Abstract
Clinical successes with dual energy CT, aggressive development of energy discriminating x-ray detectors, and novel, target-specific, nanoparticle contrast agents promise to establish spectral CT as a powerful functional imaging modality. Common to all of these applications is the need for a material decomposition algorithm which is robust in the presence of noise. Here, we develop such an algorithm which uses spectrally joint, piece-wise constant kernel regression and the split Bregman method to iteratively solve for a material decomposition which is gradient sparse, quantitatively accurate, and minimally biased. We call this algorithm spectral diffusion because it integrates structural information from multiple spectral channels and their corresponding material decompositions within the framework of diffusion-like denoising algorithms (e.g. anisotropic diffusion, total variation, bilateral filtration). Using a 3D, digital bar phantom and a material sensitivity matrix calibrated for use with a polychromatic x-ray source, we quantify the limits of detectability (CNR = 5) afforded by spectral diffusion in the triple-energy material decomposition of iodine (3.1 mg/mL), gold (0.9 mg/mL), and gadolinium (2.9 mg/mL) concentrations. We then apply spectral diffusion to the in vivo separation of these three materials in the mouse kidneys, liver, and spleen.
Keywords: spectral CT, split Bregman method, material decomposition, sparsity, bilateral filtration, kernel regression
1. INTRODUCTION
Spectral CT exploits the energy and material dependent attenuation of x-ray photons to enable quantification of the concentrations of high atomic number elements. Imaging probes based on high atomic number elements are required to create spectral contrast for functional CT imaging. Of particular significance are iodine (I; K-edge: 33.2 keV) and gadolinium (Gd; K-edge: 50.2 keV) which have K-edge energies within the diagnostic x-ray range (~20–150 keV) and which are integrated into clinically approved contrast agents for CT and MRI, respectively (e.g. Omnipaque from GE Healthcare, Isovue from Bracco Diagnostic, Magnevist from Bayer Schering Pharma AG). Gold-based contrast agents (Au; K-edge: 80.7 keV) show great promise for clinical CT imaging owing to their strong biocompatibility (Connor et al 2005) and their 2–3 fold contrast improvement over iodine per unit weight (Hainfeld et al 2006). Furthermore, gold may be a safer alternative to iodine-based CT contrast agents which are known to produce adverse reactions and kidney failure in some patients (Curry et al 2014). Several gold-based agents are currently undergoing clinical trials (e.g. Aurimune from CytImmune, Inc.; AuroShell from Nanospectra, Inc.).
In preclinical imaging, which we focus on here, the circulation half-life of low molecular weight contrast agents is too short for vascular imaging (on the order of seconds, (Lin et al 2008)), spurring the development of nanoparticle contrast agents such as ~100 nm iodine (Mukundan et al 2006) and gadolinium-based liposomes (Ghaghada et al 2008). Gold-based contrast agents (e.g. 15 nm AuroVist from Nanoprobes, Inc.) have gained importance in preclinical imaging because of the aforementioned contrast improvement over iodine contrast agents. Previously, we have demonstrated many preclinical, functional imaging applications using dual-energy micro-CT involving the separation of iodine and calcium or iodine and gold, including classification of atherosclerotic plaque composition (Bhavane et al 2013), non-invasive measurement of lung (Badea et al 2012), lung tumor (Ashton et al 2014b), and myocardial perfusion (Ashton et al 2014a), and the classification of tumor aggressiveness and therapy response in primary sarcoma tumors (Clark et al 2013, Moding et al 2013).
The primary objectives in this work are to develop and demonstrate a material decomposition algorithm which can be applied to both clinical and preclinical spectral CT data, which is generic to the number of materials and energies taken as input, and which is robust in the presence of noise. Being generic to the number of materials and energies is important for the future development of passively and actively targeted nanoprobes based on different high atomic number elements for functional CT imaging (Ghadiri et al 2013). Being generic to the number of input energies also enables investigation of over-constrained material decompositions which are of potential interest for increasing material sensitivity, particularly in the case of photon counted data (Faby et al 2014). The most significant point, being robust in the presence of noise, is of critical importance for performing material decomposition in small animal micro-CT data, which is typically an order of magnitude noisier than clinical CT data, for improving the limits of detectability for each material, for application to low dose scanning with an energy integrating detector, and for application to photon-starved, K-edge imaging with a photon counting detector (Ghadiri et al 2013).
We call the proposed algorithm that accomplishes these objectives spectral diffusion. Spectral diffusion works by integrating estimates of the underlying image structure from multiple spectral channels and their corresponding material decomposition into an iterative denoising scheme, removing noise such that both the spectral CT data and the material decomposition become gradient sparse. Two experiments are detailed to validate the performance of spectral diffusion in solving the three energy, three material decomposition of iodine, gold, and gadolinium. The first experiment illustrates and quantifies the efficacy in separating each individual material from the other two at varying concentrations and spatial resolutions using a digital bar phantom. The second experiment applies spectral diffusion to in vivo data which is fully sampled (using a polychromatic x-ray source) and reconstructed at each of the three energies. For validation purposes, we deal with the case of full x-ray dose, preclinical CT scans; however, we note that even full-dose preclinical data is typically an order of magnitude nosier than clinical CT data given the required spatial resolution (Ford et al 2003, Schindera et al 2014).
2. MATERIALS AND METHODS
Section 2.1 covers the post-reconstruction material decomposition approach used to perform quantitative separation of iodine, gold, and gadolinium concentrations. Section 2.2 recaps previous work using joint bilateral filtration to regularize spectral CT data for improved material decomposition accuracy and sensitivity. Spectral diffusion is then proposed to extend joint bilateral filtration to enforce gradient sparsity in the input spectral CT data and in the material decomposition of the data in tandem, a novel basis for regularization. Section 2.3 formally derives the spectral diffusion algorithm using the split Bregman method. Sections 2.4 and 2.5 then outline digital and in vivo experiments used to validate the performance of spectral diffusion in the quantitative separation of iodine, gold, and gadolinium concentrations using a polychromatic x-ray source.
2.1. Post-Reconstruction Material Decomposition
Post-reconstruction material decomposition solves the following least-squares optimization problem:
| (2.1) |
Given the input spectral CT data, X, the objective is to find the material decomposition, C. In the case where the number of CT data sets matches the number of materials, D and DT perform material decomposition (spectral data, X, to material maps, C; Equation 2.2) and synthesis (material maps to spectral data; Equation 2.3) using a sensitivity matrix, B:
| (2.2) |
| (2.3) |
where the entries of the sensitivity matrix, b, are scaled in enhancement/concentration (e.g. HU/mg/mL; HU: Hounsfield units) and are constant for a given material (I, Au, Gd) and energy (E1, E2, E3; accelerating voltage). The entries of the sensitivity matrix are determined in advance using a calibration phantom (Figure 1, 2) containing vials of known material concentrations in water:
| (2.4) |
where ||.||F denotes the Frobenius norm (square-root sum of squared matrix entries) and where M is an operator which measures the mean concentration in a region (volume) of interest defined within each vial. The measured values are compared with the expected values, Q:
| (2.5) |
Figure 1. Simulated spectral properties of our dual source micro-CT system.
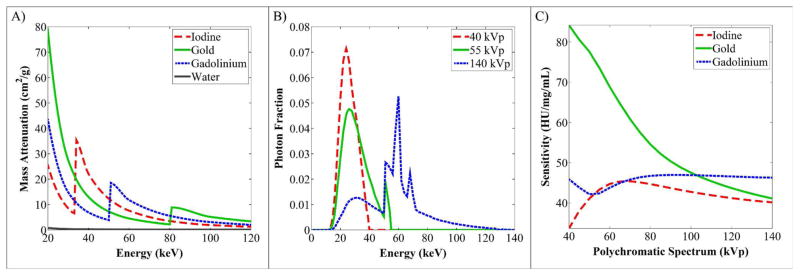
(A) Mass attenuation curves for the four materials of interest: iodine, gold, gadolinium, and water. (B) Simulated polychromatic spectra. (C) Resultant, expected material sensitivities used for material decomposition.
Figure 2. 3D physical calibration phantom.

A single, 2D slice through a 3D, physical calibration phantom consisting of vials containing unmixed concentrations of iodine, gold, and gadolinium in water as marked in mg/mL. Shown are the 55 kVp CT data after filtration with 3 iterations of spectral diffusion (calibration bar: Hounsfield units) and the corresponding three-material decomposition after the application of subspace projection (Equation 2.27; calibration bars: concentration in mg/mL). The RMSE of the mean concentrations measured in each vial over all vials is 1.04 mg/mL.
The first subscript in Q (the row) denotes the decomposition map in which the measurement is taken. The columns of Q assign arbitrary numerical indices to each material vial. Material vials can contain any number of the three materials in water, including water only. Here, Equation 2.4 is solved using MATLAB’s simplex solver, fminsearch (The Mathworks, Inc. Natick, MA). Also, a constraint can be placed on the condition number of the resulting sensitivity matrix based on the expected value (from simulated results) to prevent over fitting given a limited number of vials.
We note that Equation 2.4 can be modified with a residual weighting function to emphasize accuracy for specific materials (e.g. higher weights for specific materials), for low concentrations of materials (e.g. proportionally smaller weights for high concentrations), etc.; however, weighting was not used for the experiments illustrated here. Intrinsically, without weighting, Equation 2.4 emphasizes accuracy in decomposing materials with low sensitivity (e.g. iodine and gadolinium relative to gold), since these materials must typically be present in higher concentrations for detection, contributing more strongly to the un-normalized errors. Here, this dependence was viewed as a desirable feature because iodine and gadolinium are more difficult to differentiate from each other than from gold.
Figure 1A plots literature values for the mass attenuation of iodine, gold, gadolinium, and water with photon energy (Siewerdsen et al 2004). Of particular interest are the K-edges of iodine (33.2 keV) and gadolinium (50.2 keV) which fall within the range of effective energies produced by the polychromatic x-ray spectra of our micro-CT system (Figure 1B). Specifically, the imaging chain of our micro-CT system consists of a Varian G297 x-ray tube (tungsten rotating anode; focal spot sizes: 0.3, 0.8 mm; Varian Medical Systems, Inc., Palo Alto, CA) with 0.7 mm of aluminum filtration and 3 mm of PMMA filtration. Combined with the Gd2O2S scintillator used in our x-ray camera (XDI-VHR CCD; Photonic Science, East Sussex, UK; (Johnston et al 2012)), which is particularly efficient above the K-edge of gadolinium, adequate spectral sensitivity is produced to separate iodine, gold, and gadolinium (Figure 1C). Using the approach in (Badea et al 2011), the accelerating voltages (kVps, “energies”) used to separate these three materials (40, 55, and 140 kVp) were chosen to minimize the condition number of the resulting sensitivity matrix. The condition number of the sensitivity matrix is equal to the ratio of its largest to its smallest singular value (with singular values computed via singular value decomposition). Minimizing the condition number is important because it quantifies the potential amplification of errors when performing material decomposition. Using these three kVps and sensitivity values plotted in Figure 1C yielded the following sensitivity matrix:
| (2.6) |
which has a condition number of 24.42. This sensitivity matrix was used to initialize the optimization problem outlined in Equation 2.4 with an additional constraint that the condition number be ≤ 25. Using the physical calibration phantom illustrated in Figure 2 to perform the optimization yielded the following result:
| (2.7) |
which has a condition number of 22.81. This optimized sensitivity matrix was used for the application of spectral diffusion to the digital bar phantom (Section 2.4) and to the in vivo data (Section 2.5). The data acquisition and reconstruction parameters used for of the calibration phantom were identical to the parameters used for the in vivo data (Section 2.5).
2.2. Spectral Denoising with Bilateral Filtration
In the spectral diffusion algorithm, we robustly estimate the underlying material decomposition in the presence of noise using bilateral filtration (BF). BF is a locally adaptive, edge-preserving, smoothing filter which replaces the intensity of each voxel in the noisy data with a weighted average of the intensities of neighboring voxels (Tomasi and Manduchi 1998). Weights are assigned based on the Euclidean distance from the voxel being filtered both in space (domain weights) and in intensity (range weights):
| (2.8) |
In Equation 2.8, x indexes the voxel being filtered, y indexes a spatially invariant neighborhood relative to x, t is the total number of voxels within the neighborhood, D(y) produces domain weights (here, constant within a radius of 6 voxels around x, (Clark et al 2012)), and R(x,y) produces Gaussian range weights. f(x,y) evaluates to the intensity of voxels in the noisy input data, and f′(x) indexes the resulting, filtered intensities. For piece-wise constant signals with zero-mean, Gaussian noise (a close approximation for contrast-enhanced CT data), a single application of BF reduces image noise and increases intensity gradient sparsity similar to total variation denoising (Rudin et al 1992), with two significant differences. First, unlike total variation, BF considers and weights multiple scales of image derivatives within the filtration domain, minimizing gradients between distant neighbors, which can prevent oversmoothing (Farsiu et al 2004). Second, because the range kernel of BF abstracts intensity information as probabilistic weights, it provides a convenient platform for integrating several images of the same underlying image structure into a single denoising problem, regardless of differences in or lack of image contrast.
Previously, we exploited these observation to jointly denoise in vivo, dual energy micro-CT data, resulting in a factor of 10 improvement in the limits of detectability for concentrations of iodine and gold (relative to the unfiltered data, (Clark et al 2013)). For CT data of the same field of view acquired at an arbitrary number of energies, e, joint BF is performed as follows:
| (2.9) |
| (2.10) |
where Equation 2.9 indicates that a single set of filtration weights is applied to each component data set: i = 1, …, e. Equation 2.10 indicates that the range weights are computed from the element-wise product of two sub-sets of Gaussian range weights:
| (2.11) |
| (2.12) |
where RE computes the element-wise product of energy-specific range weights and RL computes additional range weights using the low noise, energy-averaged data, fL. The relative contribution of each subset of range weights to the final range weights and the desired level of smoothing are determined by the constant parameters mE (Equation 2.11) and mL (Equation 2.12), with larger values of m resulting in greater smoothing. For the iterative, three energy, three material problem discussed here, mE was set to 12 and mL was set to 3.5. These constants serve as multipliers for the standard deviations of the Gaussian range weighting functions: σi and σL. Unlike the constant m parameters, these standard deviations are measured within each component data set before filtration by computing the median absolute deviation (Donoho and Johnstone 1995):
| (2.13) |
| (2.14) |
where HH1 denotes the high-pass, high-pass component of the first level of the redundant Haar wavelet transform in a 2D region of interest. This component is used because it is presumed to be dominated by noise, particularly in band limited CT reconstructions. We note that the accuracy of these noise estimates need only be relative since the estimates are scaled by the chosen m parameters. We also note that this dynamic noise estimation scheme is highly appealing within the context of an iterative algorithm since it intrinsically reweights the contribution of each component data set, promoting fast and stable convergence of the algorithm as the median absolute deviation of the average component (RL) approaches 0.
The final component of Equations 2.11 and 2.12 is the spatially invariant resampling kernel, K(y):
| (2.15) |
where w0 and w2 are positive weights for the Gaussian and second derivative of Gaussian components, respectively. The appropriate weights are determined by solving the linear system presented for classic kernel regression in (Takeda et al 2007) for a given choice of σk. In (Clark et al 2013), we demonstrated that when σk (i.e. the bandwidth of K(y)) is calibrated to match the 10% cutoff of the modulation transfer function (MTF) of our micro-CT system (3.4 lp/mm, (Badea et al 2008)), denoising performance is substantially improved. This value, σk = 1, was used for all experiments in this work. In Equations 2.11 and 2.12, <K(y),f(x,y)> denotes the inner product of the resampling kernel weights and the filtration neighborhood intensities which evaluates to the mean of the Gaussian range weighting function.
As previously discussed, BF abstracts intensity information as probabilistic weights which can be used to integrate multiple images with differing noise levels and contrasts into a single, jointly computed range kernel (Equation 2.10) used to filter each image. Because of this abstraction, it is possible to construct joint range kernels which include both material decompositions and CT data. In practice, however, the sensitivity matrix for material decompositions (B in Equations 2.2 and 2.3) is poorly conditioned when working with micro-CT data acquired with a polychromatic x-ray source. For example, in (Clark et al 2013), the reported condition number for iodine and gold decompositions was ~7, meaning that errors could be amplified by as much as 7 times by the decomposition operation. In that work, joint BF of the input data was found to be adequate for controlling errors in the resulting decomposition. Here, where we attempt to separate three materials, the condition number is 22.81 (Equation 2.7), requiring more sophisticated regularization. Specifically, the proposed spectral diffusion algorithm jointly filters both the CT data (X, d1) and the material decomposition (DX, d2):
| (2.16) |
| (2.17) |
where Rd1 is a single range kernel applied to each CT data set and Rd2 is a single range kernel applied to each material decomposition. Rd1 is equivalent to R in Equation 2.10. RC,L is the decomposition domain analogue to RL (e.g. the average material concentration), while RC is the analogue of RE. The noise standard deviation multiplier used for RE (mE = 12, Equation 2.11) was also used for RC, and the multiplier used for RL (mL = 3.5, Equation 2.12) was also used for RC,L. These kernels are structured such that the average components with low multipliers provide bounds to prevent oversmoothing while the energy and material specific components allow recovery of specific features (which may have low contrast in the average images) as the noise level in each individual data set is reduced.
2.3. Spectral Diffusion
The objective of spectral diffusion is summarized by the following optimization problem:
| (2.18) |
Given the input data, Y, the objective is to find a denoised version of the data, X, which best minimizes the cost specified by Γ(.) for both the data and the material decomposition of data, DX, while maintaining data fidelity. The relative contribution of each term is controlled by the regularization parameters μ1 and μ2. A popular choice for Γ when working with piece-wise constant signals is intensity gradient sparsity:
| (2.19) |
where W is an image gradient operator. Image gradients are computed and penalized at a single scale of derivatives (total variation denoising, (Rudin et al 1992); edge weighting, (Niu et al 2014)) or across multiple scales of derivatives (B-spline tight frame transform, (Gao et al 2011); wavelet soft thresholding, (Daubechies et al 2004)). As previously discussed, considering multiple scales of derivatives can prevent oversmoothing.
When processing data sets with heterogeneous contrast, such as spectral CT data, intensity gradient sparsity is typically enforced on each component data set independently (Gao et al 2011, Niu et al 2014); however, as we have shown in previous work, joint consideration of spectral CT data can notably improve denoising performance (Clark et al 2013). Along these lines, the spectral diffusion algorithm enforces gradient sparsity using bilateral total variation (BTV, (Farsiu et al 2004)). As the name suggests, BTV is related to the previously discussed bilateral filtration (BF) weights in the following way:
| 2.20 |
| 2.21 |
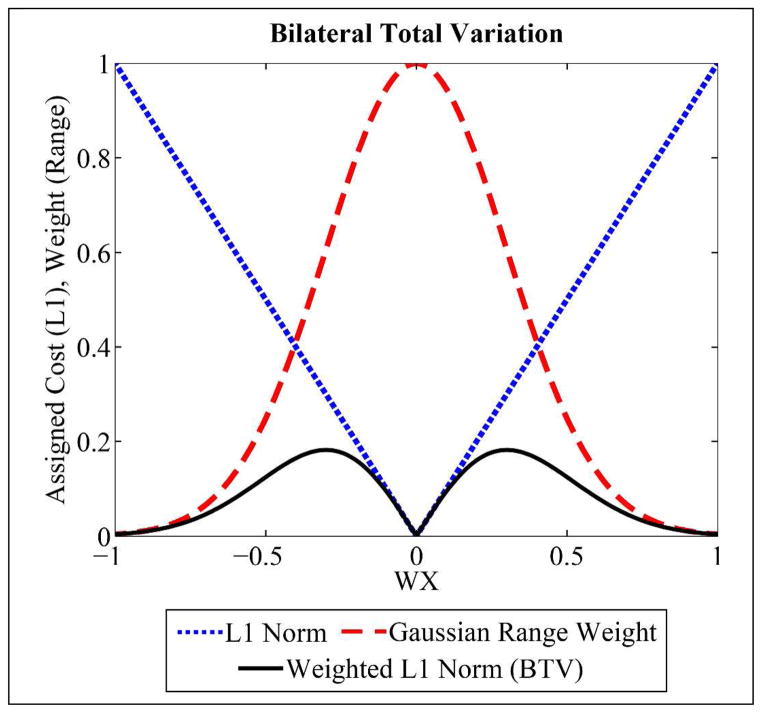
Equation 2.20 relates that each range weight computation can be rewritten as a function of the intensity gradient operator, W(y). Inherently, the filtration domain, indexed by y, defines the scales of derivatives considered. Equation 2.21 defines BTV. BTV can be understood in two ways. In relation to BF, BTV applies the BF weights to the magnitude of the intensity gradients. The result is the same size as the original image. Computing the L1 norm yields a single scalar value for each component data set (each energy). In relation to TV and Equation 2.19, Equation 2.21 can be viewed as BF-weighted, anisotropic total variation, computed across multiple scales of derivatives (Farsiu et al 2004). Figure 3 provides further intuition on the relationship between BF and BTV. Specifically, the product of the magnitude of the image gradients (blue) and the BF weights (red) assigns low cost to gradients of small magnitude (black, analogous to L1 minimization with total variation) and also to gradients of large magnitude (presumed to be edge features). The result is that only image gradients of intermediate magnitude (as determined by the bandwidth of the Gaussian range weights, 2m2σ2) are penalized, and, therefore, significantly smoothed by the action of the bilateral filter.
Figure 3.
Bilateral total variation (BTV, black) is measured as the product of the range weight assigned for bilateral filtration (red) and the intensity gradient magnitude (blue, L1 norm). Mirroring the objective of bilateral filtration (“edge preserving smoothing,” (Tomasi and Manduchi 1998)), BTV assigns low cost to intensity differences near zero (gradient sparsity) and to large intensity differences (edge preserving), while assigning a higher cost to gradients of intermediate magnitude (smoothing). BTV is reduced by application of the bilateral filter (Elad 2002, Farsiu et al 2004).
We solve Equations 2.18 and 2.21 using the split Bregman method (Goldstein and Osher 2009, Osher et al 2005) which replaces each L1 (BTV) term with its Bregman distance, splitting the optimization problem into three highly efficient sub-problems:
| (2.22) |
| (2.23) |
| (2.24) |
The variable n tracks the split Bregman iteration number (Figure 4). The method introduces the variables d1 and d2 which approach X (Equation 2.22) and DX (Equation 2.23) as the algorithm converges and the variables v1 and v2 which track the remaining residuals. The costs in Equations 2.22 and 2.23 are reduced by application of BF (Elad 2002) initialized with and (Figure 4, Step 1) and using the range weights outlined in Equations 2.16 and 2.17, respectively. We note that (Elad 2002) recommends multiple iterations of BF for further cost reduction. In practice, because the split Bregman method itself is solved iteratively, we found that a single application of BF per split Bregman iteration was adequate. Since DTD evaluates to the identity matrix (Equation 2.3), setting the derivative of Equation 2.24 equal to zero (Equation 2.25) and simplifying it results in an equation which can be solved for X by explicit evaluation (Equation 2.26; Figure 4, Step 4), making the algorithm particularly efficient:
| (2.25) |
| (2.26) |
Figure 4. Spectral diffusion.
Spectral diffusion uses bilateral filtration and the split Bregman method to remove noise from spectral CT data while ensuring a gradient-sparse material decomposition.
In general, convergence is declared when the rate of change in the magnitude of any of the variable terms falls below a specified threshold or when a maximum allowable number of iterations is reached (nmax, Figure 4).
The final step of spectral diffusion (Figure 4, Step 6), solves the following optimization problem:
| (2.27) |
This optimization, called subspace projection, reflects the physical reality that concentrations cannot be negative. In general, negative concentrations in contrast enhanced regions result from noise and beam hardening artifacts present in the source data. Equation 2.27 is solved by orthogonal projection of the columns of X (Equation 2.2) onto the subspace bounded by the columns of the sensitivity matrix, B, (Equation 2.3) before decomposition and then by setting negative concentrations to zero after decomposition.
2.4. Bar Phantom
Inspired by the experiments in (Clark et al 2013), a digital bar phantom was used to investigate the tradeoffs between material concentration, spatial resolution, and decomposition accuracy for the three material, three energy decomposition problem. Specifically, the accuracy with which one of the three materials (even bars) could be separated from mixtures of the other two (odd bars) at varying concentrations and spatial resolution was investigated. The phantom (Figure 5A) consists of two bars at each spatial resolution corresponding to 0.36 through 5.68 line pairs per mm (lp/mm; isotropic voxels; 1 voxel width = 88 microns). We note that this configuration effectively models mixtures of all three materials at intermediate to high spatial frequencies due to the resampling kernel applied during BF (Equation 2.15) which is calibrated to match the frequency response of our micro-CT system (10% cutoff of the MTF: 3.4 lp/mm). Focusing on low contrast detectability, iodine and gadolinium concentrations were varied between 0 and 9 mg/mL in increments 1.5 mg/mL while the concentration of gold was varied from 0 to 3 mg/mL in increments of 0.5 mg/mL, resulting in 1029 total combinations (3 materials, 343 combinations/material).
Figure 5. 3D digital bar phantom.
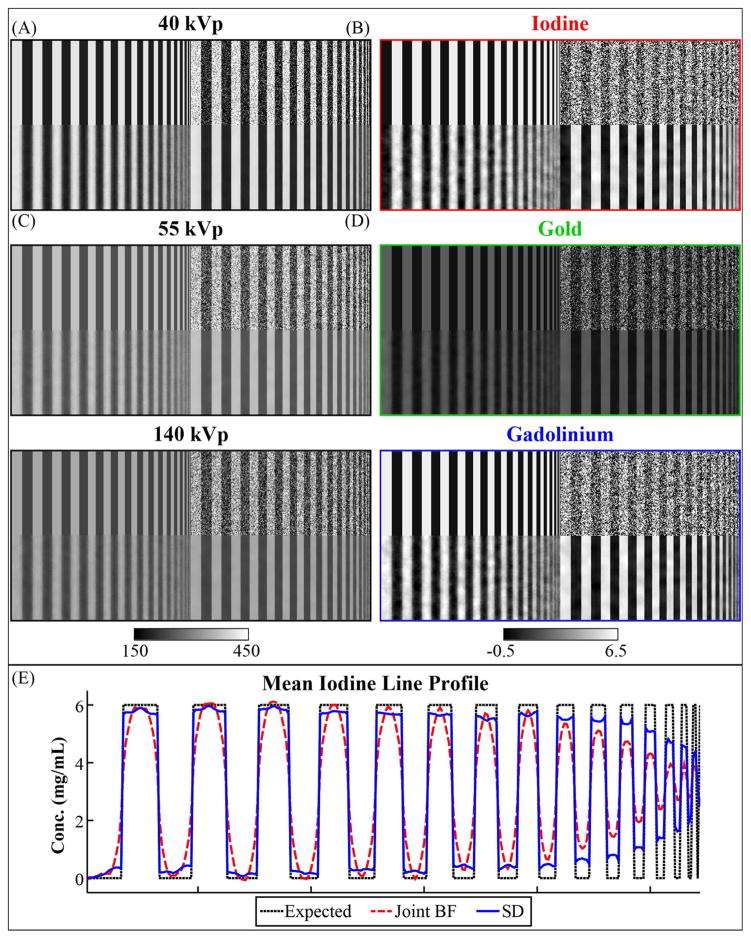
The central slice of sample, high contrast results comparing joint bilateral filtration (Joint BF) with spectral diffusion (SD) using equivalent filtration parameters. In this instance of the phantom, the task is to separate 6 mg/mL of iodine (even bars) from 6 mg/mL of gadolinium and 2 mg/mL of gold (mixed in odd bars). (A) Reference phantom. (B) Reference phantom after adding zero-mean, Gaussian noise with a standard deviation of 80 HU. (C) Image (B) after 3D, joint bilateral filtration integrating data from all three energies. (D) Image (B) after three iterations of spectral diffusion. Corresponding, post-filtration, material decomposition results are as shown in the second column before applying subspace projection. (E) Column-mean line profile for the iodine decomposition showing the iodine concentration bias as a function of spatial resolution (i.e. iodine modulation transfer).
For a given combination of material concentrations, 40, 55, and 140 kVp versions of the phantom were generated using the calibrated sensitivity matrix (Equation 2.7). The resultant 2D phantoms were then replicated along the z-axis to allow 3D filtration (dimensions: 128×272×13 voxels). Finally, zero-mean Gaussian noise with a standard deviation of 80 HU was added to each phantom, approximating the pre-filtration noise level in water measured in the calibration phantom at each energy. Because spectral diffusion is iterative, all 13 slices were filtered at every iteration with edge mirroring used to pad the image data to accommodate the six pixel radius of the filtration domain. For comparison purposes, results produced by a single application of joint filtration of the CT data only (Equation 2.16) using identical filtration parameters were also recorded and analyzed. Improvement upon the results of joint filtration builds upon the work in (Clark et al 2013), where joint filtration was shown superior to naïve sensitivity matrix inversion, “classic” bilateral filtration (Tomasi and Manduchi 1998), and to independent bilateral filtration as a preprocessing step for dual-energy material decomposition of iodine and gold. The central slice (slice 7) of the target material decomposition (iodine in Figure 5) was then used to compute performance metrics:
| (2.28) |
| (2.29) |
RMSE computed the root-mean-square error between the expected material concentration, [C]0, and the measured material concentration, [C]j, over all N voxels known to contain non-zero concentrations of the target material (i.e. the even bars). A separate RMSE was computed for the bar representing each spatial resolution. Also in the target material decomposition, CNR computed the contrast-to-noise ratio between the odd and even bar at each spatial resolution where m1, m2 and σ1, σ2 were the means and standard deviations measured within the paired bars. Averaging the RMSE over all 343 combinations per target material quantified the decomposition error as a function of spatial resolution for each material. Averaging the CNR for each target material over all spatial resolutions quantified the limits of detectability for each material using the Rose criterion (i.e. CNR ≥ 5, (Rose 1948)). Subspace projection (Equation 2.27) was not applied to the bar phantom decompositions to avoid skewing the average metrics with non-linear corrections, and, in general, was not required given the absence of beam hardening artifacts. Cubic spline interpolation was used to fill in the gaps between sampled points.
2.5. In Vivo Data
The animal experiment in this study was approved by the Duke University Institutional Animal Care and Use Committee. To illustrate the potential of spectral diffusion in in vivo applications, a single C57BL/6 mouse was scanned using our custom micro-CT scanner (Badea et al 2008). Iodine contrast was provided by tail vein injection of 0.0120 mL/g liposomal iodine (Mukundan et al 2006), 96 hours prior to scanning. Immediately prior to scanning, gold and gadolinium contrast were provided by tail vein injection of 0.008 mL/g of gold nanoparticles (AuroVist, Nanoprobes, Inc.) and 0.0140 mL/g of gadolinium-based Magnevist (Bayer HealthCare Pharmaceuticals, Inc.) at a concentration of 166 mM. The objective was to differentiate enhancement from large liposomal iodine nanoparticles (~100 nm diameter; half-life: ~40 hours) which are slowly cleared by the liver and spleen (Mukundan et al 2006) from low molecular weight gadolinium contrast which is rapidly cleared by the kidneys. The gold nanoparticles provided non-specific enhancement of the vasculature (~15 nm diameter; half-life: ~15 hours). In other words, at the time of scanning, mixed iodine and gold enhancement was expected in the in the liver while mixed gold and gadolinium enhancement was expected in the kidneys with the concentrations of each respective material to be determined by material decomposition. Following contrast injection, cone-beam projections were acquired using kVp switching and the following currents and exposures: 40 kVp, 250 mA, 16 ms; 55 kVp, 200 mA, 10 ms; 140 kVp, 50 mA, 10 ms. Following conclusions drawn in (Guo et al 2012), kVp switching and a single rotation was chosen over sequential scanning (i.e. one kVp per rotation) for optimal registration between data sets. The whole scan took approximately 36 minutes. The size of the projections was 1002×667 pixels. The associated radiation dose was ~ 0.3 Gy. Before reconstruction, a beam hardening correction was applied to the projection data using the method outlined in (Herman 1979). After correction, the projections were reconstructed with an isotropic voxel size of 88 microns (volume size: 5123 voxels) using the Feldkamp algorithm (Feldkamp et al 1984) and 360 projections per energy.
2.6. Limitations
We note a limitation of our post-reconstruction material decomposition approach which must be considered when performing quantitative measures of material concentrations in vivo. To enable the separation of three materials using three spectral CT data sets, we first normalize each component data set to the Hounsfield scale. As outlined in Section 2.1, normalization of water to zero at each energy allows calibration of a sensitivity matrix using a physical calibration phantom in which known concentrations of the target materials (iodine, gold, and gadolinium) are diluted in water (Figure 2). Because these target materials are implied to form a complete material basis, using this sensitivity matrix to perform material decomposition of in vivo data results in non-zero apparent concentrations of the target materials for common, biological tissues, even in the absence of contrast media. Apparent, target material concentrations for several biological tissues are listed in Table 1. These concentrations were derived using the model of our micro-CT system outlined in Section 2.1, mass attenuation coefficients and material densities from Spektr (Siewerdsen et al 2004), and the optimized sensitivity matrix (Equation 2.7). The practical consequences of this limitation are discussed in the Discussion and Conclusions section. For emphasis, here we note that the bias in our in vivo decompositions is a product of our material decomposition approach only. Spectral diffusion can be applied to any material decomposition problem as long as the decomposition is expected to be gradient sparse and to mirror the image structure of the input spectral CT data.
Table 1.
Apparent 3-material decompositions for biological compounds (mg/mL).*
| Compound | Iodine | Gold | Gadolinium |
|---|---|---|---|
| Fat | 0 | 0 | 0 |
| Blood | 0.43 | 0.72 | 0.61 |
| Cortical Bone | 7.05 | 91.43 | 0 |
| Lung Tissue | 0.33 | 0.52 | 0.51 |
| Skeletal muscle | 0.33 | 0.36 | 0.53 |
| Soft Tissue | 0.40 | 0.42 | 0.66 |
| Water | 0 | 0 | 0 |
3. RESULTS
3.1. Bar Phantom Results
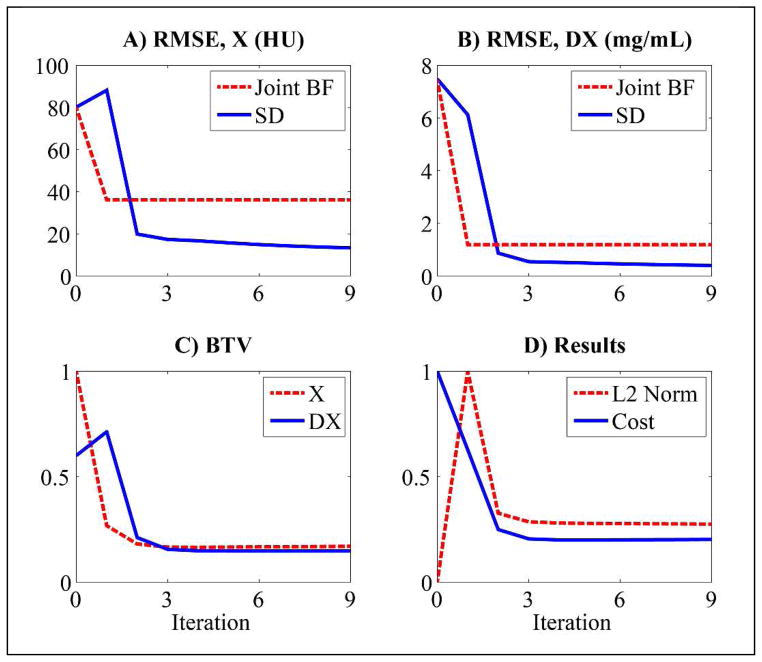
Figure 5 illustrates sample results from the bar phantom experiment, comparing the reference phantom (A) with the CT data and three material decomposition after the addition of noise (B), after joint BF of the noisy CT data (C), and after three iterations of spectral diffusion (D). This particular example illustrates the fidelity with which 6 mg/mL of iodine (even bars) can be separated from 6 mg/mL of gadolinium mixed with 2 mg/mL of gold (odd bars). Figure 5E shows the average line profile through the iodine decomposition, comparing the modulation transfer characteristics of joint filtration and spectral diffusion. While both filtration schemes illustrate systematic over and underestimation of the true concentrations, it is noteworthy that for the same filtration parameters, spectral diffusion largely prevents oversmoothing at edges. Table 2 quantifies the noise standard deviation in the lowest frequency bars before and after filtration. For this case, spectral diffusion reduces the noise standard deviation more than 10 times relative to the original data and more than 2 times relative to joint BF. Figure 6 summarizes the convergence properties of spectral diffusion for the example in Figure 5. Consistent with the results in Table 2, spectral diffusion is seen to outperform joint filtration in terms of the energy and material average RMSE values (A, B). Furthermore, the spectral diffusion cost function outlined in Section 2.3 is seen to reach a stable, minimum value after only 3 iterations (C, D).
Table 2.
Noise standard deviation at 0.36 lp/mm.*
| Component | Noisy | Joint Bilateral Filtration | Spectral Diffusion |
|---|---|---|---|
| 40 kVp (HU) | 79.50 | 22.20 | 6.03 |
| 55 kVp (HU) | 79.79 | 12.99 | 4.40 |
| 140 kVp (HU) | 79.98 | 11.12 | 4.13 |
| Iodine (mg/mL) | 9.25 | 0.78 | 0.25 |
| Gold (mg/mL) | 2.36 | 0.23 | 0.09 |
| Gadolinium (mg/mL) | 8.78 | 0.64 | 0.27 |
Measured in the bar with maximum intensity
Figure 6.
A breakdown of the denoising and decomposition results by iteration for the problem summarized in Figure 5. (A) Energy-average RMSE of the spectral CT data in Hounsfield units (HU) after a single application of joint bilateral filtration (Joint BF) and after each of 9 iterations of spectral diffusion (SD). (B) Corresponding material-average RMSEs. (C) Normalized bilateral total variation (BTV) for the spectral CT data (X) and for the material decomposition (DX) after each of 9 iterations of SD (Equation 2.21). (D) Normalized data fidelity (L2 Norm) and overall cost (Equations 2.18 and 2.21) after each of 9 iterations of SD. For both the bar phantom experiments and the in vivo data, only 3 iterations of SD were performed.
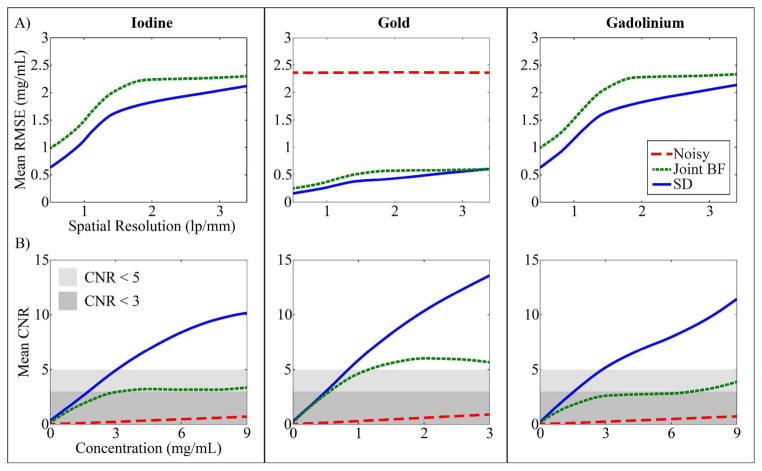
Figure 7 summarizes the results produced from all 1029 instances of the phantom. As hinted in Figure 5E, spectral diffusion provides a notable increase in the accuracy of the material decomposition across all spatial resolutions and materials with an average reduction of the RMSE by 7.52 (iodine), 1.96 (gold), and 7.17 mg/mL (gadolinium) relative to the noisy data and by 0.34, 0.09, and 0.36 mg/mL relative to joint filtration over the relevant range of spatial resolutions (10% cutoff of the MTF of our micro-CT system: 3.4 lp/mm). Figure 7B summarize the limits of detectability afforded by each processing scheme and for each material. Consistent with the noise levels reported in Table 2 (which apply the example in Figure 5 only), spectral diffusion is seen to maintain or improve upon the CNR at any given concentration of each material. Furthermore, spectral diffusion is seen to be required to meet the Rose criterion for all three materials within the concentration ranges tested (Table 3).
Figure 7. 3D digital bar phantom simulation results.
(Row A) Mean RMSE by spatial resolution (i.e. RMSE averaged over concentration) in separating the title material from mixtures of the other two. Results are shown for the original, “Noisy” data as well as after joint bilateral filtration (“Joint BF”) or three iterations of spectral diffusion (“SD”) with equivalent filtration parameters. “Noisy” results for iodine and gadolinium are constant at all spatial resolutions and are as listed in Table 2. Note that, in general, the results in Table 2 apply to the example in Figure 5 only. (B) Mean CNR by concentration (i.e. CNR averaged over spatial resolution) in separating the title material from mixtures of the other two. Shaded boxes indicate limits of detectability as labeled.
Table 3.
Limits of detectability (mg/mL).
| Component | Noisy | Joint Bilateral Filtration | Spectral Diffusion | |||
|---|---|---|---|---|---|---|
|
| ||||||
| CNR = 3 | 5 | 3 | 5 | 3 | 5 | |
| Iodine | N/A | N/A | 3.2 | N/A | 1.8 | 3.1 |
| Gold | N/A | N/A | 0.6 | 1.2 | 0.5 | 0.9 |
| Gadolinium | N/A | N/A | 7.0 | N/A | 1.6 | 2.9 |
3.2. In Vivo Results
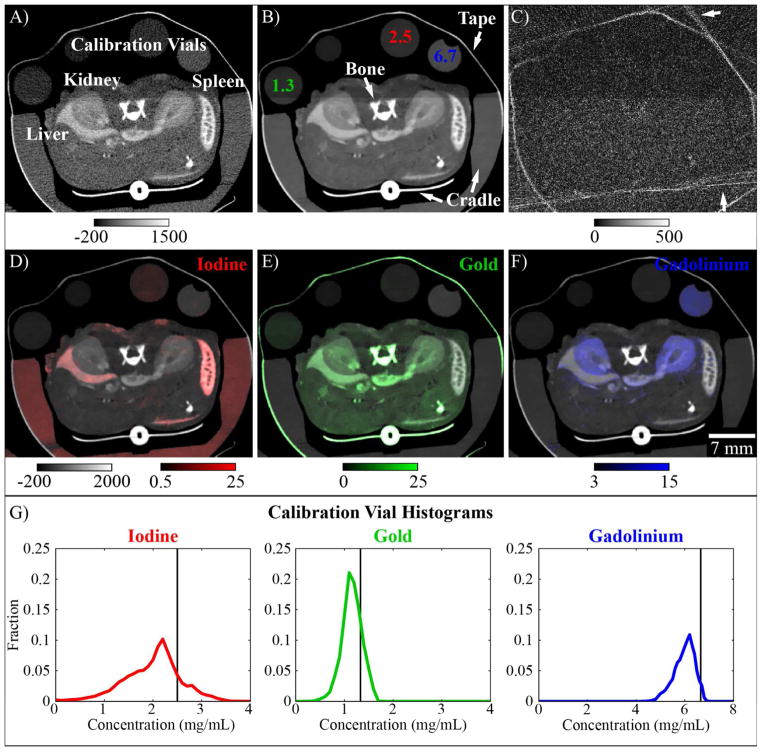
Figure 8 summarizes the results of spectral diffusion applied to the in vivo, C57BL/6 mouse data set. As empirically demonstrated in Figure 8A–C in a single, transverse, 2D slice through the 55 kVp data set, three iterations of spectral diffusion resulted in highly effective noise removal with minimal bias. White arrows in Figure 8C highlight a notable exception, the smoothing of high frequency artifacts which are introduced along highly attenuated rays by the projection-based beam hardening correction. Because these artifacts are inconsistent between energies, they are largely removed by the joint filtration process. Figure 8D–F show the resultant material decomposition using the calibrated sensitivity matrix (Equation 2.7) and after subspace projection (Equation 2.27). The material maps are overlaid on the 55 kVp data to highlight the structural correlation established between the CT data and the material maps by the iterative filtration process and to improve visibility over a wide range of material concentrations. As expected (Section 2.5), liposomal iodine contrast is largely isolated to the liver and spleen while low molecular weight gadolinium contrast is largely isolated to the kidneys. Non-specific gold contrast is seen in the liver, kidneys, and vasculature. The histograms in Figure 8G illustrate the accuracy and precision of the material decompositions within the included material calibration vials. The expected concentrations in these vials are labeled in Figure 8B and are indicated by vertical black lines in Figure 8G. A strong correlation is seen between the expected and measured material concentrations, indicating high fidelity decomposition performance.
Figure 8. In vivo application of spectral diffusion.
(A) A single, 2D slice through the 55 kVp CT data with anatomy as labeled in white. (B) The 2D slice in (A) after three iterations of spectral diffusion. Calibration vials contain concentrations of the target materials in water as marked (mg/mL). The unlabeled vial contains water. Additional materials not accounted for in the decomposition are labeled in white (e.g. “Cradle”). (C) Absolute difference between (A) and (B). White arrows indicate removed high frequency artifacts which are caused by beam hardening correction of highly attenuating features. (D)–(F) Iodine, gold, and gadolinium maps (after subspace projection, Equation 2.27) overlaid on the 55 kVp data and scaled as shown in HU (CT data) and mg/mL (materials). (G) Histograms of material concentrations measured in the calibration vials labeled in (A) and (B). A black vertical line in each histogram indicates the known concentration in each calibration vial.
Figure 9 shows the results of spectral diffusion by iteration, culminating in a composite image of the results presented in Figure 8 with identical intensity scaling (“Iteration 3+”). “Iteration 0” refers to the unfiltered input data and provides strong motivation for the use of regularization in solving the three energy, three material decomposition problem discussed here. Limited improvement is seen after the first iteration of the algorithm (“Iteration 1”) because of the large difference between smoothing in the domain of the CT data and smoothing in the domain of the decomposition (i.e. because of the poor conditioning of the decomposition problem). By contrast, a large improvement is seen after the second iteration because the estimate for X computed during the first iteration effectively averages the filtration results computed in both domains (Figure 4, Step 4, n = 0) before repeating the filtration process during the second iteration (Figure 4, Step 1, n = 1). Reminiscent of the convergence properties for the bar phantom (Figure 6), a substantially smaller improvement is seen after the third iteration. Additional iterations of the algorithm produced inconsequential changes both in the visual appearance of the results and in the values of the intermediate variables (e.g. v, d). “Iteration 3+” denotes the application of subspace projection to the “Iteration 3” results. White arrows denote a reduction in the apparent gadolinium concentration within the vasculature feeding the kidneys following subspace projection, consistent with the expectation that the low molecular weight gadolinium contrast agent is cleared from the vasculature within a few seconds of injection.
Figure 9. Spectral diffusion results by iteration.
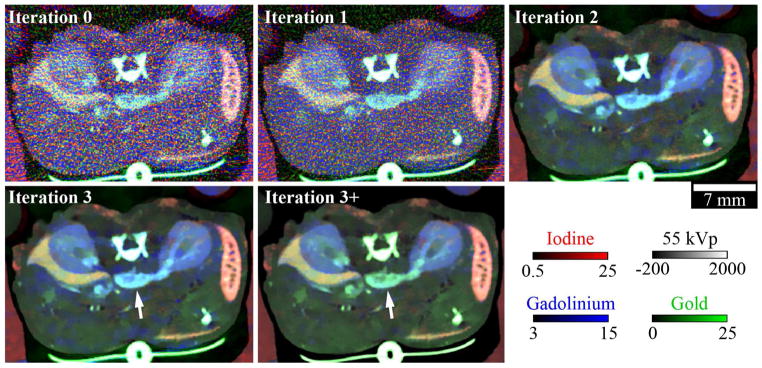
Material maps overlaid on a single, 2D slice of the 55 kVp CT data after 0, 1, 2, and 3 iterations of spectral diffusion. “Iteration 3+” indicates the iteration 3 results after the application of subspace projection (Equation 2.27). White arrows indicate a blood vessel affected by subspace projection. The CT data and material maps are scaled as shown in HU (55 kVp data) and mg/mL (material maps).
3.3. Computational Considerations
To create the in vivo results presented in Figures 8 and 9, spectral diffusion was applied to a subvolume of 427×353×21 voxels with a computation time of ~4 minutes per iteration using MATLAB’s parallel (CPU) computing toolbox and a Mac OS X workstation with dual, 2.66 GHz, quad-core Xeon processors and 16 GB of RAM. Although this computation time is substantial relative to highly efficient gradient regularization schemes such as total variation, the number of iterations required for convergence is very small (here, 3) thanks to the joint consideration of image gradients across component data sets. In future application, it may be possible to reproduce the results of spectral diffusion using highly-efficient GPU computing. The split Bregman method inherently sub-divides the required BF operations into two sub-problems which can be solved in parallel (Equations 2.22, 2.23). Furthermore, a single joint filtration operation with a large domain can be sliced into several memory-efficient update steps where each update builds upon the previous update and covers a unique scale of derivatives (Elad 2002).
4. DISCUSSION AND CONCLUSIONS
The objective of this work was to develop and demonstrate a material decomposition algorithm for spectral CT which is generic to the number of materials and energies taken as input and which is robust in the presence of noise. The proposed algorithm, spectral diffusion, simultaneously exploits the gradient sparse nature of contrast-enhanced CT data and the complimentary image structure shared between every input spectral CT data set and their resultant material decomposition. Building on previous success in improving the accuracy of dual energy decomposition using joint BF of the input CT data only (Clark et al 2013), we demonstrated further success in solving a more poorly conditioned and largely unprecedented three energy, three material decomposition by filtering both the input CT data and the material decomposition and then by combining the residuals within the iterative split Bregman framework. Joint consideration of the input data sets and decompositions was found to promote fast convergence (3 iterations), potentially offsetting the computational expense associated with non-linear, adaptive filtration in the image domain.
Two experiments were conducted to validate the performance of the spectral diffusion algorithm and to gauge its feasibly in solving the three energy, three material decomposition problem. Using a 3D, digital bar phantom, the first experiment illustrated and quantified the efficacy of spectral diffusion in separating each iodine, gold, and gadolinium from the other two materials at varying concentrations and spatial resolutions and compared the results with joint filtration for reference. Interestingly, the joint filtration scheme which proved effective in the two material problem (Clark et al 2013), yielding limits of detectability (CNR = 5) of 2.3 (iodine) and 1.0 (gold) mg/mL, proved inadequate for material separation in the three material problem (Table 3). Spectral diffusion proved capable of solving the three material decomposition problem within the relevant range of concentrations, with limits of detectability of 3.1 (iodine), 0.9 (gold), and 2.9 (gadolinium) mg/mL; however, the limit of detectability for iodine notably increased relative to the two material case. We note that the concentrations considered here (gold: 0–3 mg/mL; iodine: 0–9 mg/mL; gadolinium: 0–9 mg/mL) were lower than those considered in the previous two material case (gold: 0–9 mg/mL; iodine: 0–24 mg/mL) to emphasize low contrast detectability, to reflect the expectation that three material in vivo applications will deal in lower concentrations to control injected dose, and, to a lesser extent, to control the total number of concentration combinations. We also note that the noise level used here (standard deviation: 80 HU) was slightly higher than the noise level used in the two material case (standard deviation: 70 HU), reflecting the slight increase in noise resulting from our recently added beam hardening correction (Herman 1979).
The second experiment applied spectral diffusion to in vivo data which was fully sampled and reconstructed at each of the three energies. In addition to demonstrating the in vivo applicability of the proposed spectral diffusion algorithm, this experiment suggested a motif for future spectral CT applications; specifically, the localization, detection, and quantification of extrinsic contrast agent concentrations based on their molecular weight, tagging with target-specific ligands, and on physiological factors such increased vascular permeability in cancer. As noted in Section 2.6, however, our water-normalized, post-reconstruction material decomposition approach carries a slight bias for mixtures of biological tissues and contrast agent (Table 1). We choose to accept this limitation for several reasons. First, using a polychromatic, clinical x-ray source as in our micro-CT system, it is difficult to generate significant x-ray contrast above the K-edge of gold (80.7 keV); however, under the assumption that the target contrast materials (iodine, gold, gadolinium) form a complete basis for all materials with an enhancement above 0 HU, gold can be separated from two other contrast materials which have significant K-edge contrast (iodine, gadolinium; Figure 1C). Second, the bias introduced by common biological tissues is spread fairly evenly between the target materials (Table 1) and is generally less than the limits of detectability for each material (CNR ≥ 5, Table 3). The only exception is bone, which appears as a high concentration of gold, but which can be easily segmented from other tissues. Previously, we have demonstrated that quantitative measures of iodine and gold concentrations in several tissue types closely match ex vivo measurements using ICP-OES in spite of this bias (Ashton et al 2014b). Additionally, the bias is additive, meaning the contribution of the biological tissues can be factored out using intensity measurements from the same tissue in the absence of contrast agent. We have successfully applied such corrections in the past (Moding et al 2012, Clark et al 2013). Because the bias is additive and roughly constant for a given material type, it does not significantly influence correlation measurements between material concentration measurements and related biomarker measurements such as myocardial perfusion with Tc99m micro-SPECT (Ashton et al 2014a) and immunohistological measurements of microvascular tumor density (Ashton et al 2014b). Finally, spectral diffusion can be applied to any material decomposition problem regardless of the decomposition approach used as long as the decomposition is expected to be gradient sparse and to mirror the image structure of the input spectral CT data.
We are excited by the potential future application of spectral diffusion and similarly structured algorithms to a wide range of CT denoising and reconstruction problems. For preclinical, spectral CT, specifically, we expect spectral diffusion will allow significant radiation dose reduction in the cases of decreased x-ray exposure and projection undersampling, particularly when integrated into an iterative reconstruction scheme. We are equally excited by the future application of spectral diffusion to photon-counted x-ray CT data, allowing the separation of multiple extrinsic contrast agents with a single CT scan via joint filtration of appropriately chosen energy bins and their material decomposition. In conclusion, we believe that a computationally efficient implementation of spectral diffusion (and joint filtration schemes in general), will enable unprecedented performance in in a wide range of preclinical, and eventually clinical, functional CT imaging applications.
Acknowledgments
All work was performed at the Duke Center for In Vivo Microscopy, an NIH/NIBIB national Biomedical Technology Resource Center (P41 EB015897). Liposomal contrast agent was provided by Ketan Ghaghada and Ananth Annapragrada (Texas Children’s Hospital).
References
- Ashton JR, Befera N, Clark D, Qi Y, Mao L, Rockman HA, Johnson GA, Badea CT. Anatomical and functional imaging of myocardial infarction in mice using micro-CT and eXIA 160 contrast agent. Contrast media & molecular imaging. 2014a;9:161–168. doi: 10.1002/cmmi.1557. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ashton JR, Clark DP, Moding EJ, Ghaghada K, Kirsch DG, West JL, Badea CT. Dual-Energy Micro-CT Functional Imaging of Primary Lung Cancer in Mice Using Gold and Iodine Nanoparticle Contrast Agents: A Validation Study. PLoS ONE. 2014b;9:e88129. doi: 10.1371/journal.pone.0088129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Badea CT, Guo X, Clark D, Johnston SM, Marshall CD, Piantadosi CA. Dual-energy micro-CT of the rodent lung. American Journal of Physiology-Lung Cellular and Molecular Physiology. 2012;302:L1088–L1097. doi: 10.1152/ajplung.00359.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Badea CT, Johnston S, Johnson B, Lin M, Hedlund LW, Johnson GA. A dual micro-CT system for small animal imaging. Proc SPIE. 2008;6913:691342. doi: 10.1117/12.772303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Badea CT, Johnston SM, Qi Y, Ghaghada K, Johnson GA. Dual energy micro-CT imaging for differentiation of iodine and gold-based nanoparticles. Proc SPIE. 2011;7961:79611X. [Google Scholar]
- Bhavane R, Badea C, Ghaghada KB, Clark D, Vela D, Moturu A, Annapragada A, Johnson GA, Willerson JT. Dual-energy computed tomography imaging of atherosclerotic plaques in a mouse model using a liposomal-iodine nanoparticle contrast agent. Circ Cardiovasc Imaging. 2013;6:285–94. doi: 10.1161/CIRCIMAGING.112.000119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clark D, Johnson GA, Badea CT. Denoising of 4D cardiac micro-CT data using median-centric bilateral filtration. Proc SPIE. 2012;8314:83143Z. doi: 10.1117/12.911478. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clark DP, Ghaghada K, Moding EJ, Kirsch DG, Badea CT. In vivo characterization of tumor vasculature using iodine and gold nanoparticles and dual energy micro-CT. Phys Med Biol. 2013;58:1683. doi: 10.1088/0031-9155/58/6/1683. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Connor EE, Mwamuka J, Gole A, Murphy CJ, Wyatt MD. Gold nanoparticles are taken up by human cells but do not cause acute cytotoxicity. Small. 2005;1:325–327. doi: 10.1002/smll.200400093. [DOI] [PubMed] [Google Scholar]
- Curry T, Kopelman R, Shilo M, Popovtzer R. Multifunctional theranostic gold nanoparticles for targeted CT imaging and photothermal therapy. Contrast Media Mol Imaging. 2014;9:53–61. doi: 10.1002/cmmi.1563. [DOI] [PubMed] [Google Scholar]
- Daubechies I, Defrise M, De Mol C. An iterative thresholding algorithm for linear inverse problems with a sparsity constraint. Communications on Pure and Applied Mathematics. 2004;57:1413–1457. [Google Scholar]
- Donoho DL, Johnstone IM. Adapting to unknown smoothness via wavelet shrinkage. Journal of The American Statistical Association. 1995;90:1200–1224. [Google Scholar]
- Elad M. On the origin of the bilateral filter and ways to improve it. IEEE Trans Image Process. 2002;11:1141–51. doi: 10.1109/TIP.2002.801126. [DOI] [PubMed] [Google Scholar]
- Faby S, Kuchenbecker S, Simons D, Schlemmer H-P, Lell M, Kachelrieß M. CT calibration and dose minimization in image-based material decomposition with energy-selective detectors. Proc SPIE. 2014;9033:903318–903318-12. [Google Scholar]
- Farsiu S, Robinson MD, Elad M, Milanfar P. Fast and robust multiframe super resolution. IEEE Transactions on Image Processing. 2004;13:1327–1344. doi: 10.1109/tip.2004.834669. [DOI] [PubMed] [Google Scholar]
- Feldkamp LA, Davis LC, Kress JW. Practical cone-beam algorithm. Journal of The Optical Society of America A. 1984;1:612–19. [Google Scholar]
- Ford N, Thornton M, Holdsworth D. Fundamental image quality limits for microcomputed tomography in small animals. Medical Physics. 2003;30:2869–2877. doi: 10.1118/1.1617353. [DOI] [PubMed] [Google Scholar]
- Gao H, Yu H, Osher S, Wang G. Multi-energy CT based on a prior rank, intensity and sparsity model (PRISM) Inverse Probl. 2011:27. doi: 10.1088/0266-5611/27/11/115012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghadiri H, Ay M, Shiran M, Soltanian-Zadeh H, Zaidi H. K-edge ratio method for identification of multiple nanoparticulate contrast agents by spectral CT imaging. British Journal of Radiology. 2013:86. doi: 10.1259/bjr.20130308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghaghada K, Hawley C, Kawaji K, Annapragada A, Mukundan S. T1 relaxivity of core-encapsulated gadolinium liposomal contrast agents—effect of liposome size and internal gadolinium concentration. Academic Radiology. 2008;15:1259–1263. doi: 10.1016/j.acra.2008.04.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldstein T, Osher S. The split Bregman method for L1-regularized problems. SIAM Journal on Imaging Sciences. 2009;2:323–343. [Google Scholar]
- Guo X, Johnston SM, Johnson GA, Badea CT. A comparison of sampling strategies for dual energy micro-CT. Proc SPIE. 2012;8313:831332. [Google Scholar]
- Hainfeld JF, Slatkin DN, Focella TM, Smilowitz HM. Gold nanoparticles: a new X-ray contrast agent. British Journal of Radiology. 2006;79:248–253. doi: 10.1259/bjr/13169882. [DOI] [PubMed] [Google Scholar]
- Herman GT. Correction for beam hardening in computed tomography. Physics in Medicine and Biology. 1979;24:81–106. doi: 10.1088/0031-9155/24/1/008. [DOI] [PubMed] [Google Scholar]
- Johnston SM, Johnson GA, Badea CT. Temporal and spectral imaging with micro-CT. Med Phys. 2012;39:4943–58. doi: 10.1118/1.4736809. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin MD, Ning L, Badea CT, Mistry NN, Qi Y, Johnson GA. A high-precision contrast injector for small animal x-ray digital subtraction angiography. IEEE Transactions on Biomedical Engineering. 2008;55:1082–1091. doi: 10.1109/TBME.2007.909541. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moding EJ, Clark DP, Qi Y, Li Y, Ma Y, Ghaghada K, Johnson GA, Kirsch DG, Badea CT. Dual-Energy Micro-Computed Tomography Imaging of Radiation-Induced Vascular Changes in Primary Mouse Sarcomas. International Journal of Radiation Oncology* Biology* Physics. 2012 doi: 10.1016/j.ijrobp.2012.09.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moding EJ, Clark DP, Qi Y, Li Y, Ma Y, Ghaghada K, Johnson GA, Kirsch DG, Badea CT. Dual-energy micro-computed tomography imaging of radiation-induced vascular changes in primary mouse sarcomas. International Journal of Radiation Oncology, Biology, Physics. 2013;85:1353–1359. doi: 10.1016/j.ijrobp.2012.09.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mukundan S, Jr, Ghaghada KB, Badea CT, Kao CY, Hedlund LW, Provenzale JM, Johnson GA, Chen E, Bellamkonda RV, Annapragada A. A liposomal nanoscale contrast agent for preclinical CT in mice. AJR Am J Roentgenol. 2006;186:300–7. doi: 10.2214/AJR.05.0523. [DOI] [PubMed] [Google Scholar]
- Niu T, Dong X, Petrongolo M, Zhu L. Iterative image-domain decomposition for dual-energy CT. Medical physics. 2014;41:041901. doi: 10.1118/1.4866386. [DOI] [PubMed] [Google Scholar]
- Osher S, Burger M, Goldfarb D, Xu J, Yin W. An iterative regularization method for total variation-based image restoration. Multiscale Modeling & Simulation. 2005;4:460–489. [Google Scholar]
- Rose A. The sensitivity performance of the human eye on an absolute scale. Journal of the Optical Society of America. 1948;38:196–208. doi: 10.1364/josa.38.000196. [DOI] [PubMed] [Google Scholar]
- Rudin LI, Osher S, Fatemi E. Nonlinear total variation based noise removal algorithms. Phys D. 1992;60:259–268. [Google Scholar]
- Schindera ST, Odedra D, Mercer D, Thipphavong S, Chou P, Szucs-Farkas Z, Rogalla P. Hybrid Iterative Reconstruction Technique for Abdominal CT Protocols in Obese Patients: Assessment of Image Quality, Radiation Dose, and Low-Contrast Detectability in a Phantom. American Journal of Roentgenology. 2014;202:W146–W152. doi: 10.2214/AJR.12.10513. [DOI] [PubMed] [Google Scholar]
- Siewerdsen JH, Waese AM, Moseley DJ, Richard S, Jaffray DA. Spektr: a computational tool for x-ray spectral analysis and imaging system optimization. Med Phys. 2004;31:3057–67. doi: 10.1118/1.1758350. [DOI] [PubMed] [Google Scholar]
- Takeda H, Farsiu S, Milanfar P. Kernel regression for image processing and reconstruction. IEEE Transactions on Image Processing. 2007;16:349–366. doi: 10.1109/tip.2006.888330. [DOI] [PubMed] [Google Scholar]
- Tomasi C, Manduchi R. Bilateral filtering for gray and color images. Proc of the 1998 IEEE International Conference on Computer Vision. 1998:839–46. [Google Scholar]