Visualization of microscale particle focusing in diluted and whole blood using particle trajectory analysis^,

Abstract

Inertial microfluidics has demonstrated the potential to provide a rich range of capabilities to manipulate biological fluids and particles to address various challenges in biomedical science and clinical medicine. Various microchannel geometries have been used to study the inertial focusing behavior of particles suspended in simple buffer solutions or in highly diluted blood. One aspect of inertial focusing that has not been studied is how particles suspended in whole or minimally diluted blood respond to inertial forces in microchannels. The utility of imaging techniques (i.e., high-speed bright-field imaging and long exposure fluorescence (streak) imaging) primarily used to observe particle focusing in microchannels is limited in complex fluids such as whole blood due to interference from the large numbers of red blood cells (RBCs). In this study, we used particle trajectory analysis (PTA) to observe the inertial focusing behavior of polystyrene beads, white blood cells, and PC-3 prostate cancer cells in physiological saline and blood. Identification of in-focus (fluorescently labeled) particles was achieved at mean particle velocities of up to 1.85 m s⁻¹. Quantitative measurements of in-focus particles were used to construct intensity maps of particle frequency in the channel cross-section and scatter plots of particle centroid coordinates vs. particle diameter. PC-3 cells spiked into whole blood (HCT = 45%) demonstrated a novel focusing mode not observed in physiological saline or diluted blood. PTA can be used as an experimental frame of reference for understanding the physical basis of inertial lift forces in whole blood and discover inertial focusing modes that can be used to enable particle separation in whole blood.

Introduction

Inertial focusing of particles in microchannels has demonstrated potentially useful effects for a wide range of applications in basic science and clinical medicine,¹ including flow cytometry^2,3 and particle enrichment.^4–7 Fluid flow in microchannels has often been assumed to be governed by viscous forces based on the notion that small length scales require a correspondingly small Reynolds number. Particle migration across streamlines on the microscale was observed in straight square channels, in which randomly distributed particles focus to four positions centered along each face of the channel.^8–11 As the aspect ratio of the channel increases (i.e., a very wide or very tall channel), particle focusing reduces to predominantly two equilibrium positions centered on the long face of the channel.^12,13 Inertial lift forces induce lateral migration of particles to distinct equilibrium positions at finite particle Reynolds number, R_p = R_c(aD_h⁻¹)², where R_c is the channel Reynolds number, a is the particle diameter, and D_h is the hydraulic diameter of the channel, defined as D_h = 2wh(w + h)⁻¹, where w and h are the channel width and height. Numerical modeling and direct experiments of varying size particles flowing through straight square channels have yielded scalings of the inertial lift force F_L.¹² The inertial lift force on a particle near the channel centerline scales as F_L α ρU²a³H⁻¹, while F_L α ρU²a⁶H⁻⁴ near the channel wall, where ρ is the fluid density, U is the mean flow velocity, a is the particle diameter, and H is the channel dimension. The spatial variation in how the force scales along the width dimension suggests the formation of equilibrium positions from two disparate fluid dynamic effects: 1) a “wall effect” lift that acts away from the wall towards the channel centerline, and 2) a “particle shear” lift that acts down the gradient in the shear rate of the flow.^14,15

One aspect of inertial focusing that has not been studied is how particles suspended in complex fluids such as whole or minimally diluted blood respond to inertial forces in microchannels. Particle focusing in whole or minimally diluted blood has not been studied or utilized due to performance limitations in the imaging techniques (e.g., high-speed brightfield imaging and long exposure fluorescence (streak) imaging) commonly used to observe particle migration. In high-speed bright-field imaging, resolution speeds exceeding 10⁵ frames per second using shutter speeds down to 1 µs have been used to measure size, rotation rate, and/or interparticle spacing of individual particles flowing through the channel.^4,12,16 In long exposure fluorescence imaging, the signal intensity of fluorescently labeled particles accumulated over a time interval on the order of 1 s has been used to measure mean equilibrium position, full width at half maximum, and/or separation efficiency of multiple particles flowing through the channel.^3,11,17 Both of these imaging techniques have been used to characterize particle focusing in samples consisting of physiological saline or highly diluted blood.^2,4,5 The utility of these imaging techniques becomes limited in samples consisting of whole or minimally diluted blood. In 1 ml of whole blood, there are approximately 5 × 10⁹ RBCs, 5 × 10⁶ WBCs, and 3 × 10⁸ platelets suspended in plasma. High-speed bright-field imaging is limited by the overwhelming presence of RBCs obscuring vision of individual particles in the channel, while long-exposure fluorescence imaging is limited by attenuation of incident light by hemoglobin absorption and RBC light scattering in the visible region. For both imaging techniques, it is difficult to gather information along the y-axis (i.e., along the height dimension of the channel).

In vitro studies of blood flow through capillary tubes have shown that blood behaves as a Newtonian fluid for tube diameters larger than 500 µm, and as a non-Newtonian fluid for tube diameters smaller than 500 µm. This non-Newtonian behavior, known as the Fahraeus-Lindqvist effect, is marked by a decrease in apparent blood viscosity for smaller tube diameters.¹⁸ This is due to the formation of a cell-free layer near the tube wall that has a lower viscosity relative to the RBC-rich tube core.^19,20 Initial studies on the behavior of RBCs in shear flow were primarily limited to dilute blood suspensions due to the lack of imaging techniques capable of obtaining both direct and quantitative measurements of multiple RBC motions in concentrated blood suspensions. Visualization and detection of tracer RBCs at HCT > 10% was first achieved using ghost cells (i.e., ruptured RBCs that were resealed in the absence of hemoglobin) and a traveling microscope for channel Reynolds numbers R_c = U_mD_h/v = 0.3, where U_m is the maximum channel velocity, D_h is the hydraulic diameter, and v is the kinematic viscosity.²¹ Ghost cells were used as models of RBCs due to attenuation of incident light by hemoglobin absorption and RBC light scattering when measuring high concentrations of normal RBCs.

The development of spinning disk (Nipkow) confocal microscopy combined with laser illumination made it possible to generate a sufficient signal-to-noise ratio for detecting RBC motion for HCT > 10%.²² Recent work utilized fluorescent dye labeling, scanning confocal microscopy, and micro-particle image velocimetry (µPIV) to observe near-wall RBC motion at physiological values of hematocrit (i.e., HCT = 48%) blood in a rectangular microchannel for R_c = 0.03.²³ The intensity of Nd:YAG (or comparable) laser illumination is such that only brief pulses (~10 ns) of light are needed to detect fluorescently labeled particles found in the optical path. Such an imaging technique could be used to identify various properties (e.g., three-dimensional position, particle diameter, rotation rate) of individual particles in whole blood flowing through the channel at high R_p. These experimental measurements can be used to make quantitative measurements of particle focusing behavior in whole blood. Moreover, an experimental frame of reference can be provided for in silico studies of RBC (and other particle) motion in blood that account for both the deformability of an individual RBC and the cell-cell interactions from a large number of RBCs. In particular, it may be possible to provide a physical basis for particle focusing in blood using computational models that quantitatively predict the rheological properties and dynamics of blood flow.^24,25

In this study, particle tracking analysis (PTA) is used to characterize the effect of RBCs on particle motion in inertia-dominated flow. Fluorescently labeled particles are suspended in physiological saline, diluted blood, or whole blood prior to being processed in a straight rectangular channel with a 2 : 1 aspect ratio. Images taken at multiple vertical positions in the channel are used to find in-focus particles and determine their particle diameter and two-dimensional spatial coordinates within the channel cross-section. The inertial focusing behavior of polystyrene beads, WBCs, and PC-3 human prostate cancer cell lines is characterized as a function of flow rate Q and RBC volume fraction f_RBC. Rheometer measurements of blood viscosity and shear rate are used to provide insight into PTA measurements of PC-3 cell focusing behavior in diluted and whole blood.

Materials and methods

Device fabrication

A straight rectangular channel (h = 93 µm, w = 45 µm, L = 3.5 cm) was formed in polydimethylsiloxane (PDMS) using a master mold fabricated via photolithography.²⁶ A 4-inch silicon wafer was spin-coated with a 93 µm thick layer of negative photoresist (SU-8 100, Microchem, Newton, MA), exposed to UV-light through a Mylar photomask (Fineline Imaging Colorado Springs, CO), and developed (BTS-220, J.T. Baker, Phillipsburg, NJ). A 10 : 1 mix of PDMS elastomer and curing agent (Sylgard 184, Dow Corning, Midland, MI) were poured onto the master mold and degassed for 60 min to remove all trapped bubbles. The master mold was placed in a 80 °C oven for 72 h to thoroughly cure the PDMS. The cured PDMS replica was peeled away from the master mold before inlet, outlet, and height calibration holes were punched using a coring tool (Harris Uni-Core, Redding, CA) with a hole diameter of 1.5 mm. The hole-punched PDMS replica was irreversibly bonded to a glass coverslip by exposing both PDMS and glass surfaces to O₂ plasma for 30 s (Harrick Plasma, Ithaca, NY).

Particle suspensions

Fluorescently labeled polystyrene beads (FluoSpheres, Invitrogen, Carlsbad, CA) were supplied as stock suspensions in 0.15M NaCl with 0.05% Tween 20 and 0.02% thimerosal. PC-3 human prostate cancer cells (CRL-1435, ATCC) were grown in F-12 K medium (30–2004, ATCC, Manassas, VA) containing 10% fetal bovine serum (Invitrogen, Carlsbad, CA) and 1% penicillin streptomycin (Invitrogen, Carlsbad, CA) at 37 °C under 5% CO₂ conditions. PC-3 cells were fluorescently labeled in physiological saline (Invitrogen, Carlsbad, CA) containing 5 µM calcein red-orange AM (Invitrogen, Carlsbad, CA). Whole blood samples from healthy donors were obtained (Research Blood Components, Boston, MA) in venous blood collection tubes containing EDTA (Vacutainer, BD Biosciences, San Jose, CA). The RBC volume fraction (i.e., hematocrit count) in each sample was determined using a blood analyzer (KX-21, Sysmex, Mundelein, IL). WBCs were recovered from whole blood via RBC lysis buffer (Miltenyi Biotec, Auburn, CA) and fluorescently labeled in physiological saline containing 5 µM calcein red-orange AM. Samples with a specific RBC volume fraction were generated by suspending particles in appropriate amounts of physiological saline and whole blood. The particle concentration was set at 3.0 × 10⁶ particles/ml.

µPIV image capture of fluorescently labeled particles

The starting sample containing fluorescently labeled particles was injected into the microchannel using an automated syringe pump (PhD 2000, Harvard Apparatus, Holliston, MA) at flow rates of Q = 50, 150, and 450 µl min⁻¹. This corresponds to particle velocities of U = 0.21, 0.62, and 1.85 m s⁻¹. The sample loading system consisted of 5-ml syringe (BD Biosciences, San Jose, CA), 22-gauge blunt needle (Small Parts, Seattle, WA), 0.02-inch inner diameter tubing (Tygon, Small Parts, Seattle, WA), and cyanoacrylate adhesive (Loctite, Henkel, Rocky Hill, CT). Images of particles flowing through the channel were captured using Nd:YAG laser-light illumination (LaVision, Ypsilanti, MI), an epi-fluorescent inverted microscope (TE-2000, Nikon, Melville, NY), and a charge-coupled device camera (TSI, Shoreview, MN). The laser generated 10-ns pulses of light with an excitation wavelength of 532 nm, and the camera detected light from fluorescent particles with an emission wavelength exceeding 565 nm. At a stationary location 3.5 cm downstream from the channel entrance, images were captured at 8 different height positions spaced 6 µm apart. Prior to image capture, 2 µm polystyrene beads (FluoSpheres, Invitrogen, Carlsbad, CA) were placed in open wells formed when one side of the height calibration holes in the PDMS replica was bonded to a glass coverslip. In-focus polystyrene beads found at the bottom of the well were used to establish the zero height position (i.e., floor) of the channel. For each height position, a set of 400 images were collected at a rate of 5 frames per second.

µPIV image analysis of fluorescently labeled particles

ImageJ software (NIH, Bethesda, MD) was used to process raw images and identify in-focus particles at each height position. For an in-focus particle at a given height location, images were taken at multiple height positions in order to observe corresponding changes in fluorescence signal intensity indicative of an out-of-focus particle. An in-focus particle was predominantly found to exhibit both a higher mean 8-bit grayscale value and a steeper edge signal intensity gradient relative to an out-of-focus particle. For each set of 400 images at a given height location, an image threshold was automatically set using an iterative procedure based on the isodata algorithm.²⁷ Using a specific cutoff for particle size based on size distribution measurements from a cell analyzer, the image filtering technique automatically generated a table of potential in-focus particles. All particles were marked in the set of images and referenced numerically in the table, and each particle was characterized based on a user-defined set of parameters (e.g., 2-D particle area, mean signal intensity, x–y coordinates, and circularity). The collection of potential in-focus particles were examined manually to ensure that in-focus particles were identified and measured properly. For a given flow rate and RBC volume fraction, quantitative measurements from the collection of in-focus particles were used to construct surface and scatter plots characterizing various aspects of particle focusing behavior using MATLAB (Mathworks, Natick, MA).

Results

Image capture of individual in-focus particles in diluted blood

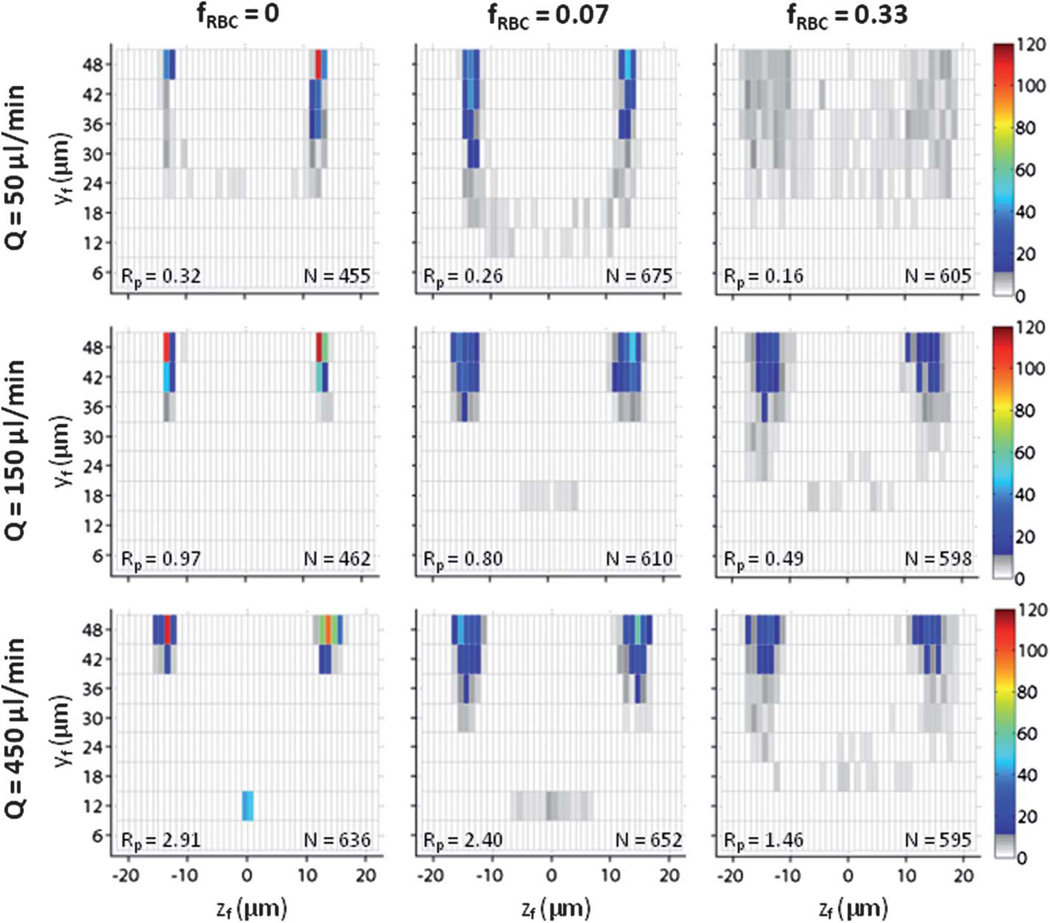
Particle trajectory analysis (PTA) was used to identify polystyrene beads, white blood cells, and PC-3 cells over a range of flow rates Q and RBC volume fractions f_RBC, where f_RBC is the ratio of RBC volume to the starting sample volume. For example, HCT = 45% (i.e., whole blood in this study) corresponds to f_RBC = 1, while HCT = 15% corresponds to f_RBC = 0.33 (diluted using physiological saline). A straight rectangular channel with a 2 : 1 (h/w) aspect ratio was used to focus randomly distributed particles to two lateral equilibrium positions centered on the long face of the channel (Fig. 1a). These equilibrium positions resulted from a balance of a “wall effect” lift that acts away from the wall towards the channel centerline and a “particle shear” lift that acts away from the channel centerline towards the wall (Fig. 1b). Polystyrene beads (mean particle diameter a_m = 9.9 µm) used in this study were monodisperse in nature, while white blood cells (a_m = 9.0 µm, size range of 7–11 µm) and PC-3 cells (a_m = 17.8 µm, size range of 10–35 µm) were polydisperse in nature. Given a 20× objective with a numerical aperture of 0.4, the depth of field was calculated²⁸ to be δ_y = 5.8 µm. In order to reliably differentiate between in-focus particles found at neighboring vertical positions, the spacing between all vertical positions was set to 6 µm. The imaging locations were confined to the bottom half of the channel since particle focusing was expected to be symmetric across the x–z plane at y = 48 µm.

Fig. 1.

Using particle trajectory analysis (PTA) to observe particle focusing behavior in diluted blood. (a) Randomly distributed particles predominantly focus to two lateral positions centered on the long face of a straight microchannel with 2 : 1 aspect ratio. (b) The equilibrium positions result from a balance of a “wall effect” lift that acts away from the wall towards the channel centerline and a “particle shear” lift that acts away from the channel centerline towards the wall. (c) Particle focusing behavior is observed in the x–z plane from eight different vertical positions spanning the bottom half of the channel. Focused particles are shown to be in focus at y₈ = 48 µm (scale bar = 20 µm). (d) For high-speed bright-field (HSB) microscopy with an exposure time of 2 µs, individual white blood cells can be identified in physiological saline (f_RBC = 0) but not in diluted blood (f_RBC = 0.07). For long-exposure fluorescence (LEF) microscopy with an exposure time of 1 s, a bulk white blood cell distribution profile can be identified, but the profile cannot be de-constructed based on height position or particle diameter. For particle trajectory analysis (PTA) with an exposure time of 10 ns, individual white blood cells re-suspended in physiological saline or diluted blood can be identified at multiple vertical positions in the channel (scale bar = 20 µm). (e) At a flow rate Q = 450 µl min⁻¹, PTA images of polystyrene beads (R_p = 2.91 for f_RBC = 0), white blood cells (R_p = 2.41 for f_RBC = 0), and PC-3 prostate cancer cells (R_p = 9.11 for f_RBC = 0) suspended in physiological saline and diluted blood demonstrate that individual in-focus particles can be identified in starting samples with higher RBC volume fractions (f_RBC) without significant degradation in fluorescence signal quality.

In diluted blood samples where the utility of high-speed bright-field imaging and long-exposure fluorescence is limited, PTA demonstrated the ability to capture images of individual in-focus particles moving at ultra-fast velocities (Fig. S1). Image capture of individual in-focus particles (with no evidence of particle streaks) was achieved at flow rates up to Q = 450 µl min⁻¹ in physiological saline initially, which corresponds to a mean flow velocity of U = 1.85 m s⁻¹ and a channel Reynolds number of R_c = 158. We limited our study to this range of flow rates, as flow rates beyond Q = 450 µl min⁻¹ for f_RBC = 1 generated a fluid pressure at the device inlet that exceeded the critical de-bonding pressure of the PDMS-glass interface. At a given vertical position (e.g., y = 48 µm), in-focus particles exhibited peak and uniform fluorescence signal intensity, while out-of-focus particles exhibited sub-optimal and radially diffuse fluorescence signal intensity (Fig. 1c). Using the appropriate image threshold, it was possible to differentiate in-focus particles at a given vertical position from in-focus particles at neighboring vertical positions. As a result, in-focus particles found at all vertical positions were used to make quantitative measurements of particle focusing behavior. Once PTA-based identification of individual in-focus particles was established in physiological saline, we repeated these experiments for polystyrene beads, white blood cells, and PC-3 prostate cancer cells suspended in diluted blood (Fig. 1d). As f_RBC increased, in-focus particles exhibited a fluorescence signal intensity that was weaker and less uniform. However, it was still possible to distinguish likely in-focus particles from undoubtedly out-of-focus particles for a given Q and f_RBC.

Quantitative measurements of particle focusing behavior in diluted blood

For a given Q and f_RBC, in-focus particles from all vertical positions were used to make quantitative measurements of particle focusing behavior. The distribution of particles in the channel cross-section (y–z plane) was visualized using an intensity map in which each individual rectangle represented a possible location for the centroid (y_c, z_c) of an in-focus particle. The color scale used to represent the particle frequency n_f at a given point in the y–z plane consisted of full color (for n_f > 10), grayscale (for 1 < n_f < 10), and white (for n_f = 0). Given the polydisperse nature of white blood cells and PC-3 cells, a scatter plot of lateral centroid coordinate z_c vs. particle diameter a was constructed. For a straight rectangular channel with a 2 : 1 (h/w) aspect ratio, particle focusing is predominantly reduced to two lateral equilibrium positions centered on the long face. Particle focusing to lateral equilibrium positions has been shown to occur both at a single vertical position⁸ and over a wide range of vertical positions.²⁹ Applications in flow cytometry would require the former, while applications in rare cell isolation can utilize the latter provided that particle focusing achieves the desired particle separation benchmarks (e.g., yield of target cell capture, purity of total cell capture). Given that particle focusing was observed across multiple vertical locations in these experiments, we evaluated inertial focusing quality of in-focus particles at vertical positions ${\displaystyle {\sum }_{i=5}^8}{y}_i$ (i.e., near the center of the long channel face). Since no accepted metric exists to define inertial focusing quality, we established a non-dimensional term “bandwidth efficiency” β_z that is dependent on mean particle diameter a_m, the mean lateral distance z_m of an in-focus particle (as an absolute value) from the channel centerline, and the standard deviation µ_z of in-focus particles in the z-direction (Table 1). Bandwidth efficiency was defined as β_z = w_b/a_m = (4σ_z + a_m)/a_m, where w_b is the edge-to-edge bandwidth in the z-direction over which 95% of all in-focus particles can be found. Note that β_z is normalized by a_m, which will vary depending on the class of particles used. As a result, β_z ≥ 1 in all cases, with β_z ~ 1 when particle focusing is nearly perfect (σ_z ~ 0). Based on the current imaging and device setup, scanning resolution in the z-direction was comprehensive and continuous, while scanning resolution in the y-direction was incomplete and segmented. Nonetheless, we established a non-dimensional term “focusing utility” Φ_y to serve as a crude measure of particle frequency at vertical positions where predicted particle focusing was unlikely to occur. Focusing utility Φ_y was defined as Φ_y = n_f/N, where n_f is the number of in-focus particles at vertical positions ${\displaystyle {\sum }_{i=5}^8}{y}_i$ and N is the number of in-focus particles at vertical positions ${\displaystyle {\sum }_{i=1}^8}{y}_i$. As a result, Φ_y ≤ 1 in all cases, with Φ_y ~ 1 when particle focusing is nearly perfect (n_f ~ N).

Table 1.

Quantitative measurements of particle focusing behavior as a function of flow rate Q and RBC volume fraction f_RBC. For a given Q and f_RBC, the particle Reynolds number R_p, the mean in-focus lateral distance z_m from the channel centerline, the bandwidth efficiency β_z, and the focusing utility Φ_y were calculated for polystyrene beads, white blood cells, and PC-3 prostate cancer cells

	Q (µl min−1)	fRBC	Rp	zm(µm)	σz(µm)	βz	Φy
Polystyrene Beads	50	0	0.32	12.7	0.7	1.27	0.91
		0.07	0.28	13.5	0.9	1.35	0.73
		0.33	0.18	12.5	4.5	2.86	0.81
	150	0	0.97	12.9	0.5	1.08	1
		0.07	0.84	14.1	1.4	1.56	0.96
		0.33	0.56	13.9	2.1	1.82	0.87
	450	0	2.91	13.6	1.1	1.45	0.86
		0.07	2.53	14.2	1.4	1.54	0.91
		0.33	1.68	14.4	2.0	1.79	0.86
White Blood Cells	50	0	0.27	14.4	0.9	1.43	0.79
		0.07	0.23	15.6	2.0	1.56	0.55
		0.33	0.16	11.2	5.3	3.13	0.40
	150	0	0.80	15.5	0.6	1.28	0.72
		0.07	0.70	16.5	1.9	1.82	0.61
		0.33	0.46	15.3	3.3	2.44	0.54
	450	0	2.41	16.1	1.0	1.43	0.75
		0.07	2.10	16.5	1.9	1.82	0.61
		0.33	1.39	16.2	2.9	2.33	0.57
PC-3 Cells	50	0	1.01	8.6	2.1	1.47	1
		0.07	0.88	8.6	2.5	1.56	1
		0.33	0.58	9.9	2.0	1.45	0.92
		1	0.25	1.0	0.9	1.22	0.17
	150	0	3.04	10.1	1.1	1.25	1
		0.07	2.64	10.3	1.4	1.32	1
		0.33	1.76	10.2	1.8	1.41	1
		1	0.76	1.1	1.0	1.22	0
	450	0	9.11	9.9	1.2	1.28	1
		0.07	7.92	11.0	1.3	1.28	1
		0.33	5.27	10.8	1.5	1.35	1
		1	2.28	1.7	1.4	1.32	0

Inertial focusing behavior of polystyrene beads in blood

Polystyrene beads have been used extensively to study particle focusing behavior in microchannels.^8,12,14 As ready-to-use monodisperse particles exhibiting strong and uniform fluorescence intensity, polystyrene beads were an ideal choice for this study. Given the mean particle diameter and channel dimensions, the particle Reynolds numbers of polystyrene beads in physiological saline for flow rates Q = 50, 150, and 450 µl min⁻¹ were R_p = 0.32, 0.97, and 2.91. Using flow rates that correspond to R_p < 1, R_p ~ 1, and R_p > 1, polystyrene beads served as a reference standard for white blood cells and PC-3 cells. For Q = 50 µl min⁻¹ in physiological saline (f_RBC = 0), bead focusing in both the z-direction (β_z = 1.27) and the y-direction (Φ_y = 0.91) approached optimal levels (Fig. 2). When f_RBC = 0.07, bead focusing decreased moderately in the y-direction (Φ_y = 0.73) with minimal decrease in the z-direction (β_z = 1.35). When f_RBC = 0.33, bead focusing was poorly organized in both the z-direction (β_z = 2.86) and y-direction (Φ_y = 0.81). For Q = 150 µl min⁻¹ in physiological saline (f_RBC = 0), bead focusing in both the z-direction (β_z = 1.08) and the y-direction (Φ_y = 1) reached optimal levels. When f_RBC = 0.07, bead focusing decreased moderately in the z-direction (β_z = 1.56) with minimal decrease in the y-direction (Φ_y = 0.96). For f_RBC = 0.33, bead focusing decreased further in a similar manner (β_z = 1.82, Φ_y = 0.87) but remained largely intact. For Q = 450 µl min⁻¹ in physiological saline (f_RBC = 0), bead focusing became suboptimal in both the z-direction (β_z = 1.45) and the y-direction (Φ_y = 0.86), as multiple beads occupied a previously unstable equilibrium position despite a non-unity channel aspect ratio. When f_RBC = 0.07, bead focusing decreased minimally in the z-direction (β_z = 1.54) but improved minimally in the y-direction (Φ_y = 0.91). When f_RBC = 0.33, bead focusing remained largely intact despite a moderate decrease in the z-direction (β_z = 1.79) and a minimal decrease in the y-direction (Φ_y = 0.86).

Fig. 2.

Polystyrene bead focusing behavior as a function of flow rate Q and RBC volume fraction f_RBC. For f_RBC = 0, values of Q correspond to R_p = 0.32, 0.97, and 2.91. For f_RBC = 0.07, values of Q correspond to R_p = 0.26, 0.80, and 2.40. For f_RBC = 0.33, values of Q correspond to R_p = 0.16, 0.49, and 1.46. The in-focus vertical position y_f and in-focus lateral distance z_f from the channel centerline for polystyrene beads were used to construct a cross-sectional particle histogram, and calculate the measures β_z and Φ_y given in Table 1.

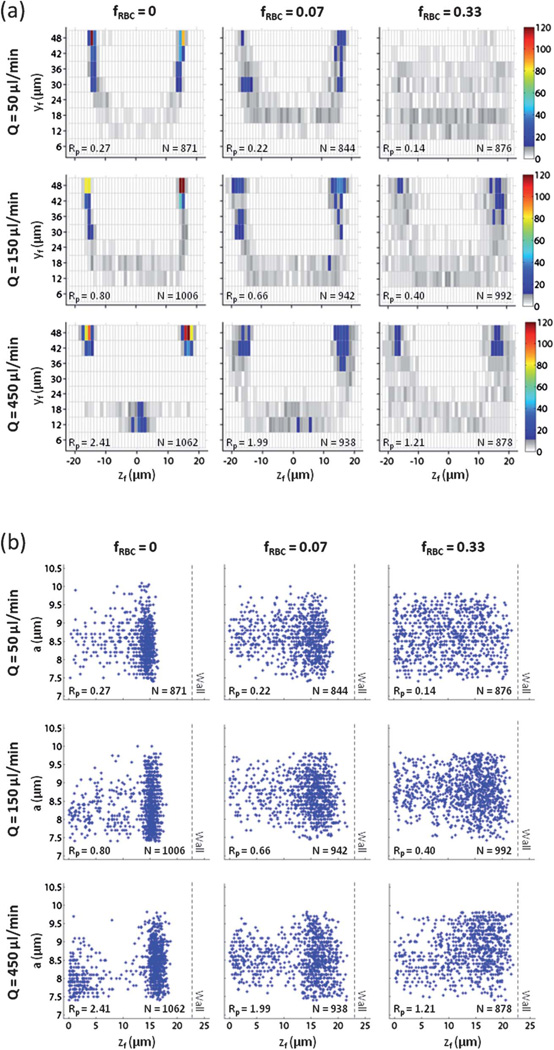
Inertial focusing behavior of white blood cells in blood

There is significant interest in incorporating inertial focusing into more portable and cost-effective flow cytometry technologies,^2,3 but the focusing behavior (and separation efficiency) of white blood cells (WBCs) in whole or minimally diluted blood has not been studied. Given the mean particle diameter and channel dimensions, the particle Reynolds numbers of WBCs in physiological saline for flow rates Q = 50, 150, and 450 µl min⁻¹ were R_p = 0.27, 0.80, and 2.41. Since WBCs have a size range of 7–11 µm, the lower bound of R_p = 0.16, 0.48, and 1.46, while the upper bound of R_p = 0.40, 1.20, and 3.60. For Q = 50 µl min⁻¹ in physiological saline (f_RBC = 0), WBC focusing in both the z-direction (β_z = 1.43) and the y-direction (Φ_y = 0.79) was weaker relative to polystyrene beads (Fig. 3a). In particular, multiple WBCs were found unfocused at vertical positions near the channel floor (i.e., ${\displaystyle {\sum }_{i=1}^4}{y}_i$). When f_RBC = 0.07, WBC focusing decreased moderately in both the z-direction (β_z = 1.85) and y-direction (Φ_y = 0.55). When f_RBC = 0.33, WBC focusing was poorly organized in both the z-direction (β_z = 3.13) and y-direction (Φ_y = 0.40). For Q = 150 µl min⁻¹ in physiological saline (f_RBC = 0), WBC focusing improved in the z-direction (β_z = 1.28) but deteriorated in the y-direction (Φ_y = 0.72) as more WBCs were found unfocused at vertical positions near the channel floor. When f_RBC = 0.07, particle focusing deteriorated moderately in both the z-direction (β_z = 1.82) and the y-direction (Φ_y = 0.61). However, most WBCs were found near a channel wall to the extent that a loose annulus of WBCs appeared to form. When f_RBC = 0.33, WBC focusing decreased further in both the z-direction (β_z = 2.44) and the y-direction (Φ_y = 0.54) as the annulus of WBCs became more radially diffuse. For Q = 450 µl min⁻¹ in physiological saline (f_RBC = 0), WBC focusing decreased moderately the z-direction (β_z = 1.43) with minimal improvement in the y-direction (Φ_y = 0.75) as WBCs occupying vertical positions near the channel floor became organized around a previously unstable equilibrium position despite a non-unity aspect ratio. When f_RBC = 0.07, WBC focusing decreased moderately in the z-direction (β_z = 1.82) and reversed in the y-direction (Φ_y = 0.61) as an annulus of WBCs appeared to form. When f_RBC = 0.33, WBC focusing decreased moderately in the z-direction (β_z = 2.33) and minimally in the y-direction (Φ_y = 0.57) as the annulus of WBCs became more radially diffuse. Since the WBCs used were polydisperse in nature, we investigated the relationship between particle diameter a and lateral distance z_f of an in-focus WBC (as an absolute value) from the channel centerline (Fig. 3b). Despite the narrow size range observed, larger WBCs were found to be slightly closer to the channel centerline (i.e., smaller z_f).

Fig. 3.

White blood cell focusing behavior as a function of flow rate Q and RBC volume fraction f_RBC. For f_RBC = 0, values of Q correspond to R_p = 0.27, 0.80, and 2.41. For f_RBC = 0.07, values of Q correspond to R_p = 0.22, 0.66, and 1.99. For f_RBC = 0.33, values of Q correspond to R_p = 0.14, 0.40, and 1.21. (a) The in-focus vertical position y_f and in-focus lateral distance z_f from the channel centerline for white blood cells were used to construct a cross-sectional particle histogram. (b) The dependence of particle diameter a on in-focus lateral distance z_f can be illustrated using a particle scatter plot. The dotted line represents the location of the sidewall given a non-deformable microchannel.

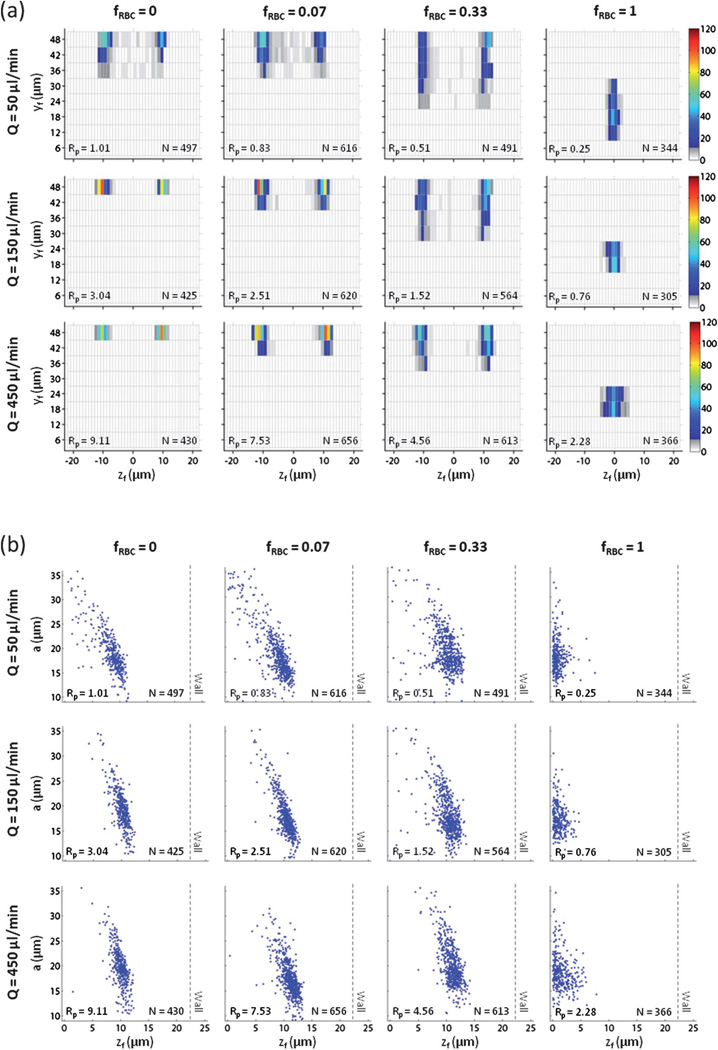
Inertial focusing behavior of PC-3 cells in blood

There is significant interest to incorporate inertial focusing into cell-friendly and high-throughput rare cell isolation technologies,^4,5 but the focusing behavior (and separation efficiency) of rare cells such as circulating tumor cells (CTCs) in whole or minimally diluted blood has not been studied. We used a model prostate cancer cell line (PC-3) to assess CTC focusing behavior in blood. Given the mean particle diameter and channel dimensions, the particle Reynolds number of PC-3 cells in physiological saline for the given set of flow rates were R_p = 1.01, 3.04, and 9.11. Since the particle diameter ranged from 10–35 µm, the lower bound of R_p = 0.33, 0.99, and 2.97, while the upper bound of R_p = 3.91, 11.76, and 35.26. For Q = 50 µl min⁻¹ in physiological saline (f_RBC = 0), PC-3 cell focusing in both the z-direction (β_z = 1.47) and the y-direction (Φ_y = 1) approached optimal levels (Fig. 4a). When f_RBC = 0.07, PC-3 cell focusing was largely unaffected in both the z-direction (β_z = 1.56) and y-direction (Φ_y = 1). When f_RBC = 0.33, PC-3 cell focusing decreased moderately in the y-direction (Φ_y = 0.92) but improved minimally in the z-direction (β_z = 1.45). Since PC-3 cell focusing remained strong, particularly in the z-direction, we repeated this experiment using whole blood (HCT = 45%). For f_RBC = 1, PC-3 cell focusing shifted radically (β_z = 1.22, Φ_y = 0.17) as PC-3 cells were predominantly found along the channel centerline (z = 0) around a previously unstable equilibrium position (due to the non-unity channel aspect ratio). No PC-3 cells occupied the previously stable equilibrium positions observed at lower f_RBC. For Q = 150 µl min⁻¹ in physiological saline (f_RBC = 0), PC-3 cell focusing in both the z-direction (β_z = 1.25) and the y-direction (Φ_y = 1) reached optimal levels. When f_RBC = 0.07, PC-3 cell focusing was largely unaffected in both the z-direction (β_z = 1.32) and y-direction (Φ_y = 1). When f_RBC = 0.33, PC-3 cell focusing decreased moderately in both the z-direction (β_z = 1.41) and the y-direction (Φ_y = 1). For f_RBC = 1, PC-3 cell focusing again shifted radically (β_z = 1.22, Φ_y = 0) as PC-3 cells predominantly occupied an equilibrium position (centered on the short face of the channel) not observed at lower f_RBC. For Q = 450 µl min⁻¹ in physiological saline (f_RBC = 0), PC-3 cell focusing in both the z-direction (β_z = 1.28) and the y-direction (Φ_y = 1) remained at optimal levels due to the lack of PC-3 cells found at vertical positions near the channel floor (in contrast to the observations for polystyrene beads and white blood cells). When f_RBC = 0.07, PC-3 cell focusing was largely unaffected in both the z-direction (β_z = 1.28) and y-direction (Φ_y = 1). When f_RBC = 0.33, PC-3 cell focusing decreased moderately in both the z-direction (β_z = 1.35) and the y-direction (Φ_y = 1). When f_RBC = 1, PC-3 cell focusing again shifted radically (β_z = 1.32, Φ_y = 0) as described previously for Q = 150 µl min⁻¹, but PC-3 cell focusing decreased moderately in the z-direction. Since the PC-3 cells used were polydisperse in nature, we investigated the relationship between particle diameter a and lateral distance z_f of an in-focus PC-3 cell (as an absolute value) from the channel centerline (Fig. 4b). When f_RBC = 0, 0.07, or 0.33, a linear correlation between the two parameters was observed, such that large PC-3 cells were situated closer to the channel centerline (z = 0), while small PC-3 cells were situated closer to the channel wall (z = ±22.5 µm). When f_RBC = 1, large PC-3 cells formed a tighter distribution around the channel centerline relative to small PC-3 cells.

Fig. 4.

PC-3 prostate cancer cell focusing behavior as a function of flow rate Q and RBC volume fraction f_RBC. For f_RBC = 0, values of Q correspond to R_p = 0.27, 0.80, and 2.41. For f_RBC = 0.07, values of Q correspond to R_p = 0.22, 0.66, and 1.99. For f_RBC = 0.33, values of Q correspond to R_p = 0.14, 0.40, and 1.21. (a) The in-focus vertical position y_f and in-focus lateral distance z_f from the channel centerline for PC-3 cells were used to construct a cross-sectional particle histogram. (b) The dependence of particle diameter a on in-focus lateral distance z_f for PC-3 cells was illustrated using a particle scatter plot. The dotted line represents the location of the sidewall given a non-deformable microchannel.

Rheological properties of test fluids

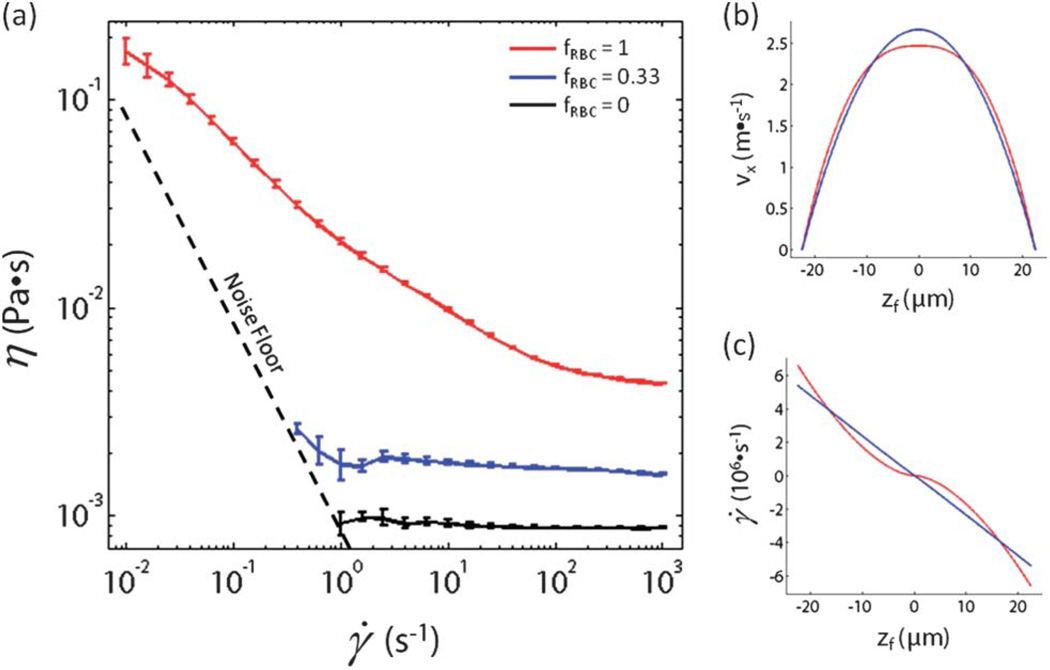
In an attempt to gain insight into the radical shift in PC-3 cell focusing behavior when f_RBC increased from 0.33 to 1, we used a torsional rheometer with a concentric cylinder geometry to measure the effective viscosity of the test fluid at f_RBC = 0, 0.33, and 1 as a function of shear rate (Fig. 5a). The governing equations of motion for a non-Newtonian fluid (such as blood) in a rectangular geometry cannot be reduced to simple equations and solved analytically. However, we used a power-law model to describe the test fluid in the x–z plane for the ideal case of y = 48 µm (i.e., the center of the long channel face) where fluid flow in the x-direction can be approximated using a simple one-dimensional equation. The viscosity η of a power-law fluid³⁰ is defined as η = m|γ̇|ⁿ⁻¹ where γ̇ is an imposed shear rate, m is a positive constant called the consistency index (with dimensions Pa·sⁿ), and n is a dimensionless positive constant. For a fluid whose viscosity is constant regardless of shear rate (i.e., Newtonian), n = 1. For a fluid whose viscosity decreases with increasing shear rate (i.e., shear-thinning), n < 1. Using a log-log plot of viscosity vs. shear rate to calculate n, the test fluid was found to be Newtonian (n = 1) for f_RBC = 0, very close to Newtonian (n = 0.98) for f_RBC = 0.33, and shear-thinning (n = 0.60) for f_RBC = 1. Assuming well-developed flow at y = 48 µm, the equation of motion in the x-direction can be approximated by v_x(z) = ((2n = 1)/(n + 1)) U_m (1 − |2z/w|^(n+1)/n), where U_m is the mean flow velocity. The shear rate γ̇(z) = dv_x(z)/dz can also be calculated from this equation. A plot of v_x(z) vs. z (Fig. 5b) and γ̇(z) vs. z (Fig. 5c) was constructed for f_RBC = 0.33 and f_RBC = 1. The velocity profile of the test fluid at f_RBC = 0.33 is expected to be parabolic, while the velocity profile of the test fluid at f_RBC = 1 is more blunted. This results in a sigmoidal shear rate profile for the test fluid at f_RBC = 1 as opposed to a linear shear rate profile for the test fluid at f_RBC = 0.33. In particular, there exists a region near the channel centerline (z = 0) where the predicted shear rate of the test fluid at f_RBC = 1 is lower than the shear rate of the test fluid at f_RBC = 0.33.

Fig. 5.

Rheometer measurements of diluted and whole blood. (a) The effective viscosity η for physiological saline, diluted blood, and whole blood was measured as a function of shear rate γ̇ using a rheometer with a concentric cylinder geometry. (b) Modeling diluted and whole blood as a power-law fluid, the flow velocity v_x down the microchannel for diluted and whole blood at height y = 48 µm was calculated as a function of in-focus lateral distance z_f from the channel centerline. (c) Modeling diluted and whole blood as a power-law fluid, the shear rate γ̇ for diluted and whole blood at height y = 48 µm was calculated as a function of in-focus lateral distance z_f from the channel centerline.

Discussion

Particle tracking analysis (PTA) was used to identify and characterize individual in-focus particles in diluted and whole blood. Given the brief (~10 ns) yet intense pulses of Nd:YAG laser illumination, individual in-focus particles could be identified (without any visual evidence of fluorescence streak formation) at mean flow velocities up to 1.85 m s⁻¹ (Q = 450 µl min⁻¹), in test fluids up to HCT = 45% (f_RBC = 1), and at multiple vertical positions across the microchannel. Direct measurements of these particles were used to generate a two-dimensional (y–z plane) profile of particle focusing behavior and its dependence on particle diameter. This represents a significant improvement over what has been achieved using high-speed bright-field imaging and long-exposure fluorescence imaging. In high-speed bright-field imaging, quantitative measurements of individual cell properties can only be made in very dilute (f_RBC < 0.07) blood, as the sheer number of RBCs occludes observation of other cell-sized particles in the channel. In long-exposure fluorescence imaging, a quantifiable intensity curve requires an aggregate fluorescence from a population of particles, which means that an ensemble of particles that are polydisperse in nature cannot be differentiated individually according to size or vertical position.

PTA was first used to observe the inertial focusing behavior of polystyrene beads in diluted blood. Polystyrene beads were chosen as an ideal test case (and reference benchmark) given their monodisperse nature and strong, uniform fluorescence intensity. For particle Reynolds numbers R_p < 1, R_p ~ 1, and R_p > 1 in physiological saline, bead focusing behavior using PTA was largely consistent with previous work in which two microchannels with inverted aspect ratios were used separately to determine the two-dimensional (y–z plane) profile of bead focusing behavior.² PTA has a significant advantage in providing three-dimensional scanning resolution of particle focusing behavior in a single device over a wide range of f_RBC, and recent work³¹ suggests that PTA image acquisition using a high-speed spinning (Nipkow) disk confocal µPIV system can provide even more comprehensive and accurate three-dimensional scanning resolution. Assuming that particle focusing behavior is well-developed, images of particles in the x–z plane can be taken at kHz frequencies in an automated and continuous manner in the y-direction with exquisite scanning resolution. PTA image analysis can also be optimized by inputting collected images into a supervised machine learning system such as CellProfiler Analyst³² for automated recognition of complicated and subtle phenotypes found in millions of particles.

PTA was then used to observe the inertial focusing behavior of white blood cells (WBCs) in diluted blood. Despite the relative similarity in particle diameter between WBCs (a_m = 9.0 µm) and beads (a_m = 9.9 µm), WBC focusing in both the z-direction and the y-direction was visibly weaker at f_RBC = 0. PTA demonstrated the ability to deconstruct WBC focusing behavior based on particle diameter and centroid position of individual particles in the channel cross-section (y–z plane). As a result, the decrease in WBC focusing behavior (relative to beads) could be partially attributed to smaller WBCs found unfocused at vertical positions near the channel floor. These results are consistent with the notion that small WBCs experience weaker inertial lift forces relative to large WBCs since R_p α a² and are thus more likely to remain unfocused at a given R_p. PTA also captured the formation of a WBC annulus in the channel cross-section (y–z plane) at f_RBC = 0.07 and 0.33. Leukocyte margination in a straight rectangular channel has been observed at much lower Reynolds numbers but not at the flow rates used in this study.^33,34 In vitro experiments characterizing the radial distribution of WBCs have shown that leukocyte margination from the center of a blood vessel depends on rheological factors such as hematocrit, blood suspension medium and shear stress.^35,36 Further investigation into leukocyte margination in inertia-dominated flow will be necessary.

PTA was finally used to observe the inertial focusing behavior of PC-3 cells in diluted blood and whole blood. A model prostate cancer (PC-3) cell line was used as a surrogate for circulating tumor cells (CTCs). CTC isolation poses an immense technical challenge, as CTCs are present in as few as one cell per 10⁹ haematologic cells in the blood of patients with metastatic cancer.^37,38 At f_RBC = 0, PC-3 cell focusing was strong in both the z-direction and the y-direction, and it remained relatively intact at f_RBC = 0.07 and f_RBC = 0.33. Since PC-3 cells are widely polydisperse in nature (a = 10–35 µm) and can be much larger than polystyrene beads, the inertial lift force on a PC-3 cell is expected to be up to an order of magnitude larger. However, it was unexpected for PTA to not only identify in-focus PC-3 cells at f_RBC = 1, but to observe a radical shift in PC-3 cell focusing behavior as opposed to further decreases in both the z-direction and the y-direction from previously observed equilibrium positions. Despite the increased RBC concentration in the channel at f_RBC = 1, the preferred equilibrium position found along the channel centerline near the channel floor made it possible to sufficiently resolve in-focus PC-3 cells. Long-exposure fluorescence (streak) imaging of PC-3 cells in straight rectangular channels with inverted aspect ratios (H/W = 0.5 and 2) was used to demonstrate that PC-3 cell focusing behavior in whole blood is symmetric across the center of the channel long face (Fig. S1) and is not the result of particle settling or imaging artifacts. However, attempts to sufficiently resolve PC-3 cells in the upper half of the channel were unsuccessful due to light absorption and scattering of RBCs (Fig. S2). The concentration of PC-3 cells spiked into the suspending fluid was orders of magnitude higher than previously observed concentrations of CTCs found in cancer patient blood samples. A higher spiking concentration was required to identify and analyze a statistically significant number of PC-3 cells in a manner that was not experimentally or computationally prohibitive. The spiking concentration of PC-3 cells should be varied in future studies to ensure that PC-3 cells can indeed serve as CTC analogs when it comes to particle focusing behavior. However, self-interactions between neighboring PC-3 cells in the channel at our spiking level will be negligible (if any) in whole blood, as the volume fraction of PC-3 cells (0.89%) is almost two orders of magnitude less than that of RBCs (45%).

In an attempt to provide a physical basis for the radical shift in PC-3 cell focusing behavior at f_RBC = 1, rheology measurements of the test fluid were made at f_RBC = 0.33 and 1. The test fluid was found to be very close to Newtonian at f_RBC = 0.33 and strongly shear-thinning at f_RBC = 1. As a result, the flow velocity and shear rate profiles indicated regions of higher viscosity near the channel centerline for the test fluid at f_RBC = 1 relative to f_RBC = 0.33. However, the shear-thinning results of dilute and whole blood do not fully explain why PC-3 cell margination differs from that of WBC margination. Deformability has also been shown to impact particle position relative to the channel wall, particularly if the cells are either soft or of comparable size to the channel dimensions.⁴ Given the capacity of PTA to resolve and identify individual particles at the typical flow rates required for inertial focusing, it would be of great interest to characterize the effect of both inertial lift forces and viscoelasticity induced forces of fluorescently labeled particles (e.g., CTCs, PDMS elastic particles, and viscous oil droplets) with varying degrees of deformability in dilute and whole blood. Furthermore, blood analogs with shear-thinning behavior similar to that of whole blood, but with substantially different relaxation times have been shown to generate considerably different extensional flow patterns.³⁹ This suggests that the elastic properties of the fluid can have a dominant effect on the flow characteristics, which has significant relevance to whole blood given the elastic and deformable RBCs found at high (38–52%) volume fractions.

To our knowledge, the flow behavior of RBCs in whole blood under inertial focusing conditions for PC-3 cells (or other target cells) has not yet been studied. However, RBCs in highly dilute (0.5% HCT) blood have been shown to focus to two streamlines centered on the long face of a 2 : 1 (H:W) straight rectangular channel.^2,40 If RBC-induced margination of PC-3 cells in whole blood is biased due to inertial focusing of RBCs, the larger PC-3 cells may not be able to able to squeeze into near-wall positions along the channel long face that the smaller WBCs can occupy. As a result, the PC-3 cells could be vertically marginated to near-wall positions along the channel short face. Direct labeling of RBCs could provide valuable insight into how RBCs manipulate the inertial focusing properties of various target cells. For example, RBCs labeled via calcein loading were used to study osmotic fragility due to malaria infection,⁴¹ while RBCs labeled with PEGylated-cationic quantum dots were used to screen for novel classes of anti-malarial drugs.⁴² By spiking a whole blood sample with a limited (1% v/v) concentration of fluorescently labeled RBCs and PC-3 cells, it could be possible to characterize the flow behavior of RBCs in whole blood under inertial focusing conditions for PC-3 cells (or other target cells). Computational simulations of particle focusing behavior have been largely limited to dilute particle suspensions in Newtonian fluids.^12,16 However, recent studies have demonstrated the capacity to predict several aspects of non-Newtonian behavior in whole blood,²⁵ platelet margination by RBCs,⁴³ and large-scale blood flow in coronary arteries.⁴⁴ Given further optimizations that account for multiple cell types, cell concentrations that are clinically relevant, and flow rates required for inertial focusing, it could be possible to develop computational simulations that accurately predict several aspects of particle focusing behavior in whole blood.

Conclusions

Particle tracking analysis (PTA) was used to identify and characterize the inertial focusing behavior of polystyrene beads, white blood cells, and PC-3 cells in diluted and whole blood. Individual in-focus particles could be identified (without any visual evidence of fluorescence streak formation) at mean flow velocities up to 1.85 m s⁻¹ (Q = 450 µl min⁻¹), in test fluids up to HCT = 45% (f_RBC = 1), and at multiple vertical positions across the microchannel. Direct measurements of these particles were used to generate a two-dimensional (y–z plane) profile of particle focusing behavior and its dependence on particle diameter. Of particular interest is the ability of PTA to not only identify in-focus PC-3 cells at f_RBC = 1, but to observe a radical shift in PC-3 cell focusing behavior as opposed to further decreases in both the z-direction and the y-direction from previously observed equilibrium positions. PTA can be used to provide an experimental frame of reference for understanding the physical basis of inertial lift forces in whole blood via numerical simulations of particle flow in non-Newtonian fluids at high Reynolds number. PTA can also be used to discover inertial focusing modes that enable particle enrichment (and ultimately isolation) directly from whole blood at high throughput for use in global health diagnostics.