Conserved patterns of incomplete reporting in pre-vaccine era childhood diseases

Abstract

Incomplete observation is an important yet often neglected feature of observational ecological timeseries. In particular, observational case report timeseries of childhood diseases have played an important role in the formulation of mechanistic dynamical models of populations and metapopulations. Yet to our knowledge, no comprehensive study of childhood disease reporting probabilities (commonly referred to as reporting rates) has been conducted to date. Here, we provide a detailed analysis of measles and whooping cough reporting probabilities in pre-vaccine United States cities and states, as well as measles in cities of England and Wales. Overall, we find the variability between locations and diseases greatly exceeds that between methods or time periods. We demonstrate a strong relationship within location between diseases and within disease between geographical areas. In addition, we find that demographic covariates such as ethnic composition and school attendance explain a non-trivial proportion of reporting probability variation. Overall, our findings show that disease reporting is both variable and non-random and that completeness of reporting is influenced by disease identity, geography and socioeconomic factors. We suggest that variations in incomplete observation can be accounted for and that doing so can reveal ecologically important features that are otherwise obscured.

1. Introduction

Observational datasets have long aided ecologists in unravelling the complex dynamical interactions of real-world populations and metapopulations. In particular, observational datasets can provide extensive spatial and temporal coverage difficult to achieve through field experiments. From disease ecology to wildlife and natural resource ecology, these datasets have allowed ecologists to evaluate the strength and significance of a wide range of dynamical processes [1–7].

Although not the core focus of ecological interest, imperfect observation is a rule rather than an exception in datasets resulting from surveillance rather than controlled experimentation. The extent to which imperfect observation can distort or obscure dynamical processes such as local extinction remains an open question, as does the ability to correct for imperfect observation. Here, we show that incomplete observation obscures classic estimates of critical community size (CCS) [8–12], which is a key dynamical feature of childhood disease. When observation processes are stationary and independent of mechanistic dynamical processes, the state variables of interest can sometimes be estimated using known constraints of the dynamical system. Knowledge of these state variables in turn allows meaningful comparisons between systems, such as different metapopulations (here, countries).

The study of human infectious diseases has yielded important insights into the nonlinear dynamics of real-world populations and metapopulations, largely owing to extensive observational datasets. For human diseases such as measles, cities comprise the basic epidemiological units of observation over which disease reporting probabilities are typically assumed to be consistent. Reporting of human infectious diseases is known to be both imperfect and variable between cities [13–18]. A reporting probability (the proportion of true infections recorded as official case reports, commonly referred to as ‘reporting rate’) can be estimated for acute, highly infectious diseases that confer permanent immunity, using a combination of demographic and case report data. Here, we show that reporting probabilities of human infectious diseases follow conserved patterns in space and time. By accounting for reporting probabilities, we also provide a more accurate estimate of the scaling of local persistence with population size.

Reporting probabilities of childhood diseases received considerable attention throughout the twentieth century in both the United States (US) [15] and England & Wales (E&W) [16]. Notable works include Bartlett [2], who reviews estimates from the early twentieth century in both countries, Black [19], who reports summary estimates for several countries, as well as Finkenstädt & Grenfell [4] and Bjørnstad et al. [20], who employ the susceptible reconstruction method. Incompleteness of modern disease reporting has also been examined via active surveillance [21–23]. However, we have found no systematic review of variation in the reporting probability of childhood diseases between populations (cities) and metapopulations (here, countries).

Stochastic extinction within host populations (e.g. cities) is driven by local processes (e.g. host demographics) and metapopulation processes (e.g. disease importation between populations). Yet, stochastic extinction is not easily distinguished from incomplete reporting. Several works have explicitly incorporated estimation of incomplete and variable reporting into dynamical models of populations [6,17] and metapopulations [7]. Nonetheless, disease reporting (and variability thereof) has been largely absent from modern population and metapopulation models that studied stochastic extinction and disease persistence in E&W [11,24–26]. These models (and results) do not necessarily generalize to metapopulations with lower and more variable reporting, such as the pre-vaccine US or modern sub-Saharan Africa.

(a). Outline

This study aims to quantify and explain variability in the reporting probabilities of two childhood diseases prior to mass vaccination. We use an extensive dataset of measles [7] and whooping cough (WC) case reports in US states and cities in the pre-vaccine era, in addition to the classic 60-city E&W measles dataset [20]. To estimate the total per-population susceptible pool, we employ two different sources of demographic records. Using case reports and susceptibles, we then compute the reporting probability of each disease and location (cities or states).

Here, we refer to sampled units (e.g. specific cities and states) as locations, while area refers to the level of geographical sampling (i.e. city versus state). For human diseases such as measles and WC, each city is a coherent epidemiological population, throughout which disease dynamics (and reporting probabilities) are typically assumed to be homogeneous. US states, on the other hand, are primarily administrative subdivisions that are socially and epidemiologically heterogeneous. Thus, state reporting probability estimates are assumed to be averaged over many discrete populations (e.g. cities and towns). Nonetheless, the unambiguous nesting of cities within states provides a useful estimate of the effect of geographical location.

We begin with a comparison of reporting probabilities between diseases and between geographical areas (e.g. between states and their respective cities). We find a very strong relationship within location between diseases, and a strong relationship within disease between geographical areas. In addition, we explore the temporal variation of reporting probability in cities. This dependence of reporting probability on geographical identity rather than time suggests that conserved socioeconomic factors strongly influence disease reporting probability. Indeed, we find that a non-trivial proportion of variation in reporting probability is explained by the proportion of a location's population that is either white or attending school.

We also include a discussion of uncertainty and sources of error. Metadata detailing the collection process of both case reports and demographic records is often sparse or altogether lacking. Here, we use several independent sources of demographic data, two different methods of calculation (per capita rates and census microdata) and bootstrap estimates for one method. Overall, we find the variability between locations and diseases greatly exceeds that between methods or time periods.

We conclude with a discussion of metapopulation dynamics and the obscuring effects of incomplete reporting. In observational datasets, poor reporting is indistinguishable from stochastic extinction in individual populations (e.g. cities). Correcting for variable reporting regenerates the hypothesized scaling relationship between population size and observed extinction in the studied metapopulations.

2. Material and methods

(a). Case reports

US weekly case reports were obtained as PDF files from the United States Public Health Reports [27] and were manually double-entered using a custom web application that automatically identified conflicts for manual resolution. Populations were removed if they contained more than 20% missing values for any disease or if demographic data was unavailable (see below). Years were excluded if more than 50% of the remaining cities had fewer than 85% of sampled weeks to avoid bias from temporally aggregated gaps. Missing case reports were excluded from further analysis.

Measles case reports in E&W were originally recorded by the United Kingdom Office of Population Censuses and Surveys [8]. We employ the publicly available 60-city subset used by Bjørnstad et al. [20]. This dataset has a two-week sampling interval, which is twice the US's interval, though sampling interval has no effect on reporting probability estimates. City-level case reports of WC in E&W have been studied extensively [10,28], but have not been publicly released.

Case report lengths and boundaries are shown in table 1, and final timeseries are shown in the electronic supplementary material, figures S10–S14. In the USA, 48 cities and 46 states were selected for final analysis, as well as 60 cities from E&W.

Table 1.

Sampled number of locations (L) and case reports (N), time range and summary statistics of estimated reporting probabilities (per capita method). (Sample coverage is limited for state WC case reports. US locations are sampled weekly; E&W cities are sampled every other week. CV, coefficient of variation.)

disease	area	L	N	start	end	mean	CV
measles	US cities	48	1148	5 Jan 1924	29 Dec 1945	0.27	0.55
measles	E&W cities	60	598	9 Jan 1944	25 Dec 1966	0.54	0.15
measles	US states	45	1089	7 Jan 1928	11 Dec 1948	0.20	0.51
WC	US cities	48	1148	5 Jan 1924	29 Dec 1945	0.10	0.71
WC	US states	46	467	1 Jan 1938	7 Dec 1946	0.06	0.67

(b). Susceptible estimation from demographic data

For US locations (cities and states), the total susceptible pool for each disease and location was estimated using two different sources of demographic data, and two different methods: per capita demographic rates and census microdata.

For the per capita method, each location's total susceptible pool was obtained from yearly population estimates and per capita birth, death and infant mortality rates (all rates are per capita unless otherwise noted). Decadal populations were obtained from the US decadal census (1920–1950) [29]. Yearly populations were estimated using an exponential growth model to interpolate between decadal populations. Yearly state birth and death rates were obtained from the US National Center for Health Statistics [30,31]. Yearly national infant mortality rates were obtained from the US Census Bureau [32].

Yearly populations and state birth rates were then used to estimate births, discounted by national infant mortality rates. These surviving births were then summed over the period of record of each disease to yield a total susceptible pool. This method assumes that pre-infection migration and (non-infant) death of susceptibles was minimal.

Census microdata refers to the individual responses to a country's census, and commonly includes variables such as location, age, gender and ethnicity. For the USA, census microdata were obtained from the Integrated Public Use Microdata Series (1920–1950, 1% sample) [33]. No census microdata is available for E&W for this time period. For US censuses, the city of residence is available only for cities meeting minimum size criteria, which vary by census date. In addition, the geographical boundaries of several cities expand to include neighbouring cities in 1940 (such as Tampa and St Petersburg, and Minneapolis and St Paul), leading to detectable overestimation of susceptibles. Cities in the above groups were excluded from further analysis.

For each US location and disease, the total susceptible pool was estimated from census microdata by summing youths (individuals ages 1 through 10, inclusive) born within the period of record of each disease. As such, this method integrates all intra-census migration and death of youths’ aged less than or equal to 10 years.

Census microdata was used to estimate the sampling distribution of susceptible pools via bootstrapping. Each decadal census was bootstrapped 10 000 times for each disease, and the total susceptible pool of each location recomputed for each bootstrap draw.

The per capita and microdata methods are not strictly comparable (e.g. electronic supplementary material, figure S2). The per capita method neglects migration and uses state birth rates as proxies for associated city birth rates (see Discussion). Census microdata, on the other hand, explicitly accounts for susceptible immigration, while potentially erroneously including immigration of recovered youths.

Yearly city births for E&W were provided by P. Rohani (2012, personal communication) and were subsequently adjusted by the national infant mortality rate. This method is functionally equivalent to the per capita method.

We assume that the microdata method is most accurate, particularly for cities. The microdata method also allows estimation of confidence intervals. Thus we use the microdata method throughout, except in comparisons that include E&W, where no microdata is available.

(c). Reporting probability

We assume that reporting probabilities (commonly referred to as reporting rates) are invariant over time within each disease and location. For each location i and disease j, we sum observed case reports C_ij and susceptibles S_ij. Note that S_i changes with disease, as the period of record varies between diseases. If the epidemiological system is approximately stationary over the time period considered (i.e. there are no major changes in the underlying processes governing the disease and demographic dynamics), then the number of susceptible individuals in the population should also be approximately stationary. This implies that the flow of new susceptibles is counterbalanced by the flow of new infections. For a disease that confers permanent immunity, new susceptibles are just surviving births (ignoring the effects of migration). The simplest estimate of reporting probability is therefore obtained by assuming that the total number of expected cases, E_ij, is approximately equal to the total accumulated susceptible pool (S_ij) over the period of interest. Thus, the reporting probability r_ij = C_ij/E_ij ≈ C_ij/S_ij [16].

(d). Comparison and validation

Our reporting probability estimates assume that the number of susceptible individuals is approximately equivalent at the beginning and end of the time period considered. Previous work [4] has regressed cumulative births against cumulative cases and estimated reporting probability as the slope of the regression line. The two estimates are the same if the deviation from the average number of susceptibles is the same at the beginning and at the end of the time period. This can be achieved in a stationary system if the time period considered begins and ends at approximately the same point in the epidemic cycle.

For completeness, we estimate reporting probabilities via this ‘susceptible reconstruction’ method [4] using per capita demographic data. Unlike previous work [34], we do not interpolate demographic data onto a weekly or bimonthly time scale, because we have no knowledge of within-year variation in birth rates.

We also assess the long-term time variability of reporting probabilities by subdividing US city case reports into two approximately equal subdivisions (Early and Late). We then re-estimate reporting probability using the per capita method.

(e). Modelling the interdependence of reporting probabilities

We employ a set of linear models to quantify the interdependence of reporting probabilities between diseases and between areas. For each location (i.e. specific city or state), we compare reporting probabilities between diseases. We use a separate model for each area, and arbitrarily model WC reporting as a response to measles reporting (between-disease). For each disease, we compare reporting probability between states and their associated cities (between-area). Here, we model city reporting as a response to the associated states' reporting.

The result is four separate model specifications. For simplicity, we use ordinary least-squares regression. All reporting probabilities were logit₂-transformed to correct for heteroskedasticity. The logit₂-transform is simply log₂(p/1 − p), such that one unit of increase equates with a doubling of the reporting probability odds, e.g. from 50% (1/1 odds, logit₂ (odds) = 0) to 66% (2/1 odds, logit₂ (odds) = 1).

For each linear model specification, 10⁴ model realizations were constructed via bootstrap resampling. For each realization, a two-step sampling process was employed. First, city identity was sampled with replacement. Second, for each sampled city, the relevant reporting probabilities were sampled with replacement from their respective bootstrap distributions, and simple linear regression was conducted on the resulting sample. This strategy, known as ‘bootstrapping pairs’ [35], accounts for uncertainty in reporting probabilities both within and between cities without making standard normality and constant-variance assumptions on the residuals. This strategy assumes only that the cities are randomly sampled from the population distribution of cities (see above for city selection criteria).

(f). Demographic predictors of reporting probabilities

US census microdata records a wide range of information about individuals and households. We examined the epidemiologically relevant variables as possible covariates of each location's reporting probability (see below). A weighted summary of each covariate was calculated by location to yield either a proportion (for categorical variables) or mean and standard deviation (for continuous variables). Tested demographic covariate predictors included the proportion of population that was white (prop.white), in school (prop.school), male (prop.male), born in the state of residence (prop.local) and in the labour force (prop.labforce), as well as the mean and s.d. of age (mean.age, sd.age) and household size (mean.housesize, sd.housesize). The 1930 decadal census was selected for this analysis. Owing to changes in census design, comparison of covariates between decades is not always possible. Nonetheless, within-census variation between locations is generally much larger than between-census changes (electronic supplementary material, figures S3 and S4), suggesting that covariates are approximately conserved over time.

A separate linear model was constructed for each disease and area, with reporting probabilities (microdata method) responding to demographic covariates. Reporting probabilities were logit₂-transformed, demographic covariate predictors were centred to zero and forward model selection was employed to select predictors using the Bayesian information criterion. While the tested covariates are broadly correlated, forward model selection parsimoniously selects the predictors with the greatest explanatory power.

3. Results

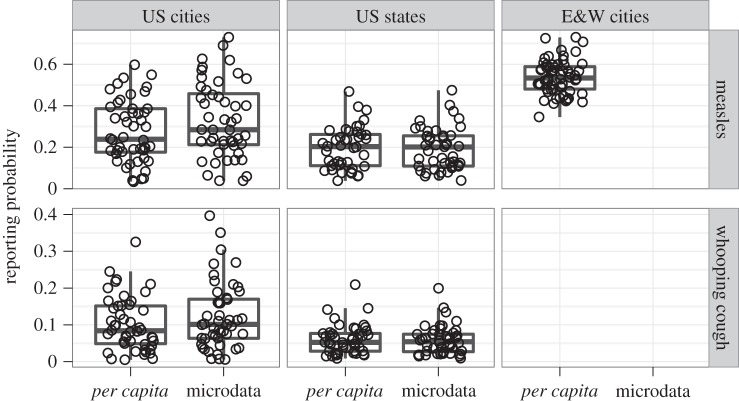
Overall, a high degree of variability in disease reporting was observed between both locations and diseases. The distribution of reporting probabilities for each area (cities, states), disease and method is shown in figure 1, and summary statistics are shown in table 1. In the USA, WC probabilities are much lower than measles probabilities, regardless of area. For US cities, per capita estimates are slightly higher than microdata estimates owing to the former method's use of state birth rates. The cities of E&W have higher and less variable measles reporting probabilities than US cities or states, consistent with previous estimates [2,15,16].

Figure 1.

Boxplot distributions of reporting probability estimates for each disease, area and method (points show individual locations). Overall, reporting of WC is less complete than measles, while US reporting is less complete than E&W. For US cities, per capita estimates are slightly higher than microdata estimates due to the former method's use of state birth rates. Extensive variation between locations is evident, particularly in the US.

(a). Comparison between methods

Case report totals for each disease are identical between methods, with different reporting probability estimates (electronic supplementary material, figure S5) resulting from variations in each location's total susceptible pool. For US states, estimated reporting probabilities were highly conserved between methods: between-method linear models yield a slope approximately equal to unity and a non-significant intercept. For US cities, reporting probabilities estimated from the census method are slightly lower than those from the per capita method.

One major limitation of the per capita method is that US city birth rates are inferred from the per capita rates of their respective states. In general, states have higher birth rates than cities in this era (electronic supplementary material, figure S1). This is probably owing to states' rural populations, which have generally higher birth rates than urban areas in this era [36]. Consequently, the census method probably overestimates US city susceptibles and underestimates reporting probabilities, as observed here (electronic supplementary material, figure S5).

For reference, the per capita method was also compared with the susceptible reconstruction method [4] for all areas (see Material and methods for important assumptions). Susceptible reconstruction yielded slightly higher estimates, particularly in E&W, although the differences are small (electronic supplementary material, figure S6).

(b). Comparison between time periods

Our reporting estimates assume that each system is approximately stationary over the period of study, and the systems in question should be assessed for major perturbations during the period of study. In addition, a sufficiently long period of time must be employed such that stochastic and seasonal fluctuations are short relative to the full period of record.

In order to assess temporal variation in reporting probabilities in the present systems, city case reports were subdivided into two time series of approximately equal length (electronic supplementary material, table S1). Electronic supplementary material, figure S7, shows that city reporting probability (per capita method) is relatively invariant across time, though more temporal variation is evident in E&W. The National Health Service was fully implemented in the UK by 1948. This change in public health infrastructure could explain some of the observed temporal variation in E&W (electronic supplementary material, figure S7), though any metapopulation-level temporal shift is slight.

(c). Conserved patterns of variation in disease reporting

The interdependence of disease identity and geographical location in the US is shown in figure 2. Reporting probabilities of WC are strongly correlated with measles probabilities, regardless of area (figure 2a). Although more scatter is evident, city reporting probabilities are correlated with their associated states' probabilities, regardless of disease (figure 2b). Estimated slopes and correlation coefficients for each linear model specification, along with bootstrapped confidence intervals, are listed in the electronic supplementary material, table S2. Overall, we find that disease reporting probability is conserved over space and time and that disease identity and geography influences reporting probabilities in consistent ways.

Figure 2.

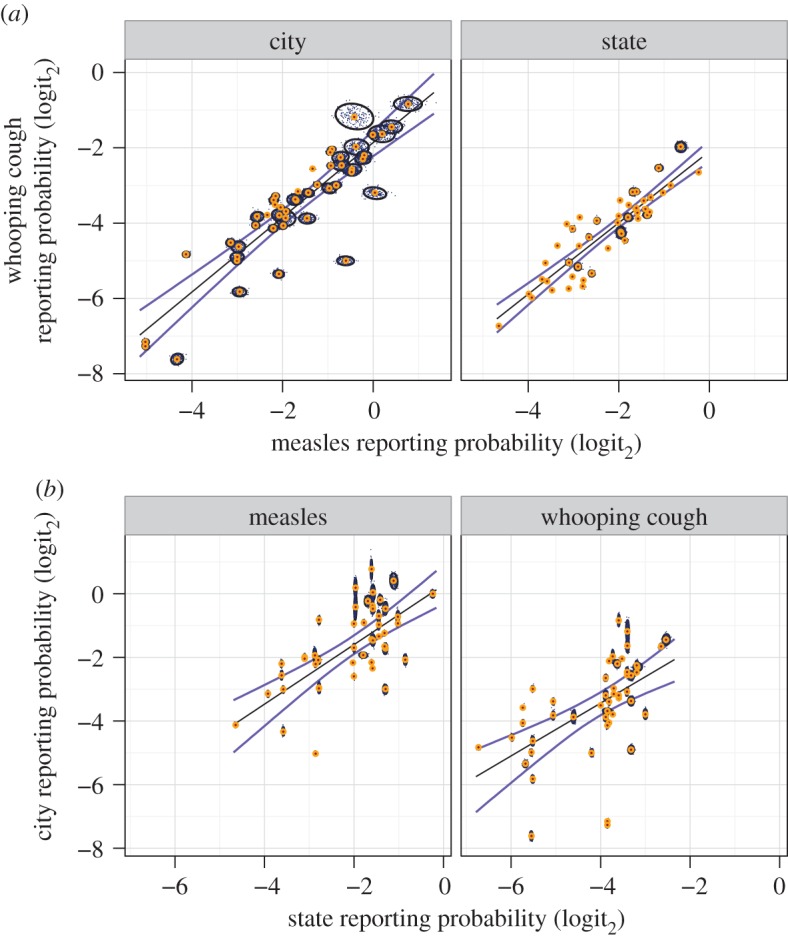
Comparison of reporting probability estimates (microdata method). (a) Within-area comparison, showing close covariation between diseases. (b) Within-disease comparison, showing covariation between areas. Variability between locations (i.e. cities or states) greatly exceeds variability within locations. 10⁴ total bootstraps were drawn (200 are plotted, small black points). For each sampled comparison, an approximate 95% confidence interval (CI) (black ovals) and median probability (orange central dot) are shown, along with median linear models (black line) and approximate model 95% CI (blue lines). See the electronic supplementary material, table S2, for linear model results.

Within-location variability estimates derived from bootstrapping of census microdata are shown in figure 2 (reporting probabilities and confidence intervals are shown in the electronic supplementary material, tables S4 and S5). Bootstrap estimates show that larger locations consistently exhibit less variation, as expected (electronic supplementary material, figure S8). Overall, between-location variation greatly exceeds within-location variation, increasing confidence in the observed patterns.

The influence of socioeconomic identity on incomplete reporting was explicitly modelled (electronic supplementary material, table S3). A range of demographic covariates were tested using forward model selection (see Material and methods). While many of these predictors are correlated, forward model selection favours a parsimonious model by selecting the best predictors first, as shown in the electronic supplementary material, table S3. The final models explain much of the observed variation in reporting probabilities: r² = 0.51 (state measles); r² = 0.4 (state WC); r² = 0.32 (city measles); r² = 0.13 (city WC). Overall, variation in measles reporting probabilities is much better explained by demographic covariates than that of WC.

Two covariates emerged as most significant: the proportion of a location's population that is either white (prop.white) or attending school (prop.school). Regardless of disease, higher reporting probabilities are correlated with a higher proportion of white for states and a higher proportion of attending school for cities. Other significant predictors include proportion in labour force (states, both diseases, positive correlation), household size s.d. (states, both diseases, positive correlation), proportion male (states, WC, negative correlation) and mean household size (cities, measles, negative correlation). Overall, selected covariates and their associated parameter estimates are generally consistent between diseases within each area.

The causal mechanisms that drive these observed correlations remain unclear. Nonetheless, the significant covariates broadly relate to measures of economic status (ethnic composition, labour force and sex ratio) as well as indicators of social structures that can influence the distribution of infection age and disease reporting (household size distribution, schooling).

4. Discussion

Observational datasets are valuable for their wide spatio-temporal extent, yet their post hoc nature means that key dynamical processes, such as stochastic extinction, can be obscured by imperfect and variable observation. Measles and WC are two well-studied childhood diseases with very different symptomology, epidemiology and temporal dynamics. Yet both infect the majority of susceptible individuals in childhood and confer lasting immunity. In addition, both diseases undergo stochastic extinction at a rate dependent on population size and birth rate [37]. Here, we estimate the extent of incomplete observation using a long-term constraint of the dynamical system, i.e. the mass balance of susceptibles in childhood diseases. We find that reporting probabilities vary greatly between disease, geographical region and metapopulation. This variability directly affects patterns of observed extinctions or ‘fade-outs’ [2,11,38] and, if not addressed, makes comparisons between diseases and metapopulations difficult.

We find that measles reporting probabilities of cities in the US are lower and more variable than in E&W. In the US, we find that measles is better reported than WC (as previously found in E&W by Clarkson & Fine [16]). In addition, we find that reporting probability varies consistently by geographical locale: those locations that report measles well also report WC well, and vice versa. On the other hand, reporting probabilities do not appear to vary appreciably by time in either country or disease in the eras considered. Likewise, bootstrapping indicates that between-location variation greatly exceeds within-location uncertainty in the USA. Finally, we show that demographic covariates, including proportion white and proportion attending school, explain a non-trivial proportion of the observed variation in US reporting probabilities: locations that have low school attendance and high minority populations have lower reporting probabilities, regardless of disease. Overall, we find substantial spatial, temporal and socioeconomic consistency within the pronounced heterogeneity of pre-vaccine era disease reporting.

(a). Sources of error and uncertainty

Observational datasets frequently lack detailed metadata, including full descriptions of sampling protocols. This introduces a persistent difficulty of estimating uncertainty and establishing concordance between varying data sources. For example, we have no detailed definition of the geographical limits used to define cities in case report collections, making concordance with census microdata estimates of city populations uncertain. For census microdata, the geographical boundaries of some cities change over time and are thus clearly incomparable with case report data. In short, we cannot unambiguously identify all sources of error and uncertainty. Nonetheless, we can often constrain uncertainty, for example by the comparison of multiple, independent data sources, as we do in this study by comparing the results from demographic data sources (i.e. census microdata and per capita birth rates).

Census microdata allows us to estimate uncertainty of reporting probabilities by bootstrapping each decadal census, yielding a bootstrap sampling distribution of each location's susceptible population. Note that this method does not account for uncertainty of case reports, which are taken as fixed. The coefficient of variation (CV) of reporting probability bootstrap draws decreases with increasing population (electronic supplementary material, figure S8). Indeed, log–log scaling of CV with population is evident for each disease and area. The sampled population of susceptibles grows as the sampled period of case reports grows. Thus, the CVs of measles and WC reporting probabilities are almost identical for cities, while the much shorter duration of state WC case reports yields higher CVs than for state measles.

Waning immunity to WC has been the subject of extensive debate in the modern era [10,39,40]. In the pre-vaccine era, adult WC was not well-recognized, and WC case reports consisted almost exclusively of childhood infections [23,39]. Thus, we have effectively estimated the reporting probability of primary infection. This estimate, in turn, provides an upper bound on total WC reporting in this era. In addition, if natural immunity is long-lasting, or repeat infections contribute little to transmission, then our estimates will be close to the reporting probability for all WC cases. In the modern era, waning vaccine-derived immunity represents another source of uncertainty, along with vaccine uptake and seroconversion rates.

The effect of migration on susceptible pools warrants closer attention. Here, we estimate each population's susceptible pool from decadal age structure. Migration can bias the results in two ways. First, recovered youths can immigrate prior to a decadal census and be erroneously counted as susceptibles. Second, susceptible youths can become infected, recover and then emigrate prior to a decadal census, and thus be erroneously neglected from the susceptible pool. Thus, immigration of previously infected youths deflates reporting probability estimates, while emigration of locally infected youths inflates them.

The overall flow of migration in the US in this era is from rural to urban areas. In addition, large rural-to-urban migration waves occurred, such as the Great Migration. Rural areas generally experienced higher levels of stochastic extinction and thus higher and more variable ages of infection than urban areas (for an extreme example, see discussion by Crum [41] of US Civil War troops). On the other hand, the low average age of infection of both measles and WC in the pre-vaccine US and E&W [42] suggests that most migrants are not susceptible to either disease. Thus, migration of recovered youths to cities could cause underestimation of reporting probabilities.

Patterns of migration can sometimes be estimated from census microdata. We cannot identify intra-census emigration here. We can, however, identify intra-census, interstate immigration by comparing individuals' resident and birth states. Assuming that all out-of-state immigrants are recovered shifts reporting probabilities upwards, though the difference is small compared with between-location variation (electronic supplementary material, figure S9).

(b). The obscuring effects of incomplete observation

Poor disease reporting and stochastic extinction cannot be easily separated, particularly in cities that regularly teeter on the boundary of extinction [7]. The proportion of zero observations (over a suitably long period of time) is one common measure of stochastic extinction [6,7,10,20,34]. This measure is appealing owing to its simplicity, but has been criticized as sensitive to disease reporting. To address these concerns, Bartlett [2] employed a three-week period of observed extinction, termed fade-out. Conlan et al. [11] propose several alternate measures on mechanistic grounds, including fade-outs post invasion and fade-outs post epidemic. Yet, the proposed measures (e.g. [11]) depend on a priori threshold values. Further, the performance of these measures under low and variable disease reporting is not well characterized.

In this regard, the large body of work on measles in E&W that neglected reporting probabilities [24,26,43] has benefitted from the happy accident of relatively high and uniform reporting probabilities. In the US, on the other hand, failing to account for the low and variable disease reporting in this era paints a false picture of the overall metapopulation dynamics and hinders a comparison between metapopulations [7].

The scaling of observed zeros with population size provides a useful example in the present systems. Previous work has demonstrated the frequent occurrence of ‘false zeros’ (apparent extinction) in pre-vaccine era US measles, particularly in medium-sized cities that hover at the edge of extinction [7]. Under the assumption of homogeneous mixing, the reporting probability is equivalent to the proportion of the population under surveillance (homogeneous mixing is a poor assumption for US states, which are not considered here). Consequently, a simple rescaling of population size by reporting probability yields the effective population size under surveillance.

The log-linear dependence of extinction risk on population size (figure 3) can be used to predict the population size at which no zero observations occur and provides a simple empirical measure of ‘total’ and ‘effective’ CCS (CCS_T and CCS_E; table 2). Failure to account for incomplete reporting yields an unrealistic measles CCS_T of more than 1.5 million for US cities, while a CCS_E of ≈400 000 is closer to theoretical predictions [37]. In E&W, the difference between the two measures is much less pronounced, but suggests that apparent extinction is still common. In addition, this simple model fails to account for the longer two-week sampling period of E&W, which should reduce the frequency of zero samples and lower both measures relative to the US. WC in the US, on the other hand, shows a drastically improved model fit using effective population size and yields a CCS_E more in line with theoretical predictions based on a similar R₀ and longer infectious period than measles [37].

Figure 3.

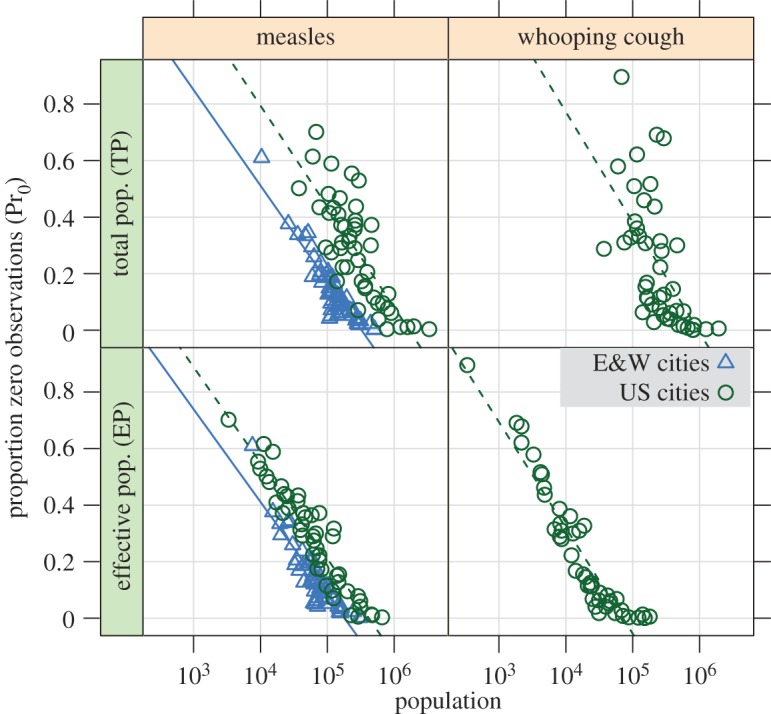
Log-linear scaling of proportion zero observations (Pr₀) with total population (TP) and effective population (EP = TP × reporting probability) of cities, excluding cities with no observed zeros. Pr₀ shows a closer scaling with EP than with TP, particularly in WC. The scaling of Pr₀ with EP in measles shows a close correspondence between countries. The longer two-week sampling interval of E&W also reduces Pr₀ in E&W. Regressions for each disease and country are overplotted (see also table 2). For the EP model, r² = 0.89 (US measles), 0.82 (E&W measles), 0.90 (US WC).

Table 2.

CCS estimates (population in thousands) and model fits for cities. Each CCS estimate is the X-intercept of a linear model of proportion zero observations (Pr₀) versus population size, excluding cities with no sampled zeros (see figure 3). Thus, each CCS estimate is the expected population size (total: CCS_T, effective: CCS_E) at which no zeros are observed. The longer two-week sampling period of E&W is expected to reduce Pr₀, and thus lower both measures of CCS, relative to the USA. WC, whooping cough.

disease	area	CCST [×103]	adj R2	CCSE [×103]	adj R2
measles	E&W	325	0.84	180	0.82
measles	USA	1678	0.63	417	0.89
WC	USA	952	0.37	71	0.90

A comparison between the US and E&W also highlights the role of socioeconomic diversity. Our results (electronic supplementary material, table S3) suggest that high levels of ethnic and cultural heterogeneity, as seen in the US compared with pre-vaccine E&W, increases variation in disease reporting. Indeed, less complete reporting in US minority populations was suggested a century ago by Crum [41]. This pattern warrants testing in the modern era in regions such as Niger, which have large rural populations and a small number of large cities [44]. In a socioeconomically heterogeneous state such as Niger, significant variation in measles reporting probabilities appears to be a conservative assumption. Furthermore, observed variation in reporting of other human infectious diseases can be explained by similar socioeconomic disparities. For example, Undurraga et al. [18] showed that the estimated probability of under-reporting of dengue episodes at a national level in southeast Asia and the Americas correlated with a measure of health quality.

(c). Broader applications

The employed method is only appropriate for fully immunizing diseases. In the modern era, vaccination introduces additional sources of variation and measurement error, since estimates of vaccine uptake and efficacy [16], as well as waning immunity rates, are required. We also assume minimal temporal variation in disease reporting and require long time periods (e.g. multiple epidemics) to generate estimates of incomplete reporting.

Nonetheless, we propose that disease ecologists and epidemiologists can often estimate between-population variation in incomplete observation. Accounting for this variation appears to be particularly important in socioeconomically diverse populations. The framework that we employ is conceptually and analytically simple, provided sufficient demographic information is available. Indeed, even when relevant demographic details are sparse or absent, rough estimates of reporting probability can suggest whether or not between-location variation overwhelms the dynamical processes or features of interest.

Data accessibility

US case report data and demographics available at Data Dryad: doi:10.5061/dryad.92p46; E&W case reports: data originally from http://www.zoo.cam.ac.uk/zoostaff/grenfell/measles.htm, no longer available. See Internet archive: https://archive.org/web/; E&W demographics: personal communication with Dr Pej Rohani (rohani@umich.edu); Integrated Public Use Microdata Series: IPUMS-USA, 1920–1950, 1% sample, https://usa.ipums.org/usa/.

Funding statement

C.G. was supported by a fellowship in the Program in Interdisciplinary Biological and Biomedical Sciences at the University of New Mexico. This publication was made possible by grant nos. P20RR018754 from the National Center for Research Resources (NCRR), T32EB009414 from the National Institute of Biomedical Imaging and Bioengineering (NIBIB), components of the National Institutes of Health (NIH). Its contents are solely the responsibility of the authors and do not necessarily represent the official views of NCRR, NIBIB or NIH.