Abstract
Morphogenesis, spontaneous formation of organism structure, is essential for life. In the pancreas, endocrine  ,
, 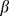 , and
, and  cells are clustered to form islets of Langerhans, the critical micro-organ for glucose homeostasis. The spatial organization of endocrine cells in islets looks different between species. Based on the three-dimensional positions of individual cells in islets, we computationally inferred the relative attractions between cell types, and found that the attractions between homotypic cells were slightly, but significantly, stronger than the attractions between heterotypic cells commonly in mouse, pig, and human islets. The difference between
cells are clustered to form islets of Langerhans, the critical micro-organ for glucose homeostasis. The spatial organization of endocrine cells in islets looks different between species. Based on the three-dimensional positions of individual cells in islets, we computationally inferred the relative attractions between cell types, and found that the attractions between homotypic cells were slightly, but significantly, stronger than the attractions between heterotypic cells commonly in mouse, pig, and human islets. The difference between  cell attraction and
cell attraction and  cell attraction was minimal in human islets, maximizing the plasticity of islet structures. Our result suggests that although the cellular composition and attractions of pancreatic endocrine cells are quantitatively different between species, the physical mechanism of islet morphogenesis may be evolutionarily conserved.
cell attraction was minimal in human islets, maximizing the plasticity of islet structures. Our result suggests that although the cellular composition and attractions of pancreatic endocrine cells are quantitatively different between species, the physical mechanism of islet morphogenesis may be evolutionarily conserved.
Introduction
Multi-cellular organisms require communications between neighboring cells, and have developed special architectures for optimizing such cellular communications. A fundamental question in life is how organisms spontaneously form their functional structures. Interestingly, a few simple rules can be sufficient to form complex organs such as the lung [1]. As a microscopic explanation of morphogenesis, Steinberg introduced the differential adhesion hypothesis that differences in adhesiveness between cell types are partially responsible for the development and maintenance of organ structures [2], [3].
Pancreatic islets of Langerhans are the critical micro-organs responsible for glucose homeostasis. Each islet consists mainly of  ,
, 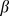 , and
, and  cells. Glucagon and insulin are the reciprocal hormones for increasing and decreasing blood glucose levels, secreted by
cells. Glucagon and insulin are the reciprocal hormones for increasing and decreasing blood glucose levels, secreted by  and
and 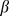 cells, respectively. The role of
cells, respectively. The role of  cells in glucose homeostasis is still mysterious. In addition, it has long been reported that endocrine cells interact with each other [4]. Considering the specific symmetries of interactions between
cells in glucose homeostasis is still mysterious. In addition, it has long been reported that endocrine cells interact with each other [4]. Considering the specific symmetries of interactions between  ,
,  , and
, and  cells, their spatial organization must have functional significance. Rodent islets have a shell-core structure where
cells, their spatial organization must have functional significance. Rodent islets have a shell-core structure where 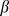 cells are located in the islet core, while non-
cells are located in the islet core, while non-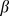 cells are located on the islet periphery. However, there are contradictory reports regarding the structure of human islets [5]. Some observations suggest more or less random structures of cells [6], [7], while others have found some order in structures, and described human islets as assemblages of
cells are located on the islet periphery. However, there are contradictory reports regarding the structure of human islets [5]. Some observations suggest more or less random structures of cells [6], [7], while others have found some order in structures, and described human islets as assemblages of  -cell-core subunits [8] or lobules [9], cloverleaf patterns [5], ribbon-like structures [10], and folded trilaminar plate [11].
-cell-core subunits [8] or lobules [9], cloverleaf patterns [5], ribbon-like structures [10], and folded trilaminar plate [11].
Dissociated islet cells spontaneously aggregate and form islet-like structures, pseudo-islets, in rat, pig, and human pancreatic cultures [12]–[15]. Different adhesion molecules have been proposed as a cause of the pseudo-islet formation expressed on rodent  and
and 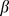 cells [16]–[20]. However, the relative adhesion strengths of such cells in native islets has not been directly measured. On one hand, this technical limitation leaves open the interesting question of whether different species have different rules for islet organization. On the other hand, current imaging methods allow to observe islet structures with high resolution. In this study, we computationally infer the organization rule from three-dimensional islet structures. In particular, we compare mouse, pig, and human islets, and find a conserved organization rule behind different islet structures.
cells [16]–[20]. However, the relative adhesion strengths of such cells in native islets has not been directly measured. On one hand, this technical limitation leaves open the interesting question of whether different species have different rules for islet organization. On the other hand, current imaging methods allow to observe islet structures with high resolution. In this study, we computationally infer the organization rule from three-dimensional islet structures. In particular, we compare mouse, pig, and human islets, and find a conserved organization rule behind different islet structures.
Results
Cellular distributions in pancreatic islets
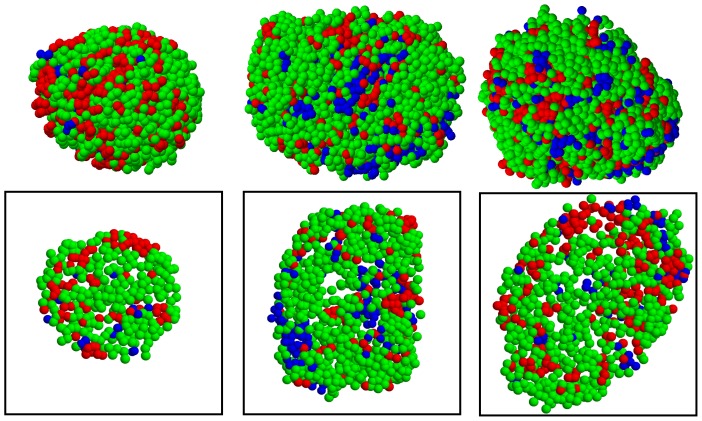
Two-dimensional cross sections of pancreatic islets have been widely used to study islet structures. Here, however, we used a confocal microscope to examine three-dimensional islet structures, as previously used [6], [21]. To precisely analyze islet structures, we obtained three-dimensional positions of every endocrine cell in individual islets. We used stained nuclei to determine the center positions of cells, and immunostaining to determine cell types. Figure 1 showed the spatial cellular organizations of pancreatic islets in different species. First, we observed two major cell types of  and
and 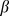 cells in mouse (Fig. 1A
), pig (Fig. 1B
), and human islets (Fig. 1C
). Mouse islets showed the typical shell-core structure in which
cells in mouse (Fig. 1A
), pig (Fig. 1B
), and human islets (Fig. 1C
). Mouse islets showed the typical shell-core structure in which 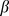 cells are located in the core, while
cells are located in the core, while  cells are located on the periphery. In pig and human islets, however,
cells are located on the periphery. In pig and human islets, however,  cells are located not only on the periphery but also distributed inside islets.
cells are located not only on the periphery but also distributed inside islets.
Figure 1. Cellular organization of pancreatic islets.
Three-dimensional spatial distribution of α cells (red) and β cells (green) is shown in (A) mouse, (B) pig, and (C) human islets. To show internal islet structures clearly, their corresponding two-dimensional sections are also shown in boxes.
We then quantified the fraction of 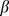 cells depending on islet size in the three species (Fig. 2). Mouse islets consisted of 90%
cells depending on islet size in the three species (Fig. 2). Mouse islets consisted of 90% 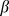 cells independent of islet size. Human islets had a smaller
cells independent of islet size. Human islets had a smaller  -cell fraction,
-cell fraction,  . In particular, larger human islets had less abundant
. In particular, larger human islets had less abundant  cells depending on size. This finding in three-dimensional islets is consistent with previous reports based on pancreatic sections [11], [22], [23]. Interestingly, pig islets (
cells depending on size. This finding in three-dimensional islets is consistent with previous reports based on pancreatic sections [11], [22], [23]. Interestingly, pig islets ( ) showed an intermediate characteristic between mouse (
) showed an intermediate characteristic between mouse ( ) and human islets (
) and human islets ( ). We also examined cell-to-cell contacts (See Materials and Methods), and quantified their ratios,
). We also examined cell-to-cell contacts (See Materials and Methods), and quantified their ratios,  ,
, 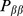 , and
, and 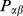 for
for  ,
,  , and
, and  contacts, respectively (Fig. 3). The higher
contacts, respectively (Fig. 3). The higher 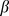 -cell fraction in mouse islets resulted in more prevalent
-cell fraction in mouse islets resulted in more prevalent  contacts (
contacts (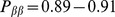 ), compared with pig (
), compared with pig ( ) and human islets (
) and human islets (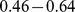 ), but less prevalent
), but less prevalent  and
and 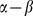 contacts.
contacts.
Figure 2. Cellular compositions in mouse, pig, and human islets.
Fractions of β cells, depending on islets size, are calculated in mouse (empty bar), pig (hatched), and human (black solid) islets. Islet size is represented by the total number of cells in islets, and categorized as small (<1000 cells), medium (1000–2000), and large (>2000) islets. Mean ± SEM (n = 30). * P<0.005.
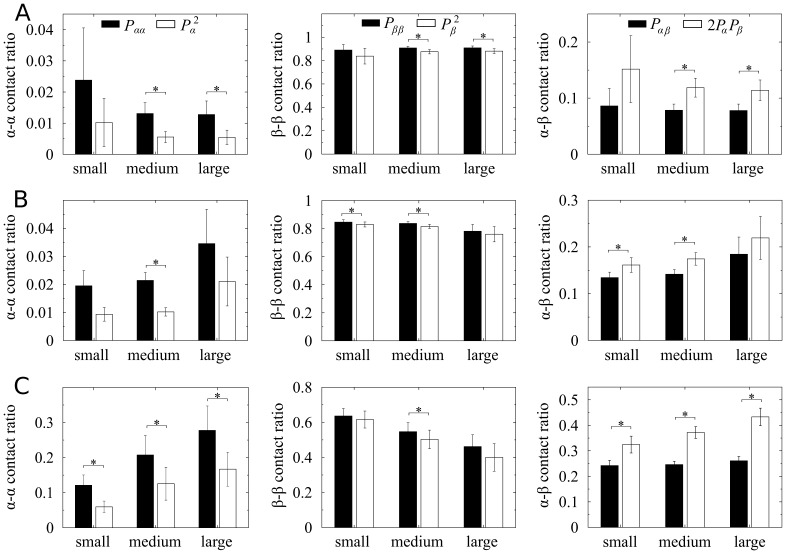
Figure 3. Cell-to-cell contact ratios in mouse, pig, and human islets.
Based on the contacts between neighboring cells, ratios of  ,
,  , and
, and  contacts (
contacts ( ,
,  , and
, and 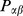 ), depending on islet size, are calculated in (A) mouse, (B) pig, and (C) human islets. Islet size is represented by the total number of cells in islets, and categorized as small (<1000 cells), medium (1000–2000), and large (>2000) islets. Given fractions of
), depending on islet size, are calculated in (A) mouse, (B) pig, and (C) human islets. Islet size is represented by the total number of cells in islets, and categorized as small (<1000 cells), medium (1000–2000), and large (>2000) islets. Given fractions of  and
and 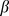 cells (
cells (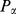 and
and 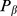 ), the
), the  ,
,  , and
, and  contact probabilities in random cell organization are theoretically
contact probabilities in random cell organization are theoretically  ,
, 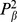 , and
, and 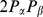 , respectively. The random organization (empty bar) is compared with the organization of native islets (black solid). Mean ± SEM. *
P<0.005.
, respectively. The random organization (empty bar) is compared with the organization of native islets (black solid). Mean ± SEM. *
P<0.005.
Given fractions of  and
and  cells, we could simulate cell-to-cell contact probabilities in random cell aggregates. The probability that two sites are occupied randomly by
cells, we could simulate cell-to-cell contact probabilities in random cell aggregates. The probability that two sites are occupied randomly by  cells is
cells is  , and the one for
, and the one for 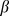 cells is
cells is 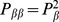 . In addition, the probability that two sites are occupied randomly by
. In addition, the probability that two sites are occupied randomly by  and
and  , or vice versa, is
, or vice versa, is 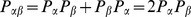 . Regardless of species, Fig. 3 shows that frequencies of homotypic contacts are significantly higher than the probabilities in random aggregates (
. Regardless of species, Fig. 3 shows that frequencies of homotypic contacts are significantly higher than the probabilities in random aggregates ( and
and  ). On the other hand, islet structures showed smaller frequencies of heterotypic contacts, compared with random (
). On the other hand, islet structures showed smaller frequencies of heterotypic contacts, compared with random (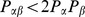 ). These results clearly demonstrated that islet structures are not random cell aggregates. This conclusion looks trivial for the shell-core structure of mouse islets (Fig. 1A
). However, this suggested that pig and human islets also had some order in their cellular organization.
). These results clearly demonstrated that islet structures are not random cell aggregates. This conclusion looks trivial for the shell-core structure of mouse islets (Fig. 1A
). However, this suggested that pig and human islets also had some order in their cellular organization.
Self-organization rule for pancreatic islets
Since islets are not random cell aggregates, we investigated rules governing islet structure. Prevalent contacts of homotypic cells could have resulted from (i) replication of neighboring cells and/or (ii) stronger attraction between homotypic cells. Islet organogenesis occurs in the milieu of developmental processes including cell differentiation, migration, aggregation, replication, and death [24], [25]. Nevertheless, when islet cells are dissociated, they can spontaneously form pseudo-islets resembling native islets [12]–[15]. This pseudo-islet formation implies that sequences of complicated developmental processes, particularly cell replication, may not be critical for the formation of equilibrium islet structures. Therefore, as proposed [2], [3], [26], we investigated if the differential adhesion hypothesis could provide a simple rule governing for islet structures. Depending on the relative adhesiveness between cell types, islets could have various equilibrium structures (Fig. 4). When homotypic attractions are stronger than heterotypic attractions, islets have a sorting phase with two homogeneous cell clusters. As heterotypic attraction becomes stronger, the two cell types start to mix [27].
Figure 4. Schematic diagram of structural dependence on relative attractions between cell types.
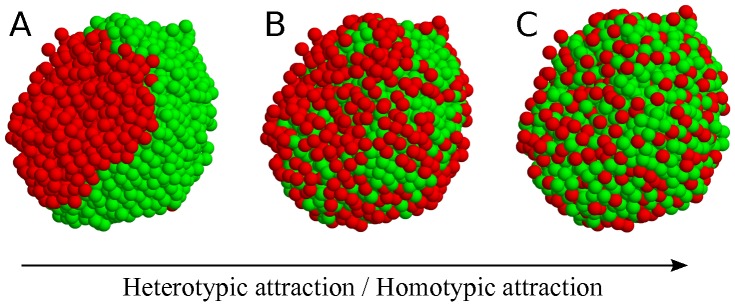
A sorting structure of two cell types is changed to mixing structures, as heterotypic attraction increased compared with homotypic attractions: (A) complete sorting, (B) shell-core sorting, and (C) mixing structures.
We specify the relative strengths of adhesiveness or attraction between cell types as  ,
,  , and
, and  for
for  ,
,  , and
, and  contacts, respectively. A stronger attraction between neighboring cells implies that it requires a larger amount of energy to dissociate them. Therefore, the total cell-to-cell contact energy, self-energy, in an islet is a sum over every contact
contacts, respectively. A stronger attraction between neighboring cells implies that it requires a larger amount of energy to dissociate them. Therefore, the total cell-to-cell contact energy, self-energy, in an islet is a sum over every contact
| (1) |
where the islet has total  ,
,  , and
, and 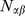 contacts of
contacts of  ,
,  , and
, and  , respectively. The negative sign in Eq. (1) represents that external energy is needed (not extracted) to dissociate cell-to-cell contacts. Given numbers of
, respectively. The negative sign in Eq. (1) represents that external energy is needed (not extracted) to dissociate cell-to-cell contacts. Given numbers of  and
and 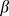 cells, the islet self-energy can have various values depending on spatial organization of cells. Our conjecture is that islets have an equilibrium structure that minimizes their self-energy. When homotypic attractions are stronger,
cells, the islet self-energy can have various values depending on spatial organization of cells. Our conjecture is that islets have an equilibrium structure that minimizes their self-energy. When homotypic attractions are stronger,  and
and  contacts are preferred. On the other hand, when heterotypic attraction is stronger,
contacts are preferred. On the other hand, when heterotypic attraction is stronger,  contacts are preferred.
contacts are preferred.
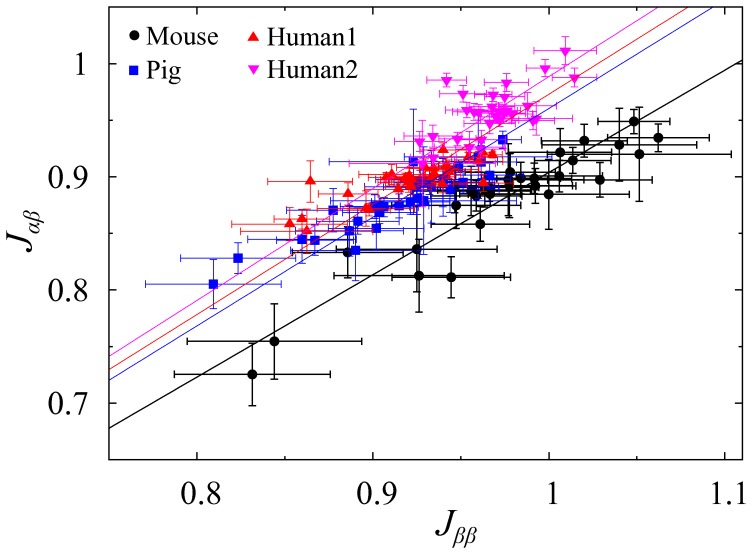
Here our problem is not to obtain equilibrium structures given cellular attractions. It is currently not possible to measure the strengths of cellular attractions inside islets. However, we could obtain cell-to-cell contact information from three-dimensional islet imaging. Thus we addressed this inverse problem to infer the strengths of cellular attractions from cell-to-cell contact information. Using Bayesian inference (See Materials and Methods), we inferred the likelihood strengths of cellular attractions that explain observed islet structures. Figure 5 showed the inferred attractions,  and
and  , relative to the reference attraction
, relative to the reference attraction 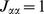 , from mouse, pig, and human islets. The relative attractions were not dependent on islet size for all species (Fig. S1). Their averages and standard deviations are summarized in Table 1. The relative attractions were not dramatically different between each other, regardless of species. The homotypic attractions,
, from mouse, pig, and human islets. The relative attractions were not dependent on islet size for all species (Fig. S1). Their averages and standard deviations are summarized in Table 1. The relative attractions were not dramatically different between each other, regardless of species. The homotypic attractions,  and
and 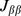 , were slightly, but significantly, larger than the heterotypic attraction,
, were slightly, but significantly, larger than the heterotypic attraction, 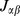 , for all species considered. This general conclusion is consistent with the cellular organization,
, for all species considered. This general conclusion is consistent with the cellular organization, 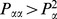 ,
,  , and
, and 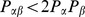 . A random organization can be obtained with equal cellular attractions, i.e.,
. A random organization can be obtained with equal cellular attractions, i.e., 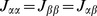 . It is thus understandable that islets have
. It is thus understandable that islets have 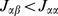 and
and  . However, the Bayesian inference quantified the dependence of relative cellular attractions on species:
. However, the Bayesian inference quantified the dependence of relative cellular attractions on species: 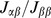 for mouse islets (0.91) is lowest, while human islets (0.98 and 0.99 for two different pancreata) show the largest ratio. Pig islets showed a similar ratio (0.97) to human islets.
for mouse islets (0.91) is lowest, while human islets (0.98 and 0.99 for two different pancreata) show the largest ratio. Pig islets showed a similar ratio (0.97) to human islets.
Figure 5. Cellular attractions in mouse, pig, and human islets.
Relative attractions between cell types and their uncertainties are inferred from three-dimensional islet structures. Symbols represent individual islets: mouse (black circle), pig (blue square), and human islets (red triangle and pink inverse triangle). Each species has n = 30 islets. In particular, two sets of n = 30 islets are provided from two human (Human1 and Human2) subjects. The relationship between  and
and  is fitted with linear functions,
is fitted with linear functions,  , represented by solid lines with colors corresponding to each species. Note that the attraction between
, represented by solid lines with colors corresponding to each species. Note that the attraction between  cells is defined as a reference attraction,
cells is defined as a reference attraction, 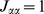 .
.
Table 1. Cellular attractions in mouse, pig, and human islets.
| Species | n | J ββ | Jαβ | Jαβ/Jββ |
| Mouse | 30 | 0.97±0.05 | 0.88±0.05a | 0.91±0.02 |
| Pig | 30 | 0.91±0.04 | 0.88±0.03a | 0.97±0.02b |
| Human1 | 30 | 0.92±0.03 | 0.90±0.02a | 0.98±0.02 |
| Human2 | 30 | 0.97±0.02 | 0.96±0.02a | 0.99±0.02 |
Relative attractions between cell types are inferred from three-dimensional islet structures, mean ± SD (n = 30 islets). Note that the attraction between  cells is defined as a reference attraction,
cells is defined as a reference attraction,  .
.
Paired Student's t-test concludes Jββ>Jαβ with  .
.
Unpaired Student's t-test concludes that mouse and pig islets have different Jαβ/Jββ with 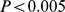 .
.
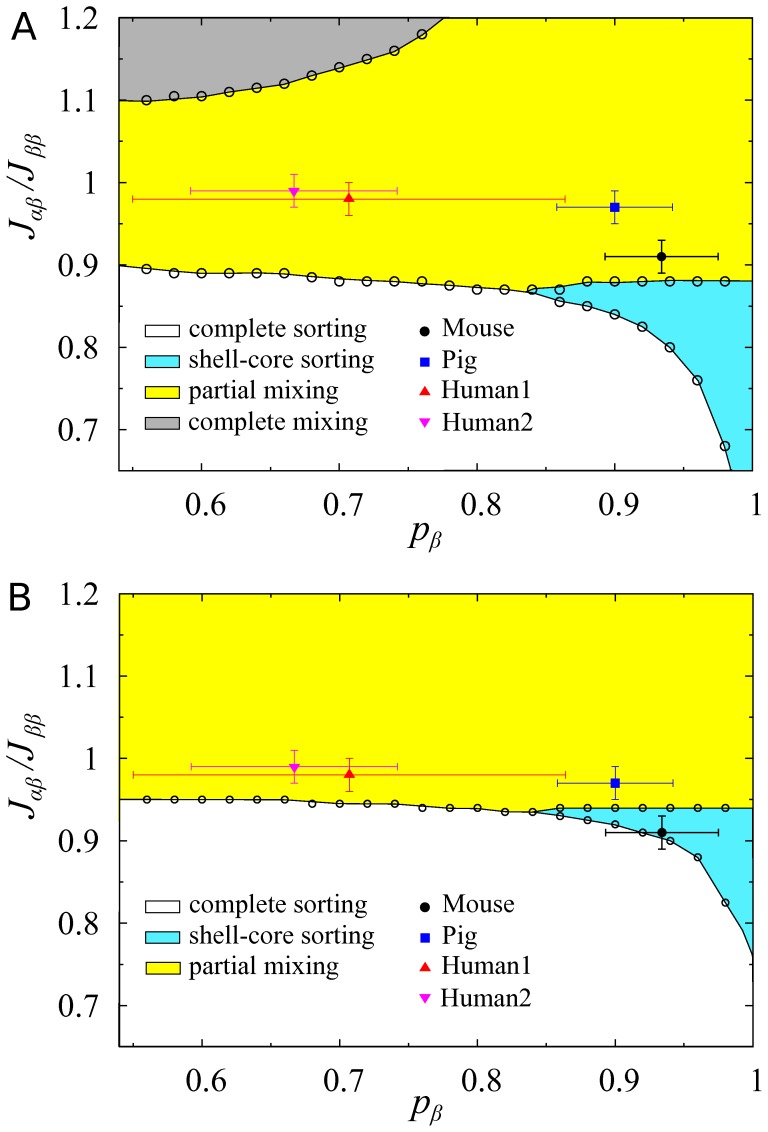
Here, an intriguing question is whether the small differences in cellular attractions can explain the structural difference between mouse and human islets. In general, binary mixture systems of finite size can generate sorting and mixing phases depending on mixture fraction and relative adhesion strengths [27]. To answer the question, we considered two theoretical lattices representing islet structures: cubic (Fig. 6A
) and hexagonal close packed (HCP) lattices (Fig. 6B
), in which  and
and 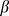 cells are distributed with various β-cell fractions
cells are distributed with various β-cell fractions  and relative attraction strengths
and relative attraction strengths 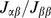 . Then we computed cell-to-cell contact numbers and their fluctuations, and obtained the phase diagrams for the cubic lattice (Fig. 7A
) and the HCP lattice (Fig. 7B
). Human and pig islets were classified to have the partial mixing structure for both cubic and HCP lattices. However, mouse islets were classified to have the partial mixing structure for the cubic lattice, but to have the shell-core sorting structure for the HCP lattice. The native islet structure could be approximated better as the HCP lattice than the cubic lattice, because its mean number of neighboring cells (
. Then we computed cell-to-cell contact numbers and their fluctuations, and obtained the phase diagrams for the cubic lattice (Fig. 7A
) and the HCP lattice (Fig. 7B
). Human and pig islets were classified to have the partial mixing structure for both cubic and HCP lattices. However, mouse islets were classified to have the partial mixing structure for the cubic lattice, but to have the shell-core sorting structure for the HCP lattice. The native islet structure could be approximated better as the HCP lattice than the cubic lattice, because its mean number of neighboring cells ( for mouse,
for mouse, 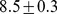 for pig,
for pig, 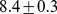 for Human1, and
for Human1, and  for Human2 islets) was closer to the HCP lattice (10.6) than the cubic lattice (5.4). Therefore, we concluded that the higher β-cell fraction
for Human2 islets) was closer to the HCP lattice (10.6) than the cubic lattice (5.4). Therefore, we concluded that the higher β-cell fraction  and the slightly weaker heterotypic attraction
and the slightly weaker heterotypic attraction  of mouse islets could be sufficient to generate the shell-core sorting structure, distinct from the partial mixing structure of human and pig islets.
of mouse islets could be sufficient to generate the shell-core sorting structure, distinct from the partial mixing structure of human and pig islets.
Figure 6. Distinct structures of binary mixtures.
Complete sorting, shell-core sorting, and partial mixing structures are plotted for (A) cubic and (B) hexagonal close packed lattices. Here each lattice consists of 1357 cells with 10%  cells (red) and 90%
cells (red) and 90% 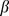 cells (green). The relative attractions are chosen to have the specific structures:
cells (green). The relative attractions are chosen to have the specific structures: 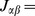 0.7 (left), 0.85 (middle), and 1.1 (right) for (A) the cubic lattice; and
0.7 (left), 0.85 (middle), and 1.1 (right) for (A) the cubic lattice; and 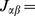 0.7 (left), 0.93 (middle), and 1.1 (right) for (B) the hexagonal close packed lattice. Note that the homotypic attractions are fixed as a reference,
0.7 (left), 0.93 (middle), and 1.1 (right) for (B) the hexagonal close packed lattice. Note that the homotypic attractions are fixed as a reference,  , and the thermal fluctuation energy is
, and the thermal fluctuation energy is  .
.
Figure 7. Phase diagrams of binary mixtures.
Binary mixtures have complete sorting (white region), shell-core sorting (cyan region), partial mixing (yellow region), and complete sorting (gray region) structures depending on mixture fraction and relative adhesion strengths. Plotted are phase diagrams for (A) cubic and (B) hexagonal close packed lattices with 1357 cells. Symbols represent the observed β-cell fraction  and the inferred relative attraction
and the inferred relative attraction  of mouse islets (black circle), pig (blue square), and human islets (red triangle and pink inverse triangle). Note that the homotypic attractions have a reference attraction,
of mouse islets (black circle), pig (blue square), and human islets (red triangle and pink inverse triangle). Note that the homotypic attractions have a reference attraction,  . Each species has n = 30 islets. Mean ± SD.
. Each species has n = 30 islets. Mean ± SD.
Spatial organization of δ cells
In addition to  and
and  cells, islets contain a minor population of somatostatin-secreting
cells, islets contain a minor population of somatostatin-secreting  cells. We further examined human islet structures including
cells. We further examined human islet structures including  cells (Fig. 8). Similarly to previous analysis, we inferred cellular attractions, relative to
cells (Fig. 8). Similarly to previous analysis, we inferred cellular attractions, relative to  attraction (
attraction (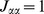 ), not only
), not only  and
and  , but also
, but also  ,
, 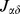 , and
, and 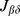 (Table 2). The result could be summarized as
(Table 2). The result could be summarized as 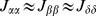
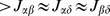 . In general, homotypic attractions were slightly stronger than heterotypic attractions.
. In general, homotypic attractions were slightly stronger than heterotypic attractions.
Figure 8. Cellular organization of human pancreatic islets.
Three-dimensional spatial distribution of  cells (red),
cells (red), 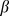 cells (green), and
cells (green), and  cells (blue) in human islets is shown. To show internal islet structures clearly, their corresponding two-dimensional sections are also shown in boxes. Note that islets are isolated from the Human3 subject for this plot.
cells (blue) in human islets is shown. To show internal islet structures clearly, their corresponding two-dimensional sections are also shown in boxes. Note that islets are isolated from the Human3 subject for this plot.
Table 2. Cellular compositions and attractions in human islets.
| No. | Size | Pα | Pβ | Pδ | Jββ | Jαβ | Jδδ | Jαδ | Jβδ |
| 1 | 588 | 0.25 | 0.54 | 0.21 | 0.97±0.02(0.96) | 0.92±0.01(0.91) | 1.03±0.02 | 0.93±0.02 | 0.90±0.02 |
| 2 | 2096 | 0.31 | 0.56 | 0.13 | 1.00±0.01(1.00) | 0.94±0.01(0.93) | 1.01±0.02 | 0.90±0.01 | 0.90±0.02 |
| 3 | 2264 | 0.19 | 0.65 | 0.16 | 0.96±0.01(0.97) | 0.91±0.01(0.91) | 1.00±0.02 | 0.90±0.01 | 0.89±0.02 |
| 4 | 2858 | 0.29 | 0.48 | 0.23 | 0.97±0.01(0.99) | 0.92±0.004(0.93) | 0.99±0.01 | 0.93±0.01 | 0.89±0.01 |
| 5 | 3253 | 0.34 | 0.47 | 0.19 | 0.98±0.01(0.99) | 0.93±0.005(0.93) | 1.00±0.01 | 0.91±0.01 | 0.89±0.01 |
| 6 | 3544 | 0.27 | 0.63 | 0.10 | 0.97±0.01(0.97) | 0.92±0.005(0.92) | 1.03±0.03 | 0.93±0.02 | 0.91±0.02 |
| Av. | 2434 | 0.28 | 0.55 | 0.17 | 0.98±0.01(0.98) | 0.92±0.01(0.92) | 1.01±0.02 | 0.92±0.02 | 0.90±0.01 |
Fractions of  ,
, 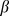 , and
, and  cells in six human islets, isolated from the Human3 subject, are calculated. Islet size is represented by the total number of cells in islets. Relative attractions between cell types are inferred from three-dimensional islet structures, mean ± SD. Note that the attraction between
cells in six human islets, isolated from the Human3 subject, are calculated. Islet size is represented by the total number of cells in islets. Relative attractions between cell types are inferred from three-dimensional islet structures, mean ± SD. Note that the attraction between  cells is defined as a reference attraction,
cells is defined as a reference attraction,  . The values
. The values 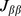 and
and  in parentheses are inferred from the three-dimensional islet structures ignoring
in parentheses are inferred from the three-dimensional islet structures ignoring  cells as empty sites.
cells as empty sites.
To validate our previous analysis with islets in which  cells are unseen, we inferred
cells are unseen, we inferred 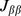 and
and 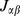 from islets in which
from islets in which  cells are seen, but ignored as empty sites. Their inferred values were not different regardless of the presence and absence of
cells are seen, but ignored as empty sites. Their inferred values were not different regardless of the presence and absence of  cells (Table 2).
cells (Table 2).
Discussion
We observed spatial distributions of endocrine cells in three-dimensional islets, and characterized their distributions in mouse, pig, and human islets. Islets from different species showed different cellular compositions and structures. An intriguing question was whether the structural difference originates from the different cellular composition or different organization rules, or both. Based on our computational inference from the high-resolution islet structures, we found that the adhesions between homotypic cells were slightly, but signficantly, stronger than the ones between heterotypic cells commonly in the three species. Furthermore, the binary mixture simulation on the HCP lattice demonstrated that the small difference of relative adhesions and the more abundant β cells could generate the shell-core structure of mouse islets, which was different from the partial mixing structure of pig and human islets. Therefore, the conserved rule could explain the different islet organizations of the three species.
We considered islet organogenesis as an equilibrium process assuming that given numbers of cells can switch their positions and minimize their total contact energy, the islet self-energy. One might consider it as a non-equilibrium process where the sequential events of cell differentiation and replication elaborately construct the specific structures of islets during development. However, sequential development is limited to explain the following two observations. First, cell replication could explain the preferential neighboring of homotypic cells, but it could not explain the regional segregation of  cells and β cells in mouse islets without extra processes such as cell polarization, migration, and death. In contrast, the equilibrium process, based on the differential adhesion hypothesis, may provide a simpler explanation for the regional segregation problem. Second, when endocrine cells are dissociated from mature islets, they can re-aggregate and form pseudo-islets resembling the native islets [12]–[15]. The pseudo-islet formation gives direct evidence suggesting that the sequence of developmental events might not be critical for the determination of islet structures. Assuming that cellular motility is sufficiently large, the detailed history of cell additions through differentiation and replication may not significantly affect the equilibrium islet structures.
cells and β cells in mouse islets without extra processes such as cell polarization, migration, and death. In contrast, the equilibrium process, based on the differential adhesion hypothesis, may provide a simpler explanation for the regional segregation problem. Second, when endocrine cells are dissociated from mature islets, they can re-aggregate and form pseudo-islets resembling the native islets [12]–[15]. The pseudo-islet formation gives direct evidence suggesting that the sequence of developmental events might not be critical for the determination of islet structures. Assuming that cellular motility is sufficiently large, the detailed history of cell additions through differentiation and replication may not significantly affect the equilibrium islet structures.
Here we proposed a dynamic structure of islets, balancing cell motility and adhesion, instead of a static structure where cellular positions were frozen. Lymphocyte homing is an extreme example of a dynamic structure because highly mobile immune cells can organize lymphoid organs such as germinal centers and Peyer's patches through chemotoxis and adhesion [28], [29]. In this study, we quantified the cellular attraction 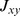 as a required energy to dissociate the contact of
as a required energy to dissociate the contact of  and
and  cells, and represented the cell motility
cells, and represented the cell motility  as a kind of fluctuation energy to help the cellular contacts dissociate. As the cell motility
as a kind of fluctuation energy to help the cellular contacts dissociate. As the cell motility  increased, cells could break their contacts to neighboring cells more frequently and move more actively. Our analysis showed that the the relative attractions between cell types were not dramatically different in pancreatic islets. Quantitatively, the energy gap between the relative cellular attractions did not exceed the fluctuation energy for cell motility to dissociate the cellular contacts,
increased, cells could break their contacts to neighboring cells more frequently and move more actively. Our analysis showed that the the relative attractions between cell types were not dramatically different in pancreatic islets. Quantitatively, the energy gap between the relative cellular attractions did not exceed the fluctuation energy for cell motility to dissociate the cellular contacts,  . Thus islet structures become rather different from random cell organization to have a few more contacts between homotypic cells. The fine balancing of cell adhesion and motility may allow islets to have flexible structures. In particular, human islets had the minimal energy gap,
. Thus islet structures become rather different from random cell organization to have a few more contacts between homotypic cells. The fine balancing of cell adhesion and motility may allow islets to have flexible structures. In particular, human islets had the minimal energy gap,  , which could maximize the structural plasticity of islets. Note that this might explain the prima facie contradictory observations of human islet structure, random versus ordered structures [5]. The morphogenetic plasticity of islets has been observed [30], and proposed to have a functional implication under altered physiological conditions [31]. The islet morphology of diabetic (db/db) and pregnant mice shows the partial mixing structure of human islets instead of the typical shell-core sorting structure of rodent islets [31].
, which could maximize the structural plasticity of islets. Note that this might explain the prima facie contradictory observations of human islet structure, random versus ordered structures [5]. The morphogenetic plasticity of islets has been observed [30], and proposed to have a functional implication under altered physiological conditions [31]. The islet morphology of diabetic (db/db) and pregnant mice shows the partial mixing structure of human islets instead of the typical shell-core sorting structure of rodent islets [31].
The differential adhesiveness between islet cells may originate from the differential expression of adhesion molecules on their cell membranes. Indeed the differential expression of neural cell adhesion molecule (NCAM) between β and non-β cells has been observed in rodent islets [17]. Furthermore, to quantify the cellular adhesiveness, the cohesivity of spherical aggregates of islet cell lines has been measured [20]. Nevertheless, it still remains to examine the expression levels of different adhesion molecules on α, β, and  cells in different species, and find the correlation between their relative expressions and the physical attractions between cell types. In addition to the experimental demonstration of the conserved rule for the islet organization, its physiological reason remains to investigate. The coupling between β cells through gap junctions has been emphasized to pronounce insulin secretion [32]. Furthermore, the functional roles of paracrine interactions between α, β, and
cells in different species, and find the correlation between their relative expressions and the physical attractions between cell types. In addition to the experimental demonstration of the conserved rule for the islet organization, its physiological reason remains to investigate. The coupling between β cells through gap junctions has been emphasized to pronounce insulin secretion [32]. Furthermore, the functional roles of paracrine interactions between α, β, and  cells have been recently investigated [33], [34]. The slight preference of
cells have been recently investigated [33], [34]. The slight preference of  contacts to
contacts to  and
and  contacts may allow islets to have both advantages of β-cell coupling and paracrine interactions.
contacts may allow islets to have both advantages of β-cell coupling and paracrine interactions.
Materials and Methods
Ethics Statement
Mouse studies were approved by the Institutional Animal Care and Use Committee of the University of Chicago. Pig studies were approved by the Institutional Animal Care and Use Committee of Meiji University. The use of human tissues in the study was approved by the Institutional Review Board at the University of Chicago.
Mouse, pig, and human islets
Mouse islets were isolated from a 3-mo old male mouse on CD-1 background. Pig islets were isolated from a 4.5-mo old female pig (a crossbred of Large white/Landrace and Duroc). Human pancreata (Human1: 60-year-old male and BMI 39.5; Human2: 40-year-old female and BMI 53; Human3: 51-year-old female and BMI 29.3) were generously provided by the Gift of Hope Organ and Tissue Donor Network in Chicago. Written informed consent from a donor or the next of kin was obtained for use of a sample in research. Specimens were collected within 12 hours of cold ischemia.
Immunohistochemistry
Isolated islets were stained with the following primary antibodies (all 1∶500): polyclonal guinea pig anti-porcine insulin (DAKO, Carpinteria, CA), mouse monoclonal anti-human glucagon (Sigma-Aldrich, St. Louis, MO), polyclonal goat anti-somatostatin (Santa Cruz, Santa Cruz, CA), and DAPI (Invitrogen, Carlsbad, CA). The primary antibodies were detected using a combination of DyLight 488, 549, and 649-conjugated secondary antibodies (1∶200, Jackson ImmunoResearch Laboratory, West Grove, PA).
Confocal microscopy
Microscopic images were taken with an Olympus IX8 DSU spinning disk confocal microscope (Melville, NY). To obtain coordinates of each islet cell, we manually scanned XYZ directions of a given islet, identified DAPI-stained nuclei, and determined corresponding cell types via endocrine hormone staining (i.e., insulin, glucagon, or somatostatin).
Determination of cellular contacts
Neighboring contacts between cells were determined based on intercellular distance and angle. Note that the neighbor determination is not trivial in soft tissues unlike regular lattices. For each cell, we defined a set of cells located within a threshold distance 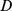 as its neighbors. Then, to discriminate some neighbors which are located close but not contacting, we measured intercellular angles between the vectors from a given vertex of each cell to its neighbors (Fig. S2). The neighbors forming narrow intercellular angles could be second-nearest neighbors. Therefore we removed those neighbors forming angles below a threshold angle
as its neighbors. Then, to discriminate some neighbors which are located close but not contacting, we measured intercellular angles between the vectors from a given vertex of each cell to its neighbors (Fig. S2). The neighbors forming narrow intercellular angles could be second-nearest neighbors. Therefore we removed those neighbors forming angles below a threshold angle  from the neighbor set of each cell. The double criteria could exclude potential errors for determining neighboring cells in large islets perhaps slightly flattened due to gravity. In practice, the mean distance between nearest nuclei can be approximated as cell diameter
from the neighbor set of each cell. The double criteria could exclude potential errors for determining neighboring cells in large islets perhaps slightly flattened due to gravity. In practice, the mean distance between nearest nuclei can be approximated as cell diameter  . In a cubic lattice (having 6 nearest neighbors) and a hexagonal close packed lattice (12 nearest neighbors), the distances to second-nearest neighbors are
. In a cubic lattice (having 6 nearest neighbors) and a hexagonal close packed lattice (12 nearest neighbors), the distances to second-nearest neighbors are 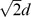 and
and  , respectively. In addition, their intercellular angles between nearest neighbors are
, respectively. In addition, their intercellular angles between nearest neighbors are 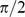 and
and 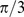 . These values could guide upper limits for
. These values could guide upper limits for 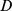 and
and  . We optimized these thresholds
. We optimized these thresholds  and
and  to obtain a reasonable neighboring number distribution (8 to 9 neighbors on average, 12 neighbors at most, and 1 neighbor at least). We have checked that our results were not sensitive to the thresholds.
to obtain a reasonable neighboring number distribution (8 to 9 neighbors on average, 12 neighbors at most, and 1 neighbor at least). We have checked that our results were not sensitive to the thresholds.
Model equilibration
The islet self-energy based on cellular attractions is
| (2) |
where 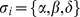 represents the cell type at the ith site,
represents the cell type at the ith site,  denotes the relative attractions between
denotes the relative attractions between 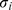 and
and 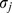 , and
, and  represents nearest neighbors of the ith site. Given cellular coordinates in an islet structure, we minimized its self-energy by exchanging positions of cells. Monte-Carlo simulation was used for the equilibration of islet structures for given cellular attractions,
represents nearest neighbors of the ith site. Given cellular coordinates in an islet structure, we minimized its self-energy by exchanging positions of cells. Monte-Carlo simulation was used for the equilibration of islet structures for given cellular attractions, 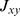 with x,
with x, [27]. We started from measured islet structures where cell positions and types were specified. Briefly, we (i) randomly distributed given numbers of
[27]. We started from measured islet structures where cell positions and types were specified. Briefly, we (i) randomly distributed given numbers of  ,
,  , and
, and  cells at the given cell coordinates in the islet; (ii) randomly chose two cells to swap, and calculated islet self-energies of
cells at the given cell coordinates in the islet; (ii) randomly chose two cells to swap, and calculated islet self-energies of 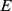 and
and  before and after exchanging their positions; (iii) accepted the exchange with the probability,
before and after exchanging their positions; (iii) accepted the exchange with the probability,  , where
, where  and
and 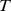 denotes thermal fluctuation, following the Metropolis algorithm [35]; and (iv) repeated these procedures in several million Monte-Carlo steps per cell to obtain an equilibrium islet structure for given cellular attractions. After equilibration, we recorded cell-to-cell contact numbers
denotes thermal fluctuation, following the Metropolis algorithm [35]; and (iv) repeated these procedures in several million Monte-Carlo steps per cell to obtain an equilibrium islet structure for given cellular attractions. After equilibration, we recorded cell-to-cell contact numbers 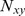 during another million Monte-Carlo steps, and calculated their mean
during another million Monte-Carlo steps, and calculated their mean 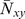 and variance
and variance  . Note that this procedure is basically the same for considering the islets having only
. Note that this procedure is basically the same for considering the islets having only  and
and 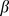 cells by ignoring
cells by ignoring  cells.
cells.
Bayesian inference of cellular attractions
Our aim is not to obtain an equilibrium structure given cellular attraction energies, but to infer these energies given an observed structure. The basic idea is to search enumerated sets of cellular attractions, 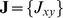 with
with  , and find the likelihood sets that can explain the observed structure (Fig. S3). Summarizing, we (i) generated a random set of
, and find the likelihood sets that can explain the observed structure (Fig. S3). Summarizing, we (i) generated a random set of  ; (ii) obtained an equilibrium structure given
; (ii) obtained an equilibrium structure given  ; (iii) calculated the mean
; (iii) calculated the mean  and the variance
and the variance 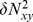 of cell-to-cell contact numbers between
of cell-to-cell contact numbers between  and
and  cell types for the equilibrium structure, as explained in the previous section; (iv) compared the equilibrium structure with the observed structure in terms of cell-to-cell contact numbers by quantifying their mismatches:
cell types for the equilibrium structure, as explained in the previous section; (iv) compared the equilibrium structure with the observed structure in terms of cell-to-cell contact numbers by quantifying their mismatches:
| (3) |
where  are the cell-to-cell contact numbers in the observed islet structures; and (v) repeated these procedures with a new set of
are the cell-to-cell contact numbers in the observed islet structures; and (v) repeated these procedures with a new set of  for several tens of thousands of trials. The likelihood of
for several tens of thousands of trials. The likelihood of  for the observed cell-to-cell contact numbers,
for the observed cell-to-cell contact numbers,  , becomes
, becomes
| (4) |
thanks to the maximum entropy principle [36]. Here the summation represents all the trials of  sets. Then, given all the trials or ensemble of
sets. Then, given all the trials or ensemble of  , we finally could infer the mean
, we finally could infer the mean 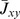 and the variance
and the variance 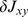 of cellular attractions for the observed islet structure:
of cellular attractions for the observed islet structure:
| (5) |
| (6) |
In order to optimize the calculation time, we choose  in a focus zone where the mismatch value
in a focus zone where the mismatch value  is not so large, instead of generating
is not so large, instead of generating 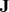 at random. For the simulation, the relative attractions
at random. For the simulation, the relative attractions  is used as unit of energy, and the fluctuation energy, which is a determinant of cell motility, is chosen large enough to escape local minimum of self-energy landscape for
is used as unit of energy, and the fluctuation energy, which is a determinant of cell motility, is chosen large enough to escape local minimum of self-energy landscape for  , but low enough not to exceed cellular attraction energies. In particular, the fluctuation energy should be clearly less than the cellular attraction energies (
, but low enough not to exceed cellular attraction energies. In particular, the fluctuation energy should be clearly less than the cellular attraction energies ( ). Otherwise, too large motility could detach cells from their aggregates under free boundary conditions. Therefore, we chose a reasonable fluctuation energy
). Otherwise, too large motility could detach cells from their aggregates under free boundary conditions. Therefore, we chose a reasonable fluctuation energy  . However, our conclusion was robust to different fluctuation energies (e.g.,
. However, our conclusion was robust to different fluctuation energies (e.g., 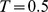 ; Table S1; Fig. S4).
; Table S1; Fig. S4).
Phase diagram of binary mixtures
Pancreatic islets could be considered as a binary mixture of  and
and  cells, the two dominant populations. In general, binary mixtures in finite systems have sorting and mixing phases depending on their composition and relative adhesion strengths between cell types. As the ratio of heterotypic attraction to homotypic attraction increases, the binary mixture has four distinct structures: complete sorting, shell-core sorting, partial mixing, and complete mixing phases [27]. We computed cell-to-cell contact numbers and their fluctuations with various β-cell fractions and relative attraction strengths for
cells, the two dominant populations. In general, binary mixtures in finite systems have sorting and mixing phases depending on their composition and relative adhesion strengths between cell types. As the ratio of heterotypic attraction to homotypic attraction increases, the binary mixture has four distinct structures: complete sorting, shell-core sorting, partial mixing, and complete mixing phases [27]. We computed cell-to-cell contact numbers and their fluctuations with various β-cell fractions and relative attraction strengths for  ,
,  , and
, and  contacts. The contact number fluctuations were peaked at the boundaries between the distinct phases (Fig. S5), representing phase transitions. Based on the fluctuations, we could identify distinct structures of the binary mixture (Fig. 6), and obtained their phase diagram. For the theoretical phase diagram, we used both cubic and HCP lattices. The lattice size was fixed to have 1357 cells for both lattices. Note that the phase diagrams were not sensitive to the lattice size within the range of islet size.
contacts. The contact number fluctuations were peaked at the boundaries between the distinct phases (Fig. S5), representing phase transitions. Based on the fluctuations, we could identify distinct structures of the binary mixture (Fig. 6), and obtained their phase diagram. For the theoretical phase diagram, we used both cubic and HCP lattices. The lattice size was fixed to have 1357 cells for both lattices. Note that the phase diagrams were not sensitive to the lattice size within the range of islet size.
Supporting Information
Relative cellular attractions and islet size. Relative attractions between cell types are inferred from three-dimensional islet structures in (A) mouse, (B) pig, and two human, (C) Human1 and (D) Human2, subjects. Islet size is represented by the total number of cells in islets. Symbols represent individual islets, and lines represent linear data fits (dotted blue). Here the linear regression analysis rejects the null hypothesis that the relative cellular attractions depend on islet size with high 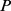 values for mouse (
values for mouse (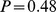 ), pig (0.87), Human1 (0.03), and Human2 (0.20).
), pig (0.87), Human1 (0.03), and Human2 (0.20).  values in the plots represent the coefficient of determination. Note that the attraction between
values in the plots represent the coefficient of determination. Note that the attraction between  cells is defined as a reference attraction,
cells is defined as a reference attraction, 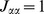 . Here thermal fluctuation energy is
. Here thermal fluctuation energy is  .
.
(TIF)
Determination of cellular contacts. Neighboring cells that contact to a given cell (cyan) are determined by cellular distance  and angle
and angle  . Sometimes second-nearest neighboring cells can be located within a threshold distance
. Sometimes second-nearest neighboring cells can be located within a threshold distance  for determining neighbors. In the diagram, nearest-neighboring (red) and second-nearest neighboring (green) cells are defined as neighbors just based on distance (
for determining neighbors. In the diagram, nearest-neighboring (red) and second-nearest neighboring (green) cells are defined as neighbors just based on distance ( ). However, once we include them, intercellular angles (
). However, once we include them, intercellular angles ( =
=  AOB) between the neighbors can be smaller than an angle threshold
AOB) between the neighbors can be smaller than an angle threshold  . The angle threshold (
. The angle threshold (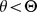 ) can be used to further discriminate neighboring cells, close to the given cell (cyan), but not contacting.
) can be used to further discriminate neighboring cells, close to the given cell (cyan), but not contacting.
(TIF)
Flow chart for model equilibration and Bayesian inference. We generate cellular attraction energies,  with
with  , which are parameters of the differential adhesion model. Then, by using Monte-Carlo simulation, we equilibrate the islet self-energy,
, which are parameters of the differential adhesion model. Then, by using Monte-Carlo simulation, we equilibrate the islet self-energy,  , given
, given 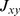 , where
, where  are the contact numbers between
are the contact numbers between  and
and 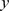 cells. After equilibration, we obtain average numbers of cellular contacts
cells. After equilibration, we obtain average numbers of cellular contacts 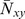 , and their fluctuations
, and their fluctuations 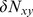 . Finally, we compute the mismatch between predicted cellular contact numbers and the measured ones,
. Finally, we compute the mismatch between predicted cellular contact numbers and the measured ones, 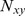 . By repeating this procedure, we can have likelihood distribution of
. By repeating this procedure, we can have likelihood distribution of  , given cellular contacts N =
, given cellular contacts N =  . This allows to estimate the likelihood
. This allows to estimate the likelihood 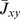 and its uncertainty
and its uncertainty 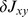 .
.
(TIF)
Cellular attractions at high thermal fluctuations. Relative attractions between cell types and their uncertainties are inferred from three-dimensional islet structures. Symbols represent individual islets: mouse (black circle), pig (blue square), and human islets (red triangle and pink inverse triangle). Each species has n = 30 islets. In particular, two sets of n = 30 islets are provided from two human (Human1 and Human2) subjects. The relationship between 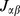 and
and  is fitted with linear functions,
is fitted with linear functions,  , represented by solid lines with colors corresponding to each species. Note that the attraction between
, represented by solid lines with colors corresponding to each species. Note that the attraction between  cells is defined as a reference attraction,
cells is defined as a reference attraction,  . Here thermal fluctuation energy is
. Here thermal fluctuation energy is  .
.
(TIF)
Cell-to-cell contact number fluctuations. The binary mixture of  cells (40%) and
cells (40%) and 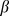 cells (60%) generates different structures depending on the relative attractions between cell types. For this plot, we fix the homotypic attractions as a reference,
cells (60%) generates different structures depending on the relative attractions between cell types. For this plot, we fix the homotypic attractions as a reference,  , and vary the heterotypic attraction
, and vary the heterotypic attraction 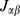 . Note that the thermal fluctuation energy is
. Note that the thermal fluctuation energy is 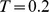 . At equilibrium, the contact numbers between cell types have fluctuations, which are peaked at the boundaries between distinct structures. Here we use (A) cubic and (B) hexagonal close packed lattices with 1357 cells.
. At equilibrium, the contact numbers between cell types have fluctuations, which are peaked at the boundaries between distinct structures. Here we use (A) cubic and (B) hexagonal close packed lattices with 1357 cells.
(TIF)
Cellular attractions at high thermal fluctuations.
(PDF)
Acknowledgments
The authors would like to acknowledge the generosity and support of Martin Jendrisak and the entire team of the Gift of Hope Organ and Tissue Donor Network in Chicago for providing the human pancreas tissues.
Data Availability
The authors confirm that all data underlying the findings are fully available without restriction. All relevant data are within the paper and its Supporting Information files.
Funding Statement
This research was supported in part by Basic Science Research Program through the National Foundation of Korea funded by the Ministry of Science, ICT & Future Planning (No. 2013R1A1A1006655) and by the Max Planck Society, the Korea Ministry of Education, Science and Technology, Gyeongsangbuk-Do and Pohang City (J.J.), the Intramural Research Program of the NIH, the National Institute of Diabetes and Digestive and Kidney Diseases (V.P.), and DK-020595 to the University of Chicago Diabetes Research and Training Center (Animal Models Core), DK-072473, AG-042151, and a gift from the Kovler Family Foundation (M.H.). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1. Metzger RJ, Klein OD, Martin GR, Krasnow MA (2008) The branching programme of mouse lung development. Nature 453: 745–750. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Steinberg MS (1963) Reconstruction of tissues by dissociated cells. Science 141: 401–408. [DOI] [PubMed] [Google Scholar]
- 3. Steinberg MS (2007) Differential adhesion in morphogenesis: a modern view. Curr Opin Genet Dev 17: 281–286. [DOI] [PubMed] [Google Scholar]
- 4. Kelly C, McClenaghan NH, Flatt PR (2011) Role of islet structure and cellular interactions in the control of insulin secretion. Islets 3: 41–47. [DOI] [PubMed] [Google Scholar]
- 5. Bonner-Weir S, O'Brien T (2008) Islets in type 2 diabetes: in honor of dr. robert c. turner. Diabetes 57: 2899–2904. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Brissova M, Fowler MJ, Nicholson WE, Chu A, Hirshberg B, et al. (2005) Assessment of human pancreatic islet architecture and composition by laser scanning confocal microscopy. J Histochem Cytochem 53: 1087–1097. [DOI] [PubMed] [Google Scholar]
- 7. Cabrera O, Berman DM, Kenyon NS, Ricordi C, Berggren PO, et al. (2006) The unique cytoarchitecture of human pancreatic islets has implications for islet cell function. Proc Natl Acad Sci USA 103: 2334–2339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Orci L (1976) The microanatomy of the islets of langerhans. Metabolism 25: 1303–1313. [DOI] [PubMed] [Google Scholar]
- 9. Erlandsen SL, Hegre OD, Parsons JA, McEvoy RC, Elde RP (1976) Pancreatic islet cell hormones distribution of cell types in the islet and evidence for the presence of somatostatin and gastrin within the d cell. J Histochem Cytochem 24: 883–897. [DOI] [PubMed] [Google Scholar]
- 10. Grube D, Deckert I, Speck PT, Wagner HJ (1983) Immunohistochemistry and microanatomy of the islets of langerhans. Biomed Res 4: 25–36. [Google Scholar]
- 11. Bosco D, Armanet M, Morel P, Niclauss N, Sgroi A, et al. (2010) Unique arrangement of α- and β-cells in human islets of langerhans. Diabetes 59: 1202–1210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Halban PA, Powers SL, George KL, Bonner-Weir S (1987) Spontaneous reassociation of dispersed adult rat pancreatic islet cells into aggregates with three-dimensional architecture typical of native islets. Diabetes 36: 783–790. [DOI] [PubMed] [Google Scholar]
- 13. Hopcroft DW, Mason DR, Scott RS (1985) Insulin secretion from perifused rat pancreatic pseudoislets. In Vitro Cell Dev Biol 21: 421–427. [DOI] [PubMed] [Google Scholar]
- 14. Britt LD, Stojeba PC, Scharp CR, Greider MH, Scharp DW (1981) Neonatal pig psedu-islets: a product of selective aggregation. Diabetes 30: 580–583. [DOI] [PubMed] [Google Scholar]
- 15. Kuo CY, Herrod HG, Burghen GA (1992) Formation of pseudoislets from human pancreatic cultures. Pancreas 7: 320–325. [DOI] [PubMed] [Google Scholar]
- 16. Halban PA, Powers SL, George KL, Bonner-Weir S (1988) Altered differentiated cell surface properties of transformed (rinm5f) compared with native adult rat pancreatic b cells. Endocrinology 123: 113–119. [DOI] [PubMed] [Google Scholar]
- 17. Rouiller DG, Cirulli V, Halban PA (1990) Differences in aggregation properties and levels of the neural cell adhesion molecule (ncam) between islet cell types. Exp Cell Res 1917: 305–312. [DOI] [PubMed] [Google Scholar]
- 18. Rouiller DG, Cirulli V, Halban PA (1991) Uvomorulin mediates calcium-dependent aggregation of islet cells, whereas calcium-independent cell adhesion molecules distinguish between islet cell types. Dev Biol 148: 233–242. [DOI] [PubMed] [Google Scholar]
- 19. Cirulli V, Baetens D, Rutishauser U, Halban PA, Orci L, et al. (1994) Expression of neural cell adhesion molecule (n-cam) in rat islets and its role in islet cell type segregation. J Cell Sci 107: 1429–1436. [DOI] [PubMed] [Google Scholar]
- 20. Jia D, Dajusta D, Foty RA (2007) Tissue surface tensions guide in vitro self-assembly of rodent pancreatic islet cells. Dev Dyn 236: 2039–2049. [DOI] [PubMed] [Google Scholar]
- 21. Brelje TC, Scharp DW, Sorenson RL (1989) Three-dimensional imaging of intact isolated islets of langerhans with confocal microscopy. Diabetes 38: 808–814. [DOI] [PubMed] [Google Scholar]
- 22. Kim A, Miller K, Jo J, Kilimnik G, Wojcik P, et al. (2009) Islet architecture: a comparative study. Islets 1: 129–136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Kilimnik G, Zhao B, Jo J, Periwal V, Witkowski P, et al. (2011) Altered islet composition and disproportionate loss of large islets in patients with type 2 diabetes. PLoS ONE 6: e27445. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Slack JMW (1995) Developmental biology of the pancreas. Development 121: 1569–1580. [DOI] [PubMed] [Google Scholar]
- 25. Edlund H (2002) Pancreatic organogenesis – developmental mechanisms and implications for therapy. Nat Rev Genet 3: 524–532. [DOI] [PubMed] [Google Scholar]
- 26. Gumbiner BM (1996) Cell adhesion: the molecular basis of tissue architecture and morphogenesis. Cell 84: 345–357. [DOI] [PubMed] [Google Scholar]
- 27. Hoang DT, Song J, Jo J (2013) Partial mixing phase of binary cells in finite systems. Phys Rev E 88: 062725. [DOI] [PubMed] [Google Scholar]
- 28. Butcher EC, Picker LJ (1996) Lymphocyte homing and homeostasis. Science 272: 60–66. [DOI] [PubMed] [Google Scholar]
- 29. Mebius RE (2003) Organogenesis of lymphoid tissues. Nat Rev Immunol 3: 292–303. [DOI] [PubMed] [Google Scholar]
- 30. Jamal AM, Lipsett M, Sladek R, Laganière S, Hanley S, et al. (2005) Morphogenetic plasticity of adult human pancreatic islets of langerhans. Cell Death Differ 12: 702–712. [DOI] [PubMed] [Google Scholar]
- 31. Steiner DJ, Kim A, Miller K, Hara M (2010) Pancreatic islet plasticity: interspecies comparison of islet architecture and composition. Islets 2: 135–145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Charollais A, Gjinovci A, Huarte J, Bauquis J, Nadal A, et al. (2000) Junctional communication of pancreatic β cells contributes to the control of insulin secretion and glucose tolerance. J Clin Invest 106: 235–243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Jo J, Choi MY, Koh DS (2009) Beneficial effects of intercellular interactions between pancreatic islet cells in blood glucose regulation. J Theor Biol 257: 312–319. [DOI] [PubMed] [Google Scholar]
- 34. Hong H, Jo J, Sin SJ (2013) Stable and flexible system for glucose homeostasis. Phys Rev E 88: 032711. [DOI] [PubMed] [Google Scholar]
- 35. Metropolis N, Ulam S (1949) The monte carlo method. J Am Statist Assoc 44: 335–341. [DOI] [PubMed] [Google Scholar]
- 36.Sivia DS, Skilling J (2006) Data Anlysis - A Bayesian Tutorial. Oxford University Press.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Relative cellular attractions and islet size. Relative attractions between cell types are inferred from three-dimensional islet structures in (A) mouse, (B) pig, and two human, (C) Human1 and (D) Human2, subjects. Islet size is represented by the total number of cells in islets. Symbols represent individual islets, and lines represent linear data fits (dotted blue). Here the linear regression analysis rejects the null hypothesis that the relative cellular attractions depend on islet size with high 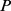 values for mouse (
values for mouse (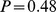 ), pig (0.87), Human1 (0.03), and Human2 (0.20).
), pig (0.87), Human1 (0.03), and Human2 (0.20).  values in the plots represent the coefficient of determination. Note that the attraction between
values in the plots represent the coefficient of determination. Note that the attraction between  cells is defined as a reference attraction,
cells is defined as a reference attraction, 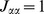 . Here thermal fluctuation energy is
. Here thermal fluctuation energy is  .
.
(TIF)
Determination of cellular contacts. Neighboring cells that contact to a given cell (cyan) are determined by cellular distance  and angle
and angle  . Sometimes second-nearest neighboring cells can be located within a threshold distance
. Sometimes second-nearest neighboring cells can be located within a threshold distance  for determining neighbors. In the diagram, nearest-neighboring (red) and second-nearest neighboring (green) cells are defined as neighbors just based on distance (
for determining neighbors. In the diagram, nearest-neighboring (red) and second-nearest neighboring (green) cells are defined as neighbors just based on distance ( ). However, once we include them, intercellular angles (
). However, once we include them, intercellular angles ( =
=  AOB) between the neighbors can be smaller than an angle threshold
AOB) between the neighbors can be smaller than an angle threshold  . The angle threshold (
. The angle threshold (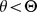 ) can be used to further discriminate neighboring cells, close to the given cell (cyan), but not contacting.
) can be used to further discriminate neighboring cells, close to the given cell (cyan), but not contacting.
(TIF)
Flow chart for model equilibration and Bayesian inference. We generate cellular attraction energies,  with
with  , which are parameters of the differential adhesion model. Then, by using Monte-Carlo simulation, we equilibrate the islet self-energy,
, which are parameters of the differential adhesion model. Then, by using Monte-Carlo simulation, we equilibrate the islet self-energy,  , given
, given 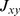 , where
, where  are the contact numbers between
are the contact numbers between  and
and 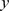 cells. After equilibration, we obtain average numbers of cellular contacts
cells. After equilibration, we obtain average numbers of cellular contacts 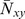 , and their fluctuations
, and their fluctuations 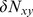 . Finally, we compute the mismatch between predicted cellular contact numbers and the measured ones,
. Finally, we compute the mismatch between predicted cellular contact numbers and the measured ones, 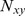 . By repeating this procedure, we can have likelihood distribution of
. By repeating this procedure, we can have likelihood distribution of  , given cellular contacts N =
, given cellular contacts N =  . This allows to estimate the likelihood
. This allows to estimate the likelihood 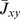 and its uncertainty
and its uncertainty 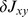 .
.
(TIF)
Cellular attractions at high thermal fluctuations. Relative attractions between cell types and their uncertainties are inferred from three-dimensional islet structures. Symbols represent individual islets: mouse (black circle), pig (blue square), and human islets (red triangle and pink inverse triangle). Each species has n = 30 islets. In particular, two sets of n = 30 islets are provided from two human (Human1 and Human2) subjects. The relationship between 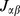 and
and  is fitted with linear functions,
is fitted with linear functions,  , represented by solid lines with colors corresponding to each species. Note that the attraction between
, represented by solid lines with colors corresponding to each species. Note that the attraction between  cells is defined as a reference attraction,
cells is defined as a reference attraction,  . Here thermal fluctuation energy is
. Here thermal fluctuation energy is  .
.
(TIF)
Cell-to-cell contact number fluctuations. The binary mixture of  cells (40%) and
cells (40%) and 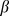 cells (60%) generates different structures depending on the relative attractions between cell types. For this plot, we fix the homotypic attractions as a reference,
cells (60%) generates different structures depending on the relative attractions between cell types. For this plot, we fix the homotypic attractions as a reference,  , and vary the heterotypic attraction
, and vary the heterotypic attraction 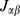 . Note that the thermal fluctuation energy is
. Note that the thermal fluctuation energy is 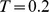 . At equilibrium, the contact numbers between cell types have fluctuations, which are peaked at the boundaries between distinct structures. Here we use (A) cubic and (B) hexagonal close packed lattices with 1357 cells.
. At equilibrium, the contact numbers between cell types have fluctuations, which are peaked at the boundaries between distinct structures. Here we use (A) cubic and (B) hexagonal close packed lattices with 1357 cells.
(TIF)
Cellular attractions at high thermal fluctuations.
(PDF)
Data Availability Statement
The authors confirm that all data underlying the findings are fully available without restriction. All relevant data are within the paper and its Supporting Information files.