GneimoSim: A Modular Internal Coordinates Molecular Dynamics Simulation Package

Abstract

The Generalized Newton Euler Inverse Mass Operator (GNEIMO) method is an advanced method for internal coordinates molecular dynamics (ICMD). GNEIMO includes several theoretical and algorithmic advancements that address longstanding challenges with ICMD simulations. In this paper we describe the GneimoSim ICMD software package that implements the GNEIMO method. We believe that GneimoSim is the first software package to include advanced features such as the equipartition principle derived for internal coordinates, and a method for including the Fixman potential to eliminate systematic statistical biases introduced by the use of hard constraints. Moreover, by design, GneimoSim is extensible and can be easily interfaced with third party force field packages for ICMD simulations. Currently, GneimoSim includes interfaces to LAMMPS, OpenMM, Rosetta force field calculation packages. The availability of a comprehensive Python interface to the underlying C++ classes and their methods provides a powerful and versatile mechanism for users to develop simulation scripts to configure the simulation and control the simulation flow. GneimoSim has been used extensively for studying the dynamics of protein structures, refinement of protein homology models, and for simulating large scale protein conformational changes with enhanced sampling methods. GneimoSim is not limited to proteins and can also be used for the simulation of polymeric materials.

1 Introduction

Molecular dynamics (MD) simulations are commonly used for studying the dynamics of proteins, protein structure prediction, and calculating thermodynamic properties such as free energy, enthalpy and entropy of conformational states of proteins.^1,2 All-atom MD simulations, also known as Cartesian MD simulations, are a classical mechanics based method routinely used for calculating statistical and thermodynamic properties of proteins. One of the attractive features of all-atom MD is its use of absolute coordinates and the resulting simplicity of the dynamics model. However, this simplicity suffers when constraints and/or bias potentials are added to increase the time-step size and/or sample large-scale conformational changes. The addition of hard constraints requires differential-algebraic equation (DAE) solvers that adversely impact simulation robustness and complexity.

The alternative Bond, Angle, Torsion (BAT) relative coordinates are more natural than Cartesian coordinates for describing the bonded structure of a protein. MD simulations in BAT coordinates are referred to as internal coordinate MD (ICMD) methods. In the ICMD model of a protein, the high frequency bond length degrees of freedom, can be constrained by simply excluding them from the model.^3–6 Not only are the resulting ICMD models of smaller dimension, but they also retain the simpler structure of ordinary differential equations (ODE) instead of the more complex DAE structure required for constrained Cartesian models. One such ICMD model is the well-known Torsional MD (TMD) model, where bond length and bond angle coordinates are frozen, and only the torsional degrees of freedom are free.^3–6 ICMD models provide a large range of options for selecting and controlling the granularity of the dynamics model of the system.^7,8 Also, in ICMD models, the six translation and orientation degrees of freedom for a molecule are explicit coordinates rather than implicit as in Cartesian models. TMD models in particular, offer additional advantages: 1) the low-frequency torsional coordinates allow larger time steps for integrating the equations of motion; 2) conformational search in the low frequency torsional degrees of freedom lead to significant conformational changes;^7,9–14 3) enhanced sampling methods are more effective when performed in torsional space.^14,15

The ability of ICMD simulation methods to control the granularity of the dynamics model makes them suitable for the development of multi-scale methods and strategies for the simulation of protein macromolecular complexes. Due to the coupled nature of the ICMD coordinates, and the higher complexity of ICMD models, solving the equations of motions for the ICMD models requires far more sophisticated mathematical techniques and algorithms.¹⁶ Thus, long standing challenges in the ICMD methods are:

1. the strong coupling among the BAT coordinates in ICMD models leads to increased analytical complexity of the dynamics model.¹⁷

2. increased computational cost of the dynamics solution, which grows cubically with the number of degrees of freedom,^5,18 limits the scalability of ICMD to larger systems.

3. the rigidity introduced by freezing degrees of freedom affects the transition barriers and probability density function of various conformational states in a protein. Although Fixman proposed a compensating potential that rigorously corrects for this bias in the probability density functions,¹⁹ it has been far too complex to compute for even moderate sized molecules, and its use has been limited to small idealized molecules^20,21

4. availability of ICMD software and application examples is very limited.

We have made significant advances in rigorously addressing these longstanding hurdles to develop the Generalized Newton-Euler Inverse Mass Operator (GNEIMO) ICMD method⁵ using a wealth of mathematical theory and analyses from the Spatial Operator Algebra (SOA) methodology¹⁶ originally developed for spacecraft and robot dynamics applications.

In this paper we describe the GneimoSim ICMD software package^* that implements the GNEIMO method. We believe that GneimoSim represents the first comprehensive ICMD simulation package that includes several advanced features not available elsewhere. Moreover, GneimoSim's modular, extensible and user-friendly design is based on software architectural features that allow its versatile use for a variety of biomolecular simulations. We begin with an overview of the recent advances in the GNEIMO method in Section 1.1 before describing the GneimoSim software architecture and design.

1.1 The GNEIMO ICMD method

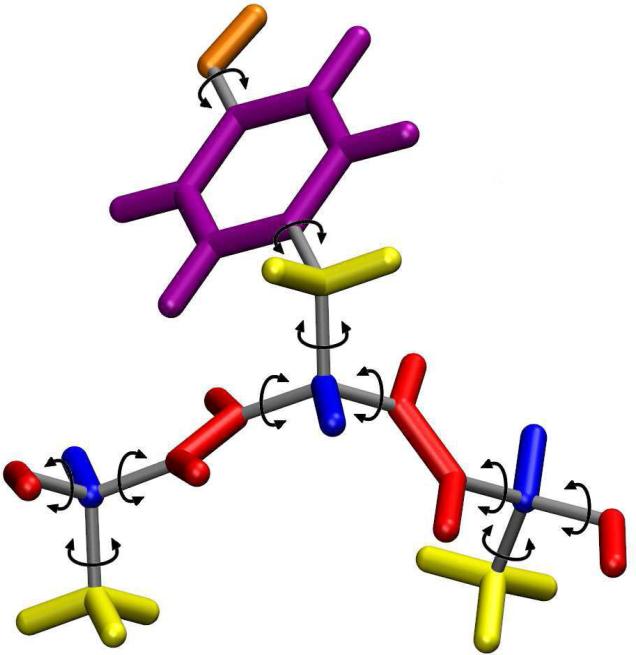
In the GNEIMO ICMD model, each molecule is modeled as a collection of rigid bodies (termed clusters) connected by one to six degrees of freedom hinges. A cluster is a group of atoms that move as a rigid unit in the molecule. it can consist of a single atom, a methyl group, a phenyl ring, an alpha helix, or even an entire domain of a protein (see Figure 1). Different choices for clusters allow users to control the granularity of the ICMD model. A hinge can have one (TMD) to six degrees of freedom, and the hinges connecting the clusters can also be frozen or thawed during a simulation to decrease or increase the total number of degrees of freedom. The default clustering removes the high frequency modes of motion, leaving the relatively low force torsion terms of the force field to act upon the model to allow longer time steps.

Figure 1.

The default clustering scheme used in GneimoSim is shown for an alanine-tyrosine-alanine section of a protein. Sections of a single color represent a rigid cluster whose atoms move together as a single unit. The gray rods and arrows represent hinges connecting two clusters.

GNEIMO includes several theoretical and algorithmic advancements that address the previously listed challenges with the ICMD method. Some of these are:

1. The SOA-based GNEIMO ICMD algorithm has been the first to overcome the computational cost bottleneck of solving the ICMD equations of motion by reducing costs to being just linearly, instead of cubically proportional to the number of degrees of freedom.^5,18 This low cost algorithm has been adopted by other groups to implement torsional MD capability.^11,22–25 The GNEIMO method also includes extensions to the SOA dynamics theory and algorithms based on graph theory ideas that generalize the mass matrix factorization^26,27 results for the low-cost recursive solution of the ICMD equations of motion.²⁶

2. GNEIMO uses a new equipartition principle¹⁷ that generalizes the classical equipartition principle to ICMD models. This forms the basis for new “modal velocity coordinates” that provide a rigorous method for the thermodynamically correct initialization of velocities in ICMD simulations.⁸

3. GNEIMO includes a low-cost and general purpose SOA-based algorithm for including the Fixman correction potential^28,29 for bias-free ICMD simulations. Our studies verify that, as predicted, the inclusion of the Fixman potential recovers the equilibrium probability density function of the conformational states, the transition barrier crossing rates, and the free energy surface for general serial and branched polymers when used without forcefields.²⁹

4. The GNEIMO ICMD methods have been expanded beyond TMD to allow freeing up of bond angle degrees of freedom. These hybrid ICMD models reduce the rigidity encountered with TMD models.

The GNEIMO method is scalable for large systems and we have tested it on proteins with 40 to 300 residues for long time scale dynamics (500ns to 1 microseconds each). We have demonstrated the benefits of the GNEIMO ICMD method for protein dynamics applications that start from protein crystal structures.⁸ We have used GNEIMO for protein homology model refinement for 7 small proteins,¹² and 30 CASP8 and CASP9 target proteins.¹³ In contrast with all-atom MD simulations used for protein model refinement,^30–32 the GNEIMO method refines homology models up to 1.5 Å without requiring the use of additional restraints from experimental data. Using temperature based replica exchange (REMD) in GNEIMO, we have also demonstrated enhanced conformational sampling allowing sampling of conformational transitions in highly flexible proteins such as calmodulin and fasciculin.¹⁴ The GNEIMO-REMD method has also been used for ab initio folding of simple proteins.^7,8

2 The GneimoSim ICMD Software

GneimoSim is a comprehensive ICMD software package designed for applications such as protein structural dynamics, protein homology model refinement, domain motion studies in proteins, protein folding etc. Our approach in developing GneimoSim has been to focus on implementing high-quality ICMD algorithms and methods, and leverage (rather than re-implement) the widely used and well-developed family of forcefield, solvation and other enhanced sampling software modules available from the MD community. GneimoSim includes several important and useful algorithms and methods in addition to the advances mentioned earlier:

1. The extension of the Nosé-Hoover NVT method for ICMD is available in GneimoSim.^7,8,18

2. GneimoSim allows the use of several integrators including Runge-Kutta, Lobatto, adaptive CVODE, and Verlet integrators for stable long timescale (microseconds) simulations.^7,8,14 Stability and Hamiltonian conservation has been verified for 40 proteins ranging in size from 30 to 300 residues.

3. The Replica Exchange MD (REMD) algorithm³³ has been integrated within GneimoSim for enhanced sampling.^12–14

4. Accelerated MD (aMD)³⁴ method has also been added as an alternative method for enhanced sampling.

5. Langevin dynamics³⁵ is also available in GneimoSim.

6. The Generalized Born Solvation (GBSA) module obtained from Simbios³⁶ has been added. Periodic boundary conditions for use with explicit solvent simulations are also supported.⁸

An important factor that influenced our GneimoSim design was the need to support a variety of run-time simulation settings required for protein dynamics studies. Meeting this objective has required a versatile architecture that provides the user with a high degree of control in configuring simulation modules as well as the simulation execution loop to best meet study objectives. Illustrative examples of various simulation scenarios possible using GneimoSim are described in more detail in Section 4. Section 6 describes scientific application studies that have been carried out using GneimoSim.

In keeping with the architectural flexibility goals, GneimoSim allows the integration and use of external modules such as established forcefields as well as custom ones developed by users. The current version of GneimoSim software interfaces with forcefield engines such as OpenMM, LAMMPS, and Rosetta and can thus be used with atomic forcefields such as AMBER, CHARMM and Rosetta. GneimoSim's Python language interface allows users to choose among several different methods and options to configure a large variety of simulations.

2.1 GneimoSim's Architecture

The extensible architecture of GneimoSim allows users to integrate and use third party force-fields, solvent models, integrators and data logging modules within GneimoSim. Key features of GneimoSim's design are:

Modularity

GneimoSim's object-oriented, open and modular architecture is based on a functional decomposition of the ICMD problem, that allows for the mixing and matching of different implementations of component modules to meet the required simulation needs. For example, it is possible to select between different all-atom forcefield implementations for the simulations.

Extensibility

It is easy to interface GneimoSim with third party software without requiring their re-implementation within GneimoSim. This has the advantage of simplifying the incorporation of new third party module versions and improvements without requiring changes to GneimoSim. For example, the OpenMM³⁶ and Rosetta³⁷ forcefield modules have been interfaced with the GneimoSim software. Any updated versions of these packages can be readily integrated into GneimoSim. Other forcefields such as coarse grain forcefield modules can also be added without having to modify the GneimoSim software.

Configurability

While the core of GneimoSim is implemented in C++ to maximize computational speed, a comprehensive Python language interface to the C++ classes and their methods is available. The Python interface provides a powerful avenue for users to configure simulations by selecting among the dynamics ensembles, enhanced sampling methods, integrators and forcefields variants. Users can take advantage of Python's full language capabilities to create simulation loops with sophisticated conditionals and simulation staging. Moreover, additional Python modules can be created by users to extend GneimoSim's functionality. Usage of a full-featured language such as Python also avoids the limited functionality and fragility associated with custom interfaces often found in MD tools.

Computational Speed

At the core of the GneimoSim software is the Dynamics Algorithms for Real Time Simulation (DARTS) module³⁸ which is an SOA-based high performance multibody dynamics solver. DARTS contains an implementation of SOA's linear cost algorithm for solving the ICMD equations of motion.⁵ GneimoSim contains interfaces to DARTS for ICMD specific computations that range from statistically rigorous velocity initialization,¹⁷ ICMD equations of motion solution, NVT dynamics adaptations^7,18 and Fixman torque computations.^28,29

2.2 Functional Decomposition

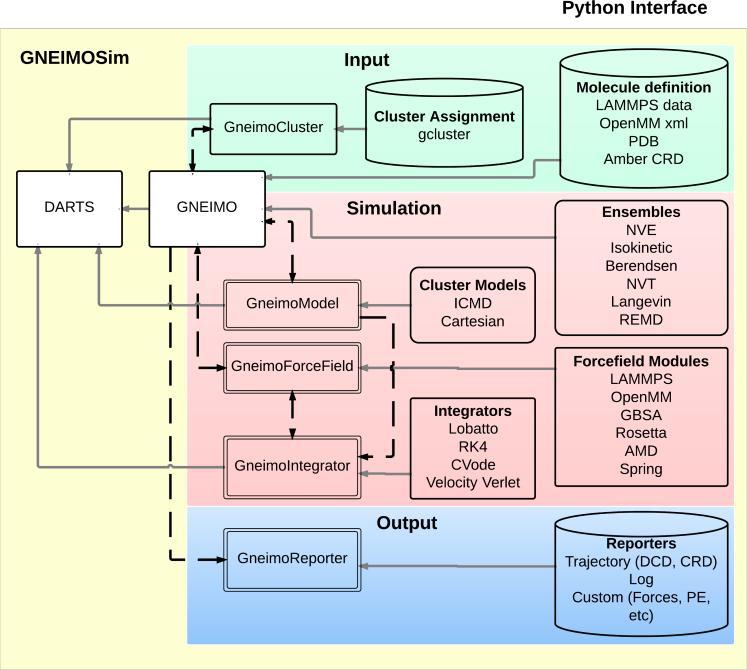
As illustrated in Figure 2, the GneimoSim design is based on a functional decomposition of ICMD simulation capability into components that support simulation, input, output, and a variety of ICMD modeling and run-time options. The input components process data files to initialize or restart a simulation. The simulation components consist of a hierarchy of classes and functions that handle the simulation run-time, while the output components support the recording of data generated by a simulation for post-analysis by the user. The organization of GneimoSim into such functional components gives users a high level of control in configuring simulations.

Figure 2.

GneimoSim Software Functional Decomposition. The GneimoSim software functional components are organized within input (green), simulation (red), and output (blue) categories. The data flow (dashed black arrows) between these components is primarily handled by the manager Gneimo class. Some of these functional components are based on abstract classes (double boundary lines) that are specialized into alternative functional implementations. Class inheritance is indicated by the solid gray arrows. GneimoSim uses the ICMD dynamics model and the SOA-based computational algorithms from the DARTS computational engine.

GneimoSim's class hierarchy has been designed to facilitate extension of the software. At the heart of the package are the following base classes that establish GneimoSim's functional interfaces:

Gneimo

This is the top level simulation class that manages the simulation run. It is instantiated with data that defines the ICMD molecular model, and various options to configure the simulation run. A Gneimo instance has methods to run, load and save a simulation. Section 2.3 describes this class in more detail.

GneimoModel

The GneimoModel class defines the clustering ICMD model of the molecule to be used for the simulation. The model options consist of either the ICMD (internal coordinates) model or a Cartesian model. The latter allows for comparison with runs from other Cartesian coordinates-based MD packages. Section 3.1 describes this class in more detail.

GneimoIntegrator

The GneimoIntegrator class is the base class for the numerical integrators supported by GneimoSim. The integrator can be chosen from among the native implementations, as well as the third party CVODE integrator from the SUNDIALS package.³⁹ Section 3.5 describes this class in more detail.

GneimoForceField

The GneimoForceField class serves as the base class for force-fields used during a simulation. The basic function of a forcefield instance is to compute the net force acting on each atom given the current model coordinates. The integrator queries these forces as needed to determine the accelerations of the atoms in the GneimoModel instance during dynamics steps. Specializations of this class provide interfaces to different forcefield implementations. The GneimoForceField instance for each of the available force fields is typically instantiated with a file in the native format for the forcefield. Preparation scripts to create these files are included in GneimoSim. Section 3.2 describes this class in more detail. Multiple forcefields can be instanced and used in a simulation.

GneimoReporter

Classes derived from the GneimoReporter class record the data generated by simulations. Commonly used reporters are ones for logging Cartesian coordinates, dihedral velocities and energies from simulation trajectories. Reporters can also log the state of a subsystem or diagnostic data such as forces within the ICMD model. Section 3.7 describes this class in more detail.

2.3 The Gneimo Simulation Manager Class

The Gneimo class is the simulation manager class and entry point for a GneimoSim simulation. The creation of a new Gneimo instance requires files describing the masses and number of atoms (system), the starting coordinates for the atoms (coords), the topology of the molecule, and the ICMD clusters. Other options to the Gneimo constructor select the model type, the integrator, and the type of simulation ensemble. The Gneimo instance has methods to add forcefield(s), turn on and off various features, initialize the temperature, and run the simulation for a number of steps.

2.4 DARTS ICMD Dynamics Solver

The DARTS ICMD dynamics solver module contains the ICMD model and the SOA-based computational algorithms for it. The Gneimo simulation manager class uses the DARTS algorithms for solving the ICMD equations of motion, the computation of the kinetic energy, the bath dynamics terms for the NVT ensemble, and the Fixman potential and torque computations. The ICMD equations of motion solver within DARTS is based on a recursive algorithm whose computational cost grows linearly with the number of degrees of freedom in the ICMD model.⁵ The algorithm is structured to allow the freezing and thawing of individual degrees of freedom during a simulation to adjust the granularity of the ICMD model. DARTS also contains the algorithms for initialization of velocities based on the equipartition principle for systems subject to constraints.¹⁷

To compensate for the systematic biases in the statistical properties caused by the rigidity in the ICMD simulations, Fixman proposed a compensating potential¹⁹ that is dependent on the mass matrix of the constrained system. Fixman potential also induces additional torques at the hinges, but due to its complexity has remained a bottleneck for computations even for simple molecules. We have implemented a computationally efficient SOA based algorithm for calculating the Fixman compensating potential and the associated torque for general branched molecules.^28,29 The GNEIMO-Fixman method can be used for polymer systems of arbitrary size. It is noteworthy that the GNEIMO-Fixman algorithm uses several terms available from the DARTS dynamics solver, and hence including the Fixman correction has only a modest impact on the overall computational cost. The GNEIMO-Fixman method has been validated and tested for both serial chain and branched polymer systems.²⁹ The GNEIMO-Fixman method is available within GneimoSim and can be enabled by specifying an option to the Gneimo simulation manager instance.

3 GneimoSim Configuration Options

As described earlier, the functional organization of GneimoSim includes a family of abstract base classes that can be specialized to develop extensions for use with GneimoSim. In this section we describe these base classes, the currently available extensions, as well as other built-in configuration options for GneimoSim.

3.1 ICMD Models and Clustering

A GneimoModel class instance defines an ICMD molecular model consisting of clusters of atoms connected by hinges. A cluster is a group of atoms moving as a rigid unit in a molecule and can consist of a single atom, a group of atoms such as an alpha helix, or even an entire domain of a protein. The internal positioning of the atoms in a cluster is set after conjugate gradient minimization of the protein structure during the structure preparation step. This sets the harmonic bond lengths and bond angles to the equilibrium values. Proline rings are currently handled as open tree structures where the ring is broken into clusters and not kept rigid as a whole. A hinge describes the relative motion between two adjacent clusters. In GneimoSim's Cartesian model, each atom is its own cluster, thus providing a convenient method for performing all-atom MD simulations within GneimoSim. The possible ICMD models thus span the range of all-atom Cartesian dynamics models, to torsional dynamics models, for simulations ranging from all-atom to torsional MD.

The default ICMD cluster model data file is generated by GneimoSim utilities to define clusters for a torsional dynamics model with all bond lengths and bond angles frozen. This cluster model data file is generated automatically by a script from an input PDB file. This data file can be modified by the user to change the cluster definition so that even whole domains of proteins can be rigidly frozen in order to sample torsion angles connecting two domains. The ability to make different clustering choices is useful for multi scale simulations. The hinges connecting clusters can also be frozen and thawed at any time during a simulation. We refer to this scheme as dynamic clustering. Dynamics clustering allows the user to remove and add torsional degrees of freedom as needed during the simulation based on user defined protocols. An example of its use is during a protein folding simulation. When using TMD with REMD, one can freeze the backbone torsions of amino acids that form a helical turn as a folding nucleus of a secondary structure motif at high temperature replicas, and thaw these motifs to allow the secondary structure growth at lower temperature replicas.

It has been shown that freeing up certain bond angles within the TMD model is important for a more accurate representation of protein structure.⁴⁰ For instance, relaxing of backbone angles has been shown to be important for protein structure dynamics.^41,42 GneimoSim supports the ICMD model where any desired or all the bond angles can be freed up in simulation runs. Simulating multiple chains is supported as required for proteins with multiple subunits and explicit water. We have cross-validated GneimoSim's all-atom simulations against corresponding all-atom simulations with the LAMMPS and OpenMM packages.

3.2 Force Field Modules

The GneimoForceField class serves as the base class for Cartesian all-atom forcefield modules within GneimoSim. The integration of a forcefield package into GneimoSim is carried out by creating an interface class derived from the GneimoForceField class whose methods transfer the coordinates and forces data between the Gneimo simulation manager and the forcefield module. Thus, the integration of third-party packages does not require modifications to the GneimoSim software. This also simplifies updating to newer versions of forcefield software packages. GneimoSim supplies atom coordinates and forcefield parameters to force-field modules, which in turn calculate the forces on each atom and pass these values back to GneimoSim.

Currently, GneimoSim contains interfaces to standard forcefield packages such as LAMMPS, OpenMM, and Rosetta that can be selected and used within simulations.

The interface classes for the currently available forcefields are as follows:

GneimoForceFieldLammps

This forcefield allows the use of forcefields from the LAMMPS software package.⁴³ This forcefield module is the fastest CPU implementation we have used. Users can select between the standard parameters for the Amber⁴⁴ and CHARMM⁴⁵ forcefields.

GneimoForceFieldLammpsGBSA

This forcefield is a CPU implementation of a Generalized Born Solvent model and is designed to work with the GneimoForceFieldLammps forcefield module.

GneimoForceFieldOpenMM

This forcefield allows the use of forcefields from the OpenMM software package. For users with CUDA-capable GPUs, the OpenMM forcefield computation module is recommended. Our testing has shown significant speedup of force calculations compared to CPU versions of forcefields.³⁶ The OpenMM forcefield comes with an implementation of GBSA.

GneimoForceFieldRosetta

This class allows the use of the Rosetta forcefield. The Rosetta forcefield is based on the Rosetta energy function⁴⁶ which has been shown to be a good predictor of native protein structures. The Rosetta forcefield module can be used within GneimoSim for protein structure prediction and refinement of protein homology models using ICMD methods.¹²

GneimoForceFieldSpring

This forcefield class implements a custom harmonic potential through which user defined constraints can be applied between any pair of atoms. This restraint potential is useful for imposing NOE restraints when refining a protein homology model and applying a harmonic restraint for steered dynamics.

GneimoForceFieldLangevin

This forcefield class provides the temperature-dependent random forces required for Langevin dynamics simulations.

Using these forcefield extensions, ICMD simulation can be carried out with the AMBER99SB, CHARMM, and Rosetta forcefields. GneimoSim also provides the ability to create custom forcefield modules for adding specialized constraint forces to simulations.

During simulation setup, instances of the desired forcefield class are created and registered with the Gneimo simulation manager instance. All registered forcefields are processed during the simulation. Thus more than one forcefield can be used by creating their instances and registering them with the simulation manager. User specified weights are used to combine the forces generated from the forcefield modules. An example of the use of multiple force-fields is the combination of GneimoForceFieldLammps and GneimoForceFieldLammpsGBSA forcefields, with the latter adding implicit solvent contributions to the all-atom forcefield.

3.3 Solvent Model

GneimoSim provides the ability to use the Generalized Born Solvation implicit solvation method as well as explicit solvent models. As described earlier, the Generalized Born Solvation implicit solvation method model can be used via the GneimoForceFieldLammpsGBSA forcefield class which adds implicit solvent contributions to the all-atom forcefield.

The explicit solvation model can be used with both the LAMMPS and OpenMM forcefield modules. Water molecules for an explicit water model in GneimoSim are treated as individual 3-atom rigid-body cluster bodies in ICMD mode, with forcefield parameters from a common force field, such as Amber. This information is input through the cluster file. GneimoSim interfaces with the forcefield module to provide the Ewald summation method and the correct periodic boundary conditions to wrap the atoms around the periodic box. Long range forces are calculated by providing the relevant parameters to the forcefield modules.

3.4 Ensembles

We have included several types of simulation ensembles in the GneimoSim software. The mathematical methods for the ICMD microcanonical ensemble (NVE) and canonical Nosé-Hoover(NVT) ensemble included in GneimoSim have been described in previous works.^18,47 GneimoSim also includes an implementation of the Berendsen thermostat⁴⁸ and the option to use Langevin dynamics³⁵ for constant temperature dynamics simulations. Selecting between the different ensemble options within GneimoSim is done by using the Gneimo class methods such as runNVE or runNoseHoover as described in Section 4.

3.5 Integrators

The GneimoSim code includes several numerical integrators. The implementation details and accuracy of the fixed time step integrators such as Lobatto, and Runge-Kutta 4 (RK4) have been described in our previous publication.⁸ We have also added a Brünger-Brooks-Karplus (BBK) integrator for Langevin dynamics simulations⁴⁹ to be used in conjunction with the GneimoForceFieldLangevin forcefield class. The CVODE⁵⁰ adaptive time step integrator in GneimoSim is the most suitable integrator for performing stable long time scale TMD simulations. We have tested the stability of this integrator in folding small proteins.⁸

3.6 Enhanced Sampling Methods

One of the main challenges for any MD simulation is the presence of energy barriers that hamper conformational transitions and effective sampling. We have implemented some of the well known algorithms for enhancing conformation sampling in GneimoSim. One such method is the REMD method.³³ REMD is a powerful method for enhancing sampling by allowing the system to escape potential energy barriers by adding replicas at higher temperatures. We have verified the benefits of applying REMD in combination with TMD for some challenging applications^7,8,14 discussed later in Section 6.

GneimoSim also includes the Accelerated Molecular Dynamics (aMD) enhanced sampling method.³⁴ Since conformational transitions in proteins involve changes in torsions to a larger extent than in other degrees of freedom, aMD has been especially successful when applied specifically to dihedral torsions.¹⁵ GneimoSim TMD includes support for aMD applied to torsional modes for studying conformational transitions in proteins.

3.7 Input/Output

GneimoSim uses file formats that are widely used by the MD community. It includes preparation scripts for generating data files needed to initialize GneimoSim. Model initialization requires the declaration of starting Cartesian coordinates, the masses of the atoms, and the cluster topology. The starting coordinates can be taken from a PDB, Amber crd, or LAMMPS data file. The masses can be taken from a LAMMPS data file, an OpenMM serialized xml system, or a simple gsystem set of masses that can be generated from a PDB file using an included script. A script for generating the default cluster definition data is also included.

Output logs are written in ascii format. The trajectory data however can be written in uncompressed crd format, or binary DCD format. These formats can be read by popular MD visualization and analysis tools, such as VMD,⁵¹ PyMOL,⁵² MDAnalysis,⁵³ and others. All output is generated using GneimoReporter instances. Any number of GneimoReporter instances can be created and used to record simulation data.

4 GneimoSim Usage

The computational algorithms and core modules within GneimoSim are implemented in C++ for speed. However, a comprehensive Python interface for the GneimoSim classes and their methods are available to the user. The SWIG⁵⁴ tool is used to auto-generate the comprehensive Python language interface for all of the C++ classes and their public methods. The Python interface provides a powerful and flexible scripting interface to fully configure a simulation at the finest level of detail without requiring a user to have to modify C++ code. The Python interface provides users with significant flexibility in managing simulations. Python scripts can be set up to replicate annealing procedures, replica-exchange MD, or any other style of MD which requires a reassessment of the state of the system during a simulation to determine how to proceed.

4.1 Example GneimoSim Simulation Script

GneimoSim simulations are typically carried out via Python scripts that create instances of the various GneimoSim classes and configure them during a setup phase, followed by an execution loop to carry out the simulation, and log data. Using the rich Python interface and language features, complex simulation flows can be implemented. Here we present an example of the calls from a basic Python simulation script for the example case of an NVT simulation of a 20 Alanine polypeptide using the Lobatto integrator.

The first step is to create a Gneimo simulation manager instance. The following call does so and sets the main options to configure the simulation.

# Creation and initialization of the Gneimo instance
g = Gneimo( system_type = SYSTEM_LAMMPS, system_filename = “20Alanine.data”, coords_type = COORDS_LAMMPS, coords_filename = “20Alanine.data”, cluster_filename = “20Alanine.gcluster”, model_type = MODEL_ICMD, integrator_type = INTEGRATOR_LOBATTO )

In this example, a LAMMPS format file provides the system and starting coordinates. The 20Alanine.data and 20Alanine.gcluster input data files are prepared using a preparation script in the GneimoSim software. The MODEL_ICMD value selects the standard ICMD cluster model type. The final variable specifies the choice of the Lobatto integrator for the simulation.

The next command creates an instance of the LAMMPS forcefield to be used. In this example, the 20Alanine.data LAMMPS format data file also has the information needed to create and configure the forcefield. Once created, the forcefield instance is registered with the Gneimo instance for use during the simulation.

# Create the Lammps force field instance
force_field_lammps = GneimoForceFieldLammps( filename = “20Alanine.data” )
# Create the GBSA force field instance
# The default dielectric constants can be changed with additional parameters force_field_gbsa = GneimoForceFieldLammpsGBSA(force_field_lammps)
# Register the force fields with the Gneimo simulation manager
g.addForceField( force_field_lammps )
g.addForceField( force_field_gbsa )

Next, reporters are created to log the energy and trajectory coordinate data from the simulation.

# Standard log (energies, temperature, etc.)
reporter_log = GneimoReporterLog( filename = “20Alanine.log”, frequency = 1 )
# Trajectory coordinate data as a DCD file
reporter_dcd = GneimoReporterTrajectoryDCD( filename = “20Alanine.dcd”, frequency = 1 )

The next command initializes the system velocities for the desired temperature in accordance with the (ICMD) equipartition principle.¹⁷ The random seed is used internally for the random initialization of velocities for the desired temperature value. The random seed can be set by the user for repeatable simulations, or to guarantee different starting conditions for the same system when running in parallel.

# Initialize velocities
g.initTemperature( temperature = 300, random_seed = 111 )

This completes the setup phase of the simulation script. The simulation is run by calling the appropriate run command for the type of ensemble to be used. This example shows the run command for an NVT simulation using the Nosé-Hoover thermostat. The following command specifies an MD run of 200000, 5.0 fs time steps. The overall system linear and angular momentum is to be reset every 100 steps to remove any numerical drift, and the temperature is maintained at 300K by the Nosé-Hoover thermostat with a bath relaxation coefficient of 500 fs.

# Run the simulation using a NOSE-Hoover thermostat.
g.runNoseHoover( step_size = 5.0, num_step = 200000, cm_reset_frequency = 100, bath_temperature = 300.0, temperature_relax_scale = 500 )

The MD parameter values can be specified directly or via variables defined elsewhere in the python script. While the above script illustrates basic usage, more complicated runs can be carried out using other GneimoSim options together with control flows involving for, if, while etc. Python loops. The following examples illustrate possible variants of this simulation script using some of the other available options.

Instead of using the LAMMPS forcefield, the above simulation can be used with OpenMM's GPU accelerated (AMBERffsb forcefield) using the following command:

force_field = GneimoForceFieldOpenMM( filename = “20Alanine.xml” )

For protein homology model refinement to higher resolution, GneimoSim's torsional MD method can be used with the ROSETTA forcefield, which can instanced as follows:

force_field = GneimoForceFieldRosetta( filename = “20Alanine.pdb” )

To the best of our knowledge, the ability to perform ICMD simulations with ROSETTA forcefield is not available in any other software package.

The clustering scheme shown in Figure 1 is the default clustering scheme used in TMD in GneimoSim. However, some of the clusters can be combined into a larger cluster, or an entire helix can be treated as a rigid body depending on the user's choice by editing the cluster definition file. Even an entire domain of a protein can be treated as rigid body. Within GneimoSim the user can choose to model any part(s) of the protein as a rigid body (or rigid bodies) connected by flexible torsional hinges. Such cluster-based coarsening of the dynamics model is useful for multi scale simulations of large protein complexes. In addition to changing the cluster definition at the start of the simulation, the dynamic clustering feature provides the ability to freeze and thaw degrees of freedom during simulation. This feature can be used in the run-time script to monitor the formation of motifs and freeze and thaw them during the course of the simulation run. The simulations can also be carried out with temperature REMD using the GneimoREMD.py script included in GneimoSim and an appropriate configuration file.

GneimoSim also offers the capability of freeing up some bond angle degrees of freedom. All the bond angles can also be selected and treated as free degrees of freedom for finer conformational sampling. In the next lines we show how to open the angle between “cluster2”, as defined in the cluster file, and atom number 3, as defined in the coordinates file.

gmodel = g.getGneimoModel()
cluster = GneimoCluster.asGneimoCluster(gmodel.body(’cluster2’,0,True))
cluster.addBondAngleDof( atom_number = 3)

5 GneimoSim Performance

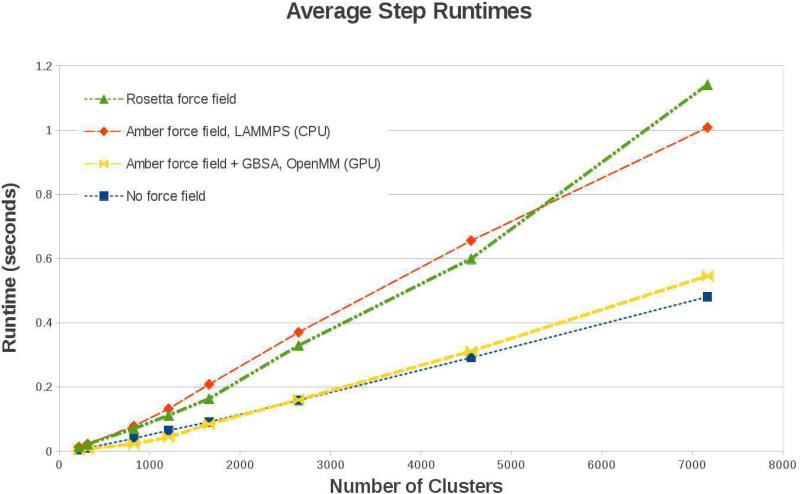
Solving the equations of motion of an ICMD model requires sophisticated algorithms that can be computationally expensive. GneimoSim includes the linear cost dynamics solver to alleviate this burden to a degree. We present an analysis of GneimoSim's performance based on the cost of the ICMD equations of motion and the cost of the force calculation as performed by the forcefield engines interfaced with GneimoSim. Figure 3 shows a comparison of the average run time per time step for the GneimoSim ICMD simulations for different forcefield options as a function of increasing number of clusters. A series of proteins with increasing number of atoms was chosen from the PDB data bank. The conventional clustering scheme illustrated in Figure 1 was used in all cases. As an example, the largest system shown (7165 clusters) corresponds to human alpha-2-macroglobulin, consisting of 20426 atoms. For each protein, 5 independent NVE ICMD simulations 300ns long were performed. The integration was performed with the Lobatto algorithm as implemented in GneimoSim with an integration time-step of 1fs. A cutoff of 17 Å was used for the long range interactions. No explicit solvent molecules were added for this study. The run time presented in Figure 3 corresponds to the average time per step as calculated for each system based on the last 100 ns of each of the 5 simulations performed. Error bars in all cases are smaller than the symbol used in the plot. All simulations were performed on a machine with an Intel Xeon E5-2670 CPU and one Nvidia Tesla K20m GPU card.

Figure 3.

Average run times per step for the GneimoSim simulation using different forcefields. Systems tested correspond to different proteins with increasing residue number. Standard clustering was used. 7165 cluster = human alpha-2-Macroglobulin with 20426 atoms.

In Figure 3 the blue line shows the average run time for a simulation without invoking a forcefield, thus reflecting the total cost of the ICMD equations of motion. It shows the effective linear scaling of the dynamics equations solver cost for the GNEIMO method in GneimoSim. We will use this line as a point of reference to compare the performance once the force calculation is invoked.

The average run time for calculating the forces using OpenMM with GBSA (on a GPU), and using LAMMPS and Rosetta forcefields on a CPU are shown in yellow, red and green lines respectively. The Rosetta and Amber forcefields force computations using LAMMPS on CPUs show an increase in computational cost that dominates the average run time from a small number of clusters. For the case of OpenMM for a run with Amber plus GBSA on the GPU, the GneimoSim solver takes slightly less time, however the cost of the forcefield does not entirely dominate the cost of the simulation with this number of clusters.

The ICMD model in GneimoSim has a higher up-front cost, but the run-time cost scales as O(N) while force calculations scale at a higher order. Thus, we find that the relative cost of the simulation dynamics decreases with increasing system size while the force computation cost increases. The increase in computational time for ICMD is compensated to an extent by the ability to take larger time steps than are possible in a Cartesian simulation. We have used integration time steps as large as 10fs in stable GneimoSim simulations. In contrast, all-atom Cartesian model-based simulations are generally restricted to a 2 fs time step with SHAKE constraints on the bond lengths. From a purely simulation speed perspective, we have found that the larger time steps result in similar simulation speed for ICMD and Cartesian MD simulations for CPU implementations. On GPUs however, Cartesian simulations are significantly faster since there are no ICMD implementations on the GPU available to date.

While important, the raw simulation speed metric does not capture attractive properties of ICMD models such as increased conformational sampling, and the ability to control the model coarseness for multi-scale models that are very important for MD problems. Section 6 presents such examples of successful applications of the GneimoSim ICMD method to important MD problems.

6 GneimoSim Applications

GneimoSim has been been used for multiple applications such as folding of small proteins,⁷ refinement of homology models,^12,13 simulation of proteins from crystal structure,⁸ and large scale conformational changes in proteins.¹⁴ These applications are briefly described below.

6.1 Folding and torsional MD simulations

We have used GneimoSim for studying the folding of small proteins starting from extended structures and performing NVT Nosé-Hoover dynamics with REMD using 12 temperature replicas. We used the fixed time step integrator Lobatto for these simulations.⁷ To demonstrate how one can control the granularity of the ICMD model during dynamics, we performed folding of small proteins using the dynamic clustering scheme described earlier in this paper, on the experimentally resolved portions of four proteins with PDB IDs: 1BDD (res. 11-56), 1EON (res. 7-31), 1PRB (res. 11-53), and 1UB.⁸ For example, the helical regions in the starting crystal structures were kept rigid and the rest of the torsions were flexible. We have also studied folding of small proteins using dynamic clustering where the partially formed helical regions in the initial stretch of the all-torsion folding simulation trajectory of small proteins such as Trp-cage are frozen as the simulation proceeded. These NVT Hoover REMD simulations, performed with the CVODE adaptive time step integrator, showed a better sampling of near native structures than all-torsion constrained MD simulations. Dynamic clustering is an adaptive scheme for coarse graining. Using the dynamic clustering tool we have folded four different proteins starting from their extended structure to molten globule-like native structures within 4 to 5Å of the crystal.

6.2 Protein Structure Refinement

Refinement of low resolution protein homology models to high resolution is an important challenge in protein structure prediction. We have used GneimoSim with temperature replica REMD, NVT Hoover dynamics and the Lobatto integrator to refine the homology models for various CASP target proteins. CASP is the Critical Assessment of Protein Structure Prediction (http://predictioncenter.org/). These studies were done using GneimoSim and with no known knowledge of the predicted structures. We observed that GNEIMO TMD method led to refinement in most cases when used with REMD.^12,13 This is in contrast with the performance of all-atom MD methods which do not lead to refinement of homology model of proteins unless restraints from known structures are used.³⁰ Currently, we are testing the use of GneimoSim with Rosetta FF for structure refinement.

6.3 Large Scale Conformational Changes

We have also studied the mapping of large scale conformational changes using GNEIMO TMD simulations for fasciculin and calmodulin.The application of GNEIMO with REMD to study the conformational dynamics of fasciculin produced sampling of two of its experimentally-established conformational substates. We also observed that the conformational transition of calmodulin from the Ca²⁺-bound to the Ca²⁺-free conformation occurred readily with GneimoSim TMD simulations. Moreover, GneimoSim generated an ensemble of conformations satisfying about half of both short and long-range inter- residue distances obtained from NMR structures of calmodulin. In contrast, unconstrained all-atom Cartesian simulations have failed to sample transitions between the substates of fasciculin and calmodulin, GneimoSim simulations demonstrated the transitions in both systems in a relatively short simulation time scale.¹⁴

7 Conclusions

The GneimoSim software is a computationally efficient implementation of the GNEIMO method for ICMD simulations. We believe that GneimoSim is the first package to include advanced features such as the ICMD equipartition principle and methods for including the Fixman potential to eliminate systematic statistical biases introduced by the use of hard constraints. Moreover, GneimoSim's architecture allows it to be extended and easily interfaced with third party forcefield packages for ICMD simulations. GneimoSim currently includes interfaces to LAMMPS, OpenMM, Rosetta forcefield packages. The availability of a comprehensive Python interface to the underlying C++ classes and their methods provides a powerful and versatile mechanism for users to develop simulation scripts to configure the simulation and to control the simulation flow.

The GneimoSim software has been used for a number of studies including ones for large-scale domain motion, protein folding and protein structure prediction and refinement. GneimoSim is not restricted to proteins and can also be used for the simulation of materials. We believe that GneimoSim will be a valuable ICMD tool for the research community.

We are continuing to develop and optimize the GneimoSim software and use it for protein dynamics applications. While the initial emphasis has been on supporting TMD models, we plan to support the full range of ICMD models that include free non-torsional degrees of freedom. We will also investigate the development of an analysis toolkit that makes direct use of the BAT coordinate trajectories such as for entropy computations. Another area of investigation is the integration with third party specialized forcefields and enhanced sampling modules for improving structure refinement and conformational sampling.