Abstract
Purpose
To investigate age related changes in diffusion tensor indices and fiber architecture of the medial and lateral gastrocnemius (MG and LG) muscles using diffusion tensor imaging (DTI).
Materials and Methods
The lower leg of five young and five senior subjects was scanned at 3T and DTI indices extracted using three methods: ROI, histogram and tract based. Tracked fibers were automatically edited to ensure physiologically relevant tracks. Pennation angles were measured with respect to the deep and superficial aponeuroses of both muscles.
Results
The three methods provided internally consistent measures of the DTI indices (correlation coefficient in the range of 0.90-0.99). The primary, secondary and tertiary eigenvalues in the MG and LG increased significantly in the senior cohort (p<0.05), while the small increase in fractional anisotropy (FA) with age was not significant (MG/LG: p=0.39/0.85; 95% CI:[ −0.059/-0.056, 0.116/0.064]). Fiber lengths of MG fibers originating distally were significantly decreased in seniors (p<0.05) while pennation angles decreased with age in the MG and LG but this was not significant.
Conclusion
Fiber atrophy and increased fibrosis have opposing effects on the diffusion indices resulting in a complicated dependence with aging. Fiber architectural changes could play a role in determining aging muscle function.
Keywords: Diffusion Tensor Imaging, muscle aging, muscle fiber architecture, gastrocnemius muscle
Introduction
Fascicle lengths and pennation angles, jointly referred to as muscle architecture, reflect the structural arrangement of sarcomeres within a skeletal muscle and are known to strongly affect its contractile properties that determine its force producing capacity (1), as evidenced by the force-length and force-velocity relationships. Fukunaga, et al. (2) and Maganaris, et al. (3) were among the first to develop ultrasound techniques to visualize and study muscle architecture in vivo. While ultrasound is generally considered a valid and reliable tool for measurements of fascicle lengths and pennation angles (4), it is limited in that it allows for muscle architecture to be studied only in 2D and in a relatively small area of interest (determined by the size of the probe). Since architecture may vary considerably along a muscle’s length (5), measurements obtained in a single location do not allow for conclusions to be drawn regarding the structural arrangement of fascicles in other parts of the muscle. Moreover, ultrasound is only partially applicable to the study of muscles lying deeper in the body. Therefore, the development of alternative imaging techniques, which may help circumvent these limitations, is imperative.
MRI-based muscle diffusion tensor imaging (DTI) is a relatively new modality which allows the noninvasive in-vivo determination of diffusion of water molecules is an excellent probe of tissue micro architecture. As highly organized tissues, in which connective tissues (endo-, peri- and epimysium) create a complex network to enclose fibers, fascicles and total muscles, human skeletal muscles are anisotropic media and, thus, ideal candidates for DTI studies (6). The eigenvector corresponding to the lead eigenvalue of the diffusion tensor has been shown through histology and Direct Anatomic Inspection (DAI) to correspond to the fiber directions (7). Thus, the determination of the diffusion tensor enables fiber tracking and measurements of fiber architecture (fiber length and pennation angles) in 3D, as opposed to the 2D data typically obtained with ultrasound.
One clinical condition that is believed to result in significant remodeling of skeletal muscle architecture is sarcopenia, i.e. the age-associated loss of muscle mass and strength MS6 (8) MS6. Ultrasound-based studies performed on the human calf (9,10) have demonstrated that the total loss of muscle mass with aging is reflected by a reduction of both fascicle lengths and pennation angles. In addition to macroscopic changes in architecture, histology based studies have revealed age-associated changes in fiber type and diameter (11-13), which are indicative of a preferential atrophy of fast twitching type II fibers. While the resolution of MRI precludes direct observations at the microscopic scale, the DTI indices may allow for indirect inferences about the microarchitecture of skeletal muscles. DTI provides information on both the fiber architecture (tracking of the lead eigenvector) as well as the microarchitecture through the DTI indices. Given that current models of diffusion in skeletal muscle propose a direct proportionality of fiber diameter to the tertiary or to the secondary and tertiary eigenvalue (14-17), it is likely that age-associated changes in fiber type composition and, thus, diameter would be reflected in a decrease of one or both of these parameters. As the lead eigenvalue is not expected to be sensitive to fiber length changes, a decrease of the secondary or tertiary eigenvalue would increase the asymmetry of the diffusion, leading to higher fractional anisotropy. The hypothesis then is that muscle atrophy (decrease in fiber diameter) with age will be reflected as a decrease in the tertiary eigenvalue with a concomitant increase in the fractional anisotropy. This study focuses on the medial and lateral gastrocnemius (MG and LG) muscles to investigate age related changes in diffusion tensor indices and fiber length and pennation angle to identify changes at the microarchitecture and whole muscle architecture levels respectively.
Methods
Diffusion tensor Models
Galban, et al. (14) proposed that the lead eigenvector was along the long axis of the muscle fiber, the second eigenvector was along the sheets of individual muscle fibers within the endomysium while the eigenvector associated with the third eigenvalue is related to diffusion within the muscle fiber. An extension of this model includes the muscle fiber volume fraction (15) and was used to explain the higher ADC/ lower FA value in females compared to males. Karampinos, et al. proposed an interesting diffusion tensor model that took into account the cross-sectional asymmetry of muscle fiber geometry (16,17). In their model, diffusion occurs within the muscle fiber and the extracellular space and λ2 and λ3 reflect the principal diameters of the elliptical cross sectional area of the myofibrils.
The model of diffusion for aging muscle proposed here is an extension of previous models proposed earlier (14-17). A voxel in the muscle volume is composed of both muscle fibers (fraction, f) and extracellular space (endomysium/perimysium, 1-f). Diffusion in the muscle fiber is anisotropic (and hindered) with eigenvalues λ1m, λ2m, and λ3m, with λ1m representing diffusion along the muscle fiber direction, and λ2m and λ3m reflecting the principal diameters of the elliptical cross-section of the myofibrils. Diffusion in the endomysium/perimysium, λp, is isotropic and less hindered. In a slow exchange, two pool model, the resulting eigenvalues for a voxel are given by: [fλ1m+(1-f)λp],[ fλ2m+(1-f)λp], [fλ3m+(1-f)λp]. Based on the histological studies on aging muscle, both fiber loss and diameter decrease is assumed to occur with aging. While a direct quantification of the endomysium is limited by the resolution of MR images, it would be reasonable to assume a similar increase of connective tissue in the endomysium as in the perimysium (~15% increase in the older cohort of the current study estimated from connective tissue imaging), since the two tissues are continuous (18).
In-Vivo Experiments
Five young adult (age: 31.6 ± 7.0 yrs, height: 155.7 ± 4.9 cm, mass: 48.4 ± 2.6 kg) and five senior adult (age: 83.4 ± 3.2 yrs, height: 153.7 ± 1.5 cm, mass: 57.4 ± 4.9 kg) Japanese women were recruited via advertisements and from within retirement homes for Japanese people, respectively. All participants were screened and the exclusion criteria were myocardial infarction, unstable angina pectoris, pericarditis, acute infections and fever as well as severe osteoarthritis and arthroplasty of the hip or knee. The participants were scanned after they signed the Institutional Review Board-approved consent form.
Diffusion weighted images were acquired at 3T (GE Medical Systems, Milwaukee, WI, USA). The MRI pulse sequence used in the image acquisition was a fat suppressed single shot EPI sequence without dual 180° pulses. Thirty-two non-collinear gradient directions with a b-factor of 400 s/mm2 were used to map the direction dependent diffusion. Imaging parameters were echo time (TE)/repetition time (TR): 49 ms/4000 ms with 4 signal averages. The field of view (FOV), slice thickness/gap, and acquisition matrix were 240 × 240 mm2, 5 mm/0 mm, and 80 × 80 (extrapolated to 256×256), respectively; yielding a voxel resolution of 0.9375 mm × 0.9375 mm × 5.00 mm. A custom built coil with a large field of view was used to image approximately 22 cm of the lower leg without moving the subject or coil; the intent was to cover the medial and lateral gastrocnemius muscles from their origin to insertion in a single acquisition. It was of particular importance to maintain shorter scan times to accommodate the senior cohort who could tolerate limited scan times only.
In addition to the diffusion weighted images, a morphological volume was acquired with a fat saturated fast gradient echo (fgre) sequence with the following parameters: TE/TR/FA::2.15 ms/775 ms/30°; all geometry parameters were the same as the DTI scans. Images were acquired using two custom sequences for fat and connective tissue quantification: Connective tissue imaging of the very short T2 species was performed using a FAST Gradient-echo based, 2D double echo ultralow (UTE) sequence. Sequence parameters were: TR= 200ms, TE1= 8μs, TE2=2.6ms, FA=30°, BW=+/− 62.5kHz, NEX=2 (19). Fat quantification was performed using the iterative decomposition of water and fat with echo asymmetry and least-squares estimation (IDEAL): axial 3D fast gradient 6 echo sequence with 3 Echo Train Length (20).
Image Pre-Processing
All diffusion weighted image volumes were registered to the baseline (b0) image to correct for eddy current and motion related artifacts. The baseline and diffusion weighted images were then denoised using a Rician linear minimum mean square error (LMMSE) estimator (3DSlicer; http://wiki.slicer.org/slicerWiki/index.php/Documentation/4.3/Modules/DWIRicianLMMSEFilter; Planning Laboratory, Harvard Medical School, Boston, MA, USA). The tensor was calculated from the denoised data using a Gaussian model of diffusion followed by correction for susceptibility based distortion artifacts (3D Slicer). The deformation fields were estimated from the registration of the baseline (b0) diffusion volume to the fat suppressed gradient echo images (volume with geometric fidelity) using a series of transformations starting from rigid to 3D B-Spline. A visual check of the color maps from the original tensor as well as the reoriented tensor (smoothed and corrected) was performed to confirm that the distortion correction did not intro duce any artifacts in the eigenvector reorientation. The distortion corrected tensor was processed to generate the eigenvalues and fractional anisotropy maps.
Diffusion Tensor Indices
We compared three methods of evaluating DTI indices: ROI based (regional and global), histogram based, and tract based. The regional and global analysis of the eigenvalues and fractional anisotropy was performed in two ways: (i) the mid-50% muscle (MG or LG) was chosen for analysis with manual contours of the muscles in the axial view generated from the matched reference images. The mid-50% of the muscle includes the slices the cover 25% to 75% of the total muscle length measured from the insertion point. (ii) ROIs in the muscle compartments (manual contour of the whole muscle cross section) were defined in slices located at specified distances from the insertion (25%, 50% and 75% of total muscle length; these slices are referred to as 25%, 50% and 75% slices ). The latter analysis was used to investigate regional differences in the diffusion tensor indices.
The second method is similar to the ROI analysis but was based on editing the histogram of the apparent diffusion coefficient (ADC) values for each muscle (whole volume) using the quantitative information of connective and adipose tissue voxels for each subject that were calculated from the customized image sequences. This editing utilizes the fact that the ADC of voxels containing fat and connective tissue is close to zero (as the signal in these voxels at baseline is close to the noise level). It should be noted that an intensity threshold was applied to the baseline b0 image to eliminate background (noise) voxels from the calculated images; this same threshold was not effective in eliminating voxels with a high % of fat and/or connective tissue. The latter was due to ‘partial volume’ effects with high signal intensity muscle. The variable intensity scaling of MR image volumes precluded selection of a common baseline intensity threshold to exclude voxels with high % of fat and or connective tissue. In contrast, calculated ADC values were reproducible across image volumes. Voxels corresponding to the lowest ADC values (cutoff determined by the % adipose and % connective tissue voxels for a given subject) were flagged and excluded from the DTI indices analysis. It should be noted that the connective tissue voxels flagged here do not belong to the endomysium which surround each muscle fiber (~ 50 μm) as this layer is not imaged separate from muscle fiber due to the resolution limits of even the high resolution structural MR images. The connective tissue identified in the structural MR images refers primarily to the perimysium enclosing fascicles (~ 1-2 mm).
The last method calculated the DTI indices for selected fiber tracts that originate from the distal and middle regions of the respective muscles. Values of the DTI indices were reported as the average of all voxels in the selected fiber tracts. No voxels were excluded as it was presumed that all voxels on a track belonged to muscle (based on the tracking criteria).
Fiber Tracking
The corrected and smoothed tensor volumes were masked with the muscle volume of interest: MG or LG. Fiber tracking was performed using DTIStudio (https://www.dtistudio.org/) on the (MG or LG) masked tensor volumes. The stopping criteria for the fiber tracking algorithm were: FA < 0.15 and an angle change > 20° between successive voxels. DTIStudio uses the ‘fiber assignment by continuous tracking’ (FACT) algorithm for fiber tracking and performs tracking with every point in the volume considered as a seed point if it exceeds the FA threshold. ROIs (1 pixel wide) were selected on coronal (reformatted) eigenvector images near the deep aponeurosis at distal and middle locations to extract fibers passing through these ROIs. Several (tens of) fibers pass through each ROI due to the ‘brute-force’ nature of the fiber tracking algorithm. Average eigenvalues and FA values for all the fibers passing through a ROI were calculated.
The surfaces corresponding to the deep and superficial aponeuroses were automatically identified from the manually contoured muscle masks by a raster scan. This raster scan was along the x-axis for the MG masks and identified the first point of intersection with the mask along the scan line as the deep MG aponeurosis surface and the last point of intersection as the superficial MG aponeurosis surface. In the case of the lateral gastrocnemius, the raster scan was along the y-axis to identify the deep and superficial aponeurosis. Pennation angle and fiber lengths were calculated for each fiber through a given ROI and averaged. The pennation angle was calculated at the deep aponeurosis as follows: the closest point on the deep aponeurosis surface to the start point of the fiber was identified (start point of the fiber is not necessarily the same as the selected ROI). A 3×3 neighborhood on the aponeurosis surface near the intersection point was fit to a 3rd order polynomial. The normal to this surface was calculated and the pennation angle was calculated as: (90°-angle between the surface normal and the line joining a point on the fiber to the surface intersection point). A similar procedure was followed for the superficial aponeurosis using the fiber end point. Pennation angles were calculated for the fiber start and end points with respect to both aponeuroses; this can provide information on fiber curvature as well as the relative orientations of the distal/superficial aponeuroses. For each location, the pennation angles reported here represent the average of 5 points around it. Several automated checks were incorporated to ensure the integrity of the fibers and, consequently, the accuracy of the extracted architecture parameters. These included (i) exclusion of fibers that tracked entirely along an aponeurosis (ii) exclusion of fibers that terminated far (greater than 3 voxels) from the superficial aponeurosis, and (iii) trimming of fibers running parallel to an aponeuroses at either surface. This latter trend was observed on many tracts where, close to the surface, the fibers ran parallel to the aponeurosis over several slice lengths. This was attributed to artifacts that may arise from the admixture of connective, adipose and muscle tissue close the aponeurosis surface. Inclusion of these long ‘tails’ to the fibers biased the pennation angle to lower and the fiber lengths to longer values.
Statistical Analyses
Unless stated otherwise, data are presented as means ± SD. Normality of data was verified visually by histograms and numerically using Shapiro-Wilk’s test (p > 0.05). The Shapiro-Wilk test is a regression-type test that assesses how well the observed frequency distribution matches the expected (normal) frequency curve. Among statistical tests to check distributional normality, it yields the greatest power (21) and is therefore most suitable when dealing with small sample sizes. In addition, Q-Q plots were used to graphically assess the normality of data. Differences between age groups and muscle regions were then tested for statistical significance using two-tailed t-tests for independent samples. For correlational analyses of the three methods proposed for extracting DTI indices, Pearson’s correlation coefficients were calculated. In cases when the Shapiro-Wilk test indicated that the assumption of normality had been violated, Spearman’s coefficients were calculated instead.
Results
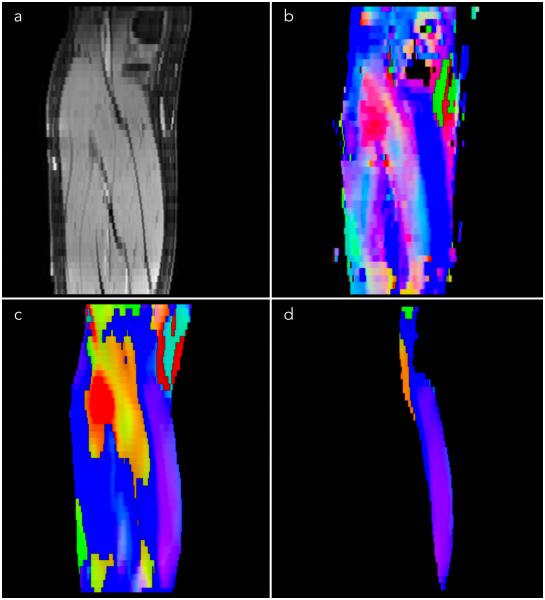
Figure 1 shows the efficacy of the distortion correction algorithm on one slice from a subject from the young cohort. The improvement in the match between the anatomical image and the baseline diffusion weighted images can be appreciated from the contour overlays. The algorithm performed well at the distal and middle regions but was less effective at the proximal ends. Further, the distortion correction was better in senior cohort than in the young cohort. Figure 2 is an example eigenvector color map comparing the tensor generated from the original image to that after denoising and distortion correction. Reduced noise is seen in the processed tensors and, though some blurring is present, the post processing introduced no artifacts into the eigenvector direction (represented by the color map).
Figure 1.
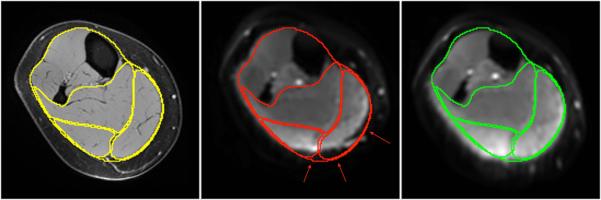
An image at one anatomic location from a subject in the young group illustrating the effects of the distortion correction: fat saturated GRE reference images (a); original uncorrected baseline images (b); and distortion corrected baseline images (c). Contours from the reference image are shown superposed on the distorted and corrected images. The contours of the calf, soleus, medial gastrocnemius, and lateral gastrocnemius are shown to illustrate distortion in the original DTI image (b) and the correction (c) in the calf and in each muscle compartment. The red arrows in (b) indicate the location of significant distortion where the tissue has been mismapped (shifted up from the true contour); these regions are correctly mapped after the distortion correction (c).
Figure 2.
Comparison of eigenvector color maps from the original uncorrected DTI data to the corrected DTI data. The same anatomical slice is shown in all the images: fat saturated GRE image (a); eigenvector color map calculated from the uncorrected data (b); eigenvector color map calculated from the distortion corrected and smoothed data with the lower leg mask from (a) excluding subcutaneous fat (c); and medial gastrocnemius mask from (a) applied to the corrected, smoothed eigenvector (d).
Table 1 summarizes the DTI indices averaged for the mid-50% muscle volume and at three specific anatomical locations for the medial and lateral gastrocnemius. Compared to the young cohort, all three eigenvalues increased in the senior cohort for both muscles and these differences were statistically significant. The FA values were higher in the older cohort in both the MG and the LG but not significantly so. There were no significant regional differences (comparing 25%, 50%, and 75% slices) of the DTI indices in either the junior or senior cohort. It should also be noted that significant differences between young and senior cohorts in the eigenvalues could not be detected using a ROI in one slice.
Table 1.
DTI indices using ROI analysis of selected slices and mid-50% medial gastrocnemius (MG) and lateral gastrocnemius (LG) muscle volumes for young (Y) and senior (S) subjects.
| Medial gastrocnemius | Lateral gastrocnemius | ||||||
|---|---|---|---|---|---|---|---|
| Young (Y) | Senior (S) | %4 | Young (Y) | Senior (S) | % | ||
| FA1 | tot2 | 0.2340 ± 0.0207 | 0.2380 ± 0.0444 | 1.7 | 0.2520 ± 0.0311 | 0.2840 ± 0.0783 | 12.7 |
| 253 | 0.1850 ± 0.0173 | 0.2420 ± 0.1085 | 30.8 | 0.1967 ± 0.0751 | 0.1575 ± 0.0236 | −19.9 | |
| 503 | 0.2580 ± 0.0610 | 0.2200 ± 0.0707 | −14.7 | 0.2000 ± 0.0283 | 0.2620 ± 0.0396 | 31 | |
| 753 | 0.2640 ± 0.0336 | 0.2300 ± 0.0455 | −12.9 | 0.2367 ± 0.0513 | 0.2200 ± 0.0600 | −7.1 | |
| λ 1 5 | tot | 0.0018 ± 0.0001 | 0.0020 ± 0.0001 | 11.1* | 0.0018 ± 0.0001 | 0.0020 ± 0.0001 | 11.1* |
| 25 | 0.0014 ± 0.0006 | 0.0018 ± 0.0005 | 28.6 | 0.0013 ± 0.0005 | 0.0014 ± 0.0005 | 7.7 | |
| 50 | 0.0018 ± 0.0002 | 0.0020 ± 0.0003 | 11.1 | 0.0021 ± 0.0003 | 0.0020 ± 0.0010 | −4.8 | |
| 75 | 0.0017 ± 0.0002 | 0.0019 ± 0.0001 | 11.8 | 0.0020 ± 0.0003 | 0.0017 ± 0.0009 | −15 | |
| λ 2 5 | tot | 0.0013 ± 0.0001 | 0.0014 ± 0.0001 | 7.7* | 0.0013 ± 0.0001 | 0.0014 ± 0.0001 | 7.7* |
| 25 | 0.0012 ± 0.0005 | 0.0015 ± 0.0005 | 25.0 | 0.0011 ± 0.0005 | 0.0013 ± 0.0005 | 18.2 | |
| 50 | 0.0013 ± 0.0002 | 0.0015 ± 0.0003 | 15.4 | 0.0016 ± 0.0001 | 0.0015 ± 0.0007 | −6.3 | |
| 75 | 0.0012 ± 0.0002 | 0.0014 ± 0.0002 | 16.7 | 0.0014 ± 0.0001 | 0.0012 ± 0.0007 | −14.3 | |
| λ 3 5 | tot | 0.0011 ± 0.0001 | 0.0013 ± 0.0001 | 18.2* | 0.0011 ± 0.0001 | 0.0012 ± 0.0002 | 9.1* |
| 25 | 0.0010 ± 0.0004 | 0.0011 ± 0.0004 | 10.0 | 0.0010 ± 0.0005 | 0.0010 ± 0.0003 | 0 | |
| 50 | 0.0011 ± 0.0002 | 0.0013 ± 0.0003 | 18.2 | 0.0014 ± 0.0001 | 0.0012 ± 0.0006 | −14.3 | |
| 75 | 0.0011 ± 0.0002 | 0.0012 ± 0.0002 | 9.1 | 0.0013 ± 0.0002 | 0.0010 ± 0.0006 | −23.1 | |
FA: fractional anisotropy, unitless (range: 0-1)
tot: mid- 50% (from 25% to 75%) medial gastrocnemius muscle voxels
25, 50, 75: muscle voxels at anatomical location 25%, 50% and 75% from the muscle origin.
% is change calculated with respect to the young group
Eigenvalues λ1, λ2, λ3 are in units of mm2/sec.
significant at p<0.05; two-tailed t-test for independent samples (young-senior age groups)
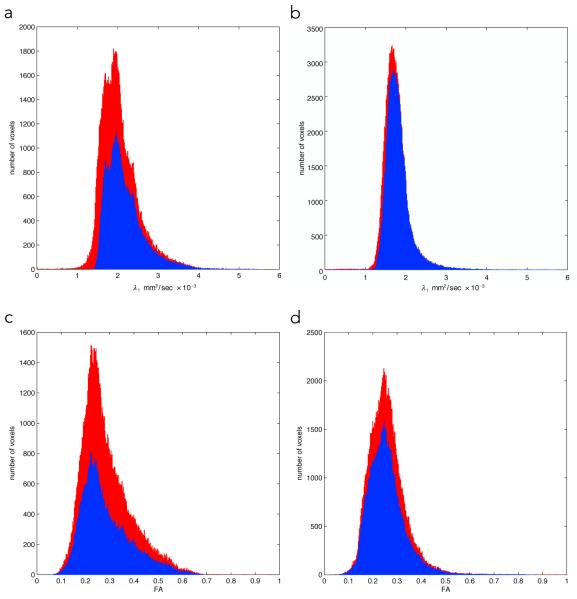
The summary of the histogram analysis of the whole MG and LG muscle after deletion of voxels with a high % of adipose and/or connective tissue is summarized in Table 2. Histograms of the λ1 and FA values for the young and senior cohorts are shown in Fig. 3. In both the LG and MG, histogram analysis showed that the older cohort had larger values for all three eigenvalues compared to the younger cohort. The differences were significant except for λ2 of the LG (for λ2, there was a trend towards significance with p = 0.06). The FA values of both the MG (~11%) and LG (~2%) showed small increases, neither of which was significant (MG: p=0.39; 95% CI:[ −0.06, 0.12] and (LG: p=0.85; 95% CI:[ −0.06, 0.06]. In addition to the eigenvalues, histogram shape parameters characterized by kurtosis and skew are also shown in Table 2. Values were greater for skewness and lower for kurtosis in the older cohort, though differences with the younger cohort were not significant (MG kurtosis: p=0.09, 95% CI:[ −4.11, 0.70]; MG skewness: p=0.55, 95% CI:[ −1.16, 0.73]; LG kurtosis: p=0.08, 95% CI:[ −6.26, 0.94]; and LG skewness: p=0.14, 95% CI:[ −1.91, 0.48]).
Table 2.
DTI indices using whole muscle histogram analysis of the medial gastrocnemius (MG) and lateral gastrocnemius (LG) muscles for young (Y) and senior (S) subjects.
| Medial gastrocnemius | Lateral gastrocnemius | ||||||
|---|---|---|---|---|---|---|---|
| Young(Y) | Senior (S) | %2 | Young(Y) | Senior (S) | % | ||
| FA1 | Mean | 0.2527 ± 0.0785 | 0.2813 ± 0.1004 | 11.3 | 0.2378 ± 0.0617 | 0.2419 ± 0.0707 | 1.7 |
| Kurtosis | 4.69 | 2.98 | −36.4 | 6.67 | 4.01 | −39.9 | |
| Skewness | 0.5 | 0.28 | −43.2 | 0.79 | 0.08 | −89.9 | |
| λ 1 3 | Mean | 0.0018 ± 0.0004 | 0.0022 ± 0.0005 | 20.1* | 0.0018 ± 0.0003 | 0.0021 ± 0.0003 | 13.7* |
| Kurtosis | 10.07 | 6.54 | −35.1 | 14.42 | 14.36 | −0.4 | |
| Skewness | 1.22 | 1.58 | 29.2 | 1.62 | 2.13 | 32 | |
| λ 2 3 | Mean | 0.0013 ± 0.0003 | 0.0015 ± 0.0003 | 16.0* | 0.0014 ± 0.0002 | 0.0015 ± 0.0003 | 11.8 |
| Kurtosis | 9.74 | 6.56 | −32.7 | 15.71 | 12.42 | −20.9 | |
| Skewness | 1.22 | 1.56 | 27.8 | 1.77 | 2.03 | 14.4 | |
| λ 3 3 | Mean | 0.0011 ± 0.0002 | 0.0012 ± 0.0003 | 13.9* | 0.0012 ± 0.0002 | 0.0013 ± 0.0003 | 13.8* |
| Kurtosis | 10.49 | 6.39 | −39.1 | 12.96 | 12.37 | −4.5 | |
| Skewness | 0.92 | 1.32 | 43.9 | 1.32 | 1.94 | 47.8 | |
FA: fractional anisotropy, unitless (range: 0-1)
% is change calculated with respect to the young group
Eigenvalues λ1, λ2, λ3 are in units of mm2/sec.
significant at p<0.05; two-tailed t-test for independent samples (young-senior age groups)
Figure 3.
Histograms of the lead eigenvalue and FA in one subject of the senior (a, c) and young cohort (b, d) respectively. The red histograms refer to the original ‘all voxels’ while the blue refers to the histogram with adipose and connective tissue excluded. Editing removed low ADC values (presumably from muscle and non-muscle tissue partial volume effects); the smaller change in the young subject is due to smaller % adipose and connective tissue. The FA histograms show that voxels with higher FA values were removed by the editing and could be a consequence of artifactual high FA on voxels with low SNR.
Table 3 lists the results from fibers originating from the middle and distal end of the MG and LG muscles. As in the ROI and in the histogram analysis, the eigenvalues of the older cohort increased compared to the younger; differences were significant in the MG for fibers originating in the middle of the muscle. The differences in the eigenvalues for the LG were much smaller than in the MG and were significant only for the lead eigenvalue for fibers originating in the distal part of the muscle. To establish whether the three methods explored here provided internally consistent measures of the DTI indices, the measures obtained with each of the approaches were correlated against each other. With the only exceptions of λ2 in the GM (0.78 < r < 0.95) and λ3 in the GM (0.85 < r < 0.88), correlation coefficients were consistently in the range of 0.90 < r < 0.99, testifying to the fact that the three methods provided internally consistent measures of the DTI indices.
Table 3.
DTI indices extracted from fibers that originate from distal (D) and middle (M) regions of the medial gastrocnemius (MG) and lateral gastrocnemius (LG) muscles for young (Y) andsenior (S) subjects.
| Medial gastrocnemius | Lateral gastrocnemius | ||||||
|---|---|---|---|---|---|---|---|
| Young (Y) | Senior (S) | % | Young (Y) | Senior (S) | % | ||
| FA1 | Distal | 0.2436 | 0.2264 | −7.1 | 0.2698 | 0.3267 | 21.1 |
| Middle | 0.2065 | 0.2096 | 1.5 | 0.2902 | 0.3125 | 7.7* | |
| λ 1 3 | Distal | 0.0018 | 0.0020 | 9.7 | 0.0019 | 0.0022 | 17.2* |
| Middle | 0.0017 | 0.0020 | 17.6* | 0.0019 | 0.0020 | 8.3 | |
| λ 2 3 | Distal | 0.0014 | 0.0015 | 5.3 | 0.0013 | 0.0014 | 5.4 |
| Middle | 0.0013 | 0.0016 | 20.1* | 0.0013 | 0.0013 | −1.5 | |
| λ 3 3 | Distal | 0.0011 | 0.0013 | 16.5* | 0.0011 | 0.0012 | 6.0 |
| Middle | 0.0011 | 0.0014 | 19.4 | 0.0010 | 0.0011 | 5.4 | |
FA: fractional anisotropy, unitless (range: 0-1)
% is change calculated with respect to the young group
Eigenvalues λ1, λ2, λ3 are in units of mm2/sec.
significant at p<0.05; two-tailed t-test for independent samples (young-senior age groups)
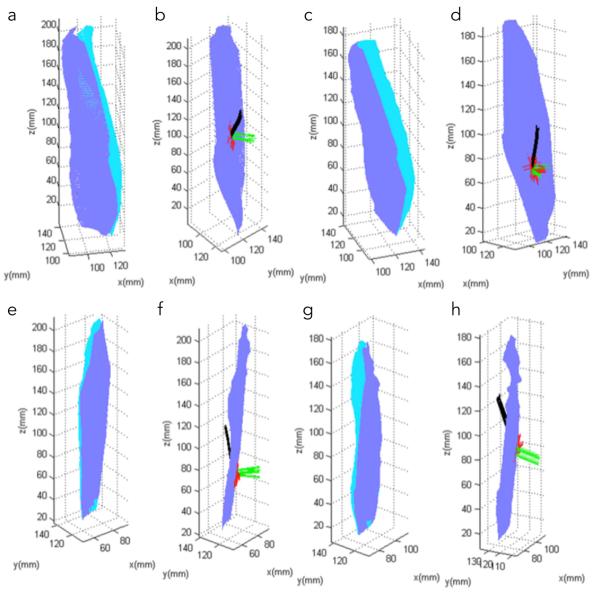
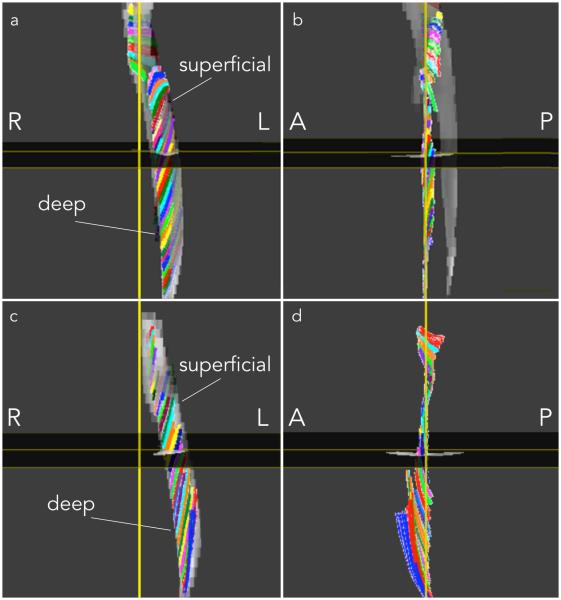
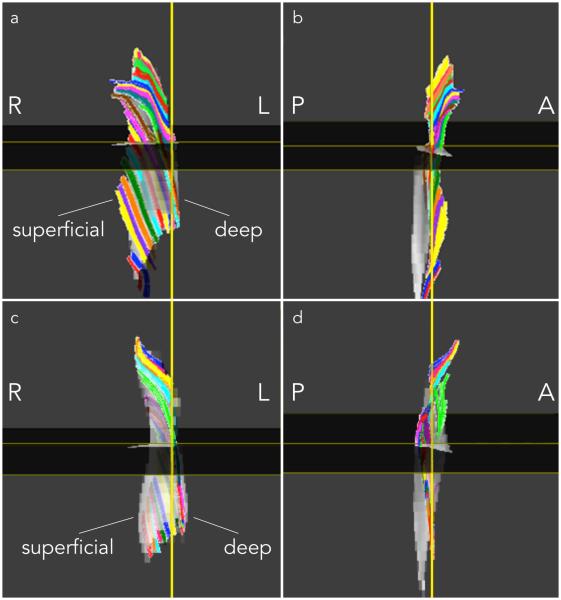
Figure 4 a, c, e, g shows the automatically identified deep and superficial aponeurosis of the MG and LG in one young and one senior subject. Figure 4 b, d, f, h are example of fibers through a single ROI with the corresponding normal and tangent to the aponeurosis surface at the point of intersection of the fiber with the deep aponeurosis surface. It should be noted that the fibers through a single ROI were tightly clustered and tracked each other closely from deep to superficial aponeurosis. Figure 5 shows the medial gastrocnemius fibers from one young and senior subject: similar fiber tracts were found in the other subjects. Visual examination of the MG fibers showed that three clusters of fibers could be identified in most subjects based on fiber shape. In the young (senior) subjects, fibers at the distal end of the muscle were initially in the coronal plane and then turned posteriorly (anteriorly) away from the coronal plane before terminating at the superficial aponeurosis (Fig. 5). For both young and old, the fibers were mostly in the coronal plane of the ROI in the middle regions while at the proximal end, the fibers were anteriorly displaced from the coronal plane to terminate on the proximal gastrocnemius tendon (Fig. 5). It was difficult to track fibers at the proximal end primarily due to the larger geometric distortions at this level. Figure 6 shows the lateral gastrocnemius fibers tracked from one young and senior subject, respectively. As in the MG, LG fibers, for many subjects, could be clustered based on shape and orientation: for young (senior) subjects, fibers originating in the distal end were displaced anteriorly (posteriorly) (Fig. 6). For both young and old, fibers originating in the middle regions were primarily in the coronal plane while those in the proximal regions were displaced anteriorly from the coronal plane to terminate in the distal gastrocnemius tendon; the middle and proximal fibers also exhibited more curvature (Fig. 6).
Figure 4.
Top row: medial gastrocnemius surface and fibers in one young subject (a, b) and one senior subject (c, d), respectively. Bottom row: lateral gastrocnemius surface and fibers in one young subject (e, f) and one senior subject (g, h) respectively. Deep and superficial aponeuroses are shown in dark and light blue, respectively (a, c, e, g). Fibers are shown in black, the normal to the deep aponeurosis surface in green, while the lines joining the intersection point on the aponeurosis to its nearest neighbors on the surface are shown in red (b, d, f, h).
Figure 5.
Medial Gastrocnemius fibers tracked in one subject from the young (a, b) and senior cohort (c, d). Fibers passing through region of interest points selected close to the deep aponeurosis on the coronal reformatted plane extending from distal to proximal are displayed in 3D, viewed from a coronal (a, c) and a sagittal perspective (b, d). ROIs of 1 pixel dimension were selected at each (axial) level to generate the tracts shown below. Colors were assigned randomly to fibers passing through each ROI to facilitate visualization. (R: Right, L: Left, A: Anterior, P: Posterior)
Figure 6.
Lateral Gastrocnemius fibers tracked in one subject from the young (a, b) and senior cohort (c, d). Fibers passing through region of interest points selected close to the deep aponeurosis on the coronal reformatted plane extending from distal to proximal are displayed in 3D, viewed from a coronal (a, c) and a sagittal perspective (b, d). The sagittal view was rotated by 180° compared to Fig. 5 as the LG fibers were better viewed from this perspective. ROIs of 1 pixel dimension were selected at each (axial) level to generate the tracts shown below. Colors were assigned randomly to fibers passing through each ROI to facilitate visualization. (R: Right, L: Left, A: Anterior, P: Posterior)
Table 4 is a summary of the fiber length and pennation angle differences for fibers through ROIs placed in the distal (within 25% from origin) and middle (between 25- 50% from origin) medial and lateral gastrocnemius in the young and senior subjects. In the MG, fibers were shorter by 41% and 17% in the older cohort compared to the younger cohort, in the distal and middle regions respectively; this difference was significant in the distal region. Further, in the MG, fibers were also longer in the distal compared to the middle muscle region in the young (43%) and in the senior (19%) subjects and the regional difference was significant in both age groups. Three angles were measured for each fiber: d-d: the angle of the deep end of the fiber to the deep aponeurosis surface (i.e., the ‘pennation’ angle typically measured in ultrasound studies), s-s: the angle of the superficial end of the fiber to the superficial aponeurosis surface, and sd: the angle of the superficial end of the fiber to the deep aponeurosis surface. Summarizing the pennation angle findings for the MG, the pennation angle (d-d) was larger in the young compared to the senior cohort and larger for fibers originating in the middle compared to the distal region. Significant differences between the young and senior cohort were found for the superficial pennation angles; however the superficial pennation angle was larger in the older cohort. Similar differences between young and senior were also present in the superficial-deep (s-d) angles, which were significant in the distal region. Regional differences were significant in both age cohorts with angles increasing from distal to middle regions. Comparing the MG pennation angles (d-d, s-s and s-d), differences were seen between each pair in both the young and senior subjects, and these differences were significant in the young cohort. In the LG, the findings were qualitatively similar to those found in the MG (longer fibers, larger pennation angles at the deep aponeurosis in the younger cohort, and longer fibers, lower pennation angles distal compared to medial origin fibers). However, the differences were all smaller and significant differences between young and old were only found for the superficial pennation angle. Comparing the LG pennation angles (d-d, s-s and s-d), differences were seen between each pair in both the young and senior subjects, and these differences were significant in the older cohort.
Table 4.
Fiber Length (mm) and pennation angles for fibers that originate from distal (D) and middle (M) regions of the medial gastrocnemius (MG) and lateral gastrocnemius (LG) muscles for young (Y) and senior (S) subjects.
| Medial gastrocnemius | Lateral gastrocnemius | ||||||
|---|---|---|---|---|---|---|---|
| Young (Y) | Senior (S) | %8 | Young (Y) | Senior (S) | % | ||
| Length (mm) |
Distal(D) | 67.1 | 39.7 | −40.8* | 56.5 | 41.1 | −27.2 |
| Middle(M) | 38.3 | 32.0 | −16.5 | 37.8 | 41.7 | 10.1 | |
| dd-PA1 | Distal | 19.4 | 17.8 | −8.4 | 17.2 | 14.8 | −13.7 |
| Middle | 36.5 | 24.9 | −31.9 | 20.3 | 14.8 | −27.2 | |
| ss-PA2 | Distal | 12.5 | 24.6 | 97.3* | 17.2 | 23.8 | 38.8 |
| Middle | 16.3 | 32.1 | 96.8* | 22.3 | 26.1 | 17.0 | |
| sd-PA3 | Distal | 21.0 | 28.0 | 33.3* | 14.2 | 20.5 | 44.7* |
| Middle | 28.8 | 33.3 | 15.3* | 21.8 | 24.4 | 12.0 | |
| distal | %diff dd-ss4 | −35.7* | 38.5 | 0.1 | 60.9* | ||
| middle | %diff dd-ss5 | −55.2 | 33.9 | 9.6 | 76.1* | ||
| distal | %diff ss-sd6 | 68.4* | 13.7 | −17.4* | −13.9* | ||
| middle | %diff ss-sd7 | 76.6* | 3.5 | −2.3 | −6.5 | ||
dd:Deep fiber point -Deep surface pennation angle (in degrees)
ss:Superficial fiber point -Superficial surface pennation angle (in degrees)
sd: Superficial fiber point -Deep surface pennation angle (in degrees)
% difference between dd and ss w respect to dd in fibers of distal origin
% difference between dd and ss w respect to dd in fibers of middle origin
% difference between ss and sd w respect to ss in fibers of distal origin
% difference between ss and sd w respect to ss in fibers of middle origin
% is change calculated with respect to the young group
significant at p<0.05; two-tailed t-test for independent samples (young-senior age groups)
Discussion
Image Preprocessing
The susceptibility related distortions reported here were substantial due to the large field of view DTI acquisition. While the single acquisition allowed shorter scan times, it also resulted in larger geometric distortions arising from off-centered locations and the inability to effectively shim over the large field of view. While the distortion and motion algorithm from the 3D Slicer has been used in brain DTI analysis, we used the B-spline free form distortion algorithm to correct for susceptibility induced distortions in the lower leg calf muscle. The visual overlays confirmed that the algorithm was able to decrease distortions in the middle and distal muscle regions to within 2 pixels while correction in the proximal regions was less effective. This was due to the much larger distortions in the proximal regions arising from an off center location and more importantly from the susceptibility artifacts from the bone. Since the correction was not as effective in the proximal regions, quantitative analysis of fibers tracked on the corrected tensors was performed in the distal and middle regions only.
Comparison of the three methods for evaluating changes in DTI indices
It should be noted that the ROI method included voxels containing adipose and connective tissue (perimysium) which will affect the true muscle values, with a greater bias expected in the older subjects due to a higher percentage of adipose and connective tissue (22). The resolution of the DTI images is lower than the structural data which made it difficult to locate the regions of connective and adipose tissue directly from the diffusion images. One approach to remove the contribution of adipose and connective tissue from the muscle mask is to exclude the adipose/connective voxels identified from a customized protocol. However, the intramuscular adipose and connective tissues form a thin network around the muscles so that even small registration errors (between the reference fat saturated gradient echo images and DTI) can lead to identification of the wrong voxels in the DTI data. Thus, the adipose and connective tissue voxels were not masked in the ROI method.
Histograms provide a convenient method for analysis, which leverages the statistics of a large number of voxels when analyzing small changes/small cohorts. While it is true that the DTI images do not have the resolution to enable direct identification of the non-muscle voxels, the contribution from these tissues is present in the data. The non-muscle tissue seen on the high resolution images have signal close to noise level in the baseline DTI images (from the long TE of the DTI sequence which suppresses the short T2 connective tissue and from the fat suppression). Thus, the ADC of these voxels will be low (ranging from zero to some partial volume value). This was the basis for deleting, from the DTI indices histogram, the % of voxels with the lowest ADC values corresponding to non-muscle tissue for each subject (determined with an independent imaging sequence). The effect of this deletion on the eigenvalue histograms can be seen as a shift of the mean to the right as well as the greater shift on the older cohort (from the higher % of non-muscular tissue). Interestingly, this exclusion had a different effect on the FA histogram: it deleted higher rather than lower FA values. This is in agreement with the report from Williams et al (23) who showed that the low SNR voxels arising from fat had artifactual high FA values. The advantage of the histogram approach was that it did not require the direct identification of the non-muscle tissue. Further, the shape analysis of the histogram may provide additional information on the heterogeneity of the indices’ distribution. However, in this pilot study, kurtosis and skew were not significantly different between age groups.
The third approach uses tract based statistics. DTI indices are routinely measured on a ROI selected from the anatomic images. It should however be noted that these ROIs could potentially contain fibers originating from different regions (distal, middle and/or proximal). The anatomically correct unit is the fiber and comparison of fiber averaged DTI indices across cohorts may be more meaningful. While fiber tracking is challenging and not always possible (coverage, higher SNR requirements over large FOVs), the first attempts at tract based statistics of the DTI indices in muscle is reported here. The age related increase in eigenvalues is similar to that seen by the ROI and histogram methods. One point to note is that the FA values for fibers originating in the distal regions are higher than those originating at the middle. This could be related to smaller diameters for fibers of distal origin compared to the middle origin fibers.
Comparing the three methods, the tract based is the anatomically relevant measurement and should be the method of choice when the SNR is high and distortions are low and the entire muscle is imaged. Given the challenge to generate fiber tracks in the muscle, the histogram method appears to be a robust method that is based on a large number of voxels provided the non-muscle voxels are excluded. It should be noted that the histogram analysis is a global method while the ROI method has the advantage that it can measure regional changes. However, improvements in image acquisition and fiber tracking, tract based statistics may become the method of choice for regional analysis. The three methods proposed in the current paper provide internally consistent results confirming that the observed small but significant increase in eigenvalues is an accurate finding of age related differences.
Eigenvalues and Fractional Anisotropy changes with age
For a given measurement sequence, the DTI indices including the eigenvalues, ADC and FA depend on several factors including intra- and extracellular diffusion coefficients and T2 values, membrane permeability, cell sizes and the cellular volume fraction (24,25). In the current work, the eigenvalues were slightly larger (significant) in the older cohort; these findings conflict with those reported earlier by Galban, et al. (26) who found that all three eigenvalues decreased with age while the FA was unchanged. They attributed this decrease in eigenvalues to a decrease in muscle fiber cross section and length. While a decrease in fiber diameter is believed to result in a decrease of λ3 and possibly λ2 (14-17), λ1 should not be affected by the changes in fiber length, since the latter is many orders of magnitude larger than the diffusion distances. It should be noted that Galban, et al. (26) calculated the DTI indices from a region of interest placed on a single slice based on a DTI acquisition using six diffusion sensitizing directions. In contrast, the DTI sequence used in the current study was SNR optimized with 32 diffusion gradient encodings and the entire muscle volume was used to calculate the DTI indices (providing greater statistical strength). It is likely that these technical differences may bias eigenvalues and FA which may contribute to the contrasting findings between this study and that of Galban, et al. (26).
Histological studies on aging humans and rodent models show loss of sarcomeres (27), selective atrophy of the larger diameter type II fibers (12,28,29), hypotrophy of all fibers, and increase in the asymmetry of muscle fiber cross-section along with an increase in the amount of intramuscular connective tissues (22, 30, 31). All these changes will influence the measured DTI indices; their combined effect may be quite complex and can only be understood using detailed modeling combined with experimental data. The diffusion model proposed in the Methods section can be extended to include aging related decrease in fiber diameter and in the muscle fiber fraction (increasing extracellular tissue). λ1 is not affected by changes in fiber length or diameter. However, the increasing contribution of the more freely diffusing extracellular tissue contributes to an overall increase in λ1. Decreasing fiber diameters will cause reductions in λ3 and possibly, λ2. However, this reduction is offset by the increasing contribution from the extracellular tissue. This also explains why the effect of aging has a higher increase in λ1 while reduced in the other two eigenvalues (Table 2). Further, the fact that λ1 increases relatively more results in a greater asymmetry of diffusion and is reflected in the small increase in FA values. A DTI/T2 study of the rat model of sarcopenia recently reported that the FA increased significantly with age (from decreasing fiber diameter) with little increase in fibrosis (32). In human subjects reduction in fiber diameter and increase in fibrosis may lead to the observed DTI results; thus the proposed hypothesis based on muscle atrophy alone is not validated by the experimental data. One point to note here is that while the collagen content of the perimysium is high enough to render it MR invisible at the TEs used in the DTI sequence (~50 ms), the endomysium, with a higher water content, contributes to the voxel signal, and thus to the DTI indices (33). The simple model proposed here qualitatively explains the aging changes seen in the diffusion indices; the more detailed model of Karampinos (17) will be required to provide a quantitative agreement.
Fiber Tracking
The fiber length changes with age agree with that obtained by ultra-sound measurements (9,34). The regional dependence of fiber lengths seen here is also anticipated since fibers get shorter from distal to proximal locations. The age related differences in the ‘deep’ pennation angles agree with earlier findings of a decrease in pennation angle with age (9,34). However, in contrast to this, the ‘superficial’ pennation angles increased with age. The superficial angle can differ from the deep angle either due to fiber curvature or from the relative curvature of the two aponeurosis surfaces. Calculation of the angle of the superficial fiber end with the distal aponeurosis should disambiguate these two situations. From an examination of these values, it appears that in the older cohort, fiber curvature contributes to the ‘deep’ and ‘superficial’ angle differences while in the younger cohort, the relative curvature of the deep and superficial aponeurosis may contribute to these differences.
Ward, et al. (32) reported the architectural features (fiber length, pennation angle and the physiological cross-sectional area (PCSA) which is the area of the cross section of a muscle perpendicular to its fibers) of lower extremity muscles from measurements on cadavers. The mean age of the cadavers corresponds to the older cohort in the current study. A coefficient of variation (CV) was provided to account for the heterogeneity of the fiber length. In the MG, the fiber lengths reported by Ward, et al. (35) are 51.0 ± 9.8 mm with a CV of 13.4%. Even taking the CV into consideration, these lengths are 5-10% longer than reported in the current paper; this may be related to differences in body height/ tibial length. MG pennation angles (corresponding to deep-deep) are reported as ~9.9 ± 4.4° (27), which is lower than the ~17.7° measured for the GM in the distal region for the older cohort. Some of this difference in angle may arise from the fact that angle measurements were made in a single plane in the cadaver study (35), which will be the projection of the true 3D angle onto the measurement plane. However, the differences are still larger than can be accounted for by differences in methodology alone. Martin, et al. (36) compared architectural features of the triceps surae from cadavers to in-vivo ultrasound studies. The mean age of their subjects was close to the older cohort in the current study. The in-vivo relaxed fiber lengths of the MG and LG in the latter paper was 43.6 ± 8.6 mm and 41.6 ± 7.4 mm, respectively, which agrees well with the fiber lengths in the current study (Table 4). Martin, et al. (36) reported the anterior angle of pennation (deep-deep in the current study) for the MG and LG as 18.6 ± 3.6° and 16.4 ± 2.6°, which agrees well with the distal pennation angles of the older cohort in this study. However, posterior pennation angles (superficial-superficial in the current study) reported from the ultrasound study do not agree with the higher angles found in the current study. This discrepancy may arise from the fact that ultrasound is a 2D measurement and may underestimate angles where the curvature of the fiber and/or the aponeurosis surface is high.
Narici, et al. (34) explored changes in MG muscle architecture by combining CT for volume and area measurements and ultrasound for fiber length and pennation angle. US measurements were performed at the midbelly level of the muscle; thus comparisons are made to the ‘middle’ fibers. Their study included young (27-42 years) and senior (70-81 years) cohorts, similar in age to the groups compared here. The fiber lengths of the young and senior group of the current study are in general agreement with the US study; fibers were shorter by 10% in the US study compared to a 16% difference seen in the current study. However, the latter difference was not significant presumably due to the smaller sample size of the current study. Pennation angles are smaller in the US study compared to the current one; one explanation may lie in the methodological differences mentioned earlier. The change in pennation angle is a 32% decrease in the current study compared to the 13% decrease in the older cohort seen in the US study.
Morse, et al. (9) studied the lateral gastrocnemius muscles using the same method as described above for the MG. They found no difference in LG fiber length between young and senior cohorts; this is in agreement to the small (and not significant) difference between the two cohorts in this study. A 12% decrease in pennation angles was seen in the older cohort in the US study, as compared to a non-significant 27% difference seen here. It is likely that measurements on the LG are confounded by different levels of compression of the muscle as subjects were scanned supine and the LG status was indeterminate.
The study has limitations; the number of subjects in each cohort was small. However, significant differences in the DTI indices as well as in the fiber architecture were found between the two cohorts. The large field of view enabled the coverage of the MG and LG from origin to insertion in one acquisition; this had the advantage that the scan time was lower than if multiple acquisitions were used to cover the MG and LG with several slabs. However, the downside of the large coverage was the increased geometric distortion artifacts especially at the ends of the FOV. The post-processing addressed most of this distortion; however some residual deformation could still be seen in the corrected images. Another limitation is the diffusion model proposed here which qualitatively explains the results; a more sophisticated model is required to explain the results quantitatively.
In conclusion, this study shows a complicated dependence of the differences in DTI indices with age and reflects the opposing effects of fiber atrophy and fibrosis on the observed eigenvalues and fractional anisotropy changes with age. It emphasizes the need for a model to connect the microstructural differences to the measurable DTI indices. The fiber architecture measures of fiber length and pennation angle show decreases in both parameters with age and this could play an important role in determining aging muscle function. However, fiber tracts based on DTI reveal a more complex fiber arrangement in both the MG and LG, including regional changes in fiber curvature. These findings point to the need for fiber clustering and incorporation of region specific architecture into a structure-function model.
Supplementary Material
Acknowledgements
We would like to thank all subjects for volunteering to participate in this study.
Grant Support: This work was supported by the National Institute of Arthritis and Musculoskeletal and Skin Diseases Grant 5RO1-AR-053343-07 (S.S.).
References
- 1.Lieber RL, Friden J. Functional and clinical significance of skeletal muscle architecture. Muscle Nerve. 2000;23(11):1647–1666. doi: 10.1002/1097-4598(200011)23:11<1647::aid-mus1>3.0.co;2-m. [DOI] [PubMed] [Google Scholar]
- 2.Fukunaga T, Ichinose Y, Ito M, Kawakami Y, Fukashiro S. Determination of fascicle length and pennation in a contracting human muscle in vivo. J Appl Physiol (1985) 1997;82(1):354–358. doi: 10.1152/jappl.1997.82.1.354. [DOI] [PubMed] [Google Scholar]
- 3.Maganaris CN, Baltzopoulos V, Sargeant AJ. In vivo measurements of the triceps surae complex architecture in man: implications for muscle function. J Physiol. 1998;512(Pt 2):603–614. doi: 10.1111/j.1469-7793.1998.603be.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Kwah LK, Pinto RZ, Diong J, Herbert RD. Reliability and validity of ultrasound measurements of muscle fascicle length and pennation in humans: a systematic review. J Appl Physiol (1985) 2013;114(6):761–769. doi: 10.1152/japplphysiol.01430.2011. [DOI] [PubMed] [Google Scholar]
- 5.Blazevich AJ, Gill ND, Zhou S. Intra- and intermuscular variation in human quadriceps femoris architecture assessed in vivo. J Anat. 2006;209(3):289–310. doi: 10.1111/j.1469-7580.2006.00619.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Noseworthy MD, Davis AD, Elzibak AH. Advanced MR imaging techniques for skeletal muscle evaluation. Semin Musculoskelet Radiol. 2010;14(2):257–268. doi: 10.1055/s-0030-1253166. [DOI] [PubMed] [Google Scholar]
- 7.Damon BM, Ding Z, Anderson AW, Freyer AS, Gore JC. Validation of diffusion tensor MRI-based muscle fiber tracking. Magn Reson Med. 2002;48(1):97–104. doi: 10.1002/mrm.10198. [DOI] [PubMed] [Google Scholar]
- 8.Lang T, Streeper T, Cawthon P, Baldwin K, Taaffe DR, Harris TB. Sarcopenia: etiology, clinical consequences, intervention, and assessment. Osteoporos Int. 2010;21:543–559. doi: 10.1007/s00198-009-1059-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Morse CI, Thom JM, Birch KM, Narici MV. Changes in triceps surae muscle architecture with sarcopenia. Acta Physiol Scand. 2005;183(3):291–298. doi: 10.1111/j.1365-201X.2004.01404.x. [DOI] [PubMed] [Google Scholar]
- 10.Narici MV, Maganaris CN, Reeves ND, Capodaglio P. Effect of aging on human muscle architecture. J Appl Physiol (1985) 2003;95(6):2229–2234. doi: 10.1152/japplphysiol.00433.2003. [DOI] [PubMed] [Google Scholar]
- 11.Larsson L, Biral D, Campione M, Schiaffino S. An age-related type IIB to IIX myosin heavy chain switching in rat skeletal muscle. Acta Physiol Scand. 1993;147(2):227–234. doi: 10.1111/j.1748-1716.1993.tb09493.x. [DOI] [PubMed] [Google Scholar]
- 12.Lexell J. Human aging, muscle mass, and fiber type composition. J Gerontol A Biol Sci Med Sci. 1995;50(Spec No):11–16. doi: 10.1093/gerona/50a.special_issue.11. [DOI] [PubMed] [Google Scholar]
- 13.Holloszy JO, Chen M, Cartee GD, Young JC. Skeletal muscle atrophy in old rats: differential changes in the three fiber types. Mech Ageing Dev. 1991;60(2):199–213. doi: 10.1016/0047-6374(91)90131-i. [DOI] [PubMed] [Google Scholar]
- 14.Galban CJ, Maderwald S, Uffmann K, de Greiff A, Ladd ME. Diffusive sensitivity to muscle architecture: a magnetic resonance diffusion tensor imaging study of the human calf. Eur J Appl Physiol. 2004;93(3):253–262. doi: 10.1007/s00421-004-1186-2. [DOI] [PubMed] [Google Scholar]
- 15.Galban CJ, Maderwald S, Uffmann K, Ladd ME. A diffusion tensor imaging analysis of gender differences in water diffusivity within human skeletal muscle. NMR Biomed. 2005;18(8):489–498. doi: 10.1002/nbm.975. [DOI] [PubMed] [Google Scholar]
- 16.Karampinos DC, King KF, Sutton BP, Georgiadis JG. In vivo study of cross-sectional skeletal muscle fiber asymmetry with diffusion-weighted MRI. Conf Proc IEEE Eng Med Biol Soc. 2007;2007:327–330. doi: 10.1109/IEMBS.2007.4352290. [DOI] [PubMed] [Google Scholar]
- 17.Karampinos DC, King KF, Sutton BP, Georgiadis JG. Myofiber ellipticity as an explanation for transverse asymmetry of skeletal muscle diffusion MRI in vivo signal. Ann Biomed Eng. 2009;37(12):2532–2546. doi: 10.1007/s10439-009-9783-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Gillies AR, Lieber RL. Structure and function of the skeletal muscle extracellular matrix. Muscle Nerve. 2011;44(3):318–331. doi: 10.1002/mus.22094. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Du J1, Bydder M, Takahashi AM, Carl M, Chung CB, Bydder GM. Short T2 contrast with three-dimensional ultrashort echo time imaging. Magn Reson Imaging. 2011;29(4):470–482. doi: 10.1016/j.mri.2010.11.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Reeder SB, Pineda AR, Wen Z, Shimakawa A, Yu H, Brittain JH, Gold GE, Beaulieu CH, Pelc NJ. Iterative decomposition of water and fat with echo asymmetry and least-squares estimation (IDEAL): application with fast spin-echo imaging. Magn Reson Med. 2005;54:636–644. doi: 10.1002/mrm.20624. [DOI] [PubMed] [Google Scholar]
- 21.Razali NM, Wah YB. Power comparisons of Shapiro-Wilk, Kolmogorov-Smirnov, Lilliefors, and Anderson-Darling test. J Stat Modeling Anal. 2011;2:21–33. [Google Scholar]
- 22.Zoico E, Corzato F, Bambace C, et al. Myosteatosis and myofibrosis: Relationship with aging inflammation and insulin resistance. Arch Gerontol Geriatr. 2013;57:411–416. doi: 10.1016/j.archger.2013.06.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Williams SE, Heemskerk AM, Welch EB, Li K, Damon BM, Park JH. Quantitative effects of inclusion of fat on muscle diffusion tensor MRI measurements. J Magn Reson Imaging. 2013;38:1292–1297. doi: 10.1002/jmri.24045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Clark CA, Le Bihan D. Water diffusion compartmentation and anisotropy at high b values in the human brain. Magn Reson Med. 2000;44(6):852–859. doi: 10.1002/1522-2594(200012)44:6<852::aid-mrm5>3.0.co;2-a. [DOI] [PubMed] [Google Scholar]
- 25.Ababneh Z, Beloeil H, Berde CB, Gambarota G, Maier SE, Mulkern RV. Biexponential parameterization of diffusion and T2 relaxation decay curves in a rat muscle edema model: decay curve components and water compartments. Magn Reson Med. 2005;54(3):524–531. doi: 10.1002/mrm.20610. [DOI] [PubMed] [Google Scholar]
- 26.Galban CJ, Maderwald S, Stock F, Ladd ME. Age-related changes in skeletal muscle as detected by diffusion tensor magnetic resonance imaging. J Gerontol A Biol Sci Med Sci. 2007;62(4):453–458. doi: 10.1093/gerona/62.4.453. [DOI] [PubMed] [Google Scholar]
- 27.Narici MV, Maffulli N. Sarcopenia: characteristics, mechanisms and functional significance. Br Med Bull. 2010;95:139–159. doi: 10.1093/bmb/ldq008. [DOI] [PubMed] [Google Scholar]
- 28.Andersen JL. Muscle fibre type adaptation in the elderly human muscle. Scand J Med Sci Sports. 2003;13(1):40–47. doi: 10.1034/j.1600-0838.2003.00299.x. [DOI] [PubMed] [Google Scholar]
- 29.Nilwik R, Snijders T, Leenders M, et al. The decline in skeletal muscle mass with aging is mainly attributed to a reduction in type II muscle fiber size. Exp Gerontol. 2013;48(5):492–498. doi: 10.1016/j.exger.2013.02.012. [DOI] [PubMed] [Google Scholar]
- 30.Alnaqeeb MA, Al Zaid NS, Goldspink G. Connective tissue changes and physical properties of developing and ageing skeletal muscle. J Anat. 1984;139(Pt 4):677–689. [PMC free article] [PubMed] [Google Scholar]
- 31.Serrano AL, Munoz-Canoves P. Regulation and dysregulation of fibrosis in skeletal muscle. Exp Cell Res. 2010;316(18):3050–3058. doi: 10.1016/j.yexcr.2010.05.035. [DOI] [PubMed] [Google Scholar]
- 32.Esposito A, Campana L, Palmisano A, et al. Magnetic resonance imaging at 7T reveals common events in age-related sarcopenia and in the homeostatic response to muscle sterile injury. PLoS ONE. 2013;8(3):e59308. doi: 10.1371/journal.pone.0059308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Light N, Champion AE. Characterization of muscle epimysium, perimysium and endomysium collagens. Biochem J. 1984;219(3):1017–1026. doi: 10.1042/bj2191017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Narici MV, Maganaris CN, Reeves ND, Capodaglio P. Effect of aging on human muscle architecture. J Appl Physiol. 2003;95(6):2229–2234. doi: 10.1152/japplphysiol.00433.2003. [DOI] [PubMed] [Google Scholar]
- 35.Ward SR, Eng CM, Smallwood LH, Lieber RL. Are current measurements of lower extremity muscle architecture accurate? Clin Orthop Relat Res. 2009;467(4):1074–1082. doi: 10.1007/s11999-008-0594-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Martin DC, Medri MK, Chow RS, et al. Comparing human skeletal muscle architectural parameters of cadavers with in vivo ultrasonographic measurements. J Anat. 2001;199(Pt 4):429–434. doi: 10.1046/j.1469-7580.2001.19940429.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.