3D representations of amino acids—applications to protein sequence comparison and classification

Abstract

The amino acid sequence of a protein is the key to understanding its structure and ultimately its function in the cell. This paper addresses the fundamental issue of encoding amino acids in ways that the representation of such a protein sequence facilitates the decoding of its information content. We show that a feature-based representation in a three-dimensional (3D) space derived from amino acid substitution matrices provides an adequate representation that can be used for direct comparison of protein sequences based on geometry. We measure the performance of such a representation in the context of the protein structural fold prediction problem. We compare the results of classifying different sets of proteins belonging to distinct structural folds against classifications of the same proteins obtained from sequence alone or directly from structural information. We find that sequence alone performs poorly as a structure classifier. We show in contrast that the use of the three dimensional representation of the sequences significantly improves the classification accuracy. We conclude with a discussion of the current limitations of such a representation and with a description of potential improvements.

1. Introduction

Proteins, the end products of the information encoded in the genome of any organism, play a central role in defining the life of this organism as they catalyze most biochemical reactions within cells and are responsible, among other functions, for the transport of nutrients and for signal transmission within and between cells. As a consequence, a major focus of bioinformatics is to study how the information contained in a gene is decoded to yield a functional protein. The overall principles behind this decoding are well understood. The sequence of nucleotides that forms a gene is first translated into an amino acid sequence, following the rules encoded in the genetic code. The corresponding linear chain of amino acids becomes functional only when it adopts a three-dimensional shape, the so-called tertiary, or native structure of the protein. This is by no means different from the macroscopic world: most proteins serve as tools in the cell and as such either has a defined or adaptive shape to function, much like the shapes of the tools we use are defined according to the functions they need to perform. It is worth noting that if the paradigm shape-defines-function is the rule in biology, intrinsically disordered proteins form a significant class of exceptions, as they lack stable structures [1,2]. Shape however remains important for those proteins, although it is its flexibility and plasticity that is of essence, as shown for example in the case of P53 [3].

The rules that relate the amino acid sequence of a protein to its three-dimensional structure have not yet been unraveled however. Finding these rules is in fact one of the “holy grails” in molecular biology, namely the protein structure prediction problem [4–14]. Efforts to solve this problem currently focus on protein sequence analysis, as a consequence of the wealth of sequence data resulting from various genome-sequencing projects, either completed or ongoing. There were more than 540,000 protein sequences deposited in SwissProt–Uniprot version 2014–04, the fully annotated repository of protein sequences, as of early April 2014. Data produced by these projects have already led to significant improvement in predictions of both protein 3D structures and functions (see for example [15]). However, we still stand at the dawn of understanding the information encoded in the sequence of a protein. In this paper, we focus on protein sequence representations and show how geometry can play a role in decoding the information content of a sequence.

The order in which amino acids appear defines the primary sequence of a protein. Amino acids are usually labeled using a one-letter code, and sequences are correspondingly represented as a usually long string of letters. This representation has proved very valuable, especially in the context of sequence comparisons that are performed using string-matching algorithms. It does however carry limitations: letters alone poorly represent the physical and chemical properties of amino acids and as such are usually difficult to decipher. One option to improve the interpretation of a sequence is to consider multiple letters at once, such as in the SCS package that deciphers protein sequences based on the frequencies of its short constituent sequences (SCS), or words [16]. Alternatively, computer programs that represent protein sequences often resort to different coloring schemes [17,18] to facilitate their interpretation (see, for example, the ClustalX windows interface for improving the readability of multiple sequence alignments [19]), or to increase their information content (see, for example, the SAS server that encodes the 3D structure of a protein on its sequence using a color coding scheme [20]). Note that a coloring scheme ultimately corresponds to adding dimensions to the representation of a protein sequence in order to help decipher its information content. This concept of increased dimensions was applied to the representation of multiple sequence alignments using Hilbert curves [21] as well as to the representation of individual sequences using non-Latin alphabet to represent individual amino acids [22].

Encoding amino acids as arrays of numerical values is a very attractive idea, as it results in an increase of the information associated to a protein sequence and consequently enables more sophisticated analyses of their functions. Scheraga and colleagues may have been the first to implement this concept, proposing to represent each amino acid with ten orthogonal characteristic factors obtained by principal component analyses of more than one hundred and eighty physico-chemical properties of the twenty amino acids [23]. This representation has been used to analyze and compare protein sequences using Fourier analysis [24–27], with such applications as fold recognition for homology modeling [28]. We note that a key advantage of numerical representations of amino acids is that it allows for more sophisticated metrics for comparing sequences [29].

The idea of representing amino acids with numbers can naturally be extended to the idea of a geometric representation of protein sequences, as originally introduced by Swanson [30]. She started with the observation that the 20 × 20 Dayhoff's amino acid substitution matrix [31] is equivalent to providing a representation of amino acids in a 20 dimensional feature space. By applying dimension reduction techniques, she proposed three lower dimensional representations of amino acids in 1D, 2D, and 3D spaces, and concluded that the 2D version is the most reasonable as it was consistent with other observations she had made on amino acid properties [32]. Using this 2D model, protein sequences are then visualized by concatenating the vectors representing their amino acids in the order they appear, yielding a vector representation of proteins (VRP). Since the original work of Swanson, many new geometric representations of protein sequences have been proposed [22,33–51]. These various representations have been used for detecting and measuring similarities between sequences [30,44,45,47,49], to study the evolution of protein sequences [50], to predict cleavage sites in protein [36], to predict the 3D fold of a protein [48], to predict sub-cellular locations of proteins [35], to predict the location of protein domains [34,41], and to provide a representation of the full protein sequence space [51]. Those that represent amino acids as vectors relate the directions and amplitudes of these vectors to the physico-chemical properties of the amino acids [39,43,44,46–48], to amino acid compositions in protein sequences [50], to evolution information [30,36,41], or simply follow the main axes of the feature space considered [38] or are uniformly distributed along a curve [37]. We note that among all these new representations of protein sequences, the vector representations introduced by Maetschke and colleagues [36] and Gu et al. [41] are most akin to the representation introduced by Swanson [30]. Both research groups agreed that an extension of the VRP to higher dimensions performed best in identifying either putative cleavage sites [36] or domains in proteins [41].

This paper draws from this concept and describes a feature-based representation of protein sequences, in which each amino acid is encoded by a unique three-dimensional (3D) vector of features. In a preliminary report [41], we had shown how the BLOSUM62 [52] substitution matrix can be scaled down to 3 dimensions, generating 3D vectors for all amino acid types. We then generated full 3D geometric representations of protein sequences by concatenating the vectors representing their amino acid residues in the order they appear and used this representation to detect domains in large protein sequences [41]. In this paper, we extend the field of applications of the 3D protein sequences and propose to compare two protein sequences by finding the optimal superposition between their 3D representations. We have tested this alternate method for comparing protein sequences in the context of protein sequence classification. Namely, we consider a large dataset of proteins that belong to five different folds, as defined by CATH [53]. These proteins were selected such that their sequences share little sequence similarities. We classified these proteins into five clusters using three measures of similarity based on sequence information alone, the 3D representation of a sequence described above, and full structure information, respectively. We have observed that sequence alone provides poor separation of the different folds. We show in contrast that the use of the three dimensional representation of the sequences significantly improves the classification accuracy.

The paper is organized as follows. The next section provides descriptions of the databases and computational methods used for this study. The following section extends upon our preliminary report [41] by providing more in depth analyses of the information content of different BLOSUM matrices. It also illustrates our 3D representations of amino acids and proteins. The result section provides applications of these representations for protein structure fold prediction. We then conclude with a discussion of future research directions.

2. Materials and experimental procedures

2.1. Dataset of Protein Sequences

The first set of structures considered in this study is extracted from the database of 2930 sequence-diverse CATH v2.4 domains used in a previous study [54]. As we focus on protein structure fold prediction, we consider the first three levels of CATH, Class, Architecture and Topology, to give a CAT classification. We refer to a set of structures with the same CAT classification as a fold. Using a set of structures with sufficient sequence diversity ensures that the data is duplicate-free and that the problem of detecting structural similarity is non-trivial for all pairs of proteins considered. The 2930 structures were selected as follows: (i) Sort all 34,287 CATH v2.4 domains by their SPACI score [55]; (ii) Start with the domain with highest SPACI score, and remove from the list all domains that share significant sequence similarity with it (FASTA [56] E-value < 10^− 4). (iii) Repeat step (ii) with all domains in the list that have not been removed. The set of 2930 domains resulting from this procedure is referred to as CATH2930.

There are 769 folds in CATH2930, many of which only contain a single element (482). To facilitate statistical analysis, we selected five of the most populated folds in CATH2930 as a more specific test set, including at least one fold from each CATH class: CATH fold 1.10.10, a fully α fold (arc repressor, 62 representatives), CATH fold 2.60.40, a fully β fold (immunoglobulin-like, 169 representatives), and three alternating α/β folds: 3.20.20, (TIM-like, 67 representatives), 3.30.70, (two layer sandwich, 92 representatives) and 3.40.50 (Rossmann fold, 215 representatives). These five folds include a total of 605 proteins of CATH2930 (set CATH605) [57]. Table S1 in Supplementary Materials provides the list of all 605 proteins broken down into the five different folds. Fig. 4 below shows examples of protein structures for each of these five folds.

Fig. 4.

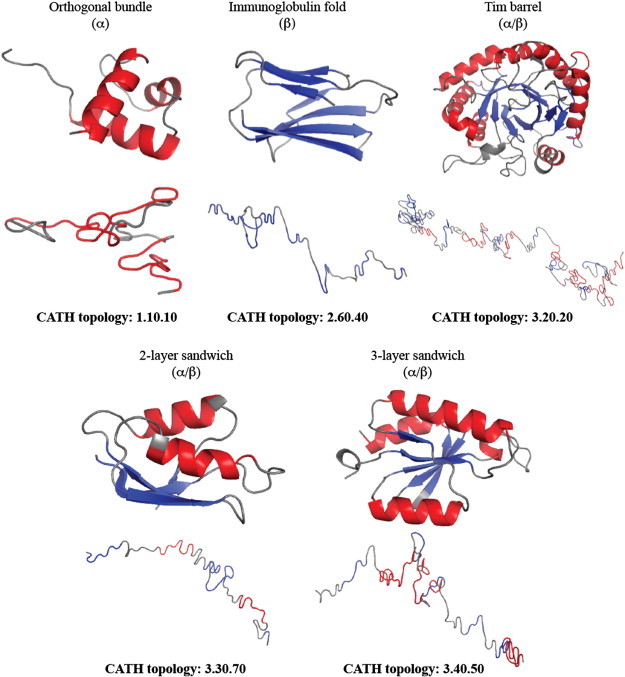
Representatives of the five fold classes in our test set. The arc repressor mutant, subunit A fold (CATH 1.10.10) is a common orthogonal helix bundle, found for example in the DNA-binding domain of the human telomeric protein HTRF1 (CATH code 1ba500). The immunoglobulin-like fold (CATH 2.60.40) is a β sandwich, found in many immunoglobulin-like proteins, such as the rat CD4 protein (CATH code 1cid02). The TIM barrel (CATH 3.20.30) is a very common α/β fold, shown in narbonin, a plant seed protein (CATH code 1nar00). The α/β plait fold (CATH 3.30.70) is a two-layer sandwich, shown here in MERP, a mercury binding protein (CATH code 2hqi00). The Rossmann fold (CATH 3.40.50) is a very common 3-layer sandwich fold in the mixed α/β class, found for example in the glycyl-tRNA synthetase from thermus thermophilus (CATH code 1atiB2). For each protein we show the cartoon representation of its structure (top) and the 3D trace of its sequence (bottom). Regions corresponding to helices and strands are shown in red and blue, respectively. All images were generated using PYMOL (http://www.pymol.org).

The second set of proteins considered in this study is extracted from a more recent release of CATH, CATH3.5, which was the release of CATH available in June 2014. A subset of domains with low sequence similarities was built using a procedure similar to the one used to generate CATH2930: (i) Randomize all 173,536 domains of CATH3.5; (ii) Start with the first domain in the randomized list, and remove all domains that share significant sequence similarity with it (FASTA [56] E-value < 10^− 4). (iii) Repeat step (ii) with all domains in the list that have not been removed. The set of 8862 domains resulting from this procedure is referred to as CATH35_E4.

2.2. Alignments of two protein structures or traces

We have used STRUCTAL [58] to perform geometric alignments of two curves representing either the 3D CA-trace of the protein structures or the 3D representations of the protein sequences (described below). STRUCTAL assumes an initial alignment (a correspondence of residues in the two structures), and gets the rigid-body transformation that superimposes the corresponding residues. It then finds an optimal alignment for this superposition. The new alignment is used to superimpose the structures again and the procedure is repeated till it converges to a local optimum that depends on the initial alignment. In an attempt to reach the global optimum, STRUCTAL starts with several different correspondences. For a given correspondence, the optimal transformation is the one with minimal coordinate root mean square displacement (cRMS, see Eq. (2) below) and STRUCTAL uses the procedure by Kabsch [59] to find it. For a given transformation, the optimal correspondence is the one with a maximal STRUCTAL score, and STRUCTAL uses dynamic programming to find it. The STRUCTAL score is defined as:

$$S={\displaystyle \sum _i\frac{20}{1+5\mathit{dist}{\left(a_i,b_i\right)}^2}}-10N_{\mathit{gap}}\text{,}$$ (1)

where the summation extends over all positions i in the correspondence, dist(a_i,b_i) the distance in space between the α-carbon (CA) atoms of the ith residue pair in the correspondence and N_gap is the total number of gaps in the alignment. Three of the initial correspondences are: aligning the beginnings, the ends and the midpoints of the two structure chains without allowing any gaps. The fourth initial correspondence maximizes the sequence identity of the chains and the fifth is based on similarity of α-carbon torsion angles between the two chains.

The traditional measure of similarity between two protein structures after optimal alignment is the root mean square displacement of atomic positions, also called cRMS for coordinate root mean square displacement, computed as:

$$\mathit{cRMS}=\sqrt{\frac{1}{N_{\mathit{mat}}}{\displaystyle \sum _i\mathit{dist}{\left(a_i,b_i\right)}^2}}\text{,}$$ (2)

where N_mat is the number of positions in the correspondence. The cRMS however is not a good measure of structural similarity [54,60]. Intuitively, a measure based on the geometric properties of an alignment should favor alignments with many matched residues, low cRMS deviations, and few gaps. Unfortunately, these properties are not independent. For example, a lower cRMS deviation can always be achieved by selecting a shorter match; given the fixed inter-CA distance there is the extreme case of many alignments of just two residues that have cRMS deviation of 0 Å. Also, by allowing additional gaps, the alignment can be lengthened without necessarily increasing the cRMS deviation. Different measures attempt to balance these values in different ways. In this work, we consider the Structural Alignment Score, SAS:

$$\mathit{SAS}=100\frac{\mathit{cRMS}}{N_{\mathit{MAT}}}\text{,}$$ (3)

originally introduced by the authors of STRUCTAL [58].

2.3. Principal Component Analyses (PCA) of BLOSUM matrices

Let us consider a set of N objects, each characterized by a set of P measured features. As such, each object can be considered as a point in a P-dimensional space, where P can be large. Not all P features are equally important however, and some of these features may be highly correlated. To capture the principal components that describe the objects and thereby reduce the dimension of the space in which they lie, it is common to perform a principal component analysis (PCA). PCA can be thought of as fitting an N-dimensional ellipsoid to the data matrix D (N rows, P columns), where each axis of the ellipsoid represents a principal component. If some axes are small, then the variance along those axes is also small, and by omitting those axes we lose only a small amount of information.

To find the axes of the ellipsoid, we first center the values for each feature by subtracting their means, which amounts to centering the data matrix D at the origin:

$$D_c\left(i,j\right)=D\left(i,j\right)-\frac{1}{N}{\displaystyle \sum _{k=1}^{N}D\left(k,j\right)}\text{.}$$ (4)

We then estimate the covariance matrix C of the data from the centered data matrix D_C:

$$C=\frac{1}{N-1}{D}_C{D_C}^T$$ (5)

where a factor N − 1 is used instead of N as the mean values for the P features are computed from the data, and not known a priori. Then, we calculate the eigenvalues of this covariance matrix and their corresponding eigenvectors. The latter provide the directions of the axes of the ellipsoid, while the former give the corresponding sizes of the ellipsoid along these axes.

2.4. Multi Dimensional Scaling (MDS) based on distance geometry

Multi Dimensional Scaling (MDS) is a technique designed to visualize the levels of similarity of individual objects in a data set S [61]. It is particularly appropriate when the similarities between the N objects in S have been computed using a distance on S, leading to a N × N distance matrix D. An MDS algorithm aims to place each object in a low dimensional space (usually two or three dimensions) such that the between-object distances are preserved as well as possible. Each object is then assigned coordinates in each of the projected dimensions.

Distance geometry is one technique that implements MDS [62]. In this technique, the distance matrix D is converted into a matrix G according to:

$$G\left(i,i\right)=\frac{1}{N}{\displaystyle \sum _{j=1}^N{d}_{\mathit{ij}}^2}-\frac{1}{2N^2}{\displaystyle \sum _{i=1}^N{\displaystyle \sum _{j=1}^N{d}_{\mathit{ij}}^2}}$$ (6)

$$G\left(i,j\right)=\frac{1}{2}\left(G\left(i,i\right)+G\left(j,j\right)-d_{\mathit{ij}}^2\right)\text{.}$$ (7)

The matrix G is then assimilated to the metric matrix of the N points in a Euclidean feature space E of dimension P, i.e. such that G(i,j) is the inner product of the vectors representing the data point i and data point j in E. The next step computes the first P principal eigenvectors V and corresponding eigenvalues λ from the matrix G and then projects all data points on these principal eigenvectors, such that the k-th coordinates of point i is given by:

$$X\left(i,k\right)=\sqrt{{\lambda }_k}V\left(i,k\right)\text{.}$$ (8)

The number of dimension P is given as input to the algorithm. It is usually chosen to be 2 or 3, thereby generating a low dimensional mapping of the points.

2.5. Evaluating clustering using the Average Inter-Cluster Separation (AIS)

Given a representation of a set of objects in a low dimensional space S, it is possible to evaluate this representation if these objects are known a priori to cluster into M clusters. If the features defining the mapping capture well the differences between the objects, these M clusters ought to be well separated. We evaluate this statement using the Average Inter-cluster Separation (AIS):

$$\mathit{AIS}=\frac{1}{M\left(M-1\right)}{\displaystyle \sum _{i=1}^{M-1}{\displaystyle \sum _{j=i+1}^{M}d\left(C_i,C_j\right)}}$$ (9)

where the distance between the two clusters C_i and C_j is defined as:

$$d\left(C_i,C_j\right)=\frac{1}{\left|C_i\right|\left|C_j\right|}{\displaystyle \sum _{i\in C_i}{\displaystyle \sum _{j\in C_j}{d}_S\left(i,j\right)}}$$ (10)

d_S(i,j) is the distance in the Euclidean space S between the data points i and j and |C_i| is the size of cluster C_i. If two clusters C_i and C_j are well separated, all inter distances between their members are expected to be large and the average distance d(C_i, C_i) is consequently large. A therefore larger value for AIS means better cluster configuration.

3. Geometric representation of protein sequences

3.1. A geometric representation of amino acids

Common measures of similarities between amino acids are usually presented in the form of a substitution matrix, which stores the odds that any given amino acid can be replaced by any other. Substitution matrices can be compiled based on substitutions observed in protein sequence families [63], or directly from amino acid physico-chemical properties (see, for example, [64]). In sequence-based substitution matrices, amino acids that are frequently mutually substituted are regarded as similar. Schwartz and Dayhoff [31] were the first to compile such a matrix, using 71 groups of closely related proteins (i.e., with more than 85% pairwise sequence identity), and collecting the data of point accepted mutations, or PAMs. Henikoff and Henikoff [52] extended this concept to include more divergent sequences and generated the BLOSUM matrices. BLOSUM matrices are derived from BLOCK sequence alignments. Different cutoffs in the accepted sequence identity within a BLOCK lead to different BLOSUM matrices. For example, BLOSUM62 is a substitution matrix derived from protein sequence alignments in which the sequences are at least 62% identical; it is considered to provide good performance for database search. The PAM and BLOSUM matrices are routinely used within protein sequence alignment programs such as FASTA [56] and BLAST [65]. As such they are available as part of the distributions of this program; they can also be downloaded directly from the public server of the National Center for Biotechnology Information (NCBI; ftp://ftp.ncbi.nih.gov).

Substitution matrices describe each amino acid with a set of twenty numerical values, henceforth defining a twenty-dimensional space. While such a high-dimensional space is useful for computer-guided sequence alignment methods, it is impractical for any form of visualization. Swanson was the first to embed the space corresponding to the original PAM matrix into a plane, using a principal component analysis (PCA) approach [30]. More recently, Maetschke et al. [36] and Gu et al. [41] proposed to embed the BLOSUM62 matrix into feature spaces of five dimensions and three dimensions, respectively, noticing that three dimensions already produce a reasonably good approximation of the high dimensional space.

To further characterize which feature space dimension to use for different BLOSUM matrices, we repeated the embedding of the latter in spaces with increasing dimensions. In their approach to lower the dimension of a substitution matrix, both Swanson [30] and Maetschke et al. [36] converted first the substitution matrix into a “distance” matrix by exponentiation of the scores included in the matrix. We keep instead the substitution matrix as it is. Each column corresponds to a different amino acid, while each row is treated as a probe of a property of that amino acid. The substitution matrix is analyzed using PCA (see Materials and Experimental Procedures). The eigenvalues E(i) for i = 1,…, 20 of the corresponding correlation matrix represent the distribution of the “energy” of the input matrix among the eigenvectors, which form an orthogonal basis for the matrix. The cumulated energy up to dimension k (also called the explained variance) is given by:

$$\mathit{Var}\left(k\right)=\frac{{\displaystyle \sum _{i=1}^{k}E\left(i\right)}}{{\displaystyle \sum _{i=1}^{20}E\left(i\right)}}\text{.}$$ (4)

In Fig. 1, we show the explained variances for feature spaces of dimension k = 2, 3, and 5 for the different BLOSUM matrices.

Fig. 1.

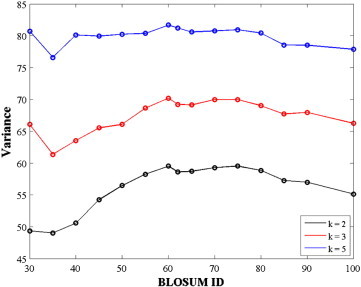
Information content of amino acid substitution matrices. The cumulative energy (variance, in %) of the two (k = 2, black), three (k = 3, red), and five (k = 5, blue) largest eigenvalues of BLOSUM substitution matrices are plotted as functions of the matrix ID.

BLOSUM matrices with high ID numbers (such as BLOSUM90) were computed from highly similar sequences, while BLOSUM matrices with low ID numbers were computed from alignments of sequences that included many mutations. Interestingly, the explained variances for these matrices in low dimensions (k = 2 and k = 3) show similar flat patterns in the range BLOSUM60 to BLOSUM80, with a weak optimum at BLOSUM60. The corresponding optimal variances are 59% and 71% for k = 2 and k = 3, respectively. We note that the differences between BLOSUM matrices decrease as the dimension of the feature space increases: for k = 5, all matrices behave similarly, with approximately 80% of their variance explained.

The principal components of a BLOSUM matrix identified by PCA correspond to linearly uncorrelated variables that best explain the data it contains. In Fig. 2, we study how the three most significant principal components vary for different BLOSUM matrices. The variations are computed as the dot products of the principal components of the matrix of interest with the corresponding principal components of the BLOSUM100 matrix.

Fig. 2.

Changes in principal components of BLOSUM matrices as a function of the BLOSUM ID. The three main components computed by PCA of the given BLOSUM matrices are compared to the corresponding component of BLOSUM100 using dot products.

The three main principal components of the BLOSUM substitution matrices do not change significantly for IDs between 100 and 45. In a previous study we had shown that these components relate to hydrophobicity, size, and secondary structure content of proteins [41]. Large changes however occur for lower IDs, i.e. for more permissive substitution matrices computed from the alignments of sequences with low cutoffs (< 40%) in sequence identity, indicating that other factors become more important for those matrices.

Once the eigenvalues and eigenvectors of the centered covariance matrix corresponding to a BLOSUM matrix are known, amino acids are assigned “coordinates” along these eigenvectors. In Fig. 3, we show the corresponding vectors in three dimensions, for BLOSUM30, BLOSUM62, and BLOSUM90. As intuitively expected from the results shown in Fig. 2, the 3D vector representations of the amino acids do not change significantly when we compare BLOSUM62 and BLOSUM90 but differ in BLOSUM30. For the latter matrix, the 3D representations of hydrophobic (in blue) and hydrophilic amino acids remain well separated. There is however more overlap between hydrophobic and aromatic amino acids (in yellow), and between hydrophilic amino acids and the two small amino acids A and G (in green). Table S2 in Supplementary Materials list the N-dimensional coordinates of the twenty amino acids derived from BLOSUM62, for N = 1, 2,3,4, and 5.

Fig. 3.

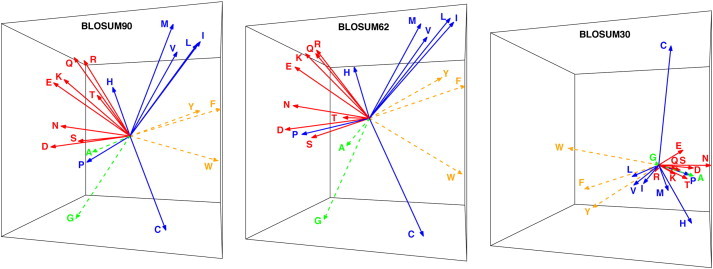
These plots represent the 3D vector representations of amino acids as derived from the BLOSUM90 (left), BLOSUM62 (center) and BLOSUM30 (right) matrices. The proximity of these vectors relate to the chemical similarities of the amino acids they represent. To highlight this fact, we show the known polar amino acids (Q, R, E, K, N, D, T, and S) in red, the hydrophobic amino acids (M, V, L, I, H, P, and C) in blue, and the aromatic amino acids (Y, F, and W) in yellow. Note that the two small amino acids, A and G, stand out. Note also that Cysteine (C), and Tryptophan (W) though non-polar, differs from all other amino acids. Cysteine can form disulfide bridges, usually highly conserved in proteins. Tryptophan is a large aromatic amino acid that is also highly conserved.

We prefer a 3D representation of amino acids as it allows for easy visualization as well as direct use of geometry for comparison. The results illustrated in Figs. 1 to 3 indicate that it is best to use BLOSUM matrices in the range of 60 to 70 for such a representation. In the following, we will therefore use BLOSUM62 as our reference matrix. This is consistent with the fact that this matrix is considered to provide good performance for database search.

3.2. A geometric representation of protein sequences

A sequence of a protein describes the succession of its amino acids from its N-terminal end to its C-terminal end. It is usually encoded as a string of letters, one for each residue in the protein, with each letter specific to one of the twenty amino acids. In the section above, we have shown that representing amino acids as 3D vectors improves the decoding of their properties. We extend this geometric concept to the representation of the whole sequence of a protein by direct “head-to-tail concatenation” of the vectors representing its constituent amino acids. A protein sequence then becomes a polyline in 3D space, which we refer to as the 3D trace of the protein sequence. In Fig. 4 we show examples of 3D traces of proteins for five proteins belonging to three different structural classes, namely α, β, and α/β classes. In the following section we show applications of this geometric representation of protein sequences for sequence comparison and prediction of protein structure classes.

4. Protein sequence classifications

Two proteins with highly similar sequences almost always share the same fold. The reverse, however, is not always true: Rost [66] has shown that pairs of proteins with similar structures possess, on average only 8–10% sequence identity: this observation is one of the main reasons that it is difficult to classify proteins based on sequence only. Here, we test an alternative approach to standard sequence comparison in which we use the 3D trace of the protein sequence to compare and classify proteins. We compare classifications obtained with the 3D trace with classifications derived from sequence only and from 3D structures. We use CATH605 as our test set. CATH605 is a database of 605 protein sequences that covers the three main classes of CATH: one fully α fold (arc repressor mutant), 1.10.10, one fully β fold (immunoglobulin fold), 2.60.40, and three α/β folds (TIM fold, 3.20.20, an α/β plait, 3.30.70, and the Rossmann fold, 3.40.50) (see Materials and Experimental Procedures section above). CATH605 was designed such that the sequences of any pair of proteins in the set have statistically no similarity (FASTA E-value > 10^− 4) [54,57].

4.1. Examples of protein comparison based on the 3D traces of their sequences

The 3D trace of a protein sequence is a polygonal chain in space, i.e. a connected series of line segment, with each segment representing one amino acid in the sequence. As such, it mimics (but is not equivalent to) the Cα trace of a protein structure, i.e. the polygonal chain obtained by drawing line segments between contiguous CA atoms in the three dimensional structure of the protein. Fig. 4 shows examples of protein structures and their corresponding 3D sequence traces for each of the five folds in CATH605. As observed, sequence traces adopt different shapes. There are no obvious correlations between kinks within the 3D trace and the presence of secondary structures in the protein (Fig. 4). Previous studies however have hinted at the possibility that significant changes in the direction of the 3D sequence trace of a protein map with domain junctions in multi-domain proteins [41].

As the 3D trace of a protein sequence is a polygonal chain, the comparison of two 3D sequence traces can be achieved through 3D superposition. In particular, it is possible to use a protein structure superposition program, as long as this program does not limit itself to the specific geometry of proteins. STRUCTAL is one such tool [58]. STRUCTAL searches for an optimal alignment of two protein structures using a trial-and-error approach in which an initial alignment is assumed and subsequently refined using dynamic programming (see Methods above for more details). We have used STRUCTAL to compare pairs of protein structures that are known to belong to the same CATH class, as well as to compare the corresponding 3D sequence traces of these proteins. Examples for the five classes included in CATH605 are shown in Fig. 5. For each pair of proteins, we show the superposition of their structures (left panels) and the superposition of their 3D sequence traces (right panels). As expected, the overlaps based on structures show that for each pair the proteins share similar geometry and topology. The cRMS values are between 1.7 and 4.2, i.e. consistent with significant similarities.

Fig. 5.

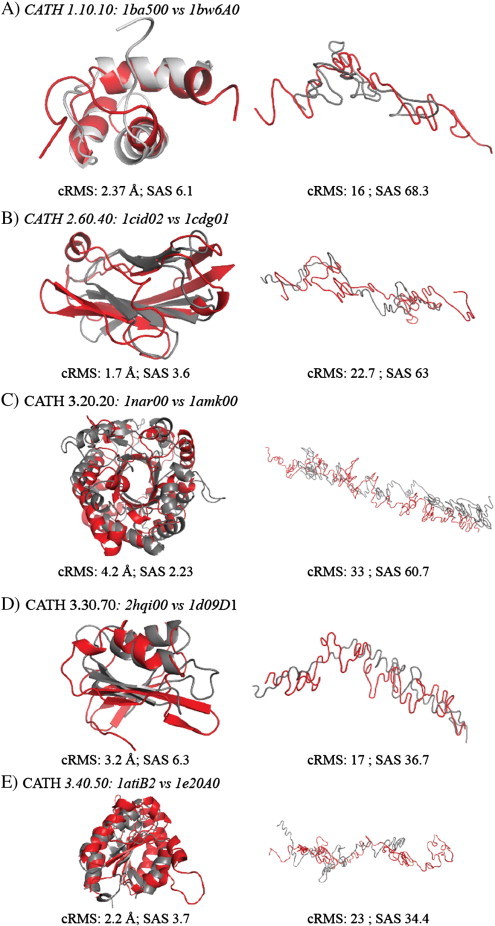
Superposition of the structures (left) and 3D sequence traces (right) for pairs of proteins belong to the five CATH classes included in CATH605.

Interestingly, the 3D sequence traces show significant similarities that parallel the similarities observed from structures. In particular, major changes in direction in the 3D sequence traces are conserved for the 3D traces of two proteins belonging to the same structural class: this is observed for the pairs (1ba500, 1bw6A0), (2hqi00, 1d09D1) and for the central kink in the proteins (1atiB2, 1e20A0). In contrast, the 3D traces of proteins (1nar00, 1amk00) that belong to the TIM fold are both mostly linear. The alignment of the two 3D sequence traces corresponding to proteins 1cid02 and 1cdg01 is the less convincing of the five alignments shown in Fig. 5. We note that the cRMS values (and corresponding SAS values) reported for the alignment of 3D sequence traces are not as easily interpreted as the cRMS obtained for a protein structure alignment. Indeed, the lengths of the linear fragments that form a 3D sequence trace are not equal and have been derived from a BLOSUM matrix that was not designed to represent geometric properties.

4.2. Fold recognition based on 3D sequence traces

The results shown above for the five pairs of structures considered, while significant for these specific structures, may be anecdotic when considering the whole fold space. To assess the relevance of comparing 3D sequence traces for fold recognition, we repeated the comparisons described above for all pairs of non-identical proteins in CATH605. For each pair, we computed the STRUCTAL alignment of their 3D structures and the STRUCTAL alignment of their 3D sequence traces. In Fig. 6, we show the distributions of SAS values obtained from these alignments, with the SAS based on 3D structure as x-axis, and the SAS based on 3D sequence trace as y-axis.

Fig. 6.

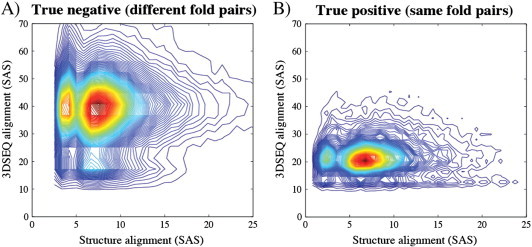
Density distributions of the SAS scores obtained when comparing proteins from CATH605, with the SAS scores based on their 3D structures on the x-axis, and the SAS scores based on their 3D sequence traces on the y-axis. Both SAS scores were computed using STRUCTAL. (A) Data from 137,221 pairs, including only those pairs of proteins in different folds. (B) Data from 45,489 pairs, including only those pairs of proteins that belong to the same fold. Comparison of A and B shows that pairs of proteins from the same fold have lower SAS values on average than those from different folds, both based on 3D structures and based on 3D sequence traces.

CATH605 contains 605 proteins that belong to 5 folds (see Materials and Experimental Procedures). Out of all 182,710 pairs of non-identical proteins it contains, 137,221 correspond to proteins that belong to different folds. While most of the alignments between two proteins from different folds are not expected to be significant globally, it is possible to find good local matches, for example at the level of secondary structures. It is therefore not surprising that the SAS scores for these pairs of proteins cover a large range of values, from 2 to 68 with a mean value of 8 for the SAS scores of the structural alignments of the proteins, and from 7 to 320 with a mean value of 38 for the SAS scores of the alignments of the 3D sequence traces of the proteins. CATH605 also contains 45489 pairs of proteins that belong to the same CATH fold. Interestingly, the SAS scores for those pairs of proteins are shifted towards lower values (i.e. better alignments) when compared to the SAS scores of different fold pairs (Fig. 6B versus Fig. 6A). The SAS scores for the same fold pairs cover a range from 0.52 to 44.2 with a mean value of 4.65 for the 3D-structure-based alignments, and a range from 7 to 162 with a mean of 33 for the 3D sequence trace alignments. The improved SAS scores for same fold pairs illustrate the effectiveness of alignments based on either 3D structures or on 3D sequence traces to identify fold similarity.

4.3. Visualizing the protein fold space for CATH605

We extended the analysis of our sequence similarity measures to the problem of detecting fold membership by generating different representations of the feature space in which the proteins of CATH605 belong, one for each similarity measure considered. For each pair of proteins, we computed the FASTA E-value obtained from comparing their sequences using the SSEARCH version 3.6 tool of FASTA, with BLOSUM62 as a scoring matrix and gap penalties of − 11 and − 1 for opening and extending a gap, respectively, the STRUCTAL SAS score obtained when comparing their 3D sequence traces, and the STRUCTAL SAS score obtained when comparing their 3D structures. These calculations yield three distance matrices for all 605 proteins. We project the information contained in these matrices on a P dimensional space using Multi Dimensional Scaling (MDS; see Materials and Experimental Procedures). Results are shown in Fig. 7 for P = 2. We also estimate the effectiveness of the 3 distance measures in identifying proteins with similar structures (folds) by measuring the Average Inter-cluster Separation (AIS; see Materials and Experimental Procedures on how to compute AIS) between the representations of the five clusters corresponding to the five folds included in CATH605, as well as the mean distances between any cluster and the four other clusters. Results are given in Table 1.

Fig. 7.

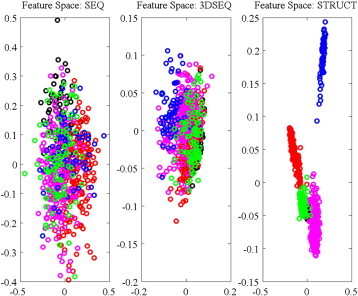
2D representations of the protein fold space corresponding to CATH605. All pairs of proteins from CATH605 are compared using FASTA on their native sequences (left panel), STRUCTAL on their 3D sequence traces (middle panel), or STRUCTAL on their 3D structures (right panel). The corresponding distance matrices are then projected on a two-dimensional plane using MDS. Each protein of CATH605 is represented as a circle on this plane, whose color is assigned based on the fold it belongs to: black for CATH class 1.10.10 (all α proteins), red for CATH class 2.60.40 (all β proteins), and blue, magenta and green for CATH classes 3.20.20, 3.30.70 and 3.40.50, respectively (mixed α/β folds) (see text for details).

Table 1.

Assessing the effectiveness of 3 distance measures (FASTA, STRUCTAL on 3D sequence traces, and STRUCTAL on 3D structures) in identifying proteins with similar structures.

	MDS spacea
	FASTA				3DSEQ				3DSTRUCT
Cluster	2	3	4	5	2	3	4	5	2	3	4	5
1	30.8b	36.6	43.6	47.6	34.5	41.7	47.0	50.6	39.7	60.7	62.2	77.0
2	32.6	38.9	45.2	49.5	31.3	39.7	46.0	50.2	56.8	71.0	72.2	76.6
3	27.7	34.4	41.4	45.5	44.1	50.9	56.7	59.4	82.5	87.1	88.00	90.9
4	28.3	34.9	42.4	47.3	31.8	40.0	45.5	49.3	40.7	54.5	56.9	71.2
5	28.7	35.0	41.3	45.6	33.2	42.2	49.3	52.9	50.2	67.0	70.4	74.6
AIS	29.6c	35.9	42.8	47.1	35.0	42.9	48.9	52.5	54.0	68.0	70.0	78.1

^aDimension P of the MDS projected space, i.e. number of coordinates representing each protein. Fig. 7 provides illustrations of this space for P = 2.

^bAverage distance dav = 0.25 ∑ _j ≠ id(C_i, C_i), where d is computed using Eq. (10). The distances are scaled as fraction of the maximum distance between any two proteins in CATH605.

^cAverage Inter-cluster Separation (AIS) computed using Eq. (10). A large value for AIS indicates a good separation between the clusters.

The five folds in the CATH605 dataset ought to be represented as five clusters in the low dimensional mapping obtained by MDS. If the distance measure defining the mapping captures well the differences between the folds, these five clusters ought to be well separated. This is indeed observed visually for the SAS distance measure based on structural alignment (right panel, Fig. 7) and quantified with the AIS as shown in Table 1. In contrast, the five folds overlap significantly in the MDS mapping based on the FASTA E-value, i.e. based on direct sequence information (left panel). For example, the AIS for the 2D representation of the five clusters based on structure comparison is 54.0, significantly larger than the 29.6 obtained for the 2D representation based on FASTA scores. The MDS mapping based on the distances between the 3D-sequence traces of the proteins show improvement compared to the latter, with an intermediate AIS of 35.0. In particular, we observe that proteins from fold 3, i.e. CATH 3.20.20 (2-layer sandwich) shown in blue start to separate from the other proteins: the mean distance between fold 3 and the other folds is 27.7 based on FASTA distances, and 44.1 based on STRUCTAL comparisons of the 3D sequence traces. This is consistent with the results obtained directly from 3D structure comparison, as we observe that fold 3.20.20 is well separated from all the other four folds based on a structure-based distance measure, with a mean separation value from the other folds of 82.5. The same overall trends were observed for higher dimensional projection spaces (see Table 1).

4.4. ROC analysis of protein homology detection

To better quantify the effectiveness of the three distance measures used in the previous section to generate the 2D-representations of the protein fold space corresponding to CATH605, we evaluate their performances using the receiver operating characteristic (ROC) analysis [67]. The five folds in CATH605 serve as the standard. A pair of proteins is defined as similar, or “positive”, if they belong to the same fold, and “negative” otherwise. All pairs of proteins in CATH605 are then compared using a similarity measure. For varying thresholds of the measure, all pairs below the threshold are assumed positive, and all above it are negative. The pairs that agree with the standard are called true positives (TP), while those that do not are false positives (FP). ROC analysis compares the rate of TP as a function of the rate of FP; it is scored with the area below the corresponding curve. A ROC score of 1 indicates that all TP are detected first: this corresponds to the ideal measure. On the other hand, a ROC score of 0.5 corresponds to the first diagonal: TP and FP appear at the same rate, and the measure is not discriminative.

ROC analysis of protein comparison based on FASTA E-values, STRUCTAL SAS scores for 3D sequence traces, and STRUCTAL SAS scores for 3D structures are shown in Fig. 8.

Fig. 8.

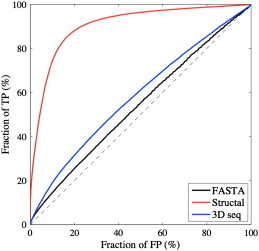
ROC analyses of three measures of protein similarity. We compare the effectiveness of sequence only (compared with FASTA), 3D sequence traces (compared with STRUCTAL), and 3D structures (compared with STRUCTAL) to detect fold similarity in a set of 605 proteins. “True” relationships are defined by CATH topologies. Curves close to the first diagonal (such as the ROC curve for FASTA) indicate poor performance, while the upper most curve (such as the 3D structure-based curve) indicates good performance.

FASTA search tool [56] implements a fast Smith and Waterman sequence comparison; the similarity is given either as a raw score, or as an E-value; we use the latter as a similarity measure. The ROC curve for the FASTA measure is marginally above the first diagonal, with a score (area) of 0.53: this is expected, as by construction all protein pairs in CATH605 have little or no sequence similarity.

Assignment of structural fold is expected to work best when it is based on 3D structural information. Indeed, The ROC curve obtained based on distances computed as the SAS STRUCTAL scores obtained when comparing the X-ray structures of the proteins illustrates excellent classification results, with a ROC score of 0.91. We note that even with X-ray structure information the classification is not perfect. This again is not a surprise. CATH is a semi-automatic classification of protein structures and some proteins are included in the same class based on more information than structure alone [53]. As such, two proteins may belong to the same class even though their structures are loosely similar. In addition, structural alignment programs work with heuristic algorithms and as such may miss the optimal alignment [54]. That said, STRUCTAL scores based on X-ray structures still perform remarkably well.

The ROC curve based on STRUCTAL alignments of 3D sequence traces is intermediate between the two other curves, although much closer to the sequence-based distance measure. Clearly, the addition of evolution information from BLOSUM62 captured in the form of 3D vectors improves the classification of proteins into fold. This improvement is small, from a ROC score of 0.53 to a ROC score of 0.59. To assess the significance of this small difference, we performed a statistical analysis on a set of ten CATH605-like datasets. We first generated ten CATH2930-like databases as follows: (i) Randomize all 34,287 CATH v2.4 domains; (ii) Start with the first domain in the randomized list, and remove from the list all domains that share significant sequence similarity with it (FASTA E-value < 10^− 4). (iii) Repeat step (ii) with all domains in the list that have not been removed. Each set of 2930 domains resulting from this procedure is referred to as SET2930I, where I is an index between 1 and 10. We then selected randomly from each of these sets 62 representatives from CATH fold 1.10.10, 169 representatives from fold 2.60.40, 67 representatives from fold 3.20.20, 92 representatives from fold 3.30.70, and 215 representatives from fold 3.40.50, to generate ten datasets similar to CATH605, albeit with a random selection process. These datasets are referred to setI, for I between 1 and 10. The average overlap (i.e. percentage of shared proteins) between any of these sets and CATH605 is 20.9%. The results of ROC analyses of protein comparison based on FASTA E-values, STRUCTAL SAS scores for 3D sequence traces, and STRUCTAL SAS scores for 3D structures, for all 10 randomized setI are given in Table 2.

Table 2.

ROC analyses of the effectiveness of three measures of protein similarity in classifying proteins in CATH folds.

	ROC areaa
Set	FASTA on native sequences	STRUCTAL on 3D sequence traces	STRUCTAL on 3D structures
Set1	0.56	0.61	0.94
Set2	0.56	0.60	0.92
Set3	0.56	0.60	0.92
Set4	0.56	0.60	0.92
Set5	0.57	0.60	0.92
Set6	0.56	0.60	0.92
Set7	0.56	0.61	0.92
Set8	0.56	0.60	0.92
Set9	0.56	0.60	0.92
Set10	0.56	0.61	0.92
CATH605	0.53	0.59	0.91

^aArea under the ROC curve, with 0.5 corresponding to the score of a random classifier, and 1.0 corresponding to the score of a perfect classifier.

The scores for all three distance measures are remarkably similar over all 10 random sets mimicking CATH605 and consistent with the scores obtained directly on CATH605. These results emphasize that though the difference between comparing native sequences and comparing 3D sequence traces is small, this difference is significant.

All ROC analyses described above relate to five specific folds. To assess the extent with which these results are influenced by the choice of these five folds, we repeated the analyses on two much larger datasets, namely CATH2930 and CATH35_e-4, which contain 2930 and 8862 proteins from 769 and 1306 folds, respectively. Results are given in Table 3.

Table 3.

ROC analyses of the effectiveness of two measures of protein similarity in classifying proteins in CATH classes, architectures, and folds.

	FASTA on native sequences			STRUCTAL on 3D sequence traces
Dataset	Classa	Architecturea	Folda	Class	Architecture	Fold
CATH2930	0.53b	0.54	0.57	0.56	0.55	0.62
CATH35_e-4	0.53	0.53	0.56	0.56	0.54	0.61

^aResults are given at three levels of the CATH hierarchy.

^bArea under the ROC curve.

CATH2930 contains proteins from 4 classes, 38 architectures, and 769 topologies, or folds based on our terminology, based on the CATH hierarchy. The differences between the classification powers at the fold level of FASTA on native sequences, and STRUCTAL on 3D sequence traces are consistent with the differences observed on the 5 folds of CATH605. Interestingly, classifications into classes and architectures are less effective than classifications into folds, for both native sequences and 3D sequence traces. The same behaviors are observed on the larger CATH35_e-4 database that contains proteins from 4 classes, 40 architectures, and 1306 topologies.

4.5. Classification of proteins into folds

The ROC analysis detects protein similarity. We extended the analysis of our protein similarity measures to the problem of detecting fold membership by performing a set of computational fold classification experiments. In each experiment, we randomly divide the sets of proteins for all five folds that form CATH605 into two groups of approximately equal size: the first group serves as a reference set to define the folds, while the second group serves as a test set. A test protein p is classified into one of the five folds F_j by computing first the average distances d(p,F_j) from i to the reference proteins belonging to F_j and second by choosing F_j such d(p,F_j) is minimal over j. The results are stored in a confusion matrix, such that element (i,j) of this matrix shows how many proteins belonging to fold i are classified as belonging to fold j. The accuracy of the classifier is then defined as the ratio of the trace of the confusion matrix over the sum of all its elements (i.e. the percentage of correctly classified proteins). To remove possible bias from the initial separation of the protein set into test and training sets, the procedure is repeated 1000 times.

We performed these experiments for the three types of distances between proteins, namely the FASTA E-values computed from sequence only, the STRUCTAL SAS scores computed from 3D sequence traces, and the STRUCTAL SAS scores computed from the X-ray 3D structures. The corresponding classification accuracies were 4.8 ± 1.0, 10.9 ± 1.1, and 97.7 ± 0.7, respectively. Clearly, sequence alone provides poor classification with only 5% on average of the sequences being correctly classified. This value is more than doubled when evolution information is added to the sequence information in the form of geometric vectors. For comparison, the classification based on 3D structure information remains one order of magnitude more accurate.

5. Discussion

The traditional approach to comparing two protein sequences starts from the strings of letters representing these sequences, where each letter corresponds to an amino acid type, a separable scoring function for comparing these letters, and uses dynamic programming to find either the best global alignment or the best local alignment between the two sequences [68]. Unfortunately, it is not easy to find the parameters of a scoring function that best captures the similarity between amino acid types. This has led to the development of many types of scores in the form of substitution matrices in the hope of producing biologically meaningful sequence alignments [31,52,63,69]. It remains that when the similarity between the two proteins to be compared is low, the quality of the corresponding sequence alignment is usually poor. This has led to sequence alignment techniques being poor methods for classifying protein into folds [57] or detecting homology [66], both essential tasks in the hope of solving the protein structure prediction problem.

There have been many methods developed to circumvent these problems. More reliable detection of structure similarity can be achieved for example if sequence similarity is defined on the basis of families of sequences, rather than on the basis of the native sequence alone [70]. This fact is at the root of all profile methods used in modern database searching programs such as PSIBLAST [71] and HMMER [72]. In this paper we have explored another alternative approach to string matching for protein sequence alignment. We have shown that amino acids can be encoded by 3D vectors, thereby allowing us to generate a geometric representation of their properties. We derived one set of 3D vectors, based on the BLOSUM62 substitution matrix [52]. Interestingly, integrating information from BLOSUM62 matrix into the protein sequence amounts to capturing information coming from evolution and as such is (distantly) related to the profile methods mentioned above. Concatenation of the vectors corresponding to the successive amino acids in a protein sequence generates the 3D sequence trace of the protein. We have shown that performing superpositions of the 3D sequence traces of proteins using the protein structure alignment STRUCTAL [58] provide better classifications of proteins into structural folds than direct comparisons of their sequences using FASTA. The performances of sequence comparison through the 3D sequence traces are not yet good enough to become a viable replacement to computationally intensive procedures such as structural alignment tools. These observations lead to two main questions: why are 3D sequence traces performing better than sequences + substitution matrices, and how can we improve comparisons of 3D sequence traces to make them more reliable?

It appears as though the alignments of two protein sequences using FASTA or using STRUCTAL on their 3D traces are based on the same information, namely the sequence of amino acids and evolution information extracted from a substitution matrix. The SSEARCH tool of FASTA proceeds by aligning the two strings of letters representing the sequences based on the local dynamic programming method [73], using a substitution matrix as a scoring scheme when comparing the letters. In this study, we have used BLOSUM62 for all FASTA alignments. In parallel, we give as input to STRUCTAL the 3D traces of the sequences, that are computed from the sequences of amino acids in the proteins and their 3D representations derived from the BLOSUM62 matrix. The key difference however between these two approaches lays in the way the BLOSUM62 matrix is used. SSEARCH only considers BLOSUM62 as a table that stores individual scores (i,j) for substituting amino acid type i into amino acid type j. The 3D vectors representing amino acid types that are computed from the BLOSUM62 matrix on the other hand take into account correlations between the values stored in the matrix. Interestingly, it was shown that the three main principal components of the BLOSUM62 matrix, from which the 3D vectors are derived, relate to properties of amino acids in proteins, namely hydrophobicity, size, and secondary structure content [41]. We believe that it is this information, implicitly included in the 3D vectors, that is responsible for the improved performances observed for 3D sequence traces.

There are several directions to explore to improve the performance of protein sequence comparison based on the 3D sequence traces.

In this study, we have encoded amino acids into 3D vectors starting from a substitution matrix (BLOSUM62), namely evolution information. Following others, we could have used instead physico-chemical properties of amino acids [39,43,44,46–48], amino acid compositions in protein sequences [50] or even combinations of these properties. It would also be possible to represent each amino acid using a vector that contains its propensities to belong to a helix, a β strand, or a turn. Such vectors, and the corresponding 3D traces, should prove useful for predicting the fold of a protein. We are currently developing this representation.

There are many ways to combine the 3D vectors corresponding to the amino acids into a complete representation for the entire sequence of a protein. We have relied on probably the simplest of such representations, namely the concatenation of the vectors. We will investigate whether other graphical representations support highly effective visual and quantitative extraction of the information contained in a protein sequence.

We have used STRUCTAL, a standard protein structure alignment program, to generate the superposition of the 3D sequence traces of two proteins. While STRUCTAL has been shown to be effective for aligning 3D structures of proteins [54], it is not clear that it is the most appropriate tools for aligning sequence traces, as those do not resemble protein structures. STRUCTAL is based on an iterative, heuristic procedure [58]. Assuming an initial alignment, STRUCTAL gets the rigid-body transformation that superimposes the corresponding positions. It then finds an optimal alignment for this superposition. The new alignment is used to superimpose the traces again and the procedure is repeated till it converges to a local optimum. This algorithm is general enough that it should apply to aligning 3D sequence traces, with one exception. The optimal alignment is selected based on a score (see Materials and Experimental Procedures) that proved adequate for protein structure alignment. There is no reason to believe however that the same score will perform well for aligning 3D sequence traces. We are aware of this limitation and we plan on resolving it by developing new geometric tools for registering 3D protein sequence traces.

Appendix A. Supplementary Data

Supplementary Material.

Table S1: The 605 proteins included in CATH605, divided according to their CATH classifications.

Table S2: Coordinates of the N-dimensional vectors representing the twenty amino acids, computed from a PCA analysis of BLOSUM62.