Harmonic Motion Imaging (HMI) for Tumor Imaging and Treatment Monitoring

Abstract

Palpation is an established screening procedure for the detection of several superficial cancers including breast, thyroid, prostate, and liver tumors through both self and clinical examinations. This is because solid masses typically have distinct stiffnesses compared to the surrounding normal tissue. In this paper, the application of Harmonic Motion Imaging (HMI) for tumor detection based on its stiffness as well as its relevance in thermal treatment is reviewed. HMI uses a focused ultrasound (FUS) beam to generate an oscillatory acoustic radiation force for an internal, non-contact palpation to internally estimate relative tissue hardness. HMI studies have dealt with the measurement of the tissue dynamic motion in response to an oscillatory acoustic force at the same frequency, and have been shown feasible in simulations, phantoms, ex vivo human and bovine tissues as well as animals in vivo. Using an FUS beam, HMI can also be used in an ideal integration setting with thermal ablation using high-intensity focused ultrasound (HIFU), which also leads to an alteration in the tumor stiffness. In this paper, a short review of HMI is provided that encompasses the findings in all the aforementioned areas. The findings presented herein demonstrate that the HMI displacement can accurately depict the underlying tissue stiffness, and the HMI image of the relative stiffness could accurately detect and characterize the tumor or thermal lesion based on its distinct properties. HMI may thus constitute a non-ionizing, cost-efficient and reliable complementary method for noninvasive tumor detection, localization, diagnosis and treatment monitoring.

1 Introduction

1.1 Imaging

Since tumors are in general harder than the surrounding tissues [1], self and clinical breast examinations using palpation are commonly used to detect the presence of abnormalities that could indicate pathologies. Several imaging techniques other than mammography [2], mainly ultrasound and MRI, have been developed to estimate tissue stiffness and thus detect tumors, with various forms of tissue perturbation for the detection of stiffer masses [3].

In the field of ultrasound, Krouskop et al. [4] applied dynamic indentation at 0.1, 1, and 4 Hz, and at different pre-compression strain levels (i.e., 5 and 20%) to measure ex vivo breast tissue elastic moduli. They showed that the elastic moduli of breast tissues do not change with the frequency of the applied displacement. This demonstrates that the breast tissue samples behave as an elastic material, i.e., viscous component is insignificant with the parameters used. ‘Sonoelasticity imaging’ or ‘sonoelastography’ has been proposed for the detection of inclusions in a vibrating medium [5–10]. They estimated the amplitude (and/or phase) of the periodic movement of tissues by estimating the resulting Doppler shift [5, 11, 12]. Sonoelastography has been applied on ex vivo breast tissues [13] and have started clinical trials for non-palpable breast lesion detection [14–19]. Ophir et al. [20] developed the method of elastography that applies a small external static compression (on the order of 1%) and used cross-correlation techniques on radio frequency (RF) signals in order to estimate tissue strains resulting from external compression [20]. This method has been proven to produce good quality strain images (or, elastograms) in the breast in vivo [21–24]. Several clinical trials have been initiated to establish elastography in a clinical setting, and the capability of the method for the noninvasive breast cancer detection and diagnosis [25] is currently being established.

Sarvazyan et al. have implemented elastography using a hand-held scanning device that combined a transducer probe and a 2D pressure sensor array. This method provides a real-time 2D pressure pattern and elasticity map, and is termed as tactile imaging (TI), or ‘stress imaging’, or ‘mechanical imaging (MI)’ [26–28].

Quasi-static elastographic techniques have also been demonstrated as feasible methods for the detection of breast cancer in vitro using magnetic resonance imaging (MRI) [29]. In MR Elastography (MRE), tissue mechanical properties (e.g., shear modulus) are mapped based on the observed phase shift of the MR signal in response to an external mechanical vibration [30]. MRE could provide a tissue displacement map incurred by the low-frequency shear wave induced by the external excitation. The shear wave velocity is dictated by the local shear modulus. MRE used the propagating shear wave to reconstruct the local shear modulus of the medium.

MRE has been applied in the imaging of breast tumors and various breast tissues, with the aim to explore shear modulus imaging for the diagnosis of breast lesions [31–37]. The in vivo measurement of the shear modulus using MRE has shown that there was good separation between malignant and benign (i.e., fibro-adenoma and mastopathy) tumors based on their shear moduli [36]. However, the measured shear viscosity did not show a clear distinction between benign and malignant masses, which might be related to different static pre-compression strain levels applied on tissues [35].

Transient elastography (TE) has also been tested and validated as a quantitative technique of soft tissue viscoelastic properties [38]. Bercoff et al. applied this technique clinically for breast tumor detection [39].

Apart from the aforementioned external excitation techniques, more recently, ultrasound-based internal perturbation methods have emerged that can produce a concentrated force in a targeted region, deep inside the tissue and can be used for probing and analyzing tissue properties within the targeted region. Several research groups have applied the so-called radiation force to induce brief mechanical excitations locally and either imaged the resulting tissue response while RF data are collected during tissue relaxation [40, 41], or analyzed the resulting shear wave propagation (Supersonic Shear Imaging (SSI) [42, 43], and shear wave elasticity imaging (SWEI) [44]) or resulting vibration (Ultrasound-Stimulated Vibroacoustography (USVA) [47–50] and Harmonic Motion Imaging (HMI) [52, 53]). Table 1 provides a summary of these internal excitation methods and their relative differences.

Table 1.

Currently available radiation force techniques

Methods	Motion is tracked		Imaging method used	Excitation
	After (relaxation)	During excitation
Acoustic radiation force impulse (ARFI)	✓		Modified linear array transducer	Impulse
Supersonic shear imaging (SSI)	✓		Modified 1D array transducer	Impulse
Shearwave dispersion ultrasound vibrometry (SDUV)		✓	Ultrasound or vibrometry	Oscillatory force
Shear wave elasticity imaging (SWEI)		✓	Ultrasound or acoustic detector	Oscillatory force (low kHz)
Vibroacoustography		✓	Hydrophone	Oscillatory force (low kHz)
Harmonic Motion Imaging (HMI)		✓	Ultrasound (pulse-echo/phased-array transducer)	Oscillatory force (10–50 Hz)

ARFI imaging applies a short-duration acoustic radiation force to generate localized displacements in tissues, and the resulting displacements are tracked during relaxation using cross-correlation based methods. The tissue response is monitored both spatially and temporally. ARFI has been applied, e.g., to detect cancerous breast lesions and lymphnodes in vivo [45] and the resulting ARFI image showed a stiffer inclusion which was determined to be an infected lymph node at core biopsy.

Initial clinical evaluation of in vivo elastography for breast lesion imaging using SSI was reported by Tanter et al. [46]. The SSI technique uses a modified 1D array transducer to generate a radiation force that results in transient shear wave propagation. An ultrafast imaging sequence is performed to acquire successive radiofrequency (RF) signals at high frame rates. The results demonstrated that the SSI elasticity maps could detect breast masses and provide quantitative information on their stiffness.

In Ultrasound-Stimulated Vibro-Acoustography (USVA) [47–50], two confocal ultrasound transducers and a hydrophone are used. The interference of two confocal ultrasound transducers at slightly different frequencies (low kHz range) causes a vibration at the focus. The amplitude or phase of the shear wave is recorded by a hydrophone and used to form an image by repeating the procedure at multiple points across the object. USVA has been applied on the human breast in vivo and shown capable of detecting microcalcifications regardless of the breast density [49, 50, 51].

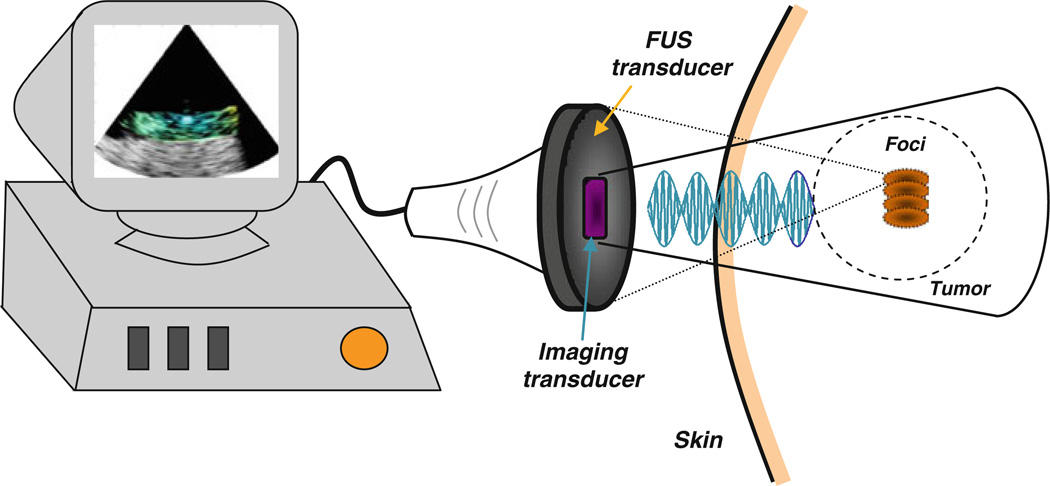
HarmonicMotion Imaging (HMI) [53–58] is an all-ultrasound based technique for both imaging of tumors and monitoring of thermal lesion formation (Fig. 1). Two separate HMI systems have been reported (Table 2). Both HMI systems consist of a single-element focused ultrasound (FUS) transducer and an ultrasound imaging transducer. Both systems use an amplitude-modulated waveform to produce an internal vibration that is spatially invariant [53]. This internal vibration is used to interrogate the tissue mechanical properties. Theoretical and experimental studies of the HMI technique using two separate FUS transducers have been previously reported [54]. Finite-element and Monte-Carlo simulations were used to simulate the oscillatory displacement within an applied force frequency range of 200–800 Hz. The force was applied at the specific nodes within the focal region in a finite-element model (FEM) [55]. However, the applied radiation force amplitude was not realistic because the 2D acoustic pressure field had not been taken into account until recently [72].

Figure 1.

Illustration of the HMI setup in vivo

Table 2.

Summary of the HMI systems used

	HMI-1	HMI-2
FUS transducer	MHz single-element FUS transducer (Imasonic)	MHz single-element FUS transducer (Imasonic)
Imaging transducer	Single-element pulse-echo transducer (Panametrics)	Phased-array transducer (64 element) (Ultrasonix)
Parameters
Center frequency	7.5 MHz	3.3 MHz
Bandwidth	60%	60%
Sampling frequency	80 MHz	40 MHz
PRFa/FRb	PRF = 5.4 kHz	FR = 200–400 frames/s
Filter process	Analog bandpass filter	Digital low pass filter
Advantages	Higher axial resolution Higher temporal resolution Integrated with current DAQ and computer control positioner	Simultaneous B-mode. 2D view of the targeted region. Image deeper into the tissue. Data acquisition up to 6 s
Disadvantages	No 2D view of the targeted region Data acquisition is limited up to 1 s	Lower axial resolution. Lower temporal resolution. Suboptimal data synchronization
Objectives	Monitoring of thermal treatment Tumor mapping for pre- and post-treatment assessment	Monitoring of thermal treatment. Tumor mapping for pre- and post-treatment assessment. Quantitative measurement of viscoelastic parameters

^aPRF pulse repetition frequency

^bFR frame rate

Localized Harmonic Motion (LHM) is a technique similar to HMI that uses a series of quasi-static excitations at a specific rate. Heikkila et al. [76, 77] have developed a LHM simulation framework to test the performance of LHM for lesion detection which they have also demonstrated in vivo [78]. Two configurations were simulated involving either a 1D linear phased array transducer, or two confocal single-element transducers, for both sonication and imaging. A burst waveform with several repetition frequencies (e.g., 50, 100, and 150 Hz) was then used to induce dynamic excitation inside a medium. Their simulation findings indicated good agreement with the in vivo LHM experimental results in rabbit muscle [76, 77].

HMI is unique among other elasticity imaging techniques in the sense that it provides a spatially localized distribution of an oscillatory acoustic radiation force that can be applied across a wide range of frequencies. The dynamic tissue response at the interrogated region can be related to the underlying tissue mechanical properties, which may differentiate healthy from diseased tissue in simulations [59], phantoms and in a transgenic breast cancer murine model in vivo [60] as well as indicate reliably the underlying stiffness [61].

The application of the HMI system for sonication and monitoring thermal ablation has been demonstrated in in vitro and ex vivo livers [62], as well as in a transgenic breast cancer murine model in vivo [60]. In this chapter, we provide examples from these studies in order to show how HMI images could be used as complementary information for detection and diagnosis of pathological tissues.

1.2 High-Intensity Focused Ultrasound Monitoring

High-Intensity Focused Ultrasound (HIFU) is the only truly noninvasive and non-ionizing tumor treatment method. Unlike RF ablation [59–64], HIFU does not require a tissue incision or needle insertion, but instead induces heat extracorporeally [64–68]. The general consensus from several studies used in vivo has been that extracorporeal HIFU is both safe and acceptable to patients [70] and has been shown as a very effective and safe treatment of uterine fibroids in the clinic [71]. The HIFU focus can lie at several centimeters within the body. The focal spot size is approximately 1–3 cm³ and the highest acoustic energy can be deposited only at the focus for the localized ablative treatment [72]. There is no or very low heating along the beam path. High acoustic energy at the localized focus can cause temperature elevation that is sufficient to initiate coagulative necrosis in tissues (thermal lesions), while the surrounding tissues and organs remain intact.

The limitations of HIFU lie in efficiently monitoring temperature changes during treatment, and the current lack of ability to optimally stop the treatment upon lesion formation. The ability of HIFU to cause irreversible cell damage in tissues has been shown to treat early-stage breast cancer [73]. HIFU typically induces thermal and mechanical (or, cavitation) effects on cells in order to annihilate their function. Despite successful monitoring using MRI-based imaging techniques [73], the current lack of low-cost and reliable monitoring methods may result in the confinement of this promising treatment technique to large research centers worldwide with the exception of certain hospitals in the US [70]. In other words, HIFU is in itself a low-cost treatment technique that currently requires an extremely costly monitoring device: an MRI system. Our group has recently shown that the same therapeutic beam used in HIFU can be used to probe the tissue before, during and after ablation. In other words, the same HIFU device can be used to detect [52, 53], monitor [62] and ablate [62] the tumor. As mentioned above, the main advantage is that the technique is stiffness-sensitive and in perfect alignment with the treatment reference frame. During monitoring, HMI is a radiation-force-based technique that induces oscillatory displacements in the focal zone of the HIFU transducer for the detection of localized stiffness changes. HMI does not thus require any contact or external tissue vibration or compression or image co-registration. The combination of detection and treatment into a single device of Harmonic Motion Imaging for Focused Ultrasound (HMIFU [58]) has been shown successful in monitoring lesion formation in real-time in porcine liver ex vivo [58, 70] and detection of tumors ex vivo and in vivo [56]. Due to its use of standard pulse-echo ultrasound methods, B-mode ultrasound images together with the HMI images can be used for both detection and monitoring. The HMIFU technique may thus constitute the low-cost, real-time, fully-integratable and noninvasive image-guidance technique for successful tumor ablation. In short, we aim at developing and assessing the potential of an integrated system for localization and treatment monitoring of tumors, fibroadenomas or invasive ductal carcinomas that can combine standard diagnostic and therapeutic ultrasound in order to more economically and efficiently translate the latter to the clinic as well as expand its range of applications.

2 Methods and Results

2.1 Theoretical Framework for HMI Performance Assessment with Experimental Validation

The performance of HMI in estimating displacements in tissues has been determined and validated in experimental phantoms [55]. In order to assess its capabilities, a theoretical framework was developed [55]. A rectangular mesh with a total of 2,771 nodes and 5,424 triangular elements was assembled. The mesh had an axial length of 35 mm and a lateral width of 30 mm (Comsol Multiphysics™, Comsol Inc., Burlington, MA, USA). For simplicity, the mesh was assumed to be a purely elastic medium with an assigned Poisson’s ratio of 0.49, density of 1.0 g/cm³ and Young’s moduli of 20, 40, and 60 kPa [55]. The model was assumed to be in a plane-strain state. Finer triangular elements allowed accurate simulation of the spatial distribution and the consequent tissue response to acoustic pressure of the HMI technique.

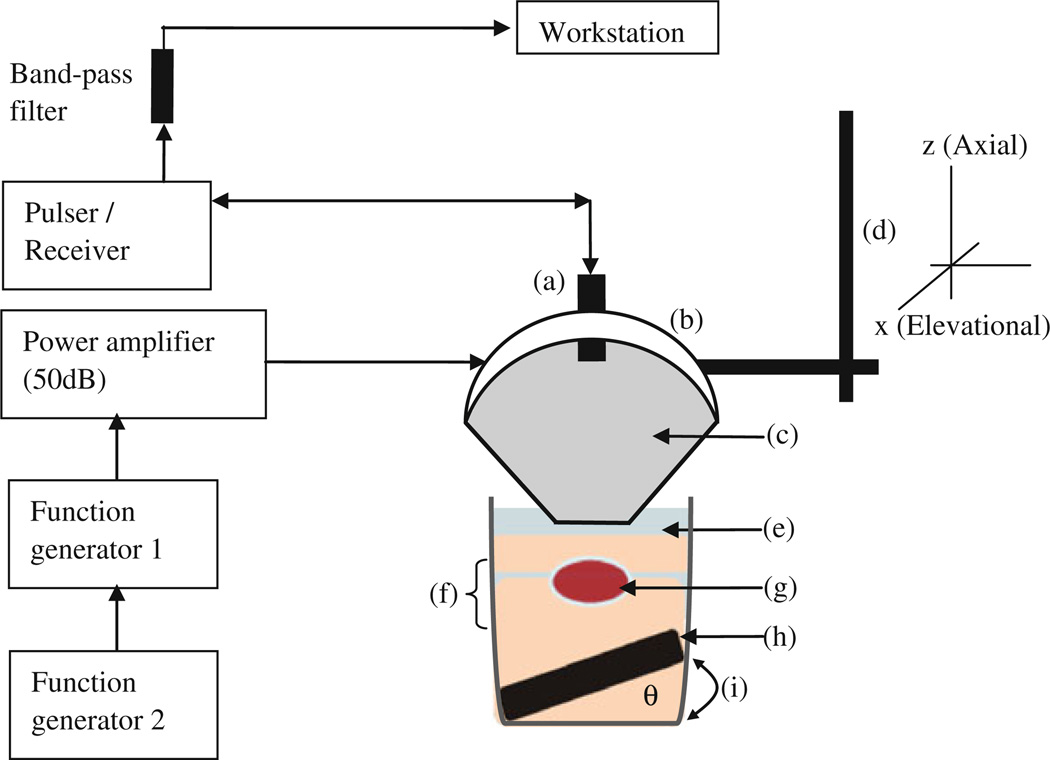
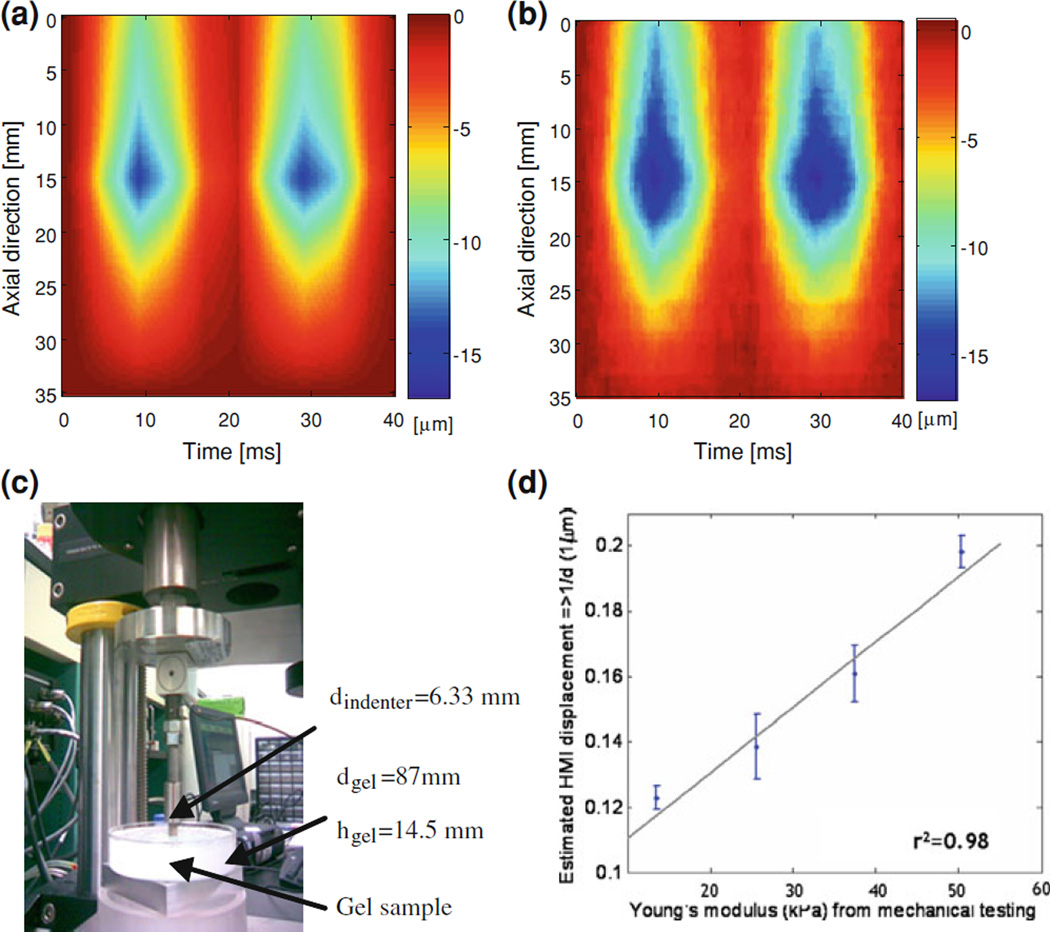
The acoustic pressure field was simulated in Field II [51] using the same transducer parameters used as in the experiments. The resulting pressure field was used as the excitation force to generate displacements. The acoustic intensity was normalized and scaled to a peak in situ, the peak average intensity value was 1,000 W/cm² at a focal depth of 15 mm. The radiation force field was calculated based on the intensity field given its definition [51]. The imaging field was simulated in Matlab 7.2 (Mathworks, Natick, MA, USA) using a linear scattering model with 64 acoustic elements, a center frequency of 7.5 and 40 MHz sampling frequency. Only the displacement estimation on the center RF signal was considered in the validation since a single-element pulse-echo transducer used in the experiments. The experimental setup is shown in Fig. 2. A 1D cross-correlation technique was used on consecutive RF signals to estimate axial displacement with a window size equal to 0.47 mm and 90% overlap. The results showed that using simulated and experimental phantoms of similar moduli led to excellent agreement between the simulation model and the experiments (Fig. 3a, b) between the HMI and mechanical testing (Fig. 3c) findings with a correlation coefficient of 0.98 (Fig. 3d).

Figure 2.

Block diagram and schematic of the HMI experimental setup ex vivo. (a) pulse-echo transducer, (b) HIFU transducer attached to (d) the 3D positioner and (c) a coupling cone filled with degassed distilled water. (g) The specimen was cased between (f) two gel layers (in the case of the phantom, there were no layers, only uniform gel material), and was submerged in (e) degassed PBS. In order to reduce potential reflections, (h) an absorber was placed on the bottom of the glass beaker tilted by a height amount (i) and an angle (theta) to avoid specular reflections

Figure 3.

a Theoretical and b experimental (in 20-kPa tissue-mimicking gel phantoms) M-mode HMI images over two full cycles at 25 Hz. Corroboration with mechanical testing: c Instron compressional testing of gel phantoms and d HMI relative stiffness measurements. d diameter and h height

2.2 Viscoelasticity Estimation

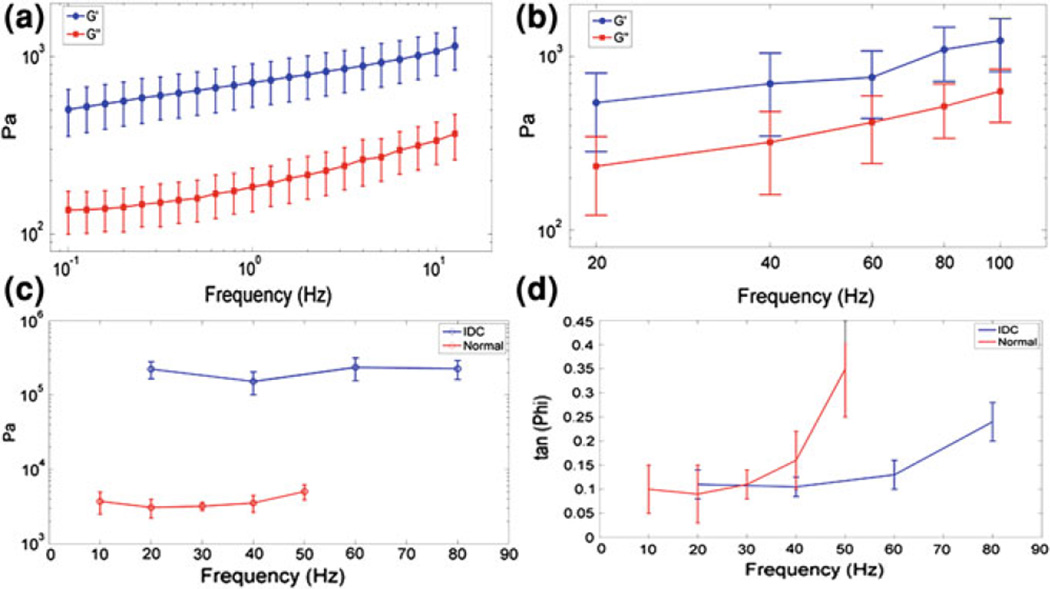
As mentioned in the introduction, one of the main drawbacks of the elasticity imaging methods is that no definite information on the underlying mechanical properties of tissues can be obtained due to either the type of tissue deformation or cumbersome inverse problem methods that need to be implemented. HMI has been shown capable of not only measuring mechanical properties of tissues directly but also take into account the viscoelasticity properties with independent mechanical testing validation [57]. This is mainly due to three important advantages of HMI namely (1) localized force application, (2) simultaneous excitation and response measurement and (3) large frequency range variation capability (Fig. 5). Imaging and quantifying the viscoelastic properties can be key in assessing the capability of the technique to distinguish tumors based on their actual properties and not only based on the displacement that also depend on the surrounding media.

Figure 5.

HMI viscoelasticity estimation: Ex vivo porcine liver specimens (n = 7): Shear storage modulus (G′) (1,070 ± 338 Pa at 10 Hz) and shear loss modulus (G″) (337 ± 90 Pa at 10 Hz) versus frequency for both a rheometry and b HMI; Ex vivo human breast specimens (n = 2): c Shear storage modulus (3.71 ± 0.2 and 223.6 ± 57.1 kPa) 0.40 ± 0.2 kPa (10 Hz) and 24.56 ± 0.7 kPa (20 Hz) and d tan(Φ) (equivalent to shear loss modulus, 0.40 ± 0.2 kPa (10 Hz) and 24.5 ± 6.7 kPa (20 Hz)) versus frequency for both normal breast and IDC, respectively. Errobars denote one standard deviation over five measurements obtained in each specimen

The measured viscoelastic properties are the shear storage modulus G′, which is related to the energy stored under deformation (elasticity) and the shear loss modulus G″, which is related to the energy lost under deformation (viscosity). In order to estimate these two independent quantities, two independent measurements must be performed. Here, viscoelastic shear parameters are measured by using (1) the local shear wavenumber and (2) the phase shift between the applied force and the resulting strain.

This hybrid method uses two different equations to solve for the elasticity and viscosity parameters. First, the shear wave propagation equation relates shear modulus (G) to the wavenumber (k) as follows:

$$G=\rho \frac{{\omega }_o^2}{k^2},$$ (1)

where ρ indicates the tissue density and ω_o indicates the excitation frequency. Second, the viscoleastic tissue can be described in terms of a complex shear modulus having both real and imaginary parts, i.e.,

$$G=G\prime +iG″,\text{and}k=k\prime +ik″.$$ (2)

The shear storage modulus (G′), the real part of G, represents the elastic component, and the loss modulus (G″), the imaginary part of G, represents the viscous component. k′ and k″ represent the real and imaginary parts of the wavenumber (k). By equating both real and imaginary parts from Eqs. (1) and (2),

$$G\prime =\rho {\omega }^2\frac{{k\prime }^2-{k″}^2}{{({k\prime }^2+{k″}^2)}^2},$$ (3)

$$G″=-2\rho {\omega }^2\frac{k\prime k″}{{({k\prime }^2+{k″}^2)}^2}.$$ (4)

In order to solve for the two parts of G, i.e., G′ and G″, two HMI parameters are used, namely the wavenumber k and the ratio of G″ to G′. The ratio (R) of G″ to G′ is given by

$$R=\frac{G″}{G\prime }=-\frac{2k\prime k″}{{k\prime }^2-{k″}^2}.$$ (5)

Solving for k″ using the quadratic formula, the positive and negative solutions are as follows:

$$k″=k\prime (R+\sqrt{1+R^2})\text{and}$$ (6)

$$k″=k\prime (R-\sqrt{1+R^2}),$$ (7)

respectively. We have shown that the response of the probed tissue undergoes wave attenuation due to its viscous properties, so negative k″ (Eq. 7) is chosen to satisfy this physical condition. If we are able to estimate k′ and R from the experimental data, G″ and G′ can be calculated based on Eqs. (5) and (7), respectively. The following sections explain how k′ and the ratio (R) of G″ to G′ can be estimated from the HMI displacement measurements.

HMI has the valuable advantage of generating motion at the focal region. This represents a clear advantage compared to the more conventional shear wave based methods (Sect. 1.1) as it allows to precisely select the location of the source of excitation inside the tissue. Hence, different effects that can be critical for the estimation of viscoelastic properties can be minimized such as rigid motion, shear wave loss by diffraction, spurious reflections, and mode conversion. The first measurement consists in estimating locally (i.e., in a small region close to the focus) the wavenumber k′, which can be calculated from the phase of the temporal Fourier transform of the displacements:

$$k\prime =-\overrightarrow{\mathit{\text{grad}}}(\text{arg}(F{T}_t(u(x,t))))$$ (8)

Another unique advantage of HMI is utilized for the second measurement, namely, the possibility of simultaneously measuring both the input force and the resulting strain. This suggests an interesting analogy with dynamic mechanical analysis (DMA), a state-of-the art widespread method for dynamic mechanical testing of soft materials. Such as in DMA, we propose to locally measure the temporal phase shift Φ between the input and output. It can be shown that Φ is related to the viscoelastic properties through tan(Φ) = G″/G′. In other words, the more viscous the medium is, the higher will the phase shift be. For an ideally purely elastic medium, the phase shift is zero as the medium responds instantaneously to the stress. By using the direct relationships between (G′, G″) and k′, both G′ and G″ can be determined locally.

2.2.1 Numerical Validation

In order to evaluate the proposed approach, numerical phantoms were generated by using ABAQUS (Simulia Multiphysics, Providence, RI, USA) finite-element software. Such phantoms were generated by simulating a focal oscillatory volumic force applied at the center of a viscoelastic phantom with well-defined viscoelastic properties, i.e., G′_input and G″_input. The inverse approach proposed above was then tested, and the calculated values of G′ and G″ were compared to the input values G′_input and G″_input. This study was performed on a set of ten phantoms with the values of G′ and G″ varying between 1–11 kPa and 0–4 kPa, respectively, and the frequency of excitation varying between 10 and 50 Hz. A very good agreement between input and calculated viscoelastic parameters was found, with relative errors of 9 and 7% for G′ and G″, respectively. This confirms the validity of the proposed approach, as previously reported [61].

2.2.2 Phantom Experiments

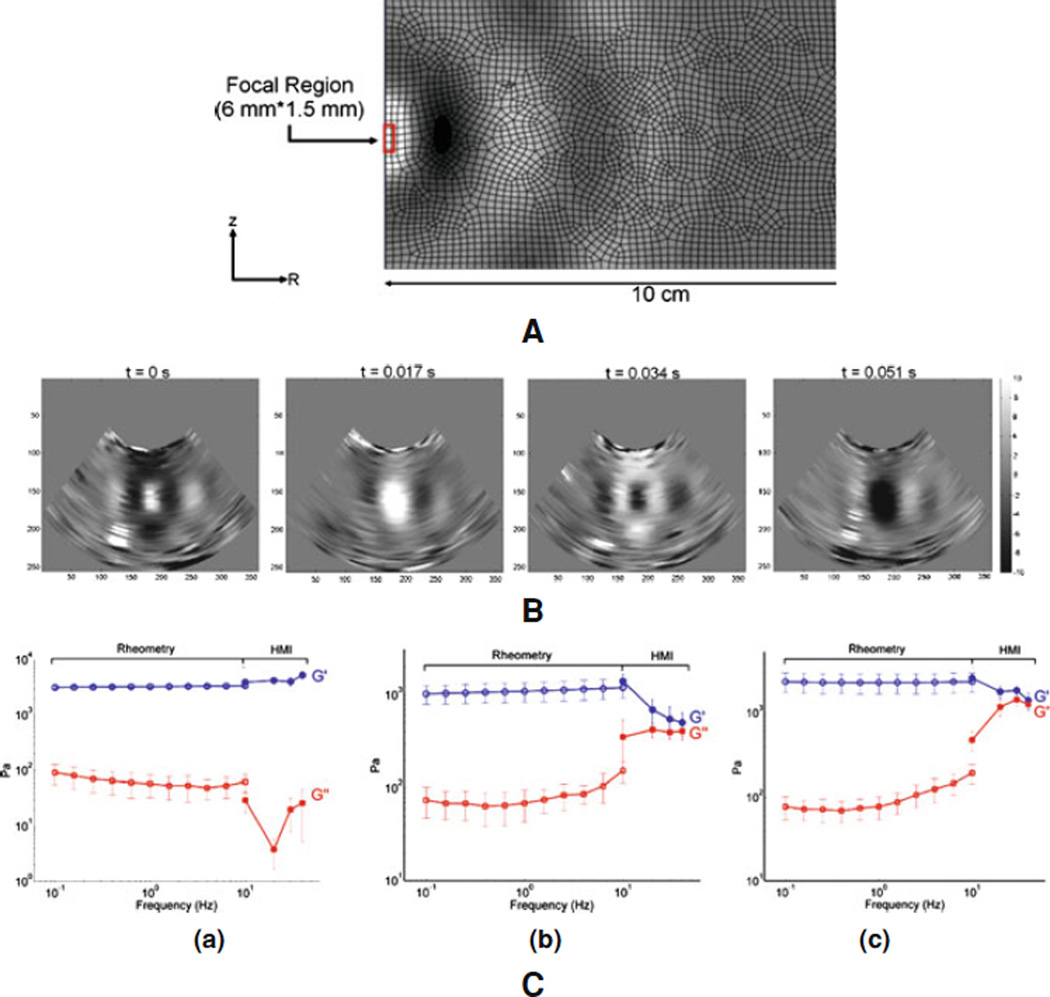
A comparison study against mechanical testing (DMA) was performed on soft tissue phantoms. This study was performed on three gel phantoms, namely, two gelatin gels and one polyacrylamide gel. HMI and mechanical tests were performed on the same day in order to ensure similar experimental conditions. Figure 4(i), (ii) indicate the good agreement between the generated shear wave propagation in simulations and gel phantom experiments, respectively. Figure 4(iii) illustrates the results obtained on the three gel phantoms in terms of their viscoelastic properties. The polyacrylamide phantom [Fig. 4(iii) (a)] seems to present a more continuous frequency-dependent variation of the shear storage modulus across the rheometry and HMI frequencies while the two gelatin phantoms appear to have distinct moduli in the rheometry and HMI ranges. This may be due to the different absorption between the polyacrylamide and gelatin phantoms.

Figure 4.

i Illustration of the axisymmetric finite-element model used for the simulations, showing the mesh, the dimensions, the location of the focus and the resulting displacements. ii Incremental displacement at four different equally spaced frames obtained in one gel, showing especially the propagation of the shear wave from the focus. iii Shear storage modulus (G′) and shear loss modulus (G″) versus frequency in the (a) polyacrylamide gel, (b) 4.7% gelatin and (c) 6.5% gelatin gel phantom for both rheometry and HMI as indicated

A good agreement was found for the shear modulus G′ (average relative error of 14%), whereas poorer agreement was found for the shear loss modulus G″ (average relative error of 55%). This disagreement is most probably related to instrumental limitations in terms of frame rate. High frame rate is required in order to ensure high accuracy of the measurement of the temporal phase shift, especially if the phase shift is low.

2.2.3 Tissue Experiments

Experiments were first performed in bovine liver ex vivo. For HMI experiments, the liver was immersed in degassed water. Mechanical testing experiments were performed on the same day as HMI experiments. Dynamic mechanical analysis was performed at small strain (ε= 0.1%) using rheometry. Figure 5a, b illustrates the results of the shear storage modulus G′ (i.e., stiffness) and shear loss modulus G″ (i.e., viscosity) versus the frequency for both HMI and rheometry. Although a similar dynamic behavior is found between the two methods, the values of shear moduli found by rheometry appear to be significantly higher than those found by HMI. Such differences can be explained by the significantly different experimental conditions (liver tissue immersed in water in HMI, small excised samples in rheometry). Nevertheless, this preliminary study illustrates the feasibility of the method in soft tissues in vitro. Experiments were performed on two samples, namely, (1) normal breast tissue and (2) invasive ductal carcinoma (IDC). Both samples were excised during breast surgery and were tested within one hour following operation. Figure 5c, d illustrate the frequency-dependent behavior of the shear storage modulus G′ and of tan(Φ) = G″/G′. Depending on the frequency, the IDC was found to be at least one order of magnitude stiffer than the normal breast tissue. A significant difference was also found in the dynamic behavior of tan(Φ), as the relative viscosity of healthy tissue was much higher than the one of IDC at a given frequency. Although those are preliminary results, they may be of high importance as they seem to indicate a significant difference between cancerous and normal tissue not only in stiffness, as it has been demonstrated by several previous studies, but also in the dynamic viscoelasticity behavior.

Reported studies have consisted of assessing the fundamental performance of HMI in detecting and estimating the viscoelasticity properties of tumors and performing similar ex vivo experiments and other types of tumors. It should be noted that one important advantage of measuring viscoelastic parameters with HMI is that no rheological model such as Voigt, Kelvin, etc. needs to be assumed [57] unlike other methods.

2.3 The HMI Technique in Breast Cancer Detection

In a recent study [77], seventeen post-surgical human breast cancer specimens (i.e., 3 normal, 5 benign, and 9 malignant tissues) were imaged using the HMI technique and the same system as described in Sect. 2.2.2. The diameter of the FUS transducer and the radius of curvature were 84 and 90 mm respectively. The oscillatory acoustic radiation force was generated by the 4.5 MHz focused transducer and a 50 Hz amplitude-modulated RF signal. A pulse-echo transducer was placed through the center of the focused transducer, so that the beams of the two transducers were properly aligned. Consecutive, filtered RF signals were acquired at a Pulse Repetition Frequency (PRF) of 6.5 kHz. The time-shift occurring between two successive RF images was calculated using a one-dimensional cross-correlation that was performed along the ultrasound beam axis with a small window size of 1.3 mm and 85% overlap [70].

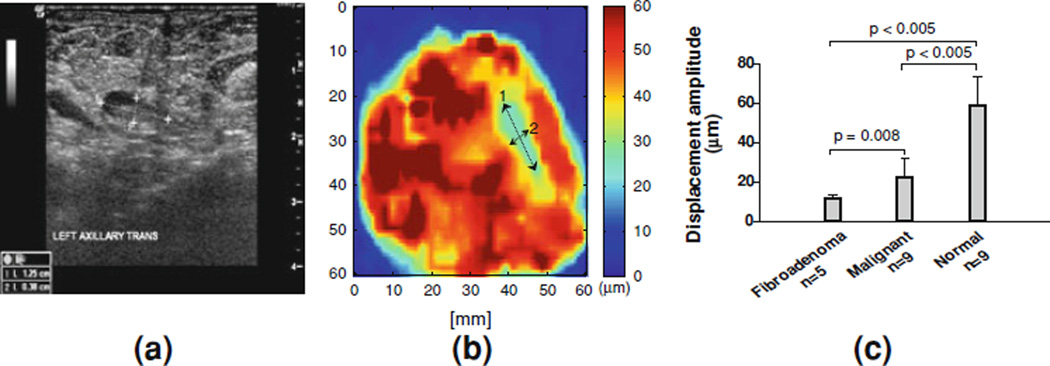
Figure 6a shows a follow up sonogram of a 70-year-old female after she received chemotherapy for 7 months. The patient had a 60 mm mass prior to chemotherapy but was no longer evident after treatment. The tumor size was reduced to 12.5 × 3.8 mm as shown in Fig. 6a. The mammogram was not presented here because it did not show enough contrast between the tumor and the surrounding breast tissue due to the high breast density. An ultrasound-guided biopsy was performed to diagnose the lesion, and the result was found to be IDC. A lumpectomy with needle localization was performed to remove the remaining lesion.

Figure 6.

Tumor localization (indicated by the arrows) in b HMI ex vivo and validated using a sonography of the subject in vivo prior to surgery. The tumor sizes and locations imaged with the two modalities were in excellent agreement. c Statistical results in 17 postsurgical specimens (in the normal specimens, six were used from excess/perilesional tissue from the same specimen). Each bar represents mean ± SD, calculated based on 3 × 3 × 3 mm³ volume. Significance was determined using an unpaired Student’s t-test with confidence interval of 90%. There are significant differences for benign versus normal (p-value < 0.005) and malignant versus normal (p-value < 0.01) [77]. Malignant tumors included invasive lobular carcinoma (ILC), invasive ductal carcinoma (IDC) and ductal carcinoma in situ (DCIS)

The HMI image (Fig. 6b) indicated the possible lesion location (blue, D_HMI is below 25 µm) surrounded by breast tissues (yellow and red, D_HMI is above 45 µm). The size of the lesion in HMI was measured to be approximately 12 mm by 4 mm, which is in good agreement with the B-mode image obtained prior the surgery, i.e., 12.5 mm by 3.8 mm (Fig. 6a). It should be noted that the HMI displacements were not corrected for depth-dependent attenuation across different tumors, but this currently is in ongoing studies.

HMI was used to accurately map all 17 breast specimens and reliably differentiate benign from malignant human breast tumors (p = 0.008) (Fig. 6c). An unpaired Student t-test with 90% confidence interval was performed to quantify whether different pathologies could be differentiated based on the HMI images. The normal breast tissue (mostly fat, glandular, and parenchyma) could be differentiated from benign and malignant at high statistical significance (p < 0.005). The benign tumors experienced a lower average displacement (i.e., stiffer) than the malignant tumors at lower significance (p = 0.008). Thus, the HMI image could categorize tumor types based on their relative stiffness. Normal, benign and malignant tumors could thus be differentiated using HMI. However, differentiation between different malignant types such as IDC and ILC proved to be more challenging (Fig. 6c), most likely due to their similar stiffnesses rendering differentiation based on the mechanical properties more difficult.

2.4 HIFU Lesion Detection

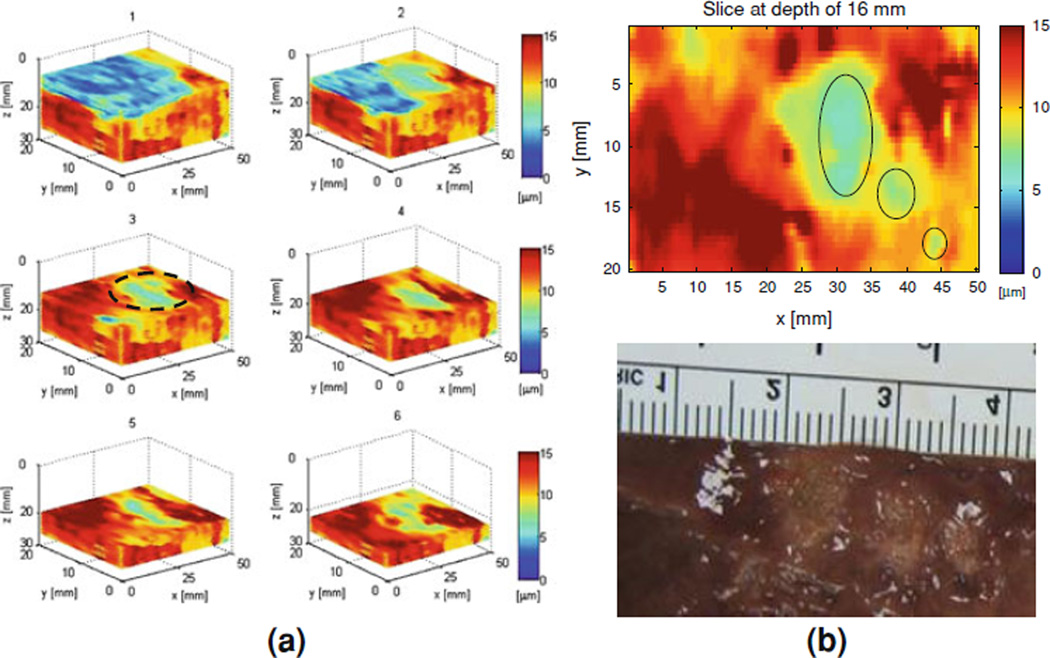
As indicated previously, it has been established that, during and after HIFU ablation, the stiffness can change up to a tenfold [75]. In order to verify the monitoring capability of the HMIFU system as intended for in vivo use, ex vivo porcine liver was used. Raster-scanning of the entire specimen in 3D led to 3D HMI mapping of three lesions at 50 Hz is shown in Fig. 7. The displacement amplitudes at the focus of the ex vivo porcine liver or the ablated regions, were approximately equal to eight microns while the normal (i.e., non-ablated) liver had an average displacement of 15 microns (Fig. 7a). Figure 7b shows the example of a 2D slice out of the 3D volume mapped in Fig. 7a identifying three HIFU lesions side-by-side at varying sizes. Both the locations and sizes of these lesions were verified using pathology (Fig. 7b). These results indicate that the HMI displacement amplitude decreases after lesion formation due to the associated higher tissue stiffness.

Figure 7.

a 3D HMI imaging (progressive sections at 5 mm steps) of the entire liver specimen ex vivo (in red, highest displacement), HIFU lesions (in green, lower displacement) and saline (in blue, null displacement), the latter used as the coupling medium; b HMI image through the dotted region in a showing three lesions side-by-side with the photograph after liver dissection (lower panel) of the liver showing the three lesions

2.5 Real-Time HIFU Monitoring

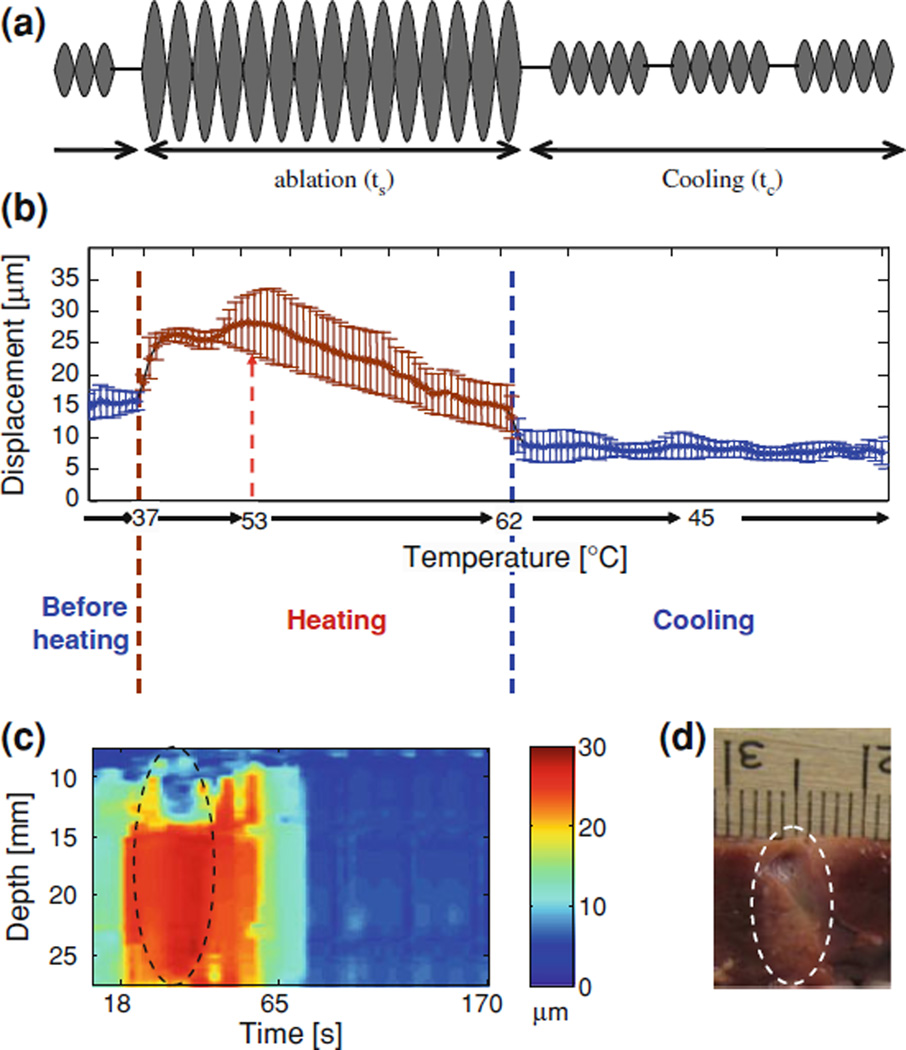
HMI has recently been shown capable of monitoring lesion formation in quasi real-time at approximately one frame/s for M-mode HMI imaging using cross-correlation techniques on Matlab and an M-mode display during HIFU ablation [56]. For the real-time monitoring application of the technique, the experiment was completed in an ex vivo porcine liver with a sonication time varying between 10 and 47 s. Figure 8 shows the monitoring curve and image of the HMI tissue displacement amplitude at the focal depth versus temperature and sonication time. The focus is located at 16.5 mm and has displacement amplitude of 30 microns, which then decreases to about 15 microns (Fig. 8b).

Figure 8.

M-mode HMI, real-time HMFU monitoring: a The HMIFU sequence used before, during and after HIFU treatment; b HMI displacement variation with temperature before (blue), during (orange), and after (blue) HIFU ablation, averaged over five different liver specimens and three locations in each liver, i.e., 15 locations total. c example of an M-mode HMI displacement image obtained in real-time during ablation (as in a) and (b, heating started at t = 18 s and ended at t = 65 s). d photograph of the liver lesion (denoted by the dashed contour) in (d). A liver vessel running through the lesion was used as a registration reference between the images in c and d. Note that in b at 53°C, coagulation occurs and the HMI displacement changes from a positive to a negative rate indicating lesion formation

The regions above and below the focus have approximately constant displacements (Fig. 8c). This indicates that the highest acoustic radiation force is produced and maintained only at the focus and that after 20 s of sonication time, the properties of the liver tissue irreversibly change due to tissue coagulation (Fig. 8b). Furthermore, it should be noted that the effect on the RF signals induced by the increase in the speed of sound with temperature also introduced a DC offset in the HMI displacement in time which could be easily filtered out due to the harmonic nature of the technique [53].

The HMI technique is therefore capable of accurately monitoring the stiffnessrelated heating process, detecting the likely onset of coagulation (Fig. 8b) as well as separating the speed-of-sound effect from stiffness-related changes. It has also been established that the HMI technique does not induce a temperature rise higher than 1°C [62]. The duration of sonication was equal to 47 s, which is within the standard duration of HIFU treatment, with the highest temperature reaching 62°C.

We have also shown similar capabilities at shorter HIFU exposures (10–30 s [56]). The coagulation onset in this case was detected to be at 53°C, beyond which the slope of displacement variation was reversed indicating nonlinear stiffening of the tissue (Fig 8). Note that the M-mode image in Fig. 8c clearly indicates that the displacement sharply decreases before the HIFU treatment stopped, indicating that coagulation was performed successfully. The cross-section of a liver vessel is also detected (near the top in both images in Fig. 8c). Table 3 shows the sensitivity of HMI in detecting small temperature variations and its specificity in detecting lesion formation. Note that during lesion formation, the HMI heating rate was switched from positive (before) to negative (after) in all 21 locations at high statistical significance (p < 0.001). This effect was due to the stiffening of the tissue as a result of coagulation. Lesion formation was verified in a preliminary study that involved interrupting the treatment by 1-s difference in different lesions to verify whether a lesion was formed.

Table 3.

Summary of HMI heating rates and lesion sizes for 10- 20- and 30-s HIFU exposures in seven (n = 7) porcine liver specimens, i.e., 21 sonication locations total

Sonication duration (s)	HMI heating rate before lesion formation (µm/°C)	HMI heating rate after lesion formation (µm/°C)	Lesion size
			Diameter (mm)	Length (mm)
10	0.87 ± 0.082	−0.88 ± 0.080	2.0 ± 0.12	6.4 ± 1.14
20	0.85 ± 0.12	−0.71 ± 0.16	3.4 ± 0.13	13.1 ± 1.15
30	0.80 ± 0.14	−0.79 ± 0.19	4.7 ± 0.18	16.4 ± 0.39

2.6 In Vivo Feasibility of the HMI Technique in Tumor Detection and HIFU Monitoring

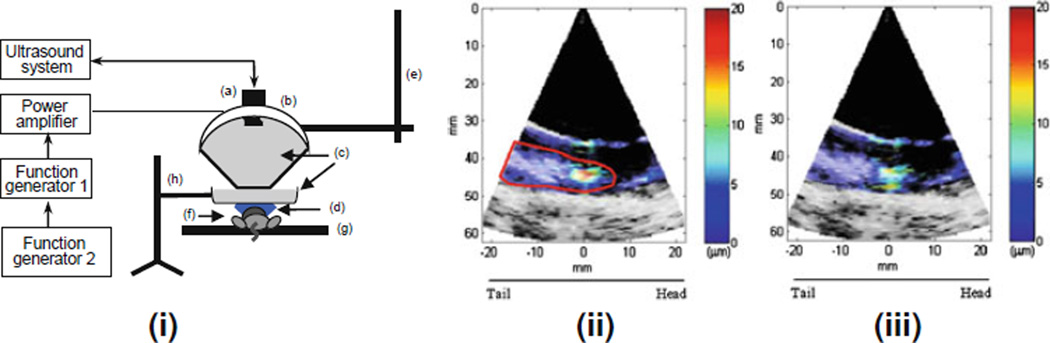
HMI was also recently shown feasible in mice in vivo for both tumor detection and treatment monitoring [60]. In vivo experiments have been performed in transgenic mouse models carrying pancreatic or mammary tumors. The in vivo experimental setup is shown in Fig. 9(i) and is very similar to what was used for the ex vivo experiments. A 4.5 MHz FUS transducer with a focal length of 45 ± 2 mm was used to generate the acoustic radiation force using a low-frequency amplitudemodulated (AM) radio-frequency (RF) waveform. Figure 9(ii) displays an example of grayscale B-mode images overlaid with color-coded peak-to-peak displacement amplitudes before and after lesion formation.

Figure 9.

i Block diagram and schematic of the experimental HMI setup in vivo: (a) imaging transducer, (b) HIFU transducer, (c) degassed water and (d) degassed ultrasound gel. HMI system was mounted on (e) the computer controlled positioner. (f) The mouse was placed on (g) a heating platform. (h) Ring stand was used to hold the water chamber. HMI images of mammary tumor (red contour) during heating in a mammary tumor mouse model in vivo. Color bars denote peakto-peak displacement amplitudes in lm. ii Beginning of heating and iii after lesion was formed. Red contour shows the targeted region (mammary tumor). For quantitative measurements, displacement amplitudes were averaged over a 3 × 3 mm² region (square). Tail (T) and head (H) of the mouse are on the left and right of the images, respectively

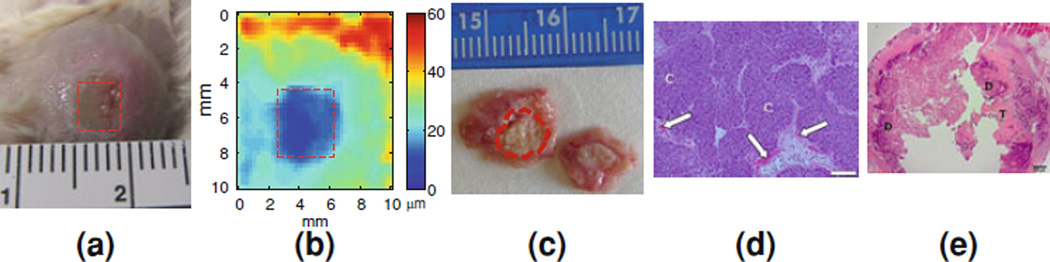
The targeted tumor region is delineated in red (Fig. 9(ii)). The focal region of the FUS beam is located at the center (0 mm) and at a depth of 45 ± 2 mm. The average displacement amplitude at the focal zone was approximately equal to 18 lm (Fig. 9(ii); in orange-red) and after the lesion was formed, the amplitude decreased to approximately 8 lm (Fig. 9(iii); in cyan). Assuming uniform application of the radiation force, the resulting tissue motion (or oscillatory displacement) can be related to the underlying relative tissue stiffness, and thus, to the stiffness change during heating. Finally, Fig. 10 demonstrates the full potential of HMI in vivo, i.e., tumor detection (Fig 10b), thermal lesion detection (Fig. 10b), thermal lesion differentiation from the tumor (Fig. 10b) with excellent size correlation with pathology findings (Fig. 10c) and evidence of tumor cell reduction in histology (Fig. 10d–e).

3 Conclusion

The capability of HMI to map and differentiate between different tumor types and thermal lesions, both ex vivo and in vivo, in a fully integrated, all-ultrasoundbased system was reviewed in terms of tumor detection, localization and treatment monitoring. The clinical objective of this technique is to provide a complementary, noninvasive method to breast detection and diagnosis for benign and malignant tumors as well as in situ thermal treatment following detection and diagnosis. Therefore, the HMI technique may significantly improve the ability to detect and ultimately assess and monitor the ablation of tumor masses and may also provide quantitative viscoelasticity information that is needed to better understand the tumor mechanical properties and thereby improve diagnosis.

Figure 10.

In vivo tumor ablation and imaging: a Visualization of the mouse mammary tumor surface after ablation with discoloration of the tumor in the ablated region (red dashed square); b HMI image of the same thermal lesion at a higher depth (red dashed square) with the unablated tumor around it; c Gross pathology of the transverse cross-section of the same tumor (red dashed contour) stained by triphenyltetrazolium chloride (TTC); d–e H&E histology images. d Non-ablated tumor cells (C; 100×). Scale bar = 100 µm. White arrows denote erythrocytes (red blood cells). e Ablated tumor cells (12.5 ×). Scale bar = 500 µm. Ablated regions are indicated as dark purple (D) surrounded by non-ablated regions (or, viable cells) are shown in pink (T)