Temporal Changes in Survival after Cardiac Surgery Are Associated with the Thirty-Day Mortality Benchmark

Abstract

Objective

To assess the hypothesis that postoperative survival exhibits heterogeneity associated with the timing of quality metrics.

Data Sources

Retrospective observational study using the Nationwide Inpatient Sample from 2005 through 2009.

Study Design

Survival analysis was performed on all admission records with a procedure code for major cardiac surgery (n = 595,089). The day-by-day hazard function for all-cause in-hospital mortality at 1-day intervals was analyzed using joinpoint regression (a data-driven method of testing for changes in hazard).

Data Extraction Methods

A comprehensive analysis of a publicly available national administrative database was performed.

Principal Findings

Statistically significant shifts in the pattern of postoperative mortality occurred at day 6 (95 percent CI = day 5–8) and day 30 (95 percent CI = day 20–35).

Conclusions

While the shift at day 6 plausibly can be attributed to the separation between routine recovery and a complicated postoperative course, the abrupt increase in mortality at day 30 has no clear organic etiology. This analysis raises the possibility that this observed shift may be related to clinician behavior because of the use of 30-day mortality as a quality metric, but further studies will be required to establish causality.

Despite substantial improvements in outcomes over the past decades (Hickey et al. 2013), cardiac surgery remains a field with comparatively high postoperative mortality. As with many areas in medicine, 30-day mortality is one of the most common outcome measures used to describe and assess the postoperative course of cardiac surgical patients. The premise behind the use of this metric is that it provides a uniform way of evaluating the aggregate outcomes that result from the performance of surgeons, hospitals, and perioperative surgical care teams (including anesthesiologists, intensivists, nurses, and consulting and supporting services). In addition to its use as a standard clinical endpoint for research, 30-day mortality has become a benchmark for quality assurance and improvement used by hospitals, professional groups, and patient safety organizations (Vaduganathan, Bonow, and Gheorghiade 2013), a metric for publicly available interhospital comparisons (for instance, by the Centers for Medicare and Medicaid Services [QualityNet 2013]), and it has been suggested for use in individual-level physician comparisons and pay-for-performance schema (Werner 2012).

Most discussions focus on the observational function of quality measures. Little attention has been paid to the possibility that use of a quality benchmark may exert feedback effects on the phenomenon being observed—for instance, that the act of measuring 30-day mortality may alter patterns of mortality. Some or all of the actors who play a role in the care of cardiac surgical patients have the potential to exhibit different behavior in response to the use of a quality benchmark. Physician decisions about the use of aggressive interventions for critically ill patients, the timing of family meetings and shifts in treatment priorities, and hospital decisions about the design and coordination of systems for caring for these patients (e.g., inpatient and outpatient rehabilitation, hospice, and palliative care services) may interact with the implicit incentives created by the use of a short-term survival outcome as a quality metric.

We used the Nationwide Inpatient Sample to examine survival patterns after major cardiac surgery and assess the hypothesis that postoperative survival exhibits a heterogeneous temporal pattern with shifts that may be associated with the timing of assessments used as quality metrics, such as 30-day mortality.

Methods

The Stanford University Institutional Review Board granted an exemption from review because this research uses publicly available, de-identified data. Administrative records were extracted from discharge datasets for the years 2005–2009 from the Nationwide Inpatient Sample (NIS), Healthcare Cost and Utilization Project (HCUP), Agency for Healthcare Research and Quality (HCUP 2013). HCUP-supplied Clinical Classifications Software (CCS) for international classification of diseases, ninth revision, clinical modification (ICD-9-CM) was used to generate procedural classification codes.

Using the HCUP definition of Procedure Classes for diagnostic and therapeutic procedures, discharge records in which a major cardiac operation (revascularization and/or valve repair or replacement) was performed were identified (L2PCCS1 codes 7.1 and 7.2). Survival analysis was carried out for the primary outcomes of all-cause in-hospital mortality, as recorded in the NIS dataset (variable DIED). Right-censoring at a survival time equal to the length of stay was performed for records without an in-hospital death. Life tables were used to estimate the day-by-day hazard rate (occurrence of mortality in a specific time interval conditional on survival to the beginning of that interval) for 1-day intervals up to 60 days after surgery.

To determine whether a change in the hazard function occurred and to identify the timing of any change(s), joinpoint regression of hazard rates was used. Joinpoint regression methodology has been described previously (Kim et al. 2000), but in brief, it is used for time-ordered data and uses least-squares estimation to fit a model with up to k_max joinpoints, that is, points of discrete change in the hazard function. The regression process begins with a model of 0 joinpoints (i.e., a straight line) and performs permutation testing with an alternate hypothesis of k_i joinpoints in an iterative fashion beginning with k = 1 up to k_max. The p-value for each iteration is obtained using Monte Carlo methods with a Bonferroni-corrected asymptotic significance level.

A number of methods have been proposed for investigating the questions we asked, that is, whether the observed hazard rate changed; if so, how many times, and when. Change point analysis using Taylor’s cumulative sums method with bootstrapping has been described for detecting multiple change points in time-ordered data (Kass-Hout et al. 2012), but it relies on assumptions of identically distributed and independent observations. Day-to-day hazard rates for postoperative mortality are not likely to be independent. Several authors have described similar data-driven, least-squares-based methods of detecting a single change point (Matthews and Farewell 1982; Gijbels and Gürler 2003). An iterative extension of these methods has been used to detect multiple change points (Goodman, Li, and Tiwari 2011), and others have employed an alternative Bayesian approach (Wilson, Nassar, and Gold 2010), but these methods all have focused on data that demonstrate a piecewise constant hazard instead of a piecewise linear hazard. In contradistinction to clinical settings with a steady hazard rate (e.g., cancer incidence in a broad population), the hazard function overall for in-hospital mortality after surgery is not constant, as routine recovery selects for increasing hazard with each postoperative day among the population remaining at risk (those still in the hospital). Therefore, a piecewise linear hazard model is more appropriate than a piecewise constant hazard model in this setting.

Joinpoint regression has similarities with the use of nonlinear least squares regression modeling (e.g., PROC NLIN in SAS) to create a piecewise linear model, but it does not require the a priori specification of the number of points of change in the hazard function. Instead, it allows iterative hypothesis testing such that model with the optimal number of points of change (joinpoints) can be determined from the data, including the calculation of confidence intervals (CIs) around the joinpoints (Lerman 1980). Joinpoint regression also allows for appropriate methodological compensation for data which do not have a constant variance (heteroscedasticity) or are not independent observations (autocorrelation).

After the timing of changes in the hazard function were identified through joinpoint regression, subsequent piecewise linear regression was performed on each segment of the hazard function to allow for discontinuity at the joinpoints in the final illustrative model. This additional step of repeating modeling with a three-segment piecewise linear regression model allowed us to combine the advantages of joinpoint regression (first using a data-driven process to determine the number and location of changes in the hazard) with the ability to model discontinuity at the points of change.

Initial dataset definition, survival analysis, and linear regression were performed using SAS (SAS 9.3; SAS Institute, Cary, NC, USA). Joinpoint regression was performed using dedicated software developed by the National Cancer Institute (Joinpoint Regression Program, Version 4.0; Statistical Methodology and Applications Branch, NCI Surveillance Research Program, Bethesda, MD, USA). With this software, a default value of k_max is determined algorithmically based on the number of data points. The highest default k_max (for large datasets) is 5, but values up to 9 can be employed at the cost of significantly increased computational intensity. We had no prior literature to suggest a k_max greater than 5 would be needed, so we accepted the default value of k_max = 5. These settings result in iterative testing for up to 5 joinpoints separated by any number of days between joinpoints. For Monte Carlo simulation, 4,500 permutations were used for testing. A standard-error-weighted least squares modification was used to account for nonconstant variance. Because the day-specific hazard rates demonstrated nonindependence, the option of fitting an autocorrelated errors model based on the data was used to correct for nonindependent observations.

Results

Out of 63.9 million NIS admission records, 595,089 records were identified that included a major cardiac operation. Death occurred in 19,454 (3.27 percent) at a mean (± standard deviation) of 17.5 ± 22.3 days. Figure 1 shows the day-by-day hazard rate for each postoperative day up to 60 days after surgery. Right-censoring was performed at a survival time equal to the length of stay for all records without an in-hospital death (n = 575,635; 96.73 percent). There was no loss to follow-up for the purposes of our analysis; in this database of inpatient admissions, the absence of a recorded death indicates an alive discharge.

Figure 1.

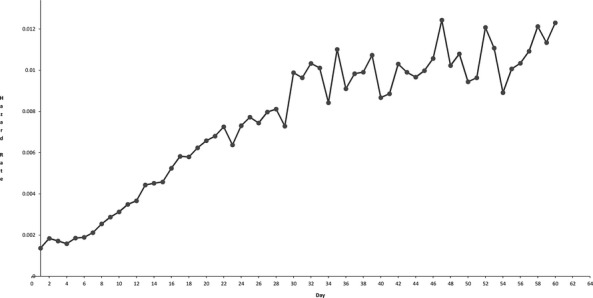
Hazard Function (Mortality Events per Day) in One-Day Intervals (Circles) for Mortality after Cardiac Surgery

Details of the iterative Monte Carlo permutation testing for joinpoint regression are shown in Table 1. The regression identified a piecewise linear model with 2 joinpoints (p = .0002), located at day 6 (95 percent CI = day 5–8) and day 30 (95 percent CI = day 20–35). The coefficient of determination for the model (R²) was 0.951. Table 2 shows the detailed parameters of the regression model. Figure 2 shows the fit of the regression model to the hazard function.

Table 1.

Monte Carlo Permutation Testing for Joinpoint Regression

Test Number (Iteration)	Number of Joinpoints, Null Hypothesis	Number of Joinpoints, Alternative Hypothesis	Selected Hypothesis	p-Value	Bonferroni-Adjusted significance level (α)
0	0	1	Alternative	.00022	0.01667
1	1	2	Alternative	.00022	0.025
2	2	3	Null	.17	0.05

Table 2.

Parameters for Joinpoint Regression Model and Piecewise Linear Regression Model with Discontinuity

	Applicable Range (Day)	Parameter Estimate	Parameter Standard Error
Parameters for joinpoint regression model
Intercept 1	1–6	0.00143157	0.000067926
Intercept 2	7–29	0.000023988	0.000115451
Intercept 3	30–60	0.007834307	0.00128956
Slope 1	1–6	0.0000773372	0.0000212525
Slope 2	7–29	0.0003119343	0.0000099508
Slope 3	30–60	0.0000515903	0.0000309763
Parameters for piecewise linear regression model with discontinuity
Intercept 1	1–6	0.0014542913	0.0001564724
Intercept 2	7–29	0.0005629491	0.0002404929
Intercept 3	30–60	0.0077530428	0.0008537572
Slope 1	1–6	0.0000729234	0.0000401784
Slope 2	7–29	0.0002754195	0.0000127790
Slope 3	30–60	0.0000560679	0.0000186084

Figure 2.

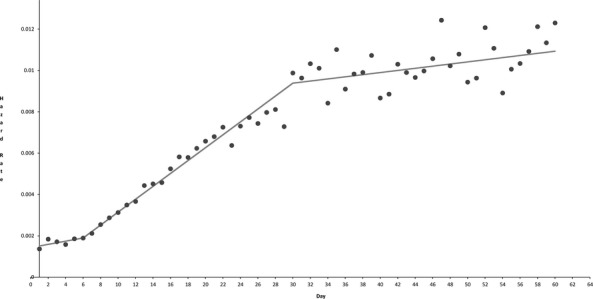
Hazard Function (Mortality Events per Day) in One-Day Intervals (Circles) for Mortality after Cardiac Surgery with Overlay of Joinpoint Regression Model (Solid Line)

Subsequent piecewise linear regression performed on each segment of the hazard function (after identification of the timing of abrupt changes in the hazard) allowed for an improved model (R² = 0.998) because of the flexibility of permitting discontinuity at the joinpoints. In particular, the joinpoint at day 30 appeared to be the locus of both an absolute increase in hazard and a change in slope of the day-to-day hazard function. This final model involved three segments: day 1–6, day 6–30, and day 30–60 (full parameters are shown in Table 2). The fit of this model to the hazard function is shown in Figure 3.

Figure 3.

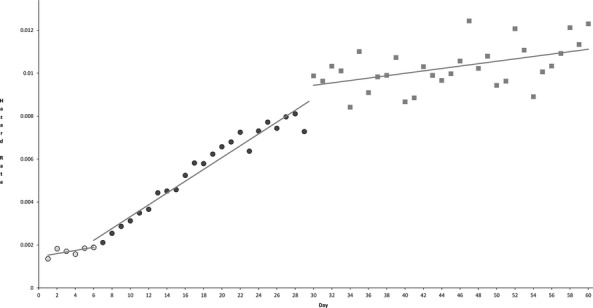
Hazard Function for Mortality after Cardiac Surgery with Overlay of Multi-Segment Discontinuous Piecewise Linear Regression Model (Solid Lines). Open circles comprise segment one (day 1–6), shaded circles comprise segment two (day 6–30), and squares comprise segment three (day 30–60)

Discussion

The principal finding of this study is that postoperative mortality after major cardiac surgery exhibits a heterogeneous temporal pattern, with abrupt changes in the hazard function observed at day 6 and 30.

The major limitation of this study is that it provides information on the occurrence of postoperative deaths, without the contextual information that would be required to ascribe specific causal explanations to the changes observed. We can only make a few informed speculations about the observed temporal patterns in mortality. The earliest phase following surgery appears to be characterized by the lowest hazard for mortality (with a relative peak at day 2); this may reflect the high success rate of modern surgical and intensive care practices in supporting even the sickest of patients through an operation and immediate postoperative period. The first change in hazard, identified at day 6, may reflect the survivorship of those patients with a routine postoperative recovery, such that those who remain at risk (in the hospital) begin demonstrating an increased hazard.

The second change in hazard, identified at day 30, appears to involve both an abrupt increase in hazard relative to the general pattern of steady per-day increases after day 6 (i.e., discontinuity) and a change in slope within that day-to-day pattern (Figure 3). Since our analysis does not provide patient-specific information on the timing of complications or clinical deterioration that ultimately lead to in-hospital postoperative death, it remains theoretically possible that the observed phenomenon reflects an organic clinical etiology. However, we cannot hypothesize a change in the risk of infection, deterioration in cardiac function, respiratory complications, renal injury, or other precipitating clinical factors which should predict an abrupt change in the risk of postoperative death at or around day 30.

An alternative explanation is an association between the use of 30-day mortality as a key quality indicator and the timing of shifts in clinical treatment priorities and strategies. Quality benchmarks have as their expressed aim the alteration of clinician behavior. Most existing discussion of quality metrics focuses on two possibilities—they will produce desirable changes in provider behavior, or they will fail to produce any significant changes in provider behavior (Werner 2012). A third possibility—that they may also have unintended and/or undesired effects on provider behavior (what has been called the “observer effect” or “Hawthorne effect”)—should be considered. Further inquiry will be needed to determine whether the observations in the present analysis can be explained by such an effect, but our results raise it as a plausible possibility.

Several other limitations should be noted. First, administrative data are always subject to coding error and a lag time in availability for analysis (e.g., this analysis only reflects patient data through 2009). We are not aware of any reason that these limitations should introduce any systematic error that would alter the internal validity of the current observations.

Second, while the iterative methods used in joinpoint regression are comparatively powerful, the observation of a joinpoint at day 30 must be interpreted with the knowledge that a narrow CI for this estimate is not present (95 percent CI = day 20–35), despite the very large sample size and a highly significant p-value (p = .0002) for the model containing that joinpoint. We suspect that the width of the CI owes itself to the subtlety of the phenomenon we observed, and it reinforces the notion that the joinpoint estimate at day 30 we observed should be confirmed with further analyses.

Third, heterogeneity exists in the use of 30-day mortality as a quality measure in addition to or in place of other metrics (Jacobs et al. 2006; Swinkels and Plokker 2010). Inpatient mortality (regardless of timing), global 30-day mortality (including patients who had already been discharged from the hospital), or combinations of these metrics are used variously by hospitals, medical groups, professional societies, local and state health departments, and consumer websites. In addition, other quality metrics that assess dimensions of quality of care beyond mortality (admittedly a crude outcome measure) are used, and they surely play into whatever complex relationship exists between quality assessment and provider behavior. However, the fact that 30-day mortality is not the sole quality benchmark should not diminish the relative importance of the present observations.

Fourth, we should note that we have included patients having more than one specific type of cardiac surgical procedure. While average mortality and recovery are not identical between, for instance, valve and nonvalve surgical populations, our reasons for not limiting the analysis to a single procedural subgroup are twofold: one, we sought to optimize sample size over as narrow a timeframe as possible to maximize the signal-to-noise ratio in examining a subtle clinical phenomenon. Two, we believe that procedural distinctions within the overall population of cardiac surgical patients may become progressively less important as one departs from the curve of routine or expected recovery. Those patients in the cardiac surgical intensive care unit at or around the 30-day mark have all experienced a similarly complicated, nonroutine postoperative course, and—we suspect—therefore represent something of a more procedure-independent single population than they might have on postoperative day 2.

Fifth, we also should note that while we have examined this phenomenon in cardiac surgery, we have no reason to believe that it should be exclusive to this setting. But identification of its presence in other clinical settings may be more difficult if the absolute mortality rate is lower, because of considerations of power.

Supporting Information

Additional supporting information may be found in the online version of this article:

Appendix SA1: Author Matrix.