Leaf Vein Length per Unit Area Is Not Intrinsically Dependent on Image Magnification: Avoiding Measurement Artifacts for Accuracy and Precision^,,

Measurements of leaf vein length per area do not increase systematically with image magnification, contrary to a recent claim, given appropriate attention toward accuracy and precision.

Abstract

Leaf vein length per unit leaf area (VLA; also known as vein density) is an important determinant of water and sugar transport, photosynthetic function, and biomechanical support. A range of software methods are in use to visualize and measure vein systems in cleared leaf images; typically, users locate veins by digital tracing, but recent articles introduced software by which users can locate veins using thresholding (i.e. based on the contrasting of veins in the image). Based on the use of this method, a recent study argued against the existence of a fixed VLA value for a given leaf, proposing instead that VLA increases with the magnification of the image due to intrinsic properties of the vein system, and recommended that future measurements use a common, low image magnification for measurements. We tested these claims with new measurements using the software LEAFGUI in comparison with digital tracing using ImageJ software. We found that the apparent increase of VLA with magnification was an artifact of (1) using low-quality and low-magnification images and (2) errors in the algorithms of LEAFGUI. Given the use of images of sufficient magnification and quality, and analysis with error-free software, the VLA can be measured precisely and accurately. These findings point to important principles for improving the quantity and quality of important information gathered from leaf vein systems.

The leaf vein system delivers water, nutrients, and signals throughout the leaf, and sugars and signal molecules back to the rest of the plant, and supports the lamina mechanically (Roth-Nebelsick et al., 2001; Sack and Scoffoni, 2013). The leaf vein length per unit leaf area (VLA; also known as venation density) has key implications for leaf development, physiology, and ecology. In typical angiosperm leaves, the venation system is constructed of three orders of major veins (i.e., one or more first-order [1°] veins entering the lamina from the petiole, second-order [2°] veins branching off along the 1° vein length, and third-order veins forming a mesh in between) along with one to several additional orders of smaller, minor veins that complete the mesh throughout the leaf, typically bounding loops known as areoles (Ellis et al., 2009). The total VLA including both systems is positively related to physiological performance (e.g. hydraulic conductance and photosynthetic rate per leaf area; for review, see Brodribb et al., 2010; Sack and Scoffoni, 2013).

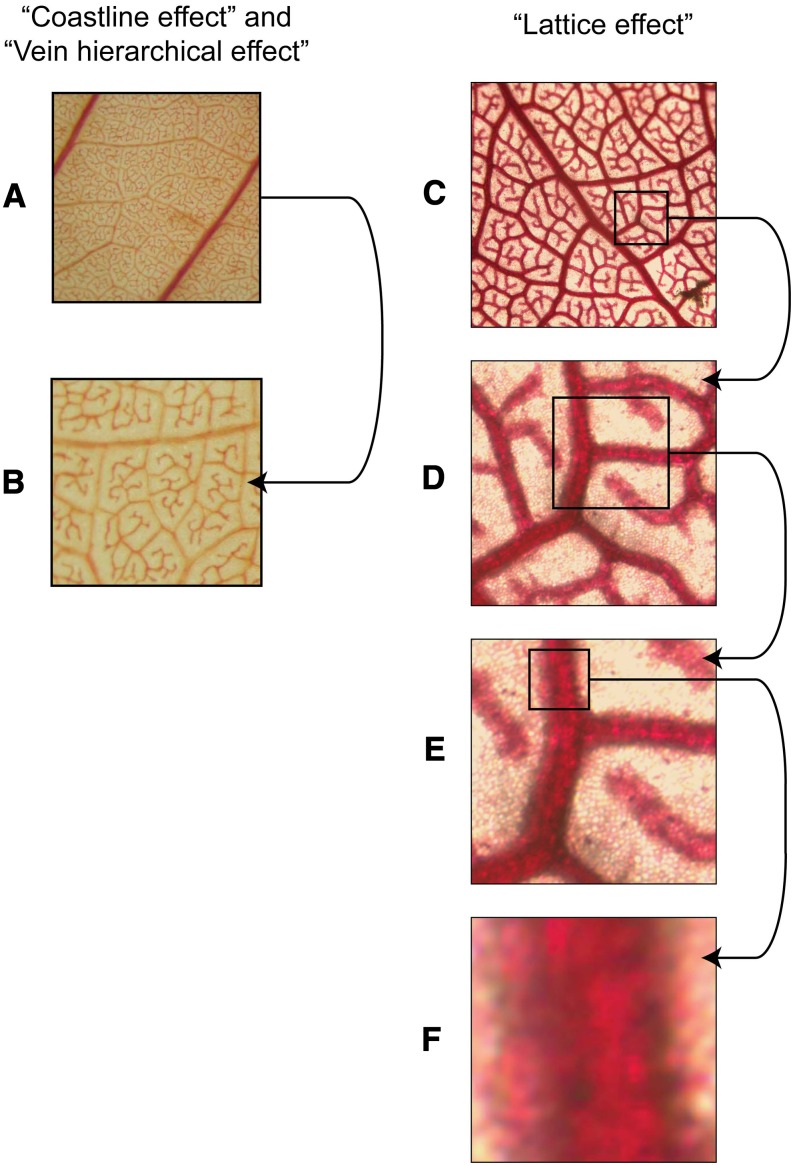
A current question is whether VLA for a given leaf can be estimated with a single number. Studies for at least 100 years had assumed so (Haberlandt, 1914). However, a fixed value was recently rejected by Price et al. (2014), who argued that VLA seemed to increase with the magnification of their image when measured with their self-designed software, LEAFGUI (for Leaf Extraction and Analysis Framework Graphical User Interface). This software measures the veins in an image of a chemically cleared leaf by thresholding or segmenting the veins (i.e. altering the contrast of the image until veins are made sharper to the eye of the user), followed by skeletonization (i.e. locating the midline of the veins) and counting for pixels (Price et al., 2011). Price et al. (2014) proposed three mechanisms to explain the apparent increase of VLA with image magnification (Fig. 1): (1) a fractal coastline effect, by which vein length would increase with magnification, like the length of the coast of Britain, for which “finer resolution imaging led to increases in the apparent length” (Mandelbrot, 1967; Fig. 1, A and B); (2) a lattice effect, by which VLA increases dramatically when zooming in on veins within areas smaller than a single areole (Fig. 1, C–F); and (3) a vein hierarchical effect, by which images at lower magnifications have lower VLA because 1° and 2° veins in the image may exclude higher order veins that have greater VLA (Fig. 1, A and B). However, these three mechanisms would not explain the increases of VLA with magnification that Price et al. (2014) reported. The problem of estimating VLA is not analogous to determining the length of a fractal frontier or surface outline, as in the example of the coast of Britain. By contrast with a natural frontier such as a coast, which has roughness features of a range of sizes (from bays to coves, to pebbles protruding from the edge, to grains of sand), the vein system is made up of approximately cylindrical tubes containing linearly arranged xylem and phloem cells, resulting in a well-defined cumulative length along the center of each vein in mature leaves; once all veins are visible, further magnification should not cause new length to appear (Liebovitch, 1998). Additionally, researchers including Price et al. (2014) generally avoided the lattice effect and hierarchical effect by choosing images that included many areoles and excluded 1° and 2° veins. An alternative explanation for the apparent scale dependency of VLA is that it was an artifact of methodology. The VLA might seem to increase with magnification if vein length was only partially resolved in the low-magnification images. Additionally, the LEAFGUI might inaccurately estimate VLA in a way that depends on image magnification.

Figure 1.

Mechanisms proposed by Price et al. (2014) for an increase of VLA with image magnification. A and B, The fractal coastline effect, by which VLA would increase systematically across all magnifications due to increasing line length at higher magnification, even in images of sufficient quality for all veins to be resolved (leaf of Plumeria alba from Price et al. [2014]), and the vein hierarchical effect, by which lower magnification images might include more 1° and 2° veins than higher magnification images, leading to lower VLA estimation. C to F, The lattice effect, by which zooming in within an image to areas of less than a single areole would lead to greater estimates of VLA because veins take up a disproportionate fraction of the image area relative to nonvein lamina; when a vein completely fills the image, the VLA equals the length of the image divided by the area of the image, which will tend to infinity as one zooms in on areas of ever smaller fractions of 1 mm (leaf of Machaerium acutifolium). Our analyses found that these mechanisms are not likely to influence typical VLA estimation or to account for the increase of VLA with magnification found by Price et al. (2014); the fractal coastline effect should not apply to the midline of veins used for VLA quantification, and typical images used for VLA estimation sample multiple areoles, typically avoiding 1° and 2° veins.

Whether a given leaf has a fixed VLA value has powerful implications for measurements and interpretation of the previous literature and its link with physiological processes. VLA values determined with a range of high magnifications have been used to compare species and to develop predictions of rates of photosynthesis and for the reconstruction of physiology or climate from fossils based on VLA (Boyce et al., 2009; Boyce and Lee, 2010; Brodribb and Feild, 2010; Brodribb et al., 2010; de Boer et al., 2012). Indeed, recent models have considered the higher mean VLA of angiosperms (7–10 mm mm⁻²) than earlier evolved lineages (less than 2 mm mm⁻²) to predict average differences in photosynthetic rate and water use by specific equations (Boyce et al., 2009; Brodribb and Feild, 2010; Sack and Scoffoni, 2013). By contrast, Price et al. (2012) measured unmagnified images of angiosperm leaves and reported VLA values more typical of previous studies of fern leaves. They argued that such low values are equally valid and recommended that low magnification be used in future comparative measurements (Price et al., 2014).

Here, we tested whether VLA increases intrinsically with magnification. We compared the precision and accuracy of LEAFGUI versus digital tracing with freely available software (ImageJ; Table I), using all the images used by Price et al. (2014), and determined the source of discrepancies. We also tested the proposal of Price et al. (2014) that low-magnification images would be sufficient to quantify how vein traits scale with leaf size.

Table I. Definitions of terms relating to image analysis and their application to the estimation of VLA from images (Ruzin, 1999).

Note that image magnification, resolution of image, scale of image, and resolving power are interrelated (Supplemental Table S1). Image quality for measuring VLA depends on magnification and resolution being sufficient to discern all veins and, additionally, on sufficient leaf clearing and staining and contrast in the image.

Term	Definition	How to Quantify for Measurement of VLA
Accuracy of estimate	Degree of conformity of a measured or calculated quantity to its actual (true) value	How close are the values to the true value? This is determined using digital tracing in high-magnification, high-quality images in which all veins can be observed sharply
Precision of estimate	Degree to which several measurements provide answers very close to each other	Coefficient of variation across experimenters
Image quality	Perceived image degradation (compared with an ideal or perfect image); this is affected by many factors, including especially sharpness, the amount of detail the image can convey	Are all the veins discernible? Low image quality may arise due to too-low magnification and/or too-low resolution, and/or blurring of the image caused by downsampling, and/or not sampling the vein network representatively (e.g. zooming in within a single areole or including large major veins in an image of minor venation)
Microscope objective magnification	Magnification contributed by the objective of the microscope: one element in the total image magnification	Given on the microscope objective
Image magnification	Ratio of the apparent size of an object in the image to its true size	Actual size of the digital image, typically embedded in the image file, relative to its actual size; because the camera magnifies the image beyond the microscope, this can be many times larger than the microscope objective magnification
Total display magnification	Ratio of the apparent size of an object of a displayed image including its zoom to its true size	Size of the image when displayed on a monitor at 100% size or with further zooming can be quantified using a ruler on the screen relative to its actual size; typically, this is many times larger than the microscope objective magnification, as it depends on image magnification (i.e. in the image file) and additionally on the computer operating system and/or software display resolution settings and/or the display monitor
Resolution of image	Ratio (pixels mm−1) of the image length in picture elements (pixels) to the length of the image (mm)	Dividing the length of the image in pixels by its actual length
Scale of image	Ratio (pixels mm−1) of the image length in picture elements (pixels) to the length of the field of view (mm)	Dividing the length of the image, or a ruler or micrometer in the image in pixels by its actual length; the scale of image equals the product of the image magnification and the resolution of the image
Resolving power	Ability to distinguish two points that are close together, and the ability to resolve minor veins in the image	Resolving power increases with the scale of the image; the diameter of the smallest vein should be larger than three pixels at minimum

RESULTS

Tests of the Precision and Accuracy of VLA Measurement by LEAFGUI Relative to Digital Tracing

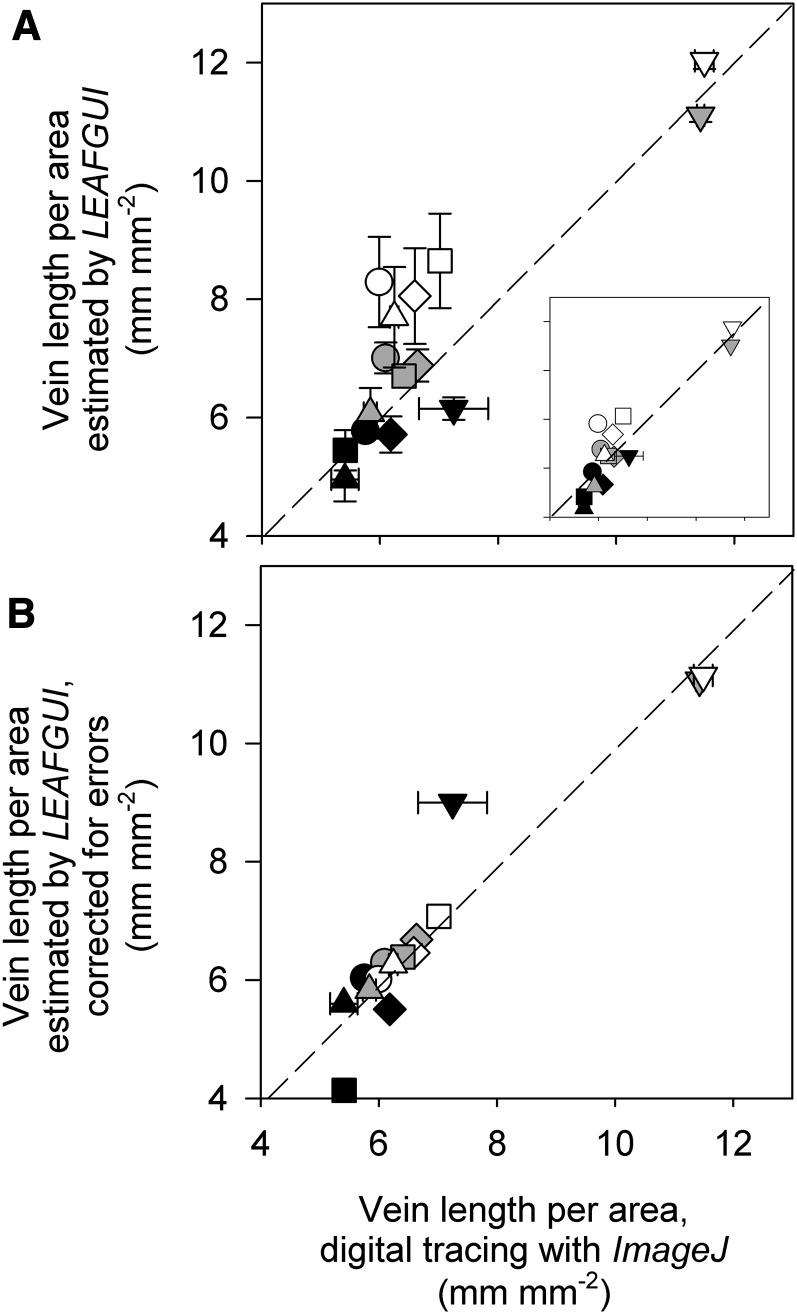
Our measurements using LEAFGUI and digital tracing with ImageJ showed that while both methods provided high accuracy and precision for line grids, LEAFGUI had low precision and accuracy for measuring venation in images of cleared leaves, using the images of Price et al. (2014; Supplemental Results S1; Supplemental Table S2). The LEAFGUI values for given leaves ranged from 15% below to 38% above the values determined using digital tracing (Fig. 2A; Supplemental Table S2; P < 0.01 for differences among methods in a repeated-measures ANOVA). The two measurement methods took users approximately the same time (10–20 min per leaf).

Figure 2.

Testing the accuracy of LEAFGUI for measurements of VLA for cleared leaves of five species imaged at three magnifications. A, Values estimated by LEAFGUI plotted against values determined by digital tracing show a wide range of scatter around the 1:1 line (errors of up to 38%), with lower magnification images typically below the line and higher magnification images above the line. Values were significantly different at P = 0.01 (repeated-measures ANOVA; see text). The main plot shows mean values ± se across three users of each software; the inset plot shows the LEAFGUI values of Price et al. (2014). B, Values estimated by Price et al. (2014) using LEAFGUI and now corrected for artifacts of the software algorithms (Table II) are very similar to those determined by digital tracing. Values were statistically similar at P = 0.99 (repeated-measures ANOVA); measurements in 5× images remained different, as veins could not be resolved accurately in these images using either method. Species symbols are as follows: circles, B. victoriae; diamonds, Hardenbergia comptoniana; squares, P. alba; triangles, Pittosporum moluccanum; and inverted triangles, Wisteria floribunda. Black symbols, 5× images; gray symbols, 20× images; white symbols, 60× images.

Sources of Error in LEAFGUI

Examination of the LEAFGUI images of Price et al. (2014) indicated four artifacts that affect its precision and accuracy (Fig. 3; see “Materials and Methods”): (1) the thresholding artifact (Fig. 3B); (2) the neglected vein length artifact (Fig. 3C); (3) the false vein artifact (Fig. 3D); and (4) the zigzag line artifact (Fig. 3E). We quantified the errors associated with each artifact using digital tracing. Notably, the images tested were those of Price et al. (2014) that had already been subjected by those authors to cleaning of the image to remove some of the artifacts, such as false veins generated during thresholding or skeletonizing to find the vein midline (see “Materials and Methods”); we quantified the artifacts remaining in these skeletonized images. Substantial errors contributed by each artifact combined to produce errors of up to 38% (Table II). Correcting these errors rendered the LEAFGUI measurements by Price et al. (2014) of VLA statistically indistinguishable from those determined by digital tracing (P = 0.99 for method effect, by repeated-measures ANOVA; Fig. 2B); several measurements made on 5× images remained different due to the impossibility of resolving all the veins in those images (Fig. 3A; see below).

Figure 3.

Artifacts that lead to errors in the estimation of VLA. A, A substantial proportion of the minor veins cannot be discerned in low-magnification images. A portion of the 5× image of W. floribunda of Price et al. [2014) was enlarged to the same magnification as the 60× image, demonstrating the low resolution of the 5× image. B to E, Artifacts of the LEAFGUI software. B, Thresholding artifact. When the cleared leaf image is transformed to a binary (black and white) image using thresholding, veins may disappear or false veins may appear. Note the appearance of vein islands, which do not actually exist in this species (detail of a P. moluccanum leaf). C, Neglected vein length artifact. The blue line shows the skeletonized vein length generated by LEAFGUI, which misses some veins (detail of a W. floribunda leaf). D, The false vein artifact. LEAFGUI interprets some roughness at vein edges as if it represented small veins and connects these, resulting in false veins (detail of an H. comptoniana leaf). E, The zigzag line artifact. LEAFGUI skeletonizes the veins by generating a midline by removing pixels at the edges of the vein, thus leading to zigzag segmented lines longer than the actual vein midline (detail of a W. floribunda leaf).

VLA Increases with Magnification for LEAFGUI, But Not for ImageJ, Given That All Veins Are Visible

We confirmed the finding of Price et al. (2014) that when measuring VLA with LEAFGUI there was a strong dependence on image magnification, averaging the values collected by three experimenters. The VLA measured with LEAFGUI increased on average by 34% from 5× to 20× images (15%–70% increase for a given species) and a further 18% from 20× to 60× images (8%–29% increase for a given species; P < 0.001 for differences among magnifications in repeated-measures ANOVA, with differences among all three magnifications at P < 0.05 in Tukey’s test; Supplemental Table S2). However, when quantifying VLA using digital tracing, again averaging values collected by three experimenters, we found an effect of magnification only when including the 5× images (P = 0.032 for magnification; only the 5× images differed from 60× images at P < 0.05 by Tukey’s comparison; no significant differences were seen for the 20× and 60× images).

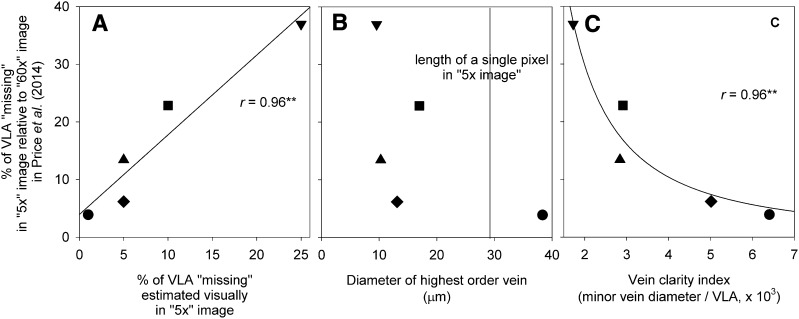
Three tests indicated that the lower VLA values for the 5× images of Price et al. (2014) found using digital tracing simply arose from their low quality for discerning all the veins (Fig. 3A). First, we found a strong correlation across the measured leaves between the percentage of the vein length not discernible, as estimated by eye, and the percentage of minor vein length missing, calculated by comparing the VLA measured by digital tracing in the 5× and 60× images (r = 0.96, P = 0.01; Table II; Fig. 4A); notably, the actual percentage of minor vein length not visible in the image was on average double that estimated by eye (paired Student’s t test on log-transformed data; P = 0.02). Second, we estimated the image resolution necessary to discern all the leaf minor veins. For an ability to discern the minor veins, these should appear at minimum as at least three pixels wide in the image (see “Materials and Methods”). In the leaves analyzed by Price et al. (2014), minor veins of the highest order were less than 30 µm in diameter (Fig. 4B), far narrower than the length of three pixels in the 5× images (87 µm) but not in the 20× (29 µm) and 60× (14 µm) images (Supplemental Table S1). Finally, we tested the correlation of an index of vein clarity (Eq. 1) with the percentage of minor vein length not visible in the 5× image, calculated by comparing the VLA measured in the 5× and 60× images using digital tracing. We found that the lower the vein clarity the greater the percentage of veins not observed across the 5× images of the leaves of different species (r = −0.96, P = 0.005 for log-transformed data; Fig. 4C).

Table II. Quantifying the artifacts of the approach of Price et al. (2014).

Errors include the use of low-magnification 5× images with veins not discernible, inclusion of 1° and 2° veins in images, and the errors arising from four artifacts in the LEAFGUI algorithms, all of which lead to inaccurate estimation of leaf VLA and the illusion of a dependency of VLA on image magnification. For each artifact, the effect on VLA was determined for the one image per leaf per species at each of three magnifications measured by Price et al. (2014). The total LEAFGUI error was determined by adding the missing vein length due to the thresholding artifact and the neglected vein length artifact and subtracting the vein length due to the false vein artifact and the zigzag line artifact. Effects are presented in absolute terms (mm mm⁻²) and as percentages of total VLA as determined by Price et al. (2014). Error percentages greater than 5% are in boldface. na, Images sufficiently magnified for veins to be discerned.

Species	Error from Using Low-Magnification Images with Nondiscernible Veins	Percentage of the Image Area Occupied by 1° and 2° Veins; Effect on VLA	Errors Arising as Artifacts of LEAFGUI Algorithms
			Thresholding	Neglected Vein Length	False Vein Length	Zigzag Line	Total LEAFGUI Error
B. victoriae
5×	−0.23 (−3.89%)	3.0%; +0.32 (+5.4%)	−0.28 (−4.9%)	−0.077 (−1.3%)	0	+0.17 (+3.0%)	−0.19 (−3.2%)
20×	na	3.6%; +0.42 (+6.3%)	+0.12 (+1.8%)	−0.078 (−1.1%)	+0.061 (+0.90%)	+0.36 (+5.4%)	+0.47 (+6.9%)
60×	na	0	−0.017 (−0.21%)	−0.053 (−0.67%)	+0.81 (+10%)	+1.1 (+14%)	+1.8 (+23%)
H. comptoniana
5×	−0.41 (−6.2%)	2.6%; −0.019 (−0.35%)	−0.12 (−2.4%)	−0.13 (−2.5%)	0	+0.084 (+1.6%)	−0.18 (−3.3%)
20×	na	0	−0.50 (−7.8%)	−0.20 (−3.1%)	+0.20 (+3.1%)	+0.29 (+4.4%)	−0.22 (−3.3%)
60×	na	0	−0.15 (−2.0%)	−0.11 (−1.5%)	+0.53 (+7.2%)	+0.65 (+8.8%)	+0.92 (+12%)
P. alba
5×	−1.6 (−23%)	3.4%; −0.018 (−0.38%)	+0.64 (+13%)	−0.13 (−2.6%)	0	+0.18 (+3.8%)	+0.69 (+14%)
20×	na	0	−0.41 (−6.3%)	−0.11 (−1.7%)	+0.083 (+1.3%)	+0.54 (+8.4%)	+0.11 (+1.7%)
60×	na	0	−0.027 (−0.34%)	−0.022 (−0.27%)	+0.27 (+3.3%)	+0.83 (+10%)	+1.0 (+13%)
P. moluccanum
5×	−0.84 (−13%)	0.56%; +0.044 (+1.0%)	−1.1 (−25%)	−0.20 (−4.7%)	0	+0.055 (+1.3%)	−1.25 (−29%)
20×	na	0	−0.94 (−18%)	−0.083 (−1.6%)	+0.13 (+2.4%)	+0.32 (+6.0%)	−0.58 (−11%)
60×	na	0	−0.47 (−7.2%)	−0.099 (−1.5%)	+0.19 (+2.9%)	+0.64 (+9.9%)	+0.27 (+4.1%)
W. floribunda
5×	−4.2 (−37%)	7.3%; −0.21 (−3.3%)	−2.6 (−40%)	−0.049 (−0.76%)	0	+0.12 (+1.9%)	−2.5 (−38%)
20×	na	0	−0.85 (−7.7%)	−0.22 (−2.0%)	+0.15 (+1.4%)	+0.88 (+8.0%)	−0.039 (−0.35%)
60×	na	0	−0.47 (−4.0%)	−0.15 (−1.2%)	+0.28 (+2.4%)	+0.97 (+8.2%)	+0.62 (+5.3%)

Figure 4.

Proving that low-image magnification in 5× images results in low estimates of VLA due to low vein clarity. Images at this magnification or lower were used by Price et al. (2011, 2012, 2014) on the basis that the low VLA was an intrinsic characteristic of vein geometry rather than due to a lack of vein clarity. The correlation of the percentage of missing VLA in 5× images relative to 60× images was plotted against a visual estimate of missing veins by an experimenter observing the 5× images (A), the diameter of the highest order vein (always smaller than the image resolving power, given that one pixel was equal to 29 µm; B), and an index of vein clarity (C), assuming that veins are easier to see in a low-magnification image if wider or spaced farther apart (Eq. 1). Species symbols are as in Figure 2. **P < 0.01. Recommendations and typical practice in the literature are to analyze images in which all veins are discernible.

By contrast with the 5× images, the veins were all visible in the 20× and 60× images, and yet VLA estimates increased using LEAFGUI but not using digital tracing. We sought the underlying mechanisms for this pattern. First, we considered the mechanisms proposed by Price et al. (2014), although any such systematic, intrinsic mechanisms also should have affected values determined by digital tracing. We considered whether the LEAFGUI effect could have arisen from a fractal coastline effect (Fig. 1, A and B), but this would not be the case for a midline (Liebovitch, 1998). We considered whether the LEAFGUI effect could have arisen from a lattice effect (i.e. from focusing on less than a single areole; Fig. 1, C–F). However, all images included more than five areoles. Furthermore, we tested for a possible vein hierarchical effect (i.e. whether the occupation of the image by major veins could have accounted for the difference; Fig. 1, A and B). However, the 1° and 2° veins presented a significant proportion of area only in the 5× images (representing mean ± se of 3.4% ± 1.1% of image area on average) and a 20× image for only one species (3.6% for Banksia victoriae; Table II). Excluding the 1° and 2° vein length and area from VLA calculation had only a small effect for only a few images (Table II) and did not remove the scale dependency of the VLA values determined by LEAFGUI (P < 0.001 for differences among magnification remained in repeated-measures ANOVA on log-transformed data, with all three magnifications different at P < 0.05 in Tukey’s test; Fig. 5).

Figure 5.

The measurement of VLA is not intrinsically dependent on image magnification. An increase of VLA across three image magnifications was found by Price et al. (2014) when determining VLA for one image per leaf at each of three magnifications for each of five species using the LEAFGUI software. The lowest magnification was too low to see veins (see “Results”; Fig. 4); the remaining two magnifications, 20× and 60×, also differed when VLA was determined using LEAFGUI. This difference was not removed when correcting the VLA for the length and area occupied by 1° and 2° veins in the images, but it was removed after correcting the LEAFGUI values of VLA for all artifacts in the algorithms of that software as determined for the skeletonized leaf images of Price et al. (2014; Table II); the difference was not found when VLA was determined using digital tracing with ImageJ. Different lowercase letters within each pair of bars indicate a statistical difference at P < 0.05 (repeated-measures ANOVA with Tukey’s comparison).

We tested whether the artifacts of the LEAFGUI described above (Fig. 3, B–E) would have contributed to the appearance of a dependency of VLA on image magnification. Indeed, correction of these errors in the images of Price et al. (2014) removed the difference between the 20× and 60× images presented in that study (no significant difference at P = 0.05, Tukey’s comparison in repeated-measures ANOVA on log-transformed data; Fig. 5). Thus, the apparent dependence of VLA on image magnification reported by Price et al. (2014) was an artifact of using low-quality images in which veins are not visible (i.e. 5× images) and of software that increases false vein length measurement with higher magnification.

Testing the Ability to Quantify the Scaling of VLA with Leaf Size Using Low-Magnification Images

We analyzed whether one can determine the scaling of VLA with leaf size using unmagnified leaf images in which all veins are not discernible, as recommended by Price et al. (2012; 2014; Supplemental Fig. S1). We found that that approach would not resolve a scaling relationship even if it had existed (Supplemental Results S2; Supplemental Fig. S1).

DISCUSSION

We found that the VLA is not intrinsically dependent on image magnification and can be accurately estimated at a range of high magnifications using digital tracing with ImageJ. Our findings did not support the claim by Price et al. (2014) that estimates of VLA depend deterministically on magnification across the full range of scales; rather, this apparent increase in VLA was due to using low-quality, low-magnification images of the leaf vein system and to errors of the LEAFGUI. With proper precautions, these issues can be avoided and VLA can be estimated with excellent accuracy and precision.

Low Accuracy and Precision of LEAFGUI Measurement

We found that LEAFGUI could accurately measure grid lines, given that these all appear sharply and they have smooth edges such that their midlines are well located as straight lines by the skeletonization algorithm. However, in processing leaf vein images, LEAFGUI produces substantial errors. The first issues arise because LEAFGUI cannot process high-quality images and requires an image of lower magnification, resolution, and quality to be generated by “downsampling” (see “Materials and Methods”). By contrast, digital tracing with ImageJ can be applied to high-quality images, providing a precision even greater than that reported here for the low-quality images used for comparison with LEAFGUI. Furthermore, at least four LEAFGUI artifacts combined to produce errors of up to 38% (Table II). The average bias depended on the magnification of the image; VLA values were low on average for the 5× images, in which missing vein length errors dominated, and high for the 60× images, in which false vein errors dominated; images with magnification in between tended to show errors in either direction. Some of these errors are related to image processing and involve the experimenter (i.e. thresholding to generate the binary black/white image identifying the veins and any cleaning of the image), but all the artifacts will lead to errors automatically for any experimenter.

The Apparent Increase of VLA with Magnification: An Artifact of Image Quality and LEAFGUI

The VLA appeared to increase with image magnification when measured by the LEAFGUI from 5× to 20× to 60× images. This effect arose from two issues: the use of low-quality, low-magnification images and LEAFGUI producing inaccurate values of VLA across the range of image magnifications. When measuring VLA using digital tracing with ImageJ, there was no intrinsic dependence on image magnification, given that the images were of high enough quality for all the veins to be discerned (Fig. 5). The 5× images were of insufficient quality, whether that was assessed by simple observation of images or by quantifying the vein length or by conducting a calculation of the resolving power or the clarity of veins in the image. By contrast, the VLA values determined by digital tracing for the 20× and 60× images were nearly identical.

We rejected the possibility that the apparent increase of VLA using LEAFGUI arose from intrinsic properties of the vein systems, as proposed by Price et al. (2014). Unlike a coastline, the midline of the leaf venation has a well-defined length. While Price et al. (2014) might have intended to include the fact of unresolved veins in low-quality images within their proposed coastline effect, making a distinction is critical. A coastline effect, if it had existed, would apply across magnifications and would imply that a fixed value for VLA does not actually exist and that VLA must always be quantified relative to its magnification. By contrast, inaccuracy due to missing veins in low-quality images can be avoided by ensuring the use of well-cleared leaves imaged at high magnification and avoiding image downsampling. For such images, and any at higher magnification, VLA will not show a significant systematic increase with magnification when measured using digital tracing, as long as a representative sample of venation is included. We also considered whether the apparent increase of VLA using LEAFGUI might arise from the lattice effect (i.e. inappropriate sampling), but all images included more than five areoles. Third, we considered whether the occupation of the image by major veins could have accounted for the apparent increase of VLA using LEAFGUI, but these large veins tended to occupy a slight proportion of the image, and correcting for this did not remove the effect. Rather, the artifacts of the LEAFGUI fully accounted for the apparent increase in VLA from the 20× to the 60× images.

To our knowledge, our quantification of LEAFGUI errors is the first of its kind. Price et al. (2014) acknowledged one of the errors affecting vein length measurement (i.e. the false vein artifact; Fig. 3D) but discounted its importance because LEAFGUI also found venation perimeter to increase with magnification, and that increase would not have been explained by that particular error. However, the other LEAFGUI errors (Fig. 3, A–C and E) would explain the apparent increase of venation perimeter with image magnification. Future investigations of VLA using novel software need to be checked against digital tracing. Furthermore, just as sufficient magnification is critical for VLA quantification, our graphical analysis demonstrated that it is necessary for accurately determining the relationships of VLA or other vein traits with leaf size (Supplemental Discussion S1).

Implications of Measurement Methods for the Interpretation and Comparison of Data across Studies

Our finding that VLA does not increase systematically with magnification has important implications for the interpretation of the published literature. Given their proposal that VLA was dependent on image magnification, Price et al. (2014) sounded a “caution against using data from multiple scales to make comparative inferences about physiological, ecological or evolutionary mechanisms driving changes in VLA.” Our analyses supported the assumption of previous studies that, given a representative and sufficiently resolved portion of the vein network, values should be comparable across a range of high magnifications. Notably, researchers tended to report the magnification of the light microscope objective rather than the total image magnification, which also includes the magnification contributed by the camera; our light microscope with a 5× objective and camera produced a digital image file with 287× magnification (for details on calculating true image magnification, see “Materials and Methods”; Table I; Supplemental Table S1).

Best Practices for the Accurate Estimation of VLA and Other Vein Traits

Our findings provide important guidance for the accurate estimation of VLA. We agree strongly with Price et al. (2014) that the magnification and resolution of images should be clearly stated (we provide a spreadsheet tool for easy calculation; Supplemental Table S1). Furthermore, we agree on the need for precision and accuracy. We disagree only on the details, as we set out here.

First, leaves need to be sufficiently cleared, and in some cases, when the epidermis is thick or hairy, the epidermis may need to be partially removed for all the minor veins to be visualized. Based on our findings, it is not necessary that all images be made at the same magnification; some leaves may require higher magnification to resolve all the veins than others. We assume that the total image magnification necessary will typically be more than 20×, attainable with a 5× microscope objective and a quality digital camera, as used in the bulk of previous studies. Our findings refute the recommendation of Price et al. (2014) that VLA measurement be made on images with 10× image magnification, which often would be too low to resolve all the veins. The “5× images” of Price et al. (2014) that we analyzed actually had >9× image magnification, and substantial portions of minor veins were not discernible for four of five species (see “Materials and Methods”; Table II; Supplemental Table S1).

We agree with Price et al. (2014) in principle that it would be ideal to measure VLA on entire leaves rather than on sampled images, but excellent estimates can be made from sampled images. One apparent advantage of LEAFGUI, its ability to measure veins for images of entire leaves, is outweighed by the fact that this can be done only for unmagnified images in which veins are not all discernible. Imaging a whole leaf with magnification is a difficult prospect, and Price et al. (2014) introduced the possibility of constructing a mosaic image of subsampled areas stitched together, although they found this to be extremely computationally intensive. Beyond this, chemically clearing entire leaves to a sufficient degree to resolve veins under high magnification is often infeasible; some regions clear only enough for major veins to be quantified. Thus, the best estimation of properties of leaf venation is currently made from images of samples of the lamina, with the optional practice of additionally measuring the major veins using scans of cleared whole leaves (Scoffoni and Sack, 2011). Some measurements of interest for studies of network properties (e.g. vein segment lengths and diameters) also can be estimated from randomly sampled sections of the venation under high magnification and statistically scaled up to allow whole-leaf estimates.

It is important to continually improve methodology by increasing precision and accuracy and, when possible, to reduce measurement effort. We found that measurement of minor vein images by digital tracing has high precision across experimenters and took a similar time as the thresholding approach of LEAFGUI (i.e. approximately 15 min per image). Vein analysis software holds the potential for increased speed, but this is only a benefit if accuracy can be preserved. Our findings led to suggestions for improving analysis software (Supplemental Discussion S2).

Improved methodology will increase not only measurement speed and accuracy but also the breadth and depth of information extracted from the venation system, a truly exciting prospect. We believe that a major advantage of digital tracing is its ability to take into account the vein orders and that this ability may be incorporated in the next generation of vein measurement software. Vein orders are precisely defined during leaf development, appearing at different times, but in mature leaves they are sometimes only distinct as different categories of sizes and connectivity, although they may be distinguished with care (Ellis et al., 2009; Scoffoni and Sack, 2011). Either the software could be guided or trained by allowing the user to click on representative veins of given orders, or the software could locate these by using diameter class categories, proceeding from low to high vein orders. Such a software algorithm could thus mimic software that simulates the development of the leaf (Runions et al., 2005) or experiments tracking the flow of water or dye through the vein system (Jeje, 1985; Canny, 1990). Such a software could quantify not only critical parameters, such as total VLA, but also other traits reflecting the development of leaf venation (e.g. VLA for different vein orders, distances between 2° veins, and angles between veins of different orders). Such parameters could be used to quantitatively summarize the complete venation architecture and thereby analyze its evolution across lineages and its relationships to function, ecology, and adaptation to climate.

MATERIALS AND METHODS

Quantifying Vein Length per Area by Digital Tracing

For quantification of VLA by digital tracing, we used ImageJ version 1.44o (National Institutes of Health), according to standard protocols (Scoffoni and Sack, 2011).

Comparing Measurements of VLA by Digital Tracing with ImageJ with Those Using the LEAFGUI

We measured a series of test grids and the images provided by Price et al. (2014) within their supplemental materials pdf document for single leaves of five species: Banksia victoriae, Hardenbergia comptoniana, Plumeria alba, Pittosporum moluccanum, and Wisteria floribunda (Supplemental Methods S1). For each leaf, Price et al. (2014) supplied one image taken at each of three magnifications, which they described as 5×, 20×, and 60×. Total vein length was measured by digital tracing with ImageJ by three users. The LEAFGUI analyses were performed by two different users, and data from the graphs of Price et al. (2014) were extracted using ImageJ, to yield data from three different users. We determined the precision of both approaches and compared the values averaged across LEAFGUI users with those determined by digital tracing with ImageJ as a test of accuracy.

Sources of Error in Measuring VLA

Low Image Quality

One source of error in measuring VLA would be low image quality: i.e., low sharpness for discerning veins, especially in the 5× images (Fig. 3A). Price et al. (2014) created high-magnification images but then downsampled by a factor of 6, averaging colors across pixels, because high-resolution images cause the software to fail by increasing the artifacts. We confirmed this: our tests of LEAFGUI using high-resolution images of leaf venation failed at the skeletonization stage; fragmented skeletons and false veins dominated the image. However, downsampling images strongly reduced the image magnification and resolution (Supplemental Table S1) and also, independently, the image sharpness; an image downsampled from a higher magnification to 10× magnification by averaging pixels will be blurrier than one originally taken at 10×. This approach resulted in 5× images of very low quality for distinguishing veins, which was a potential source of the low VLA, distinctively different from the higher magnification images. To confirm that the 5× images were of insufficient quality to accurately quantify VLA, we performed three tests. First, we visually estimated the percentage of the length of minor veins that was apparently obscure (or missing) in these images and compared this with the difference in VLA between the 5× images and the 60× images in which veins were all visible. Second, we estimated the resolving power possible using these images. Resolving power depends on many factors relating to the image and the measurer, and is strongly dependent on the scale of the image (Table I; Supplemental Table S1). If the vein diameter is smaller than one pixel, it will not be visible. If the vein diameter is equal to one pixel in the image, one could discern it only if the vein coincided exactly with a pixel centered between pixels of surrounding lamina cells with distinct colors; in many cases, the vein would not be observed. If the vein diameter were two pixels wide, in many cases, only one pixel of distinct color would be seen, with surrounding pixels averaging veins and lamina. Thus, for most veins to be visible, the vein diameter should exceed three pixels. We thus compared the diameter of the highest order veins, measured in the 60× images, with the length of three pixels in each image. Finally, we developed a theoretical index of vein clarity in an image. We hypothesized that vein clarity (VC; units millimeter squared) would be greater if veins had larger diameters and/or if veins were spaced farther apart (i.e. if VLA were lower). Thus:

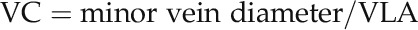(1)

The minor vein diameter was the average across fourth to sixth order veins from three replicate measurements per vein order made for each 60× image.

LEAFGUI Artifacts

Examination of the thresholded (binary) and skeletonized images of Price et al. (2014) indicated that LEAFGUI measurements involved at least four artifacts that would have contributed to inaccuracy (Fig. 2, B–E). To quantify these errors, we made additional measurements of the raw, binary, and skeletonized images of Price et al. (2014; Supplemental Methods S2).

To correct the VLA measurements reported by Price et al. (2014) based on LEAFGUI for these artifacts of measurement, we added the missing vein length due to the thresholding artifact and the neglected vein length artifact and subtracted the vein length due to the false vein artifact and the zigzag line artifact. We tested whether the artifacts of LEAFGUI could account for an apparent dependency of VLA on image magnification.

We tested the mechanisms Price et al. (2014) proposed for a dependency of VLA on image magnification (Fig. 1). To quantify the vein hierarchical effect caused by the occupation of the image by major veins, we measured the area in the images occupied by 1° and 2° veins using ImageJ and recalculated VLA after excluding their vein length and area from the image.

Statistics

When comparing the estimates of VLA using digital tracing or the LEAFGUI, we averaged values determined by the different experimenters for each image at each magnification for each species and applied repeated-measures ANOVAs after log transformation to increase normality and reduce heteroscedasticity, with method nested within magnification and species/leaf the repeated factor (Minitab Release 16; Sokal and Rohlf, 1995). Similarly, we used repeated-measures ANOVAs to compare the LEAFGUI results for VLA from Price et al. (2014) with those corrected in different ways to determine the source of the discrepancy (i.e. after correcting for artifacts of the LEAFGUI or correcting for the area occupied by major veins; see above).

To test for a dependence of VLA on image magnification, we used repeated-measures ANOVAs after averaging values across experimenters for each method and tested the effect of species/leaf and magnification, with species/leaf as the repeated factor, and applied Tukey’s comparisons among magnifications. Data were log transformed before testing to increase normality and reduce heteroscedasticity (Sokal and Rohlf, 1995).

To determine whether the inability to resolve veins in the low-quality 5× images was the determinant of their low VLA values, we tested for a correlation of the percentage of missing vein length simply estimated by eye during measurement and the percentage of minor vein length not visible, as calculated by comparing the VLA measured in the 5× and 60× images. We also tested for a correlation of the index of vein clarity (Eq. 1) with the percentage of minor vein length not visible.

We conducted a graphical analysis to test whether the scaling of VLA with leaf size can be accurately determined from the low VLA values taken from unmagnified images of cleared and stained leaves by plotting the data of Price et al. (2012) for VLA versus leaf size. We estimated the limit of resolution in those unmagnified images as their 99th percentile VLA (since 99% of measurements were below that value). We determined whether a relationship of VLA with leaf size could be hidden due to this limit of resolution, given the range of angiosperm VLA values reported in studies of magnified leaves (i.e. up to 20 mm mm⁻²).

Supplemental Data

The following materials are available in the online version of this article.

• Supplemental Figure S1. Graphical analysis of the claim that the scaling of vein length per area with leaf size can be determined accurately using data generated from unmagnified images of stained cleared leaves.

• Supplemental Table S1. Spreadsheet tool for calculating image magnification, resolution, scale, and resolving power.

• Supplemental Table S2. Values for length and vein length per area determined using LEAFGUI and digital tracing in ImageJ, for calibration grids and the images provided by Price et al. (2014).

• Supplemental Results S1. Tests of the precision and accuracy of VLA measurement by LEAFGUI relative to digital tracing.

• Supplemental Results S2. Testing the ability to determine the scaling of VLA using low-magnification images.

• Supplemental Discussion S1. Requirement of high-quality images for estimation of co-variation of vein traits with other traits.

• Supplemental Discussion S2. Suggestions for correcting or improving vein thresholding analysis software.

• Supplemental Methods S1. Comparing measurements of VLA by LEAFGUI versus digital tracing with ImageJ.

• Supplemental Methods S2. Sources of error in measuring VLA: LEAFGUI artifacts.

• Supplemental References S1. References for Supplemental “Results” and “Discussion.”

Glossary

VLA

leaf vein length per unit leaf area

1°

first-order

2°

second-order