Voltage-Sensor Transitions of the Inward-Rectifying K⁺ Channel KAT1 Indicate a Latching Mechanism Biased by Hydration within the Voltage Sensor^,,

Manipulating the electrostatic charge network that stabilizes the voltage sensor of the KAT1 K⁺ channel displaces channel gating across more than 140 mV within the physiological voltage range.

Abstract

The Kv-like (potassium voltage-dependent) K⁺ channels at the plasma membrane, including the inward-rectifying KAT1 K⁺ channel of Arabidopsis (Arabidopsis thaliana), are important targets for manipulating K⁺ homeostasis in plants. Gating modification, especially, has been identified as a promising means by which to engineer plants with improved characteristics in mineral and water use. Understanding plant K⁺ channel gating poses several challenges, despite many similarities to that of mammalian Kv and Shaker channel models. We have used site-directed mutagenesis to explore residues that are thought to form two electrostatic countercharge centers on either side of a conserved phenylalanine (Phe) residue within the S2 and S3 α-helices of the voltage sensor domain (VSD) of Kv channels. Consistent with molecular dynamic simulations of KAT1, we show that the voltage dependence of the channel gate is highly sensitive to manipulations affecting these residues. Mutations of the central Phe residue favored the closed KAT1 channel, whereas mutations affecting the countercharge centers favored the open channel. Modeling of the macroscopic current kinetics also highlighted a substantial difference between the two sets of mutations. We interpret these findings in the context of the effects on hydration of amino acid residues within the VSD and with an inherent bias of the VSD, when hydrated around a central Phe residue, to the closed state of the channel.

Plant cells utilize the potassium ion (K⁺) to maintain hydrostatic (turgor) pressure, to drive irreversible cell expansion for growth, and to facilitate reversible changes in cell volume during stomatal movements. Potassium uptake and its circulation throughout the plant relies both on high-affinity, H⁺-coupled K⁺ transport (Quintero and Blatt, 1997; Rubio et al., 2008) and on K⁺ channels to facilitate K⁺ ion transfer across cell membranes. Uptake via K⁺ channels is thought to be responsible for roughly 50% of the total K⁺ content of the plant under most field conditions (Spalding et al., 1999; Rubio et al., 2008; Amtmann and Blatt, 2009). K⁺ channels confer on the membranes of virtually every tissue distinct K⁺ conductances and regulatory characteristics (Véry and Sentenac, 2003; Dreyer and Blatt, 2009). Their characteristics are thus of interest for engineering directed to manipulating K⁺ flux in many aspects of plant growth and cellular homeostasis. The control of K⁺ channel gating has been identified as the most promising target for the genetic engineering of stomatal responsiveness (Lawson and Blatt, 2014; Wang et al., 2014a), based on the recent development of quantitative systems models of guard cell transport and metabolism (Chen et al., 2012b; Hills et al., 2012; Wang et al., 2012). By contrast, modifying the expression and, most likely, the population of native K⁺ channels at the membrane was found to have no substantial effect on stomatal physiology (Wang et al., 2014b).

The Kv-like K⁺ channels of the plant plasma membrane (Pilot et al., 2003; Dreyer and Blatt, 2009) share a number of structural features with the Kv superfamily of K⁺ channels characterized in animals and Drosophila melanogaster (Papazian et al., 1987; Pongs et al., 1988). The functional channels assemble from four homologous subunits and surround a central transmembrane pore that forms the permeation pathway (Daram et al., 1997). Each subunit comprises six transmembrane α-helices, designated S1 to S6, and both N and C termini are situated on the cytosolic side of the membrane (Uozumi et al., 1998). The pore or P loop between the S5 and S6 α-helices incorporates a short α-helical stretch and the highly conserved amino acid sequence TxGYGD, which forms a selectivity filter for K⁺ (Uozumi et al., 1995; Becker et al., 1996; Nakamura et al., 1997). The carbonyl oxygen atoms of these residues in all four K⁺ channel subunits face inward to form coordination sites for K⁺ ions between them (Doyle et al., 1998; Jiang et al., 2003; Kuo et al., 2003; Long et al., 2005) and a multiple-ion pore (Thiel and Blatt, 1991) such that K⁺ ions pass through the selectivity filter as if in free solution. The plant channels are also sensitive to a class of neurotoxins that exhibit high specificity in binding around the mouth of the channel pore (Obermeyer et al., 1994).

These K⁺ channels also share a common gating mechanism. Within each subunit, the first four α-helices form a quasiindependent unit, the voltage sensor domain (VSD), with the S4 α-helix incorporating positively charged (Arg or Lys) residues regularly positioned across the lipid bilayer and transmembrane electric field. Voltage displaces the S4 α-helix within the membrane and couples rotation of the S5 and S6 α-helices lining the pore, thereby opening or closing the channel (Sigworth, 2003; Dreyer and Blatt, 2009). For outward-rectifying channels, such as the mammalian Kv1.2 and the D. melanogaster Shaker K⁺ channels, an inside-positive electric field drives the positively charged, S4 α-helix outward (the up position), which draws on the S4-S5 linker to open the pore. This simple expedient of a lever and string secures current flow in one direction by favoring opening at positive, but not negative, voltages. This same model applies to the Arabidopsis (Arabidopsis thaliana) Kv-like K⁺ channels, including outward rectifiers that exhibit sensitivity to external K⁺ concentration (Blatt, 1988; Blatt and Gradmann, 1997; Johansson et al., 2006), and it serves equally in the gating of inward-rectifying K⁺ channels such as KAT1, which gates open at negative voltages (Dreyer and Blatt, 2009).

Studies of KAT1 gating (Latorre et al., 2003; Lai et al., 2005) have indicated that the S4 α-helix of the channel most likely undergoes very similar conformational changes with voltage as those of the mammalian and Shaker K⁺ channels. These findings conform with the present understanding of the evolution of VSD structure (Palovcak et al., 2014) and the view of a common functional dynamic to its molecular design. It is likely, therefore, that a similar electrostatic network occurs in KAT1 to stabilize the VSD. Crucially, however, experimental evidence in support of such a network has yet to surface. Electrostatic countercharges and the hydration of amino acid side chains between the α-helices within the VSDs of mammalian and Shaker K⁺ channel models are important for the latch-like stabilization of the so-called down and up states of these channels (Tao et al., 2010; Pless et al., 2011). Nonetheless, some studies (Gajdanowicz et al., 2009; Riedelsberger et al., 2010) have pointed to subtle differences in the structure of KAT1 that relate to the VSD.

We have explored the electrostatic network of the KAT1 VSD through site-directed mutagenesis to manipulate the voltage dependence of KAT1, combining these studies with molecular dynamic simulations previously shown to accommodate the plant VSDs and their hydration during gating transitions (Gajdanowicz et al., 2009; Garcia-Mata et al., 2010). We report here that gating of KAT1 is sensitive to manipulations affecting a set of electrostatic charge transfer centers. These findings conform in large measure to the mammalian and Shaker models. However, virtually all manipulations affecting a highly conserved, central Phe favor the up state of the VSD and the closed KAT1 channel, whereas mutations affecting the electrostatic networks on either side of this Phe favor the down state of the VSD and the open channel. These and additional observations suggest that hydration within the VSD is a major determinant of KAT1 gating.

RESULTS

Substitutions of Phe-102 in the S2 α-Helix Displace KAT1 Channel Opening to Negative Voltages

The S2 α-helix of the mammalian Kv and Shaker K⁺ channels incorporates highly conserved Glu or Asp and Phe residues that align with the corresponding amino acids in KAT1 as well as in other plant Kv-like K⁺ channels (Fig. 1). Phe-290 of the Shaker and Phe-233 of the Kv1.2 K⁺ channels situate roughly midway across the membrane. These Phe residues are thought to present a hydrophobic barrier that separates a set of inner and outer pockets formed between the α-helices over which residues of the S4 must pass (Jensen et al., 2012); S4 charge movement is thought to be catalyzed relative to the other α-helices by means of the π electron cloud presented by the Phe (Pless et al., 2011). Substitutions at this site with aromatic amino acids have been reported to favor the S4 α-helix extended outward, the up position (Pless et al., 2011), which for these outward-rectifying channels corresponds to the open channel. With Trp at this position, a Kv1.2-Kv2.1 VSD chimera (Protein Data Bank no. 2R9R) is stabilized in the up conformation even at voltages negative of −50 mV, whereas substitutions with nonaromatic residues, including Asn, Thr, Ser, and Leu, have been reported to give midpoint voltages for half-maximal conductance (V_1/2) near and positive of 0 mV, thus favoring the down position of the VSD when compared with the control (Tao et al., 2010).

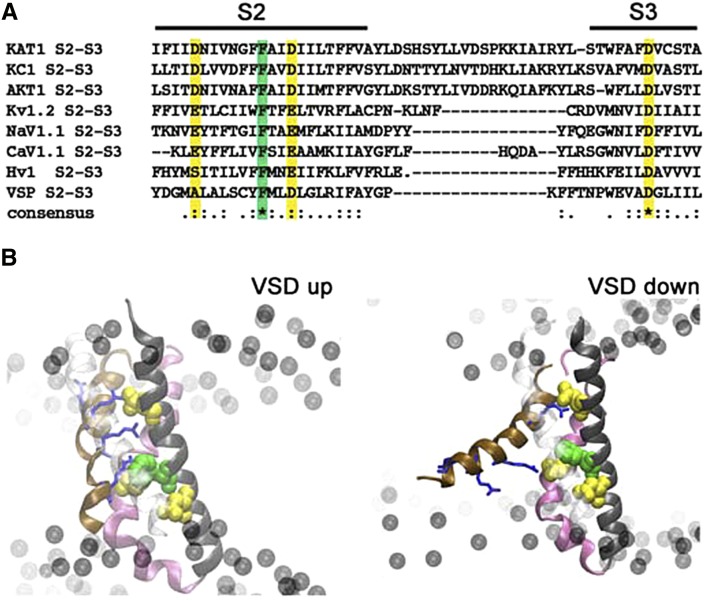
Figure 1.

Arabidopsis Kv-like channels share a set of highly conserved acid residues within the S2 and S3 α-helices and a conserved Phe positioned centrally within the S2 α-helix. A, Sequence alignment of several voltage-dependent membrane proteins: KAT1 (GI:15237407), KC1 (KAT3; GI: 15233870), AKT1 (GI:15225768), Kv1.2 (GI:52000923), Nav1.1 (115583677), Cav1.1 (GI:110349767), Hv1 (GI:91992155), and VSP (GI:76253898). Conserved residues addressed in this study are color coded: yellow, acidic; and green, aromatic. B, The KAT1 VSD shown in the up (left) and down (right) conformations with phospholipid headgroups (black balls) indicated for reference to the membrane position. The α-helices are color coded with S1 in front (transparent white), S2 (black), S3 (mauve), and S4 (ochre). Also shown are residues (top to bottom, blue stick representations) Arg-165, Arg-171, Arg-174, and Arg-177 of the S4 α-helix. Residues Asp-95, Asp-105, and Asp-141 (acidic; yellow) and Phe-102 (aromatic; green) are shown in Van der Waals representation.

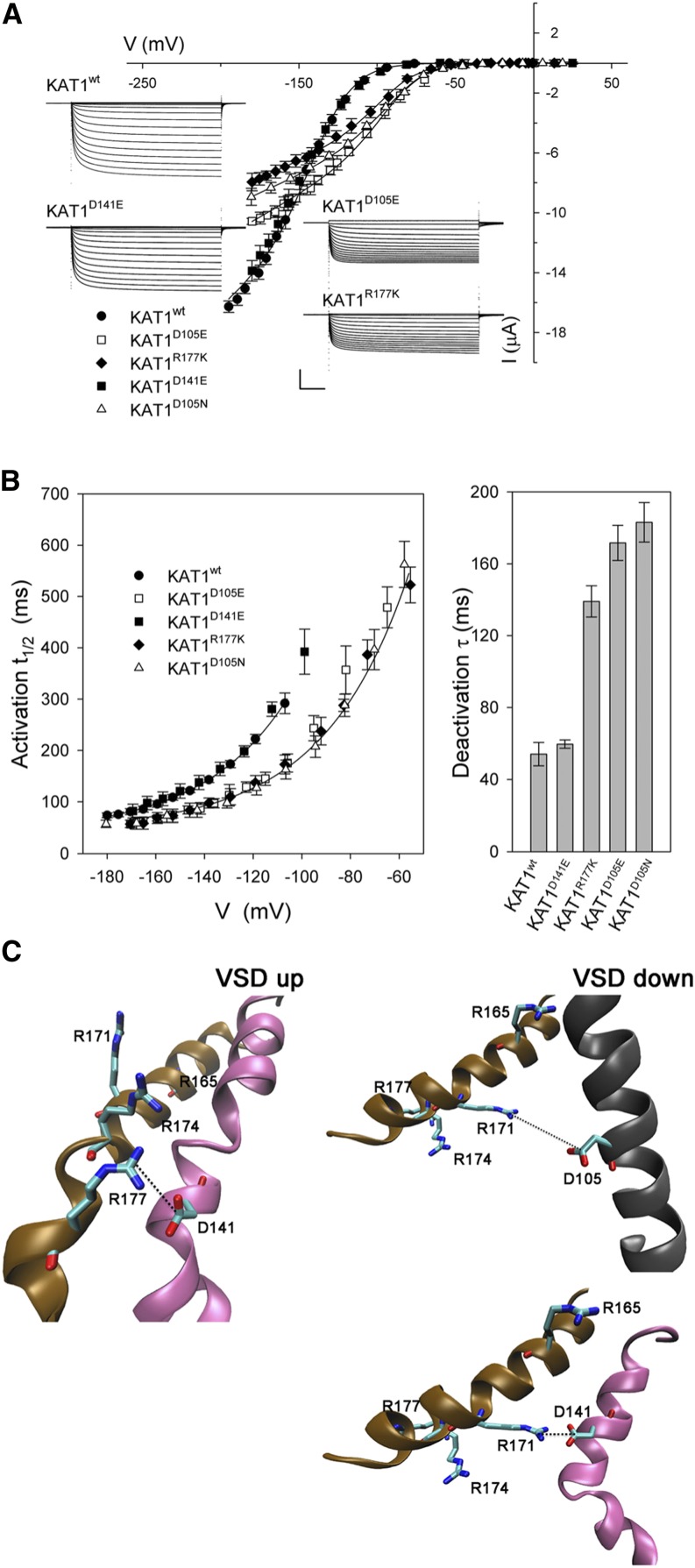
We carried out the same substitutions for Phe-102 of KAT1 (Fig. 1) to test whether similar displacements in V_1/2 would be evident in the plant K⁺ channel. When expressed in Xenopus laevis oocytes, KAT1^wt normally yields a current with a V_1/2 near −140 mV and an apparent gating charge, δ, of −1.6 to −1.8 (Hoshi, 1995; Zei and Aldrich, 1998; Latorre et al., 2003; Gajdanowicz et al., 2009; Riedelsberger et al., 2010). As expected, we found the KAT1^F102W substitution to yield a channel that activated only near the negative voltage extreme that could be achieved with oocytes under voltage clamp (Fig. 2, A and B). Substitution with Thr failed to give measurable currents. However, substitutions with each of the other nonaromatic amino acids also gave mutant KAT1 forms that activated variously at voltages negative of the wild-type K⁺ channel. Joint fitting of these data sets with a Boltzmann function yielded good fits, with gating charge and conductance maximum held in common between data sets and with values for V_1/2 that in every case were displaced to voltages negative of KAT1^wt (Fig. 2A; Table I). Fittings were to a Boltzmann function of the form

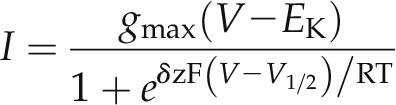(1)

where δ is the voltage sensitivity coefficient (gating charge), E_K is the K⁺ equilibrium voltage, g_max is the maximum conductance of the ensemble of channels, and F, R, and T have their usual meanings. Fittings were carried out by least square error minimization using a Marquardt-Levenberg algorithm (Marquardt, 1963) with the combined data sets, allowing a minimum of parameters to vary between data sets.

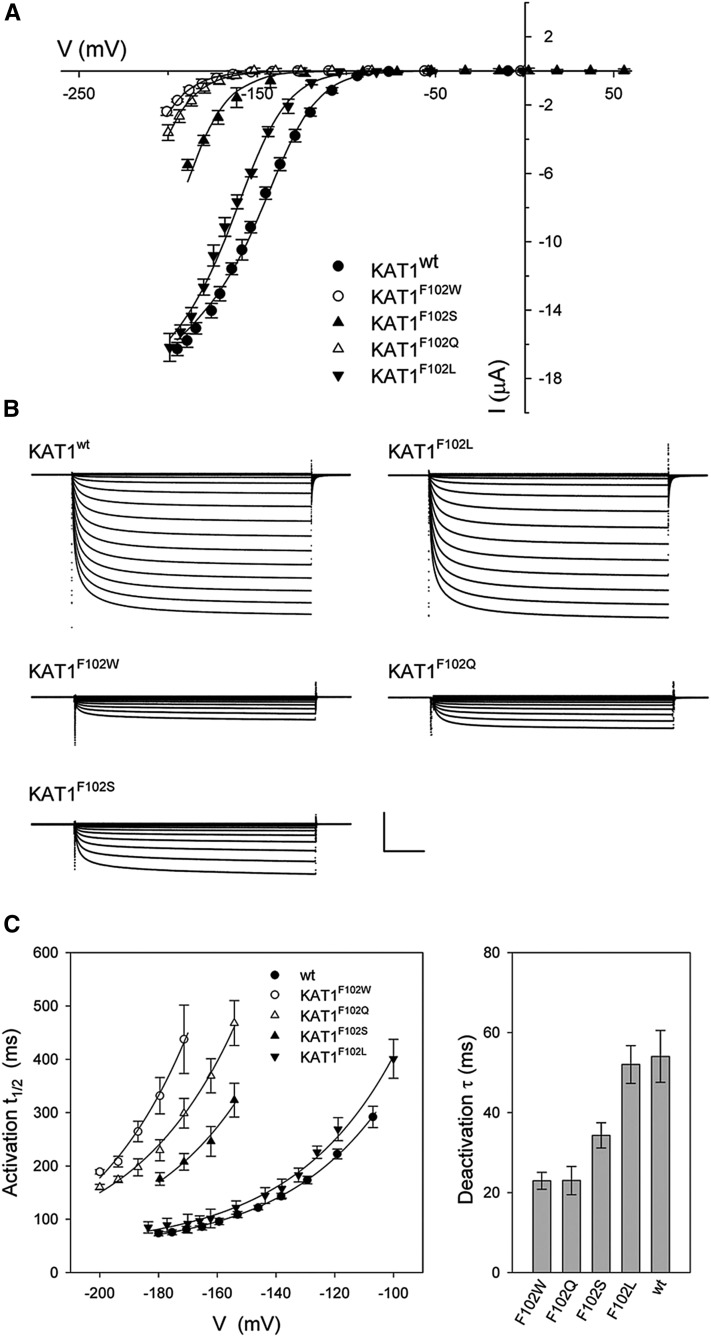
Figure 2.

Gating of the Arabidopsis KAT1 K⁺ channel is displaced negative going by mutations of Phe-102. A, Steady-state current-voltage curves for the wild-type channel (KAT1^wt) and each of four Phe-102 mutants, KAT1^F102W, KAT1^F102Q, KAT1^F102S, and KAT1^F102L. Data points are means ± se of more than seven independent experiments in each case. Solid lines indicate the results of best joint fittings to a Boltzmann function (Eq. 1). Fitted parameters are listed in Table I. B, Representative current traces for each KAT1^wt and each of the Phe-102 mutants in A. Scale bars are as follows: horizontal, 2 s; and vertical, 4 μA. C, Gating kinetics of the wild-type channel, KAT1^wt, and each of four Phe-102 mutants, KAT1^F102W, KAT1^F102Q, KAT1^F102S, and KAT1^F102L. Values shown are means ± se of the activation half-times (t_1/2) as a function of clamp voltage (left) and deactivation time constants at −50 mV (right). Data were from the same data sets as in A. Solid curves for activation half-times are empirical fittings to a simple exponential function with offset and are included for visual guidance only.

Table I. Global joint fitting of the VSD mutants of KAT1 expressed in X. laevis oocytes.

Fittings were to a Boltzmann function of the form shown in Equation 1. Listed here, and shown in Figures 2 to 6, are the results of the best fitting obtained with δ held in common between all data sets and g_max held in common between all sets apart from those of the KAT1^D105E, KAT1^D105N, and KAT1^R177K mutants. Fitted δ, 1.87 ± 0.05.

Construct	V1/2	gmax
	mV	mS
KAT1wt	−138.9 ± 0.6
KAT1F102W	−225.1 ± 0.8
KAT1F102Q	−217.0 ± 1.1
KAT1F102S	−195.5 ± 0.9	83.4 ± 0.6
KAT1F102L	−157.2 ± 0.5
KAT1D95E	−110.3 ± 0.8
KAT1D95N	−78.2 ± 0.4
KAT1D141E	−141.2 ± 0.9
KAT1D105E	−90.5 ± 1.2	59.1 ± 0.5
KAT1D105N	−78.9 ± 0.7	51.6 ± 0.4
KAT1R177K	−85.1 ± 2.1	44.0 ± 0.6

We examined the effects of Phe-102 substitutions on the kinetics of activation and deactivation of the KAT1 current. KAT1 activation is normally accelerated with negative-going voltages from −100 mV when stepped from a holding voltage of −50 mV and deactivates comparatively rapidly in steps back to voltages near and positive of −50 mV. To a first approximation, deactivation follows a simple exponential relaxation, but the current activates in sigmoid fashion (Hoshi, 1995; Zei and Aldrich, 1998), indicating two or more closed states of the channel. The current activates with half-times of approximately 300 ms at −120 mV and with half-times near 100 ms at −180 to −200 mV, while the current deactivates in roughly exponential fashion with time constants of 50 ms or less at −50 mV and more positive voltages, both in oocytes and in vivo (Chen et al., 2012a; Eisenach et al., 2012). We found that each of the mutations slowed KAT1 activation at any one voltage, the effect being most pronounced with KAT1^F102W and least with KAT1^F102L. The result was to displace activation half-times as a function of voltage for each negative-going mutant from KAT1^wt (Fig. 2C). Phe-102 substitutions also accelerated current deactivation at −50 mV in roughly antiparallel fashion (Fig. 2C). Therefore, these results indicate that the substitutions have a substantial effect on the transitions between the open and closed states of the channel.

Simulations Highlight an Extended Hydrophobic Cavity That Favors the Down State of the KAT1 VSD

It has been argued that this central Phe in the S2 α-helix forms a low-dielectric, hydrophobic barrier, isolating a water-filled pocket near the inner surface of the membrane (Tao et al., 2010; Lacroix et al., 2011). One challenge to questions of VSD conformation is that no crystal structure exists for the down state, corresponding to the open KAT1 channel, which therefore cannot be inferred directly by homology modeling. To address this problem, structural models of KAT1, with the VSD in the up and down states, were built using as template the α-subunit of Kv1.2 that was derived ab initio with Rosetta (Yarov-Yarovoy et al., 2006). The down state of this Kv1.2 model is compatible with experimental analysis of the KAT1 down state (Grabe et al., 2007) and indicates an open pore (Gajdanowicz et al., 2009) with the sequence alignment of Pathak et al. (2007). Omitted from the homology mapping were residues Tyr-114 to Lys-126 of the extended S2-S3 cytoplasmic loop of KAT1 that is not present in the Kv1.2 sequence. Residues Pro-148 to Ser-160 between the S3 and S4 α-helices were assigned to the external loop, which, in Kv1.2, includes an additional 11 amino acids. Alignments and illustration of the KAT1 subunit structure, including the pore-lining α-helices for the homology model, are included in Supplemental Figure S1. This model for the KAT1 down state yielded a net 1.76 Å root mean squared difference across the entire VSD, demonstrating the accuracy of the fit to the Kv1.2 model. It reproduced the shallow angle of the S4 α-helix and the marked kink in the S3 α-helix, both present in the Kv1.2 model (Yarov-Yarovoy et al., 2006; Pathak et al., 2007); furthermore, it is the same model used successfully for KAT1 in past molecular dynamic simulations (Gajdanowicz et al., 2009; Riedelsberger et al., 2010). For simulations, the channel was equilibrated in the open and closed states (Supplemental Fig. S2) before analysis of the water-filled space within the VSD and the atomic distances between the terminal residue carbons (CG for Asp, Glu, and Asn, CZ for Arg, and CE for Lys). We report this C-C distance and the electrostatic and solvation energies in Table II, calculated with an in-house script for the DESMOND program using the Schrödinger Python Suite 2012.

Table II. Terminal C-C carbon atom distances from residue sites and mutations to critical charged residues (indicated).

Distances determined during 10 ns of equilibration (Supplemental Fig. S1) are reported for the two states of the VSD. Values without se represent distances in the absence of key residue interactions and, hence, were not pursued further. Values in boldface highlight dominant spacings affecting charge interactions. Distances favoring the open channel (italic) and the closed channel (underlined) are indicated. Absolute electrostatic (Elec) and solvation energies (Sol) of the OPLS force field were calculated for the key residue interactions as indicated (Alves et al., 2007). The generalized Born energy for solvation was calculated according to Still et al. (1990). Note that using C-C distances adds 1 Å to the maximum for salt formation.

Site	Mutation	Residue	Down (Open) State				Up (Closed) State
			Distance	Salt Bridge?	Elec	Sol	Distance	Salt Bridge?	Elec	Sol
			Å		kJ mol−1		Å		kJ mol−1
Asp-95	Wild type	Arg-165	4.48 ± 0.08	Yes	−284 ± 6	274 ± 5	20.47 ± 1.31
		Arg-171	14.89 ± 0.08				4.43 ± 0.06	Yes	−368 ± 13	314 ± 6
		Arg-174	20.75 ± 0.83				4.62 ± 0.06	Yes	−388 ± 13	313 ± 6
		Arg-177	24.92 ± 0.76				9.35 ± 0.07
	D95E	Arg-165	4.84 ± 0.16	Yes	−453 ± 14	354 ± 8	19.52 ± 1.11
		Arg-171	15.08 ± 1.72				6.02 ± 0.06	No	−367 ± 11	306 ± 5
		Arg-174	21.44 ± 1.23				5.06 ± 0.06	No	−403 ± 12	328 ± 6
		Arg-177	26.08 ± 1.93				12.91 ± 1.79
	D95N	Arg-165	4.40 ± 0.06	No	−59 ± 6	29 ± 4	19.51 ± 1.39
		Arg-171	15.07 ± 0.71				6.06 ± 0.06	No	−1 ± 3	0 ± 3
		Arg-174	21.14 ± 1.23				5.26 ± 0.06	No	−72 ± 4	60 ± 3
		Arg-177	25.25 ± 1.28				10.56 ± 0.64
Asp-105	Wild type	Arg-165	15.16 ± 0.07				32.9 ± 1.4
		Arg-171	10.92 ± 0.06	No	−100 ± 1	99 ± 1	21.3 ± 0.7
		Arg-174	17.96 ± 1.07				15.7 ± 0.7
		Arg-177	25.78 ± 0.95				11.6 ± 0.6
	D105E	Arg-165	18.66 ± 1.05				33.88
		Arg-171	7.99 ± 0.06	No	−244 ± 3	239 ± 3	24.19
		Arg-174	16.10 ± 1.46				15.83
		Arg-177	23.68 ± 0.90				11.61
	D105N	Arg-165	17.67 ± 0.99				33.36
		Arg-171	6.13 ± 0.57	No	2 ± 11	−2 ± 11	22.84
		Arg-174	14.34 ± 0.82				14.48
		Arg-177	22.54 ± 1.20				10.24
Asp-141	Wild type	Arg-165	10.95 ± 0.07				23.8 ± 1.36
		Arg-171	3.95 ± 0.05	Yes	−506 ± 14	381 ± 5	13.4 ± 0.07
		Arg-174	11.97 ± 0.93				8.15 ± 0.07
		Arg-177	19.45 ± 0.92				3.53 ± 0.07	Yes	−389 ± 12	354 ± 6
	D141E	Arg-165	13.24 ± 1.01				25.5 ± 1.46
		Arg-171	5.27 ± 0.06	No	−374 ± 10	314 ± 5	14.11 ± 0.51
		Arg-174	14.57 ± 1.42				10.04 ± 0.35
		Arg-177	19.34 ± 0.87				5.28 ± 0.06	No	−473 ± 14	383 ± 6
Arg-177	Wild type	Asp-95	25.29 ± 0.34				9.01 ± 0.08
		Asp-105	26.42 ± 0.44				11.51 ± 0.11
		Asp-141	20.07 ± 0.46				4.13 ± 0.04	Yes	−389 ± 13	354 ± 6
	R177K	Asp-95	27.39				8.85 ± 0.09
		Asp-105	25.67				11.27 ± 0.13
		Asp-141	19.91				4.81 ± 0.07	Yes	−332 ± 10	287 ± 5

Initially, we examined Phe-102 and its residue substitutions. Previous simulations (Gajdanowicz et al., 2009; Riedelsberger et al., 2010) indicated a substantial downward and rotational motion of the S4 relative to the S2 and S3 α-helices and movement of the positively charged residues Arg-171 and Arg-174 across Phe-102. We analyzed the radial distribution function to determine the number of water molecules around residue 102 relative to free solution (Supplemental Fig. S3) and the hydrophobic versus hydrophilic surface (Lins et al., 2003) accessible between the α-helices of the VSD. The latter is summarized in Figure 3, which includes similar analysis for all of the other residue substitutions outlined in the following sections and discussed below. Significantly, both approaches predicted a substantial increase in hydration around residue position 102 in the Phe-102 mutants when compared with KAT1^wt. The results were consistent with the idea that Phe-102 forms a barrier for the transition between the closed and open states (Lacroix and Bezanilla, 2011), in effect pointing to an occluded, hydrophobic pocket bounded by Phe-102. They also suggested that the KAT1 VSD is intrinsically biased by the hydrophobic pocket bordered by Phe-102. In effect, extending the hydrophilic cavity into the space around this residue position normally favors the up state corresponding to the closed KAT1 channel.

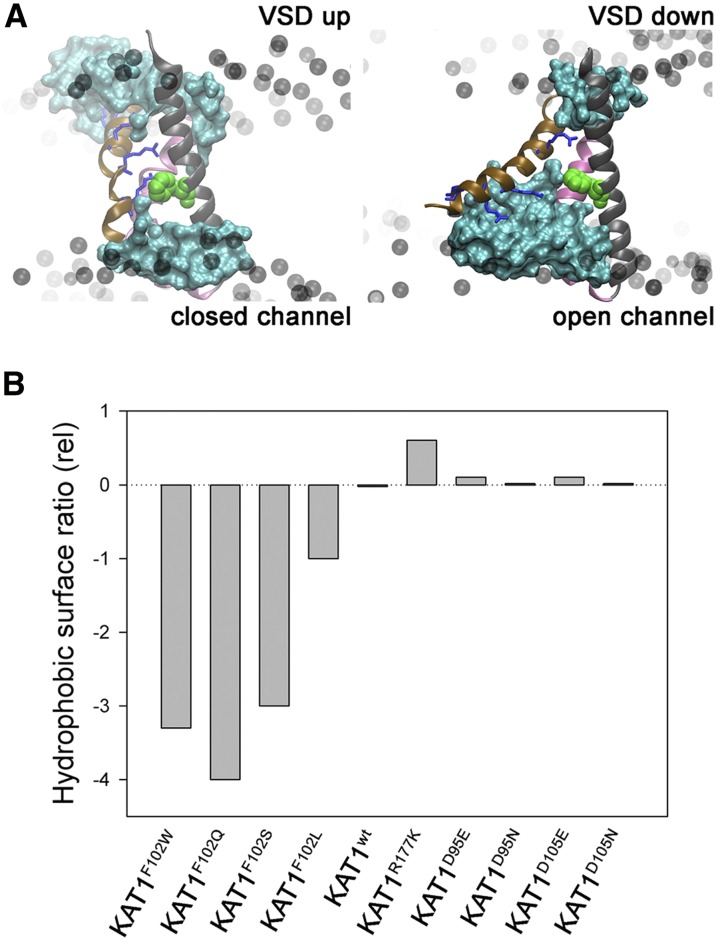
Figure 3.

The KAT1 VSD forms a stable, hydrophobic pocket to the outside of the Phe-102 residue. A, The VSD shown in the up (left) and down (right) conformations with phospholipid headgroups (black balls) indicated for reference to the membrane position. The α-helices are color coded with S1 in front (transparent white), S2 (black), S3 (mauve), and S4 (ochre). Also shown are residues (top to bottom, blue stick representations) Arg-165, Arg-171, Arg-174, and Arg-177 of the S4 α-helix. Residues Asp-95, Asp-105, and Asp-141 (acidic; yellow) and Phe-102 (aromatic; green) are shown in Van der Waals representation. The water surface within 10 Å of all of these residues is shown in aquamarine. B, Change in the ratio of hydrophobic to hydrophilic surface (Lins et al., 2003) for each of four Phe-102 mutants, KAT1^F102W, KAT1^F102Q, KAT1^F102S, and KAT1^F102L, and for KAT1^wt relative to KAT1^wt.

Substitutions of the Conserved Acidic Residue External to Phe-102 Favor the Open KAT1 Channel

KAT1 and its homologs retain three Asp residues within the S2 and S3 α-helices at positions that are conserved among many Kv and other voltage-gated channels (Fig. 1; Pless et al., 2011). Of these, Asp-95 of KAT1 aligns with the Glu-283 of the Shaker K⁺ channel to the outside of the central Phe residue. This acidic residue is thought to form part of the network of salt bridges with positively charged residues of the S4 α-helix (Papazian et al., 1995; Silverman et al., 2003; Long et al., 2005; Pless et al., 2011). Even the relatively conservative mutation to Gln in the Shaker K⁺ channel results in a roughly +70-mV displacement of the conductance-voltage curve and a suppression of the current. This effect in destabilizing the up relative to the down state of the VSD underlines the importance of the salt bridges in an otherwise hydrophobic environment (Pless et al., 2011). Glu-283 is positioned in close proximity to Arg-368 and Arg-371 of the S4 α-helix in the up state of the Shaker channel, and these residues map to Arg-171 and Arg-174 in KAT1.

We used our equilibrated models in the two states of the VSD (Fig. 3A) to determine the atomic distances between these residues and the effects of Asp-95 mutations (Table II). Comparing values with that of KAT1^wt showed, for Asp-95 mutations, that the KAT1^D95E and KAT1^D95N substitutions affect the C-C distances in the up state. The most prominent effect of the KAT1^D95E substitution was an increase in the distances to Arg-171 and Arg-174 by 1.59 Å (36%) and 0.44 Å (10%), respectively; for KAT1^D95N, the principal effects along with the loss in salt-bridge formation were increases in the distances to Arg-171 and Arg-174, in this case by 1.63 Å (37%) and 0.64 Å (14%), respectively, as well as decreases in the solvation energies of these residues (Table II). Thus, both mutations were predicted to favor the open KAT1 channel by reducing the efficacy of the electrostatic network in the up state of the VSD.

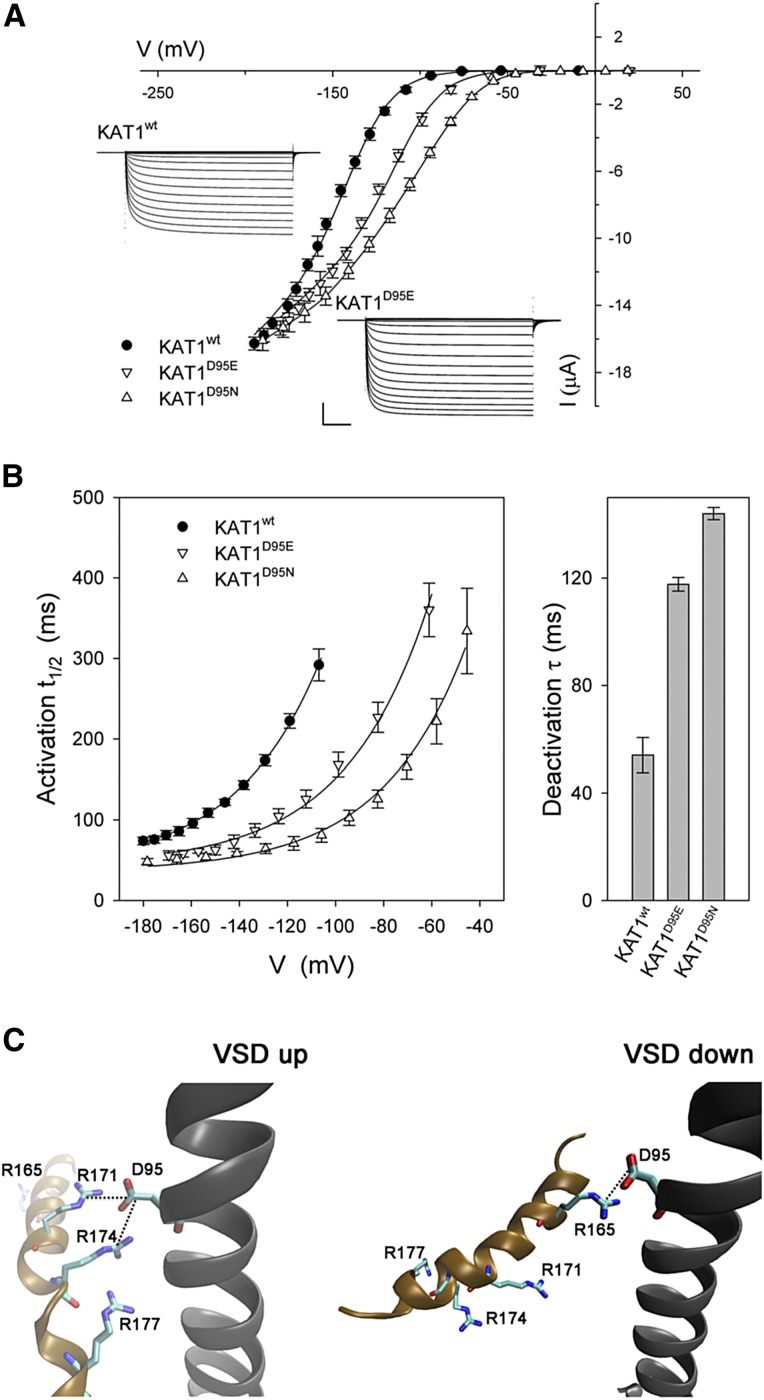
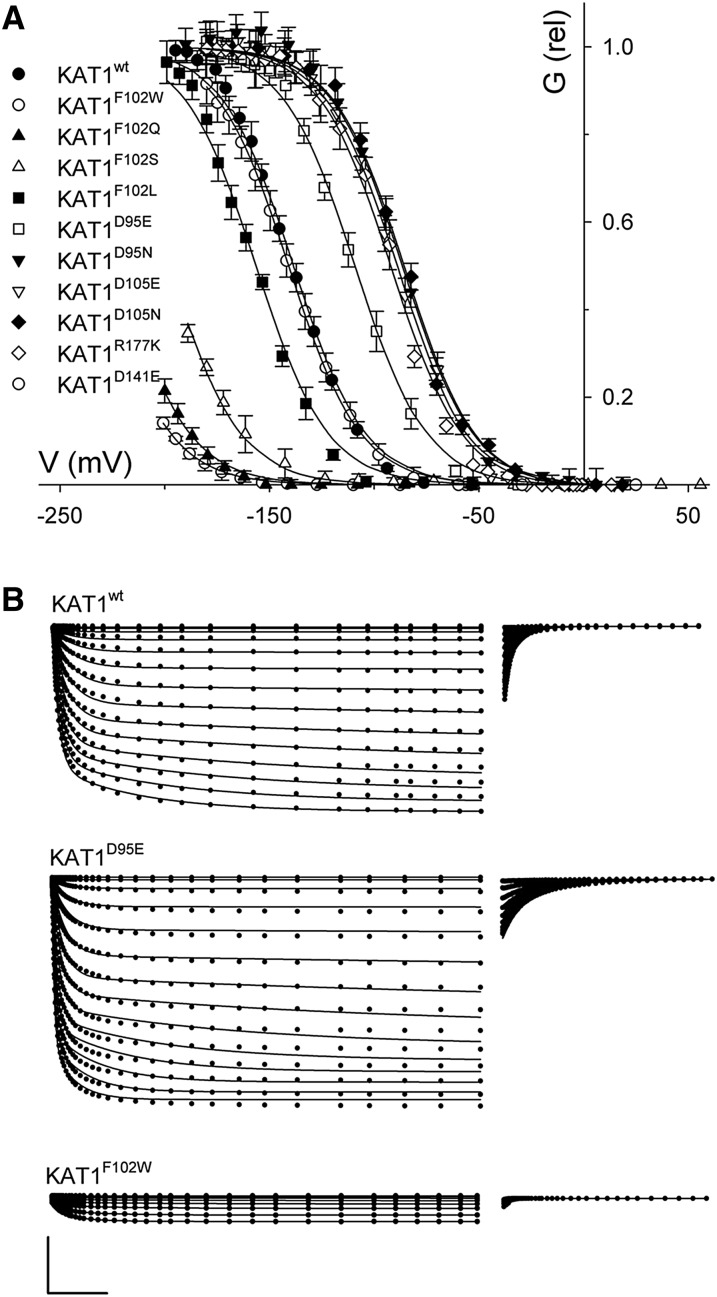
To test these predictions, we incorporated these Asp-95 substitutions in KAT1, expecting that these modest substitutions should favor the down state of the VSD, and hence the open KAT1 channel, over a wide voltage range. As expected, when expressed in X. laevis oocytes, KAT1^D95E, and to a greater extent the KAT1^D95N mutant, showed substantial positive-going shifts in current-voltage and conductance-voltage characteristics compared with KAT1^wt (Fig. 4B). Mean KAT1^D95E and KAT1^D95N currents were well fitted jointly with KAT1^wt, yielding shifts near +40 and +65 mV in the midpoint voltages, respectively (Table I). Analysis of the KAT1^D95E and KAT1^D95N current kinetics (Fig. 4C) also showed very significant decreases in relaxation half-times at any one voltage on activation, thus paralleling the displacements of the conductance-voltage curves, and a complementary increase in the apparent time constant for current deactivation at −50 mV. These results largely parallel those of Gln-283 substitution in the Kv1.2 channel, but without substantial change in the mean conductance maximum or gating charge δ (Pless et al., 2011). Note, too, that these substitutions had little effect on hydration predicted around Phe-102 (Fig. 3), including to its bounding hydrophobic pocket predicted to the outside of this residue.

Figure 4.

Gating of the Arabidopsis KAT1 K⁺ channel is displaced positive going by mutations of the S2 α-helix residue Asp-95. A, Steady-state current-voltage curves for the wild-type channel (KAT1^wt) and the mutants KAT1^D95E and KAT1^D95N. Data points are means ± se of more than six independent experiments in each case. Solid lines indicate the results of best joint fittings to a Boltzmann function (Eq. 1). Fitted parameters are listed in Table I. Insets show representative current traces for KAT1^wt and the KAT1^D95E mutant. Scale bars are as follows: horizontal, 2 s; and vertical, 4 μA. B, Gating kinetics of the wild-type channel, KAT1^wt, and the mutants KAT1^D95E and KAT1^D95N. Values shown are means ± se of the activation half-times as a function of clamp voltage (left) and deactivation time constants at −50 mV (right). Data were from the same data sets as in A. Solid curves for activation half-times are empirical fittings to a simple exponential function with offset and are included for visual guidance only. C, The S2 (black) and S4 (ochre) α-helices of the VSD shown in the up (left) and down (right) conformations. Residues (top to bottom, blue) Arg-165, Arg-171, Arg-174, and Arg-177 of the S4 α-helix and residue Asp-95 (red) are shown in stick representation. Critical distances of the terminal residue carbons are indicated by the dotted lines. Asp-95 is predicted to interact with Arg-171 and Arg-174 in the up state and with Arg-165 in the down state. Distances resolved following molecular dynamic equilibration are listed in Table II.

Substitutions of Conserved Acidic Residues at the Base of the S2 and S3 α-Helices Favor the Open KAT1 Channel

In mammalian and Shaker Kv channels, highly conserved Glu and Asp residues near the cytosolic ends of the S2 and S3 α-helices are thought to form complementary electrostatic interactions with residues at the base of the S4 α-helix. In the Shaker channel, this network most likely includes in the S4 α-helix the innermost Lys (K5), which is represented by Arg-177 in KAT1, and the next Arg residues (R3 and R4) toward the outside, which correspond to Arg-171 and Arg-174 in KAT1. Acidic Glu and Asp residues that situate to the inside of the central Phe of the Kv and Shaker models have been suggested to form an occluded site for charge coordination within the VSD (Tao et al., 2010). Substitution of the Glu and Asp residues with Gln and Asn, respectively, have a substantial effect on the conductance-voltage relations and less so on the apparent gating charge for activation in the Shaker channel (Papazian et al., 1995; Seoh et al., 1996). By contrast, conservative substitutions of the S3 Asp residue with Glu and with a neutral keto analog of Asp, 2-amino-4-ketopentanoic acid, have little effect on its conductance-voltage curve (Pless et al., 2011). These latter observations have been interpreted to reflect the importance of a local, high-dielectric environment per se, rather than of charge-charge interactions with the S4 α-helix.

Residues that might be associated with a corresponding electrostatic network in KAT1^wt are all represented by Asp. We carried out conservative substitutions of each with Glu and expressed the mutated channels in X. laevis oocytes. Figure 5 summarizes the results in comparison with data for wild-type KAT1, and the analysis of C-C distances is summarized in Table II. Comparing KAT1^wt with the KAT1^D105E and KAT1^D105N mutants in the equilibrated models indicated substantial closure in the distances to Arg-171, by roughly 2.93 Å (27%) and 4.79 Å (44%), respectively, in the down state. The energy of electrostatic interaction with Arg-171 decreased substantially in KAT1^D105E, and the solvation energy also decreased in the KAT1^D105N mutant (Table II). Both KAT1^D105E and KAT1^D105N mutants showed highly significant effects on channel gating, albeit with somewhat reduced current amplitudes (Fig. 5, A and B; Table I). The conductance-voltage relations were right shifted along the voltage axis, the V_1/2 for KAT1^D105E and KAT1^D105N were displaced roughly +40 mV relative to KAT1^wt, and were paralleled by the activation and deactivation kinetics. No significant effect could be identified in the gating charge for the mutants. By contrast, we observed little difference with the KAT1^D141E mutant (Fig. 5, A and B), despite the proximity of this residue to Arg-171 in the down state and its probable salt-bridge formation with Arg-177 in the up state (Fig. 5C). The KAT1^D141N mutant failed to give a current.

Figure 5.

Gating of the Arabidopsis KAT1 K⁺ channel is displaced positive going by mutations of the S2 and S4 α-helix residues Asp-105 and Arg-177 but not by Asp-141. A, Steady-state current-voltage curves for the wild-type channel (KAT1^wt) and the mutants, KAT1^D105E, KAT1^D105N, KAT1^D141E, and KAT1^R177K. Data points are means ± se of more than seven independent experiments in each case. Solid lines indicate the results of best joint fittings to a Boltzmann function (Eq. 1). Fitted parameters are listed in Table I. Insets show representative current traces for KAT1^wt and the KAT1^D95E, KAT1^D105E, KAT1^D141E, and KAT1^R177K mutants. Scale bars are as follows: horizontal, 2 s; vertical, 4 μA. B, Gating kinetics of the wild-type channel, KAT1^wt, and each of the mutants, KAT1^D105E, KAT1^D105N, KAT1^D141E, and KAT1^R177K. Values shown are means ± se of the activation half-times as a function of clamp voltage (left) and deactivation time constants at −50 mV (right). Data were from the same data sets as in A. Solid curves for activation half-times are empirical fittings to a simple exponential function with offset and are included for visual guidance only. C, The S2 (black), S3 (mauve), and S4 (ochre) α-helices of the VSD shown in the up (left) and down (right) conformations. Residues (top to bottom, blue) Arg-165, Arg-171, Arg-174, and Arg-177 of the S4 α-helix and residues Asp-105 and Asp-141 (red) are shown in stick representation. Critical distances of the terminal residue carbons are indicated by the dotted lines. Asp-105 is predicted to interact weakly with Arg-171 in the down state; Asp-141 is predicted to interact in the up state with Arg-177 and in the down state with Arg-171. Distances resolved following molecular dynamic equilibration are listed in Table II.

Analysis of the equilibrated KAT1^D141E substitution predicted similar effects on the C-C distances between these residues in the up and down states, suggesting that any impact in destabilizing the down state might be compensated by a similar effect in destabilizing the up state, albeit through interactions with different S4 residues. To select between these interactions, we targeted Arg-177, which is predicted to interact with Asp-141 only in the up state, reasoning that conservative substitution with a KAT1^R177K mutant might spatially constrain salt-bridge formation in the up state without affecting the electrostatic interactions of the residue in its aqueous environment in the down state. Comparisons of the KAT1 models (Table II) supported this idea, indicating that the effect of the KAT1^R177K mutant in its spacing to Asp-141 in the up state would be sufficient to reduce the energy of electrostatic interaction between these residues. Thus, we expected the KAT1^R177K mutation to favor the down state and open channel. Figure 5 and Table I show that, like the KAT1^D105E mutant, KAT1^R177K yielded a positive-going shift in the conductance-voltage curve relative to KAT1^wt and complementary changes in the activation and deactivation kinetics. Again, the KAT1^R177K mutant gave reduced currents, which may reflect a reduced stability of the expressed protein or its delivery to the plasma membrane. Nonetheless, the complementary effects of these two conservative substitutions is consistent in each case with a bias to the down state of the KAT1 VSD that favors the open channel.

A Three-State, Reaction-Kinetic Model of KAT1 Gating

The substantial effects on KAT1 gating outlined above raise the question of whether the characteristics of the several mutations might be accommodated within a single kinetic framework for channel gating. We undertook to model KAT1 gating assuming that the opening and closing of the channel are time-homogenous stochastic processes and, therefore, can be described as some combination of exponential functions. Three features of the KAT1 current guided a selection of a minimum reaction-kinetic framework for a kinetic model of gating. First, KAT1 activation is weakly sigmoidal on activation, but deactivation was roughly exponential, indicating the presence of at least two exponential components to current relaxations entering the open state and a single exponential component that dominated the transition to the closed state (Hoshi, 1995; Zei and Aldrich, 1998). Second, all of the mutations affected the midpoint voltage V_1/2; although not a specific guide in model selection, we noted above that the mutations were without substantive effect on the apparent gating charge. Finally, each of the mutations could be connected to changes in activation and, to a greater or lesser extent, to deactivation as a function of membrane voltage. Of these features, the first is consistent with n-state models comprising a series of closed states that lead to one or more open states of the channel; the second and third features justify associating the primary effects of each mutation with changes in one or more of the reaction constants rather than with gating charge per se. The simplest model that satisfies all of these requirements comprises three states and four reaction constants, with each of the reaction constants including a voltage-dependent coefficient:

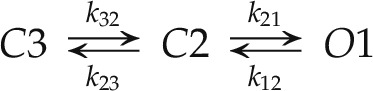(2)

Here, C3 and C2 denote two closed states that communicate serially with the open state O1, and the reaction constants k₃₂, k₂₁, k₂₃, and k₁₂ define the transitions between states and direction as indicated by the subscript ij. In effect, this scheme represents a condensed form of the model resolved by Zei and Aldrich (1998) for the wild-type KAT1 channel, in which distal closed states and the isolated burst closed state are subsumed within one or the other of the two dominant states C3 and C2 (Gradmann et al., 1987). We introduced voltage sensitivity to these transitions by assigning a voltage-sensitivity coefficient, δ_ij, for each reaction constant k_ij so that:

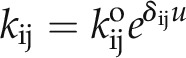(3)

where the reduced voltage u = FV/RT, V is the voltage, and F, R, and T have their usual meanings. The paired exponential terms thus correspond to a series of asymmetric Eyring barriers (δ_ij ≠ δ_ji).

Now, at any given time t, the macroscopic current I(t) comprises the sum of a steady-state component I_s and two exponential components (Bertl et al., 1988; Blatt and Gradmann, 1997):

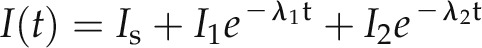(4)

The steady-state current at each voltage is given by the product of the ensemble open channel conductance g_o, the electrical driving force V − E_K from the K⁺ equilibrium voltage E_K, and the proportion of channels in the open state (steady-state open probability) p_1s:

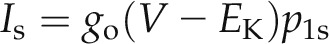(5)

where

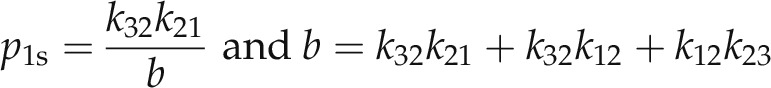(6a and 6b)

The two relaxation constants, λ₁ and λ₂, of Equation 4 denote the eigenvalues of the differential rate equations (Bertl et al., 1988; Blatt and Gradmann, 1997), each equivalent to the inverse of the corresponding time constant, and are given by:

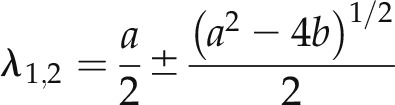(7)

where a = k₃₂ + k₂₃ + k₁₂ + k₂₁ and b is defined by Equation 6b. Finally, the current relaxation amplitudes I₁ and I₂ are defined by the changes in the relative occupation of C2 and O1, that is the changes in their relative probabilities Δp₂ and Δp₁, respectively, on a step change in voltage so that:

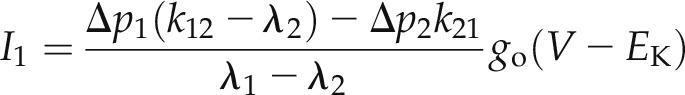(8a)

and

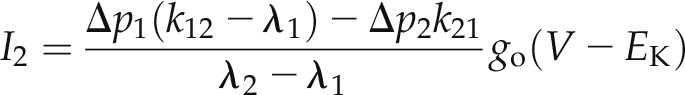(8b)

The ensemble, steady-state conductance-voltage characteristics for KAT1^wt and all of the KAT1 mutants are summarized in Figure 6. We fitted these data to Equation 6. Sets of current relaxations for activation and deactivation for each of the mutants, including the data sets shown in Figures 2, 4, and 5, were fitted to Equation 4 after thinning these data sets to a manageable size (Fig. 6B; see “Materials and Methods”). We permitted g_o to vary for KAT1^D105E, KAT1^D105N, and KAT1^DR177K only, because clear reductions in maximum conductance were evident for these constructs (Fig. 5); otherwise, fittings to both equations were carried out jointly, with the maximum number of voltage-sensitivity coefficients and reaction constants held in common between data sets for each KAT1 construct. Thus, the strategy was to seek the minimum set of reaction constants and voltage-sensitivity coefficients that were set free between KAT1 constructs in order to satisfactorily fit all of the experimental data.

Figure 6.

Reaction kinetic analysis of gating for KAT1 and the several mutations studied. Fittings were carried out by least square minimization to a three-state model (see “Results”) using a Marquardt-Levenberg algorithm (Marquardt, 1963). Best fittings were obtained with the following parameters fixed between all data sets: k₃₂^o, 6.1 × 10⁻⁶ ± 1.2 × 10⁻⁶ s⁻¹; k₂₃^o, 1.8 × 10⁻⁶ ± 0.6 × 10⁻⁶ s⁻¹; δ₃₂, −1.86 ± 0.06 e⁻; δ₂₁, −0.95 ± 0.01 e⁻; and δ₁₂, 0.48 ± 0.01 e⁻. δ₂₃ in all trials yielded values of less than 0.0002 and, therefore, was fixed to 0. Parameters for k₂₁^o and k₁₂^o varied between mutations of Phe-102, and parameters for k₂₁^o alone varied for mutations of Asp-95, Asp-105, Asp-141, and Arg-177. Values for these parameters are summarized in Figure 7. A, Steady-state conductance-voltage data sets derived from the current-voltage curves in Figures 2, 4, and 5 and fitted to Equation 6 (solid lines). B, Activation and deactivation kinetics for selected mutations. Data sets for all mutations, including those shown, were fitted to Equation 4 (solid lines) after thinning the data point density as shown for ease of handling. Scale bars are as follows: 5 μA vertical, 1 s horizontal (activation); 2.5 μA vertical, 0.3 s horizontal (deactivation).

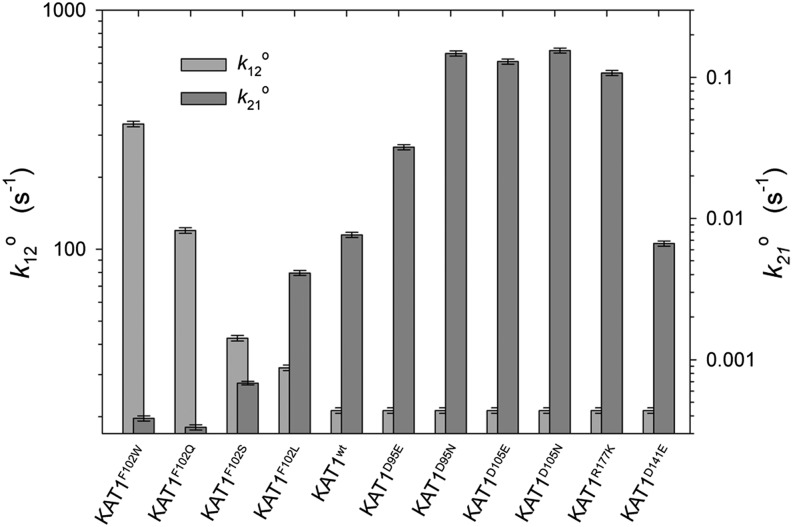
We surmised that the reaction constant k₂₁ was likely to dominate the transition to the open state, given the weak sigmoidicity to activation. Thus, it was not surprising that best fittings to all of the data sets were obtained with values for k₂₁ and k₁₂ that dominated much of the transitions between the three states of the channel. These results are summarized, and fittings to the steady-state conductance-voltage relations and to a selection of current relaxations are shown, in Figures 6 and 7. Several general observations can be drawn from the analysis. (1) All of the data sets were well fitted with a single set of parameter values for the voltage-sensitivity coefficients δ_ij (i,j = 1,2,3) common to KAT1^wt and all of the KAT1 mutants. This finding is consistent with the earlier Boltzmann analyses indicating that the various mutations affected primarily the midpoint voltage V_1/2 and had little or no influence on the apparent gating charge. The total charge associated with gating [Σ(δ_ij), for i,j = 1,2,3] was 3.29e⁻, which is roughly twice the apparent gating charge indicated from the Boltzmann analysis (Table I) and highlights the difficulties in relating the Boltzmann parameters to a mechanism when channel gating is not a simple two-state process. The value is close to the 3.42e⁻ estimated by Zei and Aldrich (1998), who also noted the much lower values derived from Boltzmann analysis. (2) All fittings indicated the predominant distribution of voltage sensitivities between reaction constants k₃₂, k₂₁, and k₁₂, with values for δ₂₃ comprising less than 0.01% of the total charge associated with gating. Virtually identical results were obtained when k₂₃ was voltage independent (δ₂₃ = 0). These findings indicate a voltage dependence in deactivation determined entirely by the initial transition out of the open state O1 and the balance of the reaction constants k₁₂ and k₂₁; by contrast, the voltage dependence in activation was spread between both transitions leading into the open state of the channel. (3) Current kinetics and conductances were well fitted, with only k₂₁^o varying between KAT1^wt, KAT1^D95E, KAT1^D95N, KAT1^D105E, KAT1^D105N, KAT1^R177K, and KAT1^D141E (Figs. 6 and 7). In kinetic terms, the primary effect of these mutations was on the rates of transition into the open state of the channel. (4) Finally, currents and conductances for KAT1^F102W, KAT1^F102Q, KAT1^F102S, and KAT1^F102L with KAT1^wt were well fitted, with only k₂₁^o and k₁₂^o varying between data sets, in other words, with the intrinsic rates both for entry to and exit from the open state determining the differences between the KAT1 constructs. These last two observations highlight the substantially different consequences of the two groups of mutations on KAT1 gating, and we return to this point below.

Figure 7.

Variable parameter values from the reaction kinetic analysis of gating for KAT1 and the several mutations studied. Parameter values are for k₂₁^o and k₁₂^o, which varied between mutations of Phe-102, and for k₂₁^o, which alone varied for mutations of Asp-95, Asp-105, Asp-141, and Arg-177. Note the logarithmic scale for both k₂₁^o and k₁₂^o.

DISCUSSION

The KAT1 K⁺ channel is one of a family of nine transmembrane K⁺ channel proteins in Arabidopsis, the members of which share many of the hallmarks of the Kv superfamily of K⁺ channels found in mammals and in D. melanogaster (Véry and Sentenac, 2003; Dreyer and Blatt, 2009). Although little is known of the molecular mechanics of gating in the plant Kv-like channels, there are many similarities implicated in coupling the charge-driven movements of the VSDs to the opening of the channel pore. The VSD conformation of KAT1, when closed, appears to correspond closely with VSD conformations, often referred to as the up state, associated with the open Shaker and mammalian Kv K⁺ channels (Latorre et al., 2003; Lai et al., 2005). Whereas the latter rectify outward, opening at positive-going voltages, KAT1 rectifies inward and gates open at negative-going voltages from approximately −100 to −120 mV. Thus, similar VSD conformations are likely for KAT1 as for the Shaker and Kv channels, albeit associated with the opposing states of the KAT1 channel (Dreyer and Blatt, 2009). Significantly, the VSDs of the Shaker and mammalian Kv channels incorporate five positively charged residues spaced at regular intervals along the fourth transmembrane α-helix. Movement of these residues within the transmembrane electric field leads to the conformational changes that drive channel gating with voltage (Dreyer and Blatt, 2009; Palovcak et al., 2014). Although only four of these residues are conserved in KAT1, their charges must nonetheless be coordinated by a network of countercharges within the VSD structure. Therefore, it has been thought likely that the VSD of KAT1 should incorporate an electrostatic network similar to the Shaker and mammalian models (Palovcak et al., 2014). This supposition had gone untested by mutational analysis to probe the conformational dynamics of the KAT1 VSD itself but is clearly central to understanding channel function as a target for future manipulation.

Here, we report a set of conserved residues within the KAT1 VSD that are likely to contribute to a network of electrostatic charge-charge interactions during gating. Our data indicate substantial parallels with electrostatic networks of the Shaker and mammalian Kv channel VSDs. In particular, they are consistent with two electrostatic interaction centers on either side of a conserved Phe residue within the S2 α-helix and positioned roughly midway across the membrane. These data nonetheless demonstrate a negative shift in the KAT1 gating characteristic as the default when this central aromatic residue is removed. These observations suggest a bias in KAT1 that favors the up state of the VSD and closed channel when this region within the VSD is hydrated, and they point to an occluded, hydrophobic pocket located to the outside of the conserved Phe residue. This interpretation is consistent also with an analysis of KAT1 gating that highlights the distinct kinetic effects of mutations within the putative electrostatic coordination centers compared with those of the central Phe residue. Finally, the observations demonstrate the feasibility of manipulating the gating of a plant Kv-like K⁺ channel over the physiological voltage range commonly found at the plant plasma membrane.

Acidic Residues of the KAT1 S2 and S3 α-Helices Identify Two Charge Coordination Centers

In the absence of a crystal structure for any plant K⁺ channel, previously we mapped the Arabidopsis Kv-like channels to the mammalian Kv1.2 (Gajdanowicz et al., 2009; Garcia-Mata et al., 2010; Riedelsberger et al., 2010; González et al., 2012) and the KvAP K⁺ channel structures (Johansson et al., 2006). These studies proved successful in predicting structural features of the plant channels, including access of water-soluble reagents within the VSD of the outward-rectifying channel SKOR (Garcia-Mata et al., 2010). Our extension of the KAT1 model in this work underscores the fundamental structural similarities between KAT1 and the Kv and Shaker K⁺ channels. Again, as template, we used the same ab initio model built from the α-subunit of Kv1.2, including the VSD as well as the α-helices forming the pore, that yielded conformations compatible with the experimental analysis of KAT1 (Grabe et al., 2007; Gajdanowicz et al., 2009; Riedelsberger et al., 2010). Most importantly, these simulations point to key roles for acidic residues within the S2 and S3 α-helices that are important for stabilizing the VSD between the up and down states previously associated with KAT1 gating (Latorre et al., 2003; Lai et al., 2005). Of these, Asp-105 and Asp-141 map to the inside of Phe-102 and are predicted to interact, alternately, between the up and down states, with Arg-177 and Arg-174 on the S4 α-helix (Fig. 5); Asp-95 maps to the outside of Phe-102 and interacts with Arg-174 and Arg-171 in the up state and with Arg-165 in the down state (Figs. 4 and 5). Indeed, the KAT1 model offered consistent and appropriate explanations for each of the mutations we introduced and analyzed experimentally at these sites (Figs. 3–5; Tables I and II; Supplemental Figs. S1–S3). Thus, like the mammalian Kv and Shaker channels (Papazian et al., 1995; Tao et al., 2010; Pless et al., 2011; Schwaiger et al., 2013), the VSD of KAT1 appears to describe a pair of countercharge interaction centers that are positioned one on either side of the pivot formed by Phe-102.

Our studies also reinforce the counterpoint with the mammalian Kv and Shaker K⁺ channels implicit in earlier studies of KAT1. The Kv1.2 and Shaker channels open with positive-going voltages that drive the VSD into the up state. This state exposes residues of the S4 α-helix otherwise buried within the membrane to modification by aqueous Cys-reactive, methanethiosulfonate reagents from the outside and hides others on the inside on the channel opening (Larsson et al., 1996), and it aligns key residues in the S4 α-helix in close proximity with amino acids near the outer surface of the S5 α-helix (Elinder et al., 2001). The same conformation in the KAT1 VSD has been associated with the closed channel (Latorre et al., 2003; Lai et al., 2005): for example, residues in the S4 α-helix move inward toward the cytosol (the down position), becoming inaccessible to the same membrane-impermeant reagents outside when the channels open at negative-going voltages (Latorre et al., 2003), and amino acids that pack against the S5 α-helix at negative voltages in the open conformation of KAT1 correspond with residues in the Shaker and Kv1.2 K⁺ channels that are similarly positioned but in the closed channel conformation (Lai et al., 2005). A similar picture now emerges for the electrostatic charge-interaction centers. Like recent studies of the Shaker channel and the Kv1.2/2.1 chimera (Pless et al., 2011; Schwaiger et al., 2013), we found that manipulations disturbing the charge-charge interactions at these centers favored the down state of the VSD and a positive-going displacement of the midpoint voltage for channel gating (Figs. 4 and 5; Table I). Significantly, these substitutions had little effect on the hydration surface within the VSD, indeed modestly increasing its hydrophobicity in the KAT1^R177K mutant (Fig. 3). It follows that the KAT1 VSD is biased to the down conformation by these manipulations independent of any substantive action on hydration around the Phe-102 and the hydrophobic pocket it bonds within the VSD. Furthermore, for KAT1, the result is to extend the voltage range for channel activity across almost the entire physiological voltage range typical of the plant cell.

Whether the same characteristics apply to the other Arabidopsis Kv-like channels, including KAT2, KC1 (KAT3), AKT1, and the outward-rectifying K⁺ channels GORK and SKOR (Dreyer and Blatt 2009), remains to be seen. Nonetheless, alignments and the topology of these channels indicate a remarkably high degree of sequence conservation, including the absolute conservation of residues contributing to the charge interaction centers and their separation by a central Phe (Fig. 1). Furthermore, a related molecular dynamic model of the SKOR K⁺ channel has yielded a very similar pattern of hydration around the S4 α-helix, correctly predicting the residue availability for methylthiosulfonate and redox modifications and their voltage dependence (Garcia-Mata et al., 2010). Thus, it is most likely that analysis of the charge interaction centers in the VSDs of these channels will yield results very similar, if not identical, to those we describe here.

Biasing the KAT1 VSD for Channel Closure

We began these studies in part to identify VSD mutations that affect the effective voltage range for gating and might thus be used in manipulating K⁺ transport. Following Tao et al. (2010), our initial efforts focused on Phe-102 of KAT1. Like the earlier study, we found that gating of the KAT1^F102W mutant was displaced strongly negative going from KAT1^wt (Figs. 2 and 6), consistent with a change in total gating energy in excess of 8 kJ. Unlike Tao et al. (2010), every other mutation we introduced at this site led to negative-going shifts in the current-voltage and conductance-voltage relations of the channel. Even the KAT1^F102Q and KAT1^F102S substitutions yielded strong, negative-going displacements in channel gating. Indeed, the characteristics of the KAT1 VSD are at odds with the mammalian Kv and Shaker models in this respect. Tao et al. (2010) observed that substituting the final, positively charged residue, a Lys (K5), on the S4 α-helix with Arg led to a reversal in the effects of Phe substitution with Trp; although V_1/2 shifted negative with Trp in the K5 form of the channel, it was displaced to more positive voltages in the R5 form of the channel. By contrast, in KAT1, this final residue of the S4 α-helix occurs naturally as Arg, yet the effect of the KAT1^F102W mutation is very similar, and qualitatively identical, to the Phe-to-Trp substitution in the K5 model of the mammalian VSD. A similar disjuncture is evident in the effects of the KAT1^R177K mutant itself: this substitution led to a substantial negative shift in V_1/2 for the Kv1.2/2.1 chimera, but in KAT1 the effect was to displace V_1/2 by roughly +60 mV (Figs. 5 and 6).

How might we understand both the similarities and differences from the mammalian Kv and Shaker channels? Molecular dynamic simulations of the KAT1 models point to an occluded, hydrophobic pocket to the outside of Phe-102, with hydration of the S4 α-helix to the inside of Phe-102 that is enhanced in the down (open channel) state. Comparison of the several mutants predicted a further hydration around and beyond position 102 with each of the Phe-102 substitutions, but with little or no effect following mutations associated with the charge interaction centers (Fig. 3; Supplemental Fig. S3). A straightforward interpretation, again, is that dehydration of the S4 surface around this outer, occluded pocket is an important factor in VSD conformation associated with the up state and its hydration favors the down state. It follows, too, that the effects of the charge interaction centers are mechanistically distinct, as noted above. In effect, in KAT1, Phe-102 may be seen to maintain a low dielectric barrier that helps immobilize Arg-171 in the down state and facilitates the transfer of Arg-177 beyond this hydrophobic barrier. This interpretation concurs with the recent studies of the Shaker channel and Kv1.2/2.1 chimera (Pless et al., 2011; Schwaiger et al., 2013), as noted above. It echoes the suggestion of Lacroix and Bezanilla (2011) that the conserved Phe in the Shaker K⁺ channel forms a hydrophobic barrier and findings of a substantial increase in aqueous accessibility to the inner half of the S4 α-helix on HCN1 channel opening (Bell et al., 2004). It also suggests that the VSD transition for KAT1 differs from that of the Kv and Shaker models in its strong dependence on a hydration/dehydration transition rather than on interactions of the K5 residue, with the π electron cloud formed by the aromatic ring at position 102 (Pless et al., 2011; Schwaiger et al., 2013). In short, the KAT1 VSD appears inherently biased to the up state; this bias is normally countered by hydration of the S4 residues to the inside of Phe-102. Manipulations that extend S4 hydration into the outer pocket beyond Phe-102 stabilize the up state and, hence, the closed KAT1 channel.

A Model for KAT1 Gating

This molecular dynamic interpretation also finds parallels with a reaction-kinetic analysis of KAT1 gating (Figs. 6 and 7). The analysis showed that a satisfactory approximation to the experimental data was realized with a serial, three-state model of gating. A systematic comparison with the six-state model arrived at by Zei and Aldrich (1998) is not possible, in the first instance because the latter incorporated an isolated closed state to account for voltage-dependent periods of high activity, so-called bursting behavior, that was identified in single-channel recordings. This behavior, as well as the longer-lived closed lifetimes, cannot be isolated in whole-cell measurements such as we have undertaken. So, expanding our model beyond the three states of Equation 2 (above) is not justified and would result in a system of gating states with substantial indetermination. Even so, this three-state analysis highlights a substantial difference in the kinetic effects of the two sets of mutations. Specifically, mutations targeted to Phe-102 were successfully accommodated by coordinate and antiparallel changes to the values for k₂₁^o and k₁₂^o; assigning the effects of substitutions at this site to a single reaction constant, or to any other combinations of paired reaction constants, was unsatisfactory. By contrast, mutations at sites associated with the electrostatic charge centers to the inside and outside of Phe-102 were well fitted, with k₂₁^o only varying between data sets for the various mutants. Again, assigning the effects of these substitutions to any other single reaction constant was uniformly unsatisfactory.

Connecting these specific kinetic constants with the dynamics of the VSD conformational transitions is not possible with the information available at present. Nonetheless, the comparison allows one set of parallels to be drawn: mutations of Phe-102 predicted to effect changes in water access to the hydrophobic pocket in the VSD also associate with kinetic effects on transitions both in and out of the open state of the channel, and they favor the up state of the VSD; mutations of the electrostatic coordination centers predicted to have little or no effect on hydration within the VSD associate principally with the kinetics of transition into the open state of the channel, and they favor the down state of the VSD. In general, these findings now add to a picture of the mechanics in K⁺ channel gating, providing evidence for a network of centers coordinating charge between the α-helices in the up and down states of the KAT1 VSD analogous to those in other Kv channels (Dreyer and Blatt, 2009). In short, voltage drives the gating process in this inward-rectifying K⁺ channel much as it does in the outward-rectifying channels characterized by the Kv and Shaker models, at least to the extent of the handover of positively charged Arg residues between two putative electrostatic charge interaction centers associated with a set of highly conserved acidic residues that localize to the S2 and S3 α-helices and either side of Phe-102 of KAT1.

Finally, our studies highlight KAT1 as a model in a very practical sense. Previous development of a quantitative systems platform for the premier plant cell model of the guard cell had shown substantial predictive power in guiding experiments (Chen et al., 2012b; Hills et al., 2012; Wang et al., 2012). A recent analysis using this platform indicated that simple manipulations of the population of ion channels at the plasma membrane and tonoplast are unlikely to have a substantial effect on cellular homeostasis and guard cell function, unlike manipulations of the primary energy-coupled transporters, including the plasma membrane H⁺-ATPase (Lawson and Blatt, 2014; Wang et al., 2014a). This prediction has found independent verification in a concurrent study (Wang et al., 2014b) reporting that overexpressing several K⁺ channels in guard cells of Arabidopsis had no measurable effect on stomatal behavior. The latter study reported a small increase in stomatal aperture and assimilation, with a 3-fold increase in the expression of AHA2, one of the three dominant H⁺-ATPases at the guard cell plasma membrane, albeit with a substantial cost in water use by the plant. By contrast, from their systems analysis, Wang et al. (2014a) concluded that even small changes of ±18 mV to the V_1/2 for gating of one or both the inward- and outward-rectifying K⁺ channels, including KAT1, could influence stomatal kinetics without a cost in water use efficiency. Our results here establish the feasibility of such manipulations, demonstrating that single point mutations within the KAT1 VSD are sufficient to drive V_1/2 across most, if not all, of the physiological voltage range, from values in excess of −200 mV to near −50 mV. We anticipate that these findings will underpin future efforts toward engineering plant membrane transport for improved efficiencies in mineral and water use in the field.

MATERIALS AND METHODS

Molecular Biology

Open reading frames for Arabidopsis (Arabidopsis thaliana) KAT1 were amplified with gene-specific primers including Gateway attachment sites (attB1 and attB2). A subsequent BP reaction in pDONR207 (Invitrogen) yielded entry clones that were verified via sequencing. Point mutants were generated by site-directed mutagenesis with SDM-Assist (Karnik et al., 2013). Gateway Destination clones were generated using LR Clonase II (Invitrogen) by LR reaction as described previously (Grefen et al., 2010b) in the oocyte expression vector pGT-Dest (Honsbein et al., 2009; Chen et al., 2011).

Electrophysiology

Electrical recordings were carried out with KAT1 constructs as described previously (Honsbein et al., 2009; Grefen et al., 2010a). Coding sequences for the wild type and point mutants were cloned in pGT-Dest (Grefen et al., 2010a), and capped copy RNA was synthesized in vitro using the T7 mMessage mMachine (Ambion). Copy RNA quality as a single band was confirmed by denaturing gel electrophoresis. To ensure uniform injections of KAT1 transcript, mixtures were made up to a standard volume as necessary with RNase-free water.

Stage VI oocytes were isolated from mature Xenopus laevis, and the follicular cell layer was digested with 2 mg mL⁻¹ collagenase (type 1A; Sigma) for 1 h. Injected oocytes were incubated in ND96 (96 mm NaCl, 2 mm KCl, 1 mm MgCl₂, 1 mm CaCl₂, and 10 mm HEPES-NaOH, pH 7.4) supplemented with gentamycin (5 μg mL⁻¹) at 18°C for 3 d. Whole-cell currents were recorded under voltage clamp using an Axoclamp 2B (Axon Instruments) two-electrode clamp circuit (Vergani et al., 1998; Leyman et al., 1999; Sutter et al., 2006). Measurements were carried out under continuous perfusion with either 30 mm KCl and 66 mm NaCl or 96 mm KCl with the addition of 1.8 mm MgCl₂, 1.8 mm CaCl₂, and 10 mm HEPES-NaOH, pH 7.2. Recordings were analyzed and leak currents subtracted using standard methods (Leyman et al., 1999; Sutter et al., 2006) with Henry IV software (Hills and Volkov, 2004; Y-Science, University of Glasgow).

Molecular Dynamic Simulations

Molecular dynamic simulations were carried out with the wild-type sequence and with the corresponding residue substitutions, first using the NAMD program (Phillips et al., 2005) and then the CHARMM27 force field (MacKerell et al., 1998). Open and closed models were embedded within a lipid bilayer in a periodic boundary condition box with water molecules, K⁺ and Cl⁻ ions, optimized using energy minimization followed by equilibration at 298 K for 5 ns with a harmonic restraint of 0.5 kcal mol⁻¹ Å⁻² applied to the backbone atoms (Gajdanowicz et al., 2009). Distances were analyzed between terminal residue carbons and salt bridge formation assessed using the VMD salt bridge plugin (www.ks.uiuc.edu/Research/vmd/plugins/saltbr/).

We used the entire α-subunit of Kv1.2 obtained by the Rosetta method as the template for KAT1 (Gajdanowicz et al., 2009) and selected the single subunit in each molecular dynamic simulation of KAT1 and the mutants that yielded most of the interactions reported for the Kv1.2 channel. The model of KAT1, with the VSD in the up and down states, was derived ab initio with Rosetta (Yarov-Yarovoy et al., 2006) and is compatible with experimental analysis of the KAT1 down state (Grabe et al., 2007) using the sequence alignment of Pathak et al. (2007). We omitted from homology mapping residues Tyr-114 to Lys-126 of the extended S2-S3 cytoplasmic loop of KAT1 that is not present in the Kv1.2 sequence. Residues Pro-148 to Ser-160 between the S3 and S4 α-helices were assigned to the external loop that, in Kv1.2, includes an additional 11 amino acids. Further information is provided in Supplemental Figure S1. Following the naming convention for the key charged residues of the VSD (Vargas et al., 2011) in KAT1, the basic residues of the S4 α-helix, R1, R3, R4, and K5, correspond to Arg-165, Arg-171, Arg-174, and Arg-177, respectively. Residue R2 is not present in KAT1 channel. The acidic residues E1 and E2 of the S2 α-helix correspond to Asp-95 and Asp-105, respectively, and D3 of the S3 α-helix corresponds to Asp-141. In the up state conformation, the interactions are formed between R3 and E1 (Pless et al., 2011), R4 and E1, and K5 and D3 (Tiwari-Woodruff et al., 2000). In the down state conformation, R1 interacts with E1 and R3 interacts with E2 and D3 (Khalili-Araghi et al., 2010). Each subunit was assembled within a homotetramer and embedded in a periodic boundary condition box (see above) and was optimized using energy minimization followed by equilibration at 300 K for 10 ns. Harmonic restraints of 50 kcal mol⁻¹ Å⁻² were applied to R1, R3, R4, K5, E1, E2, and D3 to reproduce experimental interactions. The rest of the protein structure was without harmonic restraints during molecular dynamic simulations. This second part of the molecular dynamic simulations was carried out using Desmond software (Desmond Molecular Dynamics System, version 2.2; Bowers et al., 2006) and the OPLS2005 force field (Kaminski et al., 2001).

Reaction-Kinetic Modeling

For quantitative analysis of KAT1 gating, mean steady-state conductance-voltage relationships and sets of current traces for each of the various KAT1 constructs were fitted jointly using a Marquardt-Levenberg algorithm and least square minimization (Marquardt, 1963; Press et al., 1986) to the serial (pseudo) three-state system described by Scheme 1. The differential equations for this model have been described previously (Bertl et al., 1988; Blatt and Gradmann, 1997), and their solution yields Equations 3 to 8. Steady-state conductances were fitted to Equation 4, and current relaxations were fitted to Equation 6, allowing a minimum of parameter values to vary between data sets representing each of the KAT1 constructs. Data sets representing current relaxations were thinned to a manageable size by selecting values at regular time intervals to give a total of approximately 1,000 data points per set, and residuals were adjusted to give equal weighing between data points within traces and between curves within each data set. Numerical values for each of the joint parameters were sought by sequential adjustment from starting values, and analyses were repeated after initializing with different starting values to ensure that fittings converged on a single solution.

Statistics

Statistical analysis of independent experiments is reported as means ± se as appropriate, with significance determined by Student’s t test or ANOVA. Joint nonlinear least square fittings were carried out using a Marquardt-Levenberg algorithm (Marquardt, 1963) implemented in SigmaPlot version 11 (SPSS).

Supplemental Data

The following materials are available in the online version of this article.

• Supplemental Figure S1. KAT1 model template and resolved conformations in the up (closed) and down (open) states of the channel VSD and its pore.

• Supplemental Figure S2. Equilibration of molecular dynamic simulations for KAT1^wt (above) and KAT1^D95E (below).

• Supplemental Figure S3. Radial distribution function for water around KAT1 residue at position 102 as a function of distance from the residue.

Glossary

VSD

voltage sensor domain

V_1/2

voltage for half-maximal conductance