A Two-Stage Search of Visual Working Memory: Investigating Speed in the Change-Detection Paradigm

Abstract

A popular procedure for investigating working memory processes has been the visual change-detection procedure. Models of performance in that procedure, however, tend to be based on performance accuracy and to treat working memory search as a one-step process, in which memory representations are compared to a test probe to determine if a match is present. To gain a clearer understanding of how search of these representations operate in the change-detection task, we examined reaction time in two experiments, with a single-item probe either located centrally or at the location of an array item. Contrary to current models of visual working memory capacity, our data point to a two-stage search process: a fast first step to check for the novelty of the probe and, in the absence of such novelty, a second, slower step to search exhaustively for a match between the test probe and a memory representation. In addition to these results, we found that participants tended not to use location information provided by the probe that theoretically could have abbreviated the search process. We suggest some basic revisions of current models of processing in this type of visual working memory task.

The change-detection paradigm, originally designed by Phillips (1974) and more recently popularized by Luck and Vogel (1997), is often utilized as a gold-standard method for measuring capacity limits in working memory, defined as the small amount of information that can be held in mind simultaneously to carry out various cognitive tasks. In the change-detection task, participants are presented with an array of visual objects (e.g., colored bars in various orientations, or other shapes) that are briefly presented, typically between 100 and 500 ms. Following a short retention period, participants are presented with a test probe. This test probe can consist of the entire array configuration (i.e., a whole-display probe) or a single item within the array (i.e., a single-item probe). Participants are instructed to indicate whether the displayed test probe matches the previously-viewed array or whether the probe has changed. By using this simple task across various experimental manipulations, the field has learned a great deal about the nature of storage and maintenance within visual working memory and is addressing many fundamental issues (e.g., Allen, Hitch, Mate, & Baddeley, 2012; Anderson, Vogel, & Awh, 2011; Cowan, Blume, & Saults, 2013; Gorgoraptis, Catalao, Bays, & Husain, 2011; Thiele, Pratte, & Rouder, 2011; Wheeler & Treisman, 2002; Zhang & Luck, 2009). In the present study, we add to the current body of knowledge regarding visual working memory by examining reaction or response times (RTs) in the change-detection paradigm.

For all that has been learned about visual working memory processing through this paradigm, it is surprising that most of this research has focused upon accuracy performance as the sole behavioral dependent variable of interest, even when an understanding of RTs would be helpful. A key reason for the focus upon accuracy in this task is that previous research has emphasized measures of the number of items present in working memory. These measures, by and large, are based upon accuracy. The models that have produced these measures (Bays & Husain, 2008; Cowan, 2001; Pashler, 1988; Rouder et al., 2008; Zhang & Luck, 2008), however, have also incorporated simple theoretical assumptions about how processing occurs in the change-detection task. These assumptions are predicated on the assumption that participants use the information they have in working memory in an optimal and rational manner (though see Chen & Cowan, in press).

To give an example of particular importance to the current research, consider an instance in the change-detection task in which participants are presented with a single-item probe that is in a location shown in the original array. Ideally, participants should only compare that probe to the item that was presented in a particular array location, given instructions that no other item could have changed (cf., Luck & Vogel, 1997). More recent research indicates that this assumption could be incorrect. Cowan et al. (2013, Experiment 1) presented participants with two different types of probes in a change-detection task: single-item probes in an array location, in which that particular item could change to a new color or shape; and single-item probes in the center of the array, in which case any array item could change to a new color or shape. In both cases, change probes had a color or shape different from any array item. Perhaps surprisingly, levels of accuracy performance were nearly identical across these different probe types. Cowan et al. (2013) suggested that, in instances in which a probe revealed which item may have changed from its previous presentation, location information was typically not used. Rather, the entire representation of the array stored in working memory may have been searched, even when doing so was logically unnecessary.

The means of comparing a test probe to an array can be addressed more directly with RT, which may clarify the pattern in accuracy performance obtained by Cowan et al. (2013). It has typically been used with a sequential list of items, followed by a probe that was either present within or absent from the list. For example, in Sternberg (1966), the critical data were mean RTs for trials that contained lists of 1–6 items in which responses to the probe were correct. To make a correct response, participants would need to search through list items to determine whether the probe had been presented in the list (i.e., old), or if the probe was new. Sternberg reported that as the length of the list of items increased, there was a linear increase in RT. Each increase in list size added an additional 38 ms to RT. Sternberg proposed that memory search in a list is serial in nature, given the resulting linear, additive function; this finding has since been widely-replicated. Moreover, Sternberg suggested that the search was exhaustive, given that the search functions were similar for trials with old and new probes. If the search did not have to include all list items and terminated as soon as the target was found to match a list item, search should take twice as long on average for trials with new probes than for those with old probes. Apparently, it was more efficient to search exhaustively, given the rapid rate of search. Similarly, given arrays followed by a probe that matches one item or has a color not present in the array, it might be more efficient to search through an entire array rather than searching for a single item at a specified location. If so, there should be no RT advantage for probes presented in the location of a single target item as opposed to central probes to be compared to all items at once.

The hypothesis that memory search is serial has since been contested (e.g., Donkin & Nosofsky, 2012; Ratcliff, 1978; Townsend, 1976, 1990). Given that parallel means of search can yield linear RT functions across set sizes, this difficult issue remains unresolved in our study. It should be noted, though, that a serial search is not appealing for arrays that provide no clear order of search. In any case, our study is more relevant to the issue of whether probes of a single location consistently result in content-specific searches, or whether the entire array is searched given that the procedure allows it. Search of the entire array for the purpose of change detection is a possible solution only when the changed probe has a feature that exists nowhere in the array, which was the case in our study.

The Present Study

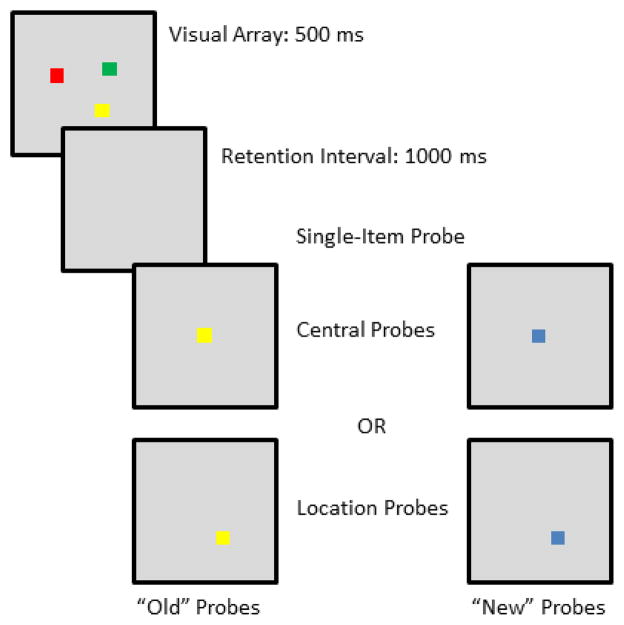
The current study was designed to investigate memory search in the change-detection paradigm using either a single-item probe that occurred at the same location as an array item, logically limiting the search to that given location, or one that occurred centrally, in which instance all array items must be searched (see Figure 1). Previous research suggests that memory search processes in change detection differ when the test probe is a whole array versus a single item (Rouder, Morey, Morey, & Cowan, 2011); given these findings, it is entirely possible that search processes may also differ with respect to probe location.

Figure 1.

Central and location probe methods in current study. For both central and location probes, there are examples of target-present and target-absent probes.

We chose to investigate this question using RT in a manner comparable to Sternberg (1966). One important difference between the list method used by Sternberg and the array method used here, however, is that a list of verbal items can be remembered with higher accuracy than an array of a comparable of nonverbal items, especially with higher set sizes (e.g., under 2% error averaged across list lengths 1–6 in Sternberg, versus about 10–15% error averaged across set sizes 1–6 in the current experiments). Additionally, as array size increases, accuracy typically declines; this means that there will be fewer data points at larger set sizes, which could affect data analyses of RTs. In order to test set sizes up to 6 array items reliably, we utilized a method in which the arrays remained at one set size until a certain number of correct responses were obtained. To move to the next array size, participants had to have correct responses on a minimum of four trials with probes that matched an array item, and a minimum of four correct responses on trials that contained probes absent from the array. These trials were randomly drawn until the participant met the criterion. If participants failed to meet the criterion after the maximum number of trials per set size (24 in both experiments), the block terminated and participants moved on to the next set size. Because of the need for a sufficient number of correct trials at larger set sizes, we presented array set sizes 1 through 6 in ascending or descending trial order. If set sizes had been randomly selected, an even greater number of trials would have to be presented to equate the number of correct trials at larger set sizes to those at smaller set sizes. By using a clear trial order, we reduced the number of trials that would have to be presented and ensured that participants received a sufficient number of change-detection trials at larger set sizes.

We hoped to examine several hypotheses in the current experiment. First, we were interested in how RTs would change in this task as a function of set size. It is possible that, similar to what Sternberg (1966) reported, RT would increase linearly as a function of array size. This need not be the case, however. If an in-location probe were used to limit search to a single item from the array, then the search function could be independent of set size (i.e., flat across set size). It is still possible that when the probed item is not in working memory, guessing processes slow down with larger set sizes. This could produce an increase in RT with set size, in which case the model would neither be confirmed nor disconfirmed by the trend across set sizes.

Further information about the nature of memory search in the change-detection task comes from examining response times for old and new probes. The model for a single-item, in-location probe task described by Cowan (2001) is based on symmetry between no-change and change trials; if the probed item is in working memory, the participant should be able to detect the match if there is one and detect the mismatch if there is one. If the item is not in working memory, the participant must guess (for further elaboration on these models, see also Donkin, Nosofsky, Gold, & Shiffrin, 2013; Rouder et al., 2008). A difference between RTs for correct responses on change and no-change trials may exist but, according to this model, this difference should not depend on set size.

For a central probe, in contrast, the existing model (Cowan et al., 2013) contains an asymmetry. If the probe item matches an item in working memory, that match can be detected. Otherwise, the participant must guess as to the likelihood that a match was not found because it was not in the array (in which case the correct response is “new”) or because it was in the array but not in working memory (in which case the correct responses is “old”). The direction of the asymmetry depends on the model. If the items are searched exhaustively (cf. Sternberg, 1966), then this search process should be no slower for trials containing new probes than for those that contain old probes. In fact, the process could be slower for target-present trials if there is some RT cost to confirm the match once it is detected.

Finally, this RT prediction for a central probe could hold true also for an in-location probe if, as was proposed for the accuracy data of Cowan et al. (2013), the location information was not used and the same model therefore applies as for the central probe.

A previous study by Hyun, Woodman, Vogel, Hollingworth, and Luck (2009) helps inform the current research. In one experiment (Experiment 1), participants were presented with a visual array of objects to be remembered, followed by a comparison array as the test probe. In one condition, the comparison array was identical to the studied array or had one array item differ in color (e.g., any-difference condition). This condition is analogous to a standard change-detection task with a whole-display probe. In a less conventional condition in that experiment, the probe array was either completely different from the studied array (i.e., no items matched), or all items except for one had changed. In this case, participants were to indicate whether any part of the array was the same at test (i.e., any-sameness condition). Finding sameness produced much steeper RT functions across set size than finding a difference. Based on these and other findings, Hyun and colleagues concluded that the search for items in visual working memory was similar to some aspects of visual search. In particular, there is a rapid detection process for detecting difference that is capacity-unlimited and searches in parallel; there is also a slower capacity-limited and serial process of search that is necessary to make decisions regarding sameness. It is unclear whether these processes would operate similarly for central and in-location probe items, as this was not examined in Hyun et al.

In sum, in addition to examining effects of set size on response time, our interest was in whether participants took probe location information into account in this task with a single-item probe. Ideally, participants in the current study could use location information provided by probes presented in an array location (as opposed to being presented centrally) to circumvent a longer memory search. This is because a probe in an array location refers to a single item; in contrast, a centrally-presented probe could refer to any item present in the array. If participants use location information to avoid search of all memory representations, we should observe an RT benefit for these probes relative to central probes. If we do not find such a benefit, this would replicate a previous finding that suggests that location information, though potentially helpful, is not being utilized (Cowan et al., 2013).

Experiment 1

Method

In the first experiment, change-detection trials with centrally-fixated probes and trials with probes in a previous array location were mixed together into trial blocks. As participants were not aware of where a given probe would be located until that probe was presented, we can assume that there were no differences in strategic encoding of the central and in-location probes in this experiment.

Participants

Thirty-one undergraduates from the University of Missouri (12 male, 19 female) took part in the experiment in exchange for credit in an introductory Psychology course. All participants reported normal or corrected-to-normal vision and were not colorblind. One male participant did not have sufficient correct trials per condition (as detailed below) and was excluded from the analysis.

Apparatus, stimuli, and procedure

Participants were tested one at a time in quiet booths. Each booth was equipped with a computer, which presented the experiment via E-Prime 2.0. All change-detection trials followed the general procedure described below and illustrated in Figure 1 Following a 1000-ms fixation, participants were shown an array of colored squares in random locations. The possible locations that were randomly selected subtended a 6.09 × 4.74 cm invisible rectangular grid, with the center of the computer screen also functioning as the center of the grid. The number of squares within each array ranged from one to six. Each square measured 0.5 × 0.5 cm and subtended 0.7 × 0.7° of visual angle. The minimal distance between squares in the array was 1.53 cm. Within an array, each square color was randomly selected from a pool of 10 possible colors and was not used more than once within that array. The pool of colors included black, white, red, green, blue, purple, yellow, cyan, orange, and teal. The array of squares was presented for 500 ms, which was followed by a blank retention period of 1000 ms. A single-item probe immediately followed that retention interval, and either matched a color present in the initial array (i.e., old probes) or changed to a unique color absent from the array (i.e., new probes). Participants were instructed to indicate whether the probe color was present or absent from the array with a keypress.

The experiment consisted of four blocks of change-detection trials, which differed with respect to whether arrays increased or decreased in set size throughout the block. Two of the blocks presented the visual arrays in ascending order, beginning with a set size of one and eventually increasing to set size six. The remaining blocks presented arrays in descending order, beginning with a set size of six and gradually decreasing to one. For each block, set size increased (or decreased, in the case of descending blocks) only after participants made correct responses to a minimum of four old probes and four new probes at each given set size. With this criterion, the task could be completed with a minimum of 384 trials. The number of trials, however, was typically larger than this minimum because the old and new probes were randomly selected, and because incorrect responses led to additional trials that were presented until the criterion above was met. In our analyses below, we have excluded data from one participant, as the participant did not meet the criterion, and this resulted in an incomplete data set.

Results

Accuracy

We have included analyses of accuracy on this task, as these results can supplement RT to provide critical insight into how participants performed the change-detection task beyond response time. The accuracy means are reported in Table 1. We examined the proportion of correct responses on change-detection trials using a repeated-measures ANOVA, including the factors of trial order within a sequence (i.e., ascending vs. descending), probe location, set size, and whether the target probe had changed at test. Most importantly, the results suggest only one complex effect of probe location, in a three-way interaction that we describe below.

Table 1.

Means and standard errors for accuracy for old and new probes for each set size and probe location in Experiment 1

Set Size
	1	2	3	4	5	6
Central Probes
Old Probes	0.98 (.01)	0.95 (.01)	0.88 (.02)	0.81 (.03)	0.74 (.03)	0.71 (.03)
New Probes	0.96 (.02)	0.97 (.01)	0.96 (.01)	0.94 (.02)	0.90 (.02)	0.85 (.03)
Location Probes
Old Probes	0.97 (.01)	0.94 (.02)	0.89 (.02)	0.84 (.02)	0.79 (.03)	0.72 (.03)
New Probes	0.97 (.02)	0.97 (.01)	0.96 (.01)	0.91 (.02)	0.88 (.02)	0.84 (.02)

There was a significant effect of set size, F(5, 145) = 92.46, MSE = .015, η_p² = .76, p < .001. Participants were most accurate on the change-detection trials when the array size was one (M = .97, SEM = .01); accuracy declined with each increase in set size (Set size 2: M = .96, SEM = .01; Set size 3: M = .92, SEM = .01; Set size 4: M = .88, SEM = .02; Set size 5: M = .83, SEM = .02; Set size 6: M = .78, SEM = .02). Post hoc tests showed that accuracy for all set sizes were significantly different from each other, except for set sizes one and two. Finally, we also observed a significant effect of whether the probe was old or new, F(1, 29) = 23.34, MSE = .08, η_p² = .44, p < .001. Compared to trials in which the single-item probe was a color that was previously presented in the array (M = .85, SEM = .02), participants were significantly more accurate on trials in which the probe changed to a unique, previously-unseen color (M = .93, SEM = .02). Interestingly, there was no discernible main effect of probe’s location upon accuracy in this task, F < 1.

The above effects were qualified by two significant interactions. First we observed a significant interaction between set size and whether the probe was old or new, F(5, 145) = 10.78, MSE = .02, η_p² = .27, p < .001. At a set size of one, participant responses were equally accurate on trials containing old and new probes. Accuracy declined with increasing set size for both probe types, but the drop in performance was significantly larger for trials in which the probe was old. Second, as shown in the table of means (Table 1), there was a significant three-way interaction between set size, probe location, and whether the probe was old or new, F(5, 145) = 2.52, MSE = .01, η_p² = .08, p < .05. The means for central and location probes seem remarkably similar except for the old probe trials for Set Size 5, for which there was a .05 advantage for location probes. Thus, at best, any advantage of location probes occurred only in narrowly-defined circumstances.

Response time

In our analyses of response time (RT) in this task, only trials with correct responses were included. Furthermore, we excluded any trials that had reaction times that were outliers, defined here as any RT larger than 5000 ms. For correct trials, using this criterion removed a very small subset of the data--less than one percent of all usable trials. Observed effects from a repeated-measures ANOVA, including F values and effect sizes, are reported in Table 2, and unweighted means can be found in Appendix A. Of note, we observed a stable pattern of different search rates for old probes versus new probes, but with little effect of probe location, which is further detailed below.

Table 2.

Results from a repeated-measures ANOVA for RT, including partial-eta squared, for all effects and interactions in Experiment 1. Significant effects and interactions are marked with an asterisk.

Effect	df	F	p	ηp2
Trial Order	(1, 29)	<1	.51	.01
Set Size*	(5, 145)	16.94	<.001	.37
Probe Location	(1, 29)	4.05	.053	.12
Probe Change (Old vs. New Probe)	(1, 29)	1.57	.22	.05
Trial Order × Set Size	(5, 145)	1.77	.12	.06
Trial Order × Probe Location	(1, 29)	1.92	.18	.06
Set Size × Probe Location	(5, 145)	<1	.99	<.01
Trial Order × Probe Change	(1, 29)	<1	.93	<.01
Set Size × Probe Change*	(5, 145)	5.85	<.001	.17
Probe Location × Probe Change	(1, 29)	2.94	.10	.09
Trial Order × Set Size × Probe Location	(5, 145)	<1	.86	.01
Trial Order × Set Size × Probe Change	(5, 145)	<1	.82	.02
Trial Order × Probe Location × Probe Change	(1, 29)	3.07	.09	.10
Set Size × Probe Location × Probe Change	(5, 145)	<1	.58	.03
Trial Order × Set Size × Probe Location × Probe Change	(5, 145)	1.44	.21	.05

Note. Trial order refers to ascending versus descending trial blocks.

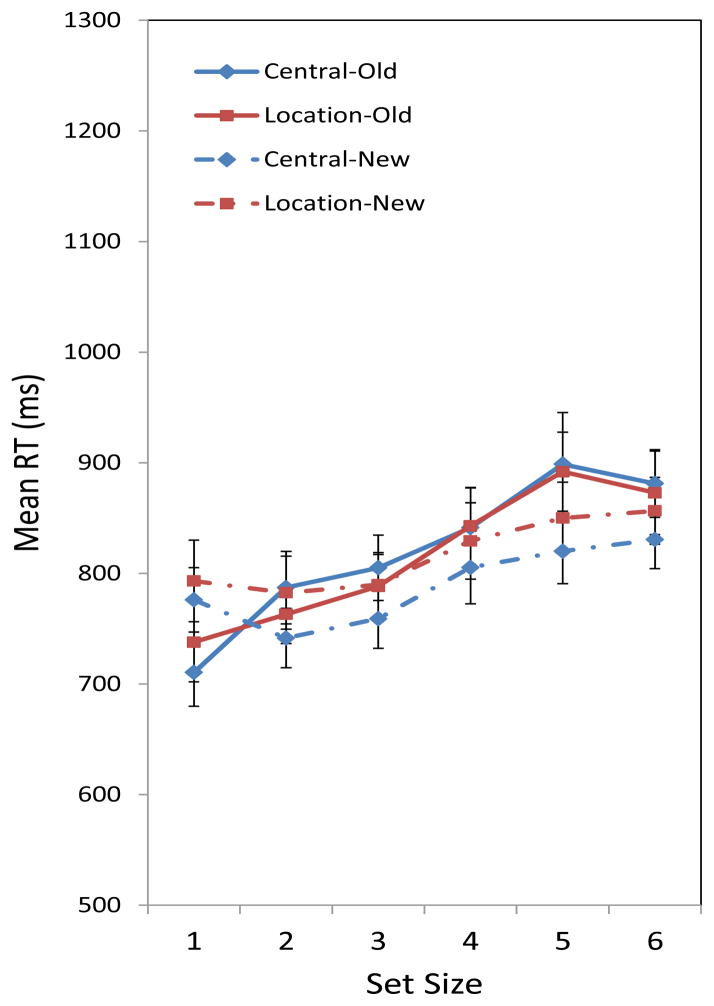
We observed that the set size of arrays significantly influenced response time in the change-detection task; RT increased as array size increased. There were no significant effects of order or probe change, and there was a marginal effect of probe location. Responses to probes that were in the center of the screen were somewhat faster than probes that were in an array location. The small effect of probe location is observable in Figure 2. It is the opposite of what would be expected if location information were used to avoid searching the entire array, in which case responses to center probes would be slower than those to location probes.

Figure 2.

Mean RT for correct responses in Experiment 1, across set size for different probe locations (Central vs. Location) and probe types (Old vs. New). Error bars are standard errors of the mean.

The significant effect of set size was qualified by a significant set size × probe change interaction. In addition to the statistics reported in Table 2, results are also illustrated in Figure 2. There was a response time advantage for old probes over new probes at set size 1. This advantage disappeared as set size increased, and at larger set sizes (i.e., 5 and 6), there was an RT advantage for new probes. These findings were confirmed in post hoc tests. To be specific, results from a Newman-Keuls test showed that RTs for set sizes 1, 2, and 3 were not significantly different from each other; we observed a similar equivalence for set sizes 4, 5, and 6. Notably, all other pairwise comparisons of RTs were significantly different from each other (p < .01 in all cases). Moreover, the RT slope functions associated with these probe types were significantly different from each other in a dependent-sample t-test, t (30) =3.70, p < .001. The slope associated with trials containing new probes (M = 15.71 ms/item, SEM = 4.70) was significantly smaller than the slope associated with old probe trials (M = 33.14 ms/item, SEM = 4.85).

The interpretation of RT can sometimes be assisted by the examination of the response time distribution (Balota & Yap, 2011). We did so to learn more about the different patterns of responses observed for Set Size 1, in which there were faster responses for old items, versus the higher set sizes, 2–6, in which there were faster responses for new items. In particular, a process that occurs on most or all trials in one condition should shift the entire RT distribution in that condition rightward, compared to conditions in which the process is absent. In contrast, a process that is quite slow and only occurs on a minority of trials will increase the right-hand tail of the distribution while leaving the rest of the distribution relatively unaffected.

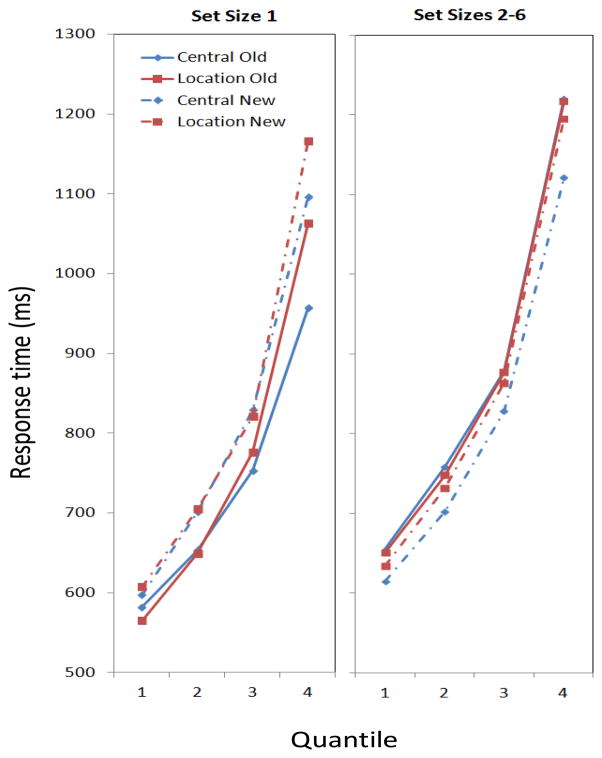
To get a portrait of the distribution we examined response time quantiles for certain conditions, which were means for each individual of RT data points between the 0–30^th, 31–50^th, 51–70^th, and 71–90^th percentiles of the valid RTs. We did this separately for data from Set Size 1 and from an aggregate of Set Sizes 2–6. Within these two sets, moreover, quantiles were figured separately for the two probe locations and the two probe change conditions. Unweighted means and standard errors across the different experimental conditions are detailed by quantile in Table 3, and the means are plotted in Figure 3.

Table 3.

Means and standard errors (in ms) for Experiment 1 quantiles (30, 50, 70, and 90 percent of the data) for set size 1 and the pooled average of set sizes 2–6.

Central Probes
Old Probes				New Probes
SS 1		SS 2–6		SS 1		SS 2–6
30	582 (23)	30	655 (23)	30	597 (22)	30	615 (18)
50	653 (26)	50	759 (26)	50	701 (29)	50	702 (21)
70	753 (30)	70	878 (31)	70	829 (36)	70	828 (27)
90	957 (57)	90	1220 (70)	90	1096 (52)	90	1121 (49)
Location Probes
Old Probes				New Probes
SS 1		SS 2–6		SS 1		SS 2–6
30	565 (24)	30	651 (24)	30	607 (23)	30	634 (20)
50	649 (26)	50	748 (24)	50	705 (27)	50	732 (23)
70	776 (38)	70	877 (29)	70	821 (32)	70	864 (28)
90	1063 (93)	90	1217 (72)	90	1166 (98)	90	1195 (53)

Figure 3.

Means from four groups of data in Experiment 1 reflecting the 0–30^th, 31–50^th, 51–70^th, and 71–90^th quantiles in the condition, respectively. Left, Set Size 1; Right, the aggregate of Set Sizes 2–6. The graph parameter is the condition, which depended on the location of the probe (Central vs. Location) and whether the probe was in the array (Old) or not (New).

Inspection of the figure shows different patterns for the different groups of set sizes. At Set Size 1 (left-hand panel), the advantage for old items is an effect that starts out small, but becomes larger at the later quantiles. It appears to reflect an extra, slow process that takes place for new items, but only on some trials (e.g., an extra check to make sure that a new probe is not the same as the target; perhaps this occurs only when the probe is still activated in memory from a recent trial). In contrast, for the larger set sizes (right-hand panel), the advantage for new items is just as large at the fastest quantile as it is at slower quantiles. It appears to be a process that occurs across the board (e.g., the rapid detection of novelty that facilitates responses; see Hyun et al., 2009). Of course, as one must expect, responses are uniformly slower for the larger set sizes.

Discussion

Two findings are especially worthy of elaboration, as these have important implications for our current understanding of search in visual working memory. First, we found that increasing set size in the change-detection task was accompanied by a steady increase in RT; this effect accounted for a sizeable portion of RT variance, along with order. It was possible that, similar to the findings reported by Sternberg (1966), participants engaged in a serial, exhaustive search of representations in working memory; however, models of parallel search may also produce linear search functions (e.g., Townsend, 1990).

Second, there was an interaction between set size and a probe target’s presence or absence from the original array. Figure 2 shows that the search function for new probes across set sizes was considerably flatter than the function associated with old probes. At Set Size 1, in fact, the responses to new probes were slower than the responses to old probes, whereas the relation reversed at the higher set sizes. Participants may check whether a color was new and was not present in the original array.

The “newness check” is relatively capacity-unlimited until working memory capacity is exceeded; as shown in Figure 2, there was little increase in RT in trials containing new probes at set sizes 3 and smaller, a number corresponding to recent estimates of capacity for array change-detection procedures (e.g., Anderson et al., 2011; Cowan, 2001; Luck & Vogel, 1997; Rouder et al., 2008). Once that capacity is exceeded, this check is considerably slower. Change-detection trials that contain old probes will fail the newness check. At that point, one should begin an exhaustive search through all possible array locations and make a response; the RT function for old probes in Figure 2 supports this notion. The exhaustive search process is capacity-limited from the start, in contrast to the newness check.

The distribution of responses (Figure 3) shows that at the higher set sizes, newness checking is a rather ubiquitous process; it affects the entire distribution of RTs, and not just the tail. Yet, it appears that the newness check does not preclude a slower search process. If it did, then RT would not have increased at all across set sizes for new objects, when in fact there was a moderate increase. The newness signal may be used in parallel with the ongoing search process, not precluding that process but sometimes terminating it early.

The other finding of note relates to the effect of probe location in the change-detection task. We originally hypothesized that single-item probes presented in an array location, as opposed to being presented in a central location, should be associated with faster and more accurate responses. This is because, when a probe is in an array location, one only has to consider a single, specific item in a given location to make a response. Furthermore, spatial location could potentially function as a cue for retrieval. In contrast, with a central probe, all items and corresponding spatial locations within the array must be searched to make a correct response. With an optimal strategy, presumably location probes would circumvent this search of all items. Perhaps surprisingly, we found a benefit for location probes only in a limited circumstance: in the proportion correct for target-present trials at one set size, and not at all in the RTs.

The RT results suggest that participants engaged in an exhaustive search of array items, even when they were presented with a spatial cue that could be used to circumvent this search. (If the search were self-terminating the slope of the search function should be steeper for new items, not for old items; see Sternberg, 1966.) As color was the relevant feature on which to base responses in this task, retrieving location information would be unnecessary in a majority of instances. These results potentially suggest that although spatial location is processed in the change-detection task, with advantages in doing so (i.e., higher accuracy as reported above), color and location are weakly bound in the current paradigm.

There is, however, an issue related to the design of the current experiment that may affect the results. In this paradigm, central probes and location probes were mixed together in the same block. As participants were not aware of which probe they would receive ahead of time, they might choose to adopt a single process of exhaustive search across all trials (which might speed responses compared to a process of selecting the search strategy after the probe appeared). If this is the case, it is likely that the current findings would not be replicated using blocked presentations of central and location probes; in these instances, utilizing different search strategies based on probe location would be more feasible. We explored this possibility in the second experiment.

Experiment 2

The second experiment utilized blocked presentation of central and location probes. We reasoned that participants may utilize different search processes for central and location probes if they were separate from each other; however, if the absence of an effect of probe location in RT remained, this would suggest that participants do not utilize spatial information to circumvent search in general. In addition to the blocked presentation of probe locations, we also counterbalanced whether participants received central probes or location probes for the first half of the experiment. It is possible that searching for working memory representations may be biased by the probe location that is presented first. We discuss the design of this experiment in further detail below.

Method

Participants

Twenty participants (12 male, 8 female) from the Georgia Institute of Technology, and thirteen participants from the University of Missouri (4 male, 9 female) took part in this study in exchange for credit in an introductory psychology course, a total of 33 participants. One male participant completed the study on a different computer setting from the other participants, which led to different visual angles for the array objects, and was excluded from further analysis. Additionally, two female participants and one male participant failed to meet the criteria of a specified number of correct responses per set size (see Experiment 1), and were also excluded from our analyses, leaving a total of 29 participants. All participants had normal or corrected-to-normal vision, and were not colorblind.

Apparatus, stimuli, and procedure

All apparatus and stimuli used for testing were identical to those used in Experiment 1. The procedure was also largely similar to the previous experiment; however, the presentation of central and location probes within the change-detection task was blocked instead of mixed. As before, the experiment consisted of four blocks of trials that differed with respect to probe location and order. First, half of the blocks contained central probes, whereas the other half contained location probes. Moreover, we designed the experiment so that participants either received two blocks of trials with central probes first, followed by location probes, or the reverse pattern. This was counterbalanced across participants. Participants were warned of the probe’s location at the beginning of each block. After receiving a warning, participants completed a small set of practice trials prior to beginning the block of trials.

Second, the blocks differed with respect to whether the change-detection trials were in either ascending or descending set size order. Order was randomized across participants so that, for half of our participants, the first and third blocks were in ascending order and the second and fourth blocks were in descending order. For the remaining half of participants, the reverse occurred. As before, for change-detection trials in ascending order, set size began at one and increased to six; for descending order, set size began at six and decreased to one. Increases (or decreases) in set size did not occur until participants met the criteria of 4 correct responses for old probes and 4 correct responses for new probes. As before, a minimum of 384 trials were needed to complete the task. However, the number of trials presented per participant was typically larger than this due to random selection of old and new probes, as well as incorrect responses leading to additional trials for a particular set size.

Results

Accuracy

We examined accuracy in this task in an ANOVA that included the same repeated-measures factors as in Experiment 1: probe location, trial order within a sequence, set size, and whether the target probe old or new. Additionally, whether participants received central or location probes first was included as a between-subjects factor. The most important aspect of the results (Table 4) was that there was no main effect or interaction involving probe location that approached significance, in contrast to the significant three-way interaction obtained in Experiment 1.

Table 4.

Means and standard errors for accuracy in Experiment 2, for old and new probes, for each set size and order.

Set Size
	1	2	3	4	5	6
Ascending Order
Old Probes	0.98 (.01)	0.94 (.01)	0.90 (.02)	0.82 (.03)	0.77 (.02)	0.70 (.03)
New Probes	0.97 (.01)	0.97 (.01)	0.96 (.01)	0.94 (.01)	0.92 (.01)	0.85 (.01)
Descending Order
Old Probes	0.98 (.01)	0.94 (.01)	0.88 (.02)	0.81 (.03)	0.73 (.03)	0.72 (.03)
New Probes	0.97 (.01)	0.96 (.01)	0.94 (.01)	0.94 (.01)	0.89 (.01)	0.89 (.01)

There was a significant effect of set size, F(5, 135) = 83.61, MSE = .02, η_p² = .76, p < .001. Accuracy was highest at set size 1 (M = .98, SEM = .004), and then steadily declined as set size increased (Set size 2: M = .95, SEM = .006; Set size 3: M = .92, SEM = .009; Set size 4: M = .88, SEM = .013; Set size 5: M = .82, SEM = .014; Set size 6: M = .79, SEM = .015). A post hoc Newman-Keuls test confirmed these findings, revealing that accuracy levels for all set sizes were significantly different from each other. There was also a significant effect of whether the single-item probe was old or new, F(1, 27) = 45.75, MSE = .06, η_p² = .63, p < .001. As expected, participants were more accurate when the probe changed (M = .93, SEM = .006) than when the probe matched an item in the array (M = .85, SEM = .013). No other main effects approached statistical significance (Central or location probe presented first, F (1, 27) = 1.20, p = .28; probe location, F(1, 27) < 1; order, F(1, 27) = 1.28, p = .27).

In addition to these effects, there were two interactions. The interaction between trial order and set size was significant, F(5, 135) = 3.59, MSE = .008, η_p² = .12, p < .01. This interaction was largely driven by differences in performance at higher set sizes, as shown in the upper portion of Table 4. The dropoff in performance as a function of set size was more noticeable in the ascending order, as one would expect if there is a contribution of proactive interference (cf. May, Hasher, & Kane, 1999). There was also a significant interaction between set size and whether the probe was old or new, F(5, 135) = 17.88, MSE = .015, η_p² = .40, p < .001. As illustrated in Table 4, the drop in accuracy performance with increasing set size was much larger for old probes than for new probes, suggesting a guessing bias toward “new.”

Last, an additional analysis was conducted to determine if location information is of any help, barring any carryover effects. For this analysis, we compared the levels of performance for the first block of every participant, which was the location-probe trials for half of them and the center-probe trials for the other half. There was no significant difference between the performance level for central probes (M=.88) versus Location probes (M=.86), t(30)=1.26, p=.22. An ANOVA of the accuracy for these first conditions of each participant that included the probe location (between participants), set size, and old/new probe status produced no effect with probe location as a factor that approached statistical significance.

Response time

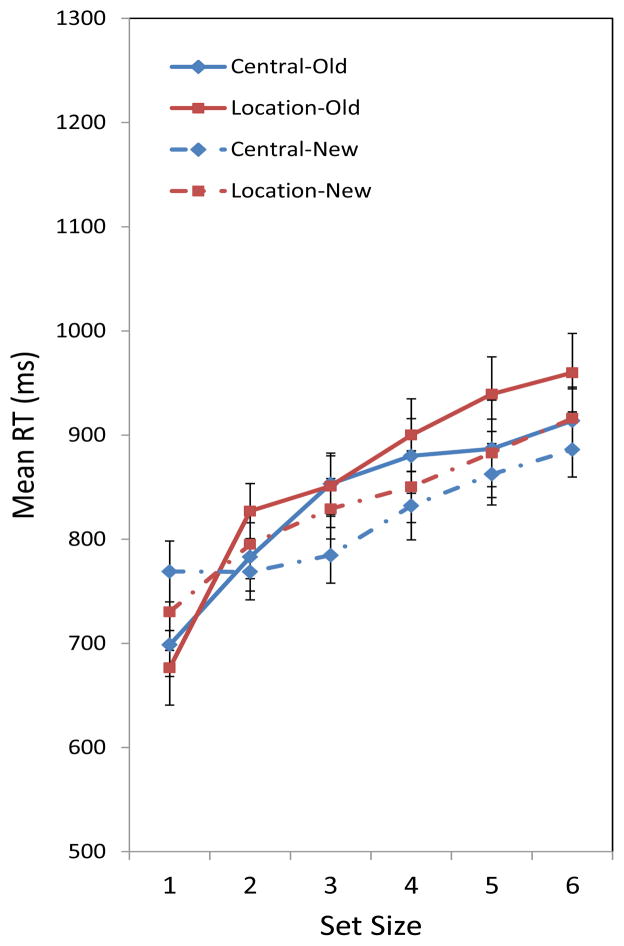
As in our previous experiment, the analysis of RT only included trials with correct responses that occurred with a delay of less than 5000 ms. As before, this criterion removed less than one percent of all correct responses that constituted usable data. We have included a table of results from a repeated-measures ANOVA in Table 5. Tables of unweighted means not included in the figure below are listed in Appendix B. Of particular note, the main effect of probe location did not approach significance (whereas in Experiment 1, a marginal effect favored central probes). Figure 4 shows a pattern of RTs quite similar to the results of Experiment 1, with different search rates for new versus old probes regardless of that probe’s location. We continued to find an effect of set size on RT. Post hoc Newman-Keuls tests confirmed that all set sizes had significantly different RTs from each other except for set sizes 5 and 6 (p < .05 in all cases). It is noteworthy that in neither experiment did participants use a location probe to speed the response by circumventing a search of the entire array.

Table 5.

Results from a repeated-measures ANOVA of RT, including partial-eta squared, for all effects and interactions in Experiment 2. Significant effects and interactions are marked with an asterisk.

Effect	df	F	p	ηp2
Trial Order	(1, 27)	<1	.92	<.01
Set Size*	(5, 135)	47.67	<.001	.64
Probe Location	(1, 27)	1.40	.25	.05
Probe Change (Old vs. New Probe)	(1, 27)	2.61	.12	.09
Trial Order × Set Size	(5, 135)	<1	.56	.03
Trial Order × Probe Location	(1, 27)	<1	.53	.02
Set Size × Probe Location	(5, 135)	1.93	.09	.07
Trial Order × Probe Change	(1, 27)	<1	.46	.02
Set Size × Probe Change*	(5, 135)	7.56	<.001	.22
Probe Location × Probe Change	(1, 27)	<1	.66	.01
Trial Order × Set Size × Probe Location	(5, 135)	<1	.76	.02
Trial Order × Set Size × Probe Change	(5, 135)	2.24	.05	.08
Trial Order × Probe Location × Probe Change	(1, 27)	<1	.46	.02
Set Size × Probe Location × Probe Change	(5, 135)	<1	.54	.03
Trial Order × Set Size × Probe Location × Probe Change	(5, 135)	<1	.88	.01
Block Order	(1, 27)	1.35	.26	.05
Block Order × Trial Order	(1, 27)	<1	.73	<.01
Block Order × Set Size*	(5, 135)	2.51	.03	.09
Block Order × Probe Location*	(1, 27)	23.35	<.001	.46
Block Order × Probe Change	(1, 27)	2.12	.16	.07
Block Order × Trial Order × Probe Location	(1, 27)	<1	.60	.01
Block Order × Set Size × Probe Location	(5, 135)	1.76	.12	.06
Block Order × Probe Location × Probe Change	(1, 27)	<1	.35	.03
Block Order × Trial Order × Probe Change	(1, 27)	<1	.36	.03
Block Order × Trial Order × Set Size	(5, 135)	<1	.51	.03
Block Order × Set Size × Probe Change	(5, 135)	<1	.71	.02
Block Order × Trial Order × Set Size × Probe Location*	(5, 135)	2.84	.02	.10
Block Order × Trial Order × Set Size × Probe Change	(5, 135)	<1	.69	.01
Block Order × Trial Order × Probe Location × Probe Change*	(5, 135)	2.43	.04	.08
Block Order × Set Size × Probe Location × Probe Change	(5, 135)	1.20	.31	.04
5-way interaction	(5, 135)	<1	.98	<.01

Note. Trial order refers to ascending versus descending trial blocks, whereas block order refers to the presentation of central or location blocks first.

Figure 4.

Mean RT for correct responses in Experiment 2 across set size. Error bars are standard errors of the mean.

We also observed several significant two-way interactions with respect to response time. Specifically, we observed a significant interaction between set size and whether the single-item probe was old or new. Similar to Experiment 1, we found that at set size 1, there was an RT advantage for old probes compared to new probes. This effect reversed as set size increased, with RTs for new probes being faster than those for old probes. Post-hoc Newman-Keuls tests showed the difference to be significant for set sizes 3–6.

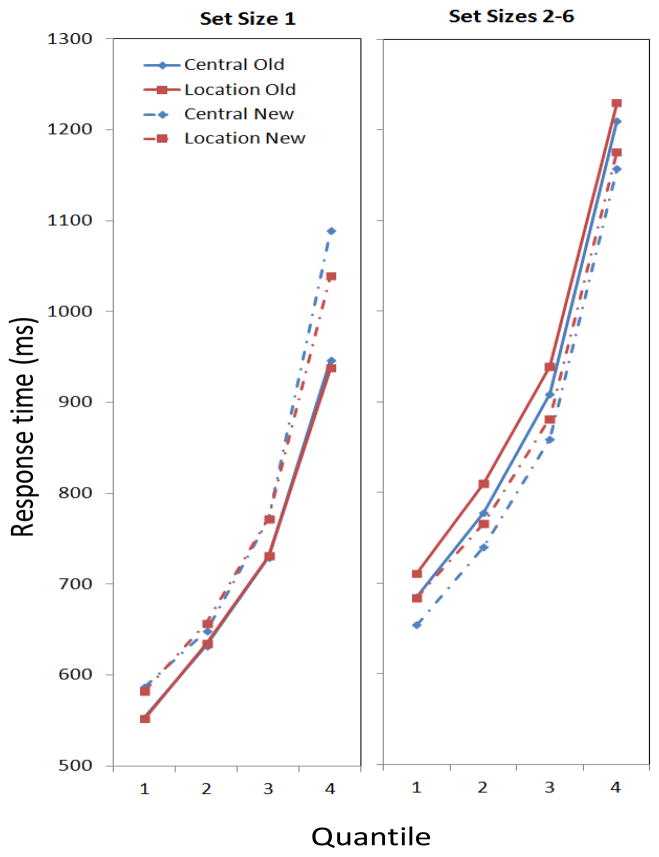
Quantiles obtained for combinations of probe location and probe change across set size provide further information about these findings; the unweighted means for these quantiles are presented in Table 6 and in Figure 5. The results are basically the same as Experiment 1, but cleaner in support of the generalizations described for that experiment. In particular, at Set Size 1, the disadvantage for new items is especially pronounced at the longer quantiles whereas, at the higher set sizes, there is an advantage for new items that occurs throughout the quantiles. The former indicates a process that is slow and only affects some trials. The latter, however, suggests a process, presumably novelty-checking, that is routinely done and does not fully replace the array search but speeds the response for new probes relative to old ones and flattens the search slope for new probes.

Table 6.

Means and standard errors (in ms) for Experiment 2 quantiles (30, 50, 70, and 90 percent of the data) for set size 1 and the pooled average of set sizes 2–6.

Central Probes
Old Probes				New Probes
SS 1		SS 2–6		SS 1		SS 2–6
30	554 (26)	30	685 (24)	30	587 (27)	30	654 (24)
50	633 (29)	50	778 (27)	50	649 (30)	50	740 (29)
70	730 (34)	70	909 (34)	70	772 (40)	70	859 (34)
90	947 (54)	90	1210 (55)	90	1089 (81)	90	1157 (59)
Location Probes
Old Probes				New Probes
SS 1		SS 2–6		SS 1		SS 2–6
30	552 (24)	30	711 (21)	30	583 (20)	30	684 (22)
50	635 (26)	50	810 (26)	50	658 (24)	50	766 (26)
70	731 (30)	70	939 (33)	70	773 (31)	70	882 (32)
90	938 (45)	90	1230 (51)	90	1040 (68)	90	1176 (55)

Figure 5.

Means from four groups of data in Experiment 2 reflecting the 0–30^th, 31–50^th, 51–70^th, and 71–90^th quantiles in the condition, respectively. Left, Set Size 1; Right, the aggregate of Set Sizes 2–6. The graph parameter is the condition, which depended on the location of the probe (Central vs. Location) and whether the probe was in the array (Old) or not (New).

The other interactions we observed in the ANOVA of RTs (Table 5) involved the order of presentation of central versus location probe trial blocks (Block Order), which had no counterpart in Experiment 1 because these probes were randomized together in that experiment. As shown in Appendix B, there was a significant interaction between probe location and whether participants were first presented with central or location probe trial blocks. Participants were fastest on trials in which the probe location matched what had been presented to participants on the first trial block. Second, the interaction between set size and whether participants received central or location probes first was significant. Appendix B shows that the central-first presentation order was advantageous, especially for the small set sizes. Two four-way interactions have been omitted for simplicity.

Last, we looked at whether there was a time savings for location probes compared to center probes, and thus the use of location information, barring any carryover effects. Thus, we compared the first procedure for every participant, a comparison that did not yield a significant difference in accuracy. Likewise, in RT, the means did not differ, t (30) = −0.76, p=.45. The nonsignificant trend was against the use of location information (location probe M=831 ms; central probe M=778 ms). An ANOVA of the RT for these first conditions of each participant that included the probe location (between participants), set size, and old/new probe status produced no effect with probe location as a factor that approached statistical significance.

Discussion

The main findings of Experiment 2 replicated the effects found in Experiment 1, this time with location and central probes in separate trial blocks. First, we found that increasing set size in the change-detection task was accompanied by a steady increase in RT; this effect accounted for a sizeable portion of RT variance. Moreover, there was an interaction set size and a probe being old or new. In particular, the search function for new probes across set size was considerably flatter than the function associated with old probes and again became faster than old probes at higher set sizes (Figure 4). A breakdown of the RT means by quantiles again showed a pattern in which, at Set Sizes 2–6, the advantage of a new probe occurred across all quantiles. In short, this was again a pattern indicative that participants carry out a “newness check” at Set Sizes 2–6 while also conducting a search, with responses to new probes facilitated by the newness factor (cf. Hyun et al., 2009).

Also of note, in neither experiment did the location probes provide a search speed advantage over the center probes, as one would expect if the probed location were accessed and the array-wide search were thereby circumvented. This finding is especially notable in Experiment 2, as the blocked presentation of central and location probes could potentially encourage participants to use different strategies to encode and retrieve central and location probes. Similar results have also recently been reported by Woodman and colleagues using a change-detection paradigm (Woodman, Vogel, and Luck, 2012).

General Discussion

The goal of the current research was to use RT to examine the nature of search in the change-detection paradigm, a task that has commonly been used to assess visual working memory capacity estimates. In two experiments, we sought to determine if, similar to findings from Sternberg (1966) using lists, searching through representations in visual working memory was subject to an exhaustive, set-size-dependent process. This process could be either serial or parallel in nature (see Donkin & Nosofsky, 2012; Ratcliff, 1978; Townsend, 1976, 1990). In either case, we were also interested in whether this process was modified by the location of a single-item probe. Would the RT function observed for probes presented in an array location be qualitatively different from the function for probes that were presented centrally? It was expected that, if this process were ideal, there should be an advantage for location probes, as that probe specified one item from the array whereas a central probe logically had to be compared to all items in the array, at least until a match was found.

In the first experiment, central and location probes occurred within the same block of trials. This was done to preclude participants engaging in different encoding strategies for the probe locations, which could potentially occur if the probes were in separate blocks. Even when participants were unaware of where the probe would be located from trial to trial, we observed an RT search function that increased as array size increased. We also observed that the RT functions for old and new probes were qualitatively different from each other. Although both functions showed a characteristic increase in RT with increasing set size, the function associated with new probes (i.e., probes that change to a new color not shown in the array) was noticeably shallower in slope than the function for old probes. We found little evidence that these search processes are influenced by probe location.

In the second experiment, in addition to keeping central and location probes in separate blocks, we also manipulated whether participants first received central probes or location probes for the first half of the experiment. This was done to examine again whether central and location probes were associated with differential encoding strategies. Similar to what we observed in Experiment 1, we found an RT search function that increased with increasing set size. Just as before, the search functions across set size for old and new probes were qualitatively different, with the RT function for old probes being associated with a steeper slope. Additionally, we again found that being presented with a single-item probe in an array location provided few benefits above central probes with respect to RT. Interestingly, we found no evidence that presenting participants with either central or location probes influences how search processes operate in working memory. While participants who received central probes first tended to be faster overall, particularly when a central probe was presented, the overall pattern of results was similar between the two groups.

In both experiments, inspection of RT results by quantiles helped to clarify the processes involved. At Set Size 1, for which the old probe responses were faster than new probe responses, it seems likely that the method of search was to attempt a direct comparison between the array item and probe colors. On some trials, though, some of the slowest responses occurred for new probes, possibly because the participant still had the color in working memory from a previous trial and had to search memory again to verify that it was not the target on the present trial. For the higher set sizes, newness of the probe speeded responses by shifting the entire distribution of responses leftward; thus, there appeared to be a routine “newness check” that was used along with the memory search process (Figures 3 and 5). Moreover, this newness check tended to make the search function for new probes more shallow than that for old probes (Figures 2 and 4). This is the opposite of what would be expected if the search were self-terminating, ending when the probe was identified in the array. If the search were exhaustive, old and new probes should yield comparable search functions (cf. Sternberg, 1966). Instead of these options, it appears that the newness check habitually takes place and can sometimes cut short the search process when a new feature is detected.

These results have significant implications for our understanding of search in visual working memory, as well as for the status of spatial location in the change-detection paradigm. We discuss each of these points in greater detail below.

Search of Visual Working Memory Representations

In this section we address two fundamental issues, the detection of sameness versus difference and the serial versus parallel nature of search.

Detection of sameness and difference

We initially designed this study to examine whether the well-replicated findings of high-speed scanning of serially-presented lists would also be found for visual arrays, in which items are presented simultaneously. Unlike lists of items, visual arrays have neither a set temporal order nor a prescribed search order. Despite this, we did find that RT increased as an effect of set sizes, similar to what has been found for lists. It appears, however, that the processes involved in this search of visual array items is more complex than the search processes that occur with list stimuli, for which old probe and new probe functions typically do not differ (e.g., Sternberg, 1966). It is also very different from visual search, in which the RT slope across visual set sizes is twice as steep for trials with new probes as for those with old probes (e.g., Treisman, 1988).

We found that RT increased across set sizes more quickly with old probes than with new probes, in both experiments and for both probe locations. In this procedure, difference detection is of no use because for multiple-item arrays, the single probe will always mismatch at least one item in the array. Search for a match cannot itself explain the RT pattern, inasmuch as the search would have to last at least as long for trials containing new probes as for those trials containing old probes.

Logically, the only possibility remaining is that the actual detection of a match takes time. It is possible, for example, that this match is mentally verified after it is detected and that the verification process depends on the array set size. As mentioned above, Hyun et al. (2009) drew similar conclusions. On the basis of several related experiments and electrophysiological data, they concluded that the change-detection procedure is akin to visual search, noting (p. 1156), “just as visual targets defined by the presence of a feature can be detected much more efficiently than targets defined by the absence of a feature …Experiment 1 showed that the presence of a difference between the sample and test arrays can be detected much more efficiently than the absence of a difference.” Reaction time slopes were much steeper for trials in which sameness must be detected than for trials in which differences must be detected. Within the condition in which differences were to be detected, either all items remained the same at test, or a single item changed. This most resembled the change-detection procedure that we used, and Hyun and colleagues observed that participants were slightly faster for new probes (i.e., 1 item changed) than for old probes (i.e., no items in the probe changed).

Nevertheless, these results do not match visual search overall. What matches visual search more closely in Hyun et al. (2009) is that, for those trials in which sameness was to be detected, the all-change condition had a steeper slope than the 1 no-change condition. This suggests that, as in visual search for features that do not pop out (Treisman, 1988), searches were not parallel or exhaustive in that condition, but terminated when a match between the studied and comparison arrays was observed. In contrast, the shallower slopes for trials in which differences must be detected suggest that a change tends to pop out mentally and need not be searched for in a slow process.

Within this relatively rapid search, though, the slightly steeper RT slopes for target-present probes (apparent in all of our data figures) cannot be explained by an analogy to visual search. It suggests an additional process in which a match must be verified. This difficulty may arise because the comparison of the probe to all of the other array items leads to the judgment of a difference; only one of the array items leads to sameness, and the response may be difficult because this relevant sameness appears to be outweighed by perceived differences. In keeping with this account, Hyun et al. (2009) also proposed that there was an additional verification process that was capacity-limited, which would be necessary to detect “sameness” between an array and a probe.

The salience of object novelty appears to fit well with certain theoretical perspectives of visual working memory. In a working memory model proposed by Wheeler and Treisman (2002), object features such as the color and location of array items are stored in parallel in feature-specific caches (i.e., a separate color and location cache). Within each cache, feature representations compete for storage in a capacity-limited working memory. It is possible that new probes are considerably easier to register because features of new probes are not stored in the color-specific cache, and thus are not subject to competition and interference.

Newness-checking can also occur within the working memory model proposed by Cowan (1988). New probes, by virtue of being a color not shown in the original array, may potentially trigger orienting selective attention toward the single-item probe, now in the focus of attention, due to the difference between the probe and the representation of the array stored in activated long-term memory. This initial attentional orienting may be noticeable enough to participants to signal a “new” response. In contrast, when the probe is old, there is no such orienting on the basis of salience; thus, the signal to make a response is not as clear. Participants must compare the probe item in the focus of attention to the array items that are stored in activated long-term memory. Taken together, this produces a more rapid “new” response and a slower “old” response.

These findings have relevance beyond the laboratory task utilized here. Although change-detection is commonly utilized in working memory research, detecting changes or sameness is critical for navigating one’s everyday environment. The general function of a working memory system is to maintain brief representations of information, potentially in the absence of external perceptual inputs, in a rapidly-changing environment. Given that one’s external environment is frequently changing, it is reasonable that it is easier to register change, compared to a lack of change, within the working memory system.

Before addressing the issue of parallel versus serial memory search, we must address a potential concern regarding the RT findings (and conclusions) reported above. It can be argued that the results that we obtained were due to encoding the visual representations, rather than searching for them. Namely, as visual array size increases, the time to encode each colored square decreases. It follows that visual representations will become poorer in quality with increasing set size, and it will become more difficult to determine whether or not a given representation matches the probe. Although this is plausible, it is not supported by previous research. In a developmental study, Cowan and colleagues presented participants with a change-detection task in which array items were presented sequentially, rather than simultaneously (Cowan, AuBuchon, Gilchrist, Ricker, & Saults, 2011). This would ensure that all items were sufficiently encoded. Despite this precaution, sequential presentation procured no additional benefit to performance, when the results were compared to a prior study that utilized simultaneous presentation. These results support the notion that the results we observed in the current study involve working memory retrieval search limitations rather than limitations in encoding.

Parallel or serial memory search?

A recent study by Donkin and Nosofsky (2012) attempted to clarify the potential search processes underlying the memory-scanning paradigm. In addition to replicating Sternberg’s original study (Sternberg, 1966), they also presented participants with a memory-scanning experiment that had a faster presentation rate. Data from both experiments, as well as simulated data, were fit to three different models that could potentially underlie memory search in the task: a serial, exhaustive model forwarded by Sternberg; a parallel, self-terminating model; and a search based on judgments of familiarity between items in short-term memory and the test probe. When this task included rapid presentation rates, the resulting RT data best fit either the familiarity or parallel model; when presentation rates were slower, as in Sternberg’s original study, all three models fit the data quite well. Moreover, what was critical to these good model fits was the inclusion of different response thresholds for old and new probes, potentially suggesting that different search processes may be involved for these probe types.

In addition to these findings, Donkin and Nosofsky were also interested in which factors drive the linear increase in RT with set size. With rapid presentation of stimuli, it was found that lag between an item’s presentation and its subsequent probe was the primary reason for this increase, with the contribution from set size being negligible. Set size, however, made a sizeable contribution to the increase in RT when presentation rate was slower. These results suggest that the processes that underlie memory search, as well as the factors that contribute to these processes, may change with different manipulations.

Unlike the memory-scanning experiments described above, there is no discernable lag between item presentations in the two experiments reported here. As such, there would be no clear marker for the order of serial search, leading us to favor the notion that search is parallel and capacity-limited. Strengthening our preference for this idea of parallel search, Donkin and Nosofsky (2012) found a poor fit to serial search for rapid list presentation rates, and the simultaneous brief presentation of array items could be viewed as similar to a rapid presentation rate.

More recently, Donkin and colleagues (2013) favored discrete over continuous models of working memory in change-detection using mathematical modeling of RT. The results strongly favored discrete models. The models assumed, however, that location information was used to narrow the search to the array item matching the location of the probe. The present results suggest that it is important to assess models in which the location information is discarded.

How is Location Processed in Change-Detection?

In the current set of experiments, we found spatial location is typically not utilized, despite the advantages it provides to memory search. When participants were presented with a single-item probe in an array location, they exhaustively searched through array items before making a response, similar to the pattern that was observed for central probes. What we find particularly surprising about this is that, ideally, the location of the single-item probe should have encouraged different search strategies. Whereas a central probe should encourage an exhaustive search of all items in memory and subsequent comparisons to the test probe, a probe in an array location picks out a single item in memory that participant should compare to the probe. Optimally, the latter process should be faster than the former; however, this was not what was observed.

What does this mean for our understanding of how location information is processed in the change-detection task? A first possibility is that if information regarding spatial location is irrelevant to making a response, a person will simply not use location information to guide search. In our studies, participants judged whether or not the probe matched an array item on the basis of color. To correctly respond in the task, participants only needed to detect whether the color matched any items in the previous array, or was a unique, new color. Although spatial location could potentially serve as a cue to guide search of these representations, it was unnecessary with respect to the decision process. If that is the case, we should expect that a study in which spatial location is relevant to making a response (e.g., change trials in which a previously-viewed color is in a different array location) should lead to RT benefits for location probes compared to central probes (e.g., Treisman & Zhang, 2006).

There is a second possibility, not mutually exclusive from the first possibility, that has implications for our broader understanding of how visual items are bound to spatial location. It is, as mentioned in earlier sections, that location information may not be tightly bound to representations stored in visual working memory. Previous evidence from visual working memory tasks suggests that location information can guide search of objects or object features; however, the bindings between feature information and its original spatial location are not so strongly bound that presenting a previously-viewed feature in a new location negatively affects retrieval of that feature (Treisman & Zhang, 2006). As we observed participants were no less accurate for central probes than for location probes, despite the fact that the former were presented in a spatial location that was different from where they were originally seen. Corroborating these results, Woodman and colleagues (2012) presented participants with a series of change-detection tasks that included manipulations that changed the spatial locations of array items. This could include changing the size of items, shifting the overall array configuration into a new location on a computer screen, or scrambling the array configuration. The first two manipulations changed specific item locations while preserving the original configuration, whereas the last manipulation changed both item locations and overall configuration. Woodman and colleagues observed that, even when these locations changed in such a way that the original configuration was violated, the working memory representations were not disrupted. Participants performed as equally well on change-detection tasks that involved these transforms as they did in the standard task with a whole-array probe. The only instance in which spatial transformations attenuated change-detection performance occurred when participants were encouraged to base their responses on a single item in a whole display, which could implicitly encourage participants to use location information to retrieve feature information. This suggests that visual working memory can be flexible in response to task demands, fitting with the first possibility above. Moreover, feature information about items in visual arrays can still be retrieved, even when spatial locations change to the point of transforming an original array configuration.

Conclusions

We suggest that the current research signals a new direction for our current conception of capacity estimates in visual working memory. Our results indicate that visual working memory search is characterized by two different processes, rather than a single process that compares stored items to a test probe. Furthermore, our results provide further evidence to a growing body of research that suggests that location information is not optimally utilized in the change-detection task, though it should be noted that this depends on the relevance of location information in the task. It is our hope that, through this research, new models of working memory storage and search can be conceived, ones that take these newfound complexities into account.

Appendix A

Unweighted RT means and standard errors (in ms) for effects and interactions not included in figures in Experiment 1. Significant effects and interactions are marked with an asterisk. Four-way interactions have been omitted for sake of simplicity.

Trial Order
Ascending: 806 (25)			Descending: 815 (30)
Set Size*
1	2	3	4	5	6
754 (29)	769 (28)	785 (25)	830 (32)	865 (32)	860 (28)
Probe Location
	Central: 805 (27)			Location: 816 (28)
Probe Change
	Old Probe: 818 (29)			New Probe: 803 (26)
Trial Order × Set Size
Ascending
1	2	3	4	5	6
772 (31)	764 (28)	783 (26)	821 (28)	844 (30)	853 (27)
Descending
1	2	3	4	5	6
736 (30)	773 (31)	788 (27)	838 (38)	886 (38)	867 (34)
Trial Order × Probe Location
Ascending
	Central: 796 (25)			Location: 817 (26)
Descending
	Central: 814 (30)			Location: 816 (30)
Trial Order × Probe Change
Ascending
	Old Probe: 814 (28)			New Probe: 799 (24)
Descending
	Old Probe: 823 (31)			New Probe: 807 (31)
Probe Location × Probe Change
Central
	Old Probe: 821 (29)			New Probe: 789 (25)
Location
	Old Probe: 816 (29)			New Probe: 817 (28)
Trial Order × Set Size × Probe Location
Ascending
1	2	3	4	5	6
Central: 752 (30)	Central: 759 (32)	Central: 777 (26)	Central: 805 (29)	Central: 840 (32)	Central: 843 (24)
Location: 793 (38)	Location: 768 (27)	Location: 789 (32)	Location: 838 (31)	Location: 848 (34)	Location: 864 (34)
Descending
1	2	3	4	5	6
Central: 735 (31)	Central: 769 (31)	Central: 787 (28)	Central: 842 (40)	Central: 879 (40)	Central: 869 (34)
Location: 738 (31)	Location: 777 (37)	Location: 789 (28)	Location: 834 (37)	Location: 894 (39)	Location: 865 (35)
Trial Order × Set Size × Probe Change
Ascending
1	2	3	4	5	6
Old Probe: 738 (35)	Old Probe: 772 (30)	Old Probe: 788 (27)	Old Probe: 831 (31)	Old Probe: 883 (39)	Old Probe: 870 (35)
New Probe: 807 (34)	New Probe: 756 (28)	New Probe: 778 (29)	New Probe: 812 (30)	New Probe: 805 (27)	New Probe: 836 (27)
Descending
1	2	3	4	5	6
Old Probe: 711 (29)	Old Probe: 778 (32)	Old Probe: 805 (33)	Old Probe: 853 (39)	Old Probe: 908 (48)	Old Probe: 884 (34)
New Probe: 762 (33)	New Probe: 768 (34)	New Probe: 771 (25)	New Probe: 823 (40)	New Probe: 865 (36)	New Probe: 851 (36)
Trial Order × Probe Location × Probe Change
Ascending
	Central			Location
	Old Probe: 806 (28)			Old Probe: 821 (30)
	New Probe: 785 (25)			New Probe: 812 (27)
Descending
	Central			Location
	Old Probe: 835 (33)			Old Probe: 811 (30)
	New Probe: 792 (29)			New Probe: 821 (34)

Note. Trial order refers to ascending versus descending trial blocks.

Appendix B

Unweighted means and standard errors for RT effects and interactions (in ms) not included in figures in Experiment 2. Significant effects and interactions are marked with an asterisk. Four- and five-way interactions have been omitted for sake of simplicity.

Block Order
	Central-First: 802 (42)			Location-First: 871 (43)
Probe Location
	Central: 826 (32)			Location: 846 (30)
Trial Order
	Ascending: 837 (31)			Descending: 836 (31)
Set Size*
1	2	3	4	5	6
719 (30)	793 (33)	829 (33)	866 (30)	893 (30)	919 (33)
Probe Change
	Old Probe: 847 (31)			New Probe: 826 (31)
Block Order × Probe Location*
Central-First
	Central: 751 (45)			Location: 852 (42)
Location-First
	Central: 902 (46)			Location: 841 (44)
Block Order × Trial Order
Central-First
	Ascending: 800 (44)			Descending: 804 (43)
Location-First
	Ascending: 875 (45)			Descending: 868 (44)
Block Order × Set Size*
Central-First
1	2	3	4	5	6
673 (42)	741 (46)	793 (46)	820 (42)	873 (41)	909 (46)
Location-First
1	2	3	4	5	6
764 (43)	846 (48)	866 (48)	911 (44)	912 (43)	928 (47)
Block Order × Probe Change
Central-First
	Old Probe: 822 (43)			New Probe:781 (42)
Location-First
	Old Probe: 872 (45)			New Probe: 870 (44)
Probe Location × Trial Order
Ascending
	Central: 831 (34)			Location: 844 (32)
Descending
	Central: 822 (33)			Location: 849 (32)
Trial Order × Set Size
Ascending
1	2	3	4	5	6
726 (33)	791 (33)	837 (35)	874 (34)	888 (33)	908 (36)
Descending
1	2	3	4	5	6
711 (30)	796 (38)	822 (35)	858 (31)	897 (30)	930 (34)
Trial Order × Probe Change
Ascending
	Old Probe: 850 (32)			New Probe: 824 (32)
Descending
	Old Probe: 845 (32)			New Probe: 827 (31)
Probe Location × Probe Change
Central
	Old Probe: 836 (33)			New Probe: 817 (33)
Location
	Old Probe: 859 (32)			New Probe: 834 (31)
Probe First × Probe Location × Trial Order
Central-First
	Central			Location
	Ascending: 749 (47)			Ascending: 850 (44)
	Descending: 752 (46)			Descending: 855 (44)
Location-First
	Central			Location
	Ascending: 912 (49)			Ascending: 837 (45)
	Descending: 892 (48)			Descending: 844 (46)
Probe First × Probe Location × Set Size
Central-First
1	2	3	4	5	6
Central: 646 (48)	Central: 693 (50)	Central: 755 (52)	Central: 748 (46)	Central: 816 (41)	Central: 846 (48)
Location: 700 (40)	Location: 789 (48)	Location: 830 (46)	Location: 892 (44)	Location: 931 (48)	Location: 972 (50)
Location-First
1	2	3	4	5	6
Central: 821 (50)	Central: 859 (52)	Central: 882 (54)	Central: 964 (47)	Central: 933 (43)	Central: 953 (50)
Location: 706 (42)	Location: 833 (50)	Location: 850 (47)	Location: 859 (45)	Location: 892 (50)	Location: 903 (52)
Probe First × Probe Location × Probe Change
Central-First
	Central			Location
	Old Probe: 773 (45)			Old Probe: 871 (44)
	New Probe: 728 (46)			New Probe: 833 (43)
Location-First
	Central			Location
	Old Probe: 898 (47)			Old Probe: 846 (45)
	New Probe: 906 (48)			New Probe: 835 (45)
Probe First × Trial Order × Probe Change
Central-First
	Ascending			Descending
	Old Probe: 825 (45)			Old Probe: 820 (44)
	New Probe: 775 (44)			New Probe: 787 (43)
Location-First
	Ascending			Descending
	Old Probe: 875 (46)			Old Probe: 869 (46)
	New Probe: 874 (46)			New Probe: 866 (45)
Probe First × Set Size × Probe Change
Central-First
1	2	3	4	5	6
Old: 657 (39)	Old: 759 (47)	Old: 823 (50)	Old: 856 (47)	Old: 911 (44)	Old: 929 (49)
New: 690 (45)	New: 723 (48)	New: 762 (49)	New: 784 (43)	New: 835 (42)	New: 890 (45)
Location-First
1	2	3	4	5	6
Old: 718 (41)	Old: 851 (49)	Old: 881 (52)	Old: 924 (48)	Old: 915 (46)	Old: 945 (51)
New: 809 (47)	New: 840 (50)	New: 852 (50)	New: 898 (45)	New: 910 (44)	New: 912 (47)
Probe Location × Trial Order × Set Size
Ascending
1	2	3	4	5	6
Central: 752 (30)	Central: 759 (32)	Central: 777 (26)	Central: 805 (29)	Central: 840 (32)	Central: 843 (24)
Location: 793 (38)	Location: 768 (27)	Location: 789 (32)	Location: 838 (31)	Location: 848 (34)	Location: 864 (34)
Descending
1	2	3	4	5	6
Central: 735 (31)	Central: 769 (31)	Central: 787 (28)	Central: 842 (40)	Central: 879 (40)	Central: 869 (34)
Location: 738 (31)	Location: 777 (37)	Location: 789 (28)	Location: 834 (37)	Location: 894 (39)	Location: 865 (35)
Probe Location × Trial Order × Probe Change
Ascending
	Central			Location
	Old Probe: 806. (28)			Old Probe: 821 (30)
	New Probe: 785 (25)			New Probe: 812 (27)
Descending
	Central			Location
	Old Probe: 835 (33)			Old Probe: 811 (30)
	New Probe: 792 (29)			New Probe: 821 (34)
Trial Order × Set Size × Probe Change
Ascending
1	2	3	4	5	6
Old Probe: 738 (35)	Old Probe: 772 (30)	Old Probe: 788 (27)	Old Probe: 831 (31)	Old Probe: 883 (40)	Old Probe: 870 (35)
New Probe: 807 (34)	New Probe: 756 (28)	New Probe: 778 (29)	New Probe: 812 (30)	New Probe: 805 (27)	New Probe: 836 (27)
Descending
1	2	3	4	5	6
Old Probe: 711 (29)	Old Probe: 778 (32)	Old Probe: 805 (33)	Old Probe: 853 (39)	Old Probe: 908 (48)	Old Probe: 884 (34)
New Probe: 762 (33)	New Probe: 768 (34)	New Probe: 77 (25)	New Probe: 823 (40)	New Probe: 865 (36)	New Probe: 851 (36)

Note. Trial order refers to ascending versus descending trial blocks, whereas block order refers to the presentation of central or location blocks first.