A kinetic mechanism for cell sorting based on local variations in cell motility

Abstract

Our current understanding of cell sorting relies on physical difference, either in the interfacial properties or motile force, between cell types. But is such asymmetry a prerequisite for cell sorting? We test this using a minimal model in which the two cell populations are identical with respect to their physical properties and differences in motility arise solely from how cells interact with their surroundings. The model resembles the Schelling model used in social sciences to study segregation phenomena at the scale of societies. Our results demonstrate that segregation can emerge solely from cell motility being a dynamic property that changes in response to the local environment of the cell, but that additional mechanisms are necessary to reproduce the envelopment behaviour observed in vitro. The time course of segregation follows a power law, in agreement with the scaling reported from experiment and in other models of motility-driven segregation.

1. Introduction

When cells of different type, from dissociated embryonic tissue, are thoroughly intermingled and then allowed to reaggregate, they spontaneously self-assemble into domains homogeneous with respect to cell type [1–3]. Such cell sorting has also been observed for dissociated Hydra cells, co-cultures of cells not in contact during normal development and mixtures of cells extracted from different species [4–7].

Understanding how such segregation emerges and is maintained offers insight into the mechanisms governing pattern formation, morphogenesis, tissue homeostasis and cancer invasion. In particular, Foty & Steinberg have demonstrated that malignant invasion may be regarded as a process of cell sorting in reverse. As tumours become invasive, cancer cells become miscible with healthy cells and the ability of the tissue to maintain compartmentalization is lost [8].

In a compact aggregate, or in a tissue, cells interact strongly with one another and factors including adhesion, cortical tension, the viscoelastic properties of cells and collective motion all affect the motility of individual cells [9–11]. Current models of sorting assume some physical difference between cell types—either in the form of adhesion [12], cortical tension [3,13] or motility [14,15].

The differential adhesion hypothesis posits that the adhesive interactions between cells give rise to surface tension and that the equilibrium configurations of the tissue are those that minimize the surface energy [16–19]. The segregation of cells into homotypic domains is therefore phenomenologically similar to the phase separation of fluids [2,18]. The differential adhesion hypothesis has been studied extensively using the Cellular Potts model, pioneered by Graner & Glazier [20,21], and has been successful in describing a range of cell-sorting phenomena [22–26]. However, the Cellular Potts model is principally an equilibrium model; the kinetics are determined by an auxiliary dynamics—typically a Markov chain Monte Carlo method—used to relax the system to its equilibrium configuration [27]. Indeed, differences in the choice of Monte Carlo algorithm may account for the discrepancies in the scaling behaviour reported for different computational implementations of the differential adhesion hypothesis (e.g. [21,22,26]). Careful work by Ouchi et al. [24] has addressed how to modify the energy function and Monte Carlo algorithm to reproduce the kinetic behaviour of cells.

It is not known to what extent local variations in cell motility might also contribute to cell sorting. Rieu et al. [9] studied the two-dimensional motion of single endodermal Hydra cells in aggregates comprised either endodermal or ectodermal cells. In both environments, the trajectories are characteristic of persistent random motion, with persistence dominating at small time scales. However, diffusion is more than two times faster for endodermal cells in an ectodermal environment, with reported diffusion constants of D_endo−ecto = 1.05 ± 0.4 μm² min⁻¹ and D_endo−endo = 0.45 ± 0.2 μm² min⁻¹. Previous mathematical and computational models [14,15,28–30] have all focused on intrinsic motility differences. Unlike implementations of the differential adhesion hypothesis, the steady-state segregated configurations of motility-driven sorting are not written in a priori as the minimum of the systems Hamiltonian, but rather emerge from the kinetics at the level of individual cells. By formulating a minimal model, in which the two cell populations are identical with respect to their physical properties, we test whether such asymmetry is a prerequisite for cell sorting. In particular, we explore here the behaviour of cell populations where motility is a dynamic quantity that changes in response to the local environment of the cell.

The model presented is related to the Schelling model [31–33], which, in the field of social sciences, is the paradigm for studying segregation phenomena at the scale of societies [34–36]. Developed by Schelling in the 1960s [31–33], it describes a system in which agents of two types move on a checkerboard according to a utility function defined by their current environment and the environment they have the option of moving to. For each agent, the utility of a site on the board is given by the proportion of neighbouring agents that are of the same type. As the system evolves, homotypic domains emerge, eventually leading to complete segregation. Schelling thereby demonstrated that even weak individual preferences for homophily can give rise to strong segregation. This type of model has since been studied on networks, in continuous-space models, and analytically [37–40]. Previous versions of the Schelling model have been non-local in that agents have information about, and are able to move to, sites not immediately adjacent to them. This is a reasonable assumption for human societies but not for populations of cells. To apply the Schelling idea in a biological context, the dynamics need to be made entirely local.

2. The model

The aim of the model is to investigate whether intrinsic differences in the physical properties of the two cell types are a prerequisite for sorting. The system consists of a binary mixture of cells that are symmetric with respect to their intrinsic motility properties. Differences in motility arise from the interaction of cells with their local environment. Specifically, the effective speed of diffusion of each cell is determined by the proportion of neighbouring cells of the same type. We demonstrate that segregation does not require asymmetry but can emerge solely from cell motility being a dynamic property that changes in response to the local environment each cell finds itself in.

The cells diffuse on a square continuous-space plane, with sides of length L and periodic boundary conditions. Each cell has a position x_i and moves according to

2.1

where we, without loss of generality, set Δt = 1.

The total number of cells is N = L². To account for volume exclusion, we introduce a radial contact force f_ij that acts if the distance r_ij between two cells i and j is smaller than the range r₀ = 1.3 at which cells can sense their neighbours. For hexagonal packing, the equilibrium distance between neighbouring cells is 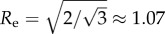. The contact force is repelling if the distance between two cells is smaller than equilibrium distance r_e, and attractive if it is larger:

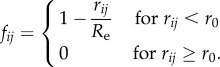2.2

The volume exclusion effects are not necessary for the segregation behaviour observed and we could equally well have chosen other functional forms that enforce an even spacing of cells (see the electronic supplementary material).

Cell motion is random with respect to orientation and, for each cell, the speed of diffusion depends on the fraction, γ_i, of neighbouring cells of the opposite type within a range r₀:

2.3

Here n₌ is the number of cells of the same type as i and n_≠ is the number of cells of opposite type within a distance r₀ from the cell. The average of γ_i over all cells is the interface index γ, which is a common measure for the degree of segregation in the system [7,14,15,26]. When γ ≈ 0 the two types of cells are completely segregated. The velocity of a cell i is given by

2.4

where u_i is a unit vector of random orientation, u_ij is a unit vector pointing from cell j to cell i, β is the intensity of the contact force and α is the diffusion speed of a cell that is surrounded only by cells of opposite type (γ_i = 1), and k determines how much faster cells diffuse when surrounded by cells of opposite type than of the same type.

Cells will continue with the same speed and direction for a number of time steps T_i, after which they will change speed and direction according to (2.4). The model is summarized in figure 1. The persistence time is given by

2.5

Figure 1.

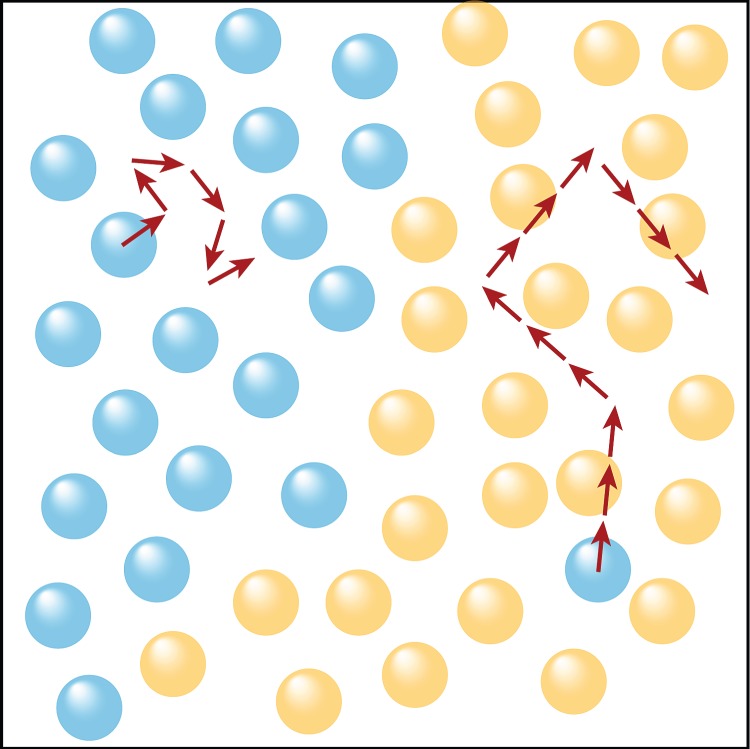
Illustration of the model. In the model, each cell performs a random walk. The step length does not vary, but the time between changes in direction is determined by the local environment. The persistence time is given by (2.5). In addition to diffusive motion with random orientation, cells interact with a radial contact force given by (2.2) which ensures that cells are evenly spaced. (Online version in colour.)

Thus, when a cell has neighbours only of its own type (γ_i = 0) we get T_i = 1, while a cell surrounded by cells of opposite type (γ_i = 1) has T_i = k. A longer persistence time, corresponding to less frequent changes in direction, results in a higher speed of diffusion.

Effectively, a cell can be described as performing a random walk where each step is of length v_iT_i and takes a duration T_i (figure 1). From this and (2.4) we can derive the diffusion coefficient of a cell as a function of γ_i, when contact forces are ignored:

2.6

In particular, we can find the ratio between diffusion constants of cells that are surrounded by opposite cell types or like cell types, respectively

2.7

This is our parameter of interest as it may be related directly to the cell-sorting experiments of Rieu et al. [9].

The model could have been formulated such that the local environment determined the velocity, rather than the persistence of motion, of each cell. In the electronic supplementary material, this version of the model is described in detail and shown to yield the same diffusion constants and segregation behaviour as the persistence of motion model (see the electronic supplementary material).

The computational work was done using Matlab and C++, and the code is available upon request.

3. Results

As shown in figure 2, the system evolves, via the formation of homotypic domains, to a steady state where the two phases are segregated. This demonstrates that, even with complete symmetry in the intrinsic motility properties of the two cell types, segregation can emerge just from cell motility being a dynamic property that changes in response to the local environment of individual cells.

Figure 2.

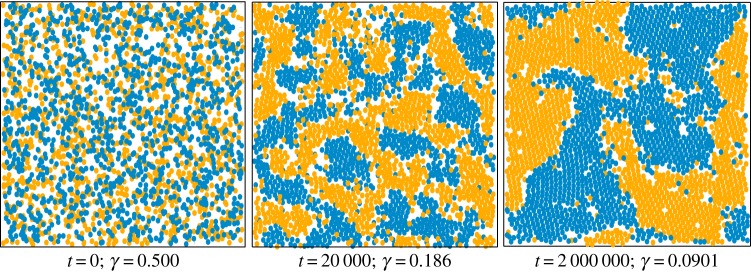
Time course of the segregation process for 2500 cells. As the cells gradually gather in larger clusters, the interface index γ decreases. The ratio of the diffusion constants is k = 64. (Online version in colour.)

The specific form of the contact force does not affect whether segregation occurs in the system. Indeed, β = 0 still results in segregation, but with the cells unevenly dispersed (see the electronic supplementary material). Consequently, we keep the parameters associated with the contact force fixed. Similarly, the parameter α relates to the balance between the contact force and the differential diffusion term and is also kept fixed.

The biologically relevant parameter in the system is the ratio, k, of the diffusion constant for a cell surrounded by cells of the opposite type (D(γ_i = 1)) and that of a cell surrounded by cells of the same type (D(γ_i = 0)).

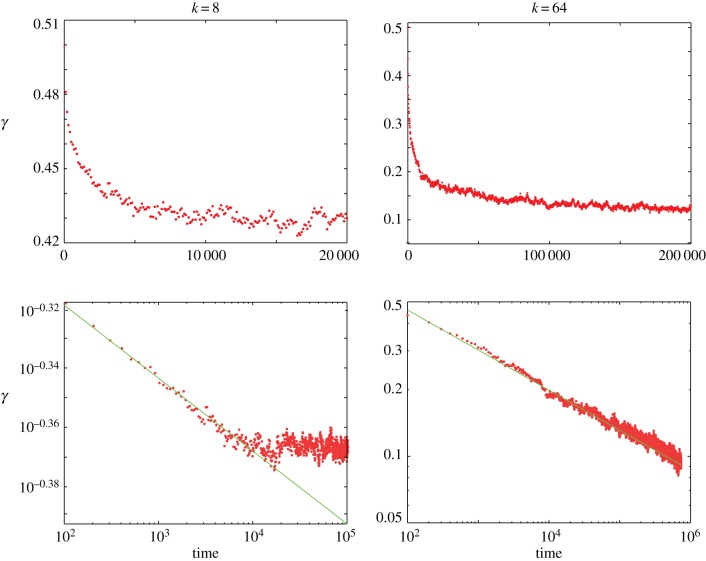
Figure 3 shows how the degree of segregation in the system, as measured by the interface index γ, develops over time. As may be seen from the log–log plot, for the range of time investigated, the interface index decreases according to a power law, before saturating. The scaling exponent quantifies the speed of segregation and, hence, increases with k. When the domain size (cluster correlation length) is much smaller than the system, finite-size effects are negligible. As shown in the electronic supplementary material, figure S6, the initial scaling behaviour does not depend on system size except for systems significantly smaller than N = 2500, used to generate figures 2–4. As sorting proceeds towards maximum segregation, finite-size effects start to play a role and the value of γ at which the system saturates depends on N.

Figure 3.

Development of the interface index γ as a function of time for k = 8 and 64. The results are the average of 10 simulations and are shown on linear and log–log scales. For high k, a more pronounced segregation is observed. The interface index is seen to decrease according to a power law until it saturates at an equilibrium value. The exponent increases with increasing k, and takes the values 0.025 for k = 8 and 0.17 for k = 64. (Online version in colour.)

Figure 4.

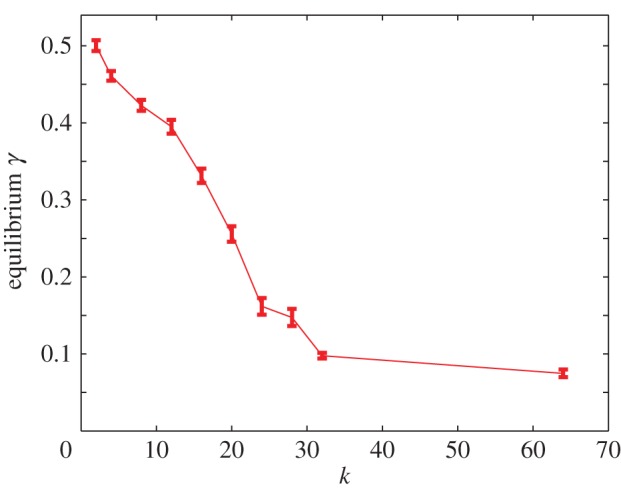
Value of the interface index γ, at which the system saturates, as a function of k. The parameter k is the ratio of the diffusion constant of cells surrounded by opposite or like cell types, respectively. For large k, the system reaches a more segregated configuration. The equilibrium interface indices are calculated as averages over 10⁵ time steps after the equilibrium is reached, and averaged over 10 simulations. (Online version in colour.)

The steady state is a dynamic equilibrium where the macroscopic configuration changes continually even though the value of γ remains stable. The steady-state value of γ is the same whether the system is initialized from a random or a segregated configuration (see the electronic supplementary material).

The figures shown are for k = 8 and 64. For k = 1, the diffusion constant of cells is the same regardless of the composition of the local environment and the degree of segregation, as quantified by the steady-state value of the interface index γ, is therefore 0.5. Segregation emerges gradually with increasing k and for low values of k almost no segregation occurs. Figure 4 shows the steady-state value of γ as a function of k. This may be compared to a vertical cross section of fig. 10 in [37], which shows the phase diagram of the Schelling model.

4. Discussion

Other models have investigated how motility affects segregation behaviour, but have tended to focus on intrinsic motility differences. Beatrici et al. [15] consider a system of two types of cells with speeds of constant modulus υ₀ and υ₁. In each time step, the direction of a cell is taken to be the average direction of its neighbours, plus a noise term. They demonstrate that differences in the intrinsic motility properties of cells, in concert with a tendency for cells to align their motion, gives rise to segregation behaviour. The model is similar to that of Belmonte et al. [14], which combines locally coherent motion with differential adhesion. The authors report that segregation in this system is characterized by power-law scaling of the interface index γ with time, and they argue that even moderate amounts of coherent motion considerably speeds up the segregation process. Using the Cellular Potts model, Kabla [28] studied a system of motile and non-motile cells in equal proportion. In this system, sorting leads to the formation of large clusters of non-motile cells surrounded by streams of motile cells. Spontaneous segregation has also been demonstrated for dense mixtures of self-propelled and passive particles using Brownian dynamics simulations [29].

In the model presented here, the two cell populations have the same physical properties and differences in motility arise solely from how cells interact with their local environment. The results demonstrate that segregation does not require asymmetry. However, comparing our results to experimental data suggests that, even though locally varying cell motility is sufficient for segregation to occur, other mechanisms are necessary to reproduce the behaviour observed in vitro.

Firstly, in vitro, cell sorting generally proceeds until the two cell types are completely segregated, with one phase enveloping the other. Computational implementations of the differential adhesion hypothesis successfully reproduce this envelopment and provide an explanation for the inside/outside order of the phases in terms of their relative surface tensions [5,41]. As the model presented here has no inbuilt asymmetry, it would not be expected to reproduce the enveloping behaviour.

Secondly, Rieu et al. [9] measured the diffusion of endodermal cells, in endodermal and ectodermal environments, and found the ratio k to be approximately 2. In our model, segregation emerges gradually with increasing k and at k = 2 the system shows almost no segregation. Other functional forms for how the diffusion coefficient depends on the interface index γ, such as a threshold instead of a linear dependence, do not significantly improve the segregation for low k values (results not shown). Endodermal and ectodermal cells studied do, however, differ in their intrinsic motility properties [42] and, based on the computational studies in [14,15], we expect that implementing this in the model would lower the value of k at which segregation occurs.

Along with asymmetry, an important aspect of cell dynamics, likely to promote segregation for lower values of k, is collective motion. As investigated computationally by Belmonte et al. [14], collective motion can emerge from differential adhesion; cells adhering more strongly to each other tend to align their motion and this speeds up segregation.

In our model, the time course of segregation follows a power law. This is qualitatively in agreement with the scaling reported from experiments. Méhes et al. [7,43] studied the kinetics of cell sorting in mixtures of keratocytes from various species. For mixtures of primary fish keratocytes and EPC keratocytes, the interface index γ and the growth of homotypic clusters were approximately linear on a log–log scale (over one decade of data). The scaling exponent quantifies the speed of segregation and therefore, in our model, increases with k. For k = 64, the exponent is similar to the values reported in [14,15], but lower than those reported by Méhes et al. [7].

We have not specified the molecular mechanism(s) that govern how the local environment determines the speed of diffusion of each cell. The motility of a cell can be a response to external cues, such as morphogens or chemotactic substances, or result from cell–cell interactions, including the adhesive properties of cells. As shown experimentally, in some systems cell motility anti-correlates with cell–cell adhesion, as strong adhesive interactions increase the effective viscosity of the local environment of the cell [9,11]. Hence, the model presented here suggests a kinetic mechanism for cell sorting where cell-specific adhesion gives rise to differences in the speed of diffusion which in turn lead to the segregation behaviour observed macroscopically.

5. Conclusion

We have presented a minimal model demonstrating that segregation does not require asymmetry in the physical properties of cells, but can arise solely from cell motility being a dynamic quantity that changes in response to the composition of the local environment of a cell. Comparison with experimental data suggests that other mechanisms are necessary to reproduce the envelopment behaviour observed in vitro. Further investigation is needed to understand the relative contributions of dynamic cell motility, differences in intrinsic motile properties, and collective motion to the kinetics of cell sorting.

The model suggests a simple kinetic mechanism for cell sorting whereby differential adhesion, or other local cell–cell interactions, give rise to differences in the effective speed of diffusion, which drive the segregation behaviour observed macroscopically.