Stress distributions and cell flows in a growing cell aggregate

Abstract

We discuss the short-time response of a multicellular spheroid to an external pressure jump. Our experiments show that 5 min after the pressure jump, the cell density increases in the centre of the spheroid but does not change appreciably close to the surface of the spheroid. This result can be explained if the cells are polarized which we show to be the case. Motivated by the experimental results, we develop a theory for polarized spheroids where the cell polarity is radial (except in a thin shell close to the spheroid surface). The theory takes into account the dependence of cell division and apoptosis rates on the local stress, the cell polarity and active stress generated by the cells and the dependence of active stress on the local pressure. We find a short-time increase of the cell density after a pressure jump that decays as a power law from the spheroid centre, which is in reasonable agreement with the experimental results. By comparing our theory to experiments, we can estimate the isotropic compression modulus of the tissue.

1. Introduction

The regulation of tissue growth is generally analysed in biology in terms of pathways and protein networks [1,2]. Recent work has, however, shown that physical properties such as the local pressure or the local stiffness of the tissue can also be important parameters in regulating tissue growth [3–5]. It has, for example, been shown in the Drosophila embryo that certain genes are mechano-sensitive in the sense that their expression is significantly modified by changing the pressure or more generally the mechanical stress in the tissue [6]. Several experiments also show that cell division and cell death (apoptosis) can be coupled to the local stress in the tissue [7–9]. Such stress dependence provides an important feedback mechanism for tissue growth, which is essential in the determination of the final tissue morphology.

Along these lines, in our recent work, we have introduced the concept of homeostatic pressure, which is the pressure of a tissue in a steady state where cell division on average compensates apoptosis and cell density is constant [10]. We have, furthermore, shown that there is also a reverse coupling of cell division and apoptosis on the mechanical properties of the tissue. If the rates of division and apoptosis of individual cells depend on the stress acting on cells, the stress in the tissue can relax. The tissue thus behaves as a visco-elastic material with elastic behaviour at short times and a viscosity at times long compared with the cell division time 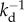[11]. Interestingly, this applies to both the isotropic and the anisotropic components of the stress. While the relaxation of shear stresses is characteristic of conventional visco-elastic fluids, the relaxation of isotropic stresses in tissues reflects an original and unconventional material property [10,11].

Multicellular spheroids are cell aggregates with a size of the order of a fraction of a millimetre that are grown from a few suspended cells. They are often made of cancerous cells and can be considered as models of tumours both to test drugs and for cell proliferation and invasion [12,13]. We have used multicellular spheroids as model tissues to study the coupling between cell division and mechanical properties. When a pressure is applied on the surface of the spheroid using osmotic effects, the growth velocity of the spheroid decreases and the finite steady-state radius reached after a few days becomes smaller [7]. The experiments can be interpreted using a simple physical description called core shell model. A spheroid of radius R is divided of into a core of radius R − e and an external shell with a thickness e of the order of a few cell sizes. In the core, the growth rate k_g = k_d − k_a is negative and the cells mostly die. Here, k_d and k_a are, respectively, the division and apoptosis rates. In the external shell, the cell division rate is increased by an amount δk_s and the growth rate k_g + δk_s is positive. The different behaviours in the core and the external shell can be revealed by imaging techniques using labels for apoptotic and dying cells [7,9]. It was shown that the core growth rate decreases and becomes even more negative when an external pressure is applied [7]. This implies that the homeostatic pressure of the tissue in the core is negative and that in the homeostatic state the tissue is thus under tension. Experiments suggest that the excess division rate δk_s in the external shell is roughly independent of pressure. The existence of two regions with cell division dominating in the outer shell and cell death dominating in the core implies an inward cell flow which has been measured directly and which agrees well with the prediction of the simple core shell model with two regions of constant division and apoptosis rates. Note that in this simplified model, the cell pressure is constant inside the core and inside the shell.

In this paper, we present a systematic continuum approach to investigate the mechanics and dynamics of a spherical aggregate of cells that divide and undergo apoptosis. We first describe in §2 experiments that reveal that the simple core shell model is insufficient to explain pressure profiles observed inside growing spheroids. We then introduce in §3 a continuum model that can account for such effects. In this model, we take into account the dependence of rates of cell division and apoptosis on local stress. The effective material properties of the tissue are captured by compressional and shear elasticities on short times and viscosities on long times. Important is the possibility of active stresses that can be anisotropic if cells are polarized. Furthermore, we allow for active anisotropic stresses to depend on local pressure. We calculate radial flow and pressure profiles in a steady state. In §4, we then discuss the short-time behaviour of the system after a pressure increase. We show that cell polarity and anisotropic active stresses are important to account for observed pressure profiles. We conclude with a discussion of the results in §5.

2. Mechanical response of a multicellular spheroid to a pressure jump

We have performed perturbation experiments in which a growing spheroid is subject to a pressure jump (see appendix C). The spheroid initially grows with no applied external pressure. After a given time, a finite pressure is applied by adding dextran which introduces an osmotic pressure difference between the spheroid and the external medium. The average cell density is then determined as a function of radius inside the spheroid. The results shown in figure 1a,b reveal that only 5 min after the pressure increase, the volume of the spheroid is decreased and that the cell density increases by approximately 50% at the centre of the spheroid while the density of cells closer to the outer shell does not change. Such a radial profile of cell density implies the existence of a pressure profile, with highest pressure in the core, even higher than the increased pressure at the surface. This observation is in disagreement with the simplified core shell model where the pressure in the core is constant and smaller than in the outer shell.

Figure 1.

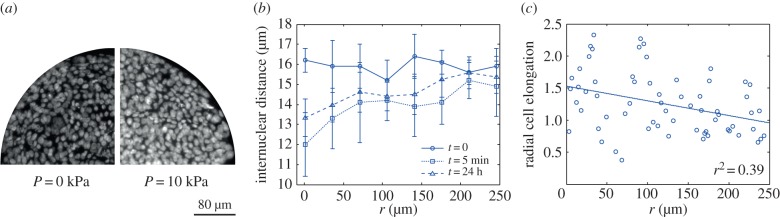
(a) Cross sections of spheroids of HT29 cells for zero external pressure (left) and pressure P_ext = 10 kPa (right) with DAPI-stained nuclei. (b) Average internuclear distance as a function of radial distance r from the centre for spheroids of HT29 cells after growth during 4 days (circles). The internuclear distance as a function of r is shown 5 min (squares) and 1 day (triangles) after a pressure jump ΔP = 10 kPa. Average of n = 3 spheroids for t = 0 and t = 5 min and n = 4 for t = 24 h; error bars indicate the standard deviation. (c) Radial cell elongation of HT29 cells shown as a function of distance r. Cell elongation is determined as the ratio of cell distances in radial and circumferential direction; see appendix C. The line is a linear fit that reveals increased cell elongation towards the spheroid centre. From the analysis of data for five different spheroids, we estimate an average slope of this line of (−1.6 ± 0.8) × 10⁻³ µm⁻¹. The value r² is the correlation coefficient obtained from the linear fit. (Online version in colour.)

The analysis of cell shape inside the spheroid furthermore reveals that cells are on average elongated radially inside the core (figure 1c). In the outer shell, the cell elongation is either weak or orthoradial without evidence of macroscopic tangential order. These observations suggest that the cells inside the spheroid are polarized radially. These observations are also confirmed when studying a different cell line called BC52. Again, we see a significant increase of cell density inside the spheroid after a pressure jump (figure 3a). Also, cells inside the spheroid tend to be radially elongated (figure 3b). The idea that cells are polarized radially is further supported by a study of centrosome position relative to cell nucleus (see appendix C). Centrosome position is an indicator of cell polarity. We find that centrosomes inside spheroids of BC52 cells point typically radially inward with respect to the cell nucleus (figure 3c).

Figure 3.

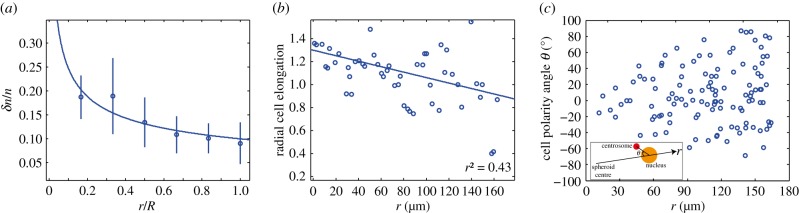
Experiments on BC52 cells. (a) Relative cell density increase δn/n = (n₀ − n(1 day))/n₀ of BC52 cells 1 day after an external pressure jump ΔP = 5 kPa as a function of radial distance r normalized by spheroid radius R (circles). Here n₀(r) denotes the cell density at radius r before the pressure jump. Fit of 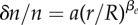to the experimental data, corresponding to the theory given by equation (4.13) (solid line). Fit parameters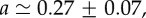 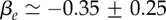and fit quality χ² = 0.8. (b) Radial cell elongation of BC52 cells shown as a function of distance r. Cell elongation is determined as the ratio of cell distances in radial and circumferential direction (see appendix C). The solid line is a linear fit, indicating an increased cell elongation towards the spheroid centre. (c) Angle of the polarity vector of BC52 cells of radial distance r from the centre. The cell polarity angle is based on the position of the centrosome relative to the nucleus of a given cell as shown in the inset. The angle θ = 0 corresponds to the centrosome positioned from the nucleus in the direction towards the spheroid centre. Note that all angles are confined between ±90° which shows strong polarity of the tissue along the radial axis. An isotropic centrosome orientation would correspond to a distribution between −180° and +180°. (Online version in colour.)

3. Dynamic equations for a growing anisotropic tissue

We now present a continuum description of the tissue, taking into account cell polarity and anisotropic active stresses. We study spherically symmetric stress and velocity profiles that emerge in spheroids where cells divide and undergo apoptosis. In a steady state, corresponding to the long-time behaviour, the flow and pressure profiles are calculated explicitly.

3.1. Hydrodynamic description

We consider a tissue in a continuum limit characterized by a cell number density n which obeys the cell number balance equation

3.1

Here, v_α is the cell velocity, k_d the cell division rate and k_a the apoptosis rate.

We distinguish the isotropic and the anisotropic parts of the stress and the deformation rate tensors. The cell stress σ_αβ and the symmetric part of the velocity gradient tensor v_αβ = (1/2)(∂_αv_β + ∂_βv_α) are decomposed into a traceless part and a part with trace

3.2

and

3.3

Force balance can then be expressed as

3.4

The tissue mechanical properties are characterized by constitutive material relations that describe visco-elastic properties with a tissue viscosity η, Maxwell relaxation time τ_t and a bulk cell compressibility K [11]. The bulk compressibility is defined by

3.5

where dn/dt = ∂_tn + v_α∂_αn is a convected time derivative. From equation (3.1), it follows that n⁻¹dn/dt = −v_γγ + k_d − k_a. The constitutive relations describing active tissue dynamics then read

3.6

and

3.7

where

3.8

is a co-rotational convected time derivative [14,15] and ω_αβ = (1/2)(∂_αv_β − ∂_βv_α) is the vorticity of the flow. Here ζ is the magnitude of an active anisotropic tissue stress 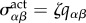. An active stress can exist as cells consume permanently chemical energy and contain contractile elements such as the cortex and stress fibres. It may include both a collective component associated with cell division discussed in [11] and a stress generated by individual cells resulting from the activity of the cytoskeleton of the cells (see appendix A). For simplicity, we consider in equation (3.6) the case where the active stress is only owing to individual cell stress.

The cell polarity defines a vector p_α which we normalize as p_γp_γ = 1 without any loss of generality. The corresponding tissue anisotropy is characterized by the traceless tensor q_αβ = p_αp_β − (1/3)δ_αβ. The dependence of the rates of cell division and apoptosis, k_d and k_a, on stress is described to linear order by a stress dependence of the net growth rate k_d − k_a as

3.9

Here, we have introduced the coefficient 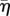which has units of viscosity and corresponds to an effective bulk viscosity. The homeostatic pressure of an isotropic tissue is denoted by P_h and we have taken into account the possible dependence of the growth rate on the anisotropic part of the stress. The dimensionless coefficient ν characterizes the coupling of growth to anisotropic stresses and their orientation with respect to tissue polarity. Combining equation (3.7) and equation (3.9) reveals that the isotropic stress shows a visco-elastic behaviour and obeys

3.10

with a longitudinal relaxation time .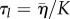

In general, the active stress may not be constant but could be regulated by the cell in response to external cues. Here, we consider the case where the active stress depends on local pressure P. To linear order we therefore write

3.11

In addition to bulk equations, we have to specify boundary conditions on the tissue surface. The force balance at the surface can be expressed as

3.12

where 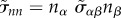is the normal stress and n_α denotes a surface normal vector. The tissue surface tension is denoted by γ and H is the local mean curvature of the surface.

We consider the outer shell of the spheroid as a thin layer of thickness e, in which the net growth rate is δk_s. The cell number balance at the interface then leads to an expression for the normal cell velocity below the surface v_n = v_αn_α:

3.13

where v_s is the normal surface velocity of the growing spheroid and v₀ = δk_sn_se/n is the extra velocity generated in the surface layer with n_s denoting the cell density in the surface layer.

3.2. Spherical geometry

We solve the dynamic equations for a cell spheroid of spherical geometry with radius R and a radial cell polarity field p = e_r in spherical coordinates. The force balance in spherical geometry reads

3.14

We first consider the long-time behaviour in which the tissue becomes a viscous fluid and elastic stresses have relaxed. In the viscous long time limit, the non-vanishing components of the traceless stress read in spherical coordinates

3.15

and

3.16

Here, v = v_r denotes the radial velocity and v_θ = v_ϕ = 0 by symmetry. The pressure can be expressed as

3.17

Using equation (3.15) together with the pressure dependence of the active stress (3.11), we find

3.18

where α = 1 − (2/3)νζ₁.

The force balance equation (3.14) then becomes an equation for the flow profile

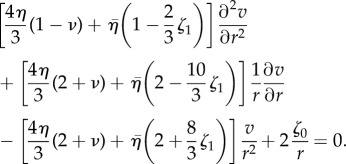3.19

This equation can be solved exactly using a power-law ansatz (see appendix B). The velocity profile in steady state reads

3.20

The boundary condition at the surface (3.13) then implies v(R) = dR/dt − v₀. Here, the exponent β can be written as

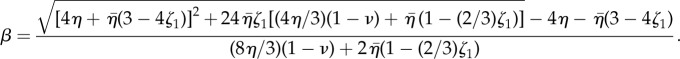3.21

Using equation (3.18) together with equation (3.20), the pressure profile can be expressed as

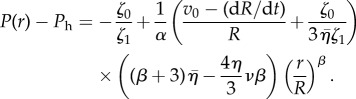3.22

The exponent β vanishes for ζ₁ = 0. This implies that in the case where the active stress becomes pressure independent, the velocity profile becomes linear and the pressure is constant. Active anisotropic stresses that depend on local pressure as described by ζ₁ lead to power-law profiles of velocity and pressure.

The pressure boundary condition 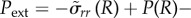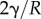implies

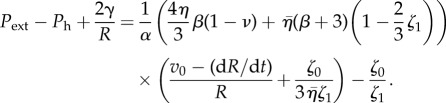In the long time limit, we can determine the density change δ_n = n − n_h from the pressure profile as 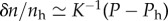, where n_h is the density at pressure P_h. The density profile is thus given by

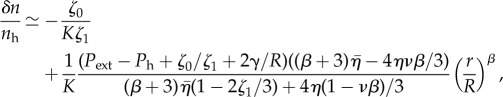3.24

which predicts a power law as a function of distance from the spheroid centre.

In a steady state, the growth rate dR/dt = 0 and equation (3.23) provides a relation between the external pressure and the steady-state radius R_∞ of the spheroid. Equation (3.23) also provides a dynamic equation for the spheroid radius in the limit where the radius changes slowly enough that the long time limit can be used inside the spheroid. The spheroid radius then changes as

3.25

where R₀ is the initial radius. The relaxation time of the spheroid radius can be written as

3.26

where

3.27

is an effective viscosity and

3.28

an effective active pressure. The steady-state radius is then given by

3.29

A stable steady-state radius is obtained if P_ext > P_h + P_a and v₀η_eff > 2γ. In this case τ > 0, and the system relaxes to a finite steady-state radius R_∞. Note that both the relaxation time and the steady-state radius diverge when the external pressure P_ext matches the sum of the homeostatic and the effective active pressure P_h + P_a. Thus, in the presence of active behaviour, the divergence of the steady-state radius does not provide a direct measure of the homeostatic pressure. For P_ext < P_h + P_a and v₀η_eff < 2γ, an unstable steady state exists. This unstable steady state corresponds to a generalization of the critical nucleus for tumour growth discussed in Basan et al. [10] in the presence of active stresses.

4. Visco-elastic response of a spherical tissue

The experiments discussed in §2 reveal that the cell density inside the spheroid changes significantly within only 5 min after a sudden increase in external pressure P_ext. To discuss the response of a spheroid to such a pressure increase, we study the mechanical short-time response of a steady state discussed in §3.

We thus calculate the time-dependent change of velocity, pressure and stress profiles as well as the response of the spheroid radius to a sudden change in pressure. We write

4.1

4.2

4.3

4.4

4.5

where v₀ and P₀ are the steady-state solutions discussed in §3 with radius R⁽⁰⁾ = R_∞ and for external pressure 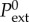. The Heaviside function θ(t) captures the external pressure jump ΔP at time t = 0.

We solve the dynamic equations by Laplace transformation 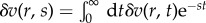and 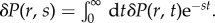The constitutive relations (3.6) and (3.10) then become

4.6

and

4.7

where we have neglected the convective nonlinearities in equation (3.6) and used the initial conditions δv_α(t = 0) = 0, δP(t = 0) = 0 and 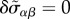. Using the force balance equation 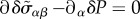, we have to solve the same equations in spherical geometry as in the steady state, however with ζ₀ = 0 and renormalized coefficients 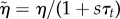, 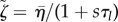and .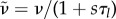

At the boundary, the interface velocity is v_s = dδR/dt and v_n = v⁽⁰⁾(R + δR(t)) + δv(R + δR). To linear order in δv and δR, we then have

4.8

Similarly, from 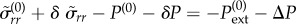we find

4.9

The solution to the force balance equation is then

4.10

where β_e is given by equation (3.21), however with parameters η, 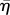and ν replaced by the renormalized coefficients 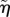, 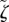and 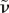, respectively, and therefore depending on s. In the large s limit (short times), we find

4.11

and

4.12

Here, 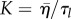and G = η/τ_t are the bulk and shear moduli, respectively. The tissue compression can be obtained from the isotropic deformation δu = δv/s and is given by δn/n = −(1/r²)d/dr(r²δu). Using the short-time solution equations (4.10)–(4.12), we then find for the cell compression profile

4.13

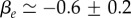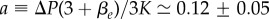Figure 2 shows a fit with the theory of the observed relative cell density increase of HT29 cells 5 min after a pressure jump. The experiment corresponds to a short-time response of the tissue (figure 1a). From the fit, we can estimate and . From this, we deduce 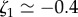and 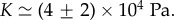In the estimate of ζ₁, we have used the fact that the compression modulus is larger than the shear modulus 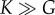. A fit to the cell density data of BC52 cells 1 day after a pressure jump is shown in figure 3a. Fit parameter values for this case are 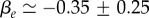and . 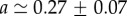From this fit, we infer 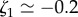and 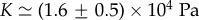. In both cases, the theory can account for the observed density profile. Because of the noise in the experimental data, the parameter values estimated by the fit show a sizeable uncertainty. Both fits, however, lead to consistent estimates.

Figure 2.

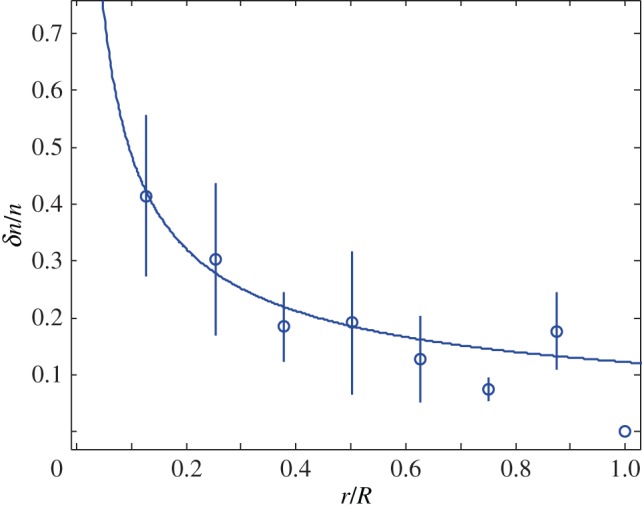
Relative cell density increase δn/n = (n₀ − n(5 min))/n₀ of HT29 cells 5 min after an external pressure jump as a function of radial distance r normalized by spheroid radius R (circles). Here n₀(r) denotes the cell density at radius r before the pressure jump. Data as shown in figure 1a. Fit of to the experimental data, corresponding to the theory given by equation (4.13) (solid line). Fit parameters 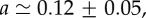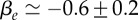and fit quality χ² = 0.73. (Online version in colour.)

5. Concluding remarks

Cell spheroids represent a very simple and fundamental model for the organization of multicellular systems. Because of the existence of a surface tension, their shape is spherical. However, the simplest picture of an isotropic material in the bulk of the spheroid is insufficient to account for the observed behaviours. In the case of isotropic material properties, the pressure in the core is constant (see equation (3.22)). This would correspond to a constant cell density inside the spheroid.

Experiments in which a pressure jump is applied to a growing spheroid reveal an interesting mechanical response. This response occurs at a time scale shorter than 5 min which is short compared with the cell division time. Deep inside the spheroid, the cell density increases significantly with less increase further outside. This clearly leaves out the possibility of biochemical signalling as a cause, as this would be maximum outside and minimum in the centre. For this deformation to develop in the centre of the spheroid, it is necessary that intersticial fluid leaves the cells. This suggests that a two-component picture of the tissue dynamics should be used in the description of the spheroid [16]. However, the mere fact that the time required for evacuating the intersticial fluid is smaller than 5 min, implies that the permeation length introduced in [16] is large compared with the spheroid radius. The permeation length characterizes the length scale beyond which a two-component description becomes necessary because stresses associated with the relative movement of cells and extracellular fluid become relevant. We therefore can ignore permeation and use here a one-component description of the tissue.

The fact that cells increase their density inside the spheroid implies that there exists, already after 5 min subsequent to an external pressure jump, a pressure profile inside the spheroid with highest pressure at the centre. This finding cannot be explained by isotropic material properties and we have to invoke ordered cell polarity in the tissue which introduces tissue anisotropies. We indeed see in experiments that the cells organize their polarity in the core along the radial direction, while it may be tangential to the surface in the outer layers. This tissue anisotropy introduces anisotropic active stresses. When these anisotropic stresses depend on local pressure, stress profiles result that can account for the observed density profiles at short times. The observed negative sign of the exponent β_e implies according to equation (4.12) that ζ₁ is negative: cells tend to overreact to an external pressure. They add up contractile stress in the radial direction in response to external pressure. Passive anisotropic stresses could also give a reasonable account of experimental data [17]. Probably both effects contribute to the experimental behaviour. We also cannot rule out a heterogeneous response of cells to stress due to, for example, position-dependent cell fates. Furthermore, our analysis allows us to provide a measure of the short-term tissue isotropic compressional modulus K. Shear modulus is measured conventionally but compressional modulus is hard to access. This is to our knowledge the first such measurement.

In the long time limit, the spheroid can reach a steady state in which cells die inside and divide near the surface. Therefore, there exists an inward flow profile in steady state. In this limit, elastic stresses can relax and the material can be regarded as a viscous fluid. Even in that limit we find a non-trivial power-law dependence of cell density as a function of distance from the centre. On short times, elastic properties become important and the power law characterizing cell density changes. Here, we have studied the steady state as well as the short-time response of a steady state to a pressure jump. Both limits are relevant to the experiments on spheroids and together provide a coherent physical picture of dynamic cell spheroids.

Appendix A

The constitutive equation for the anisotropic tissue stress can be obtained as described in Ranft et al. [11]. Here we generalize this derivation to the case where the active stress contains contributions from individual cell stress and from stress due to cell division and apoptosis events. The tissue shear stress can be expressed as a sum of an elastic and an active component

A1

where G is the cell shear modulus and 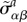denotes the total active stress. The total active stress can be expressed as a sum of two contributions

A2

Here, ζq_αβ is the anisotropic stress generated by the cytoskeleton of individual cells that are polarized as described by the anisotropy q_αβ. The second term describes active stress corresponding to force dipoles that are introduced by cell division and apoptosis events at a rate .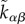

The active stress rate due to tissue growth 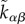is biased by local stress and also by the local cell polarity. To linear order, we can write

A3

where we introduced the stress relaxation time τ_t and a characteristic time τ_a describing the relative role of cell stress and of active stress owing to growth. The tissue stress then obeys

A4

with η = Gτ_t. In the simple case τ_a = τ_t, we find equation (3.6). Note that our calculations do not change when τ_a differs from τ_t. In the long time limit, we have to replace ζ by (τ_t/τ_a)ζ. The short time limit is unchanged.

Appendix B

Equation (3.19) for the radial velocity profile is of the form

B1

where primes denote derivatives with respect to r and

B2

B3

B4

This equation can be solved by first obtaining the general solution v_h(r) to the homogeneous problem, equation (B 1) with c = 0. This solution is then combined with the special inhomogeneous solution v = [c/(b − a)]r to equation (B 1). For c = 0, solutions to equation (B 1) are of the form v₀ = Ar^1+β, where the exponent obeys β² + (1 + a)β + a − b = 0 which is solved by

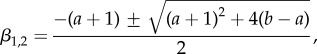B5

with β₁ > β₂. The general solution to the velocity profile is thus given by

B6

The larger exponent β₁ governs the velocity profile for distances larger than a cut-off length of the order of the cell size. This can be shown for β₂ < 0 by a detailed calculation, taking into account the cell number conservation law in the centre. Using

B7

and taking into account the boundary condition (3.13), we find the solution given in equation (3.20) with β = β₁. We can then express the exponent β defined in equation (B 5) as equation (3.21). Note that β = 0 for ζ₁ = 0.

Appendix C. Experimental methods

Experiments were performed with different cell lines (HT29, BC52) in a culture medium [9]. As spheroids are dense tissues and therefore hard to image, we performed cryosections and imaged the equatorial plane of the spheroid using confocal microscopy. This ensures a constant thickness of the optical cut which is an improvement as compared with earlier work [8]. The equatorial plane was identified by measuring the diameter of the spheroid before cutting and selecting the cuts with diameter closest to the spheroid diameter. We used DAPI staining of nuclei to determine typical distances between nuclei and used spatial intensity–intensity autocorrelation functions to determine cell density and cell elongation.

The autocorrelation method was implemented as follows: in the DAPI-stained image of a spheroid cross section, we randomly chose the centres of circular regions of interest containing of the order of 10 cells (figure 4a). The number N of regions was chosen such that typically regions do not overlap. For the analysis of a given region of interest, the image was cropped outside the region. The spatial power spectral density of this cropped image was obtained by fast Fourier transformation using Matlab. The spatial correlation function was obtained by inverse Fourier transform of this spatial power spectral density. We obtained the spatial autocorrelation function g(d), where d is the radial distance within a region of interest by averaging over all angles.

Figure 4.

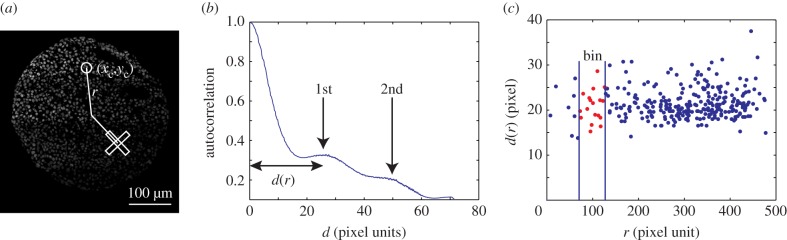
Internuclear distances and cell elongation determined by autocorrelation methods. (a) Examples of regions of interest for density–density autocorrelation functions used for internuclear distance (circle) and for cell elongation (perpendicular rectangles). The centre of the circular region is at position (x_c, y_c). (b) Angle-averaged density–density autocorrelation function g(d) of a circular region of interest as a function of distance d. Two peaks at finite distance are indicated. (c) Average internuclear distance d, corresponding to the first peak in the function g(d) in different regions of interest shown as a function of radial distance r in the spheroid (dots). Data points are grouped together in bins, such as for example the points around r = 100. For details see appendix C. (Online version in colour.)

In addition to the peak at d = 0, the autocorrelation function g(d) has a first peak at finite d, the typical distance between nuclei (figure 4b). Each region of interest with a centre at radial distance r in the spheroid provides one data point on the internuclear distance as a function of r (figure 4c). We distribute these points in bins with a width corresponding to the diameter of the regions of interest to determine average internuclear distance. The cell density is estimated as the inverse cube of the average internuclear distance. Error bars in figure 1b show the variance of data points obtained from five spheroids. The estimated cell size before the pressure increase is consistent with the value obtained using the volume of a cell population measured with a Coulter counter.

We used the same method to study the anisotropy of the cell shape before the application of the pressure jump. Instead of using circular regions of interest we used two perpendicular rectangular regions of interest, one in the radial direction, one in the orthoradial direction. From the autocorrelation functions along the long axis of the rectangular regions (figure 4a), we determined the characteristic distance between nuclei in radial and tangential directions. The radial cell elongation is defined as the internuclear distance in the radial direction divided by the internuclear distance in the circumferential direction (figures 1c and 3b).

The cell polarity can be determined from the position of the centrosome relative to the nucleus. We used immunofluorescence staining of percentrin to determine the centrosome position relative to the position of DAPI-stained nuclei. We characterize the polarity pointing from the nucleus to the centrosome by a unit vector p. The angle of the vector p with respect to the inward radial direction is shown as a function of radial distance in figure 3c. This result provides additional support for cell polarity being radially oriented in the core of the spheroid and not polarized or even tangentially polarized at the surface.