The straight and narrow path: the evolution of straight-line dispersal at a cane toad invasion front

Abstract

At the edge of a biological invasion, evolutionary processes (spatial sorting, natural selection) often drive increases in dispersal. Although numerous traits influence an individual's displacement (e.g. speed, stamina), one of the most important is path straightness. A straight (i.e. highly correlated) path strongly enhances overall dispersal rate relative to time and energetic cost. Thus, we predict that, if path straightness has a genetic basis, organisms in the invasion vanguard will exhibit straighter paths than those following behind. Our studies on invasive cane toads (Rhinella marina) in tropical Australia clearly support this prediction. Radio-tracking of field-collected toads at a single site showed that path straightness steadily decreased over the first 10 years post-invasion. Consistent with an evolved (genetic) basis to that behavioural shift, path straightness of toads reared under common garden conditions varied according to the location of their parents' origin. Offspring produced by toads from the invasion vanguard followed straighter paths than did those produced by parents from long-established populations. At the individual level, offspring exhibited similar path straightness to their parents. The dramatic acceleration of the cane toad invasion through tropical Australia has been driven, in part, by the evolution of a behavioural tendency towards dispersing in a straight line.

1. Introduction

The distance that an animal moves from its original location over some finite time period depends upon the proportion of time that it spends moving, the rate that it travels when it is moving, and the straightness of the path that it follows over time [1,2]. Thus, any situation in which evolutionary forces favour increased rates of dispersal can potentially operate via changes to any, or all, of these three parameters. Importantly, however, two of these three parameters entail an increase in energetic expenditure that scales with total distance moved. Increasing either the proportion of time spent moving, or the rate of movement, is energetically expensive. Increasing the straightness of the path followed, on the other hand, may incur little to no additional energetic cost [2,3]. Thus, perhaps the most efficient way for a dispersing individual to increase its net rate of movement is to increase the straightness of its path (i.e. to maintain a similar compass heading across successive moves).

At the expanding range edge of a species invasion, strong evolutionary forces act to increase rates of dispersal. In this situation, dispersal evolves upwards through natural selection (individuals on the invasion front may have higher absolute fitness) interacting with spatial sorting (only the fastest dispersers can be on the invasion front [4–6]). Under the latter (non-adaptive) process, genes that encode traits facilitating more rapid dispersal accumulate at the expanding range edge, simply because the bearers of those traits have moved further than conspecifics lacking such genes [5,7]. Importantly, however, both theory and empirical evidence suggest that, following a period of range advance, dispersal rates begin to push up against trade-offs [6,8–12]. Given the energetic neutrality of changes to path straightness, the evolution of straighter paths might be a particularly effective way to achieve high dispersal while avoiding the worst effects of fitness trade-offs [11].

For most biological invasions, the only evidence available to test predictions of increased dispersal involves an overall acceleration in rate of range expansion through time [13] or morphological traits at the invasion front that correlate with rapid dispersal, such as wings, or enlarged flight muscles or legs [14–17]. For a few systems, however, we also have more detailed information on individual behaviour. Some of the most intensive studies involve the spread of cane toads (Rhinella marina) through tropical Australia. The toad invasion has accelerated through time [16,18] owing, in part, to increased dispersal rates of individual toads at the invasion front [4]. These invasion-vanguard individuals tend to spend more time moving, and to follow straighter paths than do conspecifics in older, established populations [6,19,20]. When raised under standard conditions, the offspring of invasion-front toads tend to inherit the overall higher dispersal rates of their parents [21].

In this study, we explore the path straightness of individual radio-tracked cane toads, as a function of invasion phase. To test the prediction of straighter paths in invasion-vanguard animals, we use data from annual wet-season tracking of toads at a single site, for 10 years following the initial arrival of the invasive anurans. To test the prediction of a genetic basis to the divergences observed as a function of invasion phase, we use data from radio-tracking of the offspring of toads collected from a range of locations spanning the toads' invasion history in Australia. Those offspring were bred and raised in common-garden conditions at our field station so as to minimize environmental impacts on dispersal behaviour.

At the level of the individual, we examined path straightness (does each nightly movement tend to be at the same heading as the previous one?). Specifically, we asked

• (1) do toads at the forefront of the invasion move in straighter lines than toads that are monitored in later years at the same site?

• (2) do the offspring of parents from closer to the invasion front move in straighter lines than the offspring of parents from long-established populations? and

• (3) do offspring resemble their parents in the straightness of their movements?

2. Material and methods

Using data collected over several years, we were able to examine changes in path straightness over 10 years at the same location following toad arrival; changes in straightness between toads that had been collected from populations spanning the invasion history and, finally, whether straightness scores of parents predict those of their offspring.

(a). Study species

Native to southern and central America, cane toads were translocated from the Caribbean to Hawaii, and thence to Australia, in a misguided attempt to control insect pests in commercial sugarcane plantations [22]. Progeny from 101 toads were released along the northeastern coast of Queensland in 1935, and have since spread widely [18]. The annual rate of range expansion has accelerated from about 10 to 55 km [16], reflecting the evolution of higher dispersal and reproductive rates in the vanguard population during the invasion process [4].

(b). Study site and field methods

Data for this study were gathered on the Adelaide River floodplain, 60 km east of the city of Darwin, in the wet–dry tropics of northern Australia (12.621794′ S, 131.305016′ E). Temperatures are high all year, but rainfall is limited to a six-month ‘wet season’ (November to April). Cane toads arrived at this site in 2005 [23]. Adult toads are nocturnal; they remain active year-round, but disperse only when the ground is damp (i.e. during the wet season [24]). Every wet season since toads first arrived, we have radio-tracked adult animals on Beatrice Hill Farm, a pastoral property 5 km from our field station. One day after capture, toads were fitted with a bead-chain waistbelt holding a miniature radiotransmitter (less than 5% of toad body mass) and released back at their point of capture. They were subsequently radio-tracked each day, and the coordinates of their location read with a handheld GPS (using the Universal Transverse Mercator reference system). Most toads were tracked for a predefined period of 5 days, but others were tracked for longer, variable periods. For the present purposes, we used only the first 5 days of location data for any individuals tracked for periods longer than 5 days, and we excluded any individuals tracked for periods of less than 5 days.

In 2006, adult toads were collected from four sites, each approximately 500 km apart, along a 1600 km east–west transect spanning the invasion history of the species in Australia (see [6] for details). The animals were maintained in captivity at our field station, where we bred them (using within and among population pairings) and then raised their progeny under common conditions to reduce environmental effects on phenotypic traits (see [21] for details). In 2008, when the progeny were close to adult size, we released and radio-tracked them on Beatrice Hill Farm (as above) during the wet season. To quantify spatial origin of each toad's genotype in relation to invasion history, we calculated its ‘mid-parent distance’. For a given offspring, this value is the average distance of its parents' collection sites from the eastern (origin) end of the transect (Cairns).

(c). Data analysis

We assessed path straightness from movement data over 5 days of wet-season telemetry for each toad. For toads tracked for periods longer than 5 days, we used data from only the first 5 days. We then deleted data for any individual toad that did not move at least three times during that 5 day period (because at least three locations are needed to estimate path straightness). This left usable data from 254 field-collected adult toads and 129 common-garden-raised offspring (i.e. toads that had each moved on three, four or five nights over a 5 day period). The 129 offspring consisted of one to nine siblings from 34 families. Because most families contained more than one offspring, we used family as a random effect when analysing offspring traits.

We calculated two measures of path straightness for each radio-tracked toad; circular variance and fractal dimension. Circular variance is analogous to the conventional linear measure of variance associated with a mean value [25]. Like its linear counterpart, circular variance is a measure of the spread of a sample of observations taken on a circular scale (e.g. angles, compass bearings, times of day). Because such data are measured on a circular scale rather than a linear one, their mean and variance must be calculated using circular statistical methods [25]. For a series of animal movements, circular variance is calculated as

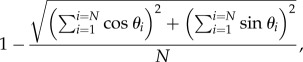where N is the number of unit-length vectors in the sample, and θ is the angular bearing of each vector. Circular variance ranges from 0 (no variance, all bearings are identical) to 1 (bearings uniformly distributed among all compass directions) (figure 1). Because circular variance represents angular dispersion on a linear scale, it can be analysed with conventional statistics [26]. And, because it is calculated using unit-length vectors (i.e. each vector originates at the centre of a circle and ends along its circumference at the appropriate compass direction), each leg of movement is given equal weight, irrespective of the actual distance travelled during that leg.

Figure 1.

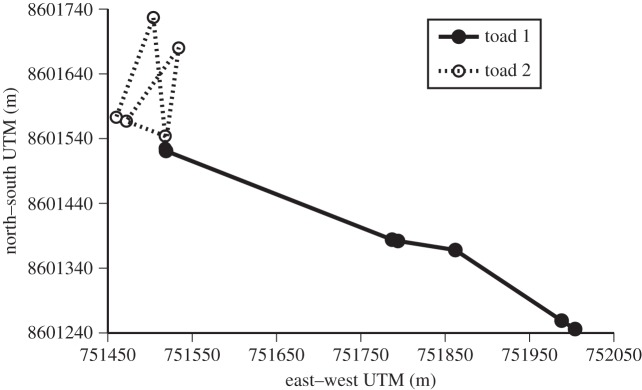
Comparison of movement paths of two toads. Both toads had been captured and released at the same point and both moved approximately 600 m in five moves over 5 days. Toad 1, represented by the solid line and closed symbols (tracked in March 2007), had a straight path, with circular variance = 0.021 and fractal D = 1.002. Toad 2, represented by the dashed line and open symbols, (tracked in February 2014), had a crooked path, with circular variance = 0.93 and fractal D = 1.182. The axes show positions along the north–south and east–west dimensions.

Fractal dimension (hereafter fractal D) is another measure of straightness that has been applied to study animal paths [27–30]. Fractal D-values are bounded between 1 and 2 and can be viewed as a measure of a linear path's ability to fill a plane. A fractal D-value of 1 describes a perfectly straight line, whereas a value of 2 describes a path so crooked that it fills an entire plane [28] (figure 1). Like circular variance, fractal D calculations ignore the length of each step [29]. We calculated D using the fractal mean estimator (described in [31]) implemented in the software package Fractal 5.26 (V. O. Nams, Faculty of Agriculture, Dalhousie University, Nova Scotia). For each dataset, we fixed the minimum and maximum scale used in calculating D for each individual. Values of D calculated across the same spatial scale can be used as a relative measure of path straightness, enabling comparison among individuals [28,30]. For each dataset, we fixed the upper scale limit as the mean final displacement value (500 m for field-collected toads and 200 m for common-garden toads) and set the lower scale limit at the minimum distance measured between locations (1 m) [30].

Data from radio-telemetry of the parents of the common-garden offspring are presented in [6]. We used data from that study to calculate circular variance and fractal D to compare path straightness of parents to those of their offspring. To calculate fractal D for the parental toads, we used the same minimum and maximum scale values used for calculating fractal D of the offspring (1 and 200 m, respectively). We standardized path straightness measures of parents and offspring to a mean of 0 and a standard deviation of 1 prior to regressing offspring values on parental values [32].

Values for circular variance were approximately normally distributed. Fractal D-values approximated a lognormal distribution however, and were transformed as ln(D − 1) [30]. Both measures of path straightness were used as dependent variables in linear and multiple regressions using JMP 9.0 (SAS Institute, Cary, NC). We assessed regression assumptions for all tests, using plots of residual and predicted values.

3. Results

(a). Field-collected adult toads

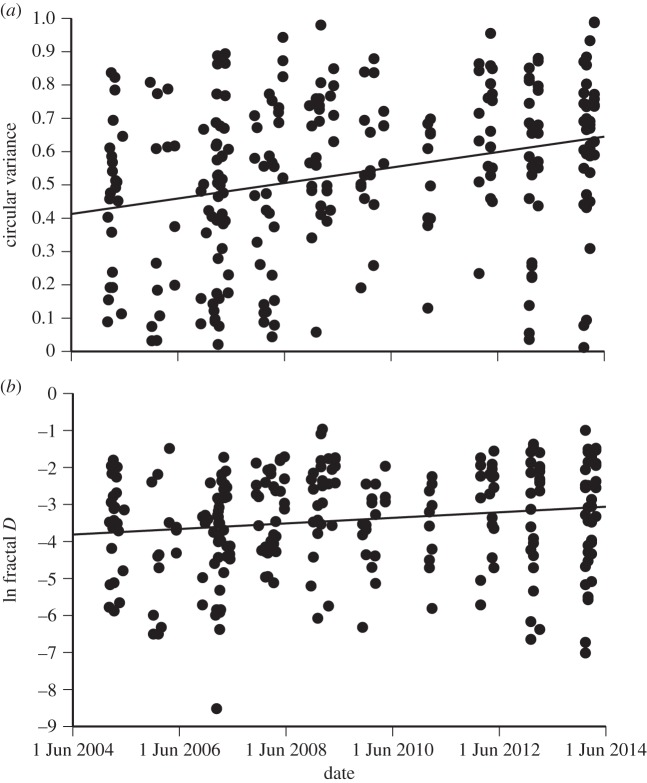
The two measures of path straightness, circular variance and fractal D, were highly correlated among the 254 wild-caught toads radio-tracked for 5 day intervals (Spearman r = 0.57, p < 0.0001). Both measures increased significantly over time since invasion (circular variance: F_1,252 = 22.1, p < 0.0001; fractal D: F_1,252 = 8.47, p = 0.0039; figure 2), indicating that toads in the invasion vanguard moved in straighter lines than did toads tracked in the same location in subsequent years. We repeated these analyses after adding three other plausible independent variables (sex, body length and mass) to the simple linear regression model, but ‘time since invasion’ remained the only significant explanatory variable for path straightness measures. Quadratic and cubic terms for time since invasion were non-significant when added to the model.

Figure 2.

Temporal changes in path straightness of 254 cane toads tracked for 5 day periods at Beatrice Hill Farm over the first 10 years post-invasion. The paths followed by individual toads became less straight through time, as indicated by (a) increasing circular variance of headings of individual toads, and (b) increasing fractal dimension (fractal D; ln-transformed) of their paths.

(b). Common-garden progeny sourced from different populations

Among the 129 common-garden-raised toads tracked over 5 day periods, values of circular variance and fractal D were highly correlated with each other (Spearman r = 0.49, p < 0.0001). We initially assessed factors affecting each of our two measures of path straightness using multiple regression models that contained sex, body size and mid-parent distance as independent variables. Because the 129 offspring originated from 34 litters, we included family identification as a random effect in the multiple regressions. Body size was non-significant in both models and was removed to form reduced models. The circular variance of a toad's path was significantly related to the location from which its parents were collected (F_1,25 = 5.16, p = 0.032). The offspring of parents that had been collected close to the point of toad introduction on the Queensland coast (low mid-parent distance) moved in more tortuous paths than did toads with parents from closer to the invasion front. Females had significantly lower circular variance values (defining straighter paths) than did males (F_1,126 = 7.14, p = 0.009). For fractal D estimation of path straightness, the effect of mid-parent distance was on the border of significance (F_1,28 = 3.97, p = 0.056; figure 3), but females again moved in significantly straighter paths (F_1,126 = 13.9, p = 0.0003). To test for curvilinear effects, we also added quadratic and cubic terms for mid-parent distance in the models. For both measures of path straightness, simple linear models provided the best fit.

Figure 3.

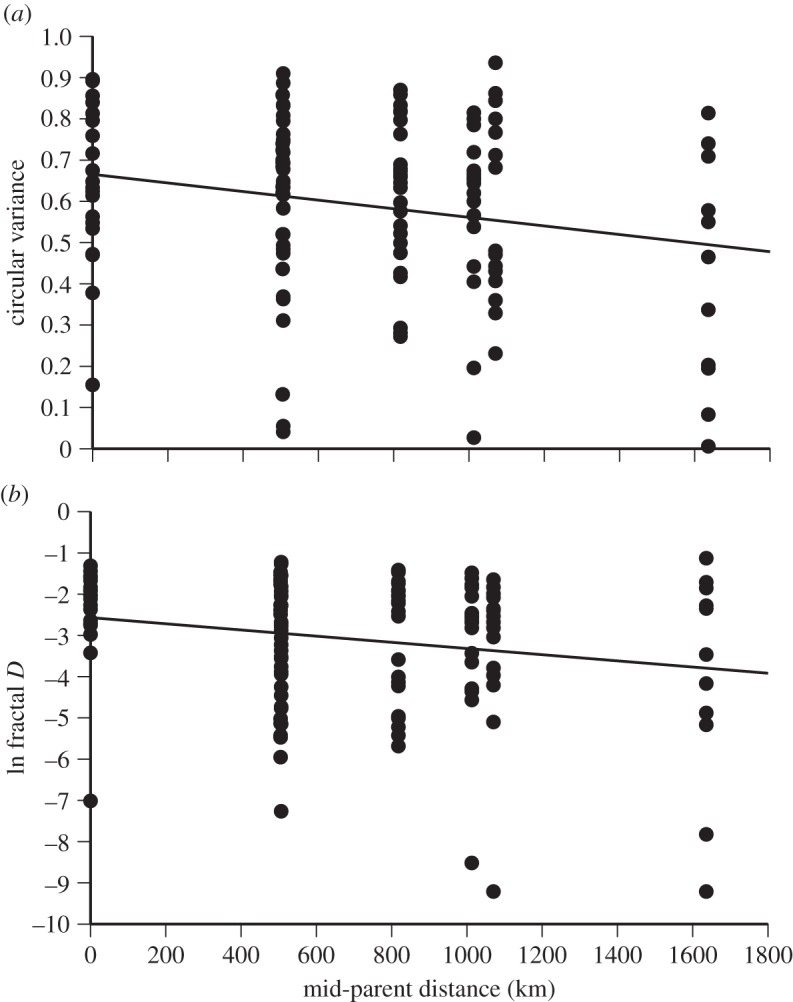
Circular variance of movement headings of captive–raised cane toads, as a function of the localities from which their parents had been collected. Data are shown for 129 toads tracked for 5 day periods at Beatrice Hill Farm. (a) Circular variance decreased significantly with mid-parent distance from Cairns, indicating that offspring produced by parents that had been collected close to the invasion front (i.e. with high mid-parent distances) moved in straighter lines. (b) Fractal dimension (fractal D) also increased significantly with mid-parent distance, indicating less tortuous paths among toads whose parents originated closer to the invasion front.

(c). Similarity in path straightness between parents and their offspring

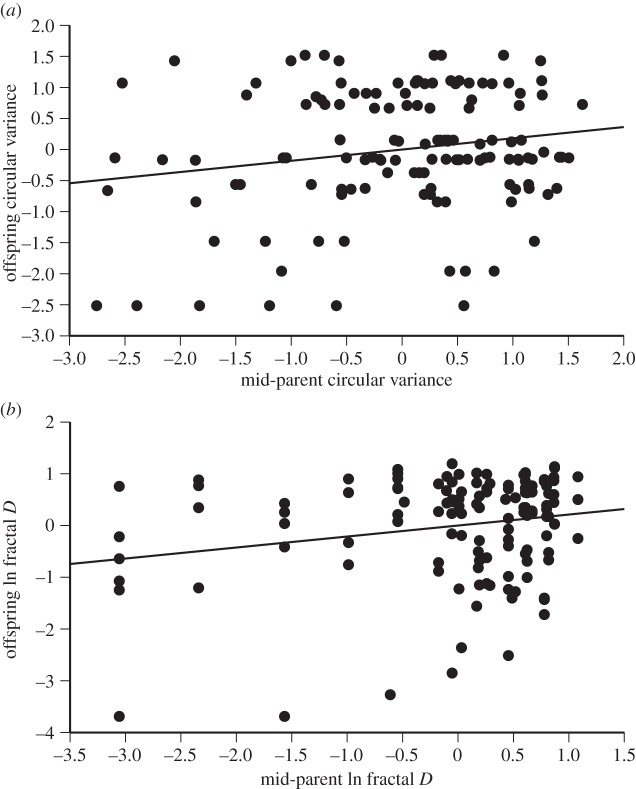
Because the parents of the common-garden offspring were radio-tracked in a previous study, at the same site [6], we can compare the path straightness of parents and offspring to estimate the degree to which the trait is heritable. Circular variances of the paths of common-garden-raised offspring were positively correlated with the average circular variance of the paths followed by their parents (F_1,127 = 4.31, p = 0.04, slope = 0.181; figure 4a). Because this parent–offspring regression uses average values for both parents, the slope of the line provides an estimate of heritability (h² = 0.181). Similarly, the fractal D-values of offspring resembled those of their parents (F_1,127 = 6.0, p = 0.016, slope = 0.212; figure 4b). However, these heritability estimates must be treated with caution because they do not account for maternal effects, which can run through several generations. In addition, epigenetic effects could produce similarities between generations, without changing gene frequencies over invasion history.

Figure 4.

Intergenerational similarity of path straightness in invasive cane toads. The graph shows the straightness of the paths followed by radio-tracked cane toads regressed on the same parameter as measured on their parents at the same study site 2 years earlier. The parental cohort were field-collected, and the graph shows the mean of maternal plus paternal path-straightness values. The offspring were reared in a standardized environment (‘common garden’) to minimize environmental influences on behaviour. Panel (a) shows circular variance, and panel (b) shows fractal dimension (fractal D). All values have been standardized to mean = 0 and s.d. = 1.

4. Discussion

Our field data, based on radio-tracking 254 field-collected adult toads and 129 common-garden-raised offspring at a single site, supported the a priori predictions that stimulated our study. First, animals at the invasion front moved in straighter paths than did conspecifics that we radio-tracked at the same site in later years. Second, the offspring of the adult toads that originated from various locations, but were raised in a common environment, exhibited straighter paths if their parents originated from closer to the invasion front. This reflects the same pattern uncovered in their parents in an earlier study [6]. Finally, the path straightness of these offspring resembled that of their parents to a significant degree, suggesting that the trait is heritable. In summary, toads from the invasion-front travelled along straighter paths than did toads from long-colonized areas, and the progeny of those toads showed the same pattern. Thus, the invasion process has evoked a significant evolutionary response in a parameter critical to dispersal rate: the degree to which an individual consistently moves in some specific direction.

Simulation models confirm that consistency in the direction of movement (i.e. path straightness) exerts a powerful influence on total distance moved [2,11,19]. Although other factors (such as speed, stamina and frequency of movement) also play a role, even a minor decrease in path straightness can substantially reduce overall displacement. Hence, this parameter may be under intense selection in any animal population in which more rapid dispersal confers a fitness benefit [2]; and also (regardless of differential fitness), be subjected to intense spatial sorting in an invasion front [5]. The cane toad invasion imposes both of these pressures. Previous research on cane toads has documented a rapid acceleration of the rate of range expansion [16,18], an accumulation of dispersal-enhancing morphological and behavioural traits at the invasion front [6,16,19,20], and significant heritability of dispersal rate [21]. Modelling incorporating all of these observations confirms that rapid evolution of dispersal is at least partly responsible for the accelerated rate of range shift [4]. This study shows that a major mode of the behavioural shift to increased dispersiveness has been through the evolution of a tendency towards forging straighter paths.

Previous studies on this system have hinted at the same result, but with less robust evidence. Radio-tracking of field-collected adult toads from several localities (the parents of the common-garden animals for which data are presented in this study) showed a shift in path straightness consistent with our data on their offspring: that is, invasion-front adults tended to follow straighter paths than did conspecifics from long-colonized areas [6]. In a more recent analysis on field-collected adults from the Adelaide River floodplain (using data from 76 of the 254 toads used for this study), Lindstrom et al. [19] calculated a ‘directionality’ parameter that differed between pioneer and post-invasion toads. With the benefit of additional and expanded datasets, we can now conclude not only that animals at the invasion vanguard travel along straighter paths, but also that path straightness has a genetic underpinning.

The tortuosity of an animal's path can provide insights into its use of space. For example, highly tortuous paths that thoroughly cover small areas can evolve to maximize search efficiency for some patchy resource [3,33]. Rapid straight-line movements, by contrast, may evolve when high-risk or low-quality areas need to be transited as quickly as possible, or when there is little cost to movement, and habitat is not clumped [1–3]. Theory predicts that rapid straight-line movements also evolve, even at the cost of individual survival, under scenarios of range expansion as seen here [11]. Thus, as predicted from theory, invasion-front toads appear to treat the landscape into which they are moving as one that needs to be traversed quickly and efficiently, whereas later-arriving toads may see the landscape and its resources as something to be explored and exploited at leisure.

Dispersal, like migration, may be a syndrome that consists of a suite of polygenic and intercorrelated morphological, physiological, behavioural and life-history traits [34,35]. Thus, life-history constraints (i.e. trade-offs) probably play an important role in regulating the evolutionary trajectory of dispersal traits [36]. Because path straightness (the degree of autocorrelation in movement direction) has a powerful influence on overall rates of movement [20,21], but probably carries fewer life-history (allocation) costs, a behavioural shift towards highly correlated walks may evolve more rapidly than a change in morphology or physiology. Of course, there may be energetic costs associated with straight-line movement. Enhancing path straightness probably involves neurological changes that improve some aspect of cognition or the acuity/efficiency of orientation or accuracy of navigation [29,37]. In elderly humans, for example, path tortuosity increases as dementia progresses [38]. Nonetheless, it seems likely that these information-processing costs will be minor relative to the energetic costs associated with moving greater distances, and moving more often.

Thus, where it is heritable, we might expect to see evolutionary shifts in path straightness whenever evolutionary pressures favour such a change. Quantifying fitness consequences of being present at the leading edge of an expanding range poses strong logistical challenges, but historical data on humans suggest an advantage to the first colonizers of an area [39]. In cane toads, invasion-front individuals have access to more food, resulting in faster growth and better body condition, but whether or not those energy-based advantages outweigh a higher risk of predation remains unclear [40]. In the absence of fitness differentials, however, genes that code for faster dispersal are expected to accumulate at an expanding range edge simply owing to spatial sorting; the majority of dispersal alleles present at a fast-moving invasion front will be those that confer high dispersal rates on their bearers [5–7].

In summary, the pressures unleashed by a biological invasion can cause rapid evolutionary changes in traits that influence rates of dispersal; and the straightness of movement may be one of the first and most important such traits to be modified. Patterns of dispersal will shift through time, such that a long-colonized area (perhaps only a decade after the initial invasion) is dominated by individuals that disperse more slowly, along more meandering routes. Those changes—critical to predicting population-level responses to environmental change, as well as the rates of invader spread—will occur at many expanding range edges.

Ethics statement

Ethical approval was granted by the University of Sydney Animal Ethics Committee under protocol no. 5805.