Abstract
Mechanics is at the heart of many cellular processes and its importance has received considerable attention during the last two decades. In particular, the tension of cell membranes, and more specifically of the cell cortex, is a key parameter that determines the mechanical behavior of the cell periphery. However, the measurement of tension remains challenging due to its dynamic nature. Here we show that a noninvasive interferometric technique can reveal time-resolved effective tension measurements by a high-accuracy determination of edge fluctuations in expanding cell blebs of filamin-deficient melanoma cells. The introduced technique shows that the bleb tension is ∼10–100 pN/μm and increases during bleb growth. Our results directly confirm that the subsequent stop of bleb growth is induced by an increase of measured tension, possibly mediated by the repolymerized actin cytoskeleton.
Introduction
Cellular membrane blebbing is a well-known and highly dynamic phenomenon that occurs throughout the lifecycle of many cell types. Cell blebs have been described in the context of apoptosis (1), cell division (2), cell spreading (3), and notably in cell motility (4). The time course of a bleb (its growth and retraction) has been carefully characterized (5–8), but a dynamic and time-resolved measurement of the tension is still missing. Blebs are driven by hydrostatic pressure generated by cortical tension, which is maintained by the contractile acto-myosin cortex that is physically linked to the membrane. The actin cortex is composed of a dense actin network that is connected to the plasma membrane and gives mechanical rigidity to the cell periphery. This connection limits the mobility of the membrane and prevents the formation of blebs in most cell types, despite the presence of hydrostatic pressure. However, if the actin cortex ruptures, or if the cortex to membrane connection is lost, the pressure pushes the membrane outwards, and a cell bleb grows.
Experimental techniques such as micropipette aspiration or the fluctuation analysis used here measure the effective tension. In the general case, the effective tension consists of both a contribution from the membrane and the actin cortex. Because the two structures are mechanically coupled, the fluctuations of the cell edge contain contributions from both. In principle, the membrane and the cortex have different tension, but it remains difficult to experimentally dissect the contribution from each component. Under steady-state conditions, the hydrostatic pressure that pushes against the plasma membrane is balanced by the mechanical rigidity of the actin cortex to which the membrane is connected. However, if this balance is broken by a local fracture of the actin cortex or by a local detachment of the actin cortex from the plasma membrane, hydrostatic pressure pushes the membrane outward to form a fast-expanding membrane bleb. Until a new actin cortex repolymerizes in the growing bleb, no mechanical support structure hinders its expansion, and the growth is determined by the pressure driving it and the friction forces of both the flowing fluid and membrane that enter the expanding bleb (9,10).
Techniques like micropipette aspiration made it possible to measure the tension of the cell cortex and to relate this tension to the growth velocity and final size of cell blebs (8). These experiments confirm that the mechanical origin of the hydrostatic pressure that drives bleb extension is the active contractility of the cellular acto-myosin cortex. Tension within the bleb is an important mechanical parameter for bleb dynamics. For a better characterization of the mechanical events during bleb growth, direct access to the bleb tension is required.
It is also important to have access to both the membrane tension and the cortex tension, which are not necessarily equal. Although in previous work it was possible to derive an estimation of the bleb tension and directly measure the cortex tension away from the bleb position (7,8), direct and time-resolved measurements at the site of blebbing is required to understand the mechanics of bleb formation. Such measurements are experimentally challenging using the micropipette aspiration method, because the structure is highly dynamic. Hence, we introduce what we believe to be a new method, one that provides direct insight into the effective tension during bleb growth.
In addition to the micropipette aspiration technique, membrane tethers have been successfully used to determine the membrane tension in blebs (11). In these measurements it became clear that the measured membrane tension in blebs is lower than tension at sites of no bleb appearance. Although this finding seems to challenge the prediction of higher tension in growth-arrested blebs, it is important to note that the pure membrane tension differs from the effective tension of the combined membrane and actin cortex system. Technically, the micropipette aspiration also includes the cortex that is aspirated together with the membrane, whereas in tether-forming experiments, only membrane is pulled. Tether measurements include both membrane tension and membrane to cortex adhesion energy. The tether formation technique is therefore well suited to determine the membrane tension and other parameters such as contributions from the cytoskeletal adhesion energy. However, it does not probe the mechanics of the underlying actin cortex. In this view, these first investigations of blebs did indeed suggest a decrease of adhesion energy in the bleb membrane if compared to the nonblebbing cell cortex.
The method we introduce in this article uses membrane fluctuations to estimate the evolution of tension in blebs by measuring before, during, and after repolymerization of the actin cortex. Measurements are performed in filamin-depleted M2 melanoma cells, a common model system for membrane blebs because they continuously produce blebs all over their surface (12) and have been well studied previously (5,7). To determine the tension during bleb growth and growth arrest, we measure the membrane movement by a laser-based interferometric method capable of determining the membrane position with subnanometer precision and at submillisecond time resolution (13,14). This allows observation of the thermal fluctuations of the membrane during bleb growth. Separation of timescales is used to differentiate between the high frequency fluctuations that are considered in equilibrium and the low-frequency, active movement.
In this work, we focus on the growth phase, and show that a separation of timescales allows determination of the fluctuation amplitude even during the rapid extension phase of the cell bleb. A simplified equilibrium model for thermal fluctuations at short timescales allows extraction of an effective tension from the data that increases systematically during bleb growth. Although the blebbing phenotype of the M2 cells suggests strong mechanical differences to other, nonblebbing cells, it is interesting to see that the measured tension in the bleb membrane is only slightly smaller than previously determined values for the cell cortex in nonblebbing cells, such as L929 fibroblasts (8).
Materials and Methods
Cell culture and Cytochalasin D application
Filamin A-deficient M2 cells (15) are cultured in DMEM (1 ×) + GlutaMAX medium (Gibco, Life Technologies, Carlsbad, CA) supplemented with 10% fetal bovine serum (FBS Gold; PAA, GE Healthcare, Pasching, Austria) under standard conditions (37°, 5% CO2, maximal humidity) and passaged every 3–4 days at 80–90% confluence. For passaging, cells are washed with phosphate-buffered saline and trypsinized (TrypLE Express (1 ×) + Phenol red; Gibco, Life Technologies, Grand Island, NY) at 37° for 10 min. Trypsin is inactivated by FBS-containing media and the cell solution is centrifuged for 3 min at 1000 relative centrifugal force for subsequent medium exchange, resuspension, and seeding in new flasks. Cells are counted using an automated cell counter (Countess; Invitrogen, Carlsbad, CA). Twenty-four hours before measurements, 40,000 cells are seeded on 18 × 18 mm2 coverslips. Immediately before imaging, coverslips are placed on a glass slide, sealed, and the measurements are performed for up to 1 h.
Cytochalasin D (CD) (Sigma Aldrich, St. Louis, MO) was applied at 2.5 μM 30 min before starting the experiment.
Experimental setup and data acquisition
The membrane position was detected with a recently developed interferometric detection method using an NIR laser (YLM, 1064 nm; IPG Photonics, Oxford, MA) with a low average laser power of 40 μW per laser focus at the sample, to avoid optical trapping effects (14). The position of the laser beam in the sample plane is controlled using an xy acousto-optical deflector (AOD) device (MT80-A1,5-1064 nm; AA Opto Electronic, Orsay, France), that allows a fast repositioning of the laser focus with a switching time of 10 μs. As sketched in Fig. 1 A, the beam first passes the AOD, and is subsequently imaged into the back focal plane of a 60× NA = 1.2 water immersion objective (UPLSAPO 60×W/IR; Olympus, Rungis, France) using a 1:2 telescope and a dichroic mirror. After interaction with the sample, the scattered and unscattered light is collected by a long-distance water immersion objective (U LUMPL FL 60×W/IR, 60×, NA 0.9; Olympus) that also serves as condenser. Subsequently, the light is imaged onto a quadrant photodiode (QPD) using a 2:1 telescope. The signal from the QPD (InGaAs QPD G6849; Hamamatsu Photonics, Massy, France) is preprocessed by an analog circuit that delivers the asymmetry of the light in the x and y directions and the total sum of the signal (Öffner MSR-Technik, Plankstadt, Germany). Briefly, the asymmetry is calculated by Here Qi corresponds to the light intensity that is measured at the four different photodiodes of the detector. These signals are digitized at 500 kHz using multichannel DAQ cards (NI-DAQ 6363 PCIe; National Instruments, Austin, Texas) and further processed using the softwares LABVIEW (National Instruments) and MATLAB (The MathWorks, Natick, MA). The detection method works reliably if the bleb edge is in the focal volume of the laser, which has a diameter of ≈500 nm. However, due to the rapid growth, the bleb may leave this area quickly (timescale, 1 s). To ensure recording of the bleb during movement, we rapidly scan the laser over 50 positions normal to the bleb edge with a step size of 100 nm between each scan point. Every 500 μs, a full scan is completed, leading to an effective acquisition frequency of 2 kHz. Data acquisition and trap position are synchronized by using a common 500 kHz TTL trigger generated by the acquisition card. Careful calibration was performed to assure synchronization of laser positioning and data acquisition. The resulting Δx, Δy, and sum signals are recorded as a function of the laser position for later analysis.
Figure 1.
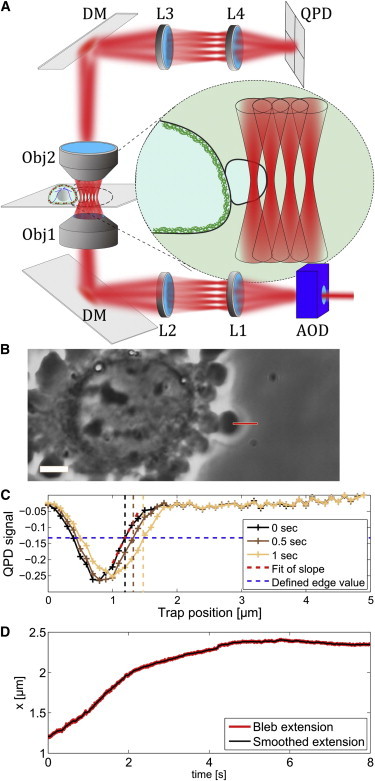
Experimental procedure: (A) sketch of the setup, where the laser position is controlled by an acousto-optical deflector (AOD) and imaged in the back focal plane of the objective 1 (Obj1) via a telescope formed by the lenses L1 (f = 15 cm) and L2 (f = 30 cm) and the dichroic mirror (DM). After interaction with the bleb (see inset) the light is collected by the objective 2 (Obj2) and the back focal plane of Obj2 is imaged to the QPD via L3 (f = 9 cm) and L4 (f = 4.5 cm). (B) Example of the experimental procedure, where a bleb is identified and the position and direction of the scan line is controlled by the experimenter via a custom-programmed user interface (LABVIEW; National Instruments, Austin, TX). Scale bar, 5 μm. (C) Example of three scan results at different time-points. The edge position is defined by the first scan and used in the following sequence to determine the edge movement. (D) Measured time evolution of the bleb membrane during bleb growth and arrest.
Experimental protocol and edge detection
For experiments, M2 cells are plated on uncoated coverslips one day before observation. Cells are sealed in a chamber formed between two coverslips. An average distance of ≈500 μm between the coverslips ensures that cells are not compressed between the glass faces. After mounting the sample on the microscope, an isolated cell is observed in video microscopy. The temperature during the experiment is typically between 29° and 31°, and represents the room temperature during the experiments. This is the maximal temperature tolerated by the electronics and the laser in the room, and it presents a technical limitation of the setup used. Heating chambers are incompatible with the laser and the QPD detection system used.
Once a growing bleb is identified by observation of the cell edge, 50 traps with a distance of 100 nm between each trap are positioned in a trap array normal to the bleb surface and in parallel to the bleb growth direction (see Fig. 1 B, red line). The trap power is adjusted to 40 μW per trap so that the actual pulling force can be neglected (16). The total laser power delivered to the sample is 50 × 40 μW = 2 mW, which is still low compared to typical situations of optical tweezers. The heating due to this laser power can be estimated to be ∼20 mK, which can be neglected (17). The resulting signal on the QPD is recorded and analyzed to detect the relative membrane position of the cell edge with a time resolution of 500 μs. The construction of the laser beams typically takes several seconds, which has the effect that, with this protocol, we can only record the final phase of bleb growth. When the bleb size has reached its maximum, data acquisition is stopped and the protocol starts again on a new bleb.
To extract the edge position, the minimum of the scan curve as shown in Fig. 1 C was determined and the QPD signal that corresponds to the edge was defined to be the QPD signal at the position 500 nm to the right of the minimum (blue dotted line in Fig. 1 C). The width of the scan reflects the size of the laser focus and can be described by a convolution between the point-spread function of the laser focus and the spatial change of refractive index at the cell interface (18). Changes in the width may result from slight defocusing due to drift or changes in the surface morphology of the bleb. The position of the edge was defined to be 500 nm to the right of the minimum to obtain the maximum sensitivity of the method, inasmuch as this corresponds approximately to the size of the laser focus. Using the scan points that are in the region of highest slope increases sensitivity.
Please note that the trap position of 0 μm always refers to the position determined by the experimenter when initiating the laser array, and is highly variable between different experiments. To follow the edge over time, we analyze the time evolution of the scans. In each scan we use the three closest points to the predefined QPD value that represents the edge. Due to the size of the linear regime of ≈400 nm, and the distance of 100 nm between scan points, we can use multiple points to detect the edge position by fitting a line through these points. The relative edge position is then defined by the intersection of the fitted curve with the previously defined QPD value. This gives an edge value every 500 μs, which can be followed over the full recording time. The resulting edge movement is shown in Fig. 1 D. Velocities are calculated by v = Δx/Δt, with Δt = 500 ms to avoid influence of the fluctuations.
Experimental Results
Models to estimate effective tension: power spectral density (PSD) method
To determine an effective tension from the recorded fluctuations, it is necessary to separate the fluctuations from the bleb extension. As shown previously in Betz and Sykes (14), the tension-dominated fluctuations show a typical power-law behavior for the power spectral density (PSD) derived from the edge movement, PSDtension (f) ∝ f−1, whereas a constant movement exhibits a −2 exponent, as shown in Fig. 2 A and calculated at the end of this section.
Figure 2.
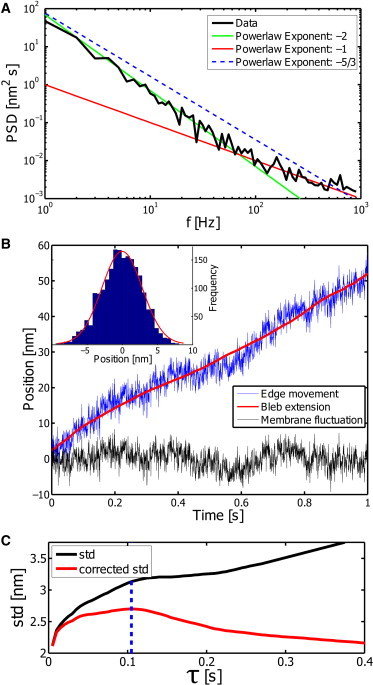
To calculate the effective tension from the fluctuations of the bleb edge, we explored two different methods that both rely on a separation of timescales. (A) The power spectrum of the edge movement for the data shown in panel B) is calculated, and the power law of −1 is detected in the high-frequency part. The prefactor for this region of the PSD depends on the effective tension. (B) The edge movement x(t) (blue) is averaged to determine the bleb extension xbleb (red). The membrane fluctuations are recovered as the difference between edge movement and bleb extension xfluc = x − xbleb (black). (Inset) Using the determined fluctuations, we construct a position histogram and fit a Gaussian distribution to it. The variance of the Gaussian is related to the tension of a free membrane. (C) To determine the smoothing window size, the SD of xfluct(τ) is determined as a function of τ. (Black) Directly determined SD. The long time slope is determined and subtracted from the original function to obtain the corrected SD (red). The idea of the correction is to remove the effect of the continuous growth on the SD. The maximum of the resulting function is used as an estimate for the window size. (Blue dotted line) Timescale for the smoothing in this example.
Briefly, the PSD can be derived from the Helfrich free energy,
| (1) |
where h represents the membrane displacement from its equilibrium position, and the integral is taken over the whole surface, σ is the membrane tension, and κ is the bending modulus. Applying the equipartition theorem and solving the equation in spatial Fourier transformation gives the wave-vector q-dependent amplitude
| (2) |
Including the viscous dissipation of the solvent allows us to calculate the autocorrelation function,
| (3) |
where ω(q) = (κq3 + σq)/(4η) is the mode-dependent relaxation frequency, and η is the mean viscosity of the surrounding fluid.
According to the Wiener-Khinchin theorem (19), the PSD can be calculated as the Fourier transform of the autocorrelation function. Additionally, we need to integrate over all q-modes, because we only observe a single point on the membrane. After some algebra (14), we find the following expression for the PSD,
| (4) |
where qmin and qmax are the cut-off wave-numbers. Inasmuch as this integral cannot be expressed analytically in a simple form, we use the limiting cases of tension- or curvature-dominated fluctuations:
| (5) |
| (6) |
Interestingly, the tension-dominated regime of the PSD depends only on the tension and not the viscosity. This is surprising, inasmuch as the PSD represents a dynamic measurement, but it can be explained by the fact that the PSDσ depends inversely on the frequency. With increasing viscosity, the frequency for a given oscillation mode decreases. However, the PSD value is simultaneously increased, inasmuch as it presents a density and is normalized by frequency bins. When increasing the viscosity, the curve is shifted to the left and simultaneously upwards. Both changes compensate, and thus the PSD for the tension-dominated regime becomes independent of the viscosity. The crossover between the −1 and the −5/3 power law can be calculated to be
(14), which is expected for blebs to be ∼10 kHz using σ = 50 pN/μm, κ = 10 kT, and η = 0.003 Pas. We only expect to see the tension-dominated regime with the bandwidth of 2 kHz. The low-frequency power law of −2 observed in the data is due to the continuous movement of the bleb, and not the bending-dominated regime. In the case of extending blebs, we need to consider the steady movement of the bleb at low frequencies, whereas at high frequency, fluctuations dominate over the continuous movement of the edge. Therefore, analyzing the PSD can be used to determine two things:
-
1.
The nature of the fluctuation, and
-
2.
The effective tension.
Power-law regions of −1 correspond to tension-dominated regimes, −5/3 to bending-dominated regimes as shown above, and −2 to a constant movement of the membrane. We can exploit the finding of a −1 power law to determine the effective tension σeff (14). It should be noted that the effective tension σeff is used in the analysis, because we can only determine the tension of the membrane plus the cytoskeleton. In contrast, σ is used in the theoretical expressions of membrane tension that are used in literature. The different notation of σ and σeff is used to highlight the difference between a purely theoretical model and the expression applied to the measurement. The expression used to describe the measured PSD uses the effective tension σeff:
As shown in Fig. S1 in the Supporting Material, we also simulated the movement of a bleb and successfully recovered the tension that was used to generate the data.
To understand the −2 power law that is found at low frequencies, we can analytically calculate the Fourier transform of a linear function in the time span 0 to T:
| (7) |
| (8) |
Noting that the PSD is proportional to the absolute value squared of the Fourier-transform, one easily finds the −2 power law:
| (9) |
| (10) |
| (11) |
Models to estimate effective tension: variance (VAR) method
We directly use the amplitude of the fluctuations quantified by the variance of the edge movement. Again, we have to consider the fact that the measured edge movement represents the overlay of continuous bleb growth and the fluctuations. To best detect how much of the variance results from fluctuations, we need to correct for the continuous movement. This was done by first detecting the average bleb extension xbleb from the curve via smoothing by averaging values from a moving window of length τ. The resulting bleb extension is considered smooth on the timescale of ∼100 ms. Nevertheless, it remains interesting to discuss possible changes in the bleb extension, as described later. However, the short-term extension is still assumed to be continuous. The membrane fluctuations are then simply calculated by where x(t) is the measured edge movement (see Fig. 2 B, blue). Fitting a Gaussian distribution to the histogram of the corrected fluctuations yields the variance of the fluctuations that are used for further analysis. A central point in this method is to determine the size of the applied smoothing window τ. This is important, because the size of this window will have direct impact on the calculated tension. We estimate this parameter for each dataset independently using the fact that the variance of the corrected data as a function of the window size first increases rapidly, whereas for longer τ-values it is less pronounced. The aim is to find a smoothing window where the variance does not depend strongly on the smoothing window τ. We approximate this timescale by analyzing the curve of the standard deviation (SD) as a function of τ (Fig. 2 C). For large smoothing windows, the increase of the SD is less pronounced than for short windows. By removing the large τ trend from the original curve (black in Fig. 2 C), we approximate the corrected SD. The maximum value of that curve is then found at a reasonable estimate of the smoothing window. This trend is determined by the slope of the last 10 values of the black line in Fig. 2 C.
To check whether this strategy does indeed reproduce reasonably well the edge fluctuations, we simulated the expected edge movement of a bleb that extends with a velocity similar to Fig. 2 C. Results of this simulation are shown in Fig. S1. It should be noted that the timescale of the smoothing window does not correspond to the timescale of crossover between the different slopes in the PSD as shown in Fig. 2 A. Although the crossover timescale in the PSD depends on the tension and the growth velocity, τ is a timescale at which the fluctuations are expected to have explored all possible regimes. This is typically one order-of-magnitude longer than the crossover in the PSD (see also Fig. S1).
Once we have determined the variance of the corrected fluctuations, we can use the theory of spherical membranes to estimate the variance (VAR) as a function of tension. This was previously introduced to be (20)
| (12) |
where the sum is taken over the accessible modes and
is the highest accessible mode. In principle, this mode depends on the bleb radius R at a given time and the size of the laser focus Δx; however, because the sum in Eq. 12 converges with 1/l2, only the first 20 values are important. Using typical values, we estimate lmax = 25, which then leads to constant value for the sum of
The tension can be calculated from the variance of the corrected fluctuations, using
| (13) |
Comparison of the two analytical models
Although the two introduced models rely on the same physical model, they do use different regimes and require different analytical procedures. The PSD method focuses on the dynamics of the fluctuations; the VAR method focuses on a static measure of the membrane fluctuations. In both cases, however, we ignore the contribution of the bending regime. This is justified by the observation that our experimental data does not show the bending-dominated −5/3 power law. Confirmed in a previous analysis (14) is that we expect to see such a crossover at higher frequencies (10 kHz) than are accessible with the bandwidth of 2 kHz. We also assume that the viscous dissipation is mainly due to the solvent, and that the models neglect the contributions of the cytoskeleton, which is polymerizing under the membrane. During the initial phase of the bleb growth, this assumption seems to be valid, inasmuch as the actin cortex requires some time to repolymerize. However, during growth arrest, we do not yet have an experimental reason to dismiss an actin cortex contribution.
Membrane movement during bleb growth shows different growth phases
The movement of the bleb edge typically shows a fast growth at the beginning of the measurement and then a reduction of the growth speed until growth fully stops. However, the growth speed often changes rapidly on the timescale of 1 s as can be seen in Fig. 1 D and Fig. 3 A at t ≈ 2 s. To quantify the occurrence of such kinks, we created a histogram of the measured velocities. Such a velocity distribution is shown in Fig. 3 D. The appearance of multiple peaks in the distribution can then be interpreted as cases in which the velocity shows fast changes. Please note that the dominant height of the first peak at v ≈ 0 μs represents the stop phase. We quantify the cases where peaks were separated by fitting multiple Gaussian functions to the histograms. If the distance between the peaks is bigger than the SD of the neighboring Gaussians, we count these cases as clearly separated growth velocities. We observe clearly separated velocity peaks in 78% of all blebs analyzed.
Figure 3.
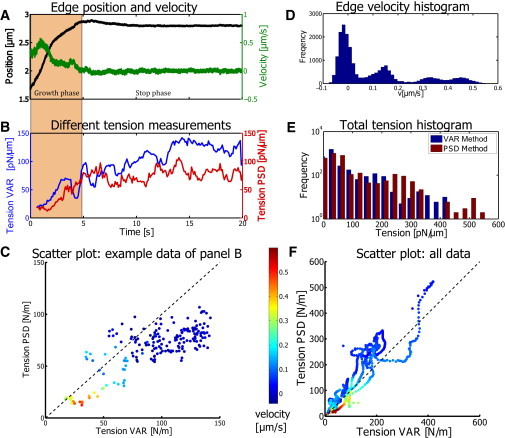
(A) Direct comparison between the time-dependent edge position (black) and velocity (green). The decay of the correlation is given in the autocorrelation plot of Fig. S3 in the Supporting Material. (B) Tension (bleb panel A) resulting from the VAR method (blue) and the PSD method (red) is presented. The tension measured by different methods is consistent and suggests a systematic increase over time. The growth phase (light-brown background) is defined by the growth arrest. (C) Scatter plot of the data presented in panel B, where the markers are color codes for the edge velocity. (D) Histogram of the velocities found in the data shown in panel A. This is used to determine whether there are different phases during bleb growth that are marked by different velocities. In this example, we can identify three different growth phases that are indicated by the three peaks at positive velocities. (E) Distribution of the measured tension for all blebs and all the time-points. The distribution shows a large variation starting at 5 pN/μm up to almost 600 pN/μm. Again, the different methods show consistent values. (F) To finally check whether the two measurements are indeed consistent, we also analyzed the data using a scatter plot, where all obtained experimental values are shown. Again, the edge velocity was used as the color coding. This plot confirms that the two methods provide consistent values, inasmuch as most points lie on the diagonal (dashed line). The highest tensions typically correspond to the low velocity. The color bar of panels C and F is equivalent.
PSD method
The PSD method offers the possibility to separate the direct advancement of the edge and the fluctuations that are added to this advancement in a direct and visual representation. For the timescales that are dominated by bleb growth, a power law with a −2 exponent is expected, which is verified in the measurements for low frequencies. However, if fluctuations are sufficiently high, a crossover to a new power law is observed. Using the high-frequency regime, we determine the effective tension and find a large variation of tension over all measurements and all times (see Fig. 3 E). The PSD methods reveals the tension to be in the range of 5 pN/μm < σeff < 600 pN/μm. The distribution of values visualizes the large variation of tension for this cell type. The average value for all measurements (17 blebs, 3149 tension measurements) for the PSD method is
and the spreading is reflected in the large SD of
These numbers give an impression of the tension in blebs. As mentioned, the actual values in a particular situation may be quite different. Due to the high speed of the membrane bleb advancement, the region where the −1 power law is found remains limited to approximately one order of magnitude, and it remains questionable whether this is sufficient to reliably establish the power law. We tried to use an analytical method that does not rely on the high-frequency limit to approximate the tension.
VAR method
In addition to investigating the PSD, we examined the variance of the fluctuations from the data after correcting for constant bleb growth. The resulting values are quite similar to the values found by the PSD method, and an example is shown in Fig. 3 B. Over all analyzed blebs, we find the same range of values as in the PSD method (Fig. 3, E and F), with an average value of
and SD of
As can be seen in Fig. 3 E and the scatter plot in Fig. 3 F, the two different methods give similar results over the full tension range that was measured.
Tension increases during growth phase and depends on actin
Our analysis shows that the effective tension values can vary drastically. This reflects not only the temporal changes that we measure during the growth of a single bleb but also the variations between different blebs. To get further insight into the time dynamics of the effective tension, we investigated the time evolution of tension as shown in Fig. 3 B. Although we have access only to the last seconds of the growth phase, we can still determine an increase of tension that was consistently observed in the two methods of analysis. To quantify whether this increase is commonly observed, we split the datasets into a growth phase and a rest phase, and compare the average tension in both phases (see Fig. 4 A). Again, the individual values vary extensively, but we do find that the tension increases significantly (p = 0.045, single-tail students t-test) by almost a factor of 2. Because the PSD method is typically less noisy, we show in Fig. 4 only the tensions extracted from the PSD. The VAR method gives qualitatively similar results, but values are, on average, 10–20% smaller.
Figure 4.
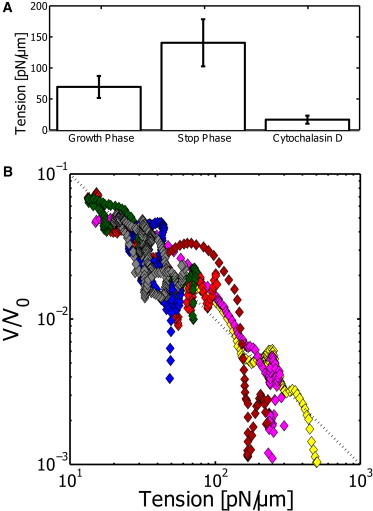
(A) Direct comparison of the growth and the stop phase. The average tension in these phases increases, whereas the tension that is found for CD-treated cells decreases significantly. (B) Plotting the normalized velocity over the measured tension shows a clear inverse relation in the log-log plot. Here we limit the data to blebs that showed at least a twofold increase of tension during measurement. This was the case for 7 out of 17 blebs (41%). Each color corresponds to a different dataset. (Dashed diagonal) Power law of −1. The same data using the VAR method can be found in Fig. S4.
Finally, we test the tension in cells that have a perturbed actin cytoskeleton due to treatment with 2.5 μM Cytochalasin D (CD), a drug that is known to cap actin filaments and thereby hinders the repolymerization of an actin cortex. When cells were treated with CD, the dynamic growth and retraction phases of blebbing were not observed, and thus only a single value for tension is reported. Tension values after drug treatment of
(n = 10, mean ± SE) are significantly smaller than the tension found in both the growth and the stop phase of untreated cells.
Inverse relation between tension and growth velocity
Although the increase of tension over time was apparent, we further investigated the relation between growth velocity and tension. The example shown in Fig. 3 B suggests an inverse relation between tension and growth velocity. This is further supported by the scatter plot of Fig. 3 E, where the highest tensions correspond to the lowest velocities. To check whether this is systematically true, we analyzed the dependence between the tension and the growth on a subset of the data (7 out of 17) shown in Fig. 4 B. The subset presents the data where the tension changed by at least a factor of two over the observation time. This selection was necessary because we do not have access to the beginning of the bleb, which means that we have to select for data that shows a change in tension during the measurement.
Because the tensions and velocities are highly variable, we normalize the velocity by the average product between velocity and tension as v0 = 〈v(t) × σ(t)〉t. This normalization is chosen to force the area under the plots to be similar. Plotting the normalized velocity over tension confirms an inverse relation, as shown in the log-log plot of Fig. 4 B. Part of the rescaled curves collapses on an inverse relation with a power-law exponent of −1, as shown by the dotted line in Fig. 4 B. It is also observed that, in some cases, the tension remains constant during the growth stop (far-red data in Fig. 4 B), and thus gives a marked deviation from the inverse law. However, in other cases, this phenomenological inverse relation seems to be a good description of the data.
The presented inverse relation should not be taken as a general feature that is commonly observed, but as a rather phenomenological finding that may only be present in a subset of the data and, more importantly, only occurring in certain phases of a bleb. This is also obvious when considering that the tension is sometimes increasing even while the growth has arrested.
Limits
Our method to measure the effective tension is based on a high-speed interferometric approach that allows the detection of membrane fluctuations with spatial resolution <1 nm. Thanks to the high signal/noise provided by the interferometric method, it is possible to detect the edge fluctuations of growing blebs. To test the limits of this detection method, we placed the laser at the membrane of fixed cells, where we assume that the fixing process has generated a highly crosslinked cell that suppresses membrane fluctuations. The measured fluctuation then provides a lower limit for fluctuation measurements. In Fig. S2, we plot the PSD of the fixed cell together with the data already shown in Fig. 2, to validate that the measured edge fluctuations are higher than the detection limit of the system. Using the PSD method, we can also estimate a detectable upper limit of σmax ≈ 2000 pN/μm—an order of magnitude above the typical values from our measurements, which correspond to fluctuation amplitudes of ≈1 nm. The reason for the −2 power law in the fixed cells is due to thermal drift of the cell and the detection laser, inasmuch as random thermal movement leads to −2 power laws. An example of such a dependence is used in the calibration of optical tweezers (21).
In addition to the theoretical limits of the methods, we compare all determined tension values of the two methods and find a median difference of 18% between them.
Discussion
Comparison with literature
The tension of cell blebs has been investigated previously using techniques such as fluorescence-based fluctuation detection and static micropipette aspiration (7). From fluorescence-based fluctuation detection methods in M2 cells, tension values of σ = 0.8 pN/μm were determined, which is almost two orders-of-magnitude smaller than values from our measurements (7). Interestingly, such work also finds a slight increase in tension for the stop phase compared to the growth phase, and an overall decrease of tension when CD is applied. And while the values are quite different when compared quantitatively, the qualitative reasoning of our work is similar. The reason for the differences in absolute values might be found in the different measurement methods. Another possible explanation is that the temperature used in our experiments is ∼30°C, which is below the optimal physiological conditions of 37°C. This difference may lead to changes in the contractility, resulting in systematically different tensions.
Additionally, measurements in Dictyostelium give an estimate of the cortical tension, which was measured to be σ ≈ 2 nN/μm (22,23)—approximately two orders-of-magnitude higher than the values measured in this work. However, it should be mentioned that the mechanical properties of Dictyostelium are drastically different from typical mammalian cells.
The tension of cell cortices has also been measured directly using micropipette aspiration (8,24). This method allows direct determination of the effective tension by pulling on the membrane, including the actin cortex, and observing the resulting deformations. In L929 fibroblasts, effective tension was measured and blebs were induced by local ablation of the actin cortex using UV laser cutting. The measurement method of micropipette pulling, however, did not allow determination of the tension within the bleb, but only at the nonblebbing parts of the cells. This study reports tensions in σ ≈ 400 pN/μm for normal L929 fibroblasts, and a highly reduced tension under the application of CD σCD ≈ 40 pN/μm. These values are slightly bigger than the tension we measure, but remain consistent. In addition, this difference might be due to the different measurement methods, the different position of measurement on the cells, and the different cell types. The difference between the M2 cells and the L929 cells might be found in the particular cortex defects of the M2 cells that are known to lack the actin crosslinking protein filamin A.
The threshold tension to create a bleb may be linked to the mechanical properties of the actin cortex, where a direct dependence of the cortex rupture force and the tension could be hypothesized. In this view, the lack of filamin could decrease the rupture tension, which would then directly explain the reduced tension found in the M2 cells. Although this hypothesis remains to be checked, it would explain why the overall measured tension is smaller in blebs within the stop phase of the M2 cells if compared to the cell cortex of other cell types. Additionally, it is interesting to find that the tension upon CD application is similar in the different systems, hinting for a possible general membrane tension.
We were further interested to compare the time evolution of the bleb tension with the known times of the recruitment of different proteins in the cell bleb (25). It has been shown that the recruitment of actin is correlated to the growth arrest of the bleb, and we do see an increase of effective tension when the bleb extension slows down. This suggests that actin is responsible for the increase in tension. This hypothesis is also supported by our results, which show a decrease of tension when the repolymerization of the actin cytoskeleton is inhibited by CD (Fig. 4 A). The final recruitment of actin binding proteins such as crosslinkers may further increase the mechanical rigidity of the actin cortex and increase the tension. In this view, the tension increase is indeed due to the actin cortex.
Validity of an equilibrium model of membrane fluctuations
The theoretical model used to infer information about the membrane tension from the fluctuation is based on equilibrium thermodynamics (26). Our analysis considers the active bleb extension, and uses our method of separation of timescales to isolate the random fluctuations from the edge advancement. However, it remains unclear whether these fast movements are purely thermal or might also have nonthermal and active components. Previous reports hint that the nonequilibrium fluctuation in active systems are dominant in the low-frequency part, and that the high frequencies beyond 10 Hz can be described by the passive model (27). Our analysis does rely on the validity of these findings in the investigated system of membrane fluctuations. However, unknown fast nonequilibrium processes might partially drive the measured membrane fluctuation, and lead to a systematic underestimation of the reported tension values. As of this writing, the main reason supporting the high-frequency fluctuations being in thermodynamic equilibrium is that we find the predicted power law of −1. But theoretical models of active membranes (28–30) suggest that, depending on the active process, the PSD might not be sufficient to exclude such contributions. Possible contributions to such nonthermal fluctuations could be the active polymerization of the actin cytoskeleton (31), or membrane-bound proteins such as ion pumps (32).
Interpretation of effective tension
As described above, we apply the theory of pure lipid membranes to infer an effective tension from membrane fluctuation characteristics in blebs. It should be pointed out that the validity of this theory, for composite systems such as a membrane including the underlying actin cortex, is far from evident. From a mechanical point of view, the membrane theory may be applied if the cortex remains thin compared to the typical wavelength of the fluctuations. This is indeed the case in the blebs. Different analytical approaches that either disregard the time-dependent information (VAR method) or which exploit exactly the time dependence in fluctuations (PSD method) were used to check for consistency between the model and the experimental results. Our finding that both approaches lead to similar effective tension values suggests that the underlying model can be used to describe the system. However, whether the simple lipid membrane model can be used to extract information about the cortical tension in other cell types or structures remains to be verified.
Regarding the interpretation of the effective tension, it should be also pointed out that, especially in the VAR method, we exclusively assume that fluctuations are governed by tension, and we do not consider possible mechanical stabilization effects due to the known repolymerization of the actin cortex. The main reason to still use the term “effective tension” is the observed power law from the PSD measurement. However, one might argue that even the actin cortex may lead to such a power law. In the absence of further theoretical models, we interpret the fluctuations as tension-dominated. Moreover, even if a polymerizing actin cortex experiences an area stretching (as it occurs in the extending blebs), it should simply add an additional tension to the membrane tension. In this sense we argue that the interpretation as an “effective tension” is reasonable. Again, the fact that the VAR and the PSD methods give similar results further supports this interpretation. Future experiments, such as on biomimetic liposomes that contain actin cortices (33,34), might give more insight into the expected influence of an actin network on membrane fluctuations.
Of special interest is the interpretation of the effective tension when combined with the previous results from Dai et al. (11). They directly measured the membrane tension using membrane tethers and report values for blebs that are close to the values that we find in CD-treated cells with a disrupted actin cortex. The small differences in our measurements and these tether-pulling experiments may be due to the onset of actin repolymerization in our bleb measurement. Measurements during the onset of blebbing should yield values directly comparable to tether pulling experiments; however, the experimental procedure under discussion here did not allow such measurements.
Tension increase during growth
With our experimental data, we see an increase in tension over time. From a plain mechanical point of view, the movement of the membrane has to reflect an imbalance between the forces pushing on the membrane (pressure) and the forces holding the membrane back (tension). If bleb growth stops, the system has returned to an equilibrium situation. Because the hydrostatic pressure is not vanishing at growth stop (8), the tension has to increase, which is exactly the observation reported in this article.
The molecular explanation for the tension increase, however, remains unclear. Possible explanations are an increase of mechanical rigidity during the repolymerization of the actin cortex, a limited membrane reservoir that has to flow into the bleb, a bleb growth in direct vicinity of the bleb, and changes in the bleb shape. Our hypothesis is that the repolymerized actin cortex, in fact, creates a rigid structure connected to the membrane, which resists mechanical extension. This view has been already put forward in previous reports (7). This mechanical effect requires a sufficiently rigid actin cortex that is fully connected inside the bleb. Also, the strongly reduced tension in the CD-treated cells supports this hypothesis. To show this explanation, a detailed study of the correlation between tension and the repolymerization of the actin network is required.
Conclusion
We present a fluctuation-based measurement of blebs in M2 cells which is capable of detecting the effective tension during bleb expansion with a temporal resolution of ≈1 s. The time resolution of the tension measurement is ∼2 orders-of-magnitude slower than the time resolution of the data acquisition because reasonable statistics for the fluctuations are required to get reliable values. The method is based on high-accuracy measurements of membrane fluctuations that can be distinguished from the continuous growth through a separation of timescales. The extracted tension is found to increase during bleb expansion and growth stop. This result directly confirms the model of a bleb growth stop that is mediated by the increased mechanical rigidity due to repolymerization of the actin cortex in the growth phase.
The time-resolved effective tension values are comparable to previous measurements on the cell cortex by micropipette aspiration on different, nonblebbing cells. However, when perturbing the actin cytoskeleton with CD, bleb dynamics stop and we recover similar values as found in previous studies under CD treatment. The method given here is capable of providing a direct measurement of the effective tension, with the potential to directly study the mechanical properties and its dynamic changes with 1-s time resolution. Our study shows that by using membrane fluctuations it is feasible to determine membrane tension in the physiological range, with a limit of fluctuation amplitude of 1 nm, corresponding to an upper limit of effective tension measurements of ≈2000 pN/μm.
Acknowledgments
The authors thank C. Sykes, P. Nassoy, and W. W. Ahmed for helpful discussions. The M2 cells were a kind gift from Guillaume Charras.
This work was supported by French Agence Nationale de la Recherche (ANR) grant No. ANR-11-JSV5-0002, Fondation pour la Recherche Medicale grant No. DEQ20120323737, and LabEx CelTisPhyBio grant No. ANR-10-LBX-0038, as part of Les Initiatives d’Excellence Paris Sciences and Letters (PSL) grant No. ANR-10-IDEX-0001-02 PSL.
Supporting Material
References
- 1.Robertson A.M., Bird C.C., Currie A.R. Morphological aspects of glucocorticoid-induced cell death in human lymphoblastoid cells. J. Pathol. 1978;126:181–187. doi: 10.1002/path.1711260307. [DOI] [PubMed] [Google Scholar]
- 2.Hickson G.R., Echard A., O’Farrell P.H. Rho-kinase controls cell shape changes during cytokinesis. Curr. Biol. 2006;16:359–370. doi: 10.1016/j.cub.2005.12.043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Bereiter-Hahn J., Lück M., Vöth M. Spreading of trypsinized cells: cytoskeletal dynamics and energy requirements. J. Cell Sci. 1990;96:171–188. doi: 10.1242/jcs.96.1.171. [DOI] [PubMed] [Google Scholar]
- 4.Blaser H., Reichman-Fried M., Raz E. Migration of zebrafish primordial germ cells: a role for myosin contraction and cytoplasmic flow. Dev. Cell. 2006;11:613–627. doi: 10.1016/j.devcel.2006.09.023. [DOI] [PubMed] [Google Scholar]
- 5.Charras G.T., Yarrow J.C., Mitchison T.J. Non-equilibration of hydrostatic pressure in blebbing cells. Nature. 2005;435:365–369. doi: 10.1038/nature03550. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Paluch E., Piel M., Sykes C. Cortical actomyosin breakage triggers shape oscillations in cells and cell fragments. Biophys. J. 2005;89:724–733. doi: 10.1529/biophysj.105.060590. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Charras G.T., Coughlin M., Mahadevan L. Life and times of a cellular bleb. Biophys. J. 2008;94:1836–1853. doi: 10.1529/biophysj.107.113605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Tinevez J.-Y., Schulze U., Paluch E. Role of cortical tension in bleb growth. Proc. Natl. Acad. Sci. USA. 2009;106:18581–18586. doi: 10.1073/pnas.0903353106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Paluch E.K., Raz E. The role and regulation of blebs in cell migration. Curr. Opin. Cell Biol. 2013;25:582–590. doi: 10.1016/j.ceb.2013.05.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Charras G., Paluch E. Blebs lead the way: how to migrate without lamellipodia. Nat. Rev. Mol. Cell Biol. 2008;9:730–736. doi: 10.1038/nrm2453. [DOI] [PubMed] [Google Scholar]
- 11.Dai J., Sheetz M.P. Membrane tether formation from blebbing cells. Biophys. J. 1999;77:3363–3370. doi: 10.1016/S0006-3495(99)77168-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Cunningham C.C. Actin polymerization and intracellular solvent flow in cell surface blebbing. J. Cell Biol. 1995;129:1589–1599. doi: 10.1083/jcb.129.6.1589. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Gögler M., Betz T., Käs J.A. Simultaneous manipulation and detection of living cell membrane dynamics. Opt. Lett. 2007;32:1893–1895. doi: 10.1364/ol.32.001893. [DOI] [PubMed] [Google Scholar]
- 14.Betz T., Sykes C. Time resolved membrane fluctuation spectroscopy. Soft Matter. 2012;8:5317–5326. [Google Scholar]
- 15.Cunningham C.C., Gorlin J.B., Stossel T.P. Actin-binding protein requirement for cortical stability and efficient locomotion. Science. 1992;255:325–327. doi: 10.1126/science.1549777. [DOI] [PubMed] [Google Scholar]
- 16.Betz T., Lenz M., Sykes C. ATP-dependent mechanics of red blood cells. Proc. Natl. Acad. Sci. USA. 2009;106:15320–15325. doi: 10.1073/pnas.0904614106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Peterman E.J., Gittes F., Schmidt C.F. Laser-induced heating in optical traps. Biophys. J. 2003;84:1308–1316. doi: 10.1016/S0006-3495(03)74946-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Lemière J., Guevorkian K., Betz T. Alpha-hemolysin membrane pore density measured on liposomes. Soft Matter. 2013;9:3181–3187. [Google Scholar]
- 19.Engelberg S. CRC Press; Boca Raton, FL: 2007. Random Signals and Noise: A Mathematical Introduction. [Google Scholar]
- 20.Milner S.T., Safran S.A. Dynamical fluctuations of droplet microemulsions and vesicles. Phys. Rev. A. 1987;36:4371–4379. doi: 10.1103/physreva.36.4371. [DOI] [PubMed] [Google Scholar]
- 21.Tolic-Norrelykke S.F., Schaffer E., Flyvbjerg H. Calibration of optical tweezers with positional detection in the back focal plane. Rev. Sci. Instrum. 2006;77:103101–103111. [Google Scholar]
- 22.Brugués J., Maugis B., Sens P. Dynamical organization of the cytoskeletal cortex probed by micropipette aspiration. Proc. Natl. Acad. Sci. USA. 2010;107:15415–15420. doi: 10.1073/pnas.0913669107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Dai J., Ting-Beall H.P., Titus M.A. Myosin I contributes to the generation of resting cortical tension. Biophys. J. 1999;77:1168–1176. doi: 10.1016/s0006-3495(99)76968-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Thoumine O., Cardoso O., Meister J.J. Changes in the mechanical properties of fibroblasts during spreading: a micromanipulation study. Eur. Biophys. J. 1999;28:222–234. doi: 10.1007/s002490050203. [DOI] [PubMed] [Google Scholar]
- 25.Charras G.T., Hu C.-K., Mitchison T.J. Reassembly of contractile actin cortex in cell blebs. J. Cell Biol. 2006;175:477–490. doi: 10.1083/jcb.200602085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Schmidt, D., C. Monzel, …, A.-S. Smith. 2014. Signature of a nonharmonic potential as revealed from a consistent shape and fluctuation analysis of an adherent membrane. Phys. Rev. X. 4:021023. http://link.aps.org/doi/10.1103/PhysRevX.4.021023.
- 27.Mizuno D., Tardin C., MacKintosh F.C. Nonequilibrium mechanics of active cytoskeletal networks. Science. 2007;315:370–373. doi: 10.1126/science.1134404. [DOI] [PubMed] [Google Scholar]
- 28.Loubet B., Seifert U., Lomholt M.A. Effective tension and fluctuations in active membranes. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2012;85:031913. doi: 10.1103/PhysRevE.85.031913. [DOI] [PubMed] [Google Scholar]
- 29.Gov N. Membrane undulations driven by force fluctuations of active proteins. Phys. Rev. Lett. 2004;93:268104. doi: 10.1103/PhysRevLett.93.268104. [DOI] [PubMed] [Google Scholar]
- 30.Lacoste D., Lau A.W.C. Dynamics of active membranes with internal noise. Europhys. Lett. 2005;70:418. [Google Scholar]
- 31.Brooks F.J., Carlsson A.E. Nonequilibrium actin polymerization treated by a truncated rate-equation method. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2009;79:031914. doi: 10.1103/PhysRevE.79.031914. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.El Alaoui Faris M.D., Lacoste D., Bassereau P. Membrane tension lowering induced by protein activity. Phys. Rev. Lett. 2009;102:038102. doi: 10.1103/PhysRevLett.102.038102. [DOI] [PubMed] [Google Scholar]
- 33.Pontani L.-L., van der Gucht J., Sykes C. Reconstitution of an actin cortex inside a liposome. Biophys. J. 2009;96:192–198. doi: 10.1016/j.bpj.2008.09.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Carvalho K., Lemière J., Sykes C. Actin polymerization or myosin contraction: two ways to build up cortical tension for symmetry breaking. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2013;368:20130005. doi: 10.1098/rstb.2013.0005. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


