Domain and Interdomain Energetics Underlying Gating in Shaker-Type K_V Channels

Abstract

To understand gating events with a time-base many orders-of-magnitude slower than that of atomic motion in voltage-gated ion channels such as the Shaker-type K_V channels, a multiscale physical model is constructed from the experimentally well-characterized voltage-sensor (VS) domains coupled to a hydrophobic gate. The four VS domains are described by a continuum electrostatic model under voltage-clamp conditions, the control of ion flow by the gate domain is described by a vapor-lock mechanism, and the simple coupling principle is informed by known experimental results and trial-and-error. The configurational energy computed for each element is used to produce a total Hamiltonian that is a function of applied voltage, VS positions, and gate radius. We compute statistical-mechanical expectation values of macroscopic laboratory observables. This approach stands in contrast with molecular-dynamic models which are challenged by increasing scale, and kinetic models which assume a probability distribution rather than derive it from the underlying physics. This generic model predicts well the Shaker charge/voltage and conductance/voltage relations; the tight constraints underlying these results allow us to quantitatively assess the underlying physical mechanisms. The total electrical work picked up by the VS domains is an order-of-magnitude larger than the work required to actuate the gate itself, suggesting an energetic basis for the evolutionary flexibility of the voltage-gating mechanism. The cooperative slide-and-interlock behavior of the VS domains described by the VS-gate coupling relation leads to the experimentally observed bistable gating. This engineering approach should prove useful in the investigation of various elements underlying gating characteristics and degraded behavior due to mutation.

Introduction

The voltage-controlled gating of Na⁺, K⁺, and Ca²⁺ channels is a regulatory function crucial for living cells. It involves cooperation among intramolecular domains with distinct evolutionary histories, structures, and functions (1,2). Gating events occur over a million-fold measured experimental time range, from microseconds to seconds, and this time range can in some cases be observed in a single record from a single channel (3). Discrete-state hidden Markov models have provided kinetic descriptions of gating over this time range. These models describe gating as transitions among discrete states of empirically known lifetimes but typically unknown physical structure (4–6). Another approach, molecular-dynamics simulation, computes the atomic motions in models of crystallographically defined structures for short snippets of time. The actual gating motions are seldom if ever observed in these simulations unless the system is highly biased to induce gating (7–17). These atomic simulations likely do not allow the free energies governing large reconfigurations in a channel macromolecule to reach sufficient convergence (18), and they do not extend to most gating phenomena that electrophysiological experiments typically assess.

In this article, we follow an engineering approach to voltage-controlled gating. Events evolving at different scales of time and/or length are described at different levels of resolution and organized into a hierarchical model with two tiers. The presented model incorporates known aspects of structure, computed physical interactions, and hypothesized elements to simulate actual experiments. The model can correlate structural and functional experimental data, yet it can be solved with computational methods that are both economical and rigorous.

The lower tier of our gating model comprises models describing the internal physics of the individual voltage-sensor (VS) and gate domains. Structural information is abstracted into a generic geometry of each domain and a set of physical interactions known to be involved and which we hypothesize dominate the function of each domain. The VS and gate domain models are integrated into the channel model in terms of their energetics: overall channel configurational energy is described by an energy map (Hamiltonian). Domain energetic contributions are computed and sampled over all degrees of freedom made explicit in the domain models. This makes our approach essentially different from that of the state-based hidden Markov-chain models of gating because the hidden Markov-chain approach does not compute any Hamiltonian components from given physical features, but instead infers an overall Hamiltonian from functional data, assuming that the relevant configurations are restricted to a hypothesized set of energy minima. The hidden Markov-chain approach primarily goes backward from experimental results to a constrained set of state transitions; our approach attempts to go forward from a physical model to predict experimental results, with an exception discussed below regarding coupling.

The upper tier of our hierarchical model describes the cooperation of the VS and gate domains. Domain interaction is formally described by a map of configurational energy quantifying the energetic cost of the coexistence of configurations in a VS domain and in the gate domain. With the VS and gate domains described by physical models, the model developed of a gated channel provides a constrained view of the mechanism by which these domains can be coupled. Although at this stage no structure-based physical model exists for creating this map, available functional data allow us to construct a well-defined map for the VS/gate interaction.

Unlike state-based hidden Markov models (which describe the kinetics of a single entity, the channel) and atomistic models (which describe the channel as a homogeneously modeled ensemble of interacting atoms), our two-tier model makes explicit the intrinsic energetics of the domains and the energetics of the interactions among domains. It thereby gives an engineering decomposition of the mechanism that has not been naturally provided by the hidden Markov-chain models or atomistic simulations.

Analyzing Shaker-type K_V channels, we find that relatively simple models of the VS and gate domains coupled via a simple energy landscape predict experimental charge/voltage and conductance/voltage relations quite well. The only coupling function that we have found that is consistent with known experimental results is a “two-latch” mechanism, which leads to the Shaker domains sliding and interlocking to produce gating that is essentially bistable. Our analysis also produces the most detailed accounting of gating energetics to date. Specifically, we find that the electrical work picked up by the VS domains is an order-of-magnitude larger than the work needed for reconfiguring the gate domain between conducting and nonconducting configurations. Therefore, there is disposable energy in the gating mechanism allowing, in principle, for the evolution of diverse gating characteristics. Such multiscale engineering approaches may be applicable to other large biophysical systems whose measures of interest have long characteristic times.

Model

We briefly describe here the VS and gate domain models that we embed into the full-channel model. Because these have been the subjects of previous publications (19–22), we only detail the specific model configurations used here. We then elaborate the formal framework for integrating these domain models into a statistical-mechanical model of the full channel.

Model of the VS domain

The model of a VS domain comprises an α-helical S4 transmembrane segment sliding in a “gating canal” formed between the S1–S3 and S5–S6 segments. The protein matrix is represented by a uniform dielectric and charged residues by embedded point charges (Fig. 1 A). In previous work (21), this model of a single VS domain was studied in a computational setup including membrane and water dielectrics and encapsulated by electrodes to establish voltage-clamp boundary conditions. The expected whole-body movements of the uncoupled S4 charges in response to the applied membrane voltage V_m have been computed (21,22). In constructing the channel model, we use the (electrostatic) configurational energy ${\mathcal{H}}_{\text{VS}}$(z,ϕ,V_m) and the displaced gating charge Q(z,ϕ) (Fig. 2 A) computed for a VS domain as a function of S4 position (translation z, rotation ϕ) and membrane voltage V_m in the range −100 mV to +100 mV. Our specific VS model is the α-helical model described by Peyser and Nonner (21). Variations of that VS model have been explored (22). The model produces a gating-charge/voltage relation for an isolated VS domain that is comparable in total charge and slope to the relation experimentally observed in full Shaker-type K_V channels (see Figs. 5a and 8b of Peyser and Nonner (21)). The electrostatics of that model makes the S4 charges follow an emergent helical (i.e., screw) trajectory.

Figure 1.

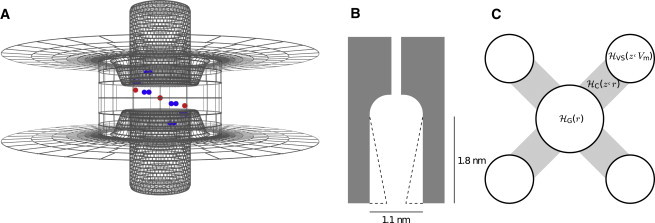
Elements of the domain-based channel model. (A) Representation of a single VS domain. Voltage is sensed by the S4 helix (central cylinder) moving in a gating canal formed between other VS transmembrane segments (represented by a dielectric domain). Displaced charge and energetics computed for this model of a single VS domain are incorporated into the channel model. Charges are indicated in color (blue, S4 charges; red, countercharges on S2 and S3). The shown (central) S4 position corresponds to translation z = 0 and displaced gating charge Q = 0. The surface grid marks the dielectric boundaries of the membrane and the protein; the electrostatics are solved on the basis of this grid. For a full description of this VS model, including the geometry of the dielectrics and the coordinates of S4 charges and countercharges, see Peyser and Nonner (21). (B) The conductive pore is gated by varying the radius r at the intracellular mouth of the pore vestibule, which controls the drying/wetting probability of that gate region. The shown gate outlines follow the outermost number density maximum of the confined water. (Shading) Maximal width of the gate (r = 0.55 nm). (Dashed outline) Pore configuration (r = 0.2 nm) in which the gate would be dry (nonconducting) most of the time. (C) The central gated pore interacts with each of the four peripheral VS domains. Each VS domain contributes the configurational energy ${\mathcal{H}}_{\text{VS}}$, and the gate domain contributes the intrinsic configurational energy ${\mathcal{H}}_{\text{G}}$, to the Hamiltonian of the channel. A specific joint configuration of a VS domain and the gate domain (defined by their translational and radius coordinates, z and r, respectively) contributes the configurational energy ${\mathcal{H}}_{\text{C}}$ to the Hamiltonian of the channel. ${\mathcal{H}}_{\text{C}}$ thus defines the coupling among VS and gate domains. To see this figure in color, go online.

Figure 2.

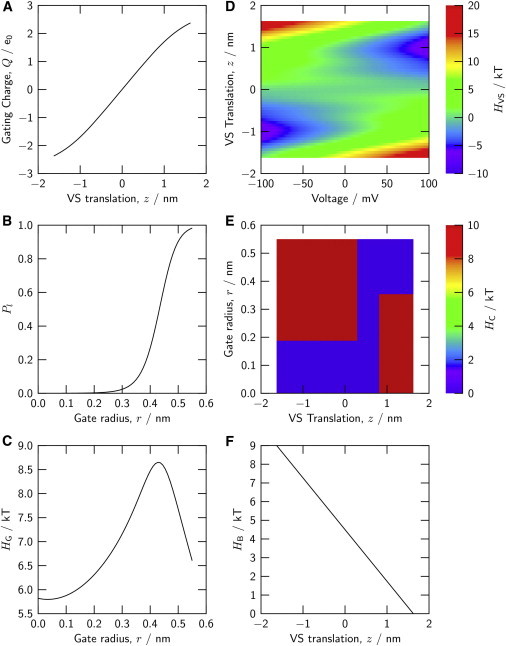
Six relations specify the domains and domain interactions of the channel model. (A) Displaced gating charge Q of a voltage sensor domain as a function of the translational S4 position, z. (B) Probability P₁ of the liquid-filled (conducting) configuration of the gate, as a function of the intracellular gate radius, r. (C) Hamiltonian component ${\mathcal{H}}_{\text{G}}$ (gate work) associated with the gate radius r. (D) Hamiltonian component ${\mathcal{H}}_{\text{VS}}$ associated with the translational position z of an individual VS domain, as a function of the transmembrane voltage (Eq. 3). (E) Hamiltonian component ${\mathcal{H}}_{\text{C}}$ describing the coupling between a VS domain at translational position z and the hydrophobic gate of radius r. (F) Hamiltonian component ${\mathcal{H}}_{\text{B}}$ describing the energetic bias acting on a VS domain, as function of translational position, z. Panels A and D are predictions by the VS model described in Peyser and Nonner (21); panels B and C are predictions by the gate model in Roth et al. (20). To see this figure in color, go online.

Our VS model describes linear dielectrics, including the protein matrix, by piecewise uniform dielectric coefficients. This continuum electrostatic model is solved consistently using a boundary element method (21). At the later stage of modeling presented in this article, our engineering model of the full channel requires only the relations ${\mathcal{H}}_{\text{VS}}$(z,ϕ,V_m) and Q(z,ϕ) to specify the behavior of the VS domain. Our channel model does not require a specification of how these relations arise. In principle, the two relations could be directly measured rather than modeled. Both relations that we use are robust: the chosen relations can arise in our generic VS model from a range of configurations (22). A coarse-grained model like that developed by Dryga et al. (18,23) might provide more accurate relations for specific structures or domains in the future.

Model of the gate domain

The model of the gate is based on the wetting/drying of a hydrophobic segment of the ion-conducting pore. Following experimental results (24), we postulate that the S4 position in the VS domains controls the width of the intracellular vestibule of the pore, which has a hydrophobic wall (25). Vestibule geometry biases the local liquid/gas phase equilibrium of water and the electrical polarizability near ions. Depending on vestibule width, the liquid-water column in the pore is disrupted by a gas bubble for a fraction of the time, which vapor-locks ionic conduction.

The pore vestibule is modeled as a generalized cylinder whose intracellular radius r is variable whereas the radius at the junction of vestibule and central pore cavity is fixed (Fig. 1 B). The intracellular radius is controlled by the transmembrane voltage via the VS domains, as described below. Water confined in the hydrophobic vestibule can exist in two equilibrium phases: liquid and/or gas. The geometry of the vestibule in this system modulates the probability of a gas bubble. A small vestibular radius promotes bubble formation (the area of a potential water-vapor interface drops with the square of gate radius whereas the interface area with the hydrophobic pore wall drops linearly with gate radius). Molecular-dynamics simulations of relevant systems (26–29) have shown that the dynamics of wetting/drying are much faster (ns) than those of the gating transitions (ms) observed in ion channels. With the liquid-filled and bubble-locked states in quasi-equilibrium, liquid-filled probability P₁ is treated as a quasi-deterministic measure of conductance that depends on the gate radius r.

Roth and Kroll (19) and Roth et al. (20) have used density functional theory of classical fluids and morphometric scaling (30) to compute the thermodynamics of the liquid/gas phase equilibrium in a hydrophobic capillary of varied geometry. Following their work, we describe water-water interaction by a square-well potential and hard core repulsion and wall-water interaction by a potential with both repulsive and attractive components (compare Fig. 6 of Roth et al. (20)). Although very simple, this water model captures the phase transition properties of water at room temperature (particularly because the potential parameters have been optimized to reproduce the relevant properties for this particular state-point (19)).

Two functional states of the gate, conducting and nonconducting, are distinguished. Conduction is blocked when a gas bubble spans the cross-section of the pore and is at least 1 water-diameter wide. Any other configurations of the liquid/gas water phase in the pore are considered conductive. Each of the two functional states is assigned a grand potential. The grand potential of the conductive state is approximated by that of the liquid-filled gate. The grand potential of the nonconductive state is approximated by the average of the grand potential systematically sampled over configurations in which a gas bubble fills the gate cross-section and spans at least 1 water diameter (0.28 nm) in the axial dimension of the pore. Over that averaging, the grand potential samples are weighed according to the partition function of the sampled bubble configurations. For the gate as a whole, the grand potential ${\mathcal{H}}_{\text{G}}$(r) associated with a radius r is then the expectation value for the grand potential taken over the two functional states of the gate.

Two relations computed from the bubble-gate model are needed for specifying the gate in the full-channel model. One is the relation between the vestibular radius r and the probability P₁ of finding liquid water throughout the vestibule (permitting ion conduction). The other is the thermodynamic work ${\mathcal{H}}_{\text{G}}$(r) associated with the gate radius r, which is given by the grand potential of the bubble gate described above. Due to the different timescales of radius variations and gate wetting/drying, this work is well averaged at the timescale of gating and is hence included as a quasi-deterministic energy into the Hamiltonian of the channel model. These relations describing the bubble gate are shown in Fig. 2, B and C. The gate work is maximal for a vestibular radius at which the probability of the liquid-filled vestibule varies most steeply. Both a narrow, gas-filled vestibule and a wide liquid-filled vestibule require less work to establish. The magnitude of the work for operating this gate is rather small.

We define the conductance G(r) of the channel by

$$G\left(r\right)=P_{\text{l}}\left(r\right).$$ (1)

This measure of conductance does not include effects that a varying pore radius would have on ion flow in a wetted pore. In some calculations, G(r) is taken to be zero when the vestibule’s radius is <0.2 nm even during the small fraction of time when the vestibule is filled with liquid water.

Statistical mechanics of the full-channel model

We base our analysis on the canonical partition function $\mathcal{Q}$(V_m) describing the partitioning of the model between channel configurations in the presence of the membrane voltage V_m. Nine degrees of freedom are explicitly considered: each S4 segment of the four VS domains moves by translation along its axis (z = (z₁, z₂, z₃, z₄)) and rotation about its axis (ϕ = (ϕ₁, ϕ₂, ϕ₃, ϕ₄)), and the pore gate varies in radius (r). Because the partition function is systematically sampled on a discrete coordinate grid, equations are presented in discrete form.

Two forms of degeneracy are considered in deriving an expression for the partition function:

• 1.The four VS domains of the channel are indistinguishable, and
• 2.The Hamiltonian component ${\mathcal{H}}_{\text{C}}$ describing the coupling between a VS domain and the gate depends on the translation z but not on the rotation ϕ of the S4 segment.

We define the Boltzmann factor

$$B\left(\mathbf{z},r,V_{\text{m}}\right)=\text{exp}\left\{-\beta \left[{\mathcal{H}}_{\text{G}}\left(r\right)+\sum _{i=1}^4\left({\mathcal{H}}_{\text{C},i}\left(z_i,r\right)+{\mathcal{H}}_{\text{B},i}\left(z_i\right)+{\mathcal{H}}_{\text{VS},i}\left(z_i,V_{\text{m}}\right)\right)\right]\right\},$$ (2)

where β = (kT)⁻¹ (k is the Boltzmann constant and T is the absolute temperature (for these calculations 25 + 273.32 K)). The contributions ${\mathcal{H}}_{\text{C},i}$(z_i,r) and ${\mathcal{H}}_{\text{B},i}$(z_i) to the Hamiltonian are described below. Summation over the rotational degree of freedom of VS domain i is implied by the definition of the contribution of VS domain i to the Hamiltonian,

$${\mathcal{H}}_{\text{VS},i}\left(z_i,V_{\text{m}}\right)=-{\beta }^{-1}\text{ln}\sum _j\text{exp}\left[-\beta {\mathcal{H}}_{\text{VS},i}\left(z_i,{\varphi }_j,V_{\text{m}}\right)\right],$$ (3)

where j is the index of the sampled rotational positions. The function ${\mathcal{H}}_{\text{VS}}$(z,V_m) resulting from the VS model is shown as a false-color map in Fig. 2 D. Because the energy ${\mathcal{H}}_{\text{VS},i}$ is electrostatic, the algebraic summation in Eq. 2 of the energies contributed by the four VS domains implies that the individual VS domains are not significantly interacting with one another through long-range electrostatic force. This latter assumption remains to be assessed by an electrostatic analysis of the full channel.

To account for the degeneracy of the VS domain positions, we introduce n(k) as the number of ways in which the four identical VS domains can be arranged among the translational positions

$${\mathbf{z}}_{\mathbf{k}}=\left(z_{k_1},z_{k_2},z_{k_3},z_{k_4}\right),$$

where k = (k₁, k₂, k₃, k₄) identifies the sampled position of each VS. Thus n varies from 1 permutation if all four VS have identical z positions to 24 permutations if every VS is in a distinct position.

The summation operator over all combinations of distinct VS positions is then

$$\sum _{\mathbf{k}}=\sum _{k_1=1}^{N_z}\sum _{k_2=k_1}^{N_z}\sum _{k_3=k_2}^{N_z}\sum _{k_4=k_3}^{N_z},$$ (4)

where N_z is the numbers of nodes sampled in the z dimension. This operator visits each combination of VS positions only once, which reduces the computational cost of the summation by a factor of ≈20 relative to summing over all permutations of all positions.

Using Eqs. 2 and 3, we write the partition function on the discretized configuration space,

$$\mathcal{Q}\left(V_{\text{m}}\right)=\sum _{l=1}^{N_r}\sum _{\mathbf{k}}n\left(\mathbf{k}\right)B\left({\mathbf{z}}_{\mathbf{k}},r_l,V_{\text{m}}\right),$$ (5)

where N_r is the number of nodes sampled in the r dimension, and the weight n(k) accounts for the degeneracy due to the equivalence of VS domains in the summation operator of Eq. 4. Computation of the partition function via Eq. 5 involves summations over five degrees of freedom (the summation about the rotational degree of freedom of a VS domain, Eq. 3, is computed only once before computing the partition function). We sample 51 discrete positions in the z dimension, and 64 discrete values of gate radius r. Then, ∼2 × 10⁷ Boltzmann factors need to be evaluated for a systematic scan over the z and r degrees of freedom. The partition function is computed in this way for the voltage range −100 mV to +100 mV in steps of 1 mV.

The general equation to calculate the expectation value of a measure X at a voltage V_m is thus

$$\langle X\left(V_{\text{m}}\right)\rangle =\frac{1}{\mathcal{Q}\left(V_{\text{m}}\right)}\sum _{l=1}^{N_r}\sum _{\mathbf{k}}n\left(\mathbf{k}\right)B\left({\mathbf{z}}_{\mathbf{k}},r_l,V_{\text{m}}\right)X\left({\mathbf{z}}_{\mathbf{k}},r_l,V_{\text{m}}\right).$$ (6)

We are also interested in the equilibrium probability of one or more of the VS domains having the translational position $z_{k_1}$,

$$P\left(z_{k_1},V_{\text{m}}\right)=\frac{1}{\mathcal{Q}\left(V_{\text{m}}\right)}\sum _{l=1}^{N_r}\sum _{\left(k_2,k_3,k_4\right)}n\left(\mathbf{k}\right)B\left({\mathbf{z}}_{\mathbf{k}},r_l,V_{\text{m}}\right),$$ (7)

where

$$\sum _{\left(k_2,k_3,k_4\right)}={\sum }_{k_2=k_1}^{N_z}{\sum }_{k_3=k_2}^{N_z}{\sum }_{k_4=k_3}^{N_z},$$

summing over combinations of VS positions as in Eq. 4 while fixing the position of 1. Of further interest is the equilibrium probability of the gate having the radius r_l,

$$P\left(r_l,V_{\text{m}}\right)=\frac{1}{\mathcal{Q}\left(V_{\text{m}}\right)}\sum _{\mathbf{k}}n\left(\mathbf{k}\right)B\left({\mathbf{z}}_{\mathbf{k}},r_l,V_{\text{m}}\right).$$ (8)

Coupling the VS and gate domains

The four VS domains and the gate domain of the model channel are coupled as suggested by channel architecture (8) so that each peripheral VS domain individually communicates with the central gated pore (Fig. 1 C). A component ${\mathcal{H}}_{\text{C},i}$(z_i,r) for each VS domain i is included in the channel energetics to quantify the energetic cost of the vestibule radius r coexisting with the translational position z_i of that VS domain. The coupling is thus assumed to be dependent on S4 translation but not rotation. The functional form of ${\mathcal{H}}_{\text{c},i}$(z_i,r) is determined empirically here rather than computed from a physical model.

One coupling function, ${\mathcal{H}}_{\text{C}}$(z_i,r), illustrated by the false-color map in Fig. 2 E, was generated by trial and error so that the model approximately reproduces experimental relations (see Results and Discussion). This map consists of plateaus at two discrete energies, 0 and +10 kT. The large energy difference between the two plateaus makes it virtually impossible for the channel to visit the high-plateau region of the (z,r) joint-configuration space. Joint configurations are restricted to a corridor after the low plateau. The ${\mathcal{H}}_{\text{C}}$(z_i,r) map is analogous to a Ramachandran plot (31).

Energetic bias acting on the VS domains

Due to intrinsic symmetry, the model used for a single VS domain reacts symmetrically to positive and negative membrane voltages. Because in the Shaker-type K_V channel the charge/voltage relation is centered about a negative membrane voltage, we include a bias component in the energetics of each VS domain i. This bias, ${\mathcal{H}}_{\text{B},i}$(z_i), decreases linearly from 9 kT at z_i = −1.6 nm to 0 kT at +1.6 nm (Fig. 2 F). Thereby, each S4 segment works against a constant force as it is moved inward under a negative applied voltage. With this bias, the model of the individual VS domain approximates the shifted midpoint voltage of the charge/voltage relation of a full Shaker-type K_V channel (21). Possible origins of such a bias include an asymmetrical distribution of surface charge on both faces of the channel (22). For the purpose of this article, we parameterize this bias rather than make its origin explicit. A uniform bias acting on each individual VS domain of the model simply shifts the voltage dependencies predicted for gating charge and conductance; it does not otherwise alter the computed gating characteristics described below.

Results and Discussion

Fig. 3, A and B, shows the equilibrium charge/voltage (Q/V) and the conductance/voltage (G/V) relations computed as thermodynamic expectation values from the full-channel model (solid lines). Experimental relations observed in Shaker-type K_V channels (32) are shown also (solid circles). Several characteristics of the data are captured by the model:

• 1.Gating charge and conductance are half-maximal at different voltages,
• 2.Conductance varies more steeply than charge,
• 3.Gating charge saturates at ∼13 unit charges displaced per channel,
• 4.Conductance saturates at <1 at positive voltage and approaches 0 at negative voltage,
• 5.Charge approaches its asymptote more swiftly with positive than with negative voltage, and
• 6.Conductance approaches its asymptote more swiftly with negative than with positive voltage.

Figure 3.

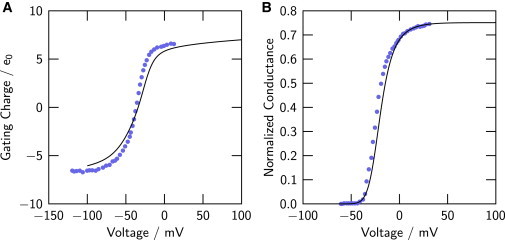
Consequences of the full-channel model compared to experiment. (A) Gating-charge/voltage (Q/V) relation of the full-channel model (solid line); experimental Q/V relation of Shaker (ShB-IR) potassium channels (from Fig. 2A in Seoh et al. (32)) (symbols). (B) Conductance/voltage (G/V) relation as defined by Eq. 1 of the model (solid line), and the experimental G/V relation from Fig. 2A in Seoh et al. (32) (symbols). To see this figure in color, go online.

The curves in Fig. 3 are computed using the energetics of coupling between the VS domains and the gate (the component ${\mathcal{H}}_{\text{G}}$(z,r) of the Hamiltonian) represented as a map in Fig. 2 E. That energy landscape is divided between two discrete energy levels, one at 0 kT allowing the respective (z,r) positions to coexist, and another at +10 kT prohibiting coexistence. The corridor (at 0 kT) allows the S4 segment of that VS domain to undergo translation (z) without concomitant variation of gate radius (r) in two regions of the z dimension, which are connected by a region centered around z = 0.58 nm that allows the gate radius to vary without energetic penalty over its full range of play.

The shape of the corridor shown in Fig. 2 E is required if the model is to predict the differences in slope and position on the voltage axis that are experimentally observed between the Q/V and G/V relations (characteristics 1 and 2 described above). An alternate shape of that corridor (see Gating Tuned by VS-Gate Coupling) gives very different predictions. The coupling energetics proposed here allow the charged particles to move independently of one another, as was originally assumed in the quantitative description made by Hodgkin and Huxley (33). As the S4 segments move away from their resting positions and approach critical locations z_c ≈ 0.58 nm, the gate can open spontaneously following its intrinsic energetics ${\mathcal{H}}_{\text{G}}$. This is only possible, however, if all S4 segments reach that critical location because a large coupling energy penalty is associated with any single S4 segment being located away from z_c (Fig. 2 E). Once the gate is open, the charged particles can continue to move. If a particle continues to move, the gate cannot close. In this way, the proposed coupling between VS domains and gate extends the original Hodgkin-Huxley model while preserving that model’s mutual independence among the charged particles through a subrange of their translation. Our model is also in general agreement with discrete-state hidden Markov-chain models in that independent configuration changes in the voltage sensors precede a concerted opening of the conduction pore (4–6). Our model, however, specifies the proposed coupling in structural and energetic terms, whereas the state-based models express the coupling in the attributes of hypothesized states.

The total gating charge displaced in the model in the range ±100 mV is 12.9 e₀, close to the experimental value obtained by dividing the number of channels into the gating charge displaced in an ensemble of channels (32).

Cooperative closure of Shaker-type channels

The conductance in Shaker-type channels is reduced exponentially when negative membrane voltages of increasing magnitude are applied. This relation has been experimentally verified down to very small open probabilities (<10⁻³) by recording (rare) single-channel openings in a membrane patch containing a known number of channels (34). Such events imply that the channel gate opens wide enough to allow a substantial rate of ion flow. An exponential relation for channel closure was established this way down to mean conductances of ∼10⁻⁷ times the maximal conductance.

We simulate this experiment in our model by setting channel conductance to zero for gate radii smaller than 0.2 nm, so that any conduction requires the gate in the model to open to a radius >0.2 nm. The G/V relation from this computation is plotted on a semi-logarithmic scale in Fig. 4 A (solid line). Indeed, negative voltage reduces the conductance exponentially, approximately e-fold per 2.6 mV, corresponding to an apparent gating charge q ≈ 9.5 e₀. The experimental charge reported by Seoh et al. (32) is 10.9 ± 1.3 e₀ in Shaker-type K_V channels (see also Schoppa et al. (35) and Aggarwal and MacKinnon (36)). The coupling effected by the Hamiltonian ${\mathcal{H}}_{\text{G}}$(z,r) of Fig. 2 E thus allows the VS domains to combine their electrical weights to maintain a gate radius that does not allow ions to flow at a rate detectable in a single channel. The apparent gating charge computed from the logarithmic slope of the model’s G/V relation is less than the total gating charge of the Q/V relation (Fig. 3 A) because S4 translations to z > z_c suffice to allow the gate radius to increase (Fig. 2 E).

Figure 4.

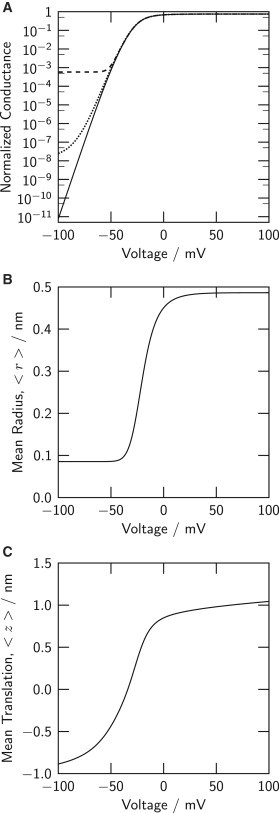
Effective channel closure by voltages ≤50 mV requires a threshold gate radius for conduction. (A) G/V relations of the full-channel model on a semi-logarithmic scale. (Solid line) Conduction is abolished at gate radii r < 0.2 nm regardless of presence of liquid water in the pore. (Dashed line) Conduction is controlled by the probability that the gate is water-filled, P₁ (compare Eq. 1). (Dotted line) Reducing VS-gate coupling energy (see text) degrades channel closure by hyperpolarization. (B) The exponential region of the G/V relation is associated with a near-asymptotic minimal gate radius. (C) The S4 segments of the VS domains change translational position z in the exponential region of the G/V relation. Voltages ≤50 mV tend to exclude VS domains from translations that allow conduction. Note that panels B and C show the expectation values 〈r〉 and 〈z〉 in the full-channel model.

A second experimental assessment of channel closure by negative voltages has been made that does not require channels to open to the extent that single-channel currents can be directly observed. Soler-Llavina et al. (37) have measured membrane current, including possible DC current leaking through closed K_V channels, that is abolished by a blocker of the ionic pathway of these channels. They determined that hyperpolarization reduces conductance to values not exceeding ∼10⁻⁵ times the maximal conductance. We simulate this experiment by allowing the probability that the gate contains liquid water (P₁) to determine conductance (Fig. 4 A, dashed line). The model conductance (Eq. 1) approaches a saturated minimal level near 10⁻³. Wetting/drying alone thus does not appear to suppress conduction to the extent observed in the experiment. A further reduction appears to be involved at small gate radii.

An analysis of pore electrostatics and ion/water packing in the gate is needed to theoretically assess ion flow through such a narrow gate. Because we describe pore boundaries by the outermost density maximum of the confined liquid water (see legend of Fig. 1), a radius of 0.2 nm, for example, implies that a single layer of water molecules (diameter 0.28 nm) covering the pore wall would leave a nominal diameter of ≈0.12 nm for the passage of ions. Ion flow through a hydrophobic constriction to r = 0.2 nm thus encounters both poor screening and difficulty of finding a trajectory for passage. Recent molecular-dynamics simulations of a hydrophobic gate in the GLIC ion channel indicate that the free energy associated with a hydrated Na⁺ ion in the gate region of the pore is up to 9 kcal (∼15 kT) larger than the free energy associated with the same amount of water but without a Na⁺ ion present in the gate region (38,39).

Fig. 4, B and C, shows the changes of gate radius and VS translation that underlie the reduction of conductance by hyperpolarization. The mean gate radius has essentially reached its asymptotic smallest value at these voltages. In contrast, the S4 segments continue inward translation throughout this voltage range. The exponential decay of conductance seen in Fig. 4 A (solid line) thus reflects a reduction in the probability that the four S4 segments all dwell at translations allowing the gate radius to exceed 0.2 nm.

The energy at the high plateau of the coupling energy map in Fig. 2 E (10 kT) was chosen to implement a simple principle: channels are virtually excluded from assuming certain joint z and r configurations. The plateau energy quantifies the strength of that restriction. It is therefore of interest to see what amount of plateau energy is needed to effect that restriction and what the consequences of weaker restriction may be for gating. Fig. 4 A (dotted line) shows the G/V relation computed for ${\mathcal{H}}_{\text{G}}$(z,r) maps with contours like those in Fig. 2 E, but with the energy of the upper-left plateau reduced from 10 to 4 kT. Channel closure at negative voltages becomes less effective (we assume conduction to cease for gate radii <0.2 nm for this test). A restrictive energy of >4 kT is needed for a Shaker-type voltage dependence of channel closure.

Energetics of gating

The model makes explicit how the electrical work picked up by the VS domains is used in gating. Fig. 5 shows the expectation values of the total electrical work received through the VS domains (solid line) and of the thermodynamic work done on the gate (dashed line) as functions of membrane voltage. Only a small fraction of the electrical work is used on the gate itself, inasmuch as gate radius is varied by voltage between the conducting and nonconducting gate configurations. The work on the gate itself is given by the Hamiltonian component ${\mathcal{H}}_{\text{G}}$(r), which is small (Fig. 2 C) and balanced: open and closed pairs of radii r exist for which ${\mathcal{H}}_{\text{G}}$(r) is the same. Due to the low energetic cost of operating this gate, the most important use of the electrical work received by the VS domains is to arrange the S4 segments into particular translational positions where, like a key, they lock or unlock the variation of gate radius. Electrical work is chiefly invested into a reduction of entropy.

Figure 5.

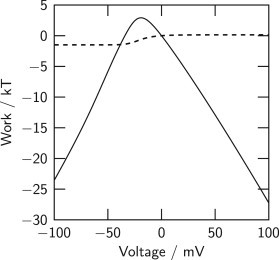
The work for operating the hydrophobic gate (dashed line) is small compared to the electrical work picked up by the four VS domains (solid line). The gate work is the expectation value 〈${\mathcal{H}}_{\text{G}}$〉, and the electrical work is computed as −〈Q〉V_m, where 〈Q〉 is the expectation value of the total gating charge displaced per channel (21). Gate work referenced here is that done at 0 mV.

Voltage sensors producing electrical work in excess of the thermodynamic work needed for operating the gate itself appear to give channels disposable energy for tuning their gating characteristics—for example, by choosing specific forms of coupling (described by the Hamiltonian component ${\mathcal{H}}_{\text{C}}$ in our model). Two variants of coupling are discussed below. Furthermore, because the amount of work picked up by a VS domain is the product of displaced gating charge and membrane voltage, these VS domains can, in principle, drive arbitrary workloads at large enough voltages. This feature allows channels to focus their open/close transition on a particular range of membrane potential. In our model for Shaker, we have introduced such an additional workload in the form of the bias component of the Hamiltonian, ${\mathcal{H}}_{\text{B}}$ (Fig. 2 F). This bias acts on each one of the VS domains individually to shift the voltage dependence of that VS domain.

The hydrophobic gate in our model requires little work to operate because its wetting/drying has intrinsic thermodynamic balance. Crucial parameters for this balance are the gate dimensions and the interaction of the pore wall with water. The gate work ${\mathcal{H}}_{\text{G}}$ shown in Fig. 2 C corresponds to a contact angle of 90.8° for a flat wall. Thus, the water-to-wall interaction is approximately halfway between fully hydrophobic and fully hydrophilic.

Channels may use variations of gate hydrophobicity or, more generally, of pore configurational energetics to tune their gating. Indeed, point mutation of the pore domain residues of Shaker changes the midpoint voltage and slope of the normalized conductance/voltage relation: left-shift is observed together with increased slope, or right-shift together with reduced slope (40).

To see how an energetically biased gate may affect gating in the model, we algebraically add to the Hamiltonian component ${\mathcal{H}}_{\text{G}}$ (Fig. 2 C) an energy that changes linearly with gate radius from 0 to a value stepwise varied between −8 and +8 kT. The pattern and the extent of change of the computed conductance/voltage relations (Fig. 6 F) are similar to those experimentally observed by Yifrach and MacKinnon (40). From a fit of their data with a hidden Markov-chain model, these authors find that an equilibrium constant L = 7.5 (kT ln 7.5 ≈ 2 kT) describes the open/close transition in WT Shaker; our Fig. 5 shows ∼2 kT for the respective work. Thus, the two kinds of model give similar estimates for the gate work. The gate work is small in proportion to the electrical work available for operating the gate (Fig. 5).

Figure 6.

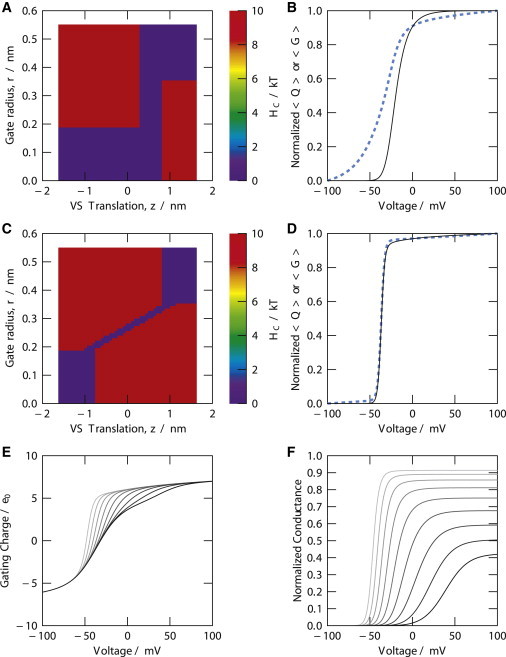
Gating tuned by VS/gate coupling or gate bias. (A and C) Maps of coupling energy ${\mathcal{H}}_{\text{C}}$(z,r); (B and D) normalized charge/voltage (dashed line) and conductance voltage relations (solid line) computed with the maps from panels A and C, respectively. (E and F) Charge/voltage and conductance/voltage relations for models with an energy bias added to ${\mathcal{H}}_{\text{G}}$(r). The bias is 0 for r = 0 and increases linearly with r toward the maximal radius, r_max = 0.55 nm. The bias at r_max is stepped from −8 kT (leftmost curve, light shaded) to +8 kT (rightmost curve, solid) in increments of 2 kT. Note that the normalized conductance is defined as the probability of the wetted gate (Eq. 1). To see this figure in color, go online.

In our model, a substantially biased gate generates a pattern of gating characteristics more complex than a simple shift of relations along the voltage axis (Fig. 6, E and F). For instance, the charge/voltage relation varies from a very steep relation indicating coupling among S4 movements to a biphasic relation. These patterns differ substantially from Shaker-type gating. The midpoints of the charge/voltage and conductance/voltage relations of Shaker are centered about negative voltages. In our model, a biased gate would bias these voltage dependencies, but with side effects not expressed in WT Shaker gating. A linear bias ${\mathcal{H}}_{\text{B}}$(z) acting on each individual VS domain (Fig. 2 F) effects a simple shift of characteristics along the voltage axis.

Gating tuned by VS-gate coupling

The energetic budget described in the preceding section is likely to support a range of possible gating characteristics. We compare here two variants of VS-gate coupling, with all the other model features unchanged, to probe this possible diversity in gating. As already described, a corridor of low configurational energy in the map ${\mathcal{H}}_{\text{B}}$(z,r), including intervals in which translation is possible in a VS domain while the gate radius is not varying, but also including an interval where the gate radius can vary without concomitant variation of VS translation, produces Shaker-type gating characteristics. The Q/V and G/V relations have different midpoints and slopes (Fig. 6, A and B).

An alternate map of coupling energy is shown in Fig. 6 C. Here, joint movements in the VS domain and the gate are enforced by a low-energy corridor involving a diagonal interval across the z,r plane. The resulting Q/V and G/V relations both are very steep and their midpoints coincide at the same voltage (Fig. 6 D). The steepness of these relations indicates that the movements of the four VS domains and the gate domain become strongly cooperative, with consequences that contrast the distinct Q/V and G/V relations experimentally observed in Shaker-type channels (Fig. 3). The cooperativity in the alternate form of coupling is global because the variation of gate radius forced by translation in one VS domain requires that all other VS domains also undergo translation. Superimposable voltage dependencies of conductance and fluorescence-monitored S4 movement similar to the G/V and Q/V relations in Fig. 6 D have been observed, for instance, in KCNQ1 channels formed in the absence of the β-subunit (41). (However, a gate biased toward the open configuration could produce such a pattern as well (Fig. 6, E and F).)

These examples of VS-gate coupling illustrate how, within constraints set by domain topology (Fig. 1 C) and homotetrameric structure, different patterns of cooperativity might arise in K_V channel gating. The calculations indicate how sensitive the gating characteristics are to the VS-gate coupling. They confirm that the coupling energy map that we have proposed for Shaker-type gating is well constrained.

Preferred configurations in gating

Experiments have shown that both displaced gating charge and ionic conductance of voltage-gated channels fluctuate essentially between two discrete values (42,43). The model allows one to compute the statistical distributions of configurations and thus to assess to what extent the physics of the model produces discrete behaviors.

Fig. 7 shows the probability distributions for VS translation (A) and gate radius (B) as computed for the full channel over a range of membrane voltage. These probabilities are defined by Eqs. 7 and 8, respectively. The S4 segment of a VS domain preferentially dwells in two well-defined translational positions near ±1 nm and is switched by voltage from one to the other. Likewise, there are two well-visited regions of gate radius, one ≥0.47 nm and associated with large conductance (Fig. 2 D), and the other <0.2 nm and associated with very small conductance. At positive voltages, an intermediate radius ≈0.38 nm is visited with a noticeable probability. This radius differs substantially from both the fully open and fully closed radii, and thus is reached from either radius by a major reconfiguration of the gate. One might therefore expect to experimentally detect, considering the available time resolution, fluctuations toward a small subconductance (compare Fig. 2 B) that persist as mean conductance saturates. Ensemble fluctuations of Shaker current indicate a saturating apparent open probability of ≈0.75 (solid circles in Fig. 3 B; Seoh et al. (32) and Islas and Sigworth (34)), and short interruptions of unitary current persist at positive voltage (44).

Figure 7.

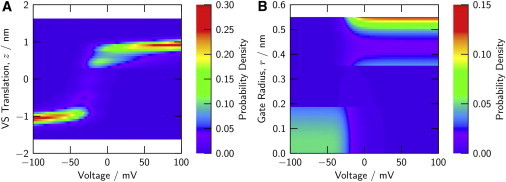
Bistability in the use of configuration space by the model channel. (A) The probability density of one or more VS domains being in translational position z versus transmembrane voltage. (B) The probability density of the gate having radius r versus transmembrane voltage. Probability density is in units of probability per length increment (0.064 nm for z and 0.0094 nm for r). Probabilities are computed from Eqs. 7 and 8, respectively. To see this figure in color, go online.

The computed distributions then predict the essentially bistable characteristics of the fluctuations of both charge displacement and conductance. The bistability in full-channel properties originates from the bistability inherent to both the VS and gate type of domains (Fig. 2, C and D) and is amplified by the interactions among these domains. A domain-based model provides insight into these internal aspects of channel energetics.

Conclusion

A model of the Shaker-type K_V channel gating process has been constructed by striking a middle ground between hidden Markov chain models that describe the kinetics of the entire channel as a single entity and molecular dynamics simulations that describe every atom of the channel. Here, we have modeled the physics of known phenomena (how the VS moves and how a change in geometry creates a bubble to stop permeation) and used an energy description for the physics of what is not explicitly known (how those two phenomena are coupled). In this way, the model quantifies the intrinsic energetics of the domains as well as the interactions among domains.

These results lead to several insights into the gating process. Realistic Q/V and G/V relations are produced only if these domains are coupled by a mechanism that allows the VS and domains to slide and interlock with regard to one another. Additionally, the electrostatics of the VS domains, the hydrophobic nature of the gate domain, and their interactions produce essentially bistable behavior in both the movement of gating charge and the conductance.

This approach provides an engineering view of how channels set their gating characteristics. These results also suggest further studies to better understand the gating process, such as charge-neutralization mutants targeting the explicit charges in the model.