Ejecting Phage DNA against Cellular Turgor Pressure

Abstract

We examine in vivo ejection of noncondensed DNA from tailed bacteriophages into bacteria. The ejection is dominantly governed by the physical conditions in the bacteria. The confinement of the DNA in the virus capsid only slightly helps the ejection, becoming completely irrelevant during its last stages. A simple calculation based on the premise of condensed DNA in the cell enables us to estimate the maximal bacterial turgor pressure against which the ejection can still be fully realized. The calculated pressure (∼5 atm) shows that the ejection of DNA into Gram-negative bacteria could proceed spontaneously, i.e., without the need to invoke active mechanisms.

Introduction

The explanation of all the relevant (thermodynamical) forces guiding the ejection of dsDNA from tailed bacteriophages into bacterial cells, despite 50 years of research, is still missing (1,2). The ejection starts as a release of DNA from the fully packed capsid (protein coating of the bacteriophage). The DNA is packed to extreme densities and exerts a pressure of 25–100 atm on the capsid (3,4). Models developed and tested in vitro (see Ponchon et al. (1) and Molineux and Panja (2) and references therein) predict that the ejecting force resulting from even such a dense packing is insufficient to completely transfer the DNA into the cell interior. Although cells have smaller turgor pressures than fully packed bacteriophages, the ejecting force (and pressure) in the capsid drops sharply as it empties (5).

A recent single-molecule Hershey-Chase experiment (6) hints that in vivo ejection is controlled not by the amount of DNA left inside the capsid but by the amount ejected into the cell. This means that once the pressure built-up in the bacteriophage is spent on the DNA ejection, a cellular mechanism takes over, e.g., as seen in vivo for T5 (7) and T7 (8). There have been various proposed mechanisms for completion of the ejection: nanomotors or enzymes that ratchet in the stalled part of the DNA (8,9); a solvent flow through the semipermeable capsid and into the cell, simultaneously flushing the DNA trough the tail (10); osmotic pressure from proteins remaining in the capsid (11); and diffusion of DNA with assisted pulling from proteins in the cell (12). It appears that none of these models give a definite answer; experiments suggest a coexistence of many different mechanisms.

We propose a scenario sufficient to explain ejection into some Gram-negative bacteria based only on thermodynamic considerations of DNA in a noncondensed state in the capsid and in a condensed state in the cell. Models of DNA ejection based on the continuum theory by Ubbink and Odijk (13,14) have been applied to explain the ejection when both the ejected and encapsidated DNA are condensed (15). In the model by Tzlil et al. (15), the capsid DNA, being confined, has a nonoptimal shape that generates the force ejecting it from the capsid until the ejection force is balanced by an external counterforce. If this in vitro model is applied to in vivo cases, it predicts that ejection stalls if the cellular turgor pressure is larger than ∼0.5 atm. Typical cellular pressures are estimated to be 0.3–5 atm for Gram-negative (16–18) and 15–25 atm for Gram-positive bacteria (17).

In our approach, we maintain the hypothesis that DNA is condensed in the cell due to the presence of multivalent cations during ejection (the concept of a condensate in the cell during ejection is not incompatible with a high reaction rate (19), and accordingly, a high DNA transcription rate after complete ejection). Typical in vitro experiments cannot obtain a clean separation between two (three) compartments, one in the virus (immersed in the extracellular fluid), and the other in the cell (20), which is a key feature of our model. The results obtained in vitro may thus have a limited applicability in the in vivo conditions. Condensing agents are found in some capsids, but this is not a general situation and has been related to reduced infectivity (21). Many viral capsids are permeable to small ions, so we expect intracapsid solvent conditions analogous to those in their exterior. Because typical extracellular fluids have no condensing agents in sufficient concentrations, DNA ejection into bacteria is expected to proceed from a noncondensed state.

Modeling the DNA

The phage DNA is one long strand of total length L₀ and persistence length L_p ≈ 50 nm (22) able to move between two compartments with different thermodynamic conditions—the virus and the cell. It is thus partitioned in two pieces, one of length L inside the virus head and tail, and the other of length L₀ – L in the cell. Assuming no attractive DNA-DNA interaction in the capsid (noncondensed DNA), the total force on the DNA will tend to eject it from the capsid. There are two major contributions to the free energy F_cell of the DNA in the cell. Because of the presence of multivalent ions and osmolytes, the ejected DNA will condense. The shape of the condensate is a result of a competition between DNA-DNA attractions mediated by the cations and unfavorable effects of DNA bending. On the other side, the major contribution to the free energy inside the capsid comes from bacteriophage tail confinement, bending from the capsid confinement, and excluded volume interactions between DNA segments.

Ubbink-Odijk model for condensed DNA in the cell

The state of the DNA inside the cell is described following the outline by Tzlil et al. (15). The volume V of the condensed DNA is proportional to the contour length L of the DNA V = A₀(L₀ – L), with A₀ as the area per unit length of DNA. The DNA condensate is treated in the Ubbink-Odijk model (13,14) with free energy F_tor = –γV + σS + E_bend consisting of: a negative (attractive) part proportional to the DNA volume –γV, where γ is an effective condensing pressure; a positive contribution proportional to the surface area σS, where σ reflects a lack of DNA neighbors at the condensate surface; and a bending energy of k_BT L_p/2R² per unit length of a circular loop of DNA wound at a radius R. The total free energy F_tor is minimal when the condensate has the shape of a torus (15), but there are other possibilities like rods (23). A different shape would only change the surface and bending energy terms to some degree.

The DNA in the condensate is assumed to be hexagonally packed with the area per unit length of DNA $A_0=\pi d_0^2/\sqrt{12}$ —the packing constant for hexagonally packed cylinders (15). Here d₀ ≈ 2.8 nm is the experimentally determined closest separation between DNA strands with added condensing agents (15,24). We note that Tzlil et al. (15) model the surface free energy contribution by assuming the loss of one-half of DNA nearest neighbors, whereas we assume the loss of one-third of the nearest neighbors as derived by Ubbink and Odijk (13). This constitutes a minor correction to the surface free energy term, but may become important if used to determine model parameters from toroid shapes.

The approximation adopted by Tzlil et al. (15) assumes the toroid to have the shape of a thin torus. In this regime, the bending energy can be approximated as if the whole length of DNA is wound at a (mean) distance R to the center. We calculate the free energy of the condensate as for a torus with major radius R as

$$F_{\text{tor}}\left(L,R\right)=-\gamma A_0\left(L-L_0\right)+\frac{2}{3}\frac{A_0\gamma }{d}\sqrt{2\left(L-L_0\right)A_0}\sqrt{R}+\frac{k_{\text{B}}T}{2}\frac{\left(L-L_0\right)L_p}{R^2},$$ (1)

and proceed with a variational approach. Minimizing Eq. 1 with respect to the major radius R yields optimal R,

$$R={\left(\frac{3d{L}_p}{A_0\gamma \sqrt{2A_0}}\right)}^{\frac{2}{5}}{\left(L-L_0\right)}^{\frac{1}{5}},$$ (2)

so that the minimal free energy of a toroidal condensate (15) is

$$F_{\text{tor}}=-{\mathit{ϵ}}_0\left(L-L_0\right)\left[1-b{\left(\frac{A_0^2{L}_p}{d_0^4{\mathit{ϵ}}_0}\right)}^{\frac{1}{5}}{\left(L-L_0\right)}^{-\frac{2}{5}}\right],$$ (3)

where ϵ₀ = A₀γ is the condensation free energy per unit length in an ideally packed hexagonal lattice and b = 1.308 a constant. This ϵ₀ was determined by Tzlil et al. (15) by fitting the toroid major axis to experimental data for λ-DNA in a solution of polylysine (23). Inasmuch as they chose a different surface term than that used by us and in the original model (14), the condensation free energy per unit length they obtain, γ_T, is smaller than ours, γ_UO. The shapes of toroids in the model of Ubbink-Odijk (14) are determined by a nondimensional parameter

$$\alpha =\frac{\sigma V^{\frac{1}{3}}{d}_0^2}{L_p},$$ (4)

which depends on the choice of surface energy σ. By using a different choice for the surface energy, the fits to toroid shapes would correspond to different values of the surface free energy σ than in the original model. Because σ is derived from γ, we have that the Ubbink-Odijk model, adopted here also by us, has γ_UO = 3/2 γ_T = 0.15 k_BT/nm³ (∼6 atm). This difference arises solely from different treatment of the missing neighbors at the surface of the toroid (one-third missing in Ubbink and Odijk (14), γ_UO ∼ 6 atm versus one-half missing in Tzlil et al. (15), γ_T ∼ 4 atm). An alternative approach to fitting is to obtain the condensing energy per unit length from osmotic force measurements (24), e.g., a 20 mM solution of Cobalt Hexamine corresponds to 0.024 k_BT nm³. The comparison of the two values obtained (0.15 k_BT nm³ vs. 0.024 k_BT nm³) shows that the thermodynamics of the condensed DNA importantly depends on the condensing agent.

When most of the viral DNA is in the condensate, L ≪ L₀, the surface and bending terms in Eq. 3 are negligible (15). This is because the largest contribution to the free energy of tori comes from the bulk term in F_tor, as can be seen from

$$1.308{\left(\frac{A_0^2{L}_p}{d_0^4{\mathit{ϵ}}_0}\right)}^{\frac{1}{5}}{L}_0^{-\frac{2}{5}}\ll 1.$$ (5)

Thus, the contributions of the surface and bending terms in the free energy are much smaller from the bulk contribution. To confirm the wider applicability of this statement, we performed a full minimization for toroids with different lengths of DNA, corresponding to different phage genomes. The minimization of free energy yielded the optimal shape together with the corresponding volume free energy F_vol = γV, surface free energy F_surf = σS, and the bending energy F_bend. The optimal condensate shapes are shown in Fig. 1 with the corresponding energy contributions. We see that for all but the smallest phage, the correction to the turgor pressure that the phage can eject against, ΔΠ, is small.

Figure 1.

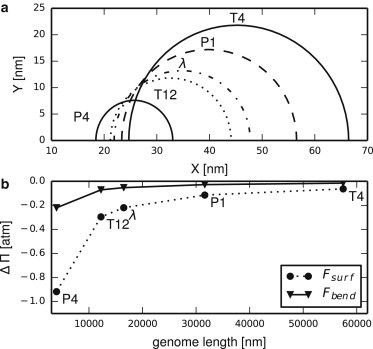
(a) Optimal DNA toroid shapes for several different lengths of DNA corresponding to well-known phages (22) (see text for details). Only the upper halves of the cross sections are shown. (b) The calculated correction to turgor pressure ΔΠ (see main text) for the DNA condensate in the cell as a function of genome length arising from the surface F_surf and bending F_bend free energies.

Excluded volume for two DNA rods in the capsid

The dominant part of the excluded volume for two DNA molecules comes from screened electrostatic interactions. Due to its rigidity DNA behaves electrostatically as a long rod with a linear charge density. The interaction between two rods is obtained from the linearized Poisson-Boltzmann equation (Debye-Hückel). If the electrostatic screening length κ and the DNA width are negligible with regard to the persistence length, then the interaction of two DNA rods that have their points of closest separation at r₁ and r₂, and a mutual angle of γ between their directors n₁ and n₂, is given by (25,26)

$$U_{12}\left({\mathbf{r}}_1,{\mathbf{r}}_2\right)=\frac{\pi {\lambda }^2}{\mathit{ϵ}\kappa }\frac{e^{-\kappa |{\mathbf{r}}_1-{\mathbf{r}}_2|}}{\text{sin}\gamma },$$ (6)

where ϵ is the solvent dielectric permittivity, and λ is the effective linear charge density of the polyelectrolyte.

The angle-dependent electrostatic excluded volume (second virial coefficient) is then calculated as (26,27)

$$\beta \left({\mathbf{n}}_1,{\mathbf{n}}_2\right)=\frac{1}{\mathcal{V}}\iint \left(e^{-\frac{U_{12}\left({\mathbf{r}}_1,{\mathbf{r}}_2\right)}{k_{\text{B}}T}}-1\right)d{\mathbf{r}}_{1}d{\mathbf{r}}_2,$$ (7)

which for the case of two charged rods of length L_p at a closest separation of x = |r₁ – r₂| evaluates to

$$\beta \left({\mathbf{n}}_1,{\mathbf{n}}_2\right)=2L_p^2\text{sin}\gamma \underset{D}{\overset{\infty }{\int }}\left(1-e^{-\frac{U_{12}\left(x,\gamma \right)}{k_{\text{B}}T}}\right)dx,$$ (8)

with D as the width of the DNA basepair. Based on the ambiguity in choosing the effective linear charge density attributable to correlations and screening, we opt to use an experimental fit that includes both hydration repulsion and screened electrostatic interactions between two parallel rods of DNA (28). We neglect the short-range hydration interactions and use only the electrostatic component of the fit

$$U\left(r\right)=b\frac{e^{-\kappa r}}{\sqrt{\kappa r}}.$$ (9)

We extend this potential to apply it to skewed rods following a scheme elaborated in Brenner and Parsegian (25) to obtain the angle-dependent potential

$$U\left(x,\gamma \right)=\sqrt{\frac{\pi }{2}}\frac{b}{\kappa }\frac{e^{-\kappa x}}{\text{sin}\gamma }.$$ (10)

From this, we calculate the angle-dependent excluded volume β(n₁, n₂) with the value of b = 85 k_BT/nm for 100 mM added monovalent salt (28).

The isotropic excluded volume v is obtained by integrating β(n₁, n₂) over all possible angles for n₁ and n₂, assuming equal probability for finding them in any orientation. From

$$v=\frac{1}{2}\iint \beta \left({\mathbf{n}}_1,{\mathbf{n}}_2\right)\frac{1}{4\pi }\frac{1}{4\pi }d{\text{Ω}}_{1}d{\text{Ω}}_2,$$ (11)

we obtain the excluded volume of one DNA persistence-length segment (26) as v ≈ L_p²DC₀, with D ≈ 2.5 nm as the width of the DNA and C₀ ≈ 2.87 as a constant depending on interaction specifics (100 mM monovalent salt concentration). A comparison with a viral capsid with R_c = 50 nm shows that v ≈ V_c/30; we see that 30 persistence-length segments of DNA are sufficient to exclude all the free volume, hinting at a large electrostatic intrastrand repulsion from confinement. The anisotropic excluded volume approximation is valid until the viral DNA transitions into a liquid crystal phase (26), which happens at roughly 30% packing (29)—well beyond the encapsidated length for which the ejecting force is comparable to the opposing cellular force.

Results and Discussion

We now study the balance of forces near the end of ejection so we can determine the maximal cellular turgor pressure that can be overcome. The crowded cellular interior exerts a turgor pressure Π on the volume V of any foreign material to banish it from the cell (30) whereas the effect of condensation tries to draw more DNA into the condensate. The balance of free energy in the cell is thus F_cell(L) = (Π – γ)A₀(L₀ – L), which is always negative if Π < γ. The DNA will tend to enter the cell despite the turgor pressure, due to the favorable condensation conditions. The value of γ can be determined by fitting minimal toroid shapes to experimentally measured toroid parameters in the presence of condensing agents found in bacteria (15,23) (see previous section). Obtained estimates for γ are between 4 and 6 atm, depending on the choice of model parameters. We take γ ≈ 4 atm for the turgor pressure that condensing agents in a cell could overcome on their own. Additional contributions, ΔΠ, come from unfavorable free energy contributions for DNA in the capsid F_cap and corrections to surface and bending energy terms in the condensate (Fig. 1).

The additional chemical potential for the DNA in the cell when the turgor pressure is increased by ΔΠ is ΔΠA₀, and this should be matched by the chemical potential in the capsid to avoid the stalling of the ejection. When the two chemical potentials are equal,

$$\mu =\frac{\partial F_{\text{cell}}}{\partial L}=\Delta \text{Π}{A}_0=\frac{\partial F_{\text{cap}}}{\partial L},$$ (12)

the ejection will stall at some length L^∗. From this we determine the maximal additional ΔΠ that can be overcome by the virus because the DNA is ejected from the cramped capsid. We now study effects due to the confinement in the capsid, which was the cause of the driving force in the early stage of ejection.

Some bacteriophages have tails of considerable length t, so we examine whether they influence the ejection process. The entropic penalty for confining a semiflexible polymer in a tube of diameter w (31) is

$$\frac{F_{\text{tail}}}{k_{\text{B}}T}\approx \frac{t}{\lambda }\text{ln}\frac{L_p}{\lambda },$$ (13)

where λ = w^2/3 L_p^1/3 is the Odijk deflection length. For a tail with w ≈ 2.75 nm (22), the effective chemical potential from the tail is F_tail/t ≈ 0.27 k_BT/nm. This is enough to oppose an additional 1.5 atm of turgor pressure in the cell and is independent of the length of the tail. However, the effect of the tail onsets only when the last DNA basepair exits the capsid and enters the tail (i.e., when L = t). This suggests a barrier in the chemical potential that needs to be overcome for total ejection when 4 atm < Π < 5.5 atm (as will be shown later).

DNA is a charged polyelectrolyte with strong repulsive electrostatic interactions between any two points on its contour. Interactions between nearby parts of the contour act to give it its large persistence length comparable to the radius of the nearly spherical capsid L_p ∼ R_c. When the DNA touches the capsid, any increase of length L will force the DNA to bend to conform to the shape of the capsid. The bending energy in such a situation can be approximated by that of a loop of DNA with radius R_c, k_BT L_p/2R_c². A comparison with the previously neglected bending energy of the condensate (see Eq. 3) reveals that they are matched for R_c ≈ 50 nm according to the thin torus model (15). Smaller capsids could enhance the chemical potential; e.g., in the case of λ-phage with R_c ≈ 30 nm (22), the change of Δμ ≈ 0.03 k_BT/nm is enough to compensate for ≈0.15 atm of turgor pressure. Any direct interactions between the DNA and capsid appear to be negligible; viral ejection experiments show no evidence of attractive forces (32), and because dsDNA bacteriophage capsids have no considerable charge (33), only weak van der Waals interactions are possible.

When the length of the DNA in the capsid is large enough, L ≫ L_p, the DNA chain statistics resemble that of a random walk of n_p = L/L_p persistence-length segments (34). This approximation is valid for steric interactions in bulk as long as L_p ≤ R_c (35). In the case of strong spherical confinement and electrostatic interactions, the effective persistence length that governs correlations along the contour becomes as small as 10 nm (36), making the approach valid even in smaller capsids. The interaction energy between different parts of the DNA strand in confinement may be estimated on the basis of the excluded volume v between two segments (35). The corresponding Flory free energy of interaction in the capsid of volume V_c is F_v ≈ k_BT n_p²v/V_c. This contribution vanishes inasmuch as L → 0, so it cannot help the ejection in its latest stages. The excluded volume between two DNA segments can be approximated as that between two charged rods. This interaction is intrinsically anisotropic, but at low packing fractions (near the end of ejection) there is no order, and we can average this over all possible mutual angles between two cylinders (see Modeling the DNA). We obtain v = L_p²DC₀, where D is the DNA diameter (D ≈ 2.5 nm) and C₀ is a numeric constant. The excluded volume interactions will contribute to the total free energy as k_BT C₀ DL²/V_c (but only in the regime when there are at least several persistence length segments inside the capsid). For R_c ≈ 50 nm in 100 mM monovalent salt, v/V_c ≈ 1/30, resulting in the effective chemical potential being an increasing function of length as ∂F_v/∂L ≈ 2L/L_p 0.013 k_BT/nm. If, say, 10 persistence lengths of DNA are in the capsid, the repulsive force is sufficient to oppose ∼0.8 atm of turgor pressure.

When the cellular turgor pressure Π is larger than the effective condensing pressure γ in the cell, the net driving pressure Π – γ > 0 on the viral DNA will tend to repel it from the cell. When the net repulsive cellular pressure is smaller than the tail confinement penalty μ_tail = F_tail/t (corresponding to ≈1.5 atm), the DNA will be stuck in the virus; the tail of length t will be completely filled, and some length L – t will reside inside the capsid. This stalling length is a result of all the repulsive interactions in the capsid canceling out with the net driving pressure in the cell. Note, however, that if the whole DNA from the capsid (of length L – t) enters the tail, the additional asymmetry in the free energy of the two thermodynamic reservoirs onsets. This is due to the confinement penalty of the DNA in the tail. With a partially filled tail, the derivatives of the free energy per unit length (the chemical potential) in the virus (the DNA length increases in the virus) and in the cell (the DNA length increases in the cell) are not the same. The thermodynamical balance is thus broken, and the thermodynamical gradient necessary for the ejection is restored. Therefore, there exists a potential barrier that the DNA needs to overcome for its capsid-side end to enter the tail and be swiftly ejected.

We now estimate whether the thermal fluctuations may overcome the free energy barrier. Because the capsid DNA is not condensed it is coupled to a solvent heat bath at temperature T. From the equipartition theorem, the encapsidated DNA will have ∼1/2 k_BT thermal energy per degree of freedom. A semiflexible polymer of length L can be partitioned into a random walk of n_p ≈ L/L_p steps with each step of length L_p having two degrees of freedom (two angles) and the origin being at the tail entrance. The resulting DNA thermal energy is ∼1 k_BT/L_p, or ∼0.02 k_BT/nm, which corresponds to a fluctuation in the maximal turgor pressure of ∼0.1 atm. We can argue that the ejection can happen in a finite time if the barrier corresponds to up to, say, three standard deviations of ∼0.3 atm.

Conclusion

We conclude that the mechanism of viral ejection from some dsDNA bacteriophages into Gram-positive bacteria could be explained as a competition between the resisting turgor pressure and a free energy gain from condensation of the ejected part of the DNA. From the experimental data for the condensation energy of DNA, we estimate that a turgor pressure in excess of 4 atm can be overcome by unassisted ejection in line with recent molecular-dynamics simulations (37). Our model does not exclude additional ejecting mechanisms such as the osmotic pressure from proteins remaining in the capsid (11) or pulling from proteins in the cell (12); such mechanisms can help to overcome even larger turgor pressures than obtained here.