Transport by Populations of Fast and Slow Kinesins Uncovers Novel Family-Dependent Motor Characteristics Important for In Vivo Function

Abstract

Intracellular cargo transport frequently involves multiple motor types, either having opposite directionality or having the same directionality but different speeds. Although significant progress has been made in characterizing kinesin motors at the single-molecule level, predicting their ensemble behavior is challenging and requires tight coupling between experiments and modeling to uncover the underlying motor behavior. To understand how diverse kinesins attached to the same cargo coordinate their movement, we carried out microtubule gliding assays using pairwise mixtures of motors from the kinesin-1, -2, -3, -5, and -7 families engineered to have identical run lengths and surface attachments. Uniform motor densities were used and microtubule gliding speeds were measured for varying proportions of fast and slow motors. A coarse-grained computational model of gliding assays was developed and found to recapitulate the experiments. Simulations incorporated published force-dependent velocities and run lengths, along with mechanical interactions between motors bound to the same microtubule. The simulations show that the force-dependence of detachment is the key parameter that determines gliding speed in multimotor assays, while motor compliance, surface density, and stall force all play minimal roles. Simulations also provide estimates for force-dependent dissociation rates, suggesting that kinesin-1 and the mitotic motors kinesin-5 and -7 maintain microtubule association against loads, whereas kinesin-2 and -3 readily detach. This work uncovers unexpected motor behavior in multimotor ensembles and clarifies functional differences between kinesins that carry out distinct mechanical tasks in cells.

Introduction

Kinesin motor proteins, which are involved in intracellular transport, spindle morphogenesis, and the regulation of microtubule dynamics, have diverse properties related to their disparate cellular roles. Single-motor assays are the clearest approach to quantifying key metrics that determine motor function, but it is often difficult to extrapolate these properties to multimotor transport. Although there has been a considerable focus on bidirectional transport involving kinesins and dynein, there have also been a number of reports describing intracellular transport by multiple plus-end-directed kinesins of either a single motor type or different motor families having differing unloaded velocities. Cargoes transported by mixed populations of fast and slow kinesins include melanosomes (1), intraflagellar transport particles (2–4), axonal transport vesicles (5,6), and chromatin (7).

Although the underlying dynamics of interacting fast and slow kinesins have been investigated previously using computational and analytical models (4,7,8), this analysis is arguably premature because there is even considerable debate over the mechanisms by which groups of identical kinesins coordinate during cargo transport (9–12). Experimental and computational studies of mechanically coupled kinesin-1 motors find that stall forces and cargo velocities under load are less than would be predicted if all motors were operating at their single-motor performance (13–16), and that forces are not shared equally by all motors in a group. Because motors exerting the most force have the highest probability of detaching, this unequal sharing leads to large fluctuations in the number of attached motors and the resulting cargo velocity. Another important conclusion from these investigations is that the predicted motor behavior is strongly dependent on the choice of parameters used to describe motor behavior (13,17,18), indicating that simple extrapolation of kinesin-1 motor properties to other kinesin families is not warranted.

Understanding coordination between mechanically linked motors is important for understanding in vivo behavior such as axonal transport of vesicles and metaphase dynamics of the mitotic spindle. However, due to the complexity of multimotor systems, it is crucial to employ computational modeling approaches together with experiments. Furthermore, although it is appreciated that kinesins have diverse motor properties (speed, run length, force-dependence of unbinding, etc.), motors beyond kinesin-1 have not been thoroughly characterized, and must be better studied to fully understand multimotor systems.

To better understand the dynamics underlying multimotor transport and characterize the mechanical properties of motors that have received less study than kinesin-1, we carried out microtubule gliding assays using defined ratios of fast and slow motors and employed a computational model to interpret the results and extract insights into multimotor behavior that are otherwise difficult or impossible to measure. A diverse set of motors was used, including both transport motors (kinesin-1, -2, and -3) and mitotic kinesins (kinesin-5 and -7) that we previously characterized at the single-molecule level (19). By developing a computational model of multimotor transport that is constrained by the extensive experimental data, we are able to show that surprisingly large intermotor forces are generated when a group of mechanically coupled motors move on the same microtubule. Furthermore, we find that the key motor property that defines multimotor transport characteristics is the dependence of motor detachment on load, and that this parameter differs significantly between kinesin families.

Materials and Methods

Motor constructs, purification, and concentration determination

Motors used were as follows: Drosophila kinesin heavy chain (kinesin-1), mouse KIF3A (kinesin-2), C. elegans UNC104 (kinesin-3), Xenopus Eg5/KSP (kinesin-5), and Xenopus CENP-E (kinesin-7). Motor domains and 14 amino acids of their neck-linker domains were fused to the kinesin-1 neck-coil and coiled-coil regions (residues 346–559), followed by a GFP and His₆ tag, as described in Shastry and Hancock (19), and were expressed in bacteria and Ni column-purified (20). Active motor concentrations were determined by incubating motors with microtubules and 1 mM AMP-PNP for 20 min, centrifuging to pellet microtubules and bound (active) motors, measuring GFP fluorescence of the resuspended pellet, and comparing it to a GFP standard quantified by absorbance at 488 nm.

Microtubule gliding assay

Standard microtubule gliding assays were used (21). Anti-His C-term antibody (20 μg/mL Cat. No. R930-25; Invitrogen, Carlsbad, CA) was adsorbed to the surface of glass flow cells, followed by Histidine-tagged kinesin motors (250 nM active motor concentration). Taxol-stabilized Cy5-labeled bovine brain microtubules (40 nM) were then introduced in the presence of an oxygen scavenging system consisting of 20 mM D-glucose, 0.02 mg/mL glucose oxidase, 0.008 mg/mL catalase, and 0.5% v/v β-mercaptoethanol in BRB80 (80 mM PIPES, 1 mM MgCl₂, 1 mM EGTA, pH 6.8). Movies were captured with a Cascade 512 charge-coupled device camera (Roper Scientific, Tucson, AZ) controlled by METAVUE software (Molecular Devices, Downingtown, PA), and gliding speeds were analyzed manually. At least 30 different microtubules were assayed for each data point over a minimum distance range of 2 μm.

Coarse-grained modeling of microtubule and motor dynamics

In the simulations, the microtubule is modeled as a rigid rod constrained to move in one dimension at a fixed height from the surface as illustrated in Fig. 1 a. A flow chart of the algorithm is given in Fig. S10 in the Supporting Material. We neglect inertial effects and therefore the motion of the microtubule is overdamped. The solvent is modeled implicitly using Langevin dynamics, i.e., at each time step the microtubule is subject to a random Brownian force due to the thermal motion of the solvent molecules at temperature T and the equation of motion is given by

$$\frac{dx\left(t\right)}{dt}=\frac{1}{{\zeta }_{\parallel }}\left(\sum _{i=1}^N{F}_{i,\parallel }^m\left(t\right)+F^B\left(t\right)\right),$$ (1)

where x(t) is the position of the microtubule, ζ_|| is the friction coefficient, F^m_i,||(t) is the parallel component of the motor force due to the ith motor, and F^B(t) is the random force. The random force is chosen to be Gaussian white noise with zero mean and a variance dictated by the fluctuation-dissipation theorem, i.e.,

$$\langle F^B\left(t\right)\rangle =0,$$ (2)

$$\langle F^B\left(t\right)F^B\left(t^{\prime }\right)\rangle =2k_{\text{B}}T{\zeta }_{\parallel }\delta \left(t-t^{\prime }\right).$$ (3)

Here the friction coefficient is given by (22)

$${\zeta }_{\parallel }=\frac{2\pi \eta L}{\text{ln}\left(4h/d\right)},$$ (4)

where L = 10 μm is the length of the microtubule, η = 0.002 Pa.s is the dynamic viscosity, h is the distance of the microtubule from the surface, and d = 25 nm is the diameter of the microtubule. The equations of motion are integrated using an Euler scheme with a time step of τ = 10 μs.

Figure 1.

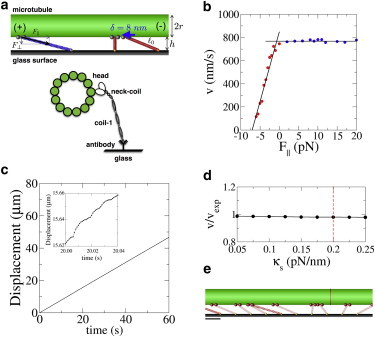
Schematic and results for the coarse-grained model of a multimotor gliding assay. (a) Geometry of motors and microtubule showing parallel and perpendicular force components, and a diagram of the motor attachment scheme. (b) Kinesin-1 force-velocity curve used (28), where red and blue points denote hindering and assisting loads, respectively. (c) Representative displacement versus time plot obtained from the simulations for a uniform kinesin-1 population. (Inset) Fluctuations at short timescales. (d) Parameter sensitivity plot for motor stiffness, κ_s. Gliding velocities from simulations were normalized to the experimentally obtained kinesin-1 velocity. (e) Still image from movie of a uniform kinesin-1 simulation (see Movie S1 in the Supporting Material), showing motors under both hindering and assisting loads (tilted left and right, respectively) and unloaded (partially transparent). Scale bar is 25 nm. To see this figure in color, go online.

The motor tether region connecting the head domains to the tail attachment point is modeled as a cable-like Hookean spring with zero stiffness up to a slack length and linear stiffness beyond, consistent with the approach taken by others (10,23). The magnitude of the force is given by

$$\left|\mathbf{F}\right|={\kappa }_s\left(\ell -{\ell }_0\right)\text{Θ}\left(\ell -{\ell }_0\right),$$ (5)

$$\text{Θ}\left(\ell -{\ell }_0\right)=\{\begin{array}{ll}1& \text{if}\ell >{\ell }_0\\ 0& \text{if}\ell \le {\ell }_0,\end{array}$$ (6)

where ℓ₀ is the rest length of the spring, and κ_s is the motor compliance. Motors are anchored on the glass surface, take steps of size δ = 8 nm along the microtubule, and are allowed to step over each other, considering the fact that the microtubules consist of multiple protofilaments. During every time-step of the simulation, τ, the probability of a motor taking a step is given by

$$p_{\text{step}}=1-e^{-v\tau /\delta },$$ (7)

where δ is the motor step size, and v is the motor velocity (thus v/δ is the stepping rate). A uniform random number $\mathcal{R}$ in the interval [0,1] is then generated, and a motor steps when the condition ${\mathit{p}}_{\text{step}}>\mathcal{R}$ is satisfied. We assume that for hindering loads the motors obey a force-velocity curve of the form

$$v=v_u\left[1-{\left(\frac{F_{\left|\right|}}{F_s}\right)}^{\omega }\right].$$ (8)

Here, F_|| is the component of the exerted force parallel to the microtubule, v_u is the unloaded motor velocity, and F_s is the stall force. A linear force-velocity relationship is obtained for ω = 1. For ω < 1, Eq. 8 results in a convex down force-velocity curve, i.e., a sublinear motor, and for ω > 1, one obtains a concave up force-velocity relation, which describes a superlinear motor (24). For assisting loads, we assume v = v_u, consistent with the experimentally measured force-velocity curve for kinesin-1 shown in Fig. 1 b, and v = 0 for forces above the stall force. Motors detach from the microtubule with different force-dependent off-rates, k_off(F). The functional forms of these off-rates are discussed in Parameter Optimization and Estimation of Critical Detachment Force, F_c, in the Supporting Material. After detachment, the elastic tether of the motor relaxes to its equilibrium position, and the motor immediately reattaches in an unstrained conformation to the nearest binding site on the microtubule. Sample movies from the simulations for different motor mixtures are shown in Movie S1, Movie S2, Movie S3, Movie S4, Movie S5, Movie S6, Movie S7, Movie S8, Movie S9, Movie S10, Movie S11, Movie S12, Movie S13, and Movie S14 in the Supporting Material.

Results

A coarse-grained model of a gliding assay

To extract force-dependent motor properties from microtubule gliding-assay experiments, we developed a coarse-grained model of a gliding assay, consisting of a microtubule being transported by motors at various densities, subject to motor and Brownian forces (see Materials and Methods for details). The motor stalk and surface-attachment (Fig. 1 a) was modeled with a cable-like spring (23), specifically an elastic tether with zero stiffness up to 40-nm extension and a 0.2 pN/nm elasticity beyond that (15,17,18). Based on previous fluorescence interference measurements (25), the microtubule was set to a height of 15 nm above the surface (Fig. 1 a). Motors were modeled as having linear force-velocity profiles with velocity equal to the unloaded velocity under hindering loads, and zero beyond the stall force of F_s = 7 pN (Fig. 1 b) (26–28). Motor detachment rates at zero load (where k_off(0) = (velocity)/(run length)) were taken from published single-molecule velocity and run-length measurements for these motors (19,28). The dependence of the motor detachment rate on hindering and assisting loads was taken from force-clamp optical tweezer measurements for kinesin-1 and kinesin-2 (28), and k_off(F) was calculated by dividing velocity by the run length at a range of hindering and assisting loads.

Simulations of kinesin-1 gliding assays

Simulations were initially run for a uniform population of kinesin-1 motors. A raw position versus time trace for a single microtubule is shown in Fig. 1 c, with a higher temporal resolution inset showing fluctuations in speed. For these kinesin-1 simulations, model parameters were generally tightly constrained by experimental results and geometrical constraints, but even this simulation of a uniform motor population revealed a number of interesting and unexpected insights that necessitate a reevaluation of the traditional picture of motor coordination in gliding filament assays. Before analyzing motor performance more thoroughly, we carried out a parameter sensitivity analysis to identify key parameters that determine performance. The first test was to investigate the effect of tether stiffness and geometry. When the stiffness of this compliant tether was varied from 0.05 to 0.25 pN/nm, there was negligible change in motor speed (Fig. 1 d), and similar insensitivity was observed for tether length (l₀), microtubule height (h), motor density (ρ), stall force (F_s), and the shape of the force-velocity curve (see Fig. S2).

When multiple identical motors work together to transport cargo, the simplest intuitive expectation is that, because they move at the same mean speed, minimal tension will be built up between different motors and to a first approximation, the speed and run length of a motor in a population will be similar to the unloaded single-molecule situation. Simulations show that this is not the case. For instance, the mean run length and association time in a kinesin-1 multimotor assay (0.56 μm and 0.74 s, respectively (Fig. 2, a and b)) are substantially lower than their values in an unloaded single-molecule experiment (1.0 μm and 1.27 s, respectively). Another way to observe this phenomenon is to examine the distribution of motor forces during transport of a microtubule by a population of kinesin-1 motors (Fig. 2 c). If motors were all moving in lock step, then no tension would be built up between motors, and the mean force at detachment would be near zero. Instead, 46.2% of motors detach under a nonzero force (with a mean absolute value of the force at detachment equal to 3.85 pN (see Fig. 2 c)), meaning that they dissociate faster than a single unloaded kinesin would.

Figure 2.

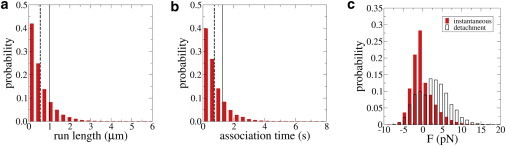
(a–c) Run-length, association time, and force distributions for uniform kinesin-1 simulations. (Dashed lines in panels a and b) Mean values of 0.56 μm and 0.74 s, respectively, which differ considerably from the single-molecule unloaded run length and (solid lines) association time inputs to the simulations of 1.0 μm and 1.27 s, respectively. (c) Instantaneous force and force at detachment for a uniform population of kinesin-1 motors are shown (see Fig. S8 in the Supporting Material for mean values). Note that 73.5% of the instantaneous forces, and 46.2% of the forces at detachment, are zeros. To see this figure in color, go online.

Mixed-motor gliding assays

Microtubule gliding assays were carried out using a constant concentration of motors (250 nM) made up of different proportions of fast and slow motors. To eliminate as variables the unloaded processivity, the mechanics of the tether domain, and the motor attachment to the surface, the neck-linker domain of every motor was adjusted to 14 amino acids and the motor and neck-linker domains were fused to the coiled-coil domain (residues 346–559) of Drosophila kinesin-1 (Fig. 1 a, and see Materials and Methods). This approach eliminates any uncertainties about coiled-coil stability and tail-dependent regulation, and avoids the possibility that results are simply dominated by differences in processivity. In a previous study, all of the motors were characterized in single-molecule motility assays to confirm that, apart from enhancing their processivity, this protein engineering strategy did not substantially alter motor properties as compared to wild-type (19). Motors had a 70-fold range of speeds with the order

$$\text{kinesin-}3>\text{kinesin-}1>\text{kinesin-}2=\text{kinesin-}7>\text{kinesin-}5.$$

The results in Fig. 3 show a diverse range of behaviors, with some combinations being dominated by the fast motor, other combinations being dominated by the slow motor, and a subset nearly following a rule of proportionality. For example, in Fig. 3 a the results from mixing kinesin-1 with the four other motors are shown. Mixing kinesin-1 with the faster kinesin-3 or the slower kinesin-2 resulted in strongly convex curves, meaning that even when kinesin-1 made up less than half of the motors present on the surface, the resulting speeds were close to the kinesin-1 speed. In contrast, for mixtures with kinesin-5 and kinesin-7, the resulting curves lie much closer to proportionality.

Figure 3.

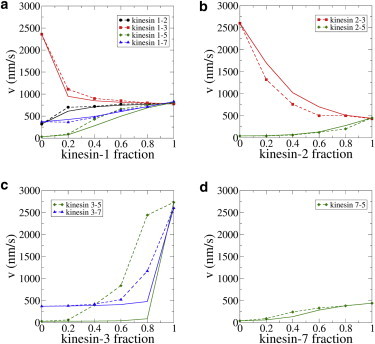
(a–d) Experimental and simulation results from gliding assays using different proportions of fast and slow motors. (Points and dashed lines) Experimental gliding velocities; (solid lines) simulations. Because of their similar velocities, no experiments were carried out for the kinesin-2/kinesin-7 mixture. Parameter sensitivities are shown in Fig. S2 and Fig. S3. To see this figure in color, go online.

Simulations used identical values for the motor contour length and stiffness, and the height of the microtubule above the surface. A parameter sensitivity analysis was carried out on 50:50 motor mixtures, confirming that results were generally insensitive to these geometric parameters (see Fig. S3). Velocities of uniform motor populations in gliding assays (i.e., kinesin fraction either 0 or 1) were matched to the experimental gliding-assay velocities by making iterative adjustments of the unloaded single-motor velocity (maximum adjustment was 10%; see Table S1 in the Supporting Material). Because optical trapping experiments have shown fairly consistent single-motor stall forces across different kinesin families (29–31), stall forces were also chosen to be identical at 7 pN and force-velocity profiles were chosen to be linear. Parameter sensitivity analysis confirmed that simulated velocities for 50:50 motor mixtures were generally insensitive to changes in stall force, the linearity of the force-velocity curve, and the motor density (see Fig. S3).

The remaining unconstrained parameter was the force-dependence of motor detachment (F_c), which was found to be the principal determinant of model behavior. The approach to finding F_c was to use experimentally available values for kinesin-1 (characterized for all loads using force-clamp optical trapping (28)) and kinesin-2 (characterized for hindering forces (28)), run simulations of kinesin-1/kinesin-2 mixtures to determine F_c for kinesin-2 under assisting loads, and then run iterations to obtain optimal F_c values for kinesin-3, -5, and -7 (see Parameter Optimization and Estimation of Critical Detachment Force, F_c, in the Supporting Material for details).

As seen in Fig. 3 a, simulations showed good quantitative agreement in all of the kinesin-1 combinations (average error compared to experimental data ranged from 3.5 to 17%; see Fig. S5 for more details). The k_off(F) and F_c values are given in Table 1. The F_c values describe the propensity of the motor to detach under load, with smaller F_c values corresponding to greater load-sensitivity. Based on the simulations, detachment of kinesin-1 is the least sensitive to load (F_c of 6 pN in hindering direction), followed by kinesin-7 (2.6 pN), kinesin-5 (1.5 pN), and kinesin-2 (2.0 pN), with kinesin-3 being the most sensitive to load (F_c = 0.5 pN). For motor combinations beyond kinesin-1 (Fig. 3, b–d), the simulations produced reasonable fits, with the exception of the kinesin-3/kinesin-5 mixtures. This pair of motors had the largest discrepancy in speed (from 30 nm/s for kinesin-5 up to 2730 nm/s for kinesin-3), and one potential explanation is simply that the model assumptions begin to break down at these extremes. However, as discussed below, the kinesin-3 motor characteristics diverged from the others, and this unique behavior may also play a role.

Table 1.

The force-dependent off-rates, k_off(F), for different motors in the hindering and assistive directions

Kinesin	khindoff (F) [s−1]	kasstoff (F) [s−1]
1	0.79e−F/6.1	0.79 + 1.56F
2	8.37e−0.07F – 7.49e0.43F	15.0eF/2.0
3	1.433e|F|/0.5
5	0.046e|F|/1.5
7	0.328e|F|/2.6

Values for kinesin-1 were taken from experimental data (28). Note that the value of F_c under hindering loads is higher than the value of 3 pN frequently used in simulations because the latter value refers to run-length data (34). Inasmuch as k_off = velocity/run length, taking into account the load dependence of velocity results in the larger F_c used here. For kinesin-2, k_off(F) in the hindering direction was measured experimentally (28), but under assisting loads motors readily dissociated, precluding a reliable estimate. The limit of detection for measuring speeds was ∼5 steps, giving a lower limit of 10 s⁻¹, and iterative fits to experimental speed data resulted in an estimate of k_off(0) = 15 s⁻¹ with an exponential dependence. All parameters obtained from modeling are shown in boldface, and forces are in picoNewtons.

Motor behavior in mixed populations

The first way to quantify the underlying motor dynamics during multimotor transport is to compare individual motor velocities to the resulting microtubule velocity. Due to the elasticity of the tether domain, the speed with which individual motors walk along the microtubule (defined as the motor run length divided by the attachment time) need not match the speed that the microtubule moves across the surface. Indeed, as shown in Fig. 4, for uniform populations of motors there was a reasonably good match between motor and microtubule velocities, but in mixed populations there was considerable divergence. For instance, in a mixture of kinesin-1 and kinesin-2, the kinesin-1 motor speeds closely matched the microtubule speed (1-2 in Fig. 4 a), whereas the kinesin-2 motor speeds were less than half of the microtubule speed (2-1 in Fig. 4 b). In contrast, in mixtures of kinesin-2 and kinesin-3, both motor velocities diverge from the resulting microtubule velocity, indicating a more balanced competition. Overall, for kinesin-1 motors, which were the most resistant to dissociation by force, motor velocities most closely matched microtubule velocities (Fig. 4 a), whereas for kinesin-3 motors, which were the most susceptible to dissociation by force, there were large discrepancies (Fig. 4 c).

Figure 4.

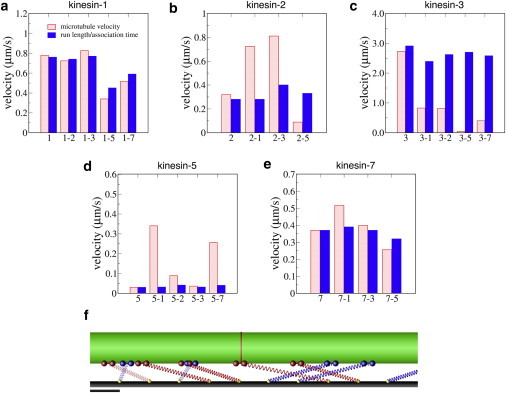
(a–e) Difference between motor velocities and resulting microtubule velocities in multimotor simulations, together with a representative snapshot from the simulations showing how motors with different speeds are pulled in different directions and stretched to different degrees (f). Motor velocity was calculated as run-length/association time (see Fig. S6), and motor mixtures were all 50:50 ratios. Scale bar is 25 nm. To see this figure in color, go online.

Another way to gain insight into competition between fast and slow motors is to examine the forces that motors generate during multimotor transport. In Fig. 5, the average proportion of motors operating under hindering or assisting load are plotted for different motor mixtures (see also Movie S1, Movie S2, Movie S3, Movie S4, Movie S5, Movie S6, Movie S7, Movie S8, Movie S9, Movie S10, Movie S11, Movie S12, Movie S13, and Movie S14). We offer the following observations:

• 1.Although most motors in uniform populations are at zero load, up to one-quarter of the motors are either pulling or being pulled, with a slightly higher fraction being under hindering load due to the asymmetric force-velocity relationship (Fig. 1 b).
• 2.In selected fast/slow mixtures, a portion of the fast motors are operating under hindering loads (e.g., the faster kinesin-1 with kinesin-2) or vice versa (the slower kinesin-1 with kinesin-3). This behavior is consistent with the fact that kinesin-1 dominates in both of these mixtures, and is a direct result of the propensity of kinesin-2 and kinesin-3 to rapidly dissociate under load. The distribution of loads at the instant of detachment, shown in Fig. S7, shows similar trends, but also shows that in many fast/slow motor mixtures nearly every motor detaches under a nonzero load. The magnitudes of the assisting or hindering loads are shown in Fig. S8.

Figure 5.

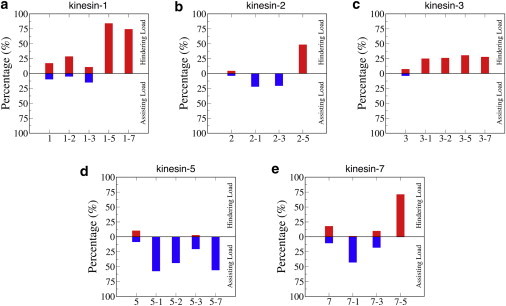
Percentage of the time spent under either an assisting (blue) or hindering (red) nonzero instantaneous load for all kinesin motors studied. (a–e) Results for both uniform motor populations and 50:50 motor mixtures. To see this figure in color, go online.

Discussion

The two key findings from this work are the following:

• 1.In multimotor transport even with uniform motor populations, significant intermotor forces are developed, which accelerate motor detachment; and
• 2.Motors from different kinesin families have different force sensitivities of their detachment rates, and this parameter is the key determinant of velocity in mixed-motor transport.

The model begins from very modest assumptions regarding the stochastic stepping characteristics and motor-surface attachment. However, even for uniform motor populations the model uncovers a diversity of motor-motor interactions not present in single-molecule measurements. The strengths of this approach are the fact that the five motors used all have the same unloaded run lengths and surface attachments (19), and that results from nine different fast/slow motor pairs were used to constrain model parameters. This approach differs from previous studies that compared only single pairs of motors (4,7,8,32).

A surprising result from the uniform kinesin-1 simulations (Fig. 2) was that the motors did not entrain and move under zero load conditions, as assumed in many mean-field models (4,7,8). Instead, because of the stochasticity in their stepping, individual motor speeds deviated considerably from the mean, and because of the finite length of their tethers, the motors built up substantial forces in both hindering and assisting directions. This phenomenon has been observed and modeled for systems of two identical motors transporting a shared cargo (13,15–18), emphasizing its importance. Although perhaps counterintuitive, this force buildup can in fact be estimated analytically by simply modeling a Poisson stepper taking 8-nm steps at ∼100 steps/s. After 100 steps, >25% of the motors will be stretched the 90-nm contour length of full-length kinesin-1 or longer (see Distribution of Instantaneous Forces and Forces at Detachment in the Supporting Material and Fig. S9 for details). For motors such as kinesin-3 that detach readily under load, this effect results in frequent motor detachments even in uniform populations, and rather ineffective transport. Inasmuch as most intracellular cargo is membrane-bound, which allows the motors to diffuse in the plane of the membrane, this competition may be less of a factor in vivo. However, for vesicles with diameters 100 nm and less (where intermotor distances are limited by vesicle size), this effect will continue to play an important role.

In mixtures of fast and slow motors, forces between motors played an even larger role, and the simulations showed that the most important motor characteristic that determined the ensemble speed was the force-dependence of detachment, F_c. The importance of F_c in determining velocity in mixtures of fast and slow processive kinesins has been noted in previous studies (4,8,32), and experiments using mixtures of nonprocessive fast and slow myosins similarly found that the crossbridge detachment rate was the principal determinant of velocity in mixed populations (33). In effect, the stubborn motors that remain walking even under load dominate the resulting transport velocity, whereas motors that detach readily under load have a much smaller influence on the overall transport speed. As it has been shown that classes of neuronal vesicles are carried by populations of kinesin-1 and kinesin-2 or kinesin-1 and kinesin-3 motors (Fig. 6 a) (5,6), it is instructive to compare the properties of these three transport motors.

Figure 6.

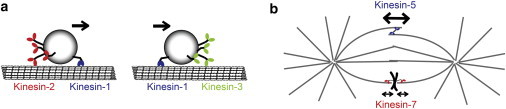
Illustration of potential in vivo scenarios involving different pairs of kinesin motors. (a) Tug-of-war between kinesin-1 and -2, and kinesin-1 and -3 pairs. In both cases, kinesin-1 dominates the cargo transport, speeding up kinesin-2 and slowing down kinesin-3. (b) Roles of kinesin-5 and kinesin-7 in mitosis. Kinesin-5 generates the outward forces required to maintain pole-pole separation, whereas kinesin-7 tethers kinetochores to spindle microtubules. To see this figure in color, go online.

Kinesin-1 has been shown to walk processively against considerable hindering or assisting loads (28,34). Kinesin-2, in contrast, has been shown experimentally to detach readily under hindering loads (28,35). Kinesin-3 is distinctive in being the fastest kinesin motor, and it is known to have a positively charged Loop 12 (K-loop) that interacts with the negatively charged C-terminal of tubulin to enhance run length in low ionic strength buffers (36). If this electrostatic tethering contributes substantially to the unloaded processivity of kinesin-3, then perhaps it is not surprising that loads substantially accelerate detachment inasmuch as this weak electrostatic interaction would not be expected to resist pN-level forces. This extreme sensitivity to load is consistent with single-molecule optical trapping of a similar C. elegans UNC104 construct to the one used here, where a 1 pN load increased k_off by 10-fold (37).

The finding that kinesin-5 is relatively insensitive to dissociation by force is consistent with the cellular role of this motor in sliding apart duplicated poles during prometaphase and maintaining mitotic spindle integrity (Fig. 6 b) (38). Because the unloaded run length of wild-type kinesin-5 is quite short (<100 nm (30,39)), processivity must be relatively force-independent for the motors to remain associated against substantial external loads. Although the modified kinesin-5 used in this study is more processive than wild-type due to its shortened neck linker, experimental work from other kinesins indicates that this difference in unloaded processivity should not affect the load-dependence of processivity (28). The insensitivity of k_off to load is supported by a single-molecule optical trapping study that found similar results (30). Kinesin-5 is also highly expressed in developing neurons and is proposed to act as a brake to resist dynein-mediated microtubule transport in axons (40), another mechanical role that would require a relative insensitivity of detachment to load.

Kinesin-7 (CENP-E) tethers kinetochores to spindle microtubules and is essential for proper metaphase chromosome alignment (41,42). CENP-E moves similarly to kinesin-1 in single-molecule optical tweezer experiments (31). Our results suggest that kinesin-7 is able to maintain association with the microtubule under both hindering and assisting loads, which is presumably very important for its tethering role, but it is still more force-sensitive than kinesin-1.

What is the underlying molecular mechanism that leads to such highly conserved motor domains having such diverse detachment rates under load?

As a processive kinesin dimer steps along the microtubule, the probability of dissociating is determined by a race between the tethered head binding to the next binding site (and releasing its bound ADP) and the bound head dissociating from the microtubule (in the low-affinity ADP-Pi or ADP state) (43). Hence, an external load can accelerate detachment either by slowing the rate of tethered head stepping or accelerating the rate of bound head dissociation (or both). A simple prediction would be that motors with strongly force-sensitive detachment rates (kinesin-2 and kinesin-3) have slower tethered-head on-rates or faster bound-head off-rates in the low-affinity ADP or ADP-Pi states. Another possibility is that ATP hydrolysis is very fast such that, during the time the tethered head is stepping forward, the bound head is predominantly in the low-affinity ADP-Pi state rather than the high-affinity ATP state. Kinesin-3 seems to be outlier in being the most sensitive to load.

One strength of the modeling approach taken here is that it provides predictions that can be tested experimentally. Encalada et al. (5) found that in kinesin-1 knockouts, synaptophysin vesicles actually moved faster than in wild-type neurons, presumably due to vesicle-attached kinesin-3 motors that dominate the transport in the absence of kinesin-1. Based on the dominance of kinesin-1 over kinesin-3 found here, one prediction would be that a kinesin-3 knockout in the same system would not necessarily lead to slower anterograde transport unless the ratio of kinesin-3 to kinesin-1 motors on each vesicle was >4:1. Similarly, Hendricks et al. (6) found a 4:1 ratio of kinesin-2 to kinesin-1 motors on purified vesicles, and due to the strong force sensitivity of kinesin-2 detachment the resulting speed would be within 10% of kinesin-1 (Fig. 4 a).

Another prediction would be that inhibiting kinesin-1 would lead to a roughly twofold decrease in velocity and inhibiting kinesin-2 would result in only a small increase in velocity. Because it is difficult to determine the functional importance of the precise speed of transport, a more relevant question is: why are vesicles and IFT cargo transported simultaneously by two different classes of kinesins?

One possibility is that, because different microtubule-associated proteins and tubulin posttranslational modifications can regulate the interaction of motors with specific subsets of microtubules (44), having more than one class of kinesin allows the cargo to move along a greater variety of microtubules or transit through regions of microtubules having specific microtubule-associated proteins or posttranslational modifications. On top of this, it is possible that the different kinesins on a cargo are differentially regulated to achieve even finer spatiotemporal control of cargo transport.

In conclusion, this work serves to categorize motors from different kinesin families by their force-dependent off-rates. For the three transport motors tested, kinesin-1 detachment is very resistant to force, whereas kinesin-2 and kinesin-3 motors detach much more readily, which will minimize their contribution to cargo transport when teamed with kinesin-1. The two mitotic motors kinesin-5 and kinesin-7 both have minimal dependence of their detachment rate on load, consistent with their requirements for sustained force generation during mitosis. However, a number of questions remain.

This study used only one member of each of the five families examined, but different motors in a given family and orthologs across different species may have divergent properties. Similarly, the coiled-coil and surface attachment domains were also kept uniform in this study and modeled as an elastic cable with a defined slack length. In reality, the length and structure of the coiled-coil domains differ substantially between motor families, which may impact their resulting performance when attached to membrane-bound cargo in their native environment.

Finally, in this work the motor dissociation rates for kinesin-3, -5, and -7 were assumed to vary exponentially with force, but in reality the detachment kinetics may depend in a more complex way on the magnitude and direction of force applied to the motor. Future work aimed at resolving these questions will help to bridge the gap between the understanding of kinesin motor properties at the single-molecule level and the complex dynamics of cargo transport in vivo.

Supporting Citations

References (45,46) appear in the Supporting Material.