Three-dimensional Ultrathin Planar Lenses by Acoustic Metamaterials

Abstract

Acoustic lenses find applications in various areas ranging from ultrasound imaging to nondestructive testing. A compact-size and high-efficient planar acoustic lens is crucial to achieving miniaturization and integration, and should have deep implication for the acoustic field. However its realization remains challenging due to the trade-off between high refractive-index and impedance-mismatch. Here we have designed and experimentally realized the first ultrathin planar acoustic lens capable of steering the convergence of acoustic waves in three-dimensional space. A theoretical approach is developed to analytically describe the proposed metamaterial with hybrid labyrinthine units, which reveals the mechanism of coexistence of high refractive index and well-matched impedance. A hyperbolic gradient-index lens design is fabricated and characterized, which can enhance the acoustic energy by 15 dB at the focal point with very high transmission efficiency. Remarkably, the thickness of the lens is only approximately 1/6 of the operating wavelength. The lens can work within a certain frequency band for which the ratio between the bandwidth and the center frequency reaches 0.74. By tailoring the structure of the metamaterials, one can further reduce the thickness of the lens or even realize other acoustic functionalities, opening new opportunity for manipulation of low-frequency sounds with versatile potential.

The focusing of acoustic energy enables nonintrusive inspection, detection and even manipulation of matters, and acoustic lenses are employed in a variety of applications ranging from nondestructive detection of damages in materials to biomedical imaging and even noninvasive cancer treatment. In retrospect, one of the leading trends in the development of modern devices is miniaturization and integration. It is therefore of paramount significance to realize an acoustic lens that has a compact size, a flattened shape as well as a high transmission efficiency. Relying on the interface of a uniform material to alter the wave trajectory, the conventional lenses can hardly serve as an ideal lens due to the inherent geometrical and wave aberrations. As a conceptually more natural but generally much less convenient approach, the refractive index can be appropriately varied to design gradient index (GRIN) acoustic lenses¹,²,³,⁴,⁵,⁶,⁷,⁸,⁹. High refractive index in the center of the GRIN lenses is crucial for providing sufficient phase delay, which will contribute significantly to the reduction of the total thickness of lenses. Moreover, the ability of GRIN lenses to have flat surfaces may simplify the mounting of lens and further facilitate the match to conventional detector and receiver arrays, remarkably increasing its potential for integration. Although the GRIN lenses have significant potential advantages over the conventional lenses, they are far less prevalent in practice due to the difficulty in finding real materials with desired parameters, since natural materials are generally unable to provide slow sound velocity and high mass density simultaneously¹⁰. The GRIN lenses made of phononic crystals¹¹,¹²,¹³,¹⁴ have slightly enhanced refractive index at long-wave regime but still suffer from the trade-off between high refractive index and acoustic impedance match, making it impossible to either shrink the lens thickness down to subwavelength regime or guarantee a flat lens shape.

Recent advances in acoustic metamaterials¹⁵,¹⁶,¹⁷,¹⁸,¹⁹,²⁰ have broadened the horizon of acoustic waves and opened new era for building diverse unconventional and fascinating devices²¹,²²,²³,²⁴,²⁵,²⁶,²⁷,²⁸,²⁹,³⁰,³¹,³²,³³,³⁴. Particularly, the coiling-up-space metamaterials proposed by Li and colleagues have the potential to yield extreme constitutive parameters including high refractive index²⁰ that should be substantially important for reducing the lens thickness. However such a structure cannot be simply piled up to construct a metamaterial lens due to the huge impedance mismatch. Moreover, GRIN lens formed by spatially varying the size of coiling structure will inevitably lead to considerable fabrication difficulty as well as large absorption effect of acoustic energy since the coiling units at the rim of the lenses have to be extremely small⁹. In addition, the previous attentions are only focused on 2D cases, heavily restricted from application in reality. So far, a 3D ultrathin planar acoustic lens, which is significant for the trends to miniaturization and integration and may take a step towards the practical application of acoustic GRIN lens, has never been achieved.

Here, we have designed and experimentally realized the first ultrathin planar acoustic lens capable of focusing low-frequency acoustic wave in 3D space, to circumvent the aforementioned limitations. As the basic building blocks of lens, a specified type of hybrid labyrinthine unit formed by coupling a modified coiling structure with air channels is proposed. To better understand the underlying physics, a theoretical approach based on the transfer matrix and Green's function theory has been developed which gives analytical description to such hybrid labyrinthine units with subwavelength scale. A monolayer of such metamaterial units with appropriate geometrical parameters is shown to act as an acoustic lens capable of yielding refractive index far greater than previously realizable while keeping the acoustic impedance well-matched. Both the theoretical and the experimental results demonstrate that the resulting lens can manipulate the 3D convergence of acoustic waves with wavelength nearly 6 times larger than its thickness, and the efficiency of acoustic focusing is very high with remarkable enhancement of acoustic energy at the predicted focal point (~15 dB). Furthermore, the lens has a flat structure which is potentially more compatible and integratable in practical applications as compared with the previous designs with curved or structured surface. We envision the realization of acoustic focusing with a subwavelength structure to pave the way for application of acoustic lenses in practical scenarios such as acoustic imaging and casual engineering.

Results

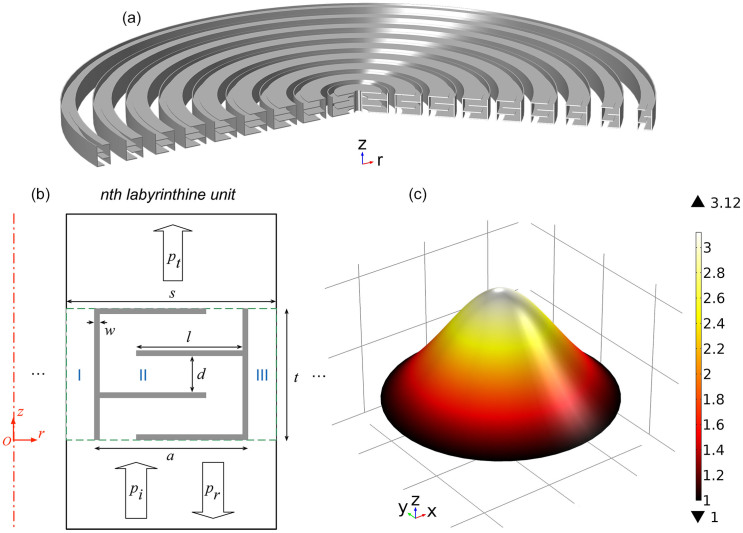
Figures 1(a) and 1(b) show the design principle of the ultrathin and planar lens, comprising a number of hybrid labyrinthine units each with a curled channel and two straight channels inside. There exists substantial phase delay as the incident wave propagates along the curled channel inside these units in comparison with the elapsed phase in a straight channel of the same physical length, which effectively provides a high refractive index⁸,⁹,²⁰. This allows a monolayer of such metamaterial units to provide sufficient phase accumulation for propagating waves at different radial distances to converge, shrinking the overall thickness of the lens down to subwavelength regime. To design the desired lens, we engineer the phase delay by changing the overall length of the channel l = a − 2w − d, while keeping the unit thickness t and the channel width d invariant. As a consequence of such a simple and intuitive design, the resulting lens has a perfectly flat surface and the channels are sufficiently wide to avoid the viscosity effect (detailed discussion can be found in Supplementary Information). Furthermore, the absence of extremely small units makes the fabrication of the prototype lens practical. As an example, a GRIN lens with a hyperbolic secant profile shown in Fig. 1(c), which has been proven capable of reducing the aberration of focal spot, is designed and fabricated. And for the sake of simplicity while without losing generality, the designed lens has an axisymmetric structure. The proposed scheme however, has the potential to build ultrathin planar lens with arbitrary index profile by properly tailoring the phase distribution of each metamaterial unit.

Figure 1. 3D axisymmetric acoustic GRIN lens.

(a) The schematic diagram of the three-dimensional axisymmetric acoustic GRIN lens, which consists of an arrangement of nine steel hybrid labyrinthine units with specified separations s = 75 mm. (b) Cross-section diagram of a unit of the proposed lens. Four transverse beams (width w = 2 mm and height l) and two standing beams (width w and height t = 47 mm) are utilized to construct a labyrinthine unit (viz. Part II) (width a) with zigzag air channel (width d = 13 mm). Two extra air channels (viz. Part I and Part III) with width, (s − a)/2, are left between the two adjacent labyrinthine units. (c) The desired profile of the relative refractive index n_r for the designed GRIN lens with maximal and minimal values of 3.12 and 1.

The desired refractive index is achieved by carefully choosing geometrical parameters in the radial plane of the lens. The particular profile of refractive index employed in this study can be described as follows

where n₀ is the refractive index at the center of the lens (r = 0) and α is the gradual coefficient, defined as

with h being the half-height of the lens, and n_h being the refractive index on the edge of the lens. To facilitate the sample fabrication, the values for n₀, n_h and h are chosen to be 3.12, 1 and 75 cm respectively. As discussed above, the high refractive index in the proposed metamaterials physically stems from the difference between actual elapsed phases in the curled channel and in straight channel of the same physical length. For an individual labyrinthine unit, therefore, the refractive index can be further enhanced by increasing the ratio of the overall length of the channel to the unit thickness. Nevertheless, the maximal refractive index in the current lens is sufficiently high, as compared with the previously realizable, to harness the convergence of incident wave with a wavelength as long as 42.1 cm (viz., operating frequency at 815 Hz).

For the proposed hybrid labyrinthine units, it is not easy to estimate n_r from the overall channel length in Part II, due to the strong coupling between acoustic fields at three inlets and outlets. To shed light on the mechanism of the proposed acoustic metamaterial, as well as providing a convenient tool for designing 3D lens, an analytical model has been developed by combining the transfer matrix method and the Green's function theory. This model allows us to predict the complex transmission and reflection coefficient from which n_r and Z_rcan be extracted. The hybrid labyrinthine unit shown in Fig. 1(b) can be divided into three parts: Parts I and III refer to two extra air channels, and Part II, the labyrinthine part. The averaged pressure and volume velocity fields 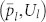(l = I, II, III) in the inlets (z = 0) and outlets (z = t) of these parts are treated separately and can be expressed as

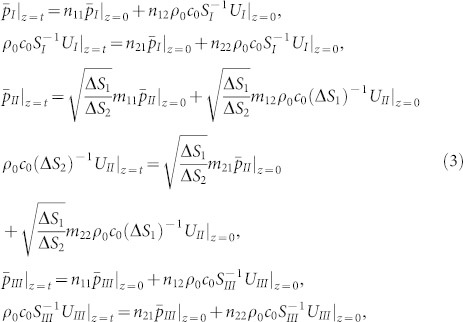where n_ij denote the transfer matrices of Parts I and III, m_ij refer to the transfer matrix of Part II; ΔS₁ and ΔS₂ represent the cross sections of the inlet and outlet in Part II, and S_I and S_III refer to the cross sections of the air channels of Part I and Part III, respectively. According to the Green's function theory for ducts, the pressure fields in the input (z < 0) and output (z > t) area can be expressed as

where G(r, z, r₀, z₀) is to the Green's function in the duct. Substituting the equation of motion into Eq. (4) yields the pressure fields of the inlets (z = 0) and outlets (z = t):

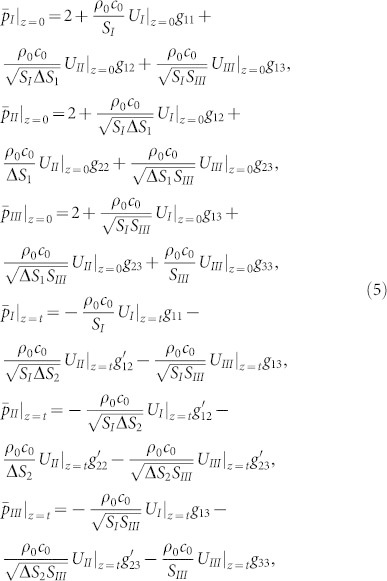with g_ij being the Green integral coupling parameters between different inlets or outlets. Substituting Eq. (3) into Eq. (5) yields the volume velocity at the inlets and outlets, referred to as U_L|_{Z = 0}(L = I, II, III) and U_L|_{Z = t}(L = I, II, III) respectively. The complex transmission and reflection coefficients of an individual metamaterial unit can be then derived according to Green's functions:

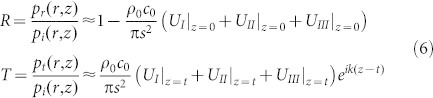Then the relative effective refractive index n_r and acoustic impedance Z_rcan be retrieved from these complex coefficients³⁵. The details of the derivations, variables and matrix definitions are given in Supplementary Information.

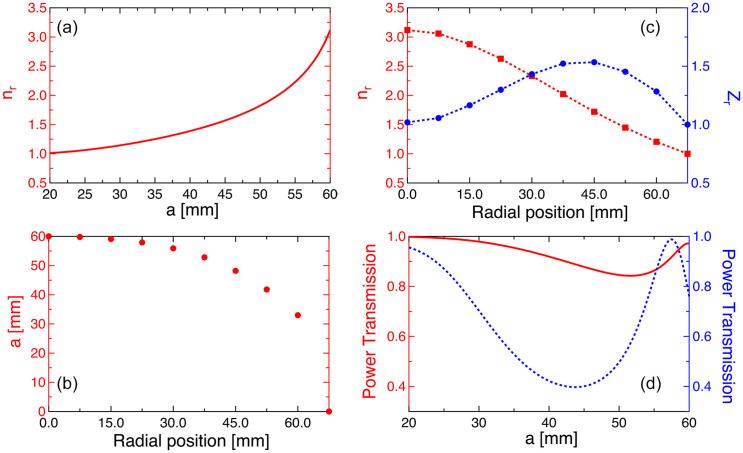
Figures 2(a) illustrates the relationship between n_rand a. It is noteworthy that the refractive index yielded by an individual metamaterials unit can be conveniently tailored to desired value by adjusting the value of a solely. Meanwhile, the widths of the steel beams and the channels in the labyrinthine units are kept invariant, and a planar structure of the presented GRIN lens is thus ensured. By comparing the curves in Fig. 1(c) and Fig. 2(a), ten different values of a are selected and shown in Fig. 2(b). At the rim of the lens, the desired refractive index should equal that of the background medium (viz., n_r = 1), indicating that no labyrinthine unit is needed here (viz., a = 0). As a result, only nine units with curled channels are required to form the GRIN lens. Figure 2(c) shows the relative effective refractive index n_r, the relative effective refractive index impedance Z_r. Despite the high refractive index provided by the hybrid labyrinthine metamaterial, the relative acoustic impedance Z_ralways approaches unity with maximal value of 1.53 for different a. Figure 2(d) illustrates the power transmission as a function of a for the case of hybrid labyrinthine units with air channels (red solid line) and the case of only the coiling units (blue dotted line). Note that that the labyrinthine units alone can only provide impedance matching at some specified frequencies, and the minimal value of the power transmission is as low as 0.39. In comparison, most acoustic energy (|p|² ≥ 84.5%) penetrates through the complex units proposed here, contributing significantly to the high efficacy of focusing. The underlying mechanism can be understood as follows. For each metamaterial unit, the transmitted waves are caused by the coupling between the wave fields at the three outlets due to the continuity of volume velocity, which can be observed in Eq. (6). For the labyrinthine units, the values of a are well tuned to support strong Fabry-Pérot resonances³⁶. Then the total transmission is determined by the transmission through the labyrinthine that depends on U_II|_{Z = t}. Note that an almost perfect impedance match is achieved here. Near the rim of lens, the units have relatively smaller a, which correspond to a variation of the resonant frequency. Therefore the transmission through the labyrinthine will be weakened, and the value of U_II|_{Z = t} will also decrease. However, the widths of the air channels have been enlarged in such cases, and the increase of U_I|_{Z = t} and U_III|_{Z = t} compensate the total transmission efficiency. As a result, the acoustic impedance Z_r throughout the whole lens matches that of background medium very well. This means the proposed structure can yield considerably high index and well-matched impedance simultaneously, suggesting the potential to serve as an ultrathin lens with high efficacy. Also, It is worth pointing out that in the proposed metamaterial unit with a hybrid structure, the air channel is introduced to compensate the impedance mismatch that is the negative effect caused by the labyrinthine structure when yielding high refractive index. Physically, the effective parameters of the lens, including the refractive index and the acoustic impedance, are determined by the whole hybrid structure. The increase of the width of the air channel helps to significantly improve the impedance match between the designed lens and the background medium, while decreasing slightly the effective refractive index due to the fact that volume fraction of the labyrinthine part becomes smaller. However, such a reduction in the effective refractive index is trivial in our design since the refractive index yielded by the labyrinthine unit is considerably high.

Figure 2. The relative effective refractive index n_rand acoustic impedance Z_r of the presented GRIN lens.

(a) The analytical n_r as a function of the width of the labyrinthine units. (b) Ten specified values of a with which GRIN lens could be arranged. (c) The analytical n_r, Z_r of the each nine units. (d) The power transmission of the proposed case of the labyrinthine unit with two extra air channels and the case with only labyrinthine unit.

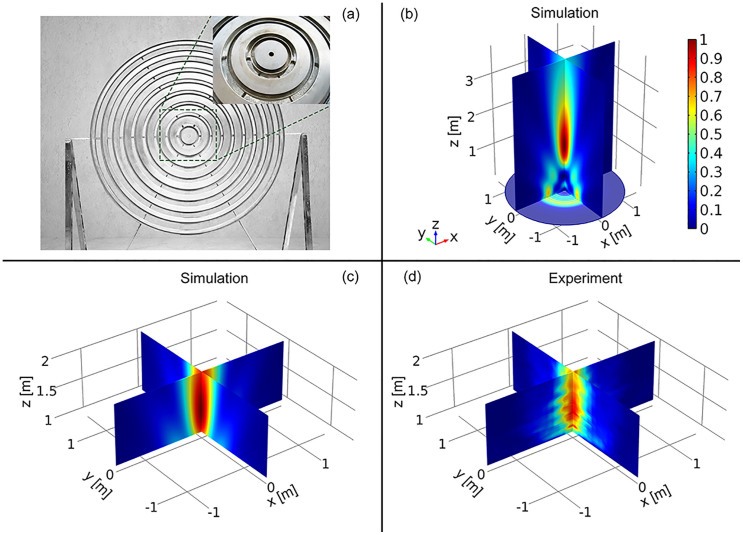
The 3D axisymmetric metamaterial lens shown in Fig. 3(a), is fabricated with designed parameters. Nine axisymmetric metamaterial units composing the lens are assembled with two supporting shelves thin enough to neglect the scattering effect within the frequency spectrum of interest. Figure 3(b) illustrates the simulated acoustic intensity distribution |p|² of the designed lens. Figures 3(c) and 3(d) display the numerical and the experimental results of acoustic intensity distribution |p|² in the focal region. Due to the axisymmetry of the lens, only the intensity distributions on two orthogonal planes are shown. The propagating waves pass through the lens and focus at the focal point z = 1.4 m with significant intensity enhancement. Good agreements can be observed between the numerical and experimental results, which verify the proposed scheme and demonstrate the performance of the fabricated lens. Slight discrepancy also exists between the calculated and measured intensity distribution, which may stem from imperfections of sample and limited precision in the measurement.

Figure 3. Acoustic focusing of the GRIN lens at 815 Hz.

(a) The sample of the designed GRIN lens. The inlet is an enlarged view near the center of lens. (b) The simulated spatial distributions of the intensity field |p|² of the GRIN lens. (c) Closer view of the simulated distributions near the focus spot. (d) The measured spatial distributions of the intensity field |p|² of the fabricated sample.

To give a quantitative analysis to the focusing performance of the prototype lens, we have measured the intensity distribution profiles along different directions crossing the focus. Results are displayed in Fig. 4. The simulated distributions are also included here for comparison. The experimental results agree excellently with the simulated results, both show the significant energy enhancement at the focal spot near z = 1.4 m. The intensity at the focal point is nearly 33.5 times (~15 dB in experiments) greater than the one without the lens. It is also noteworthy that, although the lens is designed to work at 815 Hz, the resulting lens has a frequency band that ranges from 500 to 1100 Hz, i.e., the ratio between the bandwidth and the center frequency almost reaches 0.74 (See the Supplementary Information for the demonstration of the bandwidth of the focusing effect as well as discussion on the underlying physics).

Figure 4. Experimental and theoretical demonstrations for the GRIN lens at 815 Hz.

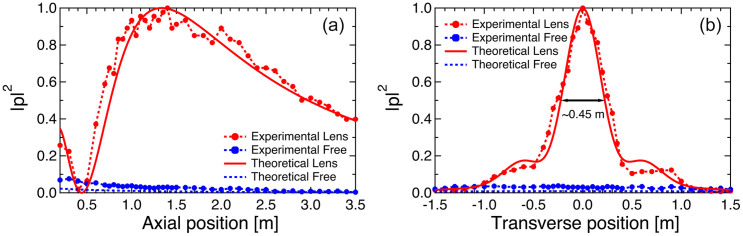
The simulated and experimental acoustic intensity distribution |p|² (a) along the axis and (b) along the transverse cross-section in the radial plane through the focal point at z = 1.4 m for the cases with and without the GRIN lens.

Discussions

In summary, we experimentally demonstrate a viable route for realizing 3D ultrathin planar acoustic lens using acoustic metamaterial units which provide high refractive index and well-matched impedance simultaneously. A theoretical method is developed for analytically describing the acoustic properties of this particular type of metamaterials. The sample lens confirms the functionality of the proposed scheme: high-efficient focusing of low-frequency sound using subwavelength-scale lens manipulating the phase of propagating wave. The experimental results agree well with the theoretical predictions. And the lens designed to work at 815 Hz actually exhibit a working bandwidth for which the ratio between the bandwidth and the center frequency almost reaches 0.74. Further optimization of our ultrathin and planar acoustic lens can pave the way to building even more compact, efficient and versatile acoustic devices for diverse applications such as acoustic imaging and casual engineering.

Method

Experiments setup and measurements

The experiment is performed in the outdoor environment with acoustic absorbing wedge placed on the ground. A 16 cm ×16 cm × 20 cm sound speaker located at the focus of a parabolic reflector is used to excite the acoustic plane waves with a frequency of 815 Hz. The sound pressure is measured by a movable 1/2-inch diameter microphone (Brüel & Kjær 4191). The recording and analysis equipment contains a Brüel & Kjær PULSE 3160-A-042 multichannel analyzer and a computer with PULSE software LabShop version 13.5.10.

Numerical Simulation

The finite Element Method (FEM) based on commercial software COMSOL Multiphysics™ 4.3 b is employed for the simulations in Figs 3 and 4. The materials used in simulations are air and steel. The mass density and sound speed of air are ρ_a = 1.21 kg/m³, c_a = 343 m/s, and the mass density and sound velocity of steel are ρ_s = 7800 kg/m³, c_s = 6100 m/s, respectively. Perfectly matched layers (PMLs) are imposed on the outer boundaries of simulated domain to eliminate the interference from reflected wave.

Author Contributions

Y. L., G.K.Y., B.L. and X.Y.Z. performed analytical and numerical computations. Y. L., G.Y.L. and C.S. conducted the experiments. B.L. and J.C.C. conceived and supervised the study. Y.L., B.L. and J.C.C. wrote the article. All authors contributed to the discussions.

Supplementary Material

Supplementary Information

Supplementary Information on