Large deformation diffeomorphic registration of diffusion-weighted imaging data

Abstract

Registration plays an important role in group analysis of diffusion-weighted imaging (DWI) data. It can be used to build a reference anatomy for investigating structural variation or tracking changes in white matter. Unlike traditional scalar image registration where spatial alignment is the only focus, registration of DWI data requires both spatial alignment of structures and reorientation of local signal profiles. As such, DWI registration is much more complex and challenging than scalar image registration. Although a variety of algorithms has been proposed to tackle the problem, most of them are restricted by the zdiffusion model used for registration, making it difficult to fit to the registered data a different model. In this paper we describe a method that allows any diffusion model to be fitted after registration for subsequent multifaceted analysis. This is achieved by directly aligning DWI data using a large deformation diffeomorphic registration framework. Our algorithm seeks the optimal coordinate mapping by simultaneously considering structural alignment, local signal profile reorientation, and deformation regularization. Our algorithm also incorporates a multi-kernel strategy to concurrently register anatomical structures at different scales. We demonstrate the efficacy of our approach using in vivo data and report detailed qualitative and quantitative results in comparison with several different registration strategies.

1. Introduction

Diffusion-weighted imaging (DWI) is widely used to non-invasively study white matter microstructure and fiber tracts in the human brain. The information provided by DWI is helpful for identifying pathological damages associated with brain diseases (e.g., stroke Schaefer et al., 2000, Alzheimer’s disease Hanyu et al., 1998; Wee et al., 2011, 2012; Zhang et al., 2013, and schizophrenia Shi et al., 2012) and brain changes associated with normal development (Yap et al., 2011).

To quantify white matter changes, a common space is required where images of patients and healthy controls can be spatially normalized and compared. Image registration is used to build such space and to spatially normalize the images by warping them to the space.

Traditional scalar image registration techniques are not directly applicable to diffusion-weighted images. When diffusion-weighted images corresponding to different diffusion gradient directions are put together, each voxel location encodes a vector-valued signal profile that provides information on the segment of the fiber bundle that traverses the voxel. As such, registration of diffusion-weighted images requires not only the spatial alignment of anatomical structures, as in scalar image registration, but also the reorientation of signal profiles with respect to the surrounding anatomical structures, which is not considered in scalar image registration. DWI registration is thus much more complicated and challenging than scalar image registration.

A common approach to registering diffusion-weighted images is to fit some diffusion model to the images to estimate angular quantities, such as orientation distribution functions (ODFs), and then incorporate such information into a registration algorithm for structural alignment. There are a number of choices of diffusion models as well as registration algorithms, leading to a variety of DWI registration methods.

Early work uses the relatively simple diffusion tensor model (Alexander et al., 2001; Cao et al., 2006; Yeo et al., 2009, 2010; Zhang et al., 2006). Alexander et al. (2001) introduced the preservation of principal direction (PPD) algorithm for the reorientation of diffusion tensors during image alignment. Instead of PPD, Yeo et al. (2009) used a finite strain reorientation strategy (Alexander et al., 2001) together with a diffeomorphic demons algorithm (Vercauteren et al., 2009) for registration. Zhang et al. (2006) broke down the image into uniform regions and estimated an affine transformation for each region by explicitly optimizing tensor orientation within that region. Cao et al. (2006) proposed a large deformation diffeomorphic metric mapping (LDDMM) algorithm (Beg et al., 2005) to tackle large-deformation non-linear registration of directional vector fields.

However, the diffusion tensor model can only characterize one principal fiber direction at each voxel and thus is unable to handle complex fiber configurations such as crossings. It has been found that at least one third of voxels in white matter have complex fiber configurations (Behrens et al., 2007). Obviously, failure to reorient the signal profiles in those voxels will lead to misalignments of microstructure.

To deal with crossing fibers, a number of researchers (Geng et al., 2011; Du et al., 2012; Hong et al., 2009; Raffelt et al., 2011; Yap et al., 2011; Dhollander et al., 2011; Zhang et al., 2012) attempted to use more complicated diffusion models. Geng et al. (2011) aligned ODFs represented by spherical harmonics (SHs) using an elastic registration algorithm. Du et al. (2012) integrated a similarity metric for the ODFs, which is defined in a Riemannian manifold, into a variant of LDDMM algorithm (Glaunès et al., 2008). Yap et al. (2011) extracted coarse-to-fine features from the ODFs for hierarchically refined alignment. Instead of using ODFs, Hong et al. (2009) performed registration with the help of T₂-weighted images and subsequently reoriented the fiber orientation distribution (FOD). Raffelt et al. (2011) registered DWI data by mapping the FODs through a subject-template-symmetric diffeomorphic framework.

However, the aligned data generated by the above approaches are not in the form of diffusion-weighted images. The ability to produce diffusion-weighted images as final registration outcome is important for common-space analysis using diffusion models without well-defined warping and reorientation methods.

To overcome this problem recent studies propose to register DWI data directly in the Q-space (Dhollander et al., 2011; Zhang et al., 2012). Dhollander et al. (2011) tackled the problem by virtue of an SH-based reorientation algorithm together with a diffeomorphic demons algorithm (Vercauteren et al., 2009). We (Zhang et al., 2012) achieved a similar goal by using a set of diffusion basis functions (DBFs) (Yap and Shen, 2012) and a geodesic shooting algorithm simplified proposed by Ashburner and Friston (2011). Both methods regard spatial alignment and local signal profile reorientation as two separate components, and perform optimization by alternating between (i) computing the spatial mapping without considering reorientation, and (ii) reorienting the data using the resulting mapping. Although this strategy is simple, it ignores the crucial role reorientation plays in correspondence establishment.

As shown by Yeo et al. (2009), a better but more complicated strategy is to integrate the two components into a single cost function and explicitly take into account reorientation during registration. In this paper we describe a method that is able to register DWI data in the Q-space in a single framework where image matching, data reorientation, and deformation regularization are considered simultaneously. Part of this work has been reported in our recently published conference paper (Zhang et al., 2013). Herein, we provide additional derivations, implementation details, and experimental results that are not available in the conference version. Compared with the conference paper, this paper uses a more general symmetric tensor model, instead of Watson distribution, as the DBFs (Yap and Shen, 2012). In addition, the cost function is reformulated such that the solution satisfies the Euler–Lagrange equation.

2. Outline of the approach

Our method consists of two components: (1) DWI data reorientation (Section 3) and (2) an LDDMM-based registration algorithm (Section 4). The first component achieves reorientation in the Q-space while the second one provides a registration framework where alignment and reorientation are considered simultaneously.

The first component is realized based on the work of Yap and Shen (2012), where reorientation is achieved by three steps: (i) decomposing the diffusion signal profile into a set of weighted DBFs; (ii) reorienting each DBF independently using a local transformation; (iii) recomposing the reoriented DBFs to obtain the desired profile. Compared with the SH-based reorientation scheme as used by Dhollander et al. (2011), this strategy avoids the computational complexity of SHs as well as the loss of sharp directional information when the maximum order of the SH basis functions is insufficient (see Yap and Shen (2012) for detailed discussion).

The second component involves the LDDMM algorithm (Beg et al., 2005). Based on the spatial mapping estimated by the LDDMM algorithm, a Jacobian matrix can be computed at each voxel location and used for DBF reorientation. The interaction between the two components is mathematically expressed as a single cost function (Section 4) and, during optimization, spatial alignment and local reorientation are considered simultaneously.

To simultaneously register anatomical structures at different scales we use a multi-kernel strategy (Risser et al., 2011). This is to introduce a natural multi-resolution property to our registration algorithm and to provide an intuitive way of parameter tuning based on the desired scales that should be captured by the registration. Details are given in Section 5.1.

This work has three major contributions. First, we propose a non-rigid registration algorithm for direct registration of DWI data. This allows any diffusion model to be fitted to the aligned data for subsequent multifaceted analysis. Second, we incorporated spatial alignment and local reorientation into a single cost function. In contrast to the works of Dhollander et al. (2011) and Hsu et al. (2012), our method does not rely on multi-shell data, which require long acquisition time. Last but not least, we derive the gradient of the cost function and describe in detail the numerical implementation.

3. Reorientation of DWI data

We now briefly review the major concepts involved in reorientation using DBFs (Yap and Shen, 2012).

3.1. Decomposition of signal profile

Let S(q_i) be the diffusion signal measured in direction q_i (i = 1, …, M). It can be represented by a set of N DBFs:

$$S({\mathit{q}}_i)=w_0{f}_0+\sum _{j=1}^N{w}_{j}f({\mathit{q}}_i\mid {\lambda }_1,{\lambda }_2,{\mathit{\mu }}_j),$$

where f(q_i∣λ₁, λ₂, μ_j) is the j-th DBF, w_j is the associated weight, and f₀ is a constant component representing isotropic diffusion. Specifically, the j-th DBF is defined by

$$f({\mathit{q}}_i\mid {\lambda }_1,{\lambda }_2,{\mathit{\mu }}_j)=\exp (-b{\mathit{q}}_i^{\mathrm{T}}{\mathit{D}}_j{\mathit{q}}_i),$$ (1)

where b is the diffusion weighting and ${\mathit{D}}_j=({\lambda }_1-{\lambda }_2){\mathit{\mu }}_j{\mathit{\mu }}_j^{\mathrm{T}}+{\lambda }_2\mathit{I}$ is a symmetric diffusion tensor. λ₁ and λ₂ control the shape of the tensor, {μ_j} is a pre-defined set of tensor principal directions and I is an identity matrix representing an isotropic tensor. We generated {μ_j} via spherical tessellation by subdividing the faces of an icosahedron.

If λ₁ ≫ λ₂, D_j can be approximated by ${\lambda }_1{\mathit{\mu }}_j{\mathit{\mu }}_j^{\mathrm{T}}$. Then, we have

$$f({\mathit{q}}_i\mid {\lambda }_1,{\lambda }_2,{\mathit{\mu }}_j)\approx \exp \left(-b{\lambda }_1{\left({\mathit{\mu }}_j^{\mathrm{T}}{\mathit{q}}_i\right)}^2\right),$$

which is essentially the p.d.f. of the Watson distribution (Jupp and Mardia, 1989). This simplified model has been used in our previous work (Zhang et al., 2012; Zhang et al., 2013). In this work we use the more general model (1).

Let S be the signal vector, then we have S = Fw, where S = [S(q₁), S(q₂), …, S(q_M)]^T, w = [w₀, w₁, …, w_N]^T, and

$$\mathit{F}=\left[\begin{array}{cccc}{f}_0& f\left({\mathit{q}}_1\mid {\lambda }_1,{\lambda }_2,{\mathit{\mu }}_1\right)& \cdots & f\left({\mathit{q}}_1\mid {\lambda }_1,{\lambda }_2,{\mathit{\mu }}_N\right)\\ ⋮& ⋮& \ddots & ⋮\\ f_0& f\left({\mathit{q}}_M\mid {\lambda }_1,{\lambda }_2,{\mathit{\mu }}_1\right)& \cdots & f\left({\mathit{q}}_M\mid {\lambda }_1,{\lambda }_2,{\mathit{\mu }}_N\right)\end{array}\right].$$

Since typically, M < N + 1, this is a set of under-determined linear equations, which can be solved by an L₁-regularized least-squares solver with a non-negative constraint (see Yap and Shen (2012) for details).

3.2. Reorientation of signal profile

At each voxel, a local affine transformation A is used to reorient the directions of the DBFs, i.e. ${\mathit{\mu }}_j^{\prime }=\mathit{A}{\mathit{\mu }}_j/\Vert \mathit{A}{\mathit{\mu }}_j\Vert$. A is estimated locally from a typically non-linear mapping and hence varies spatially. The reoriented DBF matrix, F′, is calculated based on ${\mathit{\mu }}_j^{\prime }$ as follows

$${\mathit{F}}^{\prime }=\left[\begin{array}{cccc}{f}_0& f\left({\mathit{q}}_1|{\lambda }_1,{\lambda }_2,\frac{\mathit{A}{\mathit{\mu }}_1}{\Vert \mathit{A}{\mathit{\mu }}_1\Vert }\right)& \cdots & f\left({\mathit{q}}_1|{\lambda }_1,{\lambda }_2,\frac{\mathit{A}{\mathit{\mu }}_N}{\Vert \mathit{A}{\mathit{\mu }}_N\Vert }\right)\\ ⋮& ⋮& \ddots & ⋮\\ f_0& f\left({\mathit{q}}_M|{\lambda }_1,{\lambda }_2,\frac{\mathit{A}{\mathit{\mu }}_1}{\Vert \mathit{A}{\mathit{\mu }}_1\Vert }\right)& \cdots & f\left({\mathit{q}}_M|{\lambda }_1,{\lambda }_2,\frac{\mathit{A}{\mathit{\mu }}_N}{\Vert \mathit{A}{\mathit{\mu }}_N\Vert }\right)\end{array}\right].$$

The orientation-rectified signal profile is then computed as S′ = F′ w. Note that the isotropic component is not reoriented.

4. LDDMM-based DWI registration

LDDMM techniques (Beg et al., 2005; Miller et al., 2006; Vialard et al., 2012; Ashburner and Friston, 2011) are designed for diffeomorphic registration when the object of interest undergoes large shape variation. Initially formulated for scalar image registration (Beg et al., 2005), it was later extended for registering vector fields (Cao et al., 2005). In this work, we further extend it for DWI registration.

Let I₀ be the source image and I₁ be the target image. The goal of the LDDMM algorithm is to minimize the following cost function

$$E(\mathit{\upsilon })=\frac{1}{2}{\mathit{\int }}_0^1{\Vert {\mathit{\upsilon }}_t\Vert }_V^2\mathrm{d}t+\frac{1}{{\sigma }^2}{\Vert I_0\circ {\varphi }_{1,0}-I_1\Vert }_{L^2}^2,$$ (2)

where υ_t is a time-dependent velocity field that needs to be estimated, σ > 0 is a regularization constant, and ϕ_s,t is a mapping induced by υ_t, transforming a voxel from its position at time s to its position at time t (e.g., ϕ_1,0(x) transforms a voxel at position x at time 1 to its position y = ϕ_1,0(x) at time 0). ${\Vert {\mathit{\upsilon }}_t\Vert }_V^2={\langle L^{†}L{\mathit{\upsilon }}_t,{\mathit{\upsilon }}_t\rangle }_{L^2}$, where V is a Hilbert space in which the velocity field resides, i.e. υ ∈ L²([0, 1], V) and L is a proper differential operator which, when appropriately chosen, guarantees a diffeomorphic solution (Beg et al., 2005). Instead of realizing L directly, diffeomorphism can be achieved by defining a smoothing kernel K = (L^†L)⁻¹. Here we use a multi-Gaussian kernel scheme (Risser et al., 2011) for simultaneous multi-scale registration.

Since our focus is on DWI registration, we further assume that I is a vector-valued image representing diffusion signal vector S at each position x, i.e. I(x) ≡ S(x). We denote the i-th element of I(x) as Iⁱ(x). We define the action of a mapping ϕ on I as

$$I\circ \varphi =F_{\varphi }W\circ \varphi ,$$ (3)

where W is a vector-valued weight image associated with I, containing a sparse weight vector w at each x, i.e. W(x) ≡ w(x), and F_ϕ(x) is a matrix-valued image containing the reoriented DBFs, with the voxel at x given by

$$F_{\varphi }(\mathit{x})=\left[\begin{array}{cccc}{f}_0& f\left({\mathit{q}}_1|{\lambda }_1,{\lambda }_2,\frac{{(D\varphi (\mathit{x}))}^{-1}{\mathit{\mu }}_1}{\Vert {(D\varphi (\mathit{x}))}^{-1}{\mathit{\mu }}_1\Vert }\right)& \cdots & f\left({\mathit{q}}_1|{\lambda }_1,{\lambda }_2,\frac{{(D\varphi (\mathit{x}))}^{-1}{\mathit{\mu }}_N}{\Vert {(D\varphi (\mathit{x}))}^{-1}{\mathit{\mu }}_N\Vert }\right)\\ ⋮& ⋮& \ddots & ⋮\\ f_0& f\left({\mathit{q}}_M|{\lambda }_1,{\lambda }_2,\frac{{(D\varphi (\mathit{x}))}^{-1}{\mathit{\mu }}_1}{\Vert {(D\varphi (\mathit{x}))}^{-1}{\mathit{\mu }}_1\Vert }\right)& \cdots & f\left({\mathit{q}}_M|{\lambda }_1,{\lambda }_2,\frac{{(D\varphi (\mathit{x}))}^{-1}{\mathit{\mu }}_N}{\Vert {(D\varphi (\mathit{x}))}^{-1}{\mathit{\mu }}_N\Vert }\right)\end{array}\right],$$

where D is the Jacobian operator. From (3), we can see that ϕ spatially transforms the sparse weights and reorients the DBFs via F_ϕ(x). W is computed by fitting the DBFs to the DWI data as described in Section 3.

To reflect reorientation, we rewrite the cost function (2) as

$$E(\mathit{\upsilon })=\frac{1}{2}{\mathit{\int }}_0^1{\Vert {\mathit{\upsilon }}_t\Vert }_V^2\mathrm{d}t+\frac{1}{{\sigma }^2}{\Vert F_{{\varphi }_{1,0}}{W}_0\circ {\varphi }_{1,0}-I_1\Vert }_{L^2}^2,$$ (4)

where W₀ is the weight image associated with I₀. By computing the variation of E(υ) w.r.t. υ, the gradient of (4) can be obtained as

$$\begin{array}{ll}{({\nabla }_{\mathit{\upsilon }}E)}_t& ={\mathit{\upsilon }}_t-\frac{2}{{\sigma }^2}K({\mathit{\int }}_{\Omega }|D{\varphi }_{t,1}^{\mathit{\upsilon }}|\sum _i^M(I_0^i\circ {\varphi }_{t,0}^{\mathit{\upsilon }}-I_1^i\circ {\varphi }_{t,1}^{\mathit{\upsilon }})\\ & \times \sum _j^N{w}_j\circ {\varphi }_{t,0}^{\mathit{\upsilon }}\mathrm{const}({\mathit{q}}_i,{\stackrel{\sim }{\mathit{\mu }}}_j)\\ & \times {\left({\nabla }_{{\stackrel{\sim }{\mathit{\mu }}}_j}\left[\frac{{\stackrel{\sim }{\mathit{\mu }}}_j}{\Vert {\stackrel{\sim }{\mathit{\mu }}}_j\Vert }\right]\left(D{\varphi }_{t,1}^{\mathit{\upsilon }}D({(D{\varphi }_{t,0}^{\mathit{\upsilon }})}^{-1})\right){\mathit{\mu }}_j\right)}^{\mathrm{T}}{\mathit{q}}_i\mathrm{d}\mathit{x})\\ & +\frac{2}{{\sigma }^2}\mathit{DK}({\mathit{\int }}_{\Omega }|D{\varphi }_{t,1}^{\mathit{\upsilon }}|\sum _i^M(I_0^i\circ {\varphi }_{t,0}^{\mathit{\upsilon }}-I_1^i\circ {\varphi }_{t,1}^{\mathit{\upsilon }})\\ & \times \sum _j^N{w}_j\circ {\varphi }_{t,0}^{\mathit{\upsilon }}\mathrm{const}({\mathit{q}}_i,{\stackrel{\sim }{\mathit{\mu }}}_j)\\ & \times {\left({\nabla }_{{\stackrel{\sim }{\mathit{\mu }}}_j}\left[\frac{{\stackrel{\sim }{\mathit{\mu }}}_j}{\Vert {\stackrel{\sim }{\mathit{\mu }}}_j\Vert }\right](D{\varphi }_{t,1}^{\mathit{\upsilon }}({D{\varphi }_{t,0}^{\mathit{\upsilon }})}^{-1}){\mathit{\mu }}_j\right)}^{\mathrm{T}}{\mathit{q}}_i\mathrm{d}\mathit{x})\\ & -\frac{2}{{\sigma }^2}K\left({\mathit{\int }}_{\Omega }|D{\varphi }_{t,1}^{\mathit{\upsilon }}|\sum _i^M(I_0^i\circ {\varphi }_{t,0}^{\mathit{\upsilon }}-I_1^i\circ {\varphi }_{t,1}^{\mathit{\upsilon }}){\mathit{b}}_i^{\mathrm{T}}D(W_0\circ {\varphi }_{t,0}^{\mathit{\upsilon }})\mathrm{d}\mathit{x}\right),\end{array}$$ (5)

where

$$\begin{array}{l}{\stackrel{\sim }{\mathit{\mu }}}_j={(D{\varphi }_{t,0}^{\mathit{\upsilon }})}^{-1}{\mathit{\mu }}_j,\\ \mathrm{const}({\mathit{q}}_i,{\stackrel{\sim }{\mathit{\mu }}}_j)=\exp \left\{-b\left[({\lambda }_1-{\lambda }_2){\left({\left(\frac{{\stackrel{\sim }{\mathit{\mu }}}_j}{\Vert {\stackrel{\sim }{\mathit{\mu }}}_j\Vert }\right)}^{\mathrm{T}}{\mathit{q}}_i\right)}^2+{\lambda }_2\right]\right\}\\ \times \left(-2b({\lambda }_1-{\lambda }_2){\left(\frac{{\stackrel{\sim }{\mathit{\mu }}}_j}{\Vert {\stackrel{\sim }{\mathit{\mu }}}_j\Vert }\right)}^{\mathrm{T}}{\mathit{q}}_i\right),\\ {\mathit{b}}_i={[f_0,b_{i1},\cdots ,b_{iN}]}^{\mathrm{T}},\\ b_{\mathit{ij}}=f\left({\mathit{q}}_i|{\lambda }_1,{\lambda }_2,\frac{{\stackrel{\sim }{\mathit{\mu }}}_j}{\Vert {\stackrel{\sim }{\mathit{\mu }}}_j\Vert }\right),\end{array}$$

Ω is a bounded domain in ℝ^d and x ∈ Ω. The detailed derivation is given in Appendix A.

Apart from υ_t, there are three other terms in (5). If no reorientation is involved, the first two terms will vanish and it is easy to show that (5) is equivalent to the gradient for scalar image registration as given in Beg et al. (2005). When reorientation is in effect, the first two terms contribute to updating {υ_t} by using mappings¹ estimated in the preceding iterations to reorient the directions of the DBFs. This reveals how spatial alignment and reorientation interact with each other. In contrast, spatial alignment and reorientation are regarded as two separate components by Dhollander et al. (2011) and Zhang et al. (2012).

5. Numerical implementation details

We now describe the numerical implementation details of our algorithm, including multi-Gaussian kernel, mapping computation, and gradient descent optimization.

5.1. Multi-kernel scheme

Instead of defining L, we follow the approach proposed by Risser et al. (2011) to define a multi-Gaussian kernel K to achieve the desired smoothness. Specifically, K is realized by a set of weighted Gaussian kernels

$$K=\sum a_{l}N(0,{\mathrm{\sum }}_l),$$

where a_l is the weight of the l-th Gaussian kernel and Σ_l is a diagnal covariance matrix defined by a scale factor σ_l, i.e. Σ_l = σ_lI, where I is an identity matrix.

To estimate a_l we need to perform a pre-registration step to estimate the maximum update of υ at each position x, i.e. τ_l = max({∥δυ∥∣ δυ at ∀x ∈ Ω}), where δυ can be computed via (5) by setting ϕ_t,0 = ϕ_t,1 = id, where id is an identity mapping, υ_t = 0, and K = N(0,Σ₁). Then a_l is calculated as the reciprocal of τ_l and normalized such that Σa_l = 1.

5.2. Mapping computation

Suppose the time interval is [0, 1], there are n time points {t_p∣p = 1, 2, …, n} evenly distributed in this interval, i.e. t_p = p/n and the time point 0 is denoted by t₀. To update the gradient using (5), we have to compute the forward mappings {ϕ_tp,1} and backward mappings {ϕ_tp,0} at each time point t_p. This can be obtained via a backward integration by assuming that ϕ_tn,1 = ϕ_t0,0 = id. Specifically, the forward mapping ϕ_t,1 and backward mapping ϕ_t,0 can be computed by concatenating a set of small mappings (Ashburner and Friston, 2011), i.e.

$$\begin{array}{lll}{\varphi }_{t_p,1}& =& (\mathrm{id}+\frac{1}{n}{\mathit{\upsilon }}_{t_{n-1-p}})\circ {\varphi }_{t_{p+1},1},\\ {\varphi }_{t_p,0}& =& {\varphi }_{t_{p-1},0}\circ (\mathrm{id}-\frac{1}{n}{\mathit{\upsilon }}_{t_{p-1}}),\end{array}$$

where {υ_tp} is a series of velocity fields.

5.3. Gradient descent

Once we have computed the gradient using (5), we can use any gradient descent algorithm to solve (4). In this work we use line search for gradient descent. A summary of the algorithm is given in Algorithm 1.

Algorithm 1.

LDDMM-based DWI registration

Input: I0, I1, {μj}, {qi}, λ1, λ2, b, n, {σl} and {α} (step size)

Initialization {υtp ∣ υtp ← 0, ∀p}

1: estimate kernel weights {al}

2: repeat

3:  for each p do

4:    ${\varphi }_{t_p,1}\leftarrow (\mathrm{id}+\frac{1}{n}{\mathit{\upsilon }}_{t_{n-1-p}})\circ {\varphi }_{t_{p+1},1}$

5:    ${\varphi }_{t_p,0}\leftarrow {\varphi }_{t_{p-1},0}\circ (\mathrm{id}-\frac{1}{n}{\mathit{\upsilon }}_{t_{p-1}})$

6:  end for

7:  compute current energy E using (4)

8:  for each p do

9:   compute gradient (∇υ E)tp using (5)

10:  end for

11:  (E′, α) ← linesearch (E, {υtp}, {α}, {(∇υ E)tp})

12:  if E′ < E then

13:   for each p do

14:    υtp ← υtp − α(∇υ E)tp

15:   End For

16:  end if

17: until E′ ≥ E ∨ α = inf {α} ∨ maximum number of iterations

18: function linesearch (E, {υtp}, {α}, {(∇υ E)tp})

19:  for each α do

20:   for each p do

21:     ${\mathit{\upsilon }}_{t_p}^{\prime }\leftarrow {\mathit{\upsilon }}_{t_p}-\alpha {({\nabla }_{\mathit{\upsilon }}E)}_{t_p}$

22:   end for

23:   for each p do

24:     ${\varphi }_{t_p,1}\leftarrow (\mathrm{id}+\frac{1}{n}{\mathit{\upsilon }}_{t_{n-1-p}}^{\prime })\circ {\varphi }_{t_{p+1},1}$

25:     ${\varphi }_{t_p,0}\leftarrow {\varphi }_{t_{p-1},0}\circ (\mathrm{id}-\frac{1}{n}{\mathit{\upsilon }}_{t_{p-1}}^{\prime })$

26:   end for

27:   compute current energy E′ using (4)

28:   if E′ < E then

29:    return E′, α

30:   end if

31:  end for

32:  return E, inf {α}

33: end function

6. Experiments

DWI data were acquired from 11 adults using a Siemens 3T TIM Trio MR Scanner with an EPI sequence. Diffusion gradients were applied in 120 non-collinear directions with diffusion weighting b = 2000s/mm². The imaging matrix was 128 × 128 with a field of view of 256 × 256mm². 80 contiguous slices with thickness of 2mm covered the whole brain. A diffusion tensor model was fitted to the signal vector at each voxel, leading to a field of diffusion tensors. The eigenvalues corresponding to the principal eigenvectors were then computed for each tensor. By using a region of interest (ROI) defined at the corpus callosum, which is known to contain coherent single-orientation fiber bundles, we computed λ₁ by averaging the eigenvalues corresponding to the first principal directions. We then computed λ₂ as the mean of the eigenvalues corresponding to the second and third principal eigenvectors.

We randomly chose an image as the target image and used the rest as source images. For each image, we fit the DBFs, with 321 directions uniformly distributed on a unit sphere, to estimate the associated weight image, which was then used to obtain a reconstructed version of the image. A set of affine transformations was estimated between the target image and each source image using their anisotropy images computed from the reconstructed data. We then reconstructed each source image again using the associated weight image by taking into account the affine transformation (see (3)). The resulting reconstructed source images were used for both DWI and diffusion tensor imaging (DTI) registration. We compared our method (Section 4), which we will refer to as LDDMM-DWI, with the following registration strategies:

1. Naïve LDDMM-DWI (Zhang et al., 2012): This is a registration scheme that iteratively (1) warps and reorients the source and target images based on an estimated mapping, (2) estimates a new mapping that further aligns the two resulting images via a geodesic shooting algorithm, (3) concatenates the estimated mapping with the one estimated in the previous iteration. The source image is reconstructed using the composite mapping together with an affine transformation, whereas the target is reconstructed without any transformation. At each stage the reconstruction is done by using an increasing number of diffusion directions.

2. DTI registration: For each image we computed a DT image by fitting the diffusion tensor model to the reconstructed data. We then registered each source DT image to the target DT image using DTI-TK (Zhang et al., 2006).

For LDDMM-DWI, we ran line search for 30 iterations. For naïve LDDMM-DWI (Zhang et al., 2012), we performed the registration in 6 stages: 30 iterations in the first two stages, 20 in the middle stages, and 10 and 5 in the last two stages. In each stage, the number of diffusion directions was 1, 6, 21, 81, 120, and 321, respectively. The default parameters provided on the DTI-TK website² were used for DTI registration.

To quantify the comparison, we computed the voxel-wise root mean square (RMS) error between the target image and each of source image, warped and reoriented using the estimated affine and non-linear mapping. Averaging the resulting RMS error images across subjects for each method leads to the mean images shown in Fig. 1. For reference, we also show the mean RMS error image of source images warped and reoriented using affine transformations alone. For each mean RMS error image we computed its statistics (i.e. mean, standard deviation, median, and the 90-th percentile) over all voxels and report the results in Table 1. For each method, we also computed the mean intensity value of the RMS error image associated with each subject and used these means to perform two-tailed student’s t-tests using LDDMM-DWI as the baseline. The results, given in the same table, indicate that the performance differences are statistically significant.

Fig. 1.

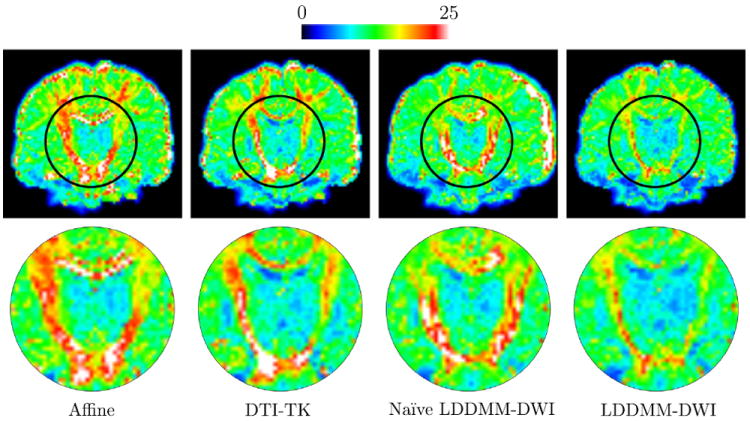
The mean RMS error images (top) and the close-ups of regions marked by black circles (bottom). Note that the images were not sliced for left–right symmetry. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Table 1.

Statistics of the mean RMS error images given by various registration strategies.

Method	Mean ± s.d.	Median	90%-ile	p-value
Affine	14.7 ± 6.3	13.4	21.4	p < 10−6
DTI-TK	13.3 ± 6.1	12.2	19.6	p < 0.01
Naïve LDDMM-DWI	12.9 ± 5.4	11.9	18.3	p < 0.05
LDDMM-DWI	11.7 ± 4.5	11.3	16.5	–

From Fig. 1, it is clear that LDDMM-DWI significantly improves the alignment of white matter structures, such as the internal capsule. Affine registration and naïve LDDMM-DWI do not take into account reorientation in the optimization process and are hence less effective in white matter alignment. Although DTI-TK explicitly considers reorientation during optimization, it can only handle one principal fiber direction per voxel and thus ambiguity will occur where fiber configuration is complex. The quantitative results given in Table 1 show that LDDMM-DWI outperforms the other methods and reduces overall mismatching error (e.g., smaller median).

To further demonstrate the efficacy of LDDMM-DWI, we compared the similarity of ODFs (for high-anisotropy voxels) computed from the target image and each source image using the symmetrized Kullback–Leibler (sKL) divergence (Chiang et al., 2008)

$$\mathrm{sKL}({\mathit{p}}_1,{\mathit{p}}_2)={\mathit{\int }}_{\mathit{s}\in {\mathrm{S}}^2}{\mathit{p}}_1(\mathit{s})\log \frac{{\mathit{p}}_1(\mathit{s})}{{\mathit{p}}_2(\mathit{s})}\mathrm{d}\mathit{s}+{\mathit{\int }}_{\mathit{s}\in {\mathrm{S}}^2}{\mathit{p}}_2(\mathit{s})\log \frac{{\mathit{p}}_2(\mathit{s})}{{\mathit{p}}_1(\mathit{s})}\mathrm{d}\mathit{s},$$

where p₁ and p₂ are the ODFs and s is a vector defined on the unit sphere S². The mean sKL divergence images resulting from each method are given in Fig. 2 and the statistics of the mean images are given in Table 2. Similarly, we can see that LDDMM-DWI works much better than other registration methods and reduces white matter misalignment.

Fig. 2.

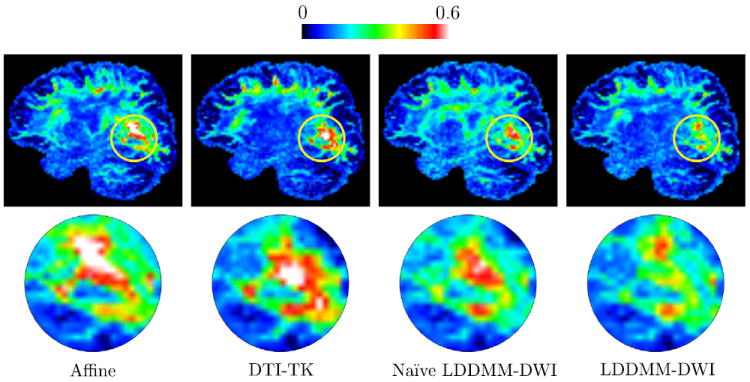
The mean sKL divergence images (top) and the close-ups of regions marked by yellow circles (bottom). Note that the low-anisotropy regions were not masked out for display purpose. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Table 2.

Statistics of the mean sKL divergence images given by different registration strategies.

Method	Mean ± s.d.	Median	90%-ile	p-value
Affine	0.22 ± 0.10	0.21	0.35	p < 0.01
DTI-TK	0.21 ± 0.10	0.20	0.36	p ≈ 0.01
Naïve LDDMM-DWI	0.21 ± 0.08	0.21	0.32	p < 0.05
LDDMM-DWI	0.19 ± 0.09	0.19	0.31	–

Figure 3 shows the anisotropy images of the target image and the mean of the aligned source images, from which we can see that LDDMM-DWI registers all main structures reasonably well. ODFs computed from the target image and the LDDMM-DWI mean image are shown in Fig. 4. It can be observed that the results produced by LDDMM-DWI are in close agreement at voxel level with the target image. This is important for applications such as white matter tractography (Yap et al., 2011; Yap et al., 2011), which is sensitive to errors in local fiber orientations.

Fig. 3.

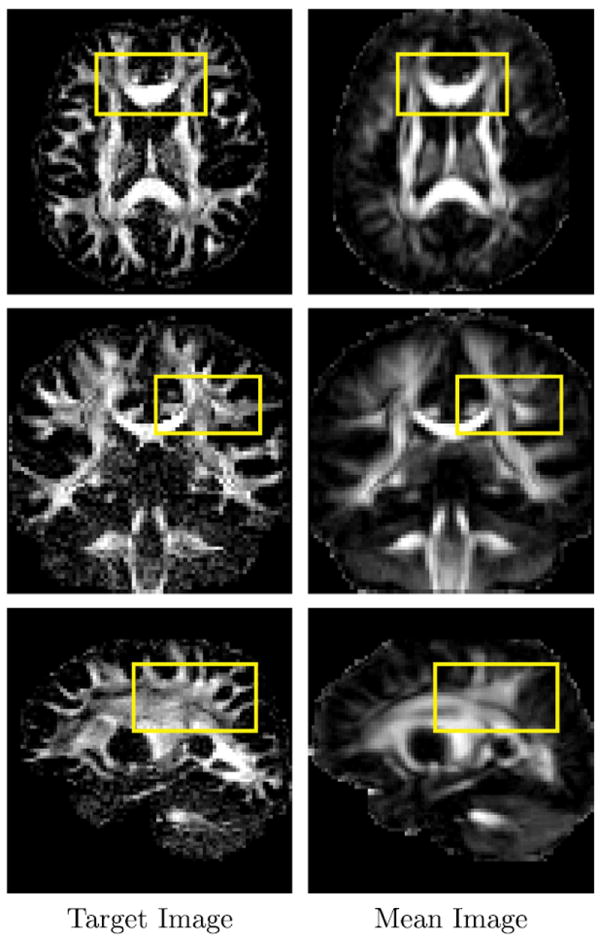
Anisotropy images of the target image and the mean of the align source images. The ODFs in regions marked by yellow rectangles are shown in Fig. 4. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Fig. 4.

ODFs in the regions marked by yellow rectangles in Fig. 3. The target anisotropy image is used as the background. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

7. Conclusion and discussions

We have described a method for directly registering the DWI data under large deformation. This is achieved by incorporating a DWI data reorientation technique (Yap and Shen, 2012) into an LDDMM algorithm (Beg et al., 2005), optimizing spatial alignment and local reorientation simultaneously. Unlike most of the existing methods, our approach eventually results in a set of diffusion-weighted images, thus allowing the fitting of any diffusion model for subsequent analysis. Experimental results indicate that our method significantly outperforms several other registration strategies as well as the method proposed in our earlier work (Zhang et al., 2012), which does not explicitly consider reorientation during optimization. In the future, to overcome the large computation cost of our method, general-purpose computing on graphics processing units (GPGPU) can be employed to significantly speed up the computation of the parallelizable portion of the algorithm.

Appendix A. Derivation of the gradient of the cost function

To minimize the cost function (4), we consider a small perturbation of υ ∈ L² ([0, 1], V) along direction h ∈ L² ([0, 1], V). The variation of energy functional E(υ) w.r.t υ can be obtained as

$${\partial }_{\mathit{h}}E(\mathit{\upsilon })\equiv \frac{\mathrm{d}}{\mathrm{d}\epsilon }E(\mathit{\upsilon }+\epsilon \mathit{h}){|}_{\epsilon =0}\equiv {{\mathit{\int }}_0^1\langle {\left({\nabla }_{\mathit{\upsilon }}E\right)}_t,{\mathit{h}}_t\rangle }_V\mathrm{d}t,$$

where ∂_h E(υ) is the Gâteaux derivative of E and ∇_υ E is the Fréchet derivative of E.

The variation of $E_1(\mathit{\upsilon })=\frac{1}{2}{\mathit{\int }}_0^1{\Vert {\mathit{\upsilon }}_t\Vert }_V^2\mathrm{d}t$ can be obtained easily as follows

$${\partial }_{\mathit{h}}{E}_1(\mathit{\upsilon })=\frac{\mathrm{d}}{\mathrm{d}\epsilon }\left(\frac{1}{2}{\mathit{\int }}_0^1{\Vert {\mathit{\upsilon }}_t\Vert }_V^2\mathrm{d}t\right){|}_{\epsilon =0}={{\mathit{\int }}_0^1\langle {\mathit{\upsilon }}_t,{\mathit{h}}_t\rangle }_V\mathrm{d}t.$$ (A.1)

Now focusing on the variation of $E_2(\mathit{\upsilon })=\frac{1}{{\sigma }^2}{\Vert F_{{\varphi }_{1,0}}{W}_0\circ {\varphi }_{1,0}-I_1\Vert }_{L^2}^2$, we have

$$\begin{array}{lll}{\partial }_{\mathit{h}}{E}_2(\mathit{\upsilon })& =& \frac{\mathrm{d}}{\mathrm{d}\epsilon }\left(\frac{1}{{\sigma }^2}{\Vert F_{{\varphi }_{1,0}^{\mathit{\upsilon }+\epsilon \mathit{h}}}{W}_0\circ {\varphi }_{1,0}^{\mathit{\upsilon }+\epsilon \mathit{h}}-I_1\Vert }_{L^2}^2\right){|}_{\epsilon =0}\\ & & =\frac{\mathrm{d}}{\mathrm{d}\epsilon }\left({\mathit{\int }}_{\Omega }\frac{1}{{\sigma }^2}{\Vert F_{{\varphi }_{1,0}^{\mathit{\upsilon }+\epsilon \mathit{h}}}{W}_0\circ {\varphi }_{1,0}^{\mathit{\upsilon }+\epsilon \mathit{h}}-I_1\Vert }^2\mathrm{d}\mathit{y}\right){|}_{\epsilon =0}\\ & & =\frac{2}{{\sigma }^2}{\mathit{\int }}_{\Omega }\langle I_0\circ {\varphi }_{1,0}-I_1,\frac{\partial }{\partial \epsilon }{F}_{{\varphi }_{1,0}^{\mathit{\upsilon }+\epsilon \mathit{h}}}{|}_{\epsilon =0}{W}_0\circ {\varphi }_{1,0}^{\mathit{\upsilon }}\\ & & {+F_{{\varphi }_{1,0}^{\mathit{\upsilon }}}\frac{\partial }{\partial \epsilon }\left(W_0\circ {\varphi }_{1,0}^{\mathit{\upsilon }+\epsilon \mathit{h}}\right){|}_{\epsilon =0}\rangle }_{L^2}\mathrm{d}\mathit{y},\end{array}$$

where Ω is a bounded domain in ℝ^d and y ∈ Ω. $\frac{\partial }{\partial \epsilon }{\mathit{F}}_{{\varphi }_{1,0}^{\mathit{\upsilon }+\epsilon \mathit{h}}}{|}_{\epsilon =0}$ at y is given by

$$\left[\begin{array}{cccc}0& \frac{\partial }{\partial \epsilon }f\left({\mathit{q}}_1|{\lambda }_1,{\lambda }_2,\frac{{(D{\varphi }_{1,0}^{\mathit{\upsilon }+\epsilon \mathit{h}})}^{-1}{\mathit{\mu }}_1}{\Vert {(D{\varphi }_{1,0}^{\mathit{\upsilon }+\epsilon \mathit{h}})}^{-1}{\mathit{\mu }}_1\Vert }\right){|}_{\epsilon =0}& \cdots & \frac{\partial }{\partial \epsilon }f({\mathit{q}}_1|{\lambda }_1,{\lambda }_2,\frac{{(D{\varphi }_{1,0}^{\mathit{\upsilon }+\epsilon \mathit{h}})}^{-1}{\mathit{\mu }}_N}{\Vert {(D{\varphi }_{1,0}^{\mathit{\upsilon }+\epsilon \mathit{h}})}^{-1}{\mathit{\mu }}_N\Vert }){|}_{\epsilon =0}\\ ⋮& ⋮& \ddots & ⋮\\ 0& \frac{\partial }{\partial \epsilon }f\left({\mathit{q}}_M|{\lambda }_1,{\lambda }_2,\frac{{(D{\varphi }_{1,0}^{\mathit{\upsilon }+\epsilon \mathit{h}})}^{-1}{\mathit{\mu }}_1}{\Vert {(D{\varphi }_{1,0}^{\mathit{\upsilon }+\epsilon \mathit{h}})}^{-1}{\mathit{\mu }}_1\Vert }\right){|}_{\epsilon =0}& \cdots & \frac{\partial }{\partial \epsilon }f\left({\mathit{q}}_M|{\lambda }_1,{\lambda }_2,\frac{{(D{\varphi }_{1,0}^{\mathit{\upsilon }+\epsilon \mathit{h}})}^{-1}{\mathit{\mu }}_N}{\Vert {(D{\varphi }_{1,0}^{\mathit{\upsilon }+\epsilon \mathit{h}})}^{-1}{\mathit{\mu }}_N\Vert }\right){|}_{\epsilon =0}\end{array}\right].$$

Note that we drop y for simplicity, i.e. ${\varphi }_{1,0}^{\mathit{\upsilon }+\epsilon \mathit{h}}(\mathit{y})\to {\varphi }_{1,0}^{\mathit{\upsilon }+\epsilon \mathit{h}}$.

The differentiation of each non-zero element in the above matrix yields

$$\begin{array}{l}\frac{\partial }{\partial \epsilon }f\left({\mathit{q}}_i|{\lambda }_1,{\lambda }_2,\frac{{(D{\varphi }_{1,0}^{\mathit{\upsilon }+\epsilon \mathit{h}})}^{-1}{\mathit{\mu }}_j}{\Vert {(D{\varphi }_{1,0}^{\mathit{\upsilon }+\epsilon \mathit{h}})}^{-1}{\mathit{\mu }}_j\Vert }\right){|}_{\epsilon =0}=\mathrm{const}({\mathit{q}}_i,{\stackrel{\sim }{\mathit{\mu }}}_j)\\ \times {\left({\nabla }_{{\stackrel{\sim }{\mathit{\mu }}}_j}\left[\frac{{\stackrel{\sim }{\mathit{\mu }}}_j}{\Vert {\stackrel{\sim }{\mathit{\mu }}}_j\Vert }\right]\frac{\partial }{\partial \epsilon }{(D{\varphi }_{1,0}^{\mathit{\upsilon }+\epsilon \mathit{h}})}^{-1}{|}_{\epsilon =0}{\mathit{\mu }}_j\right)}^{\mathrm{T}}{\mathit{q}}_i=-\mathrm{const}({\mathit{q}}_i,{\stackrel{\sim }{\mathit{\mu }}}_j)\\ \times {\left({\nabla }_{{\stackrel{\sim }{\mathit{\mu }}}_j}\left[\frac{{\stackrel{\sim }{\mathit{\mu }}}_j}{\Vert {\stackrel{\sim }{\mathit{\mu }}}_j\Vert }\right]\left({(D{\varphi }_{1,0}^{\mathit{\upsilon }})}^{-1}\frac{\partial }{\partial \epsilon }(D{\varphi }_{1,0}^{\mathit{\upsilon }+\epsilon \mathit{h}}){|}_{\epsilon =0}{(D{\varphi }_{1,0}^{\mathit{\upsilon }})}^{-1}\right){\mathit{\mu }}_j\right)}^{\mathrm{T}}{\mathit{q}}_i.\end{array}$$

Note that now ${\stackrel{\sim }{\mathit{\mu }}}_j={(D{\varphi }_{1,0}^{\mathit{\upsilon }})}^{-1}{\mathit{\mu }}_j$. According to the proof given by Beg et al. (2005),

$$\frac{\partial }{\partial \epsilon }{\varphi }_{1,0}^{\mathit{\upsilon }+\epsilon \mathit{h}}{|}_{\epsilon =0}=D{\varphi }_{1,0}^{\mathit{\upsilon }}{\mathit{\int }}_1^0{(D{\varphi }_{1,t}^{\mathit{\upsilon }})}^{-1}{\mathit{h}}_t\circ {\varphi }_{1,t}^{\mathit{\upsilon }}\mathrm{d}t.$$

Hence, $\frac{\partial }{\partial \epsilon }(D{\varphi }_{1,0}^{\mathit{\upsilon }+\epsilon \mathit{h}}){|}_{\epsilon =0}$ can be obtained by simply taking differentiation w.r.t y on both sides of the above equation, i.e.

$$\begin{array}{lll}\frac{\partial }{\partial \epsilon }(D{\varphi }_{1,0}^{\mathit{\upsilon }+\epsilon \mathit{h}}){|}_{\epsilon =0}& =& {\mathit{\int }}_1^0(D_{{\varphi }_{1,t}^{\mathit{\upsilon }}}^2{\varphi }_{t,0}^{\mathit{\upsilon }})·({\mathit{h}}_t\circ {\varphi }_{1,t}^{\mathit{\upsilon }})(D{\varphi }_{1,t}^{\mathit{\upsilon }})\mathrm{d}t\\ & & +{\mathit{\int }}_1^0(D_{{\varphi }_{1,t}^{\mathit{\upsilon }}}{\varphi }_{t,0}^{\mathit{\upsilon }})(D_{{\varphi }_{1,t}^{\mathit{\upsilon }}}{\mathit{h}}_t)D{\varphi }_{1,t}^{\mathit{\upsilon }}\mathrm{d}t,\end{array}$$

where D_y· is the value of D· at y, D²· is the Hessian operator, $D_{\mathit{y}}^2·$ is the value of D²· at y, giving a vector-valued matrix. For instance, $D_{{\varphi }_{1,t}^{\mathit{\upsilon }}}{\varphi }_{t,0}^{\mathit{\upsilon }}\equiv D{\varphi }_{t,0}^{\mathit{\upsilon }}({\varphi }_{1,t}^{\mathit{\upsilon }}(\mathit{y}))$ represents the Jacobian $D{\varphi }_{t,0}^{\mathit{\upsilon }}$ at position ${\varphi }_{1,t}^{\mathit{\upsilon }}(\mathit{y})$. Then we have

$$\begin{array}{l}{(D{\varphi }_{1,0}^{\mathit{\upsilon }})}^{-1}\frac{\partial }{\partial \epsilon }(D{\varphi }_{1,0}^{\mathit{\upsilon }+\epsilon \mathit{h}}){|}_{\epsilon =0}{(D{\varphi }_{1,0}^{\mathit{\upsilon }})}^{-1}\\ ={(D{\varphi }_{1,0}^{\mathit{\upsilon }})}^{-1}[{\mathit{\int }}_1^0(D_{{\varphi }_{1,t}^{\mathit{\upsilon }}}^2{\varphi }_{t,0}^{\mathit{\upsilon }})·({\mathit{h}}_t\circ {\varphi }_{1,t}^{\mathit{\upsilon }})(D{\varphi }_{1,t}^{\mathit{\upsilon }})\mathrm{d}t\\ +{\mathit{\int }}_1^0(D_{{\varphi }_{1,t}^{\mathit{\upsilon }}}{\varphi }_{t,0}^{\mathit{\upsilon }})(D_{{\varphi }_{1,t}^{\mathit{\upsilon }}}{\mathit{h}}_t)D{\varphi }_{1,t}^{\mathit{\upsilon }}\mathrm{d}t]{(D{\varphi }_{1,0}^{\mathit{\upsilon }})}^{-1}.\end{array}$$

We now deal with the two terms in the above equation one by one:

$$\begin{array}{l}{(D{\varphi }_{1,0}^{\mathit{\upsilon }})}^{-1}\left[{\mathit{\int }}_1^0(D_{{\varphi }_{1,t}^{\mathit{\upsilon }}}^2{\varphi }_{t,0}^{\mathit{\upsilon }})·({\mathit{h}}_t\circ {\varphi }_{1,t}^{\mathit{\upsilon }})(D{\varphi }_{1,t}^{\mathit{\upsilon }})\mathrm{d}t\right]{(D{\varphi }_{1,0}^{\mathit{\upsilon }})}^{-1}\\ ={\mathit{\int }}_1^0{(D{\varphi }_{1,0}^{\mathit{\upsilon }})}^{-1}(D_{{\varphi }_{1,t}^{\mathit{\upsilon }}}^2{\varphi }_{t,0}^{\mathit{\upsilon }})·({\mathit{h}}_t\circ {\varphi }_{1,t}^{\mathit{\upsilon }})(D{\varphi }_{1,t}^{\mathit{\upsilon }}){(D{\varphi }_{1,0}^{\mathit{\upsilon }})}^{-1}\mathrm{d}t\\ ={\mathit{\int }}_1^0{(D{\varphi }_{1,t}^{\mathit{\upsilon }})}^{-1}{(D_{{\varphi }_{1,t}^{\mathit{\upsilon }}}{\varphi }_{t,0}^{\mathit{\upsilon }})}^{-1}(D_{{\varphi }_{1,t}^{\mathit{\upsilon }}}^2{\varphi }_{t,0}^{\mathit{\upsilon }})·({\mathit{h}}_t\circ {\varphi }_{1,t}^{\mathit{\upsilon }}){(D_{{\varphi }_{1,t}^{\mathit{\upsilon }}}{\varphi }_{t,0}^{\mathit{\upsilon }})}^{-1}\mathrm{d}t\\ ={\mathit{\int }}_0^1{(D{\varphi }_{1,t}^{\mathit{\upsilon }})}^{-1}D({(D_{{\varphi }_{1,t}^{\mathit{\upsilon }}}{\varphi }_{t,0}^{\mathit{\upsilon }})}^{-1})·({\mathit{h}}_t\circ {\varphi }_{1,t}^{\mathit{\upsilon }})\mathrm{d}t\\ ={\mathit{\int }}_0^1{D}_{{\varphi }_{1,t}^{\mathit{\upsilon }}}{\varphi }_{t,1}^{\mathit{\upsilon }}D({(D_{{\varphi }_{1,t}^{\mathit{\upsilon }}}{\varphi }_{t,0}^{\mathit{\upsilon }})}^{-1})·({\mathit{h}}_t\circ {\varphi }_{1,t}^{\mathit{\upsilon }})\mathrm{d}t,\end{array}$$

and

$$\begin{array}{l}{(D{\varphi }_{1,0}^{\mathit{\upsilon }})}^{-1}\left[{\mathit{\int }}_1^0(D_{{\varphi }_{1,t}^{\mathit{\upsilon }}}{\varphi }_{t,0}^{\mathit{\upsilon }})(D_{{\varphi }_{1,t}^{\mathit{\upsilon }}}{\mathit{h}}_t)D{\varphi }_{1,t}^{\mathit{\upsilon }}\mathrm{d}t\right]{(D{\varphi }_{1,0}^{\mathit{\upsilon }})}^{-1}\\ ={\mathit{\int }}_1^0{(D{\varphi }_{1,0}^{\mathit{\upsilon }})}^{-1}(D_{{\varphi }_{1,t}^{\mathit{\upsilon }}}{\varphi }_{t,0}^{\mathit{\upsilon }})(D_{{\varphi }_{1,t}^{\mathit{\upsilon }}}{\mathit{h}}_t)D{\varphi }_{1,t}^{\mathit{\upsilon }}{(D{\varphi }_{1,0}^{\mathit{\upsilon }})}^{-1}\mathrm{d}t\\ =-{\mathit{\int }}_0^1{(D{\varphi }_{1,t}^{\mathit{\upsilon }})}^{-1}(D_{{\varphi }_{1,t}^{\mathit{\upsilon }}}{\mathit{h}}_t){(D_{{\varphi }_{1,t}^{\mathit{\upsilon }}}{\varphi }_{t,0}^{\mathit{\upsilon }})}^{-1}\mathrm{d}t\\ =-{\mathit{\int }}_0^1{D}_{{\varphi }_{1,t}^{\mathit{\upsilon }}}{\varphi }_{t,1}^{\mathit{\upsilon }}(D_{{\varphi }_{1,t}^{\mathit{\upsilon }}}{\mathit{h}}_t){(D_{{\varphi }_{1,t}^{\mathit{\upsilon }}}{\varphi }_{t,0}^{\mathit{\upsilon }})}^{-1}\mathrm{d}t,\end{array}$$

where we have used $D{\varphi }_{1,0}^{\mathit{\upsilon }}=D_{{\varphi }_{1,t}^{\mathit{\upsilon }}}{\varphi }_{t,0}^{\mathit{\upsilon }}D{\varphi }_{1,t}^{\mathit{\upsilon }}$ and $D_{{\varphi }_{1,t}^{\mathit{\upsilon }}}{\varphi }_{t,1}^{\mathit{\upsilon }}D{\varphi }_{1,t}^{\mathit{\upsilon }}=\mathit{I}$ for simplification. Hence, we have

$$\begin{array}{l}{{(D{\varphi }_{1,0}^{\mathit{\upsilon }})}^{-1}\frac{\partial }{\partial \epsilon }(D{\varphi }_{1,0}^{\mathit{\upsilon }+\epsilon \mathit{h}})|}_{\epsilon =0}{(D{\varphi }_{1,0}^{\mathit{\upsilon }})}^{-1}\\ ={\mathit{\int }}_0^1{D}_{{\varphi }_{1,t}^{\mathit{\upsilon }}}{\varphi }_{t,1}^{\mathit{\upsilon }}D({(D_{{\varphi }_{1,t}^{\mathit{\upsilon }}}{\varphi }_{t,0}^{\mathit{\upsilon }})}^{-1})·({\mathit{h}}_t\circ {\varphi }_{1,t}^{\mathit{\upsilon }})\mathrm{d}t\\ -{\mathit{\int }}_0^1{D}_{{\varphi }_{1,t}^{\mathit{\upsilon }}}{\varphi }_{t,1}^{\mathit{\upsilon }}(D_{{\varphi }_{1,t}^{\mathit{\upsilon }}}{\mathit{h}}_t){(D_{{\varphi }_{1,t}^{\mathit{\upsilon }}}{\varphi }_{t,0}^{\mathit{\upsilon }})}^{-1}\mathrm{d}t.\end{array}$$

Also, we have

$$\begin{array}{lll}\frac{\partial }{\partial \epsilon }\left(W_0\circ {\varphi }_{1,0}^{\mathit{\upsilon }+\mathrm{\epsilon }\mathit{h}}\right){|}_{\mathrm{\epsilon }=0}& =& D{W}_0\circ {\varphi }_{1,0}^{\mathit{\upsilon }}\frac{\partial }{\partial \epsilon }{\varphi }_{1,0}^{\mathit{\upsilon }+\mathrm{\epsilon }\mathit{h}}{|}_{\mathrm{\epsilon }=0}\\ & =& D{W}_0\circ {\varphi }_{1,0}^{\mathit{\upsilon }}\left(-D{\varphi }_{1,0}^{\mathit{\upsilon }}{\mathit{\int }}_0^1{(D{\varphi }_{1,t}^{\mathit{\upsilon }})}^{-1}{\mathit{h}}_t\circ {\varphi }_{1,t}^{\mathit{\upsilon }}\mathrm{d}t\right)\\ =& -{\mathit{\int }}_0^{1}D(W_0\circ {\varphi }_{1,0}^{\mathit{\upsilon }}){(D{\varphi }_{1,t}^{\mathit{\upsilon }})}^{-1}{\mathit{h}}_t\circ {\varphi }_{1,t}^{\mathit{\upsilon }}\mathrm{d}t.\end{array}$$

Now we are ready to compute $G=\frac{\partial }{\partial \epsilon }{F}_{{\varphi }_{1,0}^{\mathit{\upsilon }+\epsilon \mathit{h}}}{|}_{\epsilon =0}{W}_0\circ {\varphi }_{1,0}^{\mathit{\upsilon }}+F_{{\varphi }_{1,0}^{\mathit{\upsilon }}}\frac{\partial }{\partial \epsilon }\left(W_0\circ {\varphi }_{1,0}^{\mathit{\upsilon }+\epsilon \mathit{h}}\right){|}_{\epsilon =0}$, where G is a vector-valued image and the i-th element of its voxel at y is given by Gⁱ (y). We have

$$\begin{array}{l}G(\mathit{y})=\left[\begin{array}{ccccc}0& a_{11}& a_{12}& \cdots & a_{1N}\\ 0& a_{21}& a_{22}& \cdots & a_{2N}\\ ⋮& ⋮& \ddots & ⋮& \\ 0& a_{M1}& a_{M2}& \cdots & a_{\mathit{MN}}\end{array}\right]\left[\begin{array}{c}{w}_0\\ w_1\\ ⋮\\ w_N\end{array}\right]\circ {\varphi }_{1,0}^{\mathit{\upsilon }}\\ +\left[\begin{array}{ccccc}{f}_0& b_{11}& b_{12}& \cdots & b_{1N}\\ f_0& b_{21}& b_{22}& \cdots & b_{2N}\\ ⋮& ⋮& \ddots & ⋮& \\ f_0& b_{M1}& b_{M2}& \cdots & b_{\mathit{MN}}\end{array}\right]\left(-{\mathit{\int }}_0^{1}D(W_0\circ {\varphi }_{1,0}^{\mathit{\upsilon }}){(D{\varphi }_{1,t}^{\mathit{\upsilon }})}^{-1}{\mathit{h}}_t\circ {\varphi }_{1,t}^{\mathit{\upsilon }}\mathrm{d}t\right),\end{array}$$

where

$$\begin{array}{l}{a}_{\mathit{ij}}=-{\mathit{\int }}_0^1\mathrm{const}({\mathit{q}}_i,{\stackrel{\sim }{\mathit{\mu }}}_j)\\ \times {\left({\nabla }_{{\stackrel{\sim }{\mathit{\mu }}}_j}\left[\frac{{\stackrel{\sim }{\mathit{\mu }}}_j}{\Vert {\stackrel{\sim }{\mathit{\mu }}}_j\Vert }\right]\left(D_{{\varphi }_{1,t}^{\mathit{\upsilon }}}{\varphi }_{t,1}^{\mathit{\upsilon }}D({(D_{{\varphi }_{1,t}^{\mathit{\upsilon }}}{\varphi }_{t,0}^{\mathit{\upsilon }})}^{-1})·({\mathit{h}}_t\circ {\varphi }_{1,t}^{\mathit{\upsilon }})\right){\mathit{\mu }}_j\right)}^{\mathrm{T}}{\mathit{q}}_i\mathrm{d}t\\ +{\mathit{\int }}_0^1\mathrm{const}({\mathit{q}}_i,{\stackrel{\sim }{\mathit{\mu }}}_j)\times ({\nabla }_{{\stackrel{\sim }{\mathit{\mu }}}_j}\left[\frac{{\stackrel{\sim }{\mathit{\mu }}}_j}{\Vert {\stackrel{\sim }{\mathit{\mu }}}_j\Vert }\right]{\left(D_{{\varphi }_{1,t}^{\mathit{\upsilon }}}{\varphi }_{t,1}^{\mathit{\upsilon }}(D_{{\varphi }_{1,t}^{\mathit{\upsilon }}}{\mathit{h}}_t){(D_{{\varphi }_{1,t}^{\mathit{\upsilon }}}{\varphi }_{t,0}^{\mathit{\upsilon }})}^{-1}){\mathit{\mu }}_i\right)}^{\mathrm{T}}{\mathit{q}}_i\mathrm{d}t,\end{array}$$

$b_{\mathit{ij}}=f\left({\mathit{q}}_i|{\lambda }_1,{\lambda }_2,\frac{{(D{\varphi }_{1,0}^{\mathit{\upsilon }})}^{-1}{\mathit{\mu }}_j}{\Vert {(D{\varphi }_{1,0}^{\mathit{\upsilon }})}^{-1}{\mathit{\mu }}_j\Vert }\right)$ and [w₀, …, w_N]^T is the sparse weights of W₀ at position y. Let b_i = [f₀, b_i1, ⋯, b_iN]^T, we can then compute Gⁱ(y) as

$$\begin{array}{l}{G}^i(\mathit{y})=\sum _j^N{a}_{\mathit{ij}}{w}_j\circ {\varphi }_{1,0}^{\mathit{\upsilon }}-{\mathit{\int }}_0^1{\mathit{b}}_i^{\mathrm{T}}D(W_0\circ {\varphi }_{1,0}^{\mathit{\upsilon }}){(D{\varphi }_{1,t}^{\mathit{\upsilon }})}^{-1}{\mathit{h}}_t\circ {\varphi }_{1,t}^{\mathit{\upsilon }}\mathrm{d}t\\ =-{\mathit{\int }}_0^1\sum _j^N{w}_j\circ {\varphi }_{1,0}^{\mathit{\upsilon }}\mathrm{const}({\mathit{q}}_i,{\stackrel{\sim }{\mathit{\mu }}}_j)\times ({\nabla }_{{\stackrel{\sim }{\mathit{\mu }}}_j}\left[\frac{{\stackrel{\sim }{\mathit{\mu }}}_j}{\Vert {\stackrel{\sim }{\mathit{\mu }}}_j\Vert }\right]{\left(D_{{\varphi }_{1,t}^{\mathit{\upsilon }}}{\varphi }_{t,1}^{\mathit{\upsilon }}D({(D_{{\varphi }_{1,t}^{\mathit{\upsilon }}}{\varphi }_{t,0}^{\mathit{\upsilon }})}^{-1})·({\mathit{h}}_t\circ {\varphi }_{1,t}^{\mathit{\upsilon }})){\mathit{\mu }}_j\right)}^{\mathrm{T}}{\mathit{q}}_i\mathrm{d}t\\ +{\mathit{\int }}_0^1\sum _j^N{w}_j\circ {\varphi }_{1,0}^{\mathit{\upsilon }}\mathrm{const}({\mathit{q}}_i,{\stackrel{\sim }{\mathit{\mu }}}_j)\times ({\nabla }_{{\stackrel{\sim }{\mathit{\mu }}}_j}\left[\frac{{\stackrel{\sim }{\mathit{\mu }}}_j}{\Vert {\stackrel{\sim }{\mathit{\mu }}}_j\Vert }\right]{\left(D_{{\varphi }_{1,t}^{\mathit{\upsilon }}}{\varphi }_{t,1}^{\mathit{\upsilon }}(D_{{\varphi }_{1,t}^{\mathit{\upsilon }}}{\mathit{h}}_t){(D_{{\varphi }_{1,t}^{\mathit{\upsilon }}}{\varphi }_{t,0}^{\mathit{\upsilon }})}^{-1}){\mathit{\mu }}_j\right)}^{\mathrm{T}}{\mathit{q}}_i\mathrm{d}t\\ -{\mathit{\int }}_0^1{\mathit{b}}_i^{\mathrm{T}}D(W_0\circ {\varphi }_{1,0}^{\mathit{\upsilon }}){(D{\varphi }_{1,t}^{\mathit{\upsilon }})}^{-1}{\mathit{h}}_t\circ {\varphi }_{1,t}^{\mathit{\upsilon }}\mathrm{d}t.\end{array}$$

Now we can rewrite ∂_h E₂ (v) as

$$\begin{array}{lll}{\partial }_h{E}_2(\mathit{\upsilon })& =& \frac{2}{{\sigma }^2}{\mathit{\int }}_{\Omega }{\langle I_0\circ {\varphi }_{1,0}-I_1,G\rangle }_{L^2}\mathrm{d}\mathit{y}\\ & =& \frac{2}{{\sigma }^2}{\mathit{\int }}_{\Omega }\sum _i^M(I_0^i\circ {\varphi }_{1,0}-I_1^i)G^i\mathrm{d}\mathit{y}.\end{array}$$

Let ${\varphi }_{1,t}^{\mathit{\upsilon }}(\mathit{y})=\mathit{x}$, then $\mathit{y}={\varphi }_{t,1}^{\mathit{\upsilon }}(\mathit{x})$ and $\mathrm{d}\mathit{y}=|D{\varphi }_{t,1}^{\mathit{\upsilon }}(\mathit{x})|\mathrm{d}\mathit{x}$. By changing the variable, we have

$$\begin{array}{l}{\partial }_h{E}_2(\mathit{\upsilon })=-\frac{2}{{\sigma }^2}{\mathit{\int }}_0^1{\mathit{\int }}_{\Omega }|D{\varphi }_{t,1}^{\mathit{\upsilon }}|\sum _i^M(I_0^i\circ {\varphi }_{t,0}^{\mathit{\upsilon }}-I_1^i\circ {\varphi }_{t,1}^{\mathit{\upsilon }})\\ \times \sum _j^N{w}_j\circ {\varphi }_{t,0}^{\mathit{\upsilon }}\mathrm{const}({\mathit{q}}_i,{\stackrel{\sim }{\mathit{\mu }}}_j)\\ \times {\left({\nabla }_{{\stackrel{\sim }{\mathit{\mu }}}_j}\left[\frac{{\stackrel{\sim }{\mathit{\mu }}}_j}{\Vert {\stackrel{\sim }{\mathit{\mu }}}_j\Vert }\right]\left(D{\varphi }_{t,1}^{\mathit{\upsilon }}D({(D{\varphi }_{t,0}^{\mathit{\upsilon }})}^{-1})·{\mathit{h}}_t\right){\mathit{\mu }}_j\right)}^{\mathrm{T}}{\mathit{q}}_i\mathrm{d}\mathit{x}\mathrm{d}t\\ +\frac{2}{{\sigma }^2}{\mathit{\int }}_0^1{\mathit{\int }}_{\Omega }|D{\varphi }_{t,1}^{\mathit{\upsilon }}|\sum _i^M(I_0^i\circ {\varphi }_{t,0}^{\mathit{\upsilon }}-I_1^i\circ {\varphi }_{t,1}^{\mathit{\upsilon }})\times \sum _j^N{w}_j\circ {\varphi }_{t,0}^{\mathit{\upsilon }}\mathrm{const}({\mathit{q}}_i,{\stackrel{\sim }{\mathit{\mu }}}_j)\\ \times {\left({\nabla }_{{\stackrel{\sim }{\mathit{\mu }}}_j}\left[\frac{{\stackrel{\sim }{\mathit{\mu }}}_j}{\Vert {\stackrel{\sim }{\mathit{\mu }}}_j\Vert }\right]\left(D{\varphi }_{t,1}^{\mathit{\upsilon }}D{\mathit{h}}_t{(D{\varphi }_{t,0}^{\mathit{\upsilon }})}^{-1}\right){\mathit{\mu }}_j\right)}^{\mathrm{T}}{\mathit{q}}_i\mathrm{d}\mathit{x}\mathrm{d}t\\ -\frac{2}{{\sigma }^2}{\mathit{\int }}_0^1{\mathit{\int }}_{\Omega }|D{\varphi }_{t,1}^{\mathit{\upsilon }}|\sum _i^M(I_0^i\circ {\varphi }_{t,0}^{\mathit{\upsilon }}-I_1^i\circ {\varphi }_{t,1}^{\mathit{\upsilon }}){\mathit{b}}_i^{\mathrm{T}}D(W_0\circ {\varphi }_{t,0}^{\mathit{\upsilon }}){\mathit{h}}_t\mathrm{d}\mathit{x}\mathrm{d}t,\end{array}$$

where now ${\stackrel{\sim }{\mathit{\mu }}}_j={(D{\varphi }_{t,0}^{\mathit{\upsilon }})}^{-1}{\mathit{\mu }}_j$. As ν, h ∈ V, we have the following two equations (see (Cao et al., 2005) for details on the property of the reproducing kernel Hilbert space)

$$\begin{array}{l}{\langle \mathit{\upsilon },\mathit{h}\rangle }_{L^2}={\langle K\mathit{\upsilon },\mathit{h}\rangle }_V,\\ {\langle \mathit{\upsilon },D\mathit{h}\rangle }_{L^2}={\langle \mathit{DK}\mathit{\upsilon },\mathit{h}\rangle }_V.\end{array}$$

Hence, the variation of E₂ (v) is given by

$$\begin{array}{l}{\partial }_{\mathit{h}}{E}_2(\mathit{\upsilon })=-\frac{2}{{\sigma }^2}{\mathit{\int }}_0^1\langle K({\mathit{\int }}_{\Omega }|D{\varphi }_{t,1}^{\mathit{\upsilon }}|\sum _i^M(I_0^i\circ {\varphi }_{t,0}^{\mathit{\upsilon }}-I_1^i\circ {\varphi }_{t,1}^{\mathit{\upsilon }})\\ \times \sum _j^N{w}_j\circ {\varphi }_{t,0}^{\mathit{\upsilon }}\mathrm{const}({\mathit{q}}_i,{\stackrel{\sim }{\mathit{\mu }}}_j)\\ {\times {\left({\nabla }_{{\stackrel{\sim }{\mathit{\mu }}}_j}\left[\frac{{\stackrel{\sim }{\mathit{\mu }}}_j}{\Vert {\stackrel{\sim }{\mathit{\mu }}}_j\Vert }\right]\left(D{\varphi }_{t,1}^{\mathit{\upsilon }}D({(D{\varphi }_{t,0}^{\mathit{\upsilon }})}^{-1})\right){\mathit{\mu }}_j\right)}^{\mathrm{T}}{\mathit{q}}_i\mathrm{d}\mathit{x}),{\mathit{h}}_t\rangle }_V\mathrm{d}t\\ +\frac{2}{{\sigma }^2}{\mathit{\int }}_0^1\langle \mathit{DK}({\mathit{\int }}_{\Omega }|D{\varphi }_{t,1}^{\mathit{\upsilon }}|\sum _i^M(I_0^i\circ {\varphi }_{t,0}^{\mathit{\upsilon }}-I_1^i\circ {\varphi }_{t,1}^{\mathit{\upsilon }})\\ \times \sum _j^N{w}_j\circ {\varphi }_{t,0}^{\mathit{\upsilon }}\mathrm{const}({\mathit{q}}_i,{\stackrel{\sim }{\mathit{\mu }}}_j)\\ {\times {\left({\nabla }_{{\stackrel{\sim }{\mathit{\mu }}}_j}\left[\frac{{\stackrel{\sim }{\mathit{\mu }}}_j}{\Vert {\stackrel{\sim }{\mathit{\mu }}}_j\Vert }\right](D{\varphi }_{t,1}^{\mathit{\upsilon }}{(D{\varphi }_{t,0}^{\mathit{\upsilon }})}^{-1}){\mathit{\mu }}_j\right)}^{\mathrm{T}}{\mathit{q}}_i\mathrm{d}\mathit{x}),{\mathit{h}}_t\rangle }_V\mathrm{d}t\\ -\frac{2}{{\sigma }^2}{\mathit{\int }}_0^1{\langle K\left({\mathit{\int }}_{\Omega }|D{\varphi }_{t,1}^{\mathit{\upsilon }}|\sum _i^M(I_0^i\circ {\varphi }_{t,0}^{\mathit{\upsilon }}-I_1^i\circ {\varphi }_{t,1}^{\mathit{\upsilon }}){\mathit{b}}_i^{\mathrm{T}}D(W_0\circ {\varphi }_{t,0}^{\mathit{\upsilon }})\mathrm{d}\mathit{x}\right),{\mathit{h}}_t\rangle }_V\mathrm{d}t.\end{array}$$ (A.2)

Since h is arbitrary in L² ([0, 1], V), we obtain the gradient as given in (5) by combining results (A.1) and (A.2).