Ultrasensitivity Part I: Michaelian responses and zero-order ultrasensitivity

Abstract

Quantitative studies of signal transduction systems have shown that ultrasensitive responses—switch-like, sigmoidal input/output relationships—are commonplace in cell signaling. Ultrasensitivity is important for various complex signaling systems, including signaling cascades, bistable switches, and oscillators. In this first installment of a series on ultrasensitivity, we survey the occurrence of ultrasensitive responses in signaling systems and examine how such responses can arise. We review why the simplest mass action systems exhibit Michaelian responses, and then move on to zero-order ultrasensitivity, a phenomenon that occurs when signaling proteins are operating near saturation. We also discuss the physiological relevance of zero-order ultrasensitivity to cellular regulation.

Cooperativity and the binding of oxygen to hemoglobin

The curve that relates hemoglobin oxygen binding to the partial pressure of oxygen is, famously, sigmoidal rather than hyperbolic. The sigmoidal shape is biologically significant; it means that hemoglobin can unload a greater fraction of its oxygen in the peripheral tissues than it otherwise could (Fig 1). Building upon the work of Hill [1], Adair [2], and Pauling [3], by the 1960’s Monod, Wyman and Changeux [4] and Koshland, Némethy, and Filmer [5] had proposed plausible alternative models to account for the sigmoidal curve. The models differ in a number of respects, but share several features. Both models make use of the fact that hemoglobin is a multi-subunit protein complex, and assume allosteric regulation occurs both within its subunits and between subunits. And both assume that there is cooperativity: that the binding of oxygen to the first sites promotes the binding of oxygen to the remaining sites. Cooperativity proved to be important not just for oxygen transport, but for many other processes, including signal transduction, where multimeric ion channels, receptor proteins, and transcription factors are now known to exhibit cooperativity and sigmoidal input-output relationships. Cooperativity is important and beautiful, but complicated, because it depends upon coordinated and precise interactions among many amino acids.

Fig 1. The binding of oxygen to hemoglobin.

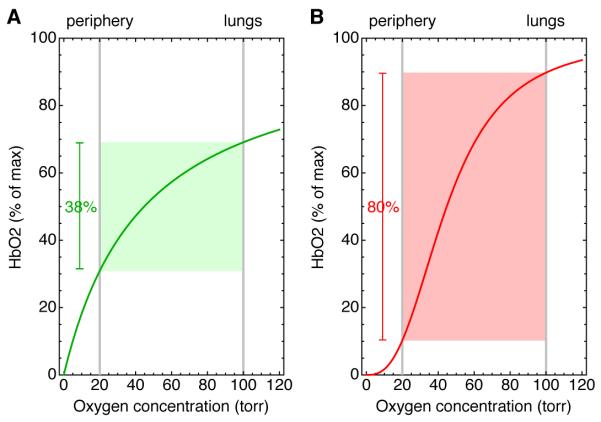
If the binding curve were hyperbolic (A), at best 38% of its oxygen could be delivered to the peripheral tissues. However, in reality the binding curve is sigmoidal with an apparent Hill coefficient of 2.7 (B). A sigmoidal curve with this Hill coefficient could allow hemoglobin to deliver as much as 80% of its oxygen.

In 1981 Goldbeter and Koshland published a landmark paper showing that, in signal transduction pathways, a much simpler mechanism can yield sigmoidal response curves that resemble those of cooperative proteins. They called the phenomenon zero-order ultrasensitivity; “zero-order” because it required that the signaling enzymes be operating close to saturation, and “ultrasensitivity” because the sensitivity of the response, as defined in a particular way (discussed later), was higher than that seen if the enzymes were operating far from saturation [6].

Over the past decade it has become clear that ultrasensitive responses do occur in natural biological systems, and may in fact be commonplace in signal transduction (Table 1). In this series we review four basic classes of mechanism that can generate ultrasensitive responses, starting with zero-order ultrasensitivity and then moving on to multistep mechanisms, stoichiometric inhibitors, and positive feedback loops, as well as the experimental evidence that these mechanisms are relevant to cell signaling. We discuss a number of interesting variations and elaborations on these mechanisms that have emerged out of recent theoretical work. And finally, we look at how ultrasensitivity can be critical in the generation of other emergent systems-level behaviors in more complex systems, such as cascades, switches, and oscillators. In this way, ultrasensitive monocycles are important elements in the generation of sophisticated biochemical behaviors.

Table 1.

Some examples of ultrasensitivity in signal transduction

Stimulus	Response	Effective Hill Exponent	Experimental System	Reference
Acetylcholine	Nicotinic cholinergic receptor conductance	1.3	Chicken neuronal homomeric α7 receptors	[23]
Delta (in trans only)	Notch production	1.7	CHO cells	[24]
Mos	MEK1	1.7	Xenopus laevis oocyte extracts	[25]
Phosphorylase kinase/phosphatase	Glycogen phosphorylase	2	Reconstituted mammalian muscle enzymes	[21]
RsbQP	σ B	2.1	Bacillus subtilis	[26]
AICAR	AMPK	2.5	Rat INS-1 cells	[27]
Ca2+	Calmodulin-dependent cAMP phosphodiesterase	2.7*	Purified beef heart proteins	[28]
IP3	Calcium release	3	Permeablized rat basophilic leukemia cells	[29]
Cdk1	Wee1A	3.5	Xenopus laevis egg extracts	[30]
Anisomycin	Jnk	3 - 10	HeLa, HEK293, and Jurkat cells	[31]
Sorbitol	Jnk	4 - 9	HeLa, HEK293, and Jurkat cells	[31]
Mos	Erk2	5	Xenopus laevis oocytes	[25]
Cln2	Cln2 synthesis	5	S. cerevisiae	[32]
KinA	σE and σF	10	Bacillus subtilis	[33]
CheY-P	Flagellar motor output	~10 - 20	Escherichia coli	[34-36]
Cdk1	Cdc25C	11	Xenopus laevis egg extracts	[37]
Delta (cis and trans)	Notch production	12	CHO cells	[24]
Cdk1	APC/CCdc20	≥ 17	Xenopus laevis egg extracts and embryos	[38, 39]
Yan	ERK	Not determined	Drosophila embryos	[22]

^*Our estimate based on the data in Fig 3 from [28].

Further perspectives on ultrasensitivity can be found in several recent papers [7-9] as well as the classic papers of Goldbeter and Koshland [6, 10-12]. Here we begin with an examination of Michaelian responses and zero-order ultrasensitivity.

Hyperbolic or Michaelian steady-state responses

Before examining how ultrasensitive responses are generated, it is helpful to thoroughly understand the responses of simple systems that are not ultrasensitive. Suppose that we have a signaling protein X that can be activated by phosphorylation and inactivated by dephosphorylation (Fig 2A). If we assume mass action kinetics, it follows (Box 1) that the steady-state input-output relationship for the system is given by Eq 1, where Input represents the concentration of the kinase driving the reaction, Output is the fraction of X in the phosphorylated form, and K is the EC50 for the system; that is, level of Input where half of the X is phosphorylated.

$$\mathit{Output}=\frac{\mathit{Input}}{K+\mathit{Input}}$$ Eq 1

Fig 2. Ultrasensitivity and the Hill function.

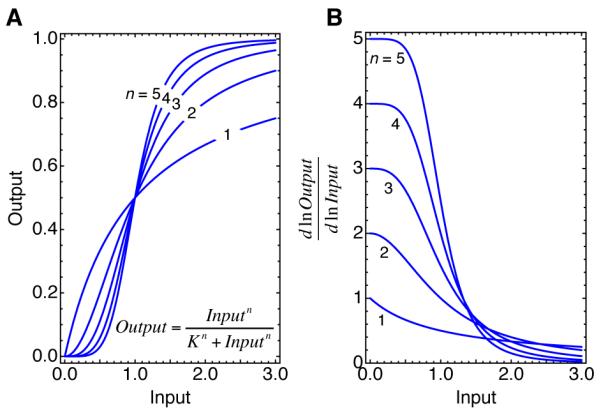
(A) Input-output relationships for Hill functions with exponents of 1, 2, 3, 4, and 5. When n = 1 the response is the same as a Michaelian response. When n > 1, the response is ultrasensitive, and the greater the value of n, the more switch-like the response. (B) Local sensitivities, as measured by the function $\frac{d\ln \mathit{Output}}{d\ln \mathit{Input}}$, for Hill curves with exponents of 1, 2, 3, 4, and 5. Note that the local sensitivity is the same as the polynomial order of the curve, and at low values of Input the sensitivity approaches n.

Box 1. Michaelian responses.

Here we derive the steady-state response of a simple phosphorylation-dephosphorylation system (Fig 2A). If we assume mass action kinetics, the net rate of phosphorylation is:

$$\frac{\mathit{dXP}}{\mathit{dt}}=k_1\mathit{kinase}(X_{\mathit{tot}}-\mathit{XP})-k_{-1}{p}^{\prime }\mathit{ase}\cdot \mathit{XP}$$ Eq 1.1

where k₁ is the rate constant for phosphorylation, k₋₁ is the rate constant for dephosphorylation, and p’ase is the concentration of the phosphatase. We do not need to write an equation for the other time-dependent species, X; because producing one molecule of XP takes away one molecule of X, this single rate equation describes the dynamics of both X and XP. This ordinary differential equation can be solved: XP exponentially approaches its steady-state level with a half-time of k₁kinase+k₋₁p’ase. However, for present purposes, we need only an expression for the steady-state level of XP, which can be obtained by solving an algebraic equation. At steady state the net rate of phosphorylation is zero; it follows that:

$$\mathit{Output}=\frac{\mathit{Input}}{K+\mathit{Input}}$$ Eq 1.2

We have taken the input to be the concentration of the kinase, the output to be the fraction of X that is phosphorylated. The constant represents the EC50 for the system, since when Input = K, $\mathit{Output}=\frac{K}{2K}=0.5$.

This relationship is plotted in Fig 2. Because the functional form of the equation is the same as that of the Michaelis-Menten equation, this type of response is sometimes referred to as Michaelian [12]. Note though that the Michaelis-Menten equation relates substrate concentrations to the initial rates of enzyme reactions, not kinase concentrations to the steady-state levels of substrate phosphorylation as we have here. Also note that here we assumed that the enzyme reactions were described by the law of mass action, not by Michaelis-Menten kinetics. This fact is perhaps worth repeating, since the terminology can be confusing: a Michaelian steady-state response is not generated by systems where enzyme activities are described the Michaelis-Menten equation. It is generated by systems where the law of mass action applies.

Michaelian responses are also obtained when an output is generated by ligand binding (e.g. activation of monomeric receptors by monomeric hormones), regulated synthesis (e.g. transcription, translation, or second messenger synthesis), or translocation (e.g. the recruitment of Raf or Akt to the plasma membrane), as long as the input regulates one step in the process and simple mass action kinetics apply.

Defining sensitivity and ultrasensitivity

In common parlance, the terms “sensitive” and “sensitivity” usually refer to how much input you need to get a certain level of output. An assay that detects 1 ng of flu virus is more sensitive than one that detects 1 μg, and one might call an assay that detects a remarkably low amount of virus ultrasensitive. If you look at recent scientific publications, sensitivity and ultrasensitivity are sometimes used in this sense, particularly in assay development (see, for example, [13]). A common measure of this type of sensitivity is the EC50, which is the amount of input required to get a half-maximal output. The lower the EC50, the higher the sensitivity.

Goldbeter and Koshland used the term sensitivity in a different sense, however, to denote the relationship between a change in input and a change in output. To make sensitivity independent of the units used, they expressed the changes in input and output as fold changes: $\frac{\Delta \mathit{Input}}{\mathit{Input}}$ and $\frac{\Delta \mathit{Output}}{\mathit{Output}}$, with the sensitivity being the ratio of the latter to the former. One can define sensitivity locally (S_local) by assuming that the change in Input is infinitesimal (Eq 2).

$$S_{\mathit{local}}=\underset{\Delta \mathit{Input}\to 0}{\lim }\frac{\Delta \mathit{Output}}{\mathit{Output}}/\frac{\Delta \mathit{Input}}{\mathit{Output}}=\frac{\mathit{dOutput}}{\mathit{dInput}}\cdot \frac{\mathit{Input}}{\mathit{Output}}=\frac{d\ln \mathit{Output}}{d\ln \mathit{Input}}$$ Eq 2

The higher the value of S_local, the higher the sensitivity. Note that S_local is the slope of a log-log plot of Input vs. Output, which makes it the polynomial order of the response. For a Michaelian response, where the response approaches first-order for small stimuli and zero-order for large stimuli, S_local is approximately 1 for small inputs, falls to 0.5 when the input equals the EC50, and approaches 0 for large inputs (Fig 2). For a Hill function, S_local is approximately equal to n for small inputs and approaches 0 for large inputs (Fig 2). Local sensitivity will be useful when we discuss signaling cascades later in this article.

Alternatively, one can calculate an overall, global value for the sensitivity of an input-output curve. Typically this is taken as the EC90:EC10 ratio. For a Michaelian response, the ratio is always 81, and so Goldbeter and Koshland defined an ultrasensitive response to be any response with an EC90:EC10 ratio smaller than 81 [6, 10, 12].

An ultrasensitive response is often (though not always) sigmoidal—flat at high and low inputs and steep in between—and often the curve is well-approximated by the Hill equation. This fact suggests another way of globally quantifying sensitivity, from the effective Hill exponent, which is defined as the Hill exponent n for a Hill curve (Eq 3 and Fig 2) that has the same EC90:EC10 ratio as the response curve in question.

$$\mathit{Output}=\frac{{\mathit{Input}}^n}{K^n+{\mathit{Input}}^n}$$ Eq 3

The effective Hill exponent is related to the EC90:EC10 ratio by Eq 4 [14]:

$$n=\frac{\mathit{Log}\left[81\right]}{\mathit{Log}[\mathit{EC}90∕\mathit{EC}10]}$$ Eq 4

There are problems with this definition if the basal level of response is high, or if the response is not well-approximated by the Hill equation (for example, if it is a bell-shaped response). In these cases, a more general, but also more complicated, integrated response coefficient can be used to characterize the global ultrasensitivity [9]. However, for present purposes, the effective Hill exponent is an adequate way of quantifying sensitivity and ultrasensitivity, and we will use this way of quantifying ultrasensitivity in most of the discussion of this article.

Zero-order ultrasensitivity

Suppose that we have a phosphorylation-dephosphorylation monocycle, but now instead of having enzymes whose activities are given by the law of mass action, the enzymes are saturable and their activities are given by the Michaelis-Menten equation. As shown in Box 2, the steady-state response of the system is now described by the formidable Goldbeter-Koshland equation (Eq 2.3). It is not easy to intuit much from just looking at this complicated equation, but if one plugs in values for the parameters so that both the phosphorylation and dephosphorylation reactions are running close to saturation, and then plots the fraction of the substrate X that is phosphorylated (XP/X_tot) as a function of kinase, the result is indeed a highly ultrasensitive, sigmoidal curve (Fig 3D). A good way to understand why the curve is shaped this way is through a simple graphical method, the rate-balance plot.

Box 2. Zero-order ultrasensitivity.

For a phosphorylation-dephosphorylation reaction with saturable enzymatic reactions rather than mass action kinetics, the situation becomes more complicated. Assuming that the total concentration of the substrate X is the sum of the concentrations of X and XP (i.e., the concentrations of the kinase•X and p’ase•XP complexes are negligible), the system can be described by a single rate equation:

$$\frac{\mathit{dXP}}{\mathit{dt}}=k_1\mathit{kinase}\frac{X_{\mathit{tot}}-\mathit{XP}}{K_{m1}+X_{\mathit{tot}}-\mathit{XP}}-k_{-1}{p}^{\prime }\mathit{ase}\frac{\mathit{XP}}{K_{m2}+\mathit{XP}}$$ Eq 2.1

Here K_m1 and K_m2 are the Michaelis constants for the kinase and phosphatase, respectively. At steady state:

$$k_1\mathit{kinase}\frac{X_{\mathit{tot}}-{\mathit{XP}}_{\mathit{ss}}}{K_{m1}+X_{\mathit{tot}}-{\mathit{XP}}_{\mathit{ss}}}-k_{-1}{p}^{\prime }\mathit{ase}\frac{{\mathit{XP}}_{\mathit{ss}}}{K_{m2}+{\mathit{XP}}_{\mathit{ss}}}=0$$ Eq 2.2

Eq 2.2 can be solved for XP_ss, the steady-state concentration of XP, analytically, yielding the Goldbeter-Koshland equation:

$${\mathit{XP}}_{\mathit{ss}}=\frac{k_1{X}_{\mathit{tot}}\mathit{kinase}-k_1{K}_{m2}\mathit{kinase}-k_{-1}{K}_{m1}{p}^{\prime }\mathit{ase}-k_{-1}{X}_{\mathit{tot}}{p}^{\prime }\mathit{ase}\sqrt{k_{-1}{\left(K_{m1}+X_{\mathit{tot}}\right)}^2{p}^{\prime }\mathit{ase}+k_1\left(K_{m2}-X_{\mathit{tot}}\right)+4k_1{K}_{m2}{X}_{\mathit{tot}}\mathit{kinase}(k_1\mathit{kinase}-k_{-1}{p}^{\prime }\mathit{ase})}}{2k_1\mathit{kinase}-2k_{-1}{p}^{\prime }\mathit{ase}}$$ Eq 2.3

Similarly, if we assume that the phosphatase reaction is saturable but the kinase reaction is described by mass action kinetics, it follows that:

$${\mathit{XP}}_{\mathit{ss}}=\frac{-K_{m2}\mathit{kinase}-p^{\prime }\mathit{ase}+X_{\mathit{tot}}\mathit{kinase}+\sqrt{4{\mathit{kinase}}^2{K}_{m2}{X}_{\mathit{tot}}+{\left(-K_{m2}\mathit{kinase}-p^{\prime }\mathit{ase}+X_{\mathit{tot}}\mathit{kinase}\right)}^2}}{2\mathit{kinase}}$$ Eq 2.4

And if we assume that the kinase reaction is saturable and the phosphatase is described by mass action kinetics, it follows that:

$${\mathit{XP}}_{\mathit{ss}}=\frac{k_1\mathit{kinase}+k_{-1}{p}^{\prime }\mathit{ase}\left(K_{m1}+X_{\mathit{tot}}\right)+\sqrt{-4k_1{k}_{-1}\mathit{kinase}\cdot p^{\prime }\mathit{ase}\cdot X_{\mathit{tot}}+{\left(k_1\mathit{kinase}+k_{-1}{p}^{\prime }\mathit{ase}\left(K_{m1}+X_{\mathit{tot}}\right)\right)}^2}}{2k_{-1}{p}^{\prime }\mathit{ase}}$$ Eq 2.5

Note that Eq 2.3 can be simplified slightly by defining V₁ = k₁kinase , V₋₁ = k₋₁p’ase , ${\widehat{K}}_{m1}=K_{m1}∕X_{\mathit{tot}}$, and ${\widehat{K}}_{m2}=K_{m2}∕X_{\mathit{tot}}$ and dividing through by X_tot:

$$\frac{{\mathit{XP}}_{\mathit{ss}}}{X_{\mathit{tot}}}=\frac{\frac{V_1}{V_{-1}}\left(1-{\widehat{K}}_{m2}\right)-{\widehat{K}}_{m1}-1+\sqrt{4{\widehat{K}}_{m2}\frac{V_1}{V_{-1}}\left(\frac{V_1}{V_{-1}}-1\right)+{\left(\frac{V_1}{V_{-1}}\left({\widehat{K}}_{m2}-1\right)+{\widehat{K}}_{m1}+1\right)}^2}}{2\left(\frac{V_1}{V_{-1}}-1\right)}$$ Eq 2.6

This is the usual form of the Goldbeter-Koshland equation.

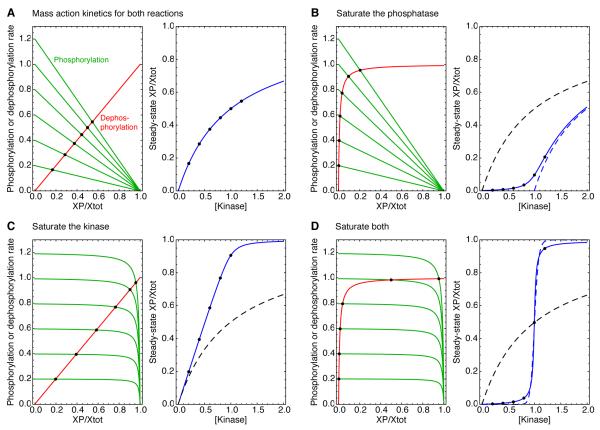
Fig 3. Michaelian responses and zero-order ultrasensitivity: rate-balance analysis.

(A) Rate balance analysis assuming mass action kinetics, which yield a Michaelian response. (B-D) Rate balance analysis assuming that one or both of the reactions is running close to saturation. In each panel, the left-hand plot shows the rate curves, with the phosphorylation rates shown in green and the dephosphorylation rates shown in red. The intersection points (solid black circles) correspond to steady states. The right-hand plots show the input ([kinase]) vs. output (the fraction of X_tot phosphorylated at steady-state) relationships in solid blue, as described by Eqs 2.3-2.5. The solid black circles are the same steady states shown in the left-hand plots. The dashed black curves in panels B-D show Michaelian input-output relationships, for comparison, and the dashed blue curve in panel B shows a Michaelian input-output curve shifted one concentration unit to the right. The assumed kinetic parameters were: k₁ = k₋₁ = X_tot = p’ase =1; K_m1 = K_m2 = 0.01; and kinase = 0.2, 0.4, 0.6, 0.8, 1.0, or 1.2. The effective Hill coefficients for the blue curves were 1, 1.18, 2, and 26.1, respectively. The dashed blue line in panel D shows a Hill function with a Hill exponent of 26.1 for comparison. Similar input-output curves can be found in [19].

Rate-balance plots

The basic idea of the rate-balance plot is to isolate the terms in the rate equation that increase the amount of XP, which contribute to the phosphorylation rate, and the terms that decrease the amount of XP, which contribute to the dephosphorylation rate [15-18]. The phosphorylation rate and dephosphorylation rate curves are then both plotted as a function of XP on one set of axes. Wherever the curves cross, the rates of phosphorylation and dephosphorylation are equal and the system is in steady state. One can then examine how the steady-state level of XP depends upon, for example, the concentration of kinase present. Following Gomez-Uribe et al. [19], we will consider four regimes of operation of the phosphorylation-dephosphorylation cycle: saturating neither reaction, both reactions, or one or the other.

If we assume mass action kinetics for both the phosphorylation and dephosphorylation reactions (Fig 3A), the rate curves are straight lines whose slopes are determined by the rate constants and enzyme concentrations. By plotting the values of XP/X_tot at the intersection points as a function of the assumed kinase concentration, one can build up an input-output curve (Fig 3A, right), which, of course, agrees with Eq 1. Note that the first increment of input (kinase) produces a reasonable increment of output, and then each successive increment produces less (Fig 3A, left). Thus the rate-balance analysis provides an intuitive feel for why mass action kinetics produces a response with a “diminishing returns” quality.

Next, we assume that the phosphatase is operating near saturation, with a K_m value 100-fold lower than the total concentration of the substrate X (Fig 3B). The phosphorylation rate curves are unchanged, but the dephosphorylation rate curve becomes a hyperbola, with the dephosphorylation rate being half-maximal when XP=0.01 units. Now the first increments of input produce very little output until the phosphorylation rate curve reaches the knee of the dephosphorylation rate curve (Fig 3B). Saturation of the phosphatase builds a threshold into the response, and as the K_m values for the phosphatase approaches zero, the input-output curve approaches a Michaelian response that has been shifted to the right by one concentration unit (Fig 3B, right). By Goldbeter and Koshland’s definition, the response is slightly ultrasensitive; as the saturation increases, the ratio $\frac{\mathit{EC}90}{\mathit{EC}10}$ approaches 41, which is less than 81, and the effective Hill exponent is 1.18. Gomez-Uribe and co-workers called this a threshold-hyperbolic response [19].

By contrast, if the kinase is operating near saturation but the phosphatase is not (Fig 3C), there is no threshold in the steady-state response (Fig 3C, right). Instead, the response approaches its maximal value more abruptly than a Michaelian response does (Fig 3C, right). This is because when the phosphorylation rate curves are virtually flat (Fig 3C left), the kinase activity does not fall off much as the output increases. The response curve approaches a straight line that does not bend over until the response is nearly maximal. By Goldbeter and Koshland’s definition, this curve is ultrasensitive, since for a straight line the EC90:EC10 ratio is 9 and the effective Hill exponent (Eq 3) is 2. However, nowhere on the curve is the local sensitivity (the polynomial order) greater than one, and for clarity it is probably better to call this a linear response rather than an ultrasensitive one.

Note that in principle linear responses could be extremely useful in signal transduction [19]. In the mating pheromone pathway in Saccharomyces cerevisiae, the response of the terminal protein kinase in the response pathway (Fus3) is, indeed, a nearly linear function of the pheromone concentration [20], and the mechanisms underpinning this linearity are not understood. Saturated signal transducers could help provide this linearity, as could some of the mechanisms that will be discussed later in this series (e.g. multisite phosphorylation with “OR gate” logic and stoichiometric inhibitors).

Finally, if both the kinase and phosphatase are assumed to be close to saturation, the response shows both a threshold and an abrupt leveling off at maximal response (Fig 3D). The result is a steeply sigmoidal input-output relationship (Fig 3D, right). The curve is similar (but not identical) in shape to a Hill function (Fig 3D, right, solid vs. dashed blue curves), and the effective Hill exponent for the degree of saturation assumed in Fig 3D is huge: 26.1. Thus, saturation of the kinase and phosphatase synergize to produce switch-like responses.

Competition in zero-order monocycles

So far we have assumed that only two species contribute significantly to the total pool of the substrate X_tot: the phosphorylated form XP and the dephosphorylated form X. However, we have also assumed that the kinase and phosphatase are operating close to saturation, which means that a large proportion of the kinase molecules are bound to X and the phosphatase to XP. These complexes will still be negligible compared to X and XP if the concentrations of the kinase and phosphatase are small compared to the concentration of the substrate. However, in signaling cascades, kinases and their substrates are sometimes comparable in concentration. What would the steady-state response of a phosphorylation-dephosphorylation monocycle be if the assumption that the kinase and phosphatase are low in concentration were relaxed?

This situation was considered by Goldbeter and Koshland in their original paper [6]. The algebra becomes more complicated; there are now four rate equations for four time-dependent species (for X, XP, X•kinase, and XP•p’ase) and a conservation equation (X_tot = X + XP+ X ×kinase+ XP×p’ase). It is no longer possible to carry out a simple one-variable rate-balance analysis or even an analytical solution, but solutions can be obtained numerically.

The results are shown in Fig. 4. When the phosphatase is assumed to be 1/100 the concentration of their substrate, there is very little difference between the exact response curve and the curve given by the Goldbeter-Koshland equation (Fig 4A). When the phosphatase reaches 1/10 the substrate concentration, the response is still highly ultrasensitive, but the maximal response is lower, since at high inputs 20% of the substrate is tied up in complexes (10% with the kinase and 10% with the phosphatase) (Fig 4B). And when the phosphatase is equal in concentration to the substrate, the maximal steady-state concentration of XP is very small (Fig 4C), with almost all of the substrate being present in complexes, and the sigmoidal character of the response is minimal (Fig 4, inset). Thus, zero-order ultrasensitivity is best generated when the converting enzymes are operating close to saturation and they are much lower in concentration than their substrate.

Fig 4. Zero-order ultrasensitivity requires that the converting enzymes be saturated and small in concentration compared to the substrate.

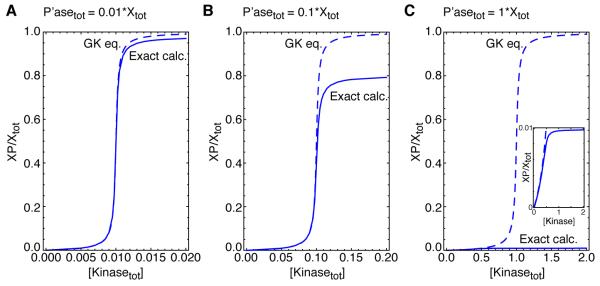
(A-C) Goldbeter-Koshland (GK) response curves (dashed blue curves) compared with exactly-calculated response curves (solid blue curves), assuming various ratios of the converting enzymes to the substrate. In each case we assumed that the association (a), dissociation (d), and catalytic (k) rate constants for both phosphorylation and dephosphorylation were a = 200, d =1 and k = 1. Thus, in each case the K_m values for both the phosphorylation and dephosphorylation reactions were 0.01, so that the total substrate concentration was 100 times as high as the K_m values (i.e. both converting enzymes were operating close to saturation). The inset in panel C shows that at low total kinase concentrations, the two curves are similar.

Physiological relevance of zero-order ultrasensitivity

Whereas the development of the theory of cooperativity was driven by experiments, most especially hemoglobin’s sigmoidal oxygen binding curve, this was not the case for zero-order ultrasensitivity. There was not some particular experimental mystery that zero-order ultrasensitivity was attempting to explain. The theory came first, and it then motivated and guided subsequent experimental studies.

The first experimental test of zero-order ultrasensitivity came in studies of isocitrate dehydrogenase (IDH) phosphorylation in a reconstituted system [15]. At concentrations of IDH above the K_m values for its phosphorylation and dephosphorylation, but still below that estimated to be present in vivo, a sigmoidal dose-response curve was obtained with a Hill coefficient of ~2 [15]. Zero-order ultrasensitivity was also demonstrated for the phosphorylation of glycogen phosphorylase in vitro [21] (Fig 5), and again the concentration of phosphorylase in vivo is thought to be high enough to make the in vitro results physiologically relevant. And finally, the response of the transcription factor Yan to the activation of the ERK MAP kinase in Drosophila ectodermal patterning has been shown to be ultrasensitive, and zero-order ultrasensitivity as a possible mechanism for this ultrasensitivity fits well with the observed insensitivity of patterning to Yan overexpression [22].

Fig 5. Zero-order ultrasensitivity in a reconstituted phosphorylase phosphorylation system.

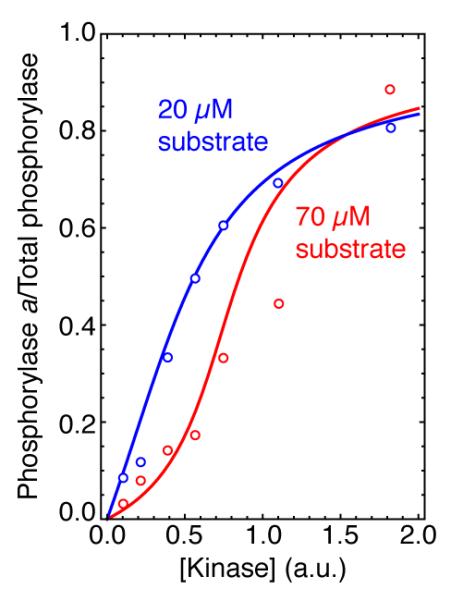
The fitted curves are from the Goldbeter-Koshland equation based on the measured K_m values, and the effective Hill coefficients were 1.35 (blue curve) and 2.35 (red curve). Adapted from [21].

However, there are a number of examples of huge Hill coefficients, including some of those seen near the bottom of Table 1, that appear not to be due to zero-order ultrasensitivity alone. This raises the question of what other mechanisms can contribute to ultrasensitive responses. We will examine one such mechanism, multisite phosphorylation, in the next installment of this series.

• The simplest signal transduction systems exhibit hyperbolic, Michaelian responses.

• But sigmoidal, ultrasensitive responses are commonplace in cell signaling.

• Zero-order ultrasensitivity is one mechanism for producing such responses.

• Zero-order ultrasensitivity is probably employed by real signaling systems.

Glossary

Cooperativity

A characteristic of some multistep processes where completing some of the early steps makes a later step more favorable. Examples include the multistep binding of oxygen to hemoglobin and priming in multisite phosphorylation.

Hill function

An input-output relationship of the form $\mathit{Output}=\frac{{\mathit{Input}}^n}{K^n+{\mathit{Input}}^n}$, where n is the Hill exponent or Hill coefficient.

Mass action kinetics

A simple kinetic scheme where the rate of a reaction is directly proportional to the concentration of the substrate or substrates involved in the reaction. This contrasts with Michaelis-Menten kinetics or kinetic schemes involving Hill functions.

Michaelis-Menten kinetics

A model for the rate of an enzymatic reaction, premised on the assumption that the enzyme is small in concentration compared to its substrate, and that the concentration of the enzyme-substrate complex is unchanging with respect to time. In the Michaelis-Menten model the rate of an enzymatic reaction is given by $\frac{\mathit{dProduct}}{\mathit{dt}}=V_{\max }\frac{\mathit{Substrate}}{K_m+\mathit{Substrate}}$.

Ultrasensitivity

A property of steady-state input-output relationships that makes them switch-like in character. Goldbeter and Koshland defined input-output relationships to be ultrasensitive if it took less than an 81-fold change in input stimulus to drive the output from 10% to 90% of maximum.

Zero-order

A zero-order chemical or biochemical reaction is one where the rate of the reaction is independent of the substrate concentration. Enzyme reactions approach zero-order when the enzyme is saturated with substrate.