Interfacial tension based on-chip extraction of microparticles confined in microfluidic Stokes flows

Abstract

Microfluidics involving two immiscible fluids (oil and water) has been increasingly used to produce hydrogel microparticles with wide applications. However, it is difficult to extract the microparticles out of the microfluidic Stokes flows of oil that have a Reynolds number (the ratio of inertia to viscous force) much less than one, where the dominant viscous force tends to drive the microparticles to move together with the surrounding oil. Here, we present a passive method for extracting hydrogel microparticles in microfluidic Stokes flow from oil into aqueous extracting solution on-chip by utilizing the intrinsic interfacial tension between oil and the microparticles. We further reveal that the thickness of an “extended confining layer” of oil next to the interface between oil and aqueous extracting solution must be smaller than the radius of microparticles for effective extraction. This method uses a simple planar merging microchannel design that can be readily fabricated and further integrated into a fluidic system to extract microparticles for wide applications.

Microfluidics involving two immiscible fluids has been increasingly used to produce hydrogel microparticles for microencapsulation of small and macromolecules, viruses, bacteria, and mammalian cells and tissues, which has wide applications in the fields of biofuel, cancer, infectious diseases, food and nutrition, tissue regeneration, and stem cell therapy.^1–4 In two-phase microfluidics, an aqueous solution is dispersed into droplets in carrier oil (or vice versa) under Plateau-Rayleigh instability.^4,5 The aqueous droplets can be physically or chemically crosslinked into hydrogel microparticles.⁶ Due to the small dimension of microfluidic channel and high viscosity of oil, the two-phase microfluidic flow is typically in the regimen of Stokes laminar flows where the viscous force dominates inertia force. The latter tends to move microparticles across streamlines to one or more equilibrium positions in microchannel.⁷ However, it is difficult to quickly extract these microparticles from oil into an aqueous solution on-chip by utilizing the intrinsic inertia force because the dominant viscous force tends to confine the microparticles within the oil phase and drives them to move together with their surrounding oil (supplementary movie S1⁸). Conventionally, these microparticles are collected together with carrier oil and the oil is removed later off-chip by multi-step washing and centrifugation, which are time-consuming and can lead to low retrieval efficiency, aggregation of microparticles, and cell injury (for cell encapsulation applications).^2,3,9 As a result, methods relying on the use of external forces (e.g., magnetophoresis, dielectrophoresis, and acoustophoresis), patterned structures (e.g., lateral displacement and filtration obstacles), and surface modification together with bifurcation law based on pressure difference have been reported to move microparticles across the streamlines in Stokes flows to achieve on-chip separation or extraction of microparticles.^9–11 In addition, moving cells/droplets across the streamlines in one-phase fluid in microchannel has been achieved by creating a gradient of polymer/surfactant concentration (and thus interfacial tension gradient and Marangoni flow along the cells/droplets) in the fluid.¹²

In this letter, we report a simple yet powerful approach for quick on-chip extraction of hydrogel microparticles confined in the Stokes flow of oil by utilizing the intrinsic interfacial tension in two-phase microfluidics. This approach uses a simple merging planar channel without the need of external force, patterned structure, or surface modification. Therefore, it can be readily fabricated and further integrated into a fluidic system to extract microparticles for wide applications. We designed and fabricated a microfluidic device consisting of two functional parts (Fig. 1(a) and supplementary Fig. S1⁸) to demonstrate the interfacial tension based approach for microparticle extraction from Stokes flows. The first part is a non-planar flow-focusing design for generating aqueous droplets of sodium alginate in the carrier oil emulsion by utilizing the Plateau-Rayleigh instability (Fig. 1(a), zoomed-in view). Due to symmetry, the generated droplets are at the center of the microchannel immediately downstream of the flow focusing. The droplets are crosslinked into hydrogel microparticles by Ca²⁺ infused in the carrier oil emulsion during flowing in the serpentine microchannel.³ The second part is a planar extraction channel with an additional inlet for aqueous extracting solution of sodium carboxymethylcellulose (with excellent biocompatibility^3,13) and two outlets. The straight outlet (green) is for the aqueous solution containing extracted microparticles, while the tilted one (red) is for the carrier oil emulsion.

FIG. 1.

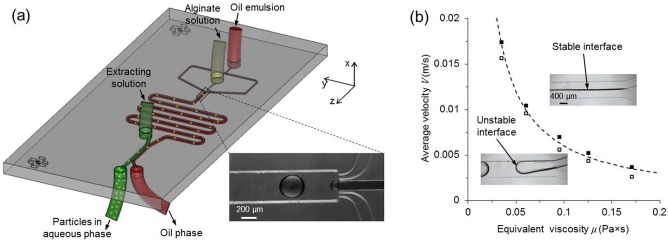
Microfluidic device used to generate and extract microparticles. (a) A schematic illustration of the microfluidic device. (b) Criterion for maintaining a stable interface between carrier oil emulsion and aqueous extracting solution. Open and solid squares represent unstable and stable interfaces, respectively. The dashed line represents the criterion of μV = 6 × 10⁻⁴ N/m for stable interface.

One of the prerequisites for continuous extraction is to maintain a stable interface between the carrier oil emulsion and aqueous extracting solution. Due to interfacial tension, the two fluids do not favor stable laminar flow and tend to form droplets.¹⁴ However, if the flows are fast enough or the fluids are viscous enough or both, viscous force can dominate over interfacial tension to establish a stable interface in the extraction channel. To gain more insight, the perturbations of the Plateau-Rayleigh instability can be assumed to propagate at speed:¹⁵ $V_p\sim \sigma /\mu$, where $\sigma$ is interfacial tension coefficient and $\mu$ is equivalent viscosity at the interface (represented by the harmonic average of the viscosities of oil (${\mu }_{o\hspace{0.17em}}$) and aqueous (${\mu }_{a\hspace{0.17em}})$ phases:¹⁶ $\mu =2{\mu }_{o\hspace{0.17em}}{\mu }_{a\hspace{0.17em}}/({\mu }_{o\hspace{0.17em}}+{\mu }_{a\hspace{0.17em}})$). The traveling time of the perturbation to pinch off a droplet $t_p=r/V_p\sim r\mu /\sigma$, where $r$ is the equivalent radius of the aqueous solution in the extraction channel.¹⁵ During the same period, the fluid would move downstream by a distance of $l_p=V{t}_p\sim rV\mu /\sigma$. As a result, if $l_p>l_e$ ($l_e$ is the length of the extracting microchannel), the interface between the two immiscible phases should be stable in the extraction channel. If the two fluids flow at the same velocity (V) with little change in their constituents, $r$ and $\sigma$ can be taken as constants for a given extraction channel geometry.^15,17 Therefore, the product $V\mu$ can be used to establish the criterion for interface stability, which is determined experimentally to be $\sim 6\times {10}^{-4}$ N/m under the conditions of this study (Fig. 1(b)).

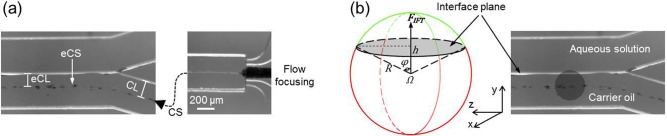
Because the Reynolds number ($\text{Re}=\rho VD/\mu ,\hspace{0.17em}$ D is microparticle diameter) and Grashof number ($\text{Gr}=\rho g{D}^3\Delta \rho /{\mu }^2$) for the microfluidic flow are much smaller than one (∼10⁻² and 10⁻³, respectively), body forces due to inertia and gravity are negligible compared to viscous force. Consequently, hydrogel microparticles suspended in the oil emulsion should move together with the surrounding fluid and do not cross the streamlines during the short travelling time in the extraction channel in the absence of an aqueous phase (supplementary movie S1⁸).^11,18 However, as shown in Fig. 2(a), the thickness of the carrier oil emulsion between solid wall and central streamline (CS), which confines hydrogel microparticles in the oil phase before entering the extraction channel and is therefore called confining layer (CL in Fig. 2(a)), reduces as the oil flow enters the extraction channel due to the disappearance of the non-slip boundary condition imposed by the solid wall. This thinned layer of oil emulsion in the extraction channel is extended from the CL and is therefore called extended CL (eCL). Therefore, in two-phase microfluidics, if the thickness of the eCL is smaller than the radius of a hydrogel microparticle, the microparticle will touch the aqueous extraction fluid (Fig. 2(b)). Once this occurs, an unbalanced hydrophobic force $F_{\mathit{I}\mathit{F}\mathit{T}}$ would be imposed on the microparticle towards aqueous solution as a result of the intrinsic interfacial tension between oil and hydrogel

$$F_{\mathit{I}\mathit{F}\mathit{T}}=-\frac{d{E}_{\mathit{I}\mathit{F}\mathit{T}}}{\mathit{d}\mathit{y}}=-\frac{\sigma R^{2}d\Omega }{-dh}=\sigma R^2\frac{d(2\pi (1+\text{cos}\hspace{0.17em}\phi \left)\right)}{d\left(R\hspace{0.17em}\text{cos}\hspace{0.17em}\phi \right)}=2\pi R\sigma ,$$ (1)

where $E_{\mathit{I}\mathit{F}\mathit{T}}$ is the potential energy due to interfacial tension between hydrogel microparticle and carrier oil emulsion, y is the coordinate, R is the radius of hydrogel microparticle, h is the distance from the interface plane to microparticle center, φ is the half of the 2D apex angle of the extracted surface (green), and Ω is the 3D solid angle of the non-extracted surface (red). This equation indicates that $F_{\mathit{I}\mathit{F}\mathit{T}}$ is constant during extraction.

FIG. 2.

Attenuation of the CL into eCL and the unbalanced hydrophobic force (F_IFT) as a result of the intrinsic interfacial tension between oil and hydrogel microparticle. (a) On the right, a typical image showing visualization of the CS of carrier oil emulsion by injecting dye Amaranth in the middle channel of flow focusing at a low flow rate (0.06 ml/h) and on the left, a typical image showing visualization of the CL and eCL by tracking the CS and eCS of carrier oil emulsion using Amaranth dye. The flow rate of carrier oil emulsion and aqueous extracting solution is all 5.5 ml/h. (b) On the right, the same image on the left of panel (a) overlaid with an imaginary hydrogel microparticle and on the left, a schematic illustration of the unbalanced hydrophobic force F_IFT imposed on the hydrogel microparticle as a result of the intrinsic interfacial tension between oil and hydrogel microparticle. R is the radius of hydrogel microparticle, h is the distance from the interface plane to microparticle center, φ is the half of the 2D apex angle of the extracted surface (green), and Ω is the 3D solid angle of the non-extracted surface (red). (Multimedia view) [URL: http://dx.doi.org/10.1063/1.4898040.1] Download video file ^{(79.8KB, mov)} DOI: 10.1063/1.4898040.1

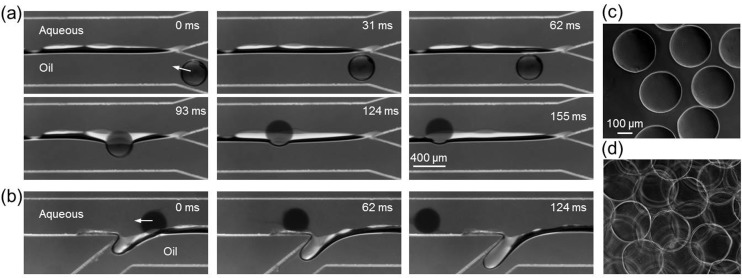
Moreover, in reality, when the hydrogel microparticle touches the aqueous solution, the interface between carrier oil emulsion and aqueous extracting solution and that between the emulsion and hydrogel microparticle will merge to minimize free energy (Fig. 3(a) at 93 ms). As a result, the interface between carrier oil emulsion and aqueous extracting solution opens up and the $F_{\mathit{I}\mathit{F}\mathit{T}}$ can easily push the hydrogel microparticles into aqueous extracting phase in a very short time (less than ∼0.03 s from ∼93 ms to less than 124 ms according to Fig. 3(a)). After the hydrogel microparticles are completely moved into the aqueous extracting solution, the interface will recover back to its original shape and position. This short extraction time and the prompt recovery of interface can effectively eliminate the disturbance of the extraction process by neighboring microparticles and are the key for achieving high throughput extraction of the microparticles. At the bifurcated exit, the hydrogel microparticles move straight along the streamlines of aqueous phase, while the oil emulsion turns into the side outlet (Fig. 3(b)). The hydrogel microparticles in aqueous phase can be directly collected with good morphology (Fig. 3(c)). On the other hand, if the hydrogel microparticles are conventionally collected without on-chip extraction and rinsed by aqueous liquid off-chip to remove oil, aggregates of the microparticles can form (Fig. 3(d)), presumably due to residual oil drop that confines the hydrogel microparticles together. Other methods, such as sonication, may be needed to further break up the microparticle aggregates.

FIG. 3.

Extraction and collection of hydrogel microparticles. (a) Typical time-lapse images (top view) showing migration of hydrogel microparticles from carrier oil emulsion into aqueous extracting solution. (b) Typical time-lapse images (top view) of hydrogel microparticles exiting from the bifurcated outlet. (c) A typical image of the hydrogel microparticles collected in the aqueous solution from on-chip extraction. (d) A typical image of the hydrogel microparticles obtained by off-chip approach showing aggregation. The flow rates of alginate solution, carrier oil emulsion, and aqueous extracting solution are 0.1, 5.5, and 5.5 ml/h, respectively. The scale bar in (a) and (c) also applies to (b) and (d), respectively. (Multimedia view) [URL: http://dx.doi.org/10.1063/1.4898040.2] Download video file ^{(233.7KB, mov)} DOI: 10.1063/1.4898040.2 [URL: http://dx.doi.org/10.1063/1.4898040.3] Download video file ^{(293.1KB, mov)} DOI: 10.1063/1.4898040.3

To quantify the thickness of the eCL in the extraction channel, we match the viscosity and flow rate of the aqueous extracting solution with that of the carrier oil emulsion (${\mu }_a={\mu }_o$ and $Q_a=Q_o$). Under this condition, when a stable interface is formed, the curvature of the interface plane between carrier oil emulsion and aqueous extracting solution is zero and the Laplace pressure on the interface due to interfacial tension vanishes. Therefore, from the viewpoint of fluid dynamics, the flow field is the same as that of one phase flow because non-slip boundary conditions are applicable for both oil and aqueous phases on polydimethylsiloxane walls.¹⁹ When the flow is fully developed, a parabolic velocity profile is anticipated across the extraction channel and the interface locates at the middle of the channel (1D model in Fig. 4, top view). The microparticles (or more precisely, their centers) should be on the extended CS (eCS, Fig. 2(a)) of the oil phase as a result of the Stokes laminar flow, which is predicted to be 0.174W (τ_eCL,1D) away from the interface according to the 1D model (dotted line in Fig. 4). If we further consider the non-slip effect of the top and bottom walls of the extraction channel, a 2D velocity field can be obtained by numerically solving the Poisson equation of the velocity component V_z in the mainstream direction (2D model in Fig. 4). The microparticle center should be on the eCS of carrier oil emulsion in the extraction channel, which is predicted by numerical integration of V_z over the channel cross section to be 0.192W (τ_eCL,2D) away from the interface (dashed line in Fig. 4). Therefore, microparticle radius should be >0.192W to achieve extraction according to the 2D model, which is greater than the 1D prediction and matches the experimental observation well, judging by the location of the center of the hydrogel microparticles (white dot) in the extraction channel (Fig. 4). These results indicate that the effect of the top and bottom walls should not be neglected in determining the positions of suspended microparticles of finite size in microfluidics. Of note, although the size of the dispersed microparticles is comparable to the channel width, it has little impact on the location of the extended central streamline and the thickness of the eCL under the flow condition of this study. This is because in Stokes flow, the dispersed microparticles move together with the surrounding fluid (and as a whole along the central streamline of the surrounding flow) with negligible relative motion between them as a result of the dominant viscous force (over inertia force) and the disturbance on the surrounding flow by the dispersed microparticles is limited to a negligible region immediately next to them.

FIG. 4.

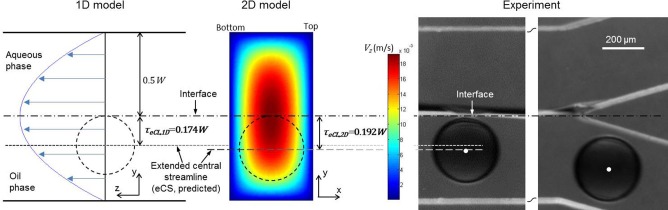
Predicted thickness of eCL (τ_eCL) as compared to the center (white dot) of hydrogel microparticle from experiment. The dashed circles indicate the predicted minimum microparticle sizes for touching the interface. The flow rates of the alginate solution, carrier oil emulsion, and extracting solution are 0.1, 6, and 6 ml/h, respectively, for both the experimental and modeling studies.

To further test this size criterion for effective extraction, hydrogel microparticles of various sizes were made by changing the flow rate of carrier oil emulsion (to maintain the stable interface position in the extraction channel, the flow rate of aqueous extracting solution is adjusted accordingly). Because the Plateau-Rayleigh instability at the flow focusing in this study falls into the dripping regime,²⁰ hydrogel microparticles of highly uniform size (relative standard deviation <2%) can be generated. Figure 5 shows that the extraction efficiency (calculated as the percentage of the extracted microparticles out of all microparticles entering the extraction channel) of these microparticles is highly dependent on their sizes. When the hydrogel microparticles are bigger than τ_eCL,2D, all of them can touch the interface and get extracted into the aqueous phase (scenario I, supplementary movie S2(a)⁸). When the size is much smaller than τ_eCL,2D but still slightly bigger than τ_eCL,1D on average, none of the microparticles can be extracted (scenario IV, supplementary movie S2(d)⁸). For the situations between these two cases (scenarios II and III, supplementary movies S2(b) and S2(c)⁸), the microparticles can be partially extracted, which probably is a result of the slight curvature and fluctuation of the interface and slight variation in microparticle size. These results show that the 2D model can be confidently used to determine the size requirement of hydrogel microparticles for effective extraction by the interfacial tension based method. According to the results shown in Figs. 4 and 5, hydrogel microparticles of various sizes can be easily extracted by varying the width (W) of the extraction channel or the ratio of the flow rates of the aqueous extracting fluid to carrier oil emulsion to change the τ_eCL (scenario I* in Fig. 5). Based on the same principle, microparticles with a hydrophobic surface confined in an aqueous phase can also be extracted into oil phase using the same simple extraction channel design. In addition, although it is insignificant compared to the interfacial tension effect in moving microparticle in Stokes flows with Re ≪ 1 (supplementary movie S1⁸), potential inertial effect at Re > ∼1 is also accounted by the merging channel design for microparticle extraction.

FIG. 5.

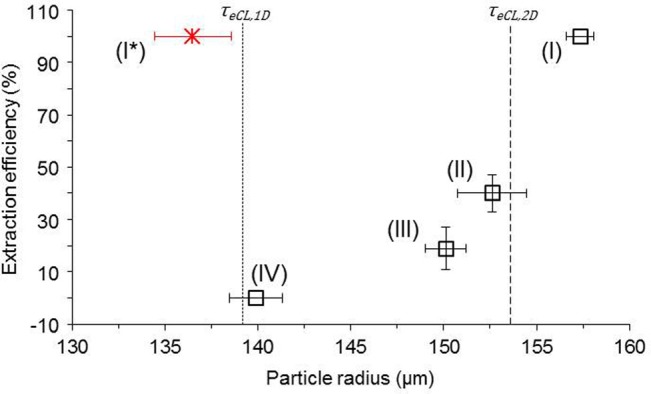
The thickness of eCL (τ_eCL) as the criterion for effective extraction of microparticles of different sizes. The error bars are standard deviations. The flow rate of carrier oil emulsion and aqueous extracting solution varies from (I) 5, (II) 6, (III) 6.5, to (IV) 8 ml/h. The flow rate of alginate solution is 0.1 ml/h. For the scenario of shifted interface (I*), the flow rates for dispersed alginate, carrier oil, and extraction solution are 0.06, 6, and 12 ml/h, respectively.

In summary, we reveal the attenuation of the CL into an eCL when two streams of fluids merge due to the partial loss of non-slip boundary condition. This attenuation from CL to eCL enables the extraction of hydrogel microparticles confined in the Stokes flow of oil with a radius greater than the thickness of the eCL (τ_eCL) using a simple merging planar microchannel design. Our study provides a simple yet powerful method and in-depth guidance to achieve quick on-chip extraction of microparticles confined in Stokes flows. This approach does not require external force, complex channel design, or complicated surface patterning and modification. As a result, it can be readily applied in a microfluidic (and non-microfluidic) system to extract microparticles for wide applications.