Wave reflections in the pulmonary arteries analysed with the reservoir–wave model

Abstract

Conventional haemodynamic analysis of pressure and flow in the pulmonary circulation yields incident and reflected waves throughout the cardiac cycle, even during diastole. The reservoir–wave model provides an alternative haemodynamic analysis consistent with minimal wave activity during diastole. Pressure and flow in the main pulmonary artery were measured in anaesthetized dogs and the effects of hypoxia and nitric oxide, volume loading and positive end-expiratory pressure were observed. The reservoir–wave model was used to determine the reservoir contribution to pressure and flow and once subtracted, resulted in ‘excess’ quantities, which were treated as wave-related. Wave intensity analysis quantified the contributions of waves originating upstream (forward-going waves) and downstream (backward-going waves). In the pulmonary artery, negative reflections of incident waves created by the right ventricle were observed. Overall, the distance from the pulmonary artery valve to this reflection site was calculated to be 5.7 ± 0.2 cm. During 100% O₂ ventilation, the strength of these reflections increased 10% with volume loading and decreased 4% with 10 cmH₂O positive end-expiratory pressure. In the pulmonary arterial circulation, negative reflections arise from the junction of lobar arteries from the left and right pulmonary arteries. This mechanism serves to reduce peak systolic pressure, while increasing blood flow.

Key points

• In the pulmonary artery, we use the reservoir–wave model to separate the effects of a charging and discharging, elastic arterial reservoir from the effects of waves created by the contracting and relaxing heart.

• Wave intensity analysis quantifies the effects of waves that cause changes in pressure and flow and precisely identifies when waves created by the heart and reflections of these waves start and end.

• We show that negative wave reflections arise from the junction of lobar arteries stemming from the left and right pulmonary arteries.

• When blood volume is increased and pulmonary arteries become distended, the strength of negative wave reflections increases when 100% O₂ is used for ventilation.

• Negative reflections suck blood downstream and, as they arrive when the heart is developing maximal pressure, negative reflections help to lower the back pressure the heart must pump against and, thus, they tend to increase the forward flow of blood.

Introduction

Conventional haemodynamic approaches attribute the measured pressure and flow to be the result of waves created by the cardiac chambers and reflections of these incident waves (Westerhof 1972; Hughes & Parker, 2009). In vascular systems, reflections can occur from branch points and therefore first appear downstream from the heart and travel backwards (i.e. against the direction of net blood flow). However, recent re-evaluation of these conventions suggests a pattern that defies physiological expectations: wave reflections appear first at the aortic valve and travel forwards (i.e. in the direction of net blood flow) (Wang et al. 2011; Tyberg et al. 2013; Westerhof & Westerhof, 2013). Therefore, a paradox occurs when, by definition, forward-going waves are created by the heart and backward-going waves are created by reflections.

The reservoir–wave model has been used to describe intuitive patterns of aortic wave propagation and reflection in the aorta, where downstream branch points cause incident waves to be reflected back to the aortic valve (Wang et al. 2003, 2011, 2013). This model provides an alternative understanding of pulmonary haemodynamics (Bouwmeester et al. 2013) and other vascular systems (Wang et al. 2003, 2006, 2008, 2011, 2013; Flewitt et al. 2007; Tyberg et al. 2009; Davies et al. 2010) by considering the contribution of a reservoir to measured pressure and flow. When applied to the pulmonary arterial circulation, the reservoir is based on a two-element windkessel (Frank, 1899; Sagawa et al. 1990), modified to take into account the zero flow (critical closing) pressure of alveolar blood vessels (Permutt & Riley, 1963). Once the reservoir pressure or flow is defined it is subtracted and the resulting wave-related ‘excess’ components of pressure and flow are analysed using wave intensity analysis (WIA) (Parker & Jones, 1990). WIA describes waves as they occur in time and quantifies the effects of waves on pressure and velocity/flow, where the prototypical wave is the forward compression wave (FCW) generated by the ventricle at the start of ejection.

The goal for a haemodynamic model of the pulmonary circulation should include the ability to discriminate between the various causes of pulmonary hypertension, either through an assessment of vascular properties or the analysis of propagated and reflected waves. Pioneering studies used Fourier analysis to determine the hydraulic impedance of the pulmonary circulation (Caro & McDonald, 1961; Patel et al. 1963) and further study of pulmonary hypertension showed that both arterial compliance and resistance have important contributions to right ventricular afterload (Milnor et al. 1969). To understand these contributions, Westerhof's three-element windkessel model (Westerhof et al. 1971) provides a good platform to quantify the independent contributions of lumped pulmonary vascular resistance and compliance (Elzinga et al. 1980). Determining these lumped vascular properties can be used to distinguish the differences between idiopathic and chronic thromboembolic pulmonary hypertension (Lankhaar et al. 2006, 2008; Saouti et al. 2010), which have distinct pressure waveforms and potentially different patterns of wave propagation and reflection (Nakayama et al. 1997; Castelain et al. 2001).

The reservoir–wave model provides a method to measure the separate contributions of lumped vascular properties with reservoir behaviour and the effects of wave propagation and reflection. Therefore, it is possible that this approach would help clarify the pathophysiology of various types of pulmonary hypertension. In the present study, we used the reservoir–wave model to describe the response of the normal pulmonary arterial circulation to decreased vascular resistance (with volume loading), potential collapse of small pulmonary vessels [with positive end-expiratory pressure (PEEP)], and active vasoconstriction and vasodilation (with hypoxia and inhaled nitric oxide, respectively).

Methods

Animal preparation

The University of Calgary animal care committee, whose criteria conformed to the ‘Guiding Principles for Research Involving Animals and Human Beings’ of the American Physiological Society, granted ethical approval of all experimental protocols. Anaesthesia was induced in 11 mongrel dogs (seven male; 18–28 kg, mean 22 kg) with an initial i.v. injection of 25 mg kg⁻¹ sodium thiopental and anaesthesia was maintained with an infusion of fentanyl (20–30 μg kg⁻¹ h^–1) and midazolam (0.01–0.015 μg kg⁻¹ h^–1). The dogs were ventilated using a constant volume respirator (model 607; Harvard Apparatus Inc., Natick, MA, USA) with a 50% O₂, 50% nitrous oxide gas mixture during surgery and with 100% O₂ during experimentation. The respiratory rate (16–18 breaths min⁻¹) and tidal volume (15 ml kg⁻¹) were adjusted to maintain physiological arterial blood gas levels (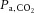 = 35–45 mmHg) and pH (7.2–7.4) (Mitchell et al. 2011). Body temperature was kept at 37°C by using a circulating warm-water blanket and heat lamp when necessary. A bladder catheter was inserted into the urethra to collect urine. During experimentation, the dogs were ventilated with 100% O₂ using a different ventilator (Servo Ventilator 900C; Siemens-Elema AB, Solna, Sweden) that allowed quick adjustment of minute ventilation, respiratory rate and PEEP. The chest remained open to allow access to the measuring devices that sometimes required adjustment.

The experimental instrumentation has been described previously (Bouwmeester et al. 2013). Briefly, pressure was measured in the right ventricle (RV), left ventricle and left atrium with 7-F catheter-tip pressure transducers with lumens (Scisense Inc., London, Ontario, Canada) and in the main pulmonary artery (PA) and a single pulmonary vein (PV) with 3.5-F catheter-tip pressure transducers without lumens (Millar Instruments Inc., Houston, TX, USA). The PA catheter was inserted through the anterior wall of the RV and advanced approximately 1 cm beyond the pulmonary valve. The PV catheter was placed in a left-sided PV, approximately 1 cm upstream of the left atrium. Flow probes (A- and S-Series models and flowmeter model T206; Transonic Systems, Ithaca, NY, USA) were placed on the main PA (immediately downstream of the tip of the PA catheter) and the PV (immediately upstream of the tip of the PV catheter). A four-limb-lead ECG was also recorded. After instrumentation was complete, the pericardium was reapproximated with interrupted loose sutures (Scott-Douglas et al. 1991).

Electronic signals were sampled at 400 Hz with data acquisition software (Sonometric Corp., London, Ontario, Canada) and data were analysed using CV Works (AccuDAQ Inc., Calgary, Alberta, Canada).

Experimental protocol

Volume loading was assessed by mean pulmonary venous pressure, which was sequentially increased with an infusion of 10% pentastarch solution (Pentaspan; Bristol-Myers Squibb Canada, Montreal, Quebec, Canada) to achieve low (∼5 mmHg), medium (∼9 mmHg) and high (∼14 mmHg) filling pressures. At each filling pressure, three ventilation strategies were used: (1) 100% O₂; (2) hypoxia; and (3) hypoxia plus nitric oxide. Ventilation with 100% O₂ was used as a baseline; hypoxia was induced by adding N₂ to the inspired gas mixture until 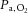was less than 50 mmHg. Then, during hypoxic ventilation, nitric oxide was added (80 ppm) to the inspired gas mixture (INOvent delivery system; Datex-Ohmeda, Helsinki, Finland). At each ventilation state, recordings were taken at 0 and 10 cmH₂O PEEP, the order of which was randomly selected.

At the conclusion of the experiments, while deeply anaesthetized, the dogs were killed with an intracardiac injection of KCl.

Reservoir analysis

The pulmonary arterial reservoir model used by Bouwmeester et al. (2013) was based upon earlier work (Wang et al. 2003) and was used to describe the PA reservoir pressure (P_res) as follows:

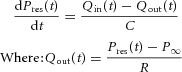(1)

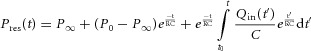(2)

For the arterial reservoir, inflow provided to this reservoir is easily measured and equivalent to measured main PA flow (Q_PA ≡ Q_in), while arterial outflow (Q_out) provided to the pulmonary capillaries is much more difficult to measure and therefore, modelled by eqn (1). Equation (2) represents the analytical solution to eqn (1), where P₀ and t₀ represent the time and PA pressure at the onset of ejection and R, C and P_∞ are the arterial reservoir parameters.

To determine the reservoir pressure in eqn (2), the reservoir parameters were assumed to be constant over the range of pressures measured during each intervention. Initial estimates of reservoir parameters were made and P_res was calculated throughout a complete cardiac cycle. The initial estimates are arbitrary and appropriate values for reservoir parameters were determined using an algorithm developed in Matlab (Mathworks, Natick, MA, USA) employing the function ‘fminsearch’ (Nelder–Mead simplex algorithm) to vary these parameters iteratively to minimize the mean-squared error between P_res and P_PA during diastole. This method is robust and relatively insensitive to the initial reservoir parameter estimates. The result of this procedure applied to the PA is shown in Fig. 1, where it was assumed that the exponential decline of P_PA during mid-to-late (approximately last two-thirds) diastole represented a decreasing reservoir pressure and therefore was used to calculate P_res.

Figure 1. Illustrating how pulmonary artery pressure and flow were analysed and showing pulmonary artery reservoir and excess pressure.

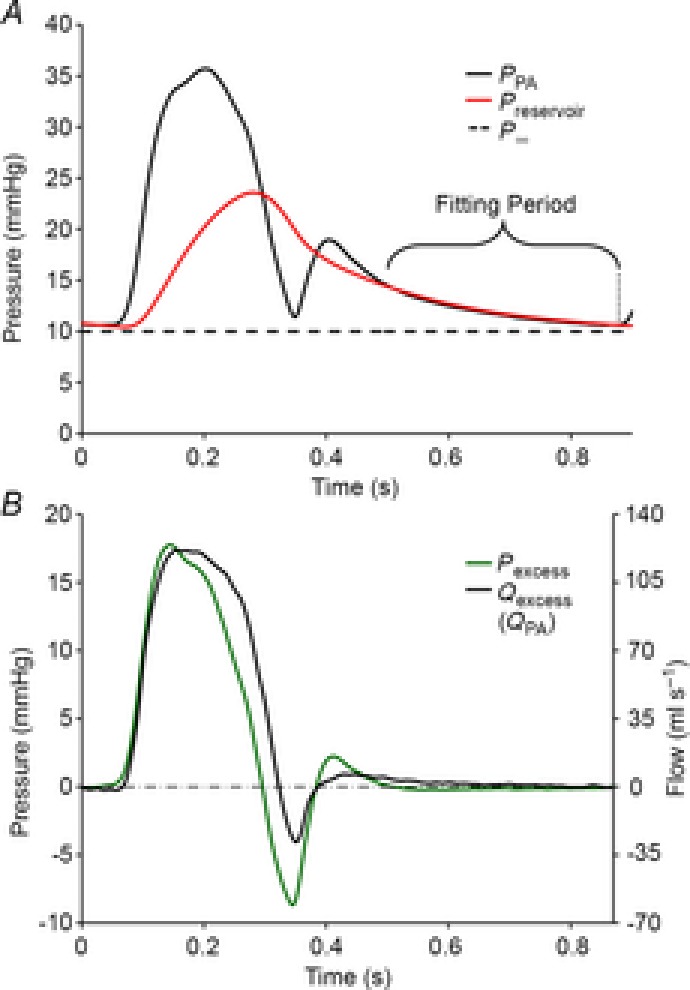
Data are taken during low blood volume, 0 cmH₂O positive end-expiratory pressure and 100% O₂ ventilation. A, measured pulmonary artery pressure (P_PA), pulmonary artery reservoir pressure (P_res) and pulmonary artery asymptotic pressure (P_∞). B, excess pulmonary artery pressure (P_excess) is shown on the left y-axis and excess pulmonary artery flow (Q_excess), which in the main pulmonary artery is equivalent to measured pulmonary artery flow (Q_PA), is shown on the right y-axis.

Excess pressure and flow/velocity

Excess pressure or flow is calculated by subtracting the reservoir contribution from the measured pressure or flow. In the PA, excess pressure (P_excess) is calculated by subtracting P_res from P_PA (P_excess = P_PA – P_res). In general, excess flow (Q_excess) is also calculated by subtracting reservoir flow (Q_res) from Q_PA (Q_excess = Q_PA – Q_res). However, the main PA is a unique location, in that there is no reservoir upstream and measured flow is negligible during diastole when the pulmonary valve is closed. Since the reservoir contribution is determined during diastole and because there is no reservoir upstream of the main PA, Q_res in this location is zero. Therefore, in the main PA Q_excess is equal to Q_PA. (NB if flow were measured further downstream, the reservoir upstream of that location would discharge, resulting in significant Q_res that would need to be subtracted to determine Q_excess at that location). P_excess and Q_excess waveforms are shown in Fig. 1B. For the purposes of WIA, Q_excess is converted to velocity (U_excess) as follows: U_excess = Q_excess/A; where the cross-sectional area (A) of the main PA was estimated from the diameter of the flow probe attached to it.

Wave intensity analysis

Defined by WIA, there are four types of waves that have different effects on pressure and velocity and, in the context of this study, account for changes in P_excess and U_excess. The forward direction is defined as the direction of net blood flow and waves might either increase (compression waves) or decrease (decompression waves) pressure as they pass. Thus, there are FCW or backward compression waves (BCW) and forward (FDW) or backward (BDW) decompression waves. In this study, the RV generates forward waves, which are transmitted downstream and backward waves arriving during systole are reflections of these incident waves. Forward waves can be separated from backward waves if the local wave speed is known (Parker, 2009). In the PA, the single point wave speed was calculated using the linear regression of the P_excess/U_excess relationship during the upstroke of systole (Khir et al. 2001) when only a FCW was assumed to be present.

WIA of P_excess and U_excess and the calculation of reflector distance and magnitude are shown in Fig. 2A. Excess wave intensity (WI_excess) is decomposed into the intensities of forward- and backward-going waves (WI_forward and WI_backward, respectively). To quantify the pressure effects of these waves, the incremental pressure changes of forward- and backward-going waves were integrated (P_forward and P_backward respectively) as shown in Fig. 2B, where the onsets of incident waves (FCW and FDW, respectively) and their reflections (BDW and BCW, respectively) are labelled. The intervals between the onsets of incident and reflected waves are indicated by δt. Together with the single-point wave speed (c), δt is used to estimate the distance from the measurement to the reflection site [d = c (δt/2)], assuming no change in the wave speed and vascular properties between where it is detected and the reflection site. The magnitude of the reflection is measured by the reflection ratio (Γ), which is calculated as: [Γ = ΔP_backward/ΔP_forward]. Taking into account experimental and analytical errors, reflections were only considered significant if the absolute value of Γ was greater than 0.15, which correlates with the ratio of daughter/mother vessels (in terms of cross-sectional area) of ∼0.8–0.9 for positive reflections and ∼1.3–1.5 for negative reflections (Parker, 2009).

Figure 2. Wave intensity analysis of pulmonary artery excess pressure and velocity.

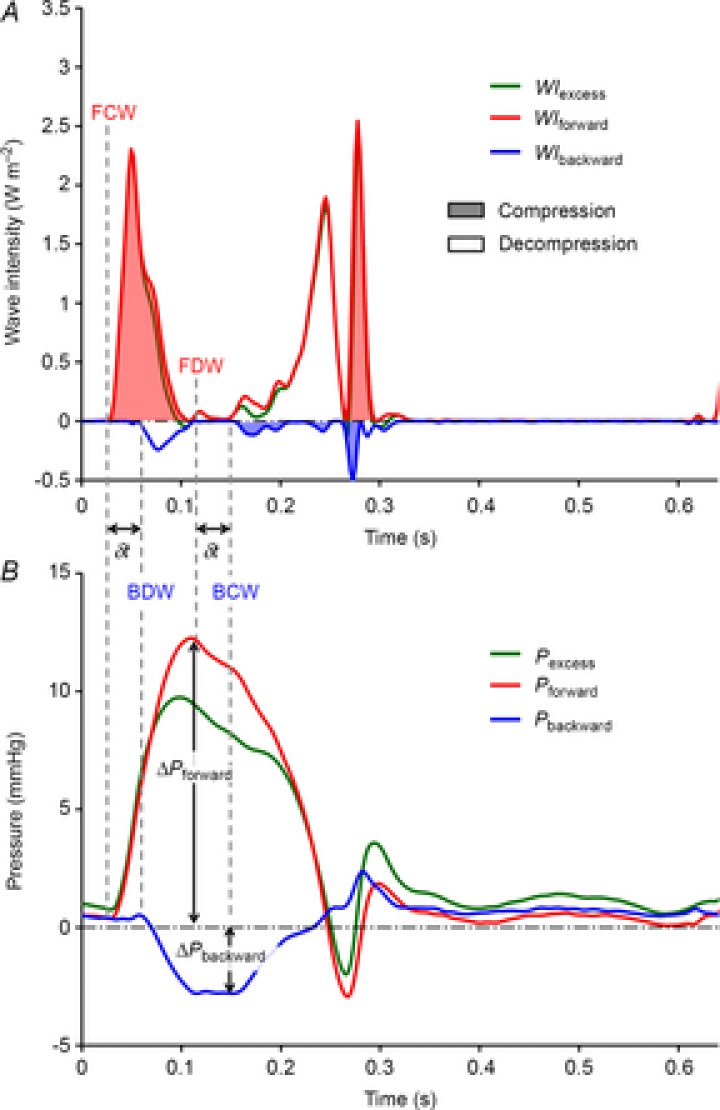
Data are taken during low blood volume, 0 cmH₂O positive end-expiratory pressure and 100% O₂ ventilation. A, net wave intensity (WI_excess) is decomposed into forward-going (WI_forward) and backward-going (WI_backward) wave components. The wave energy of compression waves is represented by shaded areas and decompression waves by open areas. B, P_excess is decomposed into the contributions of forward-going (P_forward) and backward-going (P_backward) waves. Onsets of FCW, FDW, BCW and BDW are indicated by vertical dashed lines. δt indicates the interval between the incident forward-going waves and reflected backward-going waves (i.e. FCW → BDW and FDW → BCW). The reflection ratio (Γ) is equal to ΔP_backward/ΔP_forward. BCW, backward compression wave; BDW, backward decompression wave; FCW, forward compression wave; FDW, forward decompression wave.

Statistical methods

All data were analysed with SigmaPlot software (Systat Software Inc., San Jose, CA, USA). Three-way ANOVA was used to analyse the effects of volume load, PEEP and ventilation (see Table 1). Owing to incomplete data sets, the results are presented as least-squared mean values (estimated using a general linear model) ± s.e.m. For all statistical tests, the significance level was set at 0.05. Pairwise multiple comparisons were made with the Bonferroni method.

Table 1.

Pulmonary artery reservoir parameters and wave analysis results

	Low volume	Medium volume	High volume	PEEP 0 cmH2O	PEEP 10 cmH2O	100% O2	Hypoxia	Nitric oxide
Reservoir parameters
R (mmHg s–1 ml−1)	0.28 ± 0.01*‡	0.22 ± 0.02*†	0.16 ± 0.02†‡	0.22 ± 0.01	0.22 ± 0.01	0.19 ± 0.01§	0.27 ± 0.02§+	0.21 ± 0.02+
C (ml mmHg−1)	1.21 ± 0.07	1.17 ± 0.08	1.24 ± 0.09	1.05 ± 0.06	1.36 ± 0.06	1.28 ± 0.07	1.10 ± 0.08	1.24 ± 0.08
P∞ (mmHg)	11.5 ± 0.3*‡	14.9 ± 0.4*†	19.1 ± 0.4†‡	14.9 ± 0.3	15.3 ± 0.3	13.5 ± 0.4§§	15.7 ± 0.4§	16.3 ± 0.4§
Wave Analysis Results
Wave speed (m s−1)	2.7 ± 0.1	2.5 ± 0.1	2.4 ± 0.1	2.7 ± 0.1	2.4 ± 0.1	2.6 ± 0.1	2.6 ± 0.1	2.5 ± 0.1
Absolute negative Γ (%)**	27 ± 1	29 ± 1	28 ± 2	30 ± 1	26 ± 1	28 ± 1	30 ± 1	26 ± 1
Negative reflector distance (cm)	5.0 ± 0.3	4.4 ± 0.3	4.6 ± 0.3	4.8 ± 0.2	4.5 ± 0.3	5.2 ± 0.3	4.4 ± 0.3	4.4 ± 0.3

Values represent least-squared mean values ± s.e.m. and statistical results from three-way ANOVA. Abbreviation: PEEP, positive end-expiratory pressure.

Bold numbers indicate significant (P < 0.05) differences within each volume load, PEEP and ventilation group. Within volume load, significant (P < 0.05) pairwise Bonferroni comparisons are indicated:

^*low vs. medium,

^†medium vs. high and

^‡low vs. high. Within ventilation, significant (P < 0.05) pairwise Bonferroni comparisons are indicated:

^§100 O₂ vs. hypoxia;

⁺hypoxia vs. nitric oxide; and

^¶100% O₂ vs. nitric oxide.

^**For these data, there is a significant interaction between volume load and ventilation [F(4,94) = 2.818, P = 0.029]. Therefore, the effects of volume load and ventilation cannot be interpreted singularly and Fig. 3 must be used to interpret the relation between these two factors.

Results

The RV creates two incident waves as shown by WIA of P_excess and U_PA in Fig. 2. The FCW is generated at the beginning of systole with initial contraction and the FDW is generated mid-systole when RV contraction starts to decelerate. Negative reflections are observed as the FCW is reflected as BDW and the FDW is reflected as BCW. The magnitude of the negative Γ is expressed in absolute terms, as a percentage [100 |Γ|], and the estimated distance from measurement location to negative reflection site are listed in Table 1.

Table 1 shows the results of three-way ANOVA applied to the reservoir parameters, single point wave speed, negative Γ and reflector distance. The results are organized into overlapping groups to show the effects of volume loading, PEEP and ventilation condition. None of the interventions had a significant effect on the distance between the measurement location and the negative reflection site and therefore, the mean value (4.7 ± 0.2 cm) is used as an estimate for this measurement. The absolute negative Γ data cannot be properly interpreted for both volume loading and ventilation as there is significant interaction [F(4,94) = 2.818, P = 0.029] between these interventions. To understand these data, Fig. 3 shows the absolute negative Γ data plotted at each volume load and ventilation condition. With 100% O₂ ventilation, negative reflection strengthens with progressive volume loading.

Figure 3. Negative reflection ratio as a function of volume loading for each ventilation condition.

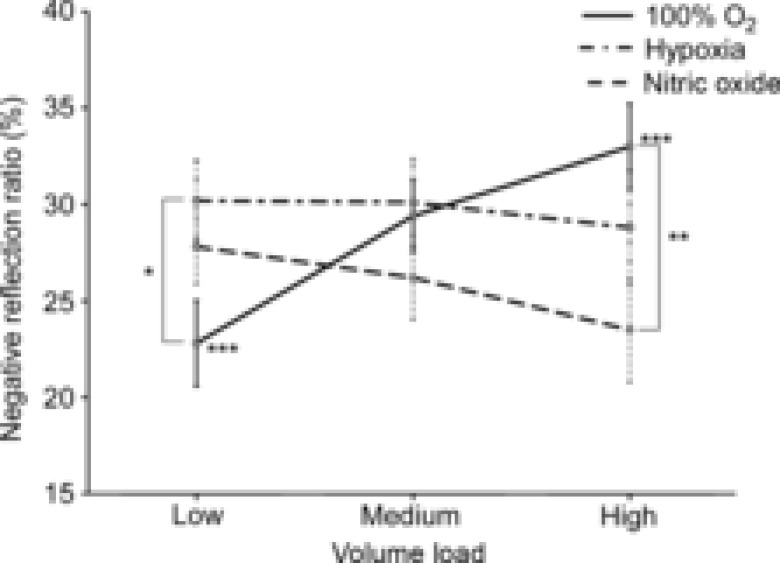
Within 100% O₂ ventilation, the absolute magnitude of negative reflection (Γ) increases. Significant Bonferroni multiple comparisons: within 100% O₂, low vs. high ***(P = 0.005); within low volume load, 100% O₂ vs. hypoxia *(P = 0.040); within high volume load, 100% O₂ vs. nitric oxide **(P = 0.035).

Discussion

We used the reservoir–wave model to analyse incident and reflected wave patterns in the pulmonary arterial circulation. In the main PA, negative wave reflections were observed; these appear to have originated from the junction of the left or right PAs and lobar arteries. The location of the negative reflection site did not change but the magnitude of this negative reflection increased with volume loading during 100% O₂ ventilation.

Pulmonary artery negative reflection site

Figure 2 shows a typical example of a negative reflection in the main PA. This has also been observed in other studies using WIA on measured PA pressure and flow/velocity (Hollander et al. 2001; Smolich et al. 2008; Dwyer et al. 2012); however, the reflection site is usually attributed to the bifurcation of the left and right PA. Considering that the distance from the main PA measurement site to the reflection site was 4.7 ± 0.2 cm and that it was approximately 1 cm from the pulmonary valve to the main PA measurement site, the distance from the pulmonary valve to the negative reflection site is estimated to be 5.7 ± 0.2 cm. This distance corresponds to a point no farther than the end of the lobar PAs (defined as the arteries that stem from the left and right PAs) (Gan & Yen, 1994). Detailed morphometric study of PA dimensions by Attinger (1963) indicate that these branch points have daughter/mother cross-sectional area ratios ranging from 0.95 to 1.22 in dogs. As shown by Attinger (1963), not all branch points are symmetrical bifurcations and therefore other studies indicate that the ratio may be as high as 1.33 in the right lung (Gan & Yen, 1994) or 1.46 from pooled data (Haworth et al. 1991). Negative reflections are possible if the cross-sectional area ratio of daughter/mother vessels is greater than approximately 1.2 (Parker, 2009). Therefore, as the area ratio of proximal lobar arteries to either the left or right PA may be greater than 1.2, the junction of the lobar branches offers a plausible site for negative reflection that matches the estimated distance to the reflection site from the pulmonary valve.

Strength of pulmonary artery negative reflection

The summarized results in Fig. 3 show that strength of absolute negative Γ increases approximately 10% with volume loading during 100% O₂ ventilation. This behaviour, which is consistent with the increase in conductance that accompanies volume loading (Bouwmeester et al. 2013), is similar to that reported by Hollander et al. (2001). Volume loading apparently dilates the lobar arteries proportionally more than the left or right PAs from which they branch. Even though mechanical testing has shown no difference in the passive properties between main, left branch and lobar PAs (Cox, 1982), the response in vivo to volume loading remains an open question as others have reported that pulmonary vascular compliance increases from proximal to distal portions of the arteries (Altinawi et al. 1991; Gan & Yen, 1994).

At the low volume load, Fig. 3 shows that hypoxia has significantly stronger negative wave reflections compared to 100% O₂ ventilation. A similar study investigating the effects of hypoxia on the pulmonary circulation showed similar patterns in regards to net wave intensity (Nie et al. 2001). Although Fig. 2 shows that net wave intensity has the potential to mask the effects of backward waves and only indicates which wave dominates at a particular time in the cardiac cycle, the results of Nie et al. could be interpreted in the context of the reservoir–wave model. Their observed increases of negative net wave intensity with hypoxia would imply greater negative wave reflection, which corresponds to the increased magnitude of negative reflections at the low volume load displayed in Fig. 3. Nie et al. also showed less wave reflection with nitric oxide inhalation, whereas the results in our study show no significant difference in the strength of negative reflections when nitric oxide was added to hypoxic ventilation.

Reservoir–wave versus conventional wave analysis

The consequences of considering reservoir effects in the PA are illustrated in Fig. 4. The reservoir–wave model shows the importance of subtracting reservoir pressure before performing wave analysis in the main PA. Once excess pressure is determined, either the impedance approach or WIA yields identical results (Hughes & Parker, 2009). This figure shows the contributions of forward- and backward-going waves to both pressure and velocity. Results are shown of the reservoir–wave model and WIA applied separately to P_excess (Fig. 4A) and U_excess (Fig. 4B). Figure 4C and D show the conventional technique (Westerhof et al. 1972; Hughes & Parker, 2009) applied separately to measured P_PA (Fig. 4C) and U_PA (Fig. 4D). In Fig. 4D, equal and opposite forward- and backward-going waves balance precisely to yield zero velocity/flow during diastole. In the PA, backward-going waves are assumed reflections of forward-going waves. Therefore, zero flow during diastole can be explained simply by the closure of the pulmonary valve or alternatively, as conventional analysis implies, reflections are always present and reduce the supposed amount of forward flow provided by the RV. In Fig. 4A and B, WIA of P_excess and U_excess demonstrates a wave pattern that is entirely consistent with minimal wave activity during diastole and furthermore, a proximal negative reflection is a mechanism that augments the blood flow provided by the RV. In a sense, blood is sucked forward, which serves to decrease pressure and increase flow.

Figure 4. Pulmonary artery reservoir-wave versus conventional wave analysis.

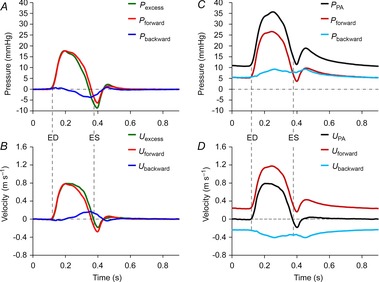
Data are taken during low blood volume, 0 cmH₂O positive end-expiratory pressure and 100% O₂ ventilation. This figure indicates the importance of subtracting reservoir pressure and velocity from the measured values before analysing wave patterns. A–D, both the pressure and velocity are decomposed into the contributions of forward-going (P_forward and U_forward) and backward-going waves (P_backward and U_backward). A, excess pressure (P_excess). B, excess velocity (U_excess). C, pulmonary venous pressure (P_PA). D, pulmonary venous velocity (U_PA). Vertical dashed lines indicate ED and ES, which were defined by the upstroke and down stroke of U_excess or U_PA crossing zero. ED, end diastole; ES, end systole.

Limitations

This study was conducted in open chest, anaesthetized dogs because it was not feasible to make such extensive measurements in a more intact preparation. Thus, our conclusions should be validated using more physiological experimental models and/or clinical observations.

Reservoir parameters were calculated during diastole. When heart rate is less than approximately 80 bpm, the reservoir parameters can be determined from regular P_PA waveforms robustly. However, if the heart rate is greater, determining reservoir parameters for regular beats becomes more difficult. In this study, to maintain the robust ability to calculate reservoir parameters at every intervention, acetylcholine was injected to extend diastole/diastasis after a series of regular beats.

Recently, a simulation consisting of three bifurcating tubes of arbitrary length, geometry and wall properties, terminated by a three-element windkessel questioned the validity of the reservoir–wave paradigm (Mynard et al. 2012). This hypothetical model showed that negative reflections were amplified and positive reflections were dampened, which applied to this study, would imply that the observed negative reflections in the main PA are questionable. As discussed by Tyberg et al. (2014) the model used by Mynard et al. (2012) with elastic (i.e. no energy loss), 1-D tubes may not represent physiological pressure–volume properties and more advanced fluid–structure interaction models that take into account viscoelastic vessel properties may be required (Giannopapa, 2004; Bessems et al. 2008). We maintain that using real physiological measurements of pressure and flow and describing waves with excess pressure yields a plausible pattern of wave propagation and reflection during normal conditions, vasoconstriction and vasodilation (Wang et al. 2011, 2013) that is not possible when using impedance analysis, as demonstrated by paradoxical reflected waves that appear to propagate downstream, when they should propagate upstream (Wang et al. 2011; Tyberg et al. 2013; Westerhof & Westerhof, 2013).

Conclusions

We conclude that there are significant negative wave reflections in the main PA that arise from the junction of lobar arteries from the left or right PAs. This reflection provides a mechanism to reduce peak systolic pressure and, at the same time, increase blood flow and effectively facilitating right ventricular ejection. This mechanism is not apparent when measured pressure and flow waveforms are analysed conventionally. It is important to define this naturally occurring negative reflection to understand normal and pathological pulmonary circulatory physiology.

Glossary

BCW

backward compression wave

BDW

backward decompression wave

C

reservoir compliance

c

wave speed

FCW

forward compression wave

FDW

forward decompression wave

P_∞

asymptotic pressure

PA

pulmonary artery

P_backward

backward-going wave pressure

PEEP

positive end-expiratory pressure

P_excess

excess pressure

P_forward

forward-going wave pressure

P_PA

pulmonary artery pressure

P_res

reservoir pressure

PV

pulmonary vein

Q_excess

excess flow

Q_in

pulmonary arterial reservoir inflow

Q_out

pulmonary arterial reservoir outflow

Q_PA

pulmonary artery flow

Q_res

pulmonary arterial reservoir flow

R

reservoir resistance

RV

right ventricle/ventricular

U_backward

backward-going wave velocity

U_excess

excess velocity

U_forward

forward-going wave velocity

U_PA

pulmonary artery velocity

WIA

wave intensity analysis

WI_backward

backward-going wave intensity

WI_excess

excess wave intensity

WI_forward

forward-going wave intensity

Γ

reflection ratio

δt

delay of reflected wave

Additional Information

Competing interests

The authors have no conflicts of interest, financial or otherwise, to declare.

Author contributions

The experiments in this study were performed in the Libin Cardiovascular Institute of Alberta at the University of Calgary. J.C.B., I.B., N.G.S. and J.V.T. conceived and designed the experiments. J.C.B. collected and analysed experimental data and J.C.B., I.B., N.G.S. and J.V.T. interpreted the experimental data. J.C.B., I.B., N.G.S. and J.V.T. drafted the article and revised it critically for important intellectual content. All authors have read and approved the manuscript.

Funding

This work was supported by the Canadian Institutes of Health Research [106520].