Wide-scale alterations in interchromosomal organization in breast cancer cells: defining a network of interacting chromosomes

Abstract

The interchromosomal spatial positionings of a subset of human chromosomes was examined in the human breast cell line MCF10A (10A) and its malignant counterpart MCF10CA1a (CA1a). The nine chromosomes selected (#1, 4, 11, 12, 15, 16, 18, 21 and X) cover a wide range in size and gene density and compose ∼40% of the total human genome. Radial positioning of the chromosome territories (CT) was size dependent with certain of the CT more peripheral in CA1a. Each CT was in close proximity (interaction) with a similar number of other CT except the inactive CTXi. It had lower levels of interchromosomal partners in 10A which increased strikingly in CA1a. Major alterations from 10A to CA1a were detected in the pairwise interaction profiles which were subdivided into five types of altered interaction profiles: overall increase, overall decrease, switching from 1 to ≥2, vice versa or no change. A global data mining program termed the chromatic median calculated the most probable overall association network for the entire subset of CT. This interchromosomal network was drastically altered in CA1a with only 1 of 20 shared connections. We conclude that CT undergo multiple and preferred interactions with other CT in the cell nucleus and form preferred—albeit probabilistic—interchromosomal networks. This network of interactions is highly altered in malignant human breast cells. It is intriguing to consider the relationship of these alterations to the corresponding changes in the gene expression program of these malignant cancer cells.

INTRODUCTION

It is widely agreed that the structural organization of the nucleus impacts genomic function. In particular, the spatial arrangement of chromosomes and genes relative to each other and the nuclear periphery has been demonstrated to be a fundamental feature in genomic expression (1–8). On a global level, the nucleus is compartmentalized with domains that have specific functions such as the nucleolus, transcription factories, PML bodies and heterochromatin (9). Chromosomes are present in the cell nucleus as discrete bodies termed chromosome territories (CT) (10–15) which interact with these functional domains (9). For example, the chromosomes which contain the nucleolar organizing regions, preferentially interact with the nucleolus (16–18). While previous studies have suggested a probabilistic nonrandom arrangement of CT based upon their radial position within the nucleus (for review, see Cremer and Cremer (19), fewer reports have investigated whether there are specific interchromosomal arrangements (20,21) and whether these are altered in different cell and tissue types (22–26), during cell differentiation and development (27) and in cancer cells (28).

Considering the possible role of interchromosomal interactions in cancer progression, increased translocation frequency has been determined between specific CT which are in closer proximity (28–31) and those that might be overlapping or intermingling (32). Moreover, within cancer nuclei, the translocated CT remain preferential partners (28). The primary method for most of the reports about CT organization involved CT centers of gravity which may or may not reflect interactions of these CT at their borders. Also, due to technical limitations, the vast majority of these studies have been limited to three or less CT pairs per nucleus.

In this report, radial and interchromosomal positioning was studied in the MCF10 breast cancer progression model. MCF10A (10A) is an immortalized human cell line that expresses many phenotypic properties characteristic of normal luminal ductal epithelial breast cells (33–35). These cells resemble morphologically normal epithelial breast cells, are noninvasive, controlled by hormones and growth factors and do not undergo any of the distinguishing morphological alterations of tumor formation (34). They are widely considered to be a normal-like breast epithelial cell line.

The MCF10CA1a (CA1a) cell line was subsequently derived from 10A (36). Unlike 10A, these cells show tumor-like morphology, anchorage-independent growth and abnormal immunocytochemistry profiles (36). They also show a high level of invasiveness consistent with their malignant state (S. Zucker and R. Berezney, unpublished observations). Further characterization using SKY and aCGH techniques demonstrated that 10A is near-diploid (47 chromosomes), whereas 10CA1a has a greater number of chromosomes and translocations (37). Microarray analysis identified ∼7000 genes that are up- or downregulated >2-fold indicating major differences in the gene expression profiles from 10A to 10CA1a (37).

The radial and interchromosomal positioning of a subset of nine chromosome pairs (CT1, 4, 11, 12, 15, 16, 18, 21 and X) were subsequently studied in 10A and CA1a cells using re-FISH. While radial positioning of CT was similarly size dependent in both cell lines, there were several alterations in the malignant cancer cells. Interchromosomal interaction profiles were generated based on the nearest border distances between all possible pairwise combinations of CT. Striking alterations were found in the interaction profiles of the malignant versus nonmalignant breast cells. Multiple interchromosomal interactions were detected at similar levels for all of the CT except the inactive CT Xi, which was much lower in 10A cells. In CA1a, however, both CTXi and Xa showed striking increases in interchromosomal interactions. Correlating with the increase of interchromosomal interactions, the gene expression levels of CTX were strikingly enhanced in CA1a (37).

Using a newly developed data mining algorithm termed the chromatic median (38), probabilistic network models were generated for the global patterns of interchromosomal positioning of all nine chromosome pairs. The preferred arrangement for the malignant CA1a was strikingly altered from MCF10A with only one of 20 interactions common between the networks. Our findings provide further support for a probabilistic ‘chromosome code’ where the overall interactive network of CT contribute to the global regulation of gene expression (25,26).

RESULTS

Re-FISH, computer imaging and computational geometric approaches (see Materials and Methods) were used to study the 3D interactions of a subset of nine human chromosomes (#1, 4, 11, 12, 15, 16, 18, 21 and X) which are representative of the entire genome by having a broad range in size and gene density. The nine CT pairs comprise ∼40% of the total number and DNA content of chromosomes in the human genome. The weighted average gene density (6.9 genes/mbp) of this nine chromosome subset is nearly identical to the entire female genome (6.7 genes/mbp). Moreover, the selected chromosomes do not show alterations in either the MCF10A or the malignant CA1a cells based on SKY and aCGH analysis (37). In brief, female MCF10A (10A) human mammary luminal ductal epithelial cells (35) or MCF10CA1a (CA1a), a malignant cell line derived from MCF10A (36) was grown on gridded cover slips and labeled with three rounds of chromosome paints. Representative images for the CT are displayed in Figure 1. A total of 108 10A and 56 CA1a cells were analyzed with our eFISHent program (see Materials and Methods) for the nine CT subsets. For each distance type, 15 552 and 8064 pairwise heterologous CT distances (36 × 4 different pairwise combinations) are generated in 10A and CA1a, respectively.

Figure 1.

Multi-FISH labeling of CT in MCF10. 2D projection images of: (A) 10 CT (1, 4, 11, 12, 15, 16, 17, 18, 21 and X) in MCF10A; (E) nine CT (1, 4, 11, 12, 15, 16, 18, 21 and X) in MCF10CA1a; (B and F) larger chromosomes (1, 4, 11, 12 and X); (C and G) smaller chromosomes (15, 16, 17, 18 and 21); and (D and H) DAPI staining to visualize the nuclei.

Labeling of replication sites with EdU (Click-iT, Life technologies, Grand Island, NY) before and after FISH (Fig. 2A–G) indicates that the FISH procedure does not alter overall genomic structure at the ∼1 Mbp level characteristic of these labeled replication domains in early S phase (15,39,40). In addition, the same CT is labeled nearly identically in consecutive rounds of FISH (Fig. 2F and G), the levels of interactions between all other CT are maintained (Fig. 2H–J) and the nearest distances between all other CT are virtually identical regardless in which round the CT was labeled (Supplementary Material, Table S1).

Figure 2.

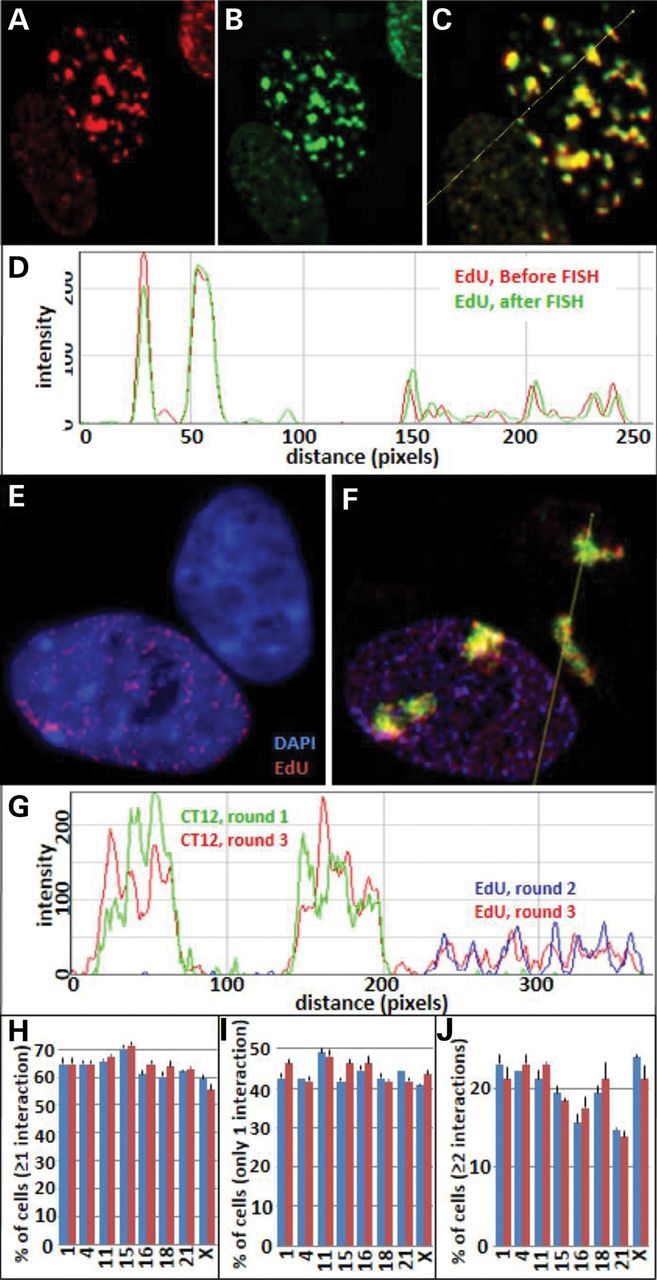
Relabeling CT and replication sites in successive rounds. EdU labeling of replication sites before and after FISH demonstrate that replication sites from small to large and their nuclear positions are not altered by FISH. (A) EdU sites before FISH (red); (B), EdU sites after FISH (green); (C) merged image of A and B; (D) line profile of the merged image; (E) EdU-labeled replication sites (red) and DAPI staining (blue); (F) merged image of DAPI (blue), EdU-labeled sites (rounds 2 and 3) and CT 12 labeling in rounds 1 (green) and round 3 (red); (G) line profile through the merged image F; (H–J) comparison interaction profiles of CT 12 with the other eight CT after labeling in the first round (blue bars) and relabeling of CT 12 in the third round (red bars).

CT volumes and radial chromosome positioning in 10A and CA1a cells

The nuclear volumes of CA1a increased an average of ∼54% compared with 10A with corresponding increases in the CT volumes (Fig. 3A–D). A significant linear relationship (r² = ∼0.7) was found between chromosome lengths in Mbp and CT volumes for both 10A and CA1a (Fig. 3C). In contrast to the active Xa, the inactive Xi fell below the linear regression trend line and decreased the overall fit (i.e. without Xi, r² = ∼0.9). The total volumes of all nine CT increased in proportion to the nuclear volumes from 10A to CA1a cells (r² = 0.73, Fig. 3D). With the exception of CTXi, the radial arrangement of CT is size dependent in both 10A and CA1a (Fig. 3E, r² ≈ 0.75; without Xi ≈ 0.90) but showed no relationship to gene density (Fig. 3F). Five of the nine CT (CT 4, 12, 15, 16 and 21) were significantly more peripherally located in CA1a compared with their 10A counterparts (Fig. 3G). In contrast, random simulations of both 10A and CA1a showed no relationship of chromosome size to radial positioning (Fig. 3E and G).

Figure 3.

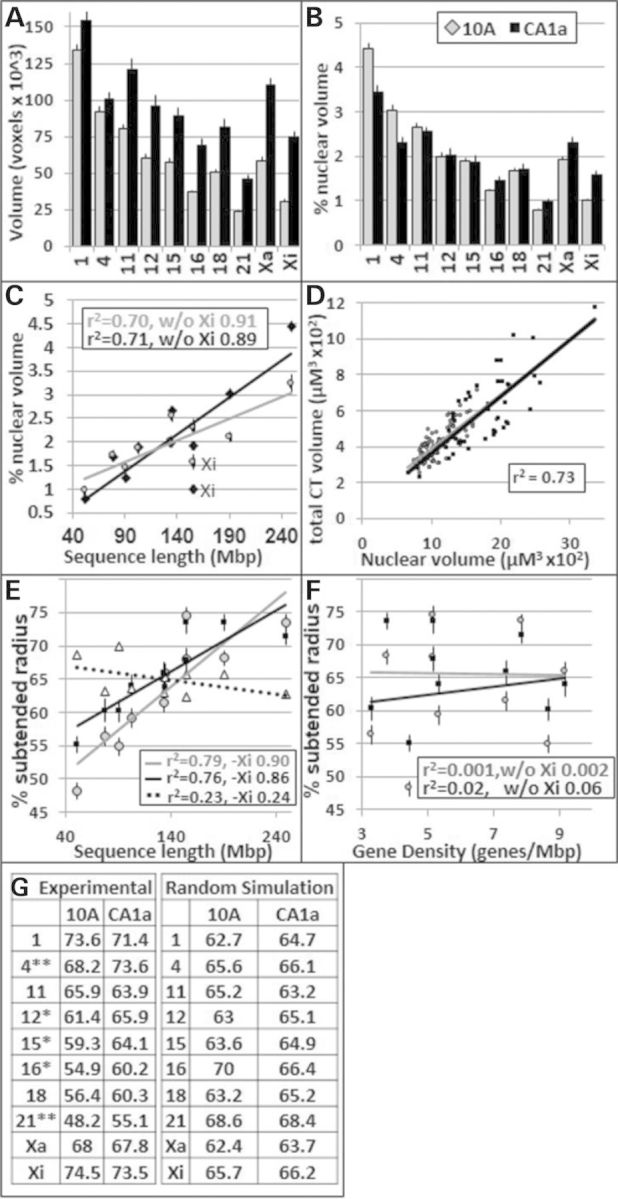
Nuclear volumes and radial positions of CT in 10A and CA1a cells. For (A)–(F), gray corresponds to 10A and black to CA1A. (A) CT absolute volumes; (B) CT volumes as a percent of total nuclear volume; (C) relationship between the total volume of CT and sequence length; (D) relationship between total CT and nuclear volumes; the relationships for 10A and CA1a CT are virtually identical as indicated by the superimposition of the trend lines; (E and F) relationship between sequence length, gene density and radial positioning (% SR), triangle points and the dashed trend line in (E) show random simulation of 10A cells; (G) % SR values for peripheral positions determined experimentally versus random simulation. *P < 0.05, **P = 0.001.

Chromosomal positions based on pairwise center distances versus pairwise border distances

While they provide insight into CT positioning and demonstrate significant levels of nonrandom positioning which is altered in CA1a (Supplementary Material, Figs S1–S4), pairwise center distances (PCDs) do not necessarily determine whether two CT are in close proximity. To directly determine the degree of interactions for each CT pair, we developed algorithms that measure the nearest neighbor distance between every possible CT pair. These distances are termed pairwise border distances (PBDs). Many PCDs do not correspond to their border distances (Supplementary Material, Figs. S3–S4). Thus, CT that may be interacting at their borders will have PCDs that are not only higher but also vary depending on the sizes of the CT and their relative structural orientations to each other (Supplementary Material, Figs. S3–S4). While only 33% of PCDs demonstrated a significant difference from random simulations, ∼90% of the PBDs are significantly different from random simulations at a threshold where virtually none of the random simulation values are significant (Supplementary Material, Table S2, P ≤ 0.01). We conclude that the PBD is the preferred approach to measuring interchromosomal distances. It avoids complications of CT size and orientation differences, directly measures the nearest 3D distances between CT and gives distance values that are predominantly nonrandom.

Pairwise CT interaction profiles of malignant CA1a cells are altered compared with 10A breast epithelial cells

A CT pair can interact once or multiple times (up to four instances, e.g. CT1a-CT2a, 1a-2b, 1b-2a and 1b-2b). We initially determined the percentage of cells that contain at least one interaction based on the PBD measurements. PBDs ≤4 pixels or ≤0.28 µm were scored as ‘interacting chromosomes’. At this threshold, ∼90% of the values were ‘zero pixels’ and virtually all of those showed potential overlap between the two CT. The degree of overlap based on the percent nuclear volume (0.10–0.60%) was similar to a previous report (32) and averaged ∼15% of the total volume of each interacting CT. The degree of overlap between CT that we measured in our study, however, is inconclusive based on the limited resolution of our microscopic images and will require further study. The % associations were then plotted for each of the 36 pairwise combinations of heterologous CT (Fig. 4A).

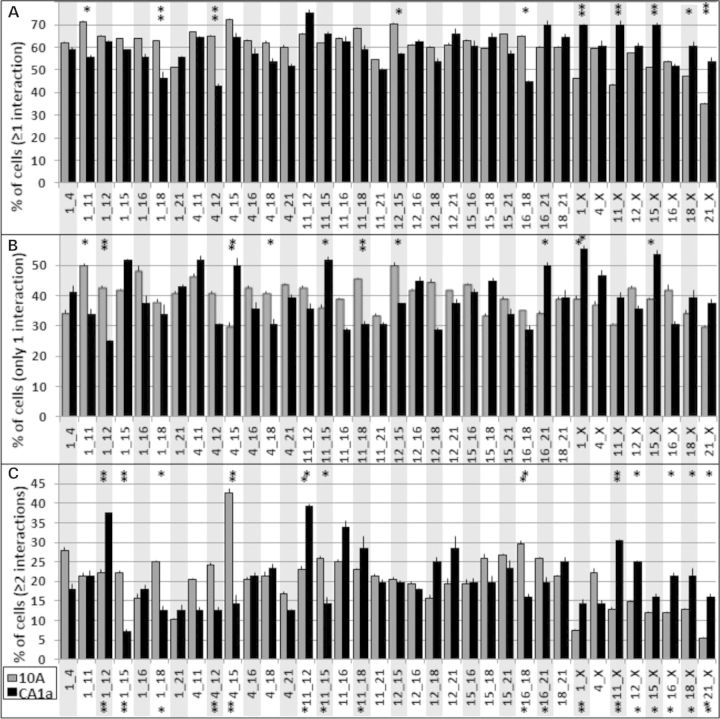
Figure 4.

Interaction profiles of CT in 10A and CA1a cells. Since each CT has two homologs, there are four possible interactions in each nucleus. The percent of cells with at least one interaction (A), percent of cells with only one interaction (B) and the percent of cells that have two or more interactions (C) are shown. 10A (gray bars), n = 108; CA1a (black bars), n = 56; error bars = SEM. Fishers exact test demonstrated significant alterations in ≥1, = 1, ≥2, and = 1 and ≥2 together. *P < 0.1, **P < 0.05.

Examination of the overall profiles revealed major differences in 10A versus CA1a (χ², P < 0.001). Of the 36 different pairwise interactions, 19 showed >10% differences between 10 and CA1a (Fig. 4A) and 33 were significantly greater than random simulations in both 10 and CA1a (Fishers exact test, P < 0.001, Supplementary Material, Figs S5 and S6). In contrast to experimental values, the levels of interaction in random simulations were size dependent (Supplementary Material, Fig. S7). Homologous CT interactions (Supplementary Material, Fig. S8) were lower than heterologous interactions and remained among the lowest interacting CT when corrected for the one possible homologous interaction compared with the four for heterologous interactions (Supplementary Material, Fig. S8).

Multiple interactions among CT pairs are altered in the malignant CA1a cells

We found that every CT homolog interacts with at least one of the other eight CT in 90–100% of the cells (Supplementary Material, Fig. S9). On average, each CT homolog interacts with ∼3.5 out of the 16 possible other heterologs (Fig. 5A). All CT have similar levels of interaction independent of their size with the exception of CT Xi. Despite being similar in volume to CT 16 and 21 (Fig. 3A and B), the inactive CT Xi interacts with much fewer CT in 10A (Fig. 5A; Supplementary Material, Fig. S9A). In CA1a, however, CT Xi is no longer the lowest interacting CT heterolog (Fig. 5A; Supplementary Material, Fig. S9B). Importantly, this increase in interaction for CT Xi is independent of radial positioning since CT Xi does not change its radial position (Fig. 3E–G) and is independent of volume since we determine no increase in interactions within simulations (Fig. 5B; Supplementary Material, Fig. S5). All CT pairs have significantly higher levels of interaction than random simulations (Student’s test, P < 0.001).

Figure 5.

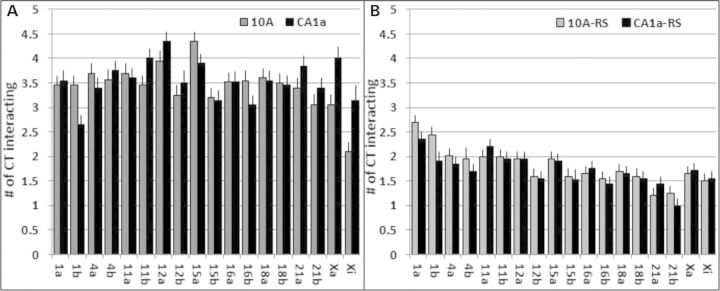
Total CT interactions. Within each nucleus, the larger homolog was designated ‘a’ and the smaller homolog was ‘b’. The total number of interactions to each CT was calculated. The average number of CT interactions is shown for experimental (A) and random simulations (B). All experimental values were significant higher than random simulations (t-test, P < 0.001). Values of 10A cells are in gray and CA1a in black.

Next we generated pairwise association profiles involving two or more interactions (Fig. 4C). The profile of CA1a was strikingly altered from 10A (χ², P < 0.001) with 26 of the 36 heterologous pairs changing by >10%. While single interactions are more prevalent than multiples, 12–60% of cells that have an interaction have multiple interactions (Fig. 4A and C). In contrast, there were lower levels of multiple interactions (1–14%) in random simulations (Supplementary Material, Fig. S5C). Of the 36 pairwise combinations, four were altered in the percent of cells with only one interaction and six were altered in the percent of cells with ≥2 interactions (Fishers exact test, P < 0.05; Fig. 4B). None were significantly different between random simulations of 10A and CA1a (Supplementary Material, Fig. S5). When considering both 1 and ≥2 together, seven pairwise CT interaction profiles were significantly altered from 10A to CA1a (Fig. 4C).

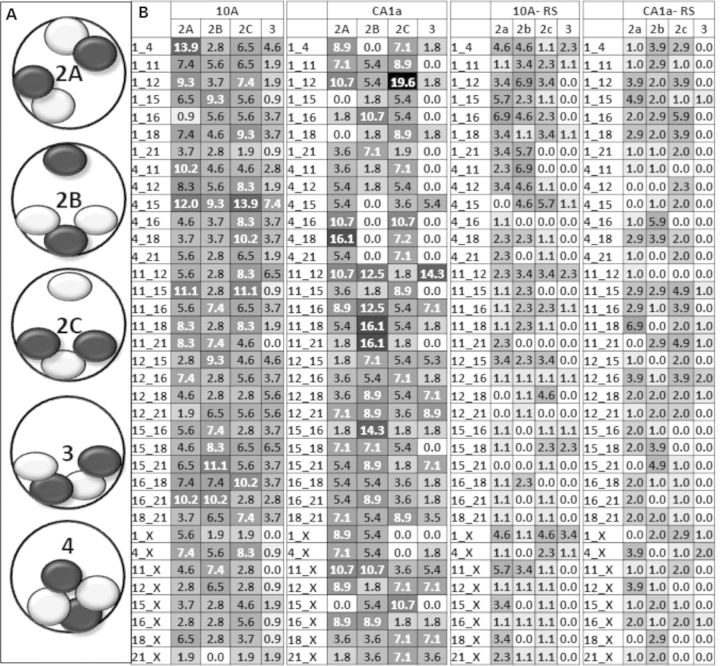
Analysis of multiple interactions of individual CT pairs, revealed three distinct configurations involving two interactions (patterns 2a, 2b and 2c, Fig. 6A). In pattern 2a, one copy of each CT forms an independent pairwise interaction with its heterologous partner CT. In pattern 2b, a triplet is formed involving one copy of one CT and two copies of the other heterologous CT (Fig. 6A). In pattern 2c, the opposite triplet is formed (Fig. 6A). For three interactions among a heterologous CT pair, all four CT form an alternating chain of CT (Fig. 6A). Four interactions can only occur when all four homologs of the two chromosomes are in close apposition (Fig. 6A). The great majority of these multiple associations involve two interactions with a smaller amount of three interactions (Fig. 6B). Four interactions are found in only trace amounts (< 2% of the cell population) or are nonexistent.

Figure 6.

Patterns of multiple interactions of CT pairs. (A) Categories of multiple interactions of CT pairs for 2, 3 and 4 interactions are illustrated; (B) the percent of total cells that have type 2a, 2b and 3 interactions were calculated and are shown for 10A, CA1a, and their corresponding random simulations (RS). Type 4 interactions were extremely rare (0–2%) and are not shown. Values are shaded in grayscale from white (low) to black (high) levels, gray are intermediate values. The top 15% of values are written in white type. None of the random simulations values were in the top 15%.

The patterns of these multiple associations change from 10A to CA1a as demonstrated in Figure 6B where the patterns of hotspots (black) and coldspots (white) are very different. Some pairwise combinations of CT are equally distributed between these patterns (e.g. CT4–15 in 10A), while others are present almost entirely in one configuration (e.g. CT11–21 in CA1a). Random simulations contain only low–to-moderate levels of each pattern (Fig. 6B).

Further comparison of 10A to CA1a revealed five different types of altered interaction profiles. Type 1 exhibits an overall increase in both single (1) and multiple (≥2) interactions, whereas type 2 alterations show an overall decrease in both 1 and ≥2. Types 3 and 4 demonstrate a switch from single to multiple associations or vice versa and type 5 represents those CT pairs that do not change in interaction from 10A to the malignant CA1a cells. The top four alterations for each type are presented in Table 1. Among the top four type 1 alterations, CTX was a member of each pair. CT12 was a member of each pair in type 3 and CT15 was a member of each pair in type 4. The presence of pairwise interactions within each of these types was independent of size. For example, CTX increased in interaction with CT1 and CT21, whereas CT12 switches from having more nuclei with a single interaction to multiple interactions with both CT1 and CT18 (Table 1; Supplementary Material, Table S3).

Table 1.

Five types of changes in CT interaction profiles

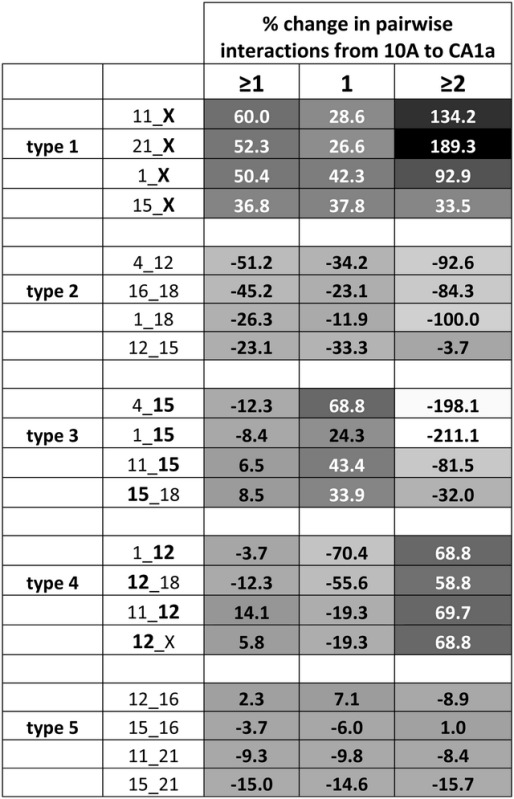Calculation of the percent difference in the level of interaction between pairwise CT reveals five types of altered CT interaction. Type 1 alterations demonstrate an overall increase in interaction, whereas type 2 have an overall decrease in interaction. Type 3 switches from having greater levels with a singular interaction to those with more nuclei with multiple interactions. Type 4 switch from having more nuclei with multiple interactions to more with singular interactions. Type 5 do not change significantly in interaction. The top 4 pairwise CT interactions from each type are presented. Values are shaded in grayscale from low (white) to high (black). The top third of values are written in white.

Microarray analysis demonstrates large changes in expression on CT

Microarray analysis (37), for the nine interacting chromosomes demonstrated alterations in gene expression in malignant CA1a compared with 10A breast cells. The percent of genes on each chromosome that are either up- or downregulated was calculated based on a 4-fold difference (Table 2). Higher amounts of downregulated genes relative to upregulated genes (18–45%) were found on all the chromosomes studied except CT4 and CTX. CTX had an unusually large increase in upregulated genes (67.5%), whereas CT4 was only slightly increased (7.7%). This relationship was maintained over a wide range of thresholds (i.e. 2- to 50-fold).

Table 2.

Chromosomes have altered levels of gene expression in malignant CA1a

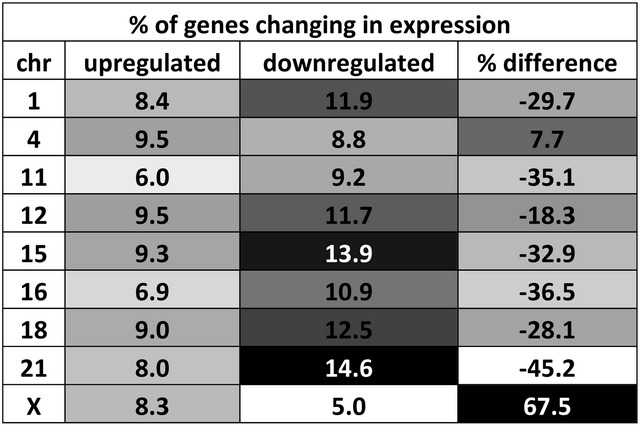The percent of genes that are up- and downregulated >4-fold are shown. The percent difference between up- and downregulation was also calculated. Values are shaded in grayscale from low (white) to high (black). The top 15% are written in white.

The preferred probabilistic model of CT interactions is altered in malignant CA1a

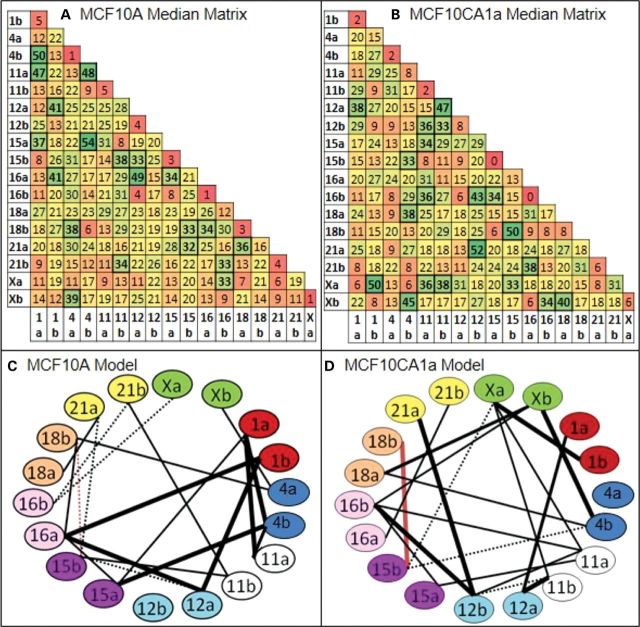
The striking differences in the profiles of CT interactions between 10A and CA1a suggested a reorganization of interchromosomal positioning on a global scale. To investigate this further, we used an algorithm termed the ‘chromatic median’ which is designed to determine the overall pattern of CT interactions across the population of cells. This program determines the corresponding homologs across all cells based upon the homolog's interactions with all other individual heterologs under investigation and switches the ‘a’ and ‘b’ labels for homologs based on its interactions with other CT (see Supplementary Material, Methods and Fig. S10). Subsequently, we determine the percent of cells that contain an interaction for each of the 153 positions in the matrices. Within these resulting median matrices, we found hot and cold spots that range from 0 to 54% of input cells (Fig. 7A and B). Random simulations were devoid of hotspots and had a lower range of values with the higher values preferentially found in interactions involving the larger CT (Supplementary Material, Figs S11A and B, S12–S13).

Figure 7.

Chromatic median analysis and preferred probabilistic models of chromosome interactions in 10A and CA1a. The chromatic median algorithm determines correspondence between homologs across nuclei based upon which other CT it interacts (see Supplementary Material, Fig. S10). This algorithm determined a median matrix for CT interactions in MCF10A (A) and MCF10CA1a (B) in which each cell in the matrix represents the percent of input nuclei that have an interaction between those homologs. Hot spots are green, cold spots are red and yellow spots are intermediate values. Thresholding of the 10A and CA1a matrices above a level of 32% interactions reveals 20 CT interactions in both 10A (C) and malignant CA1a (D). Thirty-two percent is the threshold level where there are no connections in randomizations of input matrices or random simulations (Supplementary Material, Fig. S11). A comparison of the models generated from this analysis indicates massive differences between 10A and CA1a. Nineteen of the 20 preferred pairwise associations were unique to both10A and CA1a (black lines) with only one pairwise association in common (CT 15b–18b, red line). Thick connections are within the top third of percent pairwise associations within the model while dashed connections are within the bottom third. Any given nucleus will contain an average of 39.2% (10A) and 39.4% (CA1a) of the connections within these models (41).

To determine a preferred probabilistic model of CT interactions, thresholding was performed on the matrices at 32% association. This enriched for the CT interactions found at the higher levels among the total population. Moreover at 32%, there are no connections in randomizations of input matrices or random simulations (Supplementary Material, Fig. S11). A network of 20 CT interactions were identified in both 10A (Fig. 7C) and CA1a (Fig. 7D). The interacting network was nearly completely altered in malignant CA1a with only one shared connection (15b–18b, red line, Fig. 7C and D) and the rest unique to 10A or CA1a (black lines). Sorenson's analysis (41) revealed that each individual nucleus in the population analyzed contains on average ∼40% of the network connections displayed in these probabilistic models.

Since random simulations had lower levels of interaction than experimental (Supplementary Material, Fig. S5), we determine whether the high level of interactions in the experimental data falsely lead to a model of nonrandom instead of random interactions. The range of values for randomized matrices was ∼3-fold lower than experimental values (12–31%, Supplementary Material, Figs S11–S13). This demonstrated that the process of determining corresponding homologs in a cell population with a high degree of close proximity of CT does not artificially create a nonrandom pattern of those interactions.

DISCUSSION

Major landmarks of cancer cells are alterations in nuclear shape, size and the morphological patterns of chromatin (42–44). Other studies have focused on molecular alterations in chromatin, the nuclear matrix and other nuclear components (3,42–46). Despite this progress, our understanding of the role of nuclear organization in cancer is still in its infancy. Recent studies suggest that long-range interchromosomal interactions can occur in a transcription-dependent manner to regulate gene expression (47–50). The spatial positioning of the CT, their interchromosomal associations and the resulting influence on gene regulation, however, are less clear (1–8,51–53). Indeed, only a very limited number of investigations have determined whether there are preferred chromosome-to-chromosome positional interactions (22,25,26,28,54).

With this as a basis, we examined the CT spatial positioning and interchromosomal associations in malignant breast cancer cells compared with its normal breast cell counterpart. ReFISH (25) was used to concurrently label nine CT (1, 4, 11, 12, 15, 16, 18, 21 and X) in human breast MCF10A (10A) and malignant MCF10CA1a (CA1a) cells. An integrated suite of in-house developed software (25,55) and a new 3D distance measurement program termed eFISHent was then applied to the collected images to generate an extensive database of distance measurements. A new data mining and pattern recognition algorithm termed the chromatic median (38) was then applied to determine whether there is an overall preferential organization of the CT associations in the cell nucleus of the 10A cells and if those interchromosomal positions change in the malignant CA1a cells.

Radial positioning of chromosome territories and volume relationships

The most studied property of CT is radial positioning (for review, see Cremer and Cremer (19)). Nonrandom radial positioning of genes and CT within the nucleus have been implicated in expression with highly expressed genes generally found more internal than inactive genes (56–62), although one recent investigation reported repositioning of genes independent of expression (63). At a global level, heterochromatin is found preferentially at the nuclear periphery (64–66). The inverse relationship between gene activity and heterochromatin may be the basis for the positioning of the active CTXa in more interior regions of the nucleus compared with the inactive CTXi (67,68) which in some cell lines is found as a compact Barr body along the nuclear periphery (69). Similarly, the gene poor CT18 is more compact (70) and positioned more peripherally than the gene rich CT19 (8,71,72).

The major contributing factors involved in peripheral positioning of CT are posited to be size (21,25,26,73), gene density (72,74) or both these properties (75). Differences in the nuclear shape of cells may also play a role in CT radial positioning (21,24). Furthermore, the nuclear envelope (76), evolutionary conservation (77,78), nuclear myosin (79) and nucleolar association (17,21,75) have all been implicated as contributing to the radial positioning of CT.

Expanding this analysis to a subset of nine CT pairs, we report that the radial positioning of CT in both 10A and CA1a cells are correlated with chromosome size and not gene density (Fig. 3). Moreover, we measured a significant increase in the peripheral positioning for five of these CT in the malignant CA1a cells. Importantly, random simulations demonstrated that alterations in nuclear shape or CT volume do not account for these changes in radial positioning.

Previous studies demonstrated that increases in nuclear volume coincides with increases in overall cell volumes (80) and increased gene expression (81,82) in normal cells. Other reports have shown that this relationship may be compromised in certain cancer types (83). Our analysis of both CT and nuclear volumes has revealed a direct relationship of CT volume to total nuclear volume in both 10A and CA1a cells. This could be important for gene expression at the level of the CT. For example, the active CTXa is larger than the inactive CTXi, but become similar in volume upon the inhibition of transcription (84).

Although the nuclear and CT absolute volumes in CA1a are larger than in 10A cells, the CT volumes are similar when expressed as the % of nuclear volume. The one exception is CTX which shows a significantly increase based on % of nuclear volume in CA1a compared with 10A cells. Correlating with this increased volume is a corresponding increase in overall gene expression for CTX in CA1a. In contrast, the eight other chromosomes studied in CA1a are either downregulated or show no significant increase in overall gene expression.

Alterations of interchromosomal positioning in CA1a malignant cells

Previous studies of interchromosomal associations based on measurements of the nearest edge-to-edge distances (PBDs) between individual CT have suggested an overall nonrandom nature of these interactions (25,26,28,54,85). In one study based on center to center measurements (PCDs), it was concluded that only a very limited number of the measured pairwise CT associations were significantly nonrandom (21). While studies which relied on center-to-center distance measurements between CT pairs provide some basic insight into the probabilistic nature of CT organization, they may not accurately reflect how close CT pairs actually interact. For example, we find that only one-third of CT centers (PCDs) are significantly different from random simulations compared with >90% for PBDs. Moreover, those individual CT pairs that are in close proximity based on PBD measurements have vastly different PCDs (Supplementary Material, Fig. S3).

Our eFISHnet programs have elucidated the levels of multiple interchromosomal interactions for each chromosome under investigation and demonstrate that multiple associations are common with an average of 3.5 interactions out of a maximum of 16 for each CT copy or 20–25% of the other CT copies. This extrapolates to ∼10 interactions per chromosome and >400 total interchromosomal interactions at the whole-genome level. The levels of these interactions are similar in all the CT in both 10A and CA1a cells except for CTXi and Xa which show lower amounts in 10A (∼2.2 and 3.2 interactions, respectively) but increase significantly in CA1a (3.3 and 4.0 interactions, respectively). Correlated with the increased level of CTX interactions in CA1a is an overall increase in upregulated genes for CTX. Previous studies have demonstrated defects in X inactivation in cancer cells (86). Our results further demonstrate an increase in interchromosomal interactions for CTX which correlate with an overall increase in CTX gene expression.

Using our PBD measurements, major alterations from 10A to CA1a were detected in the pairwise interaction profiles based on at least one, only one or two or more associations. We identified five types of altered interaction profiles (overall increase, overall decrease, switching from 1 to ≥2, vice versa or no change). Certain CT were found more often within a particular type. CTX, for example, not only increases in volume and overall expression, but also in its interactions with seven of eight of the other CT in the CA1a cells. CT15 was among the top 4 that decreased in singular interactions while simultaneously increasing in multiple interactions (type 3, Table 1). Conversely, CT12 increased in singular interactions and decreased in multiples (type 4, Table 1).

We are particularly interested in how the overall pattern of interactions is altered across MCF10 cancer progression. Interactions between CT have been shown to be critical in the development of cancer as CT in closer proximity in normal cells have greater frequencies of translocation (27,28,85). Chromosomes involved in translocations (CT12,14,15) in murine lymphoma AT-13 cells (t12:14 and t14:15) form a preferential cluster in normal splenocyte cells (28). Furthermore, the two translocated heterologs (t12:14 and t14:15) pair with higher frequency in the cancer cells than the normal heterologous pairing of CT12-CT14 or t12:14-CT12 (28). We now report that changes in CT clusters in cancer cells are not limited to translocated chromosomes. For example, the high-frequency CT1–4–11 cluster of 10A cells is no longer a top cluster in malignant CA1a, whereas CT16–12–21 is now found at high levels (Fig. 7).

The specific patterns of pairwise associations of CT and their striking alterations in CA1a are consistent with a preferred overall arrangement of the entire subset of CT as well as major differences between 10A and the malignant CA1a cells. We, therefore, applied a novel computational data mining and pattern recognition approach termed the chromatic median to identify overall patterns of global interactions. Not only were highly preferred and probabilistic models of interchromosomal networks identified, but the network organization was profoundly altered in the malignant CA1a breast cancer cells. Only 1 of 20 connections was shared between the 10A and CA1a overall interactive networks (Fig. 7).

Our findings support the presence of a higher order probabilistic chromosome code or network of CT interactions inside the cell nucleus (25,26). It is further proposed that the preferred interchromosomal association network defined by this code is maintained epigenetically and facilitates specific genomic expression programs characteristic of the particular cell. Superimposed on this core preferred network are additional less preferred CT interactions that number in the 100s at the whole-genome level. The probabilistic nature of the overall interactive network could in turn provide flexibility for alterations in the network and contribute to corresponding changes in the overall genomic program. Consistent with this view, gene expression is significantly altered in the CA1a cells (37) as well as in numerous other cancer cells (87,88). Moreover, altered interchromosomal interactions were detected between the IGFBP₃ gene and several other genes in breast cancer versus normal breast cells (46). Further studies using the recently developed Hi-C approach for studying interchromosomal interactions at the genomic level in both cell populations and at the single-cell level (89,90) should enable definition of the many alterations in chromosomal interactions that likely lie at the basis of the malignant state of cancer cells.

METHODS AND MATERIALS

Cell culture

MCF10A and MCF10CA1a cells (Barbara Ann Karamanos Cancer Institute, Detroit, MI) were grown in DMEM/F-10 media supplemented with 5% horse serum, 2% insulin, EGF, hydrocortisone, cholera enterotoxin and 1% penicillin/streptomycin. MCF10CA1a was cultured in DEME/F-10 media with 5% horse serum and 1% penicillin/streptomycin. All cell lines were grown at 37°C in a 5% CO₂ incubator.

Three-dimensional FISH and re-FISH

Up to 10 different CT pairs in a given nucleus were analyzed by repetitive CT FISH labeling, image collection, stripping and re-FISH as previously described (25). Briefly, cells are fixed with 4% paraformaldehyde, treated with 100 mm glycine, 0.5% Triton X-100 for 25 min, 20% glycerol (overnight), four freeze–thaw cycles in liquid N₂, 0.1 N HCl for 5 min, stored in 50% formamide/2× SSC (overnight), denatured in 70% formamide/2×` SSC at 75°C and immediately transferred to 50% formamide/2× SSC on ice. Chromosome paints (Chrombios, Germany) were prepared and denatured for 10 min prior to hybridization at 37°C for 48 h. Three posthybridization washes consisted of: (i) 50% formamide/2 SSC/0.05% Tween-20, (ii) 2× SSC/0.05% Tween-20 and (iii) 1× SSC for 30 min each at 37°C. Cover slips were then mounted in Vectashield. Following image collection, chromosome paints were stripped by immersion of the cover slips in 50% formamide/2× SSC for 35–40 s at 75°C. Another pair of denatured chromosome paint probes were then immediately added to cells and hybridized at 37°C for 48 h.

3D microscopy and image analysis

Images were collected on an Olympus BX51 fluorescence microscope equipped with a Sensicam QE (Cooke Corporation, Romulus, MI, USA) digital CCD camera, motorized z-axis controller (Prior, Rockland, MA, USA) and Slidebook 4.0 software (Intelligent Imaging Innovations, Denver, CO, USA). Three-dimensional z stacks (0.5 µm intervals) of three or four CT per in situ hybridization were collected and deconvolved with a NoNeighbor algorithm in Slidebook 4. Nuclei from each labeling were aligned using registration software developed in our laboratory by selecting one-to-one matching features between control points from corresponding optical sections of phase contrast images (25,55) and with ImageJ's translation function. Comparison of x, y, z coordinates of landmark refractile structures in corresponding phase contrast allows two different sets of images of the same nucleus to be combined into a single image. Accuracy of matching was then tested by merging of DAPI images from different rounds followed by ImageJ's line profile tool.

The CT were segmented into binary images using ImageJ's threshold feature. Three different steps are used in sequence to distinguish between signal and noise and thus determine the most accurate thresholding for each image set. (i) The threshold values are first determined by algorithms that process the intensity histograms using ImageJ threshold reference isodata. (ii) The CT borders at the thresholds selected in (i) undergo user examination at thresholds above and below to validate that the most appropriate threshold was selected. (iii) The selected threshold is decreased until background is excluded and the optimal threshold is reached [as described in 91]. Approximately 90% of the time no adjustment of the thresholds established in step (i) are required in step (ii) and/or (iii). All three of these criteria result in nearly identical selection of chromosome signals into binary segmented images.

In an effort to maximize efficiency in measuring many parameters within each nucleus, we developed a program termed eFISHent. Given an input of objects of interest (in this case, the segmented nucleus and chromosomes from above), this program reconstructs their 3D shapes based on well-known region labeling algorithms to determine the boundary of each CT (92). The eFISHent program then measures in 3D a large number of parameters including: their volumes, volume overlap between interacting CT, minimal border-to-border distances (PBDs), distances between centers of gravity (PCDs), distances between peripheries and centers (PBCDs), the distance of the line projecting from the nuclear center through the center of the chromosome/gene to the nuclear periphery (subtended radii, SR), minimal peripheral distance (MPD) to the nuclear periphery, centroid xyz coordinates and major and minor axes. This program is versatile since it will measure all of these values for any given amount of input objects simultaneously. For example, with nine chromosomes labeled, as in this study, it will measure the 18 homologs' volumes, the nuclear volume, 432 pairwise heterologous distances (144 PBDs, 144 PCDs and 144 PBCDs), 27 homologous distances (nine PBDs, nine PCDs and nine PBCDs), 18 SR, 18 MPDs, 19 centroid coordinates and 38 major/minor axes. For validation, we simulated data of known distances and found that our program accurately measures all distance combinations. We also used conventional measurement techniques in imageJ to validate distance measurements made by eFISHent in experimental FISH between BAC probe labeling.

Since the volume determination of each homolog in a CT pair are never exactly the same, this program enables us to distinguish ‘homolog a’ as having a larger volume than ‘homolog b’. This results in four pairwise distances for each CT (e.g. 1a–4a, 1a-4b, 1b-4a and 1b-4b). Any given nucleus, therefore, will have between 0 and 4 associations for each CT pair. From this data, the percentages of pairwise associations based on PBD measurements were calculated using a threshold distance of ≤4 pixels or ≤0.28 µm as the minimal nearest 3D distance for a ‘positive interaction’ (25). ∼90% of these values for each chromosome pair were ‘zero’ pixel values. We subsequently found that all the zero pixel values represented a degree of overlap or co-localization between the two CT under measurement (data not shown). Thus, the four pixel threshold used in these studies for nearest neighbor CT pairs is indicative of interchromosomal interactions and not simply the close proximity of CT.

Random simulation of nuclei and CT

While many simulations are done using an artificial nucleus and preset volumes run many times (25), to more accurately mimic the experimental conditions, we have simulated the precise nuclear and CT volumes for each image set. All images from each given nucleus are contained within its own separate folder. The simulation program reads the volumes of the CT within each CT image, selects a point at random from within the DAPI mask and grows asymmetrically from that point until the volume of the CT is reached. If a CT reaches the nuclear border it no longer grows in that direction—ensuring that all simulated CT are within the nucleus.

Chromatic median analysis and modeling CT associations

Previously an algorithm called the generalized median graph (GMG) was developed to determine the probabilistic best-fit model for global interactions of chromosome in the Go stage of WI38 human fibroblasts (25,26,93). The GMG considered all possible association matrices (i.e. all permutations of the association graphs) and simultaneously optimizes the associations of all CT under consideration. To tackle a larger population of cells with more CT and enhance the theoretical guarantee of the quality of the solution, we have developed a new algorithmic technique termed the chromatic median or CM which uses combinatorial optimization to infer the common chromosome interaction pattern or network for the overall cell population (38). Due to the computational intractability of the common pattern-finding problem, we developed several approximation algorithms. While the GMG used integer linear programming and rounding techniques, the CM is more accurate and robust. It is based on a number of new techniques, such as semi-definite programming, multilevel rounding, geometric peeling and adaptive sampling (94,95). The CM technique results in much better approximation ratios and yields near optimal solutions in all tested random or real datasets (38).

Details of the CM technique and its mathematical basis are presented elsewhere (38). In brief, this approach represents each nucleus as an 18 × 18 (nine CT for this study, two homologs per CT) binary matrix wherein a value of 1 indicates an interaction and a value of 0 indicates the absence of an interaction. This is illustrated in Supplementary Material, Figure S10. The objective is to find the best permutation (relabeling from ‘a’ to ‘b’ and vice versa for all chromosome pairs within each nucleus) which will align the association matrix of each input cell with that of the common pattern. The new CM algorithm considers all possible permutations of the interactions and simultaneously optimizes the interactions of all pairs of heterologs and homologs. For example, if there is a high frequency of nuclei wherein one homolog of CT1 associates with CT4, 11, 12, whereas the other homolog associates with CT16, 17 and 18, it will classify the first as CT1a and the second as CT1b across all cells. This process is done simultaneously for all CT studied to maximize similarity across the population. The number of input cells which have an interaction is then determined for each of the possible pairwise combinations.

After permutation analysis, the CM gives an output matrix which lists the percent of cells that have that given interaction. Using excel's conditional formatting, each interaction is filled with a color ranging from green (high/hot spots) to red (low/cold spots). Yellow indicates moderate values. After setting a threshold for interactions, probabilistic models are generated of preferred CT interactions among the entire subset of CT. A simple example of this process is illustrated in Supplementary Material, Figure S10. An extensive empirical comparison on both random and real datasets with various data sizes shows that the CM algorithm results in an improvement of ∼30% (measured using the Jaccard similarity (38,96,97) and 13% (measured using the Sorrenson similarity (41) over previously developed programs.

SUPPLEMENTARY MATERIAL

Supplementary Material is available at HMG online.

FUNDING

This research was supported by grants from the National Instititutes of Health (GM-072131) to R.B., the National Science Foundation (IIS-0713489 and IIS-1115220) to J.X. and R.B. and the University at Buffalo Foundation (9351115726) to R.B.