Reusing Cadaveric Humeri for Fracture Testing After Testing Simulated Rotator Cuff Tendon Repairs

Abstract

The financial cost of using human tissues in biomedical testing and surgical reconstruction is predicted to increase at a rate that is disproportionately greater than other materials used in biomechanical testing. Our first hypothesis is that cadaveric proximal humeri that had undergone monotonic failure testing of simulated rotator cuff repairs would not differ in ultimate fracture loads or in energy absorbed to fracture when compared to controls (i.e., bones without cuff repairs). Our second hypothesis is that there can be substantial cost savings if these cadaveric proximal humeri, with simulated cuff repairs, can be re-used for fracture testing. Results of fracture tests (conducted in a backwards fall configuration) and cost analysis support both hypotheses. Hence, the bones that had undergone monotonic failure tests of various rotator cuff repair techniques can be re-used in fracture tests because their load-carrying capacity is not significantly reduced.

Introduction

The burgeoning use of human tissues in biomedical testing and surgical reconstruction is predicted to continue to increase their cost at a rate that that is disproportionately greater than other materials used in biomechanical testing.^1–10 Our first hypothesis is that cadaveric proximal humeri that had undergone monotonic failure testing of rotator cuff repairs would not differ in ultimate fracture loads or in energy absorbed to fracture when compared with controls. Our second hypothesis is that there can be substantial cost savings if these cadaveric proximal humeri can be reused without significantly impacting the data obtained from subsequent fracture tests.

To test these hypotheses, we used cadaver proximal humeri from middle-aged and elderly cadavers that were used previously in strength testing of repairs of simulated full-thickness supraspinatus tendon tears.^11,12 We also analyzed the data to determine potential influences of: (1) proximal humerus density and volume, (2) fracture patterns, and (3) the proximity of fracture surfaces to the drill holes of the tendon repairs. The cost savings analysis was based on currently available prices of synthetic bones and cadaver bones.

Methods

Specimens and preparation

With IRB approval from our institution, thirty-two fresh-frozen cadaver shoulders (mean age 60 years, range 42–78, 18 female and 14 male) were separated into four groups: group 1, control bones with no cuff repairs (n=8); group 2, transosseous suture-only repair (n=6); group 3, single-row anchor-only repair (n=6); and group 4, quasi double-row using TOAK repairs (n=12) that combined the techniques used in groups 2 and 3: transosseous sutures laterally and Mitek™ metal or Panalock™ bioabsorbable suture anchors medially (DePuy Mitek, a Johnson and Johnson company, Norwood, MA)¹² (Fig. 1). These double-row repairs are referred to as TOAK (transosseous anchor double knot) (Fig. 1)^11,12 repairs, which resemble other “suture bridge” methods.^13,14 There were no specimens with naturally occurring rotator cuff tears, arthritis, or gross pathology.

FIG. 1.

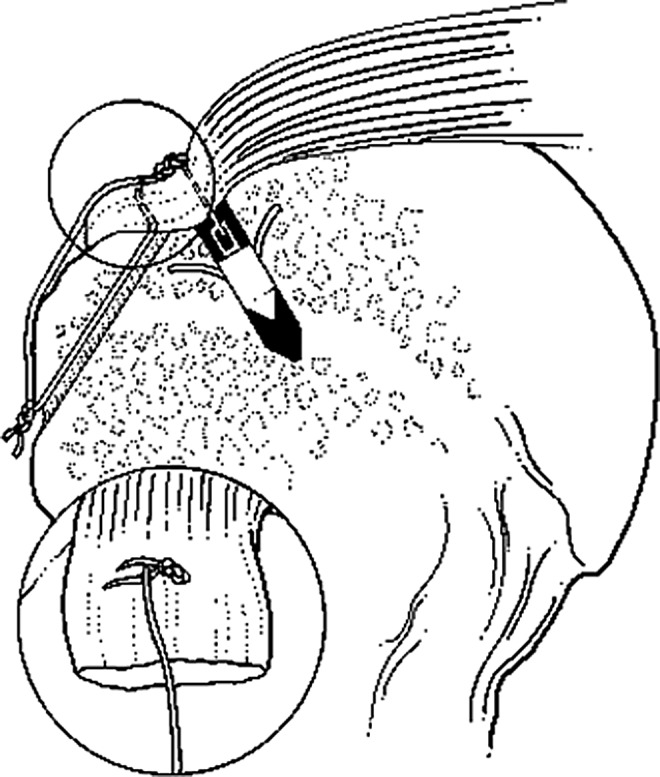
Transosseous anchor double knot (TOAK) fixation. This construct is effectively a quasi double-row repair with a suture bridge. The inset drawing shows the superficial suture of the trans-osseous component of the TOAK construct. A metal anchor is depicted in this illustration.

For each group, all of the soft tissues of the shoulder were removed except the supraspinatus tendon and muscle. In order to simulate a repair, the supraspinatus was reattached to the bones in groups 2–4. A burr was used to make a shallow, broad, roughened area (12–14 mm wide) that slightly exposed cortical bone porosity. The roughened area extended from the bicipital groove to 30 mm in the posterior direction. The detached supraspinatus tendon of each bone was then reattached using one of the three techniques.¹²

Repair of cuff tear

A 2.9-mm drill bit was used for anchor insertion near the original bone–cartilage junction; a 1.5-mm drill bit was used for the transosseous holes. Three transosseous tunnels (10 mm apart on center), had been made in the specimens for group 2, three suture anchors (10 mm apart on center) in group 3, and three transosseous tunnels combined with three suture anchors (TOAK technique, also 10 mm apart on center) in group 4. The repaired supraspinatus tendons were then tested to ultimate failure at a slow rate of loading (6 mm/min), which simulated activities during active-assisted motion during early post-operative rehabilitation.^11,12

Bone density and volume analysis

Prior to testing, a simple radiographic densitometry method was used to help detect between-group differences in the mineral content of each specimen.¹¹ This method provided a bone density score based on X-ray density (expressed in mm of aluminum [mmAl]) of the central portion of the humeral head divided by the anterior–posterior diameter of the head (as seen in anteriorposterior radiographs). This method evaluated the central portion (10 mm×10 mm) of the humeral head, where age-related osteopenia first becomes apparent in radiographs.^15,16 Using digitized X-rays, density of the bone regions and mmAl were expressed as mean gray levels using described methods.¹⁷

Dual-energy X-ray absorptiometry (DEXA) measurements (QDR-2000 Plus; Hologic Inc., Waltham, MA) were made to assess bone mineral content (BMD, g/cm²) of the entire proximal humerus (the entire head and including the upper 2 cm of the metaphysis/diaphysis).¹⁸ The volume of each proximal humerus (entire head and upper 2 cm of metaphysis/diaphysis) was determined by water displacement in a graduated cylinder (precision error±0.5 cm³). Whole-bone (“bulk”) density was calculated as the total grams of the area scanned in the DEXA analyses divided by the submerged volume. The BMD, volume, and bulk density data were incorporated in the statistical analyses in order to assess potential effects of bone size and mass on fracture load data.¹⁹

Fracture testing

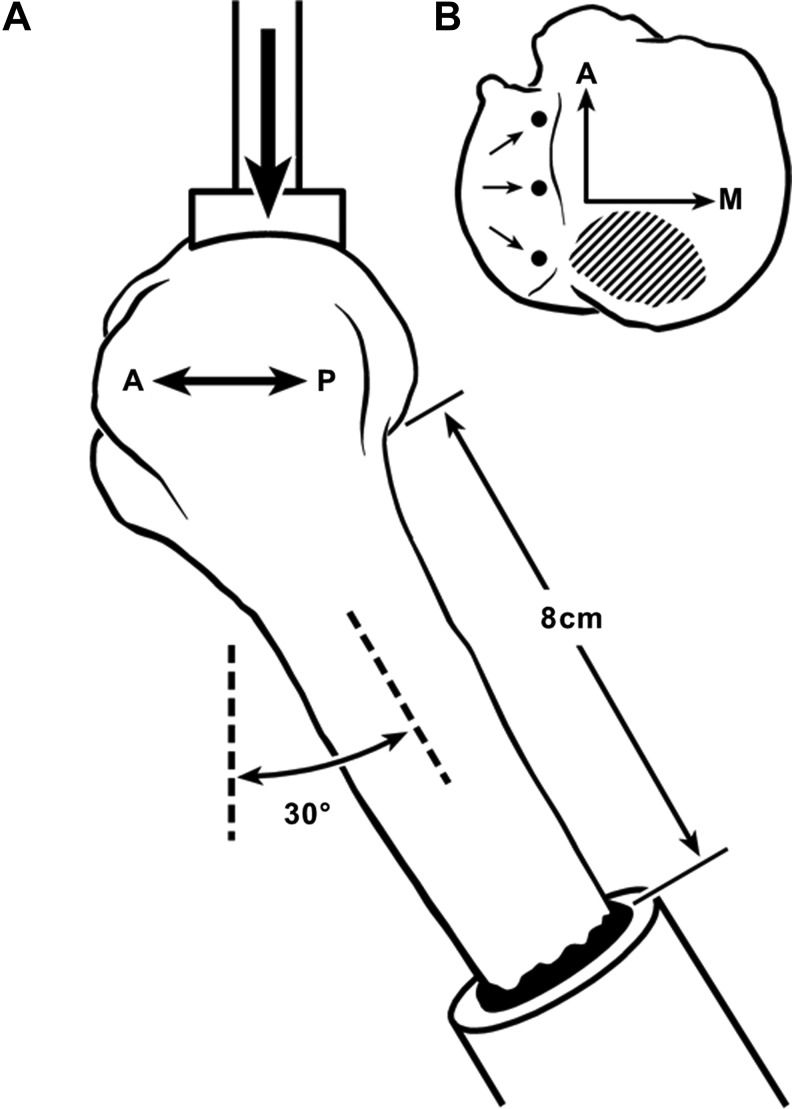
Each proximal humerus was loaded in a manner that simulated a backwards fall on the hand with the arm extended.^20,21 The fracture load was applied with a dish-like stainless steel device (2.5 cm diameter and 6.0 cm radius of curvature) that contacted the posterior-superior humeral head (Fig. 2).²² The perimeter of contact area was 10–15 mm from the posterior drill holes of the repair. Force was applied in displacement control (Bionix 858; MTS Inc., Minneapolis, MN) at a rate of 2 mm/sec until fracture occurred.^23,24 Test data were recorded on load-deformation curves. The parameters analyzed included: (1) ultimate fracture load (N) (i.e., peak of the load-deformation curve); and (2) energy absorbed to peak failure load (N-m) (i.e., area under the load-deformation curve to peak load).

FIG. 2.

(A) Diagram of load orientation; a left humerus is depicted in lateral view. A, anterior; P, posterior. (B) View of the superior humeral head showing location of anchors (medial row) and area where the force was applied to the posterior-superior aspect of the humeral head. A, anterior; M, medial.

Fracture patterns/locations were characterized numerically for statistical analysis: (1) two-part anatomical neck fracture or other two-part (non-neck) without greater tuberosity fracture, (2) greater tuberosity fracture, (3) three-part fracture, (4) four-part fracture, (5) head split fracture, (6) some combination of fracture patterns 1–5 without a greater tuberosity fracture, or (7) some combination of fracture patterns 1–5 with a greater tuberosity fracture.^25,26

Cost benefit analysis

Cost benefit was determined by gathering data on the material cost of synthetic and cadaveric humeri. The cost of additional cleaning, preparation, and storage of the cadaver bones was also considered. Cadaver bone prices were obtained from The National Disease Research Interchange (Philadelphia, PA) and Musculoskeletal Transplant Foundation (Edison, NJ). Synthetic bone prices were obtained from Sawbones (Pacific Research Laboratories, Inc., Vashon, WA; www.sawbones.com/products/productlist.aspx?111; accessed June 2014). The amount of cost savings was calculated as if 24 bones (the number used herein) were purchased. This analysis was also expanded to determine the cost of obtaining 80 bones (40 pairs), which reflects the number we have stored in anticipation that they can be reused in fracture tests.

Statistical analysis

The data were analyzed using commercially available software (NCSS 6.0, Number Cruncher Statistical System™, Kaysville, UT) with normality tests,²⁷ A power analysis performed prior to this study indicated that six specimens in each group provided 80% power (β=0.2) to detect a 600 N reduction in mean fracture load (∼15%) when comparing the cuff repair groups with controls. Differences between mean fracture loads and other parameters of the experimental groups were evaluated using one-way analysis of variance with Fisher's protected least significant difference test. Results are expressed as means plus or minus one standard deviation (SD), and p<0.05 was considered statistically significant.

Results

There were no significant differences measurable between the three cuff-repair groups and the control group in ultimate fracture load (all p-values >0.50) (Table 1). The ultimate fracture load of group 1 was 4176±2003 N, the transosseous suture-only group fractured at 4041±1568 N, which was not significantly different from the single-row anchor-only (3,885±1,170 N) (p=0.9) or quasi double-row TOAK repairs (3,700±1,227 N) (p=0.7). The latter two groups were also not significantly different (p=0.8). Additionally, combined data from both single-row repairs (transosseous-only and anchor-only) versus the quasi double-row repairs showed no statistically significant difference (p=0.6). There were no significant differences in energy absorption (N-m) in all possible comparisons (all p values >0.2).

Table 1.

Group Fracture Data and Other Characteristics

Groupsa	Ultimate fracture loadb(N)	Energy absorbed (N-m)	X-ray density(central head region) (mmAl)	X-ray density scoreb	BMDb(g/cm2)	Proximal humerus volume (cm3)	Bulk density (g/cm3)	Fracture patternc
Group 1 (control, n=8)	4176	10.7	8.0	0.18	0.38	67.7	0.13	1, 2, 5, 6, 6, 6, 7, 7
	(2003)	(7.0)	(2.2)	(0.04)	(0.13)	(16.5)	(0.04)
	866–6853	2.7–21.6	4.9–11.6	0.12–0.25	0.08–0.49	43–89	0.03–0.18
Group 2 (n=6)	4041	11.8	7.3	0.17	0.24	77.8	0.08	1, 1, 1, 1, 3, 7
	(1568)	(8.5)	(1.5)	(0.03)	(0.07)	(22.1)	(0.02)
	2224–6673	3.6–26.3	5.4–8.8	0.13–0.22	0.12–0.31	56–108	0.05–0.12
Group 3 (n=6)	3885	7.7	6.2	0.15	0.27	70.8	0.11	1, 2, 5, 7, 7, 7
	(1170)	(3.4)	(0.8)	(0.02)	(0.06)	(20.2)	(0.03)
	2714–5694	3.9–11.8	5.5–7.4	0.12–0.18	0.19–0.35	55–109	0.07–0.14
Group 4 (n=12)	3700	10.8	6.2	0.14	0.35	86.6	0.12	1, 1, 1, 1, 3, 5, 5, 5, 6, 6, 7, 7
	(1227)	(5.2)	(1.2)	(0.03)	(0.10)	(17.6)	(0.03)
	2091–6183	3.0–18.5	4.6–8.7	0.10–0.19	0.14–0.51	60–118	0.07–0.17

Mean, (standard deviation), and range provided for each category.

^aGroup 1, control bones (no rotator cuff repair); Group 2, transosseous suture-only repair (single row); Group 3, anchor-only repair (single row); Group 4, double-row TOAK repair.

^bFracture load measured in Newtons (N); X-ray density score calculated as [central head density/anteroposterior breadth; (mmAl/mm)] bone mineral density (BMD) from dual-energy X-ray absorptiometry analysis.

^cFracture pattern numerical designation described in methods section. All data are shown for fracture pattern.

There were no age, bone mass, or bone volume differences between the four groups (all p values >0.2). Groups 3 and 4 had an equal number of males and females; in the other groups, group 2 had 4 females and 2 males and group 1 had 5 females and 3 males. None of the fracture lines/surfaces were within 5 mm of the anchor drill holes. However, the fracture surfaces in 3 of 18 (17%) cases were in close proximity or entered the transosseous drill holes.

The fracture patterns are shown in Table 1. Statistical analyses were rerun after omitting the 12 specimens that incurred fracture at a low level of energy. Although statistical power is reduced in these statistical reruns, there were still no significant differences in all comparisons (all p values >0.6). These results show that even though there is a trend toward an increased proportion of the presumably lower energy fracture patterns in the non-control groups (especially in the transosseous group), this did not significantly influence the between-group differences in fracture data.

Cost analysis revealed that the price of a cadaveric humerus is approximately $400 U.S. dollars (USD). Our institutional fees and additional cost of cleaning and storing is approximately $50 USD per bone. When compared with purchasing unused cadaveric humeri, the cost savings would be approximately $450 per bone when reusing our cadaveric humeri. Approximately $11,000 USD would be the total savings when reusing the 24 cadaveric humeri in this study.

The cost of a synthetic humerus (designed for mechanical testing) is nearly $200 USD, which includes our taxes and institutional fees. When compared with purchasing synthetic bones the cost savings when reusing the 24 cadaveric humeri in this study would be nearly $5,000 USD.

Discussion

These results show that there is significant savings when reusing cadaver bones for fracture tests that were initially used for testing rotator cuff repairs at a low rate of loading. Clearly, it would not be possible to achieve this cost savings without first showing that the bones could be reused in failure testing. This was demonstrated by the results showing no significant differences in ultimate failure (fracture) loads or in energy absorbed to ultimate failure between control bones and the other groups.

The substantial cost savings also extends beyond the scope of the tissues used in this study. For example, in our laboratory storage freezer we have an additional 80 humeri that could similarly be reused for fracture testing. The savings from reusing these bones would be approximately $36,000 USD when compared with purchasing unused cadaver bones. The savings would be nearly $16,000 USD when compared with purchasing synthetic bones.

Our review of the English language publications/literature revealed nearly 110 studies in the past 10 years that used cadaveric bones in ways that might allow for their reuse in biomechanical testing. Consequently, the findings of this study can be more broadly generalized because many bioengineering laboratories are faced with the substantial financial cost of allograft tissues. The magnitude of savings when reusing our stored 80 humeri could fund additional laboratory staff, students, and/or equipment. For example, this could fund a biomedical engineering technician position, which according to the U.S. Bureau of Labor Statistics, earn a mean annual wage of approximately $54,000 USD (www.bls.gov/oes/current/oes_nat.htm#17-0000; accessed June 2014).

An advantage of synthetic bones is their uniformity in structure and material organization and composition. However, this would be a disadvantage for applications that warrant analyzing natural or pathologic differences in bone quality and structure (e.g., age- or osteoporosis-related changes). We speculate that even when rotator cuff repairs are previously tested with cyclic loading (which is commonly done), this will not adversely affect fracture data, similar to what is shown by our results. This is because failure in cyclic testing is often measured as gapping at the repair site rather than disruption/pullout of the anchors or sutures from the bone.^28–30 However, some investigators may want to reuse cadaveric humeri following cuff repair testing at relatively higher loads and/or loading rates, whether monotonic, cyclic, or mixed. In these cases where the bone strength might be significantly compromised, mechanical tests on a subset of specimens would be needed to determine if the bones can be reused.

One limitation of our study is the fracture loading rate. While our relatively low rate or loading is within the range employed in fracture studies of proximal humeri and femora,^{22,24,31–35} varying rates may yield varying results. Differences in loading rate and/or loading mode may affect the validity of bone reuse, and hence they should be tested on a subset of the sample.

Abbreviations Used

DEXA

Dual-energy X-ray absorptiometry

BMD

bone mineral content

TOAK

transosseous anchor double knot

Acknowledgments

The authors thank Casey Kiser and Peter O'Rourke for their assistance with mechanical testing and Kendra Keenan for criticisms of the manuscript.

Author Disclosure Statement

No competing financial interests exist.