A white matter lesion-filling approach to improve brain tissue volume measurements

Abstract

Multiple sclerosis white matter (WM) lesions can affect brain tissue volume measurements of voxel-wise segmentation methods if these lesions are included in the segmentation process. Several authors have presented different techniques to improve brain tissue volume estimations by filling WM lesions before segmentation with intensities similar to those of WM. Here, we propose a new method to refill WM lesions, where contrary to similar approaches, lesion voxel intensities are replaced by random values of a normal distribution generated from the mean WM signal intensity of each two-dimensional slice. We test the performance of our method by estimating the deviation in tissue volume between a set of 30 T1-w 1.5 T and 30 T1-w 3 T images of healthy subjects and the same images where: WM lesions have been previously registered and afterwards replaced their voxel intensities to those between gray matter (GM) and WM tissue. Tissue volume is computed independently using FAST and SPM8. When compared with the state-of-the-art methods, on 1.5 T data our method yields the lowest deviation in WM between original and filled images, independently of the segmentation method used. It also performs the lowest differences in GM when FAST is used and equals to the best method when SPM8 is employed. On 3 T data, our method also outperforms the state-of-the-art methods when FAST is used while performs similar to the best method when SPM8 is used. The proposed technique is currently available to researchers as a stand-alone program and as an SPM extension.

1. Introduction

Magnetic resonance imaging (MRI) permits to assess tissue abnormalities in vivo and approximate histopathological changes of the multiple sclerosis (MS) disease (Ganiler et al., 2014; Kearney et al., 2014). Several studies have shown that the percentage of change in brain atrophy tends to correlate with the progression of the disease (Pérez-Miralles et al., 2013; Sormani et al., 2014). Moreover, changes in gray matter (GM) atrophy are observed independently from white matter (WM), and hence atrophy measures based on segmentation-based methods are nowadays employed as they allow classifying brain tissues separately (Pérez-Miralles et al., 2013). The performance of different segmentation methods used to quantify brain atrophy or volume estimation has been evaluated deeply in the last 5 years (Klauschen et al., 2009; Derakhshan et al., 2010). However, it is well known that the presence of WM lesions can induce errors on brain tissue volume measurements (Chard et al., 2010; Battaglini et al., 2012; Gelineau-Morel et al., 2012) and non-rigid registration (Sdika and Pelletier, 2009; Diez et al., 2014), if lesions are processed within the images. For instance, if WM lesion voxels are classified as WM, lesion voxels with hypointense signal intensities are added into the WM tissue distribution, increasing the probability of GM voxels with similar intensity to be misclassified also as WM (Chard et al., 2010).

In the last years, some authors have proposed different techniques to overcome these issues in MS patients by filling WM lesions with intensities similar to those of WM before performing tissue segmentation and image registration. These methods can be divided into two groups: methods which use local intensities from the surrounding neighboring voxels of lesions (Sdika and Pelletier, 2009; Battaglini et al., 2012; Magon et al., 2013) and methods which use global WM intensities from the whole brain (Chard et al., 2010). In all cases, the performance of these methods is directly related with their ability to minimize the impact of refilled voxels on original tissue distribution, not only due to the addition of these voxels into the tissue distribution, but also due to the effect on the global tissue distributions of filled images.

Within local methods, Sdika and Pelletier (2009) have proposed to refill each WM lesion voxel with the mean of its three-dimensional neighboring normal appearance white matter (NAWM) voxels. Battaglini et al. (2012) have suggested refilling each WM lesion voxel with intensities derived from a histogram of NAWM voxels surrounding the two-dimensional lesions. In a recent study, Magon et al. (2013) have proposed to refill each two-dimensional lesion with the intensity from the mean of the surrounding area of the lesion. Regarding global methods, Chard et al. (2010) have proposed a different approach by using intensities re-sampled from a global WM distribution to refill WM lesion voxels, based on the mean and standard deviation of the total NAWM of the whole image. Both Chard et al. (2010) and Battaglini et al. (2012) methods are available for the community. FSL-L (Battaglini et al., 2012) runs from a computer command-line and does not provide any graphical interface that aids the process. This technique has been integrated into the latest FSL package, and therefore it depends on the whole FSL installation. In the case of LEAP (Chard et al., 2010), the method runs as a stand-alone script also from the command-line and requires the installation and configuration of several external dependencies, which may be difficult to install for non-computer experts.

In this paper we propose a new technique to refill WM lesions which is a compromise between global and local methods. Hence, for each slice composing the three-dimensional image, we compute the mean and standard deviation of the signal intensity of NAWM tissue. On the one hand, compared to local methods (Battaglini et al., 2012; Magon et al., 2013) which only make use of a limited range of voxel intensities, the fact of using global information from the whole image slice reduces the bias caused by refilled voxels on GM and WM tissue distributions, especially on images with high lesion load. On the other hand, compared to other global methods (Chard et al., 2010), which are based on the mean signal intensity of the NAWM of the three-dimensional image, our method re-computes the mean signal intensity of the NAWM at each two-dimensional slice with the aim of reproducing more precisely the signal variability between MRI slices, especially in low resolution images. In order to easily integrate it into current platforms, the proposed method called SLF is currently available as a stand-alone program and as SPM1 extension at the SALEM group site (http://atc.udg.edu/salem/slfToolbox).

To evaluate the performance of our method, we estimate the deviation in GM and WM tissue volume between a set of healthy images and the same images where artificial WM lesions have been refilled with the proposed technique. To do so, we register WM lesion masks from diagnosed MS patients into two sets of 30 1.5 and 3 T T1-weighted (T1-w) images of healthy subjects, respectively. Afterwards, we simulate realistic lesions on healthy images by replacing the signal intensities of registered lesion voxels with values similar to those of the mean GM/WM interface. Brain tissue volume is computed using both FAST (Zhang et al., 2001) and SPM8 (Ashburner and Friston, 2005) segmentation methods, in order to avoid possible correlations between the filling and segmentation processes. Furthermore, we compare our results with the same images where artificial WM lesions have been segmented as normal tissue, masked-out before tissue segmentation, and refilled using also the methods proposed by Chard et al. (2010); Battaglini et al. (2012), and Magon et al. (2013).

2. Materials and methods

2.1. Image data

The first set of images is composed of 30 images of healthy subjects (matrix size: 176 × 208 × 176, voxel size: 1 × 1 × 1.25 mm), acquired on a 1.5 T Vision scanner (Siemens, Erlangen, Germany) and obtained from the Open Access Series of Imaging Studies (OASIS) repository2 (Marcus et al., 2007). Only images from young and middle-aged subjects are selected (age < 50) as they have not been diagnosed with any related pathology. Image references included in the study are as follows: 2, 4, 5, 6, 7, 9, 11, 12, 14, 17, 18, 20, 25, 26, 27, 29, 34, 37, 38, 40, 43, 44, 45, 47, 49, 50, 51, 54, 55, and 57.

The second set of images is composed of 30 images of healthy subjects (matrix size: 256 × 150 × 256, voxel size: 0.92 × 0.92 × 1.20 mm) acquired on a Philips 3 T scanner (Philips Healthcare, Best, NL) and obtained from the Information eXtraction from Images (IXI) repository maintained by the Imperial College London in London, UK.3 We selected 30 images acquired from the Hammersmith Hospital. Image references included in the study are as follows: 12, 13, 14, 15, 33, 34, 39, 48, 49, 51, 52, 57, 59, 72, 80, 83, 92, 95, 96, 97, 104, 105, 126, 127, 128, 131, 136, 137, 146, and 159.

2.2. Preprocessing

All images are manually reoriented to match the standard MNI space. Skull-stripping is performed using the Brain Extraction Tool (BET) (Smith, 2002), following the optimization workflow suggested by Popescu et al. (2012), with the exception that cerebrospinal fluid tissue has been refilled on skull-stripped images again. This procedure is preferred over other alternatives as it provides the best performance on some lesion-filling methods such as Chard et al. (2010), being also the choice in other recent studies (Popescu et al., 2014). IXI images are corrected from possible intensity non-uniformities and acquisition artifacts using N4, the ITK (Ibáñez et al., 2003) implementation of the N3 package (Sled et al., 1997). N4 is applied on IXI images with default options. Images from the OASIS repository are provided already with N4 applied.

2.3. Lesion generation

We use a set of 37 patients with clinically confirmed MS, provided with initial and follow-up studies (Diez et al., 2014). In these patients, lesions have been annotated semi-automatically on Proton Density-weighted (PD-w) images by a trained technician using JIM software4 and afterwards co-registered with T1-w images. In order to maintain the independence between the 1.5 and 3 T sets of images, we match randomly 30 patients from the initial study into the OASIS images, and we repeat the same procedure with the follow-up study and the IXI image set.

MS lesion masks are registered into healthy images by a non-rigid transformation (Rueckert et al., 1999). To ensure that resulting lesion masks are placed on WM, we remove registered lesion voxels that have not been segmented as WM by both FAST and SPM8 on the healthy image. We computed a Wilcoxon rank sum test to analyze the difference in lesion volumes generated between OASIS and IXI datasets, obtaining that differences were not statistically significant (p = 0.162). The obtained mean lesion volume on OASIS images was 21.1 ± 20.8 ml (range from 0.5 to 65 ml), while 15.4 ± 16.2 ml (range from 0.8 to 62 ml) on IXI 3 T images. Note that due to the existing anatomical differences between 1.5 and 3 T image subjects and the enforced WM tissue constraint, the effect of registering the same MS lesion mask into a 1.5 and 3 T image results in two different lesion masks. For instance, the effect of registering lesions from the initial study into the 3 T dataset provided different lesion volumes (10.30 ± 12.10 ml) and reported statistically significantly differences (p = 0.007) on the Wilcoxon rank sum tests.

Artificial lesions are simulated by replacing registered lesion voxel intensities with ones between the GM and WM interface, following the same strategy shown in Battaglini et al. (2012). For each original image, GM and WM tissue distributions are computed using only voxels in agreement between FAST and SPM8. WM lesion voxels are filled with random intensities coming from a newly generated normal distribution, with mean equal to the average of the GM and WM mean values and standard deviation equal to the difference between mean WM and GM, divided by 4 (Battaglini et al., 2012). Artificial lesions are refilled with the aim of simulating a profile which clearly separates their signal intensity with healthy tissue. This intensity profile chosen does not reflect the entire scope of possible real lesions, but allows us to visualize the magnitude of the differences in tissue volume between images with artificial lesions and the same images where lesion have been filled with the proposed method. The intensity profile chosen would not affect any of the methods studied since they do not take into account the artificial lesion intensities.

2.4. Lesion filling

The proposed method aims to combine the global approach of Chard et al. (2010) with the similarity between refilled voxel intensities and their surrounding voxels of local methods such as Battaglini et al. (2012) and Magon et al. (2013). Basically, for each slice composing the three-dimensional image, lesion voxel intensities are replaced by random intensities of a normal distribution generated from the mean NAWM intensity of the current slice. Fig. 1 summarizes the lesion-filling process graphically.

Fig. 1.

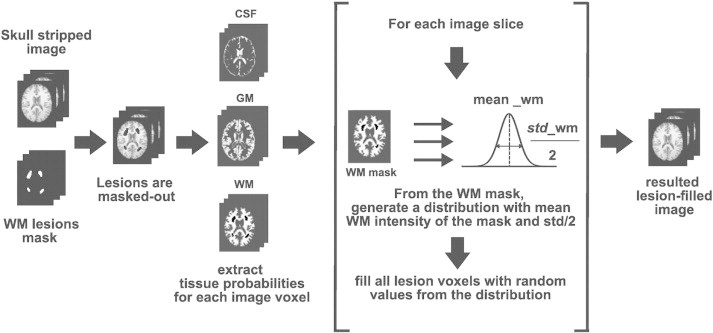
Proposed algorithm for filling WM lesions. From a preprocessed T1-w image (skull-stripping and intensity inhomogeneity corrected), WM lesions are masked out using the provided WM lesion binary mask. Using a Fuzzy-C-means approach, we estimate the probability of each image voxel to be classified as CSF, GM, and NAWM. For each slice composing the whole image, lesion voxel intensities are replaced by a random intensity derived from a normal distribution with mean and half of the standard deviation of the NAWM tissue intensities of the current slice.

The proposed algorithm requires two input images: a preprocessed T1-w image (skull-stripped and intensity inhomogeneity corrected) and its corresponding binary WM lesion mask. After testing the performance of the method with different skull-stripping approaches (Smith, 2002; Shattuck et al., 2001), we observed that including this step inside the filling process is not necessary, because the skull-stripping method employed seems to not interfere significantly in the results obtained (Wilcoxon significant rank-sum tests between differences in tissue volume between lesion-filled and original images of both datasets for GM and WM tissue, p > 0.13).

WM lesions are masked out from the T1-w image using the provided lesion mask, in order to avoid the influence of artificial lesions on tissue distributions. The resulting image is used to estimate the probability of each voxel to be classified as CSF, GM, and NAWM, by segmenting tissue with a Fuzzy-C-means approach (Pham, 2001). The Fuzzy-C-means implementation used here follows the algorithm described in Pham (2001), with clusters initialized according to Bezdek et al. (1999). Moreover, input signal intensities are constrained to the mean plus three standard deviations of the signal intensity of the image, in order to avoid outlier signal intensities, such as residual parts of the eyes or neck. From the obtained tissue segmentation output, we compute the three-dimensional NAWM mask from the image voxels with the highest probability to pertain to the WM cluster.

Finally, the lesion-filling process is achieved as follows: for each axial slice composing the three-dimensional image, we compute the mean and standard deviation of the signal intensity of NAWM tissue. Axial sampling is motivated because after testing the sampling procedure on the coronal, axial and sagittal planes, we found that the best results were obtained when we sampled the axial plane. This was due to the fact that using the axial plane reduced the variability of possible existing WM intensities, when compared to coronal and sagittal sampling. The Fuzzy-C-means approach used to estimate the tissue probabilities is a simple method which in fact does not take into account neither spatial nor neighboring information, and hyper-intense signal intensities such as residual parts of the eyes or the neck produced in the skull-stripping process can bias significantly the clusters. The risk of adding these parts into the WM distribution is minimized in the axial plane because we are reducing it to a certain slice where lesion volume is usually lower than that in central slices. The computed mean and standard deviation values are used to generate a normal distribution with mean equal to the computed NAWM mean intensity and standard deviation equal to half of the computed NAWM standard deviation. Standard deviation is always fixed to half of the WM mean independently of the dataset used. This value was chosen empirically with the aim of balancing the accuracy of the method with both 1.5 and 3 T images. Although a specific tuning of this parameter could provide a better performance on certain cases, we decided to fix it avoiding therefore the number of parameters to tune. Lesion voxel intensities from the current image slice are replaced by random values of the generated distribution. The procedure is repeated until all image slices are completed.

2.5. Volume analysis

We compute the absolute percentage % difference in normalized gray matter volume (NGMV) and normalized white matter volume (NWMV) between each original and its correspondent lesion-filled images. Normalized volumes are obtained as the ratio of voxels outside lesion regions segmented as GM or WM and the total number of segmented voxels, respectively. For instance, the % difference in NGMV is computed as:

$$\%=\frac{\left|\mathit{NGM}{V}_{\mathit{filled}}-\mathit{NGM}{V}_{\mathit{orig}}\right|}{\mathit{NGM}{V}_{\mathit{orig}}}\times 100$$

where NGMV_filled and NGMV_orig values refer to the computed volumes for the lesion-filled and original images, respectively. The higher the performance of the lesion-filling method, the lower the percentage difference between lesion-filled and original images.

In order to analyze possible correlations between the filling process and the segmentation method employed, brain tissue volume is calculated independently on the same subjects using FAST (Zhang et al., 2001) (v.5.0.5) and SPM8 (Ashburner and Friston, 2005) (v.4667) approaches.

2.6. Statistical analysis

We compare the performance of our method with respect to other existing techniques such as the ones proposed by Chard et al. (2010); Battaglini et al. (2012), and Magon et al. (2013). We also add two more sets of images into the comparison: images segmented with artificial lesions and images where WM lesions have been masked out before tissue segmentation. Given the small differences in NGMV and NWMV between original and lesion-filled images, the use of a standard Analysis of the Variance (ANOVA) or a classic t-test is impractical here. Instead, we perform a series of permutation tests to determine significant differences in tissue volume between pairs of methods (Menke and Martínez, 2004; Valverde et al., 2014). The permutation tests return the mean μ and standard deviation σ of the fraction of times that the difference in NGMV and NWMV for a current lesion-filling method is smaller than the rest of methods with p-value ≤ 0.05. Afterwards, methods are presented in 3 ranks determined by the mean and standard deviation of the best method and the distance with respect to the mean of the rest of methods (Valverde et al., 2014). In our experiments, we set the number of comparisons between each pair of methods to N = 1000.

3. Results

3.1. OASIS dataset (1.5 T data)

Fig. 2 depicts the absolute mean % difference in NGMV and NWMV between the 30 original 1.5 T images and the same images with artificial lesions (NONE), masked-out lesions before segmentation (MASKED), and lesion-filled using Magon et al. (2013) (MAGON), Battaglini et al. (2012) (FSL-L), and Chard et al. (2010) (LEAP), and finally our proposed algorithm SLF.

Fig. 2.

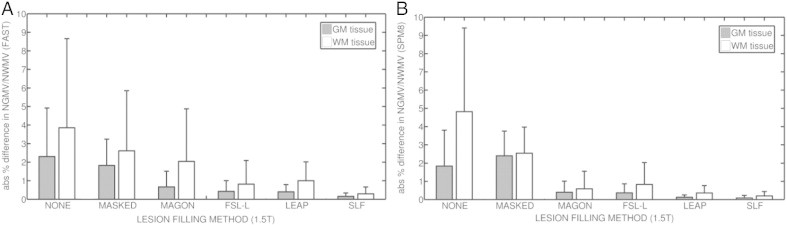
Absolute % difference in NGMV and NGWM between original and filled images from the OASIS (1.5 T) dataset. (a) Results for images segmented using FAST. (b) Results for images segmented with SPM8. Gray bars represent the absolute mean % difference in NGMV, while white bars represent the absolute mean % difference in NWMV. Lines above each bar represent the standard deviation for each method and tissue.

When FAST is used, SLF reports the lowest absolute mean difference in NGMV (0.16 ± 0.14), followed by LEAP (0.40 ± 0.30) and FSL-L (0.43 ± 0.58) methods. Our proposal also provides the lowest difference in NWMV (0.29 ± 0.36), followed by FSL-L (0.81 ± 1.28). Maximum values in NGMV are found in NONE images, with differences up to 2.30 ± 2.62 in NGMV and 3.85 ± 4.81 in NWMV.

When SPM8 is used, SLF also reports the lowest differences in NGMV (0.09 ± 0.14), followed by LEAP method (0.12 ± 0.13). Our proposed method also performs better than the rest of the methods on NWMV (0.20 ± 0.24), followed by the LEAP method (0.36 ± 0.40). Again, the highest differences in NGMV (1.84 ± 1.97) and NWMV (4.82 ± 4.58) are found in NONE images. Table 1 shows the absolute mean difference in WM volume for all methods where lesion volume has been ranged by size intervals. Results are presented for both SPM8 and FAST segmentation methods.

Table 1.

Absolute mean difference in NWMV between original and filled images from the 1.5 T OASIS images. Results are presented for both SPM8 and FAST segmentation methods. Lesion volume is ranged by size intervals with n = 6 by interval. Values indicate the mean and standard deviation of the absolute difference in volume (μ ± σ) of each lesion-filling method at a current lesion interval.

Method/lesion(ml)	0.5–4 ml (n = 6)	4–11 ml (n = 6)	11–20 ml (n = 6)	25–36 ml (n = 6)	>36 ml (n = 6)
SPM8 segmentation method
NONE	0.47 ± 0.50	1.54 ± 0.95	2.71 ± 0.60	7.09 ± 1.42	10.64 ± 3.10
MASKED	1.56 ± 0.94	2.42 ± 0.70	1.49 ± 0.43	3.16 ± 1.35	3.91 ± 1.76
MAGON	0.03 ± 0.03	0.08 ± 0.07	0.24 ± 0.25	0.32 ± 0.19	1.95 ± 1.25
FSL-L	0.03 ± 0.01	0.10 ± 0.05	0.31 ± 0.15	0.55 ± 0.07	2.38 ± 1.26
LEAP	0.04 ± 0.04	0.10 ± 0.05	0.19 ± 0.05	0.44 ± 0.22	0.92 ± 0.42
SLF	0.03 ± 0.03	0.04 ± 0.03	0.09 ± 0.06	0.23 ± 0.20	0.55 ± 0.23
FAST segmentation method
NONE	0.21 ± 0.21	0.71 ± 0.38	1.88 ± 0.56	4.55 ± 2.04	8.95 ± 4.36
MASKED	9.52 ± 1.20	8.36 ± 1.30	11.53 ± 4.91	7.42 ± 1.08	5.79 ± 1.92
MAGON	0.08 ± 0.04	0.25 ± 0.22	0.91 ± 0.63	1.28 ± 0.39	6.24 ± 2.74
FSL-L	0.03 ± 0.02	0.05 ± 0.05	0.30 ± 0.21	0.58 ± 0.19	2.13 ± 1.22
LEAP	0.08 ± 0.07	0.34 ± 0.10	0.65 ± 0.13	1.07 ± 0.66	2.50 ± 0.80
SLF	0.07 ± 0.05	0.13 ± 0.09	0.22 ± 0.15	0.36 ± 0.30	0.42 ± 0.16

Table 2 presents the performance of each filling-method after running all possible pair-wise permutation tests. With a significant p-value of ≤0.05, all tests run on images segmented with FAST show the superiority of SLF over the other methods presented. On images segmented with SPM8, all tests show a clear superiority of SLF over the other methods on NWMV, while a similar performance of SLF and LEAP over the other methods on NGMV.

Table 2.

Permutation tests for obtained absolute % differences in NGMV and NWMV on 1.5 T images. Reported values are mean and standard deviation (μ_o, σ_o) of the fraction of times when each method produces significant p-values (p ≤ 0.05). (a) Results when using FAST. (b) Results when using SPM8. Positive values indicate that in average, the method out-performs the other methods in pair-wise significant tests. Negative values indicate the contrary. Rank 1: (μ_o − σ_o, μ_o], rank 2: (μ_o − 2σ_o, μ_o − σ_o], rank 3: (μ_o − 3σ_o, μ_o − 2σ_o].

	NGMV		NWMV
	Method	μ ± σ	Method	μ ± σ
(a) FAST segmentation method (1.5 T)
Rank 1	SLF	0.83 ± 0.41	SLF	0.83 ± 0.41
Rank 2	FSL-L	0.33 ± 0.82	FSL-L	0.33 ± 0.82
	LEAP	0.33 ± 0.82	LEAP	0.33 ± 0.82
Rank 3	MAGON	−0.17 ± 0.98	MAGON	−0.17 ± 0.98
	MASKED	−0.23 ± 0.41	MASKED	−0.23 ± 0.41
	NONE	−0.50 ± 0.84	NONE	−0.50 ± 0.84
(b) SPM8 segmentation method (1.5 T)
Rank 1	SLF	0.67 ± 0.52	SLF	0.83 ± 0.41
	LEAP	0.67 ± 0.52
Rank 2	MAGON	0.00 ± 0.89	LEAP	0.33 ± 0.82
	FSL-L	0.00 ± 0.89	MAGON	0.17 ± 0.75
Rank 3	NONE	−0.67 ± 0.52	FSL-L	0.00 ± 0.89
	MASKED	−0.67 ± 0.52	MASKED	−0.50 ± 0.84
			NONE	−0.83 ± 0.41

3.2. IXI dataset (3 T data)

We also test the performance of our algorithm using 3 T data. As before, Fig. 3 shows the absolute mean % difference in NGMV and NWMV between the 30 original 3 T images and the same images with added lesions (NONE), masked-out lesions before segmentation (MASKED), and lesion-filled methods MAGON, FSL-L, and LEAP, and our proposed approach SLF.

Fig. 3.

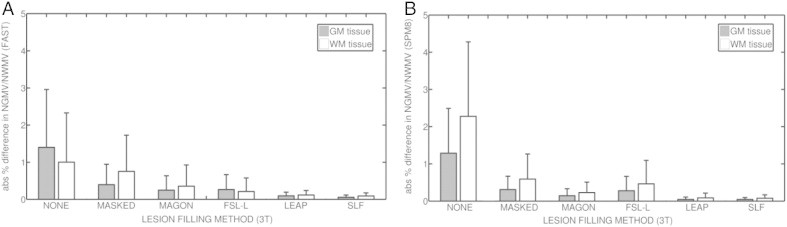
Absolute mean % difference in NGMV and NWMV between original and filled images from the IXI (3 T) dataset. (a) Results for images segmented using FAST. (b) Results for images segmented with SPM8. Gray bars represent the absolute mean % difference in NGMV, while white bars represent the absolute mean % difference in NWMV. Lines above each bar represent the standard deviation for each method and tissue.

When FAST is used, SLF reports the lowest absolute mean % difference in NGMV (0.06 ± 0.06), followed by LEAP (0.09 ± 0.10). Our method SLF also performs the lowest difference in NWMV (0.09 ± 0.09), followed again by LEAP (0.12 ± 0.08). Maximum values in NGMV are found in NONE images, with differences up to 1.40 ± 1.56 in NGMV and 1.00 ± 1.32 in NWMV.

When SPM8 is used, both LEAP (0.04 ± 0.06) and SLF (0.05 ± 0.05) yield the lowest absolute % mean difference in NGMV. On NWMV, also LEAP (0.09 ± 0.12) and SLF (0.08 ± 0.09) report the lowest absolute mean % difference in volume between original and lesion-filled images. Again, highest differences in NGMV (1.84 ± 1.97) and NWMV (4.82 ± 4.58) are found in NONE images. Table 3 shows the absolute mean difference in WM volume for all methods on IXI images, where lesion volume has been ranged by size intervals. Results are presented for both SPM8 and FAST segmentation methods.

Table 3.

Absolute mean difference in NWMV between original and filled images from the 3 T OASIS images. Results are presented for both SPM8 and FAST segmentation methods. Lesion volume is ranged by size intervals with n = 6 by interval. Values indicate the mean and standard deviation of the absolute difference in volume (μ ± σ) of each lesion-filling method at a current lesion interval.

Method/lesion(ml)	0.8–3 ml (n = 6)	4–6 ml (n = 6)	6–13 ml (n = 6)	16–21 ml (n = 6)	>21 ml (n = 6)
SPM8 segmentation method
NONE	0.68 ± 0.56	0.92 ± 0.31	1.61 ± 0.85	3.37 ± 0.81	5.16 ± 1.83
MASKED	0.07 ± 0.03	0.21 ± 0.16	0.34 ± 0.22	1.07 ± 0.79	1.42 ± 0.65
MAGON	0.05 ± 0.10	0.15 ± 0.28	0.14 ± 0.15	0.47 ± 0.44	0.41 ± 0.22
FSL-L	0.06 ± 0.06	0.06 ± 0.03	0.19 ± 0.16	0.80 ± 0.80	1.32 ± 0.53
LEAP	0.01 ± 0.01	0.03 ± 0.02	0.05 ± 0.05	0.13 ± 0.15	0.22 ± 0.18
SLF	0.03 ± 0.03	0.02 ± 0.01	0.09 ± 0.12	0.09 ± 0.06	0.16 ± 0.13
FAST segmentation method
NONE	0.14 ± 0.10	0.24 ± 0.06	0.52 ± 0.34	1.27 ± 0.35	2.94 ± 1.67
MASKED	0.07 ± 0.05	0.17 ± 0.07	0.41 ± 0.27	0.95 ± 0.25	2.23 ± 1.13
MAGON	0.05 ± 0.03	0.07 ± 0.06	0.08 ± 0.04	0.59 ± 0.55	1.07 ± 0.79
FSL-L	0.04 ± 0.02	0.03 ± 0.02	0.03 ± 0.02	0.18 ± 0.20	0.77 ± 0.45
LEAP	0.07 ± 0.05	0.03 ± 0.03	0.14 ± 0.13	0.19 ± 0.16	0.29 ± 0.13
SLF	0.03 ± 0.02	0.04 ± 0.02	0.08 ± 0.06	0.20 ± 0.15	0.34 ± 0.14

Table 4 shows the performance of each filling-method after running the permutation tests. Tests run on images segmented with FAST show a significant superiority of SLF over the rest of the methods on NWMV, and a slightly better performance of SLF with respect to LEAP on NGMV, although both methods are clearly superior to the rest of methods presented. When SPM8 is used, tests show a similar performance of SLF and LEAP over the rest of the methods on both NWMV and NGMV.

Table 4.

Permutation tests for obtained absolute % differences in NGMV and NWMV on 3 T images. Reported values are mean and standard deviation (μ_o, σ_o) of the fraction of times when each method produces significant p-values (p ≤ 0.05). (a) Results when using FAST. (b) Results when using SPM8. Positive values indicate that in average, the method out-performs the other methods in pair-wise significant tests. Negative values indicate the contrary. Rank 1: (μ_o − σ_o, μ_o], rank 2: (μ_o − 2σ_o, μ_o − σ₀], rank 3: (μ_o − 3σ_o, μ_o − 2σ_o].

	NGMV		NWMV
	Method	μ ± σ	Method	μ ± σ
(a) FAST segmentation method (3 T)
Rank 1	SLF	0.67 ± 0.52	SLF	0.67 ± 0.52
	LEAP	0.66 ± 0.51	LEAP	0.50 ± 0.55
			FSL-L	0.33 ± 0.82
Rank 2	MAGON	0.00 ± 0.8	MAGON	−0.17 ± 0.98
	FSL-L	0.00 ± 0.3
Rank 3	MASKED	−0.50 ± 0.84	MASKED	−0.50 ± 0.84
	NONE	−0.83 ± 0.41	NONE	−0.83 ± 0.41
(b) SPM8 segmentation method (3 T)
Rank 1	LEAP	0.67 ± 0.52	LEAP	0.67 ± 0.52
	SLF	0.67 ± 0.52	SLF	0.67 ± 0.52
	MAGON	0.17 ± 0.98	MAGON	0.17 ± 0.98
Rank 2	FSL-L	−0.33 ± 0.82	FSL-L	−0.17 ± 0.98
	MASKED	−0.33 ± 0.82
Rank 3	NONE	−0.83 ± 0.41	MASKED	−0.50 ± 0.84
			NONE	−0.83 ± 0.41

4. Discussion

Several studies have proposed to use different filling techniques in order to reduce the effects of WM lesions on brain tissue measurements of T1-w images. Up to date, only LEAP (Chard et al., 2010)5 and FSL-L (Battaglini et al., 2012)6 are publicly available methods that permit to refill T1-w images given a WM lesion mask. The Lesion Segmentation Toolbox (LST) proposed by Schmidt et al. (2012) also provides a lesion-filling approach based on the work of Chard et al. (2010), but it is dependent of a FLAIR image and an internal lesion-probability map obtained during the lesion segmentation step.

In general, deviation in tissue volume between original and lesion-filled images tends to be higher on 1.5 T OASIS images than on 3 T IXI images. The observed deviation is caused by differences in intensity, slice thickness and dimensionality between datasets. On IXI images, the distance between GM and WM signal intensity distributions is narrower than that of 1.5 T data. Applying the lesion generation algorithm (Battaglini et al., 2012) with identical parameters of those used with 1.5 T images creates simulated lesions whose intensity are noticeably similar to the mean WM, because the standard deviation of the generated lesion distribution is the mean between the GM and WM tissue divided by 4. However, this fact only explains the difference found on images segmented with artificial lesions. In the rest of the methods, the signal intensity of the generated lesions is not interfering with the obtained results since in all cases lesion voxels are replaced before tissue segmentation. On images where lesions have been masked before segmentation (MASKED), the lower deviation in tissue volume of 3 T images can be explained by the increase in the resolution of the images when compared to 1.5 T data, which reduces the effect of masked voxels in tissue distributions. The same reason can be behind the lower deviation found on all four lesion filling methods. By increasing the number of slices, differences produced by the methods on certain slices can be smoothed by tissue segmentation methods. Moreover, the use of a reduced sampling space or a better tuning of the parameters involved in the WM tissue distribution generated to refill lesion voxels could increase the performance of the presented method. Nevertheless, in all our experiments we decided to fix the standard deviation to 2 for simplicity.

Analyzing the results by dataset, on 1.5 T images from the OASIS dataset, our results show that compared to the available methods, the proposed algorithm SLF reduces significantly the differences in NWMV between original and filled images, independently of the brain tissue segmentation method used to measure the tissue volume. With the same data, SLF also reduces significantly the differences in NGMV when FAST is used. Although our method reports the lowest mean % difference in NGMV when SPM8 method is used, the permutation test clearly shows that differences between SLF and LEAP are not relevant. On 3 T images from the IXI dataset, SLF also yields the lowest mean % differences in NGMV and NWMV, when FAST is used to measure tissue volume. These results are clearly significant in NWMV, but not in NGMV, although our method reports also the lowest difference among all methods. When SPM8 is used, SLF presents a similar performance of that of LEAP, and both methods tie on the results of the significance tests.

Compared with local methods, our algorithm performs quantitatively better than local methods on images with high lesion load (> 36 ml). The MAGON method incorporates all neighbor voxels surrounding a WM lesion region to compute a mean intensity which is used to refill all lesion voxels. On images with high lesion load touching GM tissue, including GM voxels can decrease refilled intensities and modify the tissue distribution of filled images. FSL-L overpasses this limitation by building an intensity distribution based only on WM voxels surrounding lesions. However, on large lesion regions, all lesion voxels will be filled with a narrow range of intensities coming from the neighboring voxels that can have a direct incidence on GM and WM tissue distributions. By contrast, lesion volume appears to affect less global methods. In our case, the intensity distribution generated to refill lesion voxels will be independent of both the size and the position of lesion. Furthermore, the effect of filled voxels on the global WM tissue distribution is smoothed by the addition of intensities which try to reassemble the global NAWM of the current slice.

Compared with global methods, there are some interesting differences between our method and LEAP. Contrary to local methods, global methods have to deal with the skull-stripping process before processing images. LEAP incorporates the skull-stripping process as part of the processing pipeline. In addition, LEAP also allows the user to provide a brain mask. By contrast, our method does not deal with skull-stripping internally, and the method requires an already skull-stripped image or a brain mask. As noted previously, the skull-stripping method employed seems to not interfere significantly in the results obtained by our method. While setting up each of the different processes involved in the proposed pipeline, we found that, at least with our data, the performance of LEAP decreased or failed in 1.5 T scans when the skull-stripping methods BSE (Shattuck et al., 2001) and BET (Smith, 2002) were used with default options. By contrast, LEAP provided the best results when the optimized method proposed by Popescu et al. (2012) was used. This fact motivated the selection of this skull-stripping method for all the experiments of the study.

Furthermore, on both datasets, we have also compared the differences between our method and LEAP estimating the mean NAWM intensity used as a basis to fill lesion voxels. In most of the images, the global mean NAWM intensity does not differ significantly between fityk7 on LEAP and our Fuzzy-C-means approach. Hence, we can reject the hypothesis that observed differences in 1.5 T images can be caused by the approach employed to compute the NAWM tissue distribution before filling lesion voxels. However, on both lesion-filling approaches, tissue segmentation methods tended to increase the apparent mean WM tissue distribution on 1.5 T images with high lesion load (>40 ml) due to the increase of voxels refilled with intensities higher than the actual mean WM signal intensity. This effect is clearly more visible on LEAP than in our method, especially when FAST is used. The resolution of the OASIS 1.5 T images (176 × 208 × 176 slices) is lower than that of IXI 3 T images (256 × 150 × 256 slices). On images with low number of slices, each slice has a higher weight into the global tissue distribution. After comparing the a priori WM tissue distribution values estimated by both the LEAP and SLF methods with the already computed WM tissue distributions obtained from healthy images, we found that as lesion size increases, global methods such as LEAP and SLF tend to increase the differences in tissue volume with respect to original images. In both methods, we have observed that the a priori estimated mean intensity of the WM distribution tends to be higher than the actual tissue distribution as computed by FAST and SPM8 on healthy images. As lesion volume increases, the addition of more filled voxels with intensity higher than the actual mean tissue intensity is more prominent, causing a displacement of the mean intensity of the WM distribution returned by the segmentation methods on filled images. Consequently, more voxels bordering GM/WM are segmented as GM and WM tissue volume decreases. In this scenario, the strategy followed by SLF, where WM is sampled independently at each slice, is more robust to the increase of lesions size than a global estimation of the WM tissue (LEAP) because possible errors introduced by a particular slice are not propagated into the rest of the slices. Contrary to SPM8, which estimates the tissue distributions based on a Gaussian Mixture Model approach of the whole image, FAST builds a network of neighboring relations based on a Markov random field approach, more sensible to changes between slices. The same reason can also be behind the better performance of our method on 3 T when FAST is used. Compared with 1.5 T images, the probability of intensity change between slices is less prominent on 3 T images due to a higher resolution between slices.

Analyzing the possible deviations in tissue volume caused by each tissue segmentation process, we obtained results which suggest that the chosen tissue segmentation method does not affect significantly the performance of our filling-method. Results between the same filled images segmented with FAST and SPM8 differ (<0.1%) in the worst case on both datasets and tissues. By contrast, MAGON, FSL-L and LEAP switch their rank on 1.5 T images, depending on the segmentation method used. On 3 T images, only MAGON and FSL-L appear to switch between ranks when FAST or SPM8 is used, respectively.

The present study is not free from limitations. The most important one is the lack of images of MS patients with brain tissue expert annotations. All images from MS patients taken from Diez et al. (2014) have been only provided with lesion annotations delineated by a trained expert, but not brain tissue annotations. To overpass this limitation, we have registered WM lesions from MS patients into healthy images as performed in Battaglini et al. (2012) and double-checked that registered lesions have replaced voxels segmented as WM by FAST and SPM8. This strategy has a negligible impact on the performance of the filling-methods analyzed in this study, because we assure a priori that generated lesions are on WM, and moreover none of the methods use information from the artificial lesions generated. Furthermore, although we tested the performance of the proposed method with two datasets with different magnetic field strengths, our results are limited to these two different scanners with particular configurations, and hence it is difficult to generalize the results to all 1.5 and 3 T scanners.

In conclusion, the results of this study show that regardless of the lesion size, the SLF method performs consistently well compared to other existing methods such as LEAP, especially on 1.5 T images. Furthermore, the results obtained show that the proposed method can be an effective method for low resolution images. The skull-stripping process does not especially affect the accuracy of the method, which allows integrating it with different preprocessing pipelines. Additionally, volume estimations of lesion filled images processed by our algorithm appear to be not affected by the segmentation method employed. In contrast to other approaches, SLF may be installed by non-computer experts who can easily use it without any parameter tuning. SLF is currently available to researchers as a stand-alone script and as an SPM library extension which facilitates to incorporate the lesion filling process into the expert workflow for tissue volume segmentation.