Random Forest ensembles for detection and prediction of Alzheimer's disease with a good between-cohort robustness

Abstract

Computer-aided diagnosis of Alzheimer's disease (AD) is a rapidly developing field of neuroimaging with strong potential to be used in practice. In this context, assessment of models' robustness to noise and imaging protocol differences together with post-processing and tuning strategies are key tasks to be addressed in order to move towards successful clinical applications. In this study, we investigated the efficacy of Random Forest classifiers trained using different structural MRI measures, with and without neuroanatomical constraints in the detection and prediction of AD in terms of accuracy and between-cohort robustness.

From The ADNI database, 185 AD, and 225 healthy controls (HC) were randomly split into training and testing datasets. 165 subjects with mild cognitive impairment (MCI) were distributed according to the month of conversion to dementia (4-year follow-up). Structural 1.5-T MRI-scans were processed using Freesurfer segmentation and cortical reconstruction. Using the resulting output, AD/HC classifiers were trained. Training included model tuning and performance assessment using out-of-bag estimation. Subsequently the classifiers were validated on the AD/HC test set and for the ability to predict MCI-to-AD conversion. Models' between-cohort robustness was additionally assessed using the AddNeuroMed dataset acquired with harmonized clinical and imaging protocols.

In the ADNI set, the best AD/HC sensitivity/specificity (88.6%/92.0% — test set) was achieved by combining cortical thickness and volumetric measures. The Random Forest model resulted in significantly higher accuracy compared to the reference classifier (linear Support Vector Machine). The models trained using parcelled and high-dimensional (HD) input demonstrated equivalent performance, but the former was more effective in terms of computation/memory and time costs. The sensitivity/specificity for detecting MCI-to-AD conversion (but not AD/HC classification performance) was further improved from 79.5%/75%–83.3%/81.3% by a combination of morphometric measurements with ApoE-genotype and demographics (age, sex, education). When applied to the independent AddNeuroMed cohort, the best ADNI models produced equivalent performance without substantial accuracy drop, suggesting good robustness sufficient for future clinical implementation.

Highlights

• •Morphometric measures from 3D T1 brain MRI images (ADNI1 cohort).
• •Tree ensembles were applied for classification and prediction of AD.
• •Assessment of accuracy, robustness in different cohorts, computation and time costs.
• •Accurate and cohort-robust models were produced.
• •Several strategies for further model improvement were tested.

1. Introduction

The application of pattern recognition approaches to neuroimaging offers the potential for diagnostically relevant analysis techniques, in particular for magnetic resonance imaging (MRI), which has already been demonstrated to provide relevant support in the diagnosis of Alzheimer's disease (AD) (O'Brien, 2007). A large number of studies addressing the use of pattern recognition methods in image-based detection of AD have been published in recent years (Gray et al., 2013; Liu et al., 2012; Cuingnet et al., 2011; Klöppel et al., 2008).

The advantage of these methods over visual assessment by a medical expert is that they are fully automated and therefore unbiased towards human mistakes and can be incorporated into computerized medical decision-support systems, a growing field with especially fast research progress in radiology (Stivaros et al., 2010; Belle et al., 2013).

However, such methods do have limitations. Our previous work demonstrated that pattern recognition methods are sensitive to MR-protocol differences (Westman et al., 2011; Lebedev et al., 2013) and that a harmonization step is therefore required. Another relevant issue pertains to the comparison of high-dimensional imaging data input versus measurements extracted by neuroanatomical parcellation atlases, with the areas separated according to functional and histological maps of the human cortex (for simplicity, we will use the term “parcelled data”). Parcelled input has some obvious advantages in terms of lower computation, memory cost and processing time. However, it is possible that it could be biased by these landmarks. Normalized high-dimensional measurements without parcellation, in contrast, are unbiased, but at the same time are more difficult to handle using multivariate and machine learning approaches due to computation and memory costs. Moreover, situations where the number of measurements is much larger than the number of observations (p ≫ n) are often associated with the so-called “curse of dimensionality” (Bellman, 1961). This refers to a number of events that happen when dealing with high-dimensional input (due to increasing sparsity of the data), significantly hampering modeling efficacy. Such cases often require a preparatory step of dimensionality reduction.

Random Forest (RF) is an ensemble machine learning algorithm, which is best defined as a “combination of tree predictors such that each tree depends on the values of a random vector sampled independently and with the same distribution for all trees in the forest” (Breiman, 2001).

In many applications this algorithm produces one of the best accuracies to date and has important advantages over other techniques in terms of ability to handle highly non-linear biological data, robustness to noise, tuning simplicity (compared to other ensemble learning algorithms) and opportunity for efficient parallel processing (De Bruyn et al., 2013; Caruana and Niculescu-Mizil, 2006; Menze et al., 2009). These factors also make RF an ideal candidate for handling high-dimensional problems, where the number of features is often redundant. Although RF can itself be considered as an effective feature selection algorithm, several approaches for feature set reduction within and outside the context of RF have been proposed to further improve its performance (Tuv et al., 2009). In the current study, we use recursive feature elimination (Kuhn, 2012a) to optimize the models.

Our previous work revealed that parcelled cortical thickness together with subcortical volumetric measurements (used as an input to a multivariate model) resulted in the best performance, compared to other modalities (Westman et al., 2013). Here, we aimed not only to assess the accuracies of the classifiers trained with different morphometric modalities, but also to analyze the impact of dimensionality, parcellation strategy on models' accuracy, computation/memory/time costs of model training and feature selection. Finally, previous studies have successfully employed pattern recognition techniques to classify MRI images from different cohorts only within the combined sets (Westman et al., 2011; Lebedev et al., 2014). The present study was planned as one of the first to assess classifiers' between-cohort robustness in two independent large-scale datasets.

We hypothesized that with the use of more disease-specific parcellation atlases (in this case, when the measurements are extracted from the predefined regions, known to be affected by Alzheimer's disease), it would be possible to achieve AD-detection accuracy equivalent to that of the models trained with high-dimensional input without parcellation with shorter computational time. In addition, we hypothesized that it is possible to achieve good between-cohort generalization of the models if the MRI protocols are harmonized.

2. Methods

2.1. Subjects

The study was based on two cohorts. The first set of clinical and MRI data was obtained from the Alzheimer's Disease Neuroimaging Initiative (ADNI-1) database (http://adni.loni.ucla.edu). In short, ADNI-1 includes more than 800 subjects with up to 5 years of annual follow-up with comprehensive clinical, neuropsychological, imaging and laboratory evaluations, performed at the 57 specialized ADNI sites in North America. For details, see Aisen et al. (2010) and ADNI-Core (2011). The present cross-sectional study is focused on baseline imaging data and longitudinal information regarding conversion to dementia.

In total, 3D T1 baseline brain scans from 809 subjects passed our image quality control criteria. From this group we selected 575 subjects – 185 AD, 225 healthy controls (HC) and 165 patients with mild cognitive impairment (MCI) and long term follow up information – who met the inclusion criteria (see below).

In order to test the impact of different cohorts, we additionally included 321 subjects (AD 107, 114 MCI and 100 HCs) from the AddNeuroMed study with harmonized clinical and imaging protocols (http://www.innomed-addneuromed.com/). The standardized study harmonization workflow (described in previous publications) particularly included careful MR protocol alignment evaluated by phantom scanning and careful quality control (Simmons et al., 2011).

2.2. Inclusion criteria and clinical assessment procedures

All AD patients met the NINCDS/ADRDA criteria for probable AD, had mild level of dementia, defined as the Mini-Mental State Examination (MMSE) score between 20 and 26, and had the Clinical Dementia Rating (CDR) score of 1.0.

Inclusion criteria for MCI were: 1) MMSE score between 24 and 30, 2) memory complaints and objective memory impairment measured by the Logical Memory II subscale of the Wechsler Memory Scale (education adjusted), 3) CDR of 0.5, 4) absence of significant levels of impairment in other cognitive domains, 5) preserved activities of daily living, and 6) absence of dementia. MCI converters had to meet the criteria for Alzheimer's disease during at least two sequential evaluations (e.g., at 24 and 36 month follow-ups). Those MCI subjects who did not have the required follow-up information or had their diagnoses changed back from AD to MCI (or to HC) were excluded (n = 232 out of 397). To consider MCI subjects as being non-converters we required that their clinical status remained stable for at least 3 years of follow-up.

Controls (general inclusion/exclusion criteria): 1) MMSE scores between 28 and 30, 2) CDR of 0, and 3) they did not meet the criteria for clinical depression at baseline, MCI or dementia within 3 years of follow-up. One HC subject (ID # 0223) was excluded from the sample due to conversion to AD at follow-up. One AD subject (ID # 0805) was excluded during the outlier detection procedure, leaving 575 subjects. Subjects were between 55 and 90 years of age.

Apart from this, the standardized clinical evaluation protocol included multi-test assessment of cognitive functions and neuropsychiatric symptoms, ApoE genotyping and some other procedures (for more details see http://www.adni-info.org/).

2.3. Subsampling

From the final ADNI cohort of 575 subjects, 150 AD patients and 150 HCs were randomly selected, forming the training dataset, with the remaining AD 35 and 75 HC (coupled with 165 MCI patients) subjects included in the testing dataset.

MCI subjects were split into 6 subgroups according to the month of MCI-to-AD conversion during 4 years of follow-up (6th-, 12th-, 18th-, 24th-, 36+th-month converters and non-converters).

2.4. Study ethics

The studies were approved by the local Regional Committees for Medical Research Ethics. All patients provided written consent to participate in the study after the scheduled procedures had been explained in detail to the patient and a caregiver. All subjects were willing and able to undergo all study procedures including imaging and agreed to longitudinal follow-up.

2.5. MRI

All subjects had 1.5 Tesla T1 3D MRI images acquired using the harmonized ADNI-1 protocol (Jack et al., 2008). For details visit http://adni.loni.usc.edu.

2.6. Image post-processing

Image processing was performed at one site: Centre for Neuroimaging Sciences, IoP (KCL). Image quality control was performed using standardized procedures (Simmons et al., 2011; Simmons et al., 2009).

Next, the raw 3D T1 MRI data underwent processing for surface-based cortex reconstruction and volumetric segmentation using the Freesurfer image analysis software (http://surfer.nmr.mgh.harvard.edu/) version 5.1 installed on a CentOS4 x86_64 cluster. There are several rationales for using Freesurfer in our study. Firstly, the surface-based registration approach incorporated into this software has been shown to have better reproducibility compared to Laplacian- or Registration-based methods for cortical thickness estimation (Clarkson et al., 2011). Secondly, this framework provides a range of different kinds of surface-based and volumetric measurements, as well as different parcellation atlases for extracting averaged morphometric data. The steps of this processing are described in detail elsewhere (Ségonne et al., 2007; Ségonne et al., 2004; Fischl and Dale, 2000; Fischl et al., 1999; Dale et al., 1999; Sled et al., 1998).

The surface-based pipeline produced several morphometric modalities (cortical thickness, Jacobian maps, and sulcal depth). After the Freesurfer steps, cortical models from each individual were registered to a spherical atlas, providing matching across subjects, and finally 327,684 normalized measurements acquired for every subject were concatenated into large matrices (one for each high-dimensional morphometric modality).

41 volumetric measurements for all subjects were corrected for intracranial volume (ICV) using linear modelling (removing linear effects of ICV) and finally concatenated into an n-by-41 matrix that was used in the subsequent analysis.

The image post-processing and analysis steps are illustrated in Appendix: Fig. A1.

2.7. Statistical analysis

Statistical analysis was carried out using the R programming language (R Core Team, 2012), version 2.15.1, on R-Cloud built on EBI 64-bit Linux Cluster (Kapushesky et al., 2010). Demographic and clinical features were compared using parametric and non-parametric tests as appropriate. Principal component analysis (PCA) from the R ‘base’ package was used with visual inspection of PCA score-plot for the outlier detection (Esbensen et al., 2002). One subject was excluded during this procedure (see Results). The ‘randomForest’ package (Liaw and Wiener, 2002) was used in further analysis.

2.8. Problem formulation

The Random Forest algorithm is formally defined as a collection of tree-structured classifiers: f(x,θ_k),k=1,2,…,K; where θ_k is a random vector that meets i.i.d. (independent and identically distributed) assumption (Cover and Thomas, 2006) and each tree casts a unit vote for the most popular class at input x (Breiman, 2001). For classification problems, the forest prediction is the unweighted plurality of class votes (majority vote). The algorithm converges with a large enough number of trees. For more detailed explanation see Breiman (2001).

2.9. Parameter selection and classification

The R package ‘caret’ (Kuhn, 2012a) was used to implement recursive feature elimination (RFE) based on the Gini-criterion with 5-fold cross-validation (CV) within the context of RF (Kuhn, 2012b). Each of the steps described below was performed for all modalities: cortical thickness, sulcal depth, Jacobian maps, non-cortical volumes, combined parcelled measurements of cortical thickness and non-cortical volumes. First, the measurements with near-zero variance were removed from the feature sets and the resulting output underwent stepwise RFE. 10,000 trees were used to “grow” the first forest (using full feature set), and afterwards RFE was performed based on feature importance vector (defined in Eq. 1) derived from the first forest, by removing the lowest-ranked 5% of the features at each step (gradually reducing the dimensionality as 100%, 95%, … etc., up to 50%), and by the subsequent accuracy comparison with 5-fold CV. In order to reduce CPU, RAM and time usage the forests were trained with 1000 trees (instead of 10,000 for the first forest) at each step of RFE. After selection of the optimal feature subset, m_try-parameter adjustment was also performed using 1000 trees (search range ∈ $\left[\frac{\sqrt{N_{features}}}{4};\sqrt{N_{features}}\ast 2.5\right]$, step = $\frac{\sqrt{N_{features}}}{4}$), and finally the forests were retrained with optimal parameters using 10,000 trees. For the parcelled data (non-cortical volumes and parcelled thickness), an exhaustive search for optimal feature subset and m_try-parameter was performed, “growing” 1000 trees at each step with 10-fold CV. See diagram in Appendix Fig. A2.

The following parameters from the final models were reported to characterize performance: out-of-bag error (for the term definition see Breiman, 2001), area under the ROC curve (AUC), sensitivity/specificity and overall accuracy on the testing datasets of AD, HC and MCI subjects (see “Subsampling”). ROC-curves of the best models were compared using DeLong's test for two correlated ROCs, as implemented in the ‘pROC’ R-package (Robin et al., 2011).

The robustness of each model was also tested with respect to cohort differences (using a different cohort of AD and HC subjects from the AddNeuroMed study) (Simmons et al., 2011).

Finally, variables of importance were mapped from the best model into the brain space in order to identify the regions, which were most relevant for the classification.

At every split node τ one of the m_try variables, say x_k, is used to form the split and there is a resulting decrease in the Gini index. The mean decrease of the Gini index, ▵i(τ) (Eq. 1) was used as a metric, i.e.:

$$\Delta i\left(\tau \right)=i\left(\tau \right)-\left(p_{L}i\left({\tau }^L\right)+p_{R}i\left({\tau }^R\right)\right)$$ (1)

where $i\left(\tau \right)=1-{\sum }_{c\in C}{p}_c^2$ is the Gini index at node τ, $p_L=\frac{\left|s_j^L\right|}{\left|s_j\right|}$ and $p_R=\frac{\left|s_j^R\right|}{\left|s_j\right|}$ are the probabilities of sending a data point to the left and right nodes, respectively.

This metric reflects the contribution of a variable x_k to the node homogeneity of τ. Thus, a higher mean decrease (Eq. 1) of the Gini index for a particular feature means that the variable is present more often in nodes with higher purity among all trees in the forest (overall). The sum of all decreases in the forest due to a given variable x_k, normalized by the number of trees, therefore gives an estimate of its Gini importance (Eq. 2), i.e.:

$$I_G\left(x_k\right)=\frac{1}{n_{tree}}\sum _{t=1}^{n_{tree}}\sum _{\tau }\Delta i_{x_k}(\tau ,t).$$ (2)

Therefore, the Gini importance $I_G\left(x_k\right)$ indicates how frequent the particular feature $x_k$ was selected in a split node, and how large its overall discriminative value was for the classification task.

2.10. Morphometric modality combination

The classifiers trained with individual morphometric modality were combined by a majority vote and subsequently compared with the best model that demonstrated the highest accuracy (the one trained using parcelled thickness and volumetric measurements) on the test set.

We were also interested in assessing the effects of feature selection. For this purpose, all the steps described above (in “Parameter selection and classification”) were performed without RFE (only mtry-parameter adjustment). The resulting classifiers were assessed using the identical approach and combined together by a majority vote.

2.11. Use of different parcellation schemes

To investigate the effect of different atlases, we selected cortical thickness as a measurement type that produced the most accurate models and applied two parcellations implemented in the Freesurfer package – Desikan–Killiany (DK) and Destrieux (D) atlases – to extract averaged values from the predefined regions.

DK (Desikan et al., 2006) is a gyral-based neuroanatomical parcellation atlas that subdivides each hemisphere of the human brain cortex into 34 regions. One of the important features of this atlas, which is especially relevant for the present study, is that it has been developed using MRI scans not only from healthy controls (young, middle- and old-age groups), but also from patients with AD, and therefore this parcellation may be considered as more disease-specific. In addition, the atlas includes the entorhinal cortex as a separate region. This area is a crucial element of the episodic memory system (Lipton and Eichenbaum, 2008) and known to be affected by Alzheimer's disease from its initial stages (Braak and Braak, 1985).

The D atlas (Fischl et al., 2004; Destrieux et al., 2010) utilizes probabilistic labeling algorithm and among its advantages is that it is not tied to any specific neuroanatomical template, incorporating not only the probable location of a region of interest, but also the potential inter-subject variance of the location of the region (Fischl et al., 2004). This parcellation includes more regions than the DK atlas (74 areas for each hemisphere versus 34 in the DK atlas).

Next, after the training steps, we compared models' performance and ROC-curves as described above.

2.12. Comparison with linear SVM

Apart from this, we compared our best models with “reference classifier”, linear support vector machine (SVM) (Vapnik, 1995), tuned with recursive feature elimination. Of note, a non-linear SVM was not used as a reference, because it would be substantially more difficult and computationally expensive to tune and therefore would not be a fair comparison in terms of computation and memory costs.

2.13. Combining imaging biomarkers with ApoE genotype and demographics

The ɛ-4 allele of the gene encoding Apolipoprotein E is one of the major genetic risk factors for Alzheimer's disease (Alonso Vilatela et al., 2012). In order to investigate whether it was possible to further improve the best model (trained using combined cortical thickness and volumetric measurements) information on subjects' ApoE genotype (together with demographics) was added as an additional feature. The resulting model was trained and assessed as described above.

3. Results

3.1. Demographics

The main demographic characteristics are described in Table 1. Significant differences between AD and HC subjects were observed in education, in addition to word recall, ADAS-Cog and MMSE scores as expected.

Table 1.

Subject demographics: ADNI cohort.

	AD	HC	MCIa	AD/HC-comparison: test (p-value)
N	185	225	165	−
Age	75.2 [±7.48]	75.95 [±5.02]	75.46 [±7.37]	T = –1.17 (0.24)
M/F ratio	1.01 (93/92)	1.05 (115/110)	1.66 (103/62)	χ2 = 0.01 (0.93)
Education	14.6 [±3.24]	16.0 [±2.85]	15.65 [±2.97]	T = –4.65 (0.001)
MMSE	23.3 [±1.99]	29.1 [±0.98]	27.04 [±1.78]	T = –35.5 (0.001)

^a149 of total 165 MCI subjects developed Alzheimer's disease at some point during the 4-year follow-up period (MCI-converters).

Corresponding description of the AddNeuroMed cohort is provided in Appendix Table A3.

3.2. Outlier detection

PCA-based outlier detection revealed one subject, whose Freesurfer output was corrupted and was therefore excluded from the subsequent analysis.

3.3. Classification

Time and memory costs of RFE and m_try-adjustment varied substantially depending on the number of features. Thus, the total tuning time varied between 10 min (volumetric data) and more than 89 h (Jacobian maps). For all steps, from 6 to 10 CPU cores were used, and RAM usage also varied significantly between 1 Gigabyte (GB) (volumetric data) and 58 GB (Jacobian maps). For details see Appendix Table. A4.

Among all models, three had the best competing performances (Table 2, Fig. 1). The model trained using high-dimensional thickness measurements demonstrated AD-detection sensitivity/specificity of 88.6%/90.7%, its out-of-bag AUC (95% C.I.) was 0.93 (0.9–0.96); while the model trained using volumetric measurements resulted in sensitivity/specificity = 82.9%/86.7%, AUC = 0.91 (0.88–0.95); and using parcelled measurements of cortical thickness and subcortical structures resulted in sensitivity/specificity = 88.6%/92.0%, AUC = 0.94 (0.91–0.96).

Table 2.

AD/HC performance of the final models: ADNI cohort.

Models		OOB error [Train]	Sensitivity/specificity (OA) [Test]	AUC (95% C.I.)
Cortical thickness	RFE	14.0%	88.6%/90.7% (89.62%)	0.93 (0.9–0.96)
Sulcal depth		21.3%	80.0%/74.7% (77.3%)	0.84 (0.8–0.89)
Jacobian		21.7%	77.1%/81.3% (79.2%)	0.84 (0.79–0.88)
Volumes		15.0%	82.9%/86.7% (84.7%)	0.91 (0.88–0.95)
Thickness + volumes (ROI)		11.7%	88.6%/92.0% (90.3%)	0.94 (0.91–0.96)
Thickness	no RFE	14.7%	88.6%/89.3% (89.0%)	0.92 (0.89–0.95)
Sulcal depth		14.0%	80.0%/73.3% (76.67%)	0.83 (0.79–0.88)
Jacobian		21.0%	80.0%/80.0% (80.0%)	0.84 (0.79–0.88)
Volumes		16.7%	80.0%/86.7% (83.3%)	0.91 (0.88–0.94)
Thickness + volumes (ROI)		12%	85.7%/89.3% (87.5%)	0.93 (0.91–0.96)

AD/HC — Alzheimer's disease/healthy controls; OA — overall accuracy; OOB — out-of-bag estimate; AUC (95% C.I.) — area under the ROC curve with 95% confidence interval.

Fig. 1.

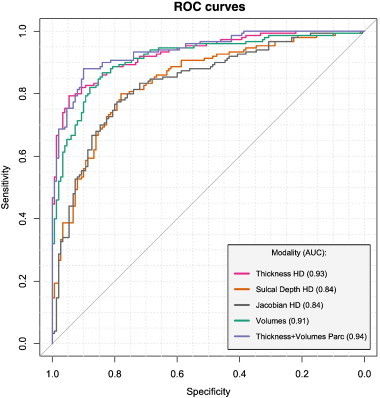
ROC curves: morphometric modalities (AD/HC). The figure illustrates ROC-curves of the models trained with different morphometric inputs. Three inputs demonstrate competing performances: high-dimensional (HD) cortical thickness, volumetric data and combined parcellated measurements. AD/HC — Alzheimer's disease/healthy controls.

Comparing these 3 models with the corresponding ones without RFE revealed significant (p < 0.001) advantages of RFE only for the model trained with high-dimensional cortical thickness measurements. The difference between the remaining two models was not significant.

Comparison of the most accurate imaging-based RF model (trained using parcelled measures of cortical thickness and volumetric data) with a corresponding SVM classifier, revealed advantages of the former. Test set AUC_RF + RFE (95% C.I.) = 0.98 (0.96–1) and AUC_SVM + RFE (95% C.I.) = 0.93 (0.87–0.98). Although there was a slight overlap between 95% C.I.s, further DeLong's test revealed significant (p = 0.03) differences.

3.4. Combined models

Combining all models by a majority vote improved the overall accuracy (OA) to 91.0% (sensitivity/specificity = 88.6%/93.3% — test set). The ROC difference between the combined models with and without RFE was significant (p = 0.017). It did not, however, differ from the ROC of the best classifier trained using parcelled measurements of cortical thickness and non-cortical volumes (see Appendix Fig. A5).

3.5. Effects of different parcellation schemes on classifier performance

Use of the D parcellation atlas resulted in lower accuracy: test set sensitivity/specificity/OA = 74.3%/82.7%/78.5% (compared to 82.9%/88.0%/85.4% for the DK atlas). ROC differences between parcellations [AUCs: 0.89 (0.85–0.93) and 0.90 (0.86–0.94), respectively] were non-significant. Both models demonstrated lower performance compared to the one trained using non-parcelled measurements of cortical thickness (sensitivity/specificity/OA = 88.6%/90.7%/89.6%, AUC = 0.93(0.9 − 0.96)). ROC differences (compared with “non-parcelled” models) were significant in both cases (p-values = 0.002 and 0.009, respectively). Test set accuracies were, however, equivalent for the DK and atlas-free measures. Results from this section are illustrated in Fig. 2.

Fig. 2.

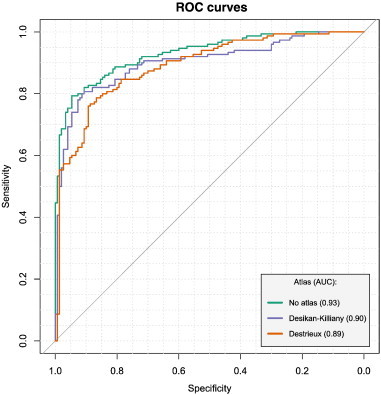
Effect of cortical parcellation using DK and D atlases on AD/HC performance. ROC-curves differed significantly when compared to one from the model trained using non-parcellated high-dimensional measurements (p-values: 0.002 and 0.009 — for Desikan-Killiany (DK) and Destrieux (D), respectively) differences were non significant between DK and D. AD/HC — Alzheimer's disease/healthy controls.

3.6. Prediction of MCI-to-AD conversion

The best ability to predict MCI-to-AD conversion based on imaging data only was observed for the model in which all RF ensembles were combined by a majority vote, and was achieved at 76.6% in overall MCI-to-AD conversion detection sensitivity, 2 years before actual dementia onset (averaged value for 6th-, 12th-, 18th- and 24th-month converters) with a specificity of 75.0% (see Table 3).

Table 3.

Ability of the AD/HC models to predict MCI-to-AD conversion: morphometric data, ADNI cohort.

Measurements	MCI-to-AD converters detection accuracya
	6 m (n = 14)	12 m (n = 44)	18 m (n = 30)	24 m (n = 35)	36 m+ (n = 26)	NC (n = 16)
Cortical thickness	78.6%	79.5%	70.0%	62.9%	65.3%	75.0%
Sulcal depth	71.4%	77.3%	53.3%	51.4%	53.8%	62.5%
Jacobian	60.2%	70.5%	76.7%	71.4%	53.8%	56.3%
Volumes	78.6%	72.7%	70.0%	68.6%	53.8%	75.0%
Combined	78.6%	79.5%	76.7%	71.4%	61.5%	75.0%

6, 12, 18, 24, 36 m+ — month of MCI-to-AD conversion; NC — non-converters (detected as HC by the classifiers); AD/HC — Alzheimer's disease/healthy controls.

^aHere the same models trained to classify images from AD and HC were used.

3.7. Combination with ApoE genotype and demographics

Adding ApoE genotype and demographics (age, sex, education) as additional predictors into our best AD/HC model, trained using combined cortical thickness and non-cortical volumetric measurements, did not improve AD/HC classification accuracy (sensitivity/specificity/OA = 90.7%/82.9%/86.7%). Meanwhile, its accuracy for MCI-to-AD conversion was relatively higher compared to other models with maximum sensitivity/specificity/OA values of 83.3%/81.3%/82.3% (See Table 4). However, this improvement was not significant with AUC for the averaged group of the 2-year converters of 0.83 (0.7–0.965) in the combined model versus AUC = 0.8(0.65 − 0.95) for cortical thickness alone (p = 0.74).

Table 4.

MCI-c/MCI-nc performance of the combined model (morphometry + ApoE+ demographics).

	OOB error	AD: Sens/spec (test)	MCI
			6 m (n = 14)	12 m (n = 44)	18 m (n = 30)	24 m (n = 35)	36 m+ (n = 26)	NC (n = 16)
Th + vol + ApoE+Age+Educ	11.3%	90.7%/82.9% (86.7%)	78.6%	75.0%	83.3%	80.0%	50.0%	81.3%

Th — cortical thickness; Vol — non-cortical volumes; Educ — education; MCI — mild cognitive impairment; ApoE — ApoE genotype; MCI-c/MCI-nc — MCI converters/MCI non-converters.

3.8. Robustness in different cohorts

Testing the ADNI models on AddNeuroMed data revealed good generalizability of the classifiers. The best stability (both for AD detection and prediction) was found for the models trained with high-dimensional measures of cortical thickness and parcelled thickness with volumetric measures. Combined models trained using both imaging and non-imaging data demonstrated absence of accuracy drop (see Table 5).

Table 5.

Classifiers’ performance in the same (ADNI) and separate (AddNeuroMed) cohorts.

Models	AD: Sens/Spec (OA)		MCI-converter 1yr sensitivity*
	Same cohort (ADNI)	Separate cohort (AddNeuroMed)	Same cohort (ADNI)	Separate cohort (AddNeuroMed)
Thickness	88.6%/90.7% (89.62%)	87%/78% (82.5%)	79.0%	76.2%
Sulcal Depth	80.0%/74.7% (77.3%)	Failed	74.4%	Failed
Jacobian	77.1%/81.3% (79.2%)	78.5%/72% (75.25%)	65.4%	57.1%
Volumes	82.9%/86.7% (84.7%)	70.1%/89% (79.5%)	75.7%	57.1%
Thickness + volumes (parc)	88.6%/92.0% (90.3%)	83.2%/89% (86.1%)	79.0%	71.4%
Morphometry + ApoE + demographics	90.7%/82.9% (86.7%)	84.2%/88.3% (86.25%)	78.0%	79%

The classifiers were trained on the subset from the ADNI dataset and then validated on testing sets from both ADNI (same) and AddNeuroMed (separate) cohorts.

Sens/Spec (OA) – Sensitivity/Specificity (Overall Accuracy);

* – for the AddNeuroMed cohort, definition of the MCI-to-AD converters subgroup (n=21) was defined based on 1-year follow-up.

NB: We did not compare accuracy to detect MCI non-converters due to only 1-year follow-up available for the AddNeuroMed cohort

3.9. Regions of relevance

As expected, the observed pattern of feature relevance was typical for AD and similar in models trained using high-dimensional and parcelled input (Figs. 3 and 4). It included atrophy in temporal areas (with more extensive changes in the entorhinal cortex, hippocampus, and amygdala), lateral ventricular size differences and parietal cortical abnormalities.

Fig. 3.

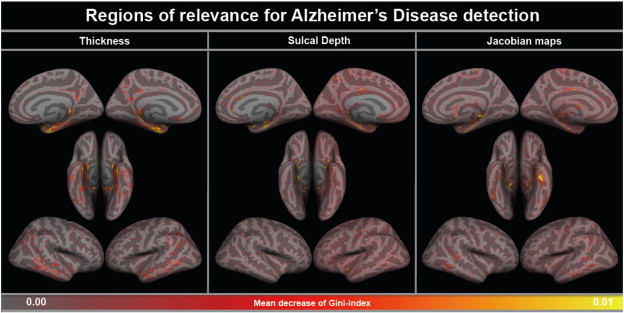
Cortical pattern of relevance for Alzheimer's disease detection: high-dimensional morphometric data. The figure illustrates regions, which were the most relevant for Alzheimer's disease detection based on the mean decrease of the Gini index (see Methods). In all three high-dimensional modalities, the pattern was AD-specific and included changes predominantly in temporal lobes (with maximum relevance of entorhinal region).

Fig. 4.

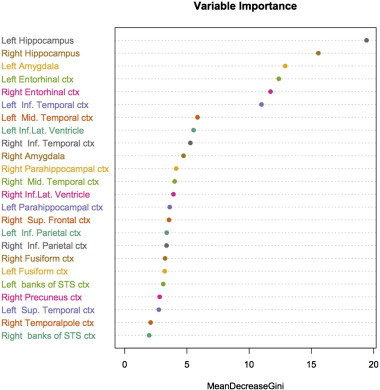
Pattern of relevance for Alzheimer's disease detection: parcelled morphometric data (cortical thickness [DK-atlas] + non-cortical volumes). The figure illustrates regions, which were the most relevant for Alzheimer's disease detection based on the mean decrease of the Gini index. Likewise in the high-dimensional input, the pattern-of-relevance is AD-specific.

4. Discussion

In the present study, we managed to produce robust and accurate models with good generalization across different cohorts. Our classifier ensembles demonstrated one of the best AD detection and prediction accuracy to date, superior over the reference model (linear SVM). It is also worth noting that performance of the best ADNI models on the AddNeuroMed dataset was equivalent to the cross-validated accuracies reported in Westman's study (Westman et al., 2011).

Of note, a recent study found no effect of the ApoE genotype on AD/HC discrimination accuracy (Aguilar et al., 2013). This is in line with our results, which however demonstrated that adding this feature may be beneficial for detecting earlier stages of the disease (MCI-to-AD converters).

To the best of our knowledge, this study is also one of the first to investigate the impact of different parcellation schemes and dimensionality of the imaging features on machine learning modeling accuracy, computation/memory and time costs.

In our experiments, the use of a parcellation with more subregions (148 versus 68) resulted in a drop in accuracy, which can be explained by the fact that the Desikan–Killiany atlas provides more AD-specific segmentation of temporal lobes compared to the Destrieux scheme, extracting measurements from the entorhinal cortex (the cortical area first affected in AD). Therefore, the use of atlases providing segmentation of the regions primarily affected by the most common neurodegenerative diseases may be beneficial in such tasks. However, this is rather speculative, since the atlases used in our study differ in many more aspects than just availability of the disease-specific regions. Measurement-specific parcellation schemes may also be useful for further accuracy improvement.

We did not find strong advantages for using high-dimensional input over parcelled measurements for our classification and prediction tasks. Both inputs produced models with equivalent performance. It is worth noting that tuning of the models with the parcelled input involved an exhaustive search for the optimal feature subset and m_try-parameter, whereas tuning of the HD-models was carried out only partially. Therefore, we cannot be sure that exhaustive tuning of the HD-models would not outperform the parcelled approach. But clarifying this currently does not appear to be feasible and practically relevant, even given abundant computational and memory resources available for our study. Nevertheless, it is worth mentioning that the use of high-dimensional raw features may have advantages for certain tasks due to the absence of spatial constraints of ROIs. Thus, we would generally expect this approach to produce better performance when a disease-specific atlas is not available.

In the present study, classifiers trained to differentiate between AD and HC demonstrated a good ability to predict MCI-to-AD conversion within 2 years before the onset of Alzheimer's disease, which is in line with previous results (Westman et al., 2012). The best accuracy was observed for the classifier produced by the combination of all “high-dimensional” models with the model trained using non-cortical volumetric measurements. Superior accuracy of this classifier over the model trained using parcelled data can be explained by the ability to detect less extensive structural changes, which are averaged in the atlas-based parcellation.

Interestingly, a drop in the ability to predict MCI-to-AD conversion over 6, 12, 18, 24 and 36+ months was substantially steeper for cortical thickness and sulcal depth compared to Jacobian maps, which demonstrated relatively stable performance over 2 years. It can be speculated that cortical thickness and sulcal depth are more dynamic measures, indicating disease progression, while Jacobian maps, as a geometric feature associated with cortical folding patterns, may be more genetically determined and therefore more stable across lifespan. Thus, it has been shown that geometric measures are associated with the formation of neuronal connections and cortical connectivity patterns, serving as characteristics of cerebral development (Armstrong et al., 1995; Van Essen, 1997). However, further research is clearly needed to support or reject this speculation.

Another interesting observation was that recursive feature elimination for the high-dimensional data improved performance of the model trained with cortical thickness, whereas other HD models did not seem to demonstrate substantial improvement. A possible explanation for this may be that the impact of neurodegeneration on cortical thickness is more localized to the entorhinal area, whereas its impact on sulcal depth and brain deformation is sparser, which complicates feature elimination.

The main strengths of the present study are:

• (a)the use of two large imaging databases of Alzheimer's disease with assessment of the classifiers' between-cohort robustness;
• (b)optimized models with one of the best accuracy to date;
• (c)evaluation of several important factors influencing classification performance, such as morphometric data modality and dimensionality, parcellation schemes;
• (d)long-term follow-up available for the MCI subgroup from the ADNI cohort that allowed the appropriate definition of MCI non-converters and assessment of models' sensitivity at different disease stages before the actual dementia onset.

It is also important to acknowledge several methodological limitations, such as an influence of possible diagnostic mislabeling of the data on our results, and possible misdiagnosis, since autopsy data were not available. Therefore, without solving these issues one should not expect perfect diagnostic class separation. The first problem can be addressed post-hoc by using computational approaches to detect mislabeled examples, whereas the second problem is organizationally more complex and pertains to the imperfection of diagnostic criteria for AD, which can potentially be overcome by employing more diagnostic procedures (for example, dopamine transporter imaging to exclude patients with Lewy body dementias), cerebrospinal fluid markers, and post-mortem diagnosis.

Another important issue pertains to robustness of the classifiers to the MR-protocol differences. Clinical implementation of such models will still require additional reliability assessment in order to make sure that models' between-cohort generalization is appropriate. Apart from this, traditional “offline” or “batch” learning framework (used in our study, where the whole training set is available to the algorithm at the beginning) does not allow any modifications of the models after the training has been completed. The latter would be very relevant especially for the clinical setting where continuous data flow is usually available. The “online” learning framework (where the system gradually “learns” using one instance at a time) may be beneficial in this context, providing not only an opportunity to update the models, but also valid estimations of the prediction confidence under a general i.i.d. assumption (independent and identically distributed) (Vovk, 2005; Gammerman and Vovk, 2007; Nouretdinov and Lebedev, 2013). Since this approach can be applied to an individual patient and gives reliable estimations of possible diagnoses, it has strong potential to be used in clinical practice and, to our opinion, would be the best candidate for diagnostic trials employing computer-aided medical decision-support systems.

To conclude, our workflow produces accurate models for detection and prediction of AD with good between-cohort robustness. The use of raw high-dimensional measurements does not appear to be effective due to its high computation/memory costs and at the same time equivalent performance compared to models trained with parcelled input. Therefore, we recommend using disease-specific parcellation schemes for image classification tasks. Combination with other imaging and non-imaging biomarker modalities may provide further improvement in accuracy and model robustness.

Conflicts of interest

The authors declare that they have no conflicts of interest that may influence the results.

Appendix.

Fig. A1.

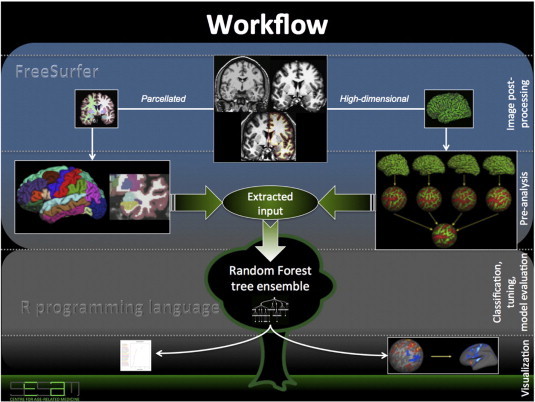
Workflow diagram. The diagram illustrates main steps of image post-processing and analysis. It starts and proceeds in two directions aimed at extraction of parcelled and high-dimensional measurements using Freesurfer software (blue box). After this part had completed, the extracted measures underwent steps for outlier detection, and the resulted output was used in further Random Forest classification runs (in R programming language — gray box). We additionally tuned our models using recursive feature elimination and m_try-parameter adjustment (which defines the number of predictors randomly sampled at each node of the classifier). Finally, feature importance vectors from the best models were either mapped into the brain space (for the high-dimensional data) or plotted (for the parcelled input).

Fig. A2.

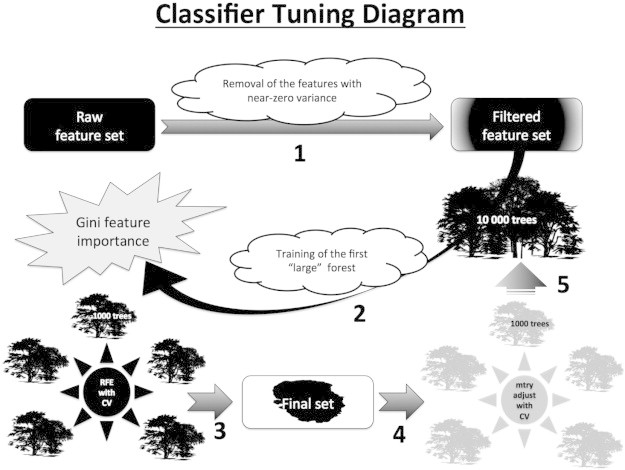
Classifier tuning diagram. The diagram describes main steps performed during the tuning of Random Forest models. This framework was employed for all modalities: cortical thickness, sulcal depth, Jacobian maps, non-cortical volumes, combined parcelled measurements of cortical thickness and non-cortical volumes. (1) First, the measurements with near-zero variance were removed from the feature sets and the resulting output underwent stepwise recursive feature elimination (RFE); (2) 10,000 trees were then used to “grow” the first forest (using full feature set), and afterwards (3) RFE was performed based on feature importance vector derived from the first forest, by removing lowest-ranked 5% of the features at each step (gradually reducing the dimensionality as 100%, 95%, … etc., up to 50%), and by the subsequent accuracy comparison with 5-fold CV; (4) after selection of the optimal feature subset, m_try-parameter adjustment was also performed using 1000 trees (search range ∈ $\left[\frac{\sqrt{N_{features}}}{4};\sqrt{N_{features}}\ast 2.5\right]$, step = $\frac{\sqrt{N_{features}}}{4}$); (5) the forests were retrained with optimal parameters using 10,000 trees.

Table A3.

AddNeuroMed cohort demographics.

	AD	HC	MCIa
N	107	100	114
Age	75.7 [±5.63]	73.2 [±6.87]	74.4 [±5.79]
M/F ratio	0.65 (42/65)	1.08 (52/48)	1.11 (60/54)
Education	7.6 [±3.78]	8.59 [±4.17]	10.5 [±4.82]
MMSE	20.8 [±4.74]	29.1 [±1.26]	27.1 [±1.68]

^a21 of total 114 MCI subjects developed Alzheimer's disease at some point over 1-year follow-up. (MCI-converters)

Table A4.

Model tuning.

Measurement	NZV	Feature subset after RFE	Opt mtry	CPU cores used	RAM usage (RFE/mtry)	Total tuning time
Thickness (HD)	14,880	156,402	356	6	51.3/44 GB	80 h 50 min
Sulcal depth (HD)	14,851	218,983	1170	6	51/46 GB	84 h 22 min
Jacobian (HD)	0	262,147	1024	6	58/45 GB	89 h 27 min
Volumes (ROI)a	0	6	2	10	1 GB	10 min
Thickness + volumes (parc)a	0	24	4	10	3.8 GB	3 h 35 min

NZV — number of features with Near-Zero Variance removed at the first step; RFE — Recursive Feature Elimination; opt m_try — optimal m_try-parameter (see Methods for details).

^aFor these models, an exhaustive search for optimal m_try parameter and feature subset has been performed.

Fig. A5.

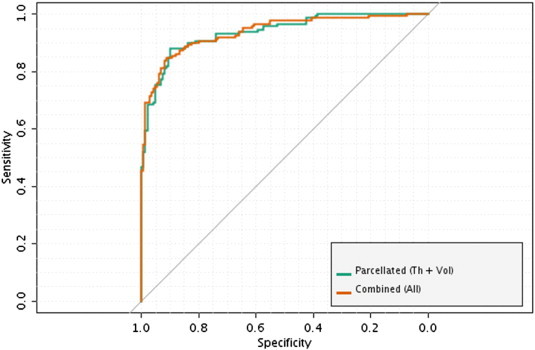
ROC curves: best models (AD/HC). The figure illustrates ROC-curves of the most accurate models trained to differentiate between AD and HC. The model trained using combined parcelled (DK atlas) cortical thickness measures and subcortical volumetric data produced equivalent accuracy compared to the higher-order ensemble model (where all classifiers were combined together by a majority vote). AD/HC — Alzheimer's Disease/Healthy Controls.