A computational study of the effect of intraglottal vortex-induced negative pressure on vocal fold vibration

Abstract

Recent studies reported the formation of intraglottal vortices for medium and high subglottal pressures in excised-larynx experiments, and hypothesized that the suction force created by these vortices might affect vocal fold vibration. However, high subglottal pressures often lead to large vocal fold elastic recoil forces, and it is unclear if the vortex-induced suction force is large enough compared with the elastic recoil force to have noticeable effects on vocal fold vibration. In this study, the validity of this hypothesis was examined using a computational model. The results suggest that intraglottal vortices might only have small effects on vocal fold vibration.

1. Introduction

The myoelastic-aerodynamic theory of phonation (van den Berg, 1958) describes the oscillation of the vocal folds based on the interaction between the glottal flow pressure and the vocal fold elastic forces. The glottal flow has known characteristics including flow separation from the surface of the vocal folds, formation of a glottal jet flow, shear layer instabilities, and transition of the glottal jet into an unsteady turbulent flow downstream of the glottis (Neubauer et al., 2007). Recent computational and experimental investigations also reported possible formation of intraglottal vortical structures near the superior medial edge of the vocal fold surface during the closing phase of the phonation cycle (Mihaescu et al., 2010; Oren et al., 2014a). Excised larynx experiments further showed that the intraglottal flow separation and the subsequent formation of the intraglottal vortices occurred only at large glottal divergent angles, which were reached only for medium to high subglottal pressures (Khosla et al., 2014b). It was shown that the intraglottal vortices can produce a local negative gauge pressure (gauge pressure is defined relative to ambient pressure) on the superior aspect of the vocal fold medial surface. Thus, it has been hypothesized that intraglottal vortices may facilitate rapid glottal closure and consequently affect voice production (Khosla et al., 2014a; Oren et al., 2014b).

In spite of these observations, the significance of the intraglottal vortex-induced negative pressure for phonation has not been established and is still a matter of debate. First, the experiments in Oren et al. (2014b) revealed that the intraglottal vortices were formed and existed only for a small fraction of the closing phase near the superior edge of the vocal folds; therefore, it is unclear whether a sufficiently large portion of the vocal fold surface was exposed to the intraglottal vortex-induced negative pressure for a long enough period to have some effect on vocal fold vibration. Second, although the peak magnitude of the negative pressure in the experiments of Oren et al. (2014b) was as high as about 55% of the subglottal pressure at the center of the vortices, this value on the surface of the vocal folds, as shown in Oren et al. (2014b), was smaller and approximately less than 30% of the subglottal pressure. Additionally, it should be noted that the peak value of the negative pressure reported in Oren et al. (2014b) varied over time and the time-averaged peak magnitude of the negative pressure during the exposure time was significantly lower than the highest negative peak value (i.e., 55% of the subglottal pressure). Finally, it is questionable whether the vortex-induced negative pressure is large enough, compared with vocal fold inertia and elastic recoil, to have a functional effect on glottal closure. The current work aims to evaluate the significance of the vortex-induced negative pressure on vocal fold vibration.

2. Method

Ideally, the effects of the intraglottal vortex-induced negative pressure on phonation can be investigated by comparing phonation at conditions with and without such negative pressures. However, this is difficult to achieve in either experiments or computational simulations using a Navier-Stokes description of the glottal flow since the vortex formation is an integral part of the flow field and is impossible to remove without affecting other aspects of the flow. In the current study, the effect of the intraglottal vortices was modeled as a negative pressure superimposed on the flow pressure predicted by a base glottal flow model. In this way, the effect of the intraglottal vortices can be selectively activated or deactivated independent of the base flow so that its contribution to phonation can be investigated.

For the base flow, a reduced-order flow solver based on Bernoulli's equation was employed to predict the air pressure on the surface of the vocal folds up to the flow separation point. The flow separation point was assumed to be the superior edge of the vocal fold medial surface for convergent glottis; whereas for divergent vocal folds, it was allowed to move upstream along the medial surface to a location where the ratio of the glottal area to the minimum area of the glottis was a user-defined constant. In this study, this constant ratio was 2, which is slightly larger than its typical value used in voice modeling studies but still within the range reported in previous computational and experimental studies (Alipour and Scherer, 2004; Šidlof et al., 2011). Implementation of typical values of this constant ratio, e.g., 1.2 or 1.47, led to very high phonation onset or vocal fold vibration with a divergent medial surface during a considerably large portion of one oscillation cycle, which was considered unrealistic and thus disregarded.

The effect of the intraglottal vortices was modeled as a sinusoidal negative pressure wave, with a magnitude proportional to the mean subglottal pressure, applied to the portion of the vocal fold medial surface between the flow separation point and the superior edge of the vocal folds,

$$\text{IVIP}\left(x\right)=-0.5\hspace{0.17em}{C}_{\text{IVIP}}{P}_{\text{sub}}\left(\text{cos}\left(2\pi \left(\frac{x}{l}\right)\right)-1\right).$$ (1)

In this equation IVIP stands for the intraglottal vortex-induced pressure, $C_{\text{IVIP}}$ is a coefficient defining the ratio of the peak negative IVIP with respect to the mean subglottal pressure (between 0 and 0.3), $P_{\text{sub}}$ is the mean subglottal pressure, $l$ is the distance between the flow separation point and the superior medial edge of the vocal folds, and $x$ is the distance from a point on the medial edge of the vocal folds to the superior medial edge of the vocal folds (Fig. 1). Equation (1) overestimates the temporal and spatial extent of the vocal fold surface exposure to the IVIP, but it allows us to have a quantitative estimate of the upper limit of the effect of the IVIP on phonation.

Fig. 1.

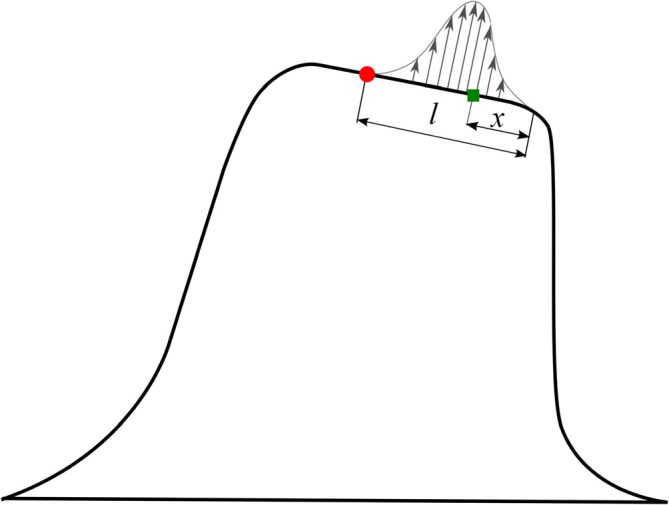
(Color online) A schematic view of the vocal fold model and the intraglottal vortex-induced suction force applied on its medial surface. The circular point is the location of flow separation. The rectangular point is an arbitrary point between the flow separation point and the superior medial edge of the vocal fold where the suction force is applied. The flow direction is from left to right.

For simplicity, a two-dimensional two-layer vocal fold model was considered in this study. The vocal fold was modeled using the non-linear finite element solver ADINA. To cover the loudness range of phonation, two model conditions were investigated in our study, namely, the Soft and the Stiff models, which roughly corresponded to conditions of soft (low muscle activities) and loud (strong muscle activities) phonation, respectively. The two models had identical geometries but different body- and cover-layer Young's moduli. The geometry of the vocal fold models was defined as in Zhang (2009), with a depth (along the medial-lateral direction) of 6 and 0.5 mm for the body and cover layers, respectively, and a medial surface thickness of 2.4 mm. The Young's moduli of the cover and body layer for the soft model were 3.2 and 16 kPa, and for the stiff model were 6 and 30 kPa, respectively. The density and Poisson ratio of both models were 1000 kg/m³ and 0.47, respectively. The damping effect was included in the simulations using a Rayleigh damping scheme with damping parameters $\alpha =0\hspace{0.17em}$ and $\hspace{0.17em}\beta =0.1035\times {10}^{-3}$. The vocal fold models were discretized using 2072 two-dimensional solid elements with four nodes per element, and the results were found to be independent of discretization. The lateral boundary of the vocal fold was fixed while the other boundaries were subject to air pressure calculated from the glottal flow model, with or without the IVIP.

The time step size of the simulations was $\hspace{0.17em}\Delta t=0.01\hspace{0.17em}\text{ms}$, and it was allowed to be adapted automatically. The simulations for the soft model were performed for the subglottal pressures of 500, 600, 700, and 800 Pa whereas the subglottal pressures for the stiff model were 1000, 1100, 1200, 1300, 1400, and 1500 Pa. For each subglottal pressure, the peak magnitude of the IVIP was varied from 0% to 30% of the mean subglottal pressure with an increment of 10%. The simulations were performed for at least 0.8 s to ensure that self-sustained vibration was established.

3. Results

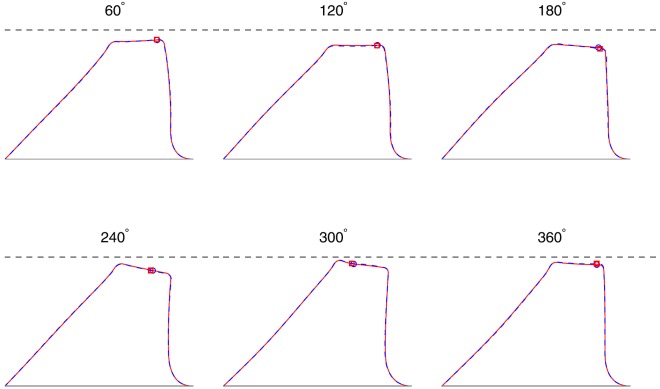
Previous experimental investigations suggested that the most significant effect of the intraglottal vortices on vocal fold vibration would be obtained only when the subglottal pressure is high (Khosla et al., 2014b). In the current computational study, the highest subglottal pressure that yielded a numerically stable solution was $P_{\mathit{s}\mathit{u}\mathit{b}}=1500\hspace{0.17em}\text{Pa}\hspace{0.17em}$ in the stiff model. Figure 2 compares the vibration of this model for peak IVIP magnitudes of 0% (without IVIP) and 30% of the subglottal pressure at six different phases of one vocal fold oscillation cycle. The beginning and end of a cycle were chosen as the instant when the superior medial edge of the vocal fold started to move away from the glottal midline. The location of the flow separation point is also depicted on the surface of the vocal fold in Fig. 2. In general, the addition of an IVIP at 30% of the subglottal pressure only yielded small difference in both the flow separation location and the vibration pattern. This observation was consistent across all conditions investigated.

Fig. 2.

(Color online) Vibration of the stiff vocal fold model during one oscillation cycle. $P_{\text{sub}}=1500\hspace{0.17em}\text{Pa}$. The solid red lines are the vocal fold surface for the condition without IVIP and the dashed blue lines are the vocal fold surface for $C_{\text{IVIP}}=0.3$. The flow separation locations are marked by the rectangular red symbols for no IVIP and blue circular symbols for $C_{\text{IVIP}}=0.3$. The black dashed lines above the vocal folds indicate the glottal midline. The flow direction is from left to right.

The volumetric fluctuation of the glottal flow is the primary sound source of phonation (Fant, 1982). The volume flow waveforms (Q) within one phonation cycle of the stiff model at $P_{\text{sub}}=1500\hspace{0.17em}\text{Pa}$ and various values of $C_{\text{IVIP}}\hspace{0.17em}$ are shown in Fig. 3(a). The corresponding time derivative of the volume flow rate is shown in Fig. 3(b). The negative peak of the time derivative of the volume flow rate, also referred to as the maximum flow declination rate (MFDR), is known to have a strong correlation with vocal intensity (Holmberg et al., 1988). For a given subglottal pressure, as the $C_{\text{IVIP}}\hspace{0.17em}$ was increased from 0 to 0.3, both the peak-to-peak amplitude of the volume flow rate and the absolute value of MFDR increased slightly.

Fig. 3.

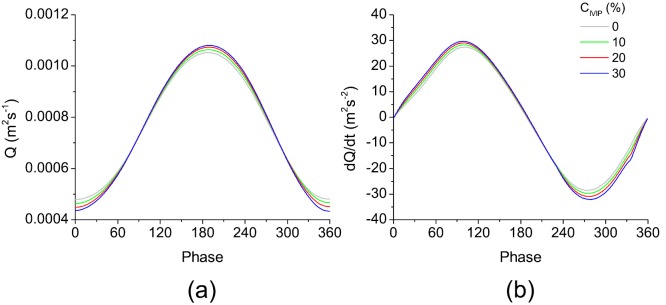
(Color online) (a) The glottal volume flow rate and (b) the time derivative of the glottal volume flow rate for the stiff model with $P_{\text{sub}}=1500\hspace{0.17em}\text{Pa}$. The legends show the percentage magnitude of the IVIP with respect to the subglottal pressure.

Figure 4 summarizes our computational observations over a wider range of the subglottal pressures and $C_{\text{IVIP}}\hspace{0.17em}$ for both the soft and stiff models. The effect of intraglottal vortices on the amplitude of vibration of the vocal folds is shown in Fig. 4(a). It was observed that for a given subglottal pressure the vibration amplitude increased as the $C_{\text{IVIP}}\hspace{0.17em}$ was increased. This effect generally increased with increasing subglottal pressures for both models, with a maximum change in the vibration amplitude of 0.08 mm observed in the soft model at $P_{\text{sub}}=800\hspace{0.17em}\text{Pa}\hspace{0.17em}$. Figure 4(b) shows the percentage changes of MFDR due to the presence of the IVIP with respect to the conditions without IVIP. The percentage changes in MFDR gradually increased with increasing subglottal pressure and $C_{\text{IVIP}}\hspace{0.17em}$ for both the soft and stiff model. In most cases, the effect of the intraglottal vortices on MFDR remained less than 10%. The maximum MFDR percentage change for the soft and stiff models was 12.53% at $P_{\text{sub}}=800\hspace{0.17em}\text{Pa}$ and 11.62% at $P_{\text{sub}}=1500\hspace{0.17em}\text{Pa}\hspace{0.17em}$, respectively, and both occurred when the peak magnitude of IVIP was 30% of the corresponding subglottal pressure.

Fig. 4.

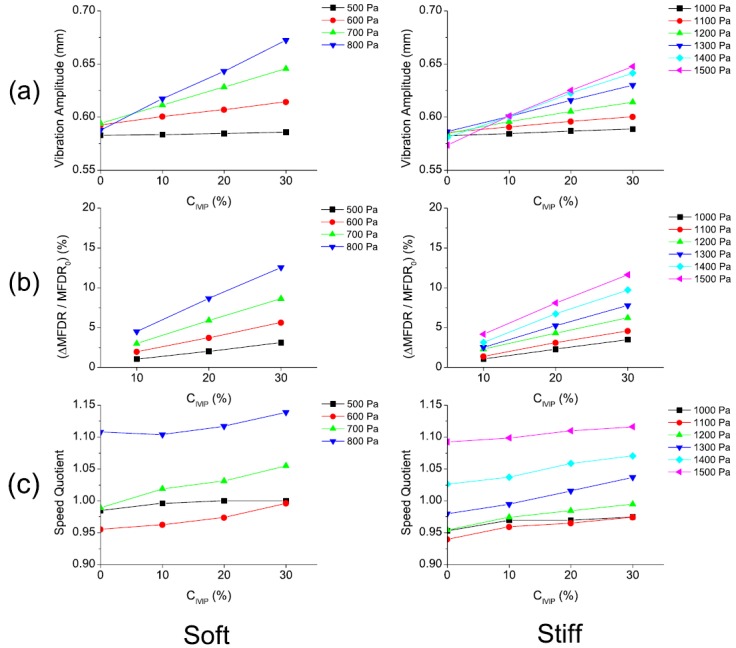
(Color online) The effect of IVIP on (a) the vibration amplitude, (b) percentage change of MFDR, and (c) speed quotient for both the soft and stiff vocal folds models. In this figure ${\text{MFDR}}_0\hspace{0.17em}$ stands for the case without IVIP and $\Delta \text{MFDR}={\text{MFDR}}_{{\mathrm{C}}_{\text{IVIP}}}-{\text{MFDR}}_0$.

An additional parameter shown in Fig. 4(c) is the speed quotient (SQ), a measure of symmetry of the glottal flow waveform, which is calculated as the ratio between the opening and closing phases within one oscillation cycle. In general, the SQ increased slightly with increasing subglottal pressure except for conditions near phonation onset (around $\hspace{0.17em}{P}_{\text{sub}}=500\hspace{0.17em}\text{Pa}$ and $P_{\text{sub}}=1000\hspace{0.17em}\text{Pa}$ for the soft and stiff models, respectively). However, for a given subglottal pressure, increasing $C_{\text{IVIP}}\hspace{0.17em}$ led to only a small increase in SQ, indicating a minimal waveform-skewing effect of the IVIP.

4. Discussion

Using a computational model of phonation, this study sought to determine possible effects of intraglottal vortices on vocal fold vibration. It was observed that the presence of the negative pressure corresponding to intraglottal vortices slightly increased the vibration amplitude and the MFDR. The largest increase in MFDR was approximately 12.5% in the soft model at the highest subglottal pressure and an IVIP magnitude of 30% of the subglottal pressure. This corresponds to a 1 dB increase in sound intensity, assuming a linear relation between the MFDR and the outside sound pressure amplitude, which is perceptually insignificant. The intraglottal vortices also caused a slight but negligible increase in SQ, indicating a negligible role of the IVIP in glottal flow waveform skewing and, thus, the excitation of high-order harmonics in the voice spectrum. In summary, the presence of the IVIP, even at extreme conditions, caused a slight increase in sound intensity but otherwise negligible effects on the shape of the glottal flow waveform.

The results of this study may be interpreted as the upper limit of the effects of IVIP, due to the inherent overestimation of the IVIP magnitude in our model as well as both the temporal and spatial extent of the IVIP influence on the vocal fold surface. In our computational investigation, the IVIP was always imposed with a constant peak magnitude proportional to the given subglottal pressure, whereas in reality the peak magnitude of the negative pressure in the experiments gradually increased before reaching its instantaneous peak and then vanished. Moreover, the IVIP in this study was applied to the part of the vocal fold surface between the flow separation point and the superior edge of the vocal fold medial surface. In reality, the vortices are convected downstream by the jet flow as they are being formed; hence, when the IVIP magnitude reaches its maximum, these vortices are already at a much downstream position. Indeed, the vortices were often observed at the superior edge of the vocal fold medial surface in previous studies (Oren et al., 2014b). Considering these possible overestimations of the IVIP, it is reasonable to expect that the effect of the intraglottal vortices in normal phonation is probably smaller than what was found in the current study.

The limitations of our study lie in the simplifications of the model used, in both the flow and the vocal fold. Particularly, a two-dimensional vocal fold model was used and glottal closure was never observed in our simulations, although the lack of the glottal closure was consistent with previous experimental observations in synthetic isotropic vocal fold models of similar geometries (Xuan and Zhang, 2014). Only two vocal fold stiffness conditions were examined in this study. Thus, this study needs to be repeated in the future using a more realistic computational model of the vocal folds for a large range of stiffness conditions before generalization to realistic human phonation. Refinement of the IVIP model based on further experimental characterization of intraglottal vortices would also allow us to more accurately evaluate their effects on phonation.