Optimizing Sedative Dose in Preterm Infants Undergoing Treatment for Respiratory Distress Syndrome

Abstract

The Intubation-Surfactant-Extubation (INSURE) procedure is used worldwide to treat pre-term newborn infants suffering from respiratory distress syndrome, which is caused by an insufficient amount of the chemical surfactant in the lungs. With INSURE, the infant is intubated, surfactant is administered via the tube to the trachea, and at completion the infant is extubated. This improves the infant’s ability to breathe and thus decreases the risk of long term neurological or motor disabilities. To perform the intubation safely, the newborn infant first must be sedated. Despite extensive experience with INSURE, there is no consensus on what sedative dose is best. This paper describes a Bayesian sequentially adaptive design for a multi-institution clinical trial to optimize the sedative dose given to pre-term infants undergoing the INSURE procedure. The design is based on three clinical outcomes, two efficacy and one adverse, using elicited numerical utilities of the eight possible elementary outcomes. A flexible Bayesian parametric trivariate dose-outcome model is assumed, with the prior derived from elicited mean outcome probabilities. Doses are chosen adaptively for successive cohorts of infants using posterior mean utilities, subject to safety and efficacy constraints. A computer simulation study of the design is presented.

1. Introduction

Respiratory distress syndrome (RDS) in pre-term newborn infants is characterized by an inability to breathe properly. RDS is associated with the facts that the infant’s lungs have not developed fully and do not have a sufficient amount of surfactant, a compound normally produced in the lungs that facilitates breathing. A relatively new but widely used procedure for preterm infants suffering from RDS is Intubation-Surfactant-Extubation (INSURE), which is carried out when the infant is a few hours old. Once RDS has been diagnosed, the INSURE procedure is carried out as soon as possible to reduce the need for mechanical ventilation and risk of bronchopulmonary dysplasia. With INSURE, the infant is intubated, surfactant is administered via the tube to the trachea, and at completion the infant is extubated. The surfactant spreads from the trachea to the surface of the alveola, where it lowers alveolar surface tension and reduces alveolar collapse, thus improving lung aeration and decreasing respiratory effort. The aim is to improve the infant’s ability to breathe and thus increase the probability of survival without long term neurological or motor disabilities (Verder, et al., 1994; Bohlin, et al., 2007; Stevens, et al., 2007). In most cases, the INSURE procedure takes no more than one hour, and ideally it is completed within 30 minutes. Because intubation is invasive, to allow it to be done safely and comfortably the infant first must be sedated. The drugs propofol (Ghanta et al., 2007) and remifentanyl (Welzing et al., 2009) are widely used for this purpose. Although the benefits of the INSURE procedure are well-established, it also carries risks associated with intubation done while the infant is awake, and risks associated with the sedative. These include possible adverse behavioral and emotional effects if the infant is under-sedated as well as adverse haemodynamic effects associated with over-sedation. The goal in choosing a sedative dose is to sedate the infant sufficiently so that the procedure may be carried out, but avoid over-sedating. While it is clear that dose should be quantified in terms of amount per kilogram (kg) of the infant’s body weight, little is known about what the optimal dose of any given sedative may be for the INSURE procedure. Propofol doses that are too high, or that are given recurrently or by continuous infusion, have been associated with serious adverse effects in the neonatal or pediatric populations (Murdoch and Cohen, 1999; Vanderhaegen, et al., 2010; Sammartino, et al. 2010). Unfortunately, there is no broad consensus regarding the dose of any sedative in the community of neonatologists. The doses of that actually are used vary widely, with each neonatologist using their preferred dose chosen based on personal clinical experience and consensus within their neonatal unit.

Pediatric clinical trials are challenging primarily due to ethical considerations, including informed consent, the fact that many pediatricians are hesitant to experiment with children, and the fact that adverse events may have lifelong consequences. These issues are especially difficult with newborn infants just a few hours old. While there is an extensive literature on adaptive dose-finding methods, these have been developed primarily for chemotherapy in oncology, which is a very different medical setting than sedation of neonates as described above. To date, no adaptive dose-finding design has been developed specifically for infants.

The primary aim of the clinical trial described here is to optimize the dose of propofol given at the start of the INSURE procedure. Six possible doses are considered: 0.5, 1.0, 1.5, 2.0, 2.5, and 3.0 mg/kg body weight. Inherent difficulties in determining an optimal propofol dose are that there are both desirable and undesirable clinical outcomes related to dose, the probability of each outcome may vary as a complex, possibly non-monotone function of dose, and the outcomes do not occur independently of each other. In any dose-finding clinical trial in humans, it is not ethical to randomize patients fairly among doses because, a priori, some doses are considered unsafe or ineffective, and as data are obtained some doses may turn out to be either unsafe or to have unacceptably low efficacy. These ethical considerations motivate the use of sequential, outcome-adaptive, “learn-as-you-go” dose-finding methods (cf. O’Quigley, et al., 1990; Thall and Russell, 1998; Chevret, 2006; Cheung, 2011). Such methods are especially important when treating newborn infants diagnosed with RDS, where sedative dose prior to intubation may have adverse haemodynamic effects and failure of the INSURE procedure may result in prolonged mechanical ventilation, a recognized risk factor for long term adverse pulmonary outcomes (Stevens, et al., 2007). Consequently, to optimize propofol dose in a reliable and ethical manner in the setting of the INSURE procedure, a clinical trial design must (1) account for unknown, potentially complex relationships between dose and key clinical outcomes, (2) account for inherent risk-benefit trade-offs between efficacy and adverse outcomes, (3) adaptively learn and make decisions using the accumulating dose-outcome data during the trial, and (4) reliably choose a final, “optimal” dose that can be recommended for future use worldwide with the INSURE procedure.

The clinical trial design described here satisfies all of these requirements. It uses a Bayesian sequentially outcome-adaptive method that relies on subjective utilities, elicited from neonatologists who perform the INSURE procedure, that account for the benefits of desirable outcomes and the risks of adverse outcomes. To characterize propofol dose effects in a realistic and practical way, we define three co-primary outcomes, including two desirable efficacy outcomes and one undesirable adverse outcome. The first efficacy outcome is that a “good sedation state,” GSS, is achieved quickly. GSS is a composite event defined in terms of five established ordinal sedation assessment criteria variables scored within five minutes of the first sedative administration (Hummel, et al., 2008). These five variables are A₁ = Crying Irritability, A₂ = Behavior State, A₃ = Facial Expression, A₄ = Extremities Tone, and A₅ = Vital Signs. Each variable takes on an integer value in the set {−2, −1, 0, +1, +2}, with A_j = −2 corresponding to highest sedation and A_j = +2 to highest infant discomfort. The Vital Signs criterion score A₅ is defined in terms of heart rate (HR), respiration rate (RR), mean blood pressure (BP), and saturated oxygen in the circulating blood (SaO₂). Supplementary Table 1 gives detailed definitions of these five assessment variables.

The overall sedation assessment score is defined as $Z={\sum }_{j=1}^5{A}_j$, and a good sedation score is defined as GSS = {−7 ≤ Z ≤ −3}. Because a GSS is required to intubate the infant, if it is not achieved with the initial propofol dose then an additional fixed dose of 1.0 mg/kg propofol is given. If this still does not achieve a GSS, then use of another sedative is allowed at the discretion of the attending clinician. A nontrivial dimension reduction is performed in defining GSS, since Z is defined in terms of the variables A₁,⋯, A₄ and A₅, which in turn is a function of three haemodynamic measurements. However, A₁,⋯, A₅, Z, and GSS were defined by neonatologists who have extensive experience with the INSURE procedure.

Because it is desirable to complete the INSURE procedure as quickly as possible, the design also accounts for the efficacy event, EXT, that the infant is extubated within at most 30 minutes of intubation. This is motivated by the desire to sedate the infant sufficiently so that the INSURE procedure may be carried out, but not over-sedate. In addition to the efficacy events GSS and EXT, it is essential to monitor adverse events and include them in the dose-finding procedure. To do this, a third, composite adverse event was defined. The adverse haemodynamic event, HEM, is defined to have occurred if the baby’s HR falls below 80 beats per minute, SaO₂ falls below 60%, or mean BP decreases by more than 5 mm Hg from a chosen inferior limit corresponding to the infant’s gestational age. The time interval for monitoring the infant’s HR, SaO₂, and BP values to score HEM includes both the period while the infant is intubated and the subsequent three hours following extubation. Thus, HEM is defined very conservatively.

Our proposed methodology is very different from adaptive dose-finding methods based on a single outcome. For example, a method based on GSS alone might choose a dose to maximize Pr(GSS | dose), maximize information using about this dose-response function using D-optimal or A-optimal designs, or possibly find the “minimum effective dose” for which it is likely that Pr(GSS | dose) ≥ $p_G^{*}$ for some fixed target $p_G^{*}$. There is an extensive literature on such methods. Some useful references are Fedorov and Leonov (2001), Atkinson, Donev, and Tobias (2006), Dette, et al. (2008), and Bornkamp, et al. (2011). In the present setting, a method that is ethically acceptable must account for more than one outcome, and must quantify the trade-offs between the risk of HEM and the benefits of GSS and EXT. This requires specifying and estimating a trivariate dose-outcome probability distribution for these three events. Even if this function were known perfectly, however, some numerical representation of the desirabilities of the eight possible elementary outcomes still would be needed to decide which dose is best. We quantify this using elicited utilities, described in Section 3, below.

The propofol trial design uses a sequentially outcome-adaptive Bayesian dose-finding method based on a numerical utility of each of the eight possible combinations of the three outcomes GSS, EXT, and HEM. The numerical utilities, given in Table 1, were elicited from the neonatologists planning the trial, who are experienced with the INSURE procedure and have observed and dealt with these events in their clinical practice. Before the elicitation, the maximum numerical utility 100 was assigned to the best possible event (GSS = yes, EXT = yes, HEM = no), and the minimum numerical utility 0 was assigned to the worst possible event (GSS = no, EXT = no, HEM = yes). The six remaining intermediate values were elicited subject to the obvious constraints that the utility must increase as either GSS or EXT goes from “no” to “yes” and must decrease as HEM goes from “no” to “yes.” The range 0 to 100 was chosen for convenience since it is easy to work with, although in general any numerical domain with which the area experts are comfortable could be used. By quantifying the desirability of each of the eight possible outcomes, the utility function formalizes the inherent trade-off between the INSURE procedure’s risks and benefits, insofar as they are characterized by these three events. An essential property of the numerical utilities is that they quantify the subjective opinions of the area experts. This is an advantage of the methodology since, inevitably, any multidimensional criterion must be reduced to a one-dimensional object if decisions are to be made. However a dimension reduction is done, it is inherently subjective.

Table 1.

Consensus elicited utilities and alternative utilities of the eight possible elementary outcomes. GSS = {good sedation score}, EXT = {extubation within 30 minutes}, HEM = {an adverse value of heartbeat, blood oxygen level, or blood pressure during the INSURE procedure or within 3 hours after extubation}.

a. Elicited Consensus Utilities.
	GSS = Yes		GSS = No
	EXT = Yes	EXT = No	EXT = Yes	EXT = No
HEM = Yes	60	20	40	0
HEM = No	100	80	90	70
b. Alternative Utilities 1, with GSS given greater importance compared to the consensus utility.
	GSS = Yes		GSS = No
	EXT = Yes	EXT = No	EXT = Yes	EXT = No
HEM = Yes	80	60	20	0
HEM = No	100	90	45	35
c. Alternative Utilities 2, with EXT given greater importance compared to the consensus utility.
	GSS = Yes		GSS = No
	EXT = Yes	EXT = No	EXT = Yes	EXT = No
HEM = Yes	80	10	70	0
HEM = No	100	40	95	35
d. Alternative Utilities 3, with HEM given greater importance compared to the consensus utility.
	GSS = Yes		GSS = No
	EXT = Yes	EXT = No	EXT = Yes	EXT = No
HEM = Yes	30	10	20	0
HEM = No	100	90	95	85

For trial conduct, the first cohort is treated at 1.0 mg/kg. The design chooses doses adaptively for all subsequent cohorts, subject to dose safety and efficacy constraints. Each decision is based on the dose-outcome data from all previously treated infants, using the posterior mean utilities of the six doses. To avoid getting stuck at a sub-optimal dose, a well-known problem with “greedy” sequential algorithms that always maximize an objective function (cf. Sutton and Barto, 1988), once a minimal sample is obtained at the current optimal dose, one version of the design randomizes adaptively among acceptable doses with posterior mean utility close to the maximum.

A variety of Bayesian decision theoretic methods have been proposed that are based on the utilities of making correct or incorrect decisions at the end of the trial. These include designs for phase II trials (cf. Stallard, 1998; Stallard, Thall, and Whitehead 1999; Stallard and Thall, 2001; Leung and Wang, 2001; Chen and Smith, 2009) and for randomized phase III trials (cf. Christen, et al., 2004; Lewis, et al., 2007; Wathen and Thall, 2008). These methods optimize benefit to future patients. This is fundamentally different from the present approach, which assigns doses based on elicited joint utilities of the clinical outcomes, and at the end of the trial relies on the same criterion, posterior mean utility of each dose, to make a final recommendation. Bayesian clinical trial designs with similar sequentially adaptive Bayesian decision structures based on utilities have been proposed by Houede, et al. (2010), Thall, et al., (2011), and Thall and Nguyen (2012). The third design is the basis for a currently ongoing trial to optimize the dose of radiation therapy for pediatric brain tumors, based on bivariate ordinal efficacy and toxicity outcomes.

Section 2 describes the Bayesian multivariate dose-outcome model. The utility function and decision criteria used for trial conduct are presented in Section 3, and outcome-adaptive randomization criteria used in a modified version of the design are given in Section 4. An extensive simulation study of the design’s behavior under a range of different possible scenarios is summarized in Section 5. We close with a brief discussion in Section 6.

2. Probability Model

2.1 Dose-Response Functions

Denote the outcome indicators Y_G = I(GSS) = I{−7 ≤ Z ≤ −3}, Y_E = I(EXT), Y_H = I(HEM). In the dose-response model, we will use the standardized doses obtained by dividing the raw doses by their mean, x₁ = 0.5/1.75 = 0.286,⋯, x₆ = 3.0/1.75 = 1.714, with unsubscripted x denoting any given dose. The observed outcome vector is O = (Z, Y_E, Y_H). Because historical data of the form (x, O) are not available, the following dose-outcome model was developed based on the collective experiences and prior beliefs of the neonatologists planning the propofol trial, and extensive computer simulations studying properties of various versions of the model and design.

Adaptive decisions in the trial are based on the behavior of Y = (Y_G, Y_E, Y_H) as a function of x. The distributions of the later outcomes, Y_E and Y_H, may depend quite strongly on the sedation score Z achieved at the start of the INSURE procedure, it is unlikely that Y_E and Y_H are conditionally independent given Z and x, and the definition of Z includes some of the haemodynamic events used to define HEM. To reflect these considerations, our joint model for [O | x] is based on the probability factorization

$$[Z,Y_E,Y_H|x,\mathit{\theta }]=[Z|x,{\mathit{\theta }}_Z][Y_E,Y_H|x,Z,{\mathit{\theta }}_{E,H}],$$ (1)

where θ_Z and θ_E,H are subvectors of the model parameter vector θ. Expression (1) says that x may affect Z, while both x and Z may affect (Y_E, Y_H). To account for association between Y_E and Y_H, we first specify the conditional marginals of [Y_E | x, Z] and [Y_H | x, Z], and use a copula (Nelsen, 1999) to obtain a bivariate distribution. Indexing k = E, H, we define these marginals using logistic regression models (McCullagh and Nelder, 1989),

$${\pi }_k(x,Z,{\mathit{\theta }}_k)=\text{Pr}(Y_k=1|x,Z,{\mathit{\theta }}_k)={\text{logit}}^{-1}\{{\eta }_k(x,Z,{\mathit{\theta }}_k)\},$$ (2)

with linear terms taking the form

$${\eta }_k(x,Z,{\mathit{\theta }}_k)={\theta }_{k,0}+{\theta }_{k,1}{x}^{{\theta }_{k,4}}+{\theta }_{k,2}f(Z)+{\theta }_{k,3}(1-Y_G),$$ (3)

where f(Z) = {(Z + 5)/15}² and we denote θ_k = (θ_k,0, θ_k,1, θ_k,2, θ_k,3, θ_k,4). For k = E, H, θ_k,1 is the dose effect, θ_k,2 is the sedation score effect, θ_k,3 is the effect of not achieving a GSS, and x is exponentiated by θ_k,4 to obtain flexible dose-response curves. We standardize Z in η_E and η_H so that its numerical value does not have unduly large effects for values in the Z domain far away from −5, with (Z + 5)/15 squared to reflect the functional form of the elicited prior in Table 2. For example, the extreme score Z = +10 is represented by f(Z) = 1 rather than 225.

Table 2.

Prior means, interval probabilities for Z and x = dose, and utilities.

	Propofol Dose (mg/kg)
	0.5	1.0	1.5	2.0	2.5	3.0
a. Elicited prior interval probabilities for Z
−10 ≤ Z ≤ −8	.05	.10	.20	.30	.40	.60
−7 ≤ Z ≤ −3	.55	.65	.75	.66	.58	.39
−2 ≤ Z ≤ 10	.40	.25	.05	.04	.02	.01
b. Elicited prior means of πE(z, x)
Z = −10	.99	.98	.90	.70	.60	.25
Z = −5	.99	.98	.97	.95	.90	.75
Z = 0	.95	.90	.80	.50	.20	.10
Z = +10	.70	.30	.10	.05	.03	.01
c. Elicited prior means of πH (z, x)
Z = −10	.01	.10	.20	.30	.50	.70
Z = −5	.01	.02	.05	.10	.15	.40
Z = 0	.01	.20	.40	.70	.80	.90
Z = +10	.30	.40	.70	.95	.98	.99
d. Prior mean utilities and probabilities, obtained by averaging over Z.
Ū (x | θ)	94.0	91.6	90.9	83.5	74.8	50.0
π̅G(x | θ)	.55	.65	.75	.66	.58	.39
π̅H (x | θ)	.02	.08	.12	.20	.32	.57
π̅E(x | θ)	.97	.95	.94	.84	.75	.46
π̅S(x | θ)	.54	.63	.71	.58	.47	.24

Specifying domains of the elements of θ_E and θ_H requires careful consideration. The intercepts θ_E,0 and θ_H,0 are real-valued, with the exponents θ_E,4, θ_H,4 > 0. Based on clinical experience with propofol and other sedatives used in the INSURE procedure, as reflected by the elicited prior means in Table 2, we assume that θ_E,1, θ_E,2, < 0 while θ_H,1, θ_H,2 > 0. This says that, given sedation score Z achieved initially, π_E(x, Z, θ) decreases and π_H(x, Z, θ) increases with dose. Similarly, failure to achieve a GSS can only increase the probability π_H(x, Z, θ) of an adverse haemodynamic event and decrease the probability π_E(x, Z, θ) of extubation within 30 minutes, so θ_H,3 > 0 while θ_E,3 < 0.

Denote the joint distribution π_E,H(a, b | x, Z, θ_k) = Pr(Y_E = a, Y_H = b | x, Z, θ_k), for a, b ∈ {0, 1}. Given the marginals π_k(x, Z, θ), k = E, H, temporarily suppressing (x, Z, θ) for brevity, the Gumbel-Morgenstern copula model is

$${\pi }_{E,H}(a,b)={\pi }_E^a{(1-{\pi }_E)}^{1-a}{\pi }_H^b{(1-{\pi }_H)}^{1-b}+\rho {(-1)}^{a+b}{\pi }_E(1-{\pi }_E){\pi }_H(1-{\pi }_H)$$ (4)

with association parameter −1 < ρ < +1. The joint conditional distribution of [Y_E, Y_H | x, Z] is parameterized by θ_E,H = (θ_E, θ_H, ρ), which has dimension 5+5+1 = 11, and θ_Z, which will be described below. Combining terms, and denoting π_Z(z | x, θ_Z) = Pr(Z = z | x, θ_Z), the joint distribution of [Z, Y_E, Y_H | x] is

$$\mathit{\text{Pr}}(Z=z,Y_E=a,Y_H=b|x,\mathit{\theta })={\pi }_Z(z|x,{\mathit{\theta }}_Z){\pi }_{E,H}(a,b|x,z,{\mathit{\theta }}_{E,H})$$ (5)

for z = −10, −9,⋯, +9, +10 and a, b ∈ {0, 1}.

An important property of the model is that the unconditional marginal distributions of the two later events, Y_E and Y_H, may be complex, non-monotone functions of x. This is because their marginals first are defined in (2) conditional on the initial sedation score, Z, and their unconditional marginals are obtained by averaging over the distribution of Z,

$${\mathrm{\pi ̅}}_k(x,{\mathit{\theta }}_k,{\mathit{\theta }}_Z){=}_{\mathit{\text{def}}}\text{Pr}(Y_k=1|x,{\mathit{\theta }}_k,{\mathit{\theta }}_Z)=\sum _{z=-10}^{+10}{\pi }_k(x,z,{\mathit{\theta }}_k){\pi }_Z(z|x,{\mathit{\theta }}_Z).$$

The unconditional joint distribution π̅_E,H(x, θ_k, θ_Z) is computed similarly, from (4) and (5). The probability π̅_H(x, θ_k, θ_Z) of HEM plays a key role in the design because it is used as a basis for deciding whether x is acceptably safe. Similarly, overall success is defined as S = (GSS and EXT) = (−7 ≤ Z ≤ −3 and Y_E = 1), which has probability π_S(x, θ) that depends on π_Z(z | x, θ_Z). Thus, a key aspect of how the outcomes are observed that affects the statistical model and method is that, for an infant given propofol dose x, π̅_H(x, θ_k, θ_Z) and π_S(x, θ) are averages over the initial sedation score distribution, and thus these probabilities depend on θ_Z.

2.2 Extended Beta Regression Model for Sedation Score

To specify a flexible distribution of [Z | x], we employ the technical device of first defining a beta regression model for a latent variable W having support [0, 1] with mean that is a decreasing function of x, and then defining the distribution of Z in terms of the distribution of W. We formulate the beta regression model for [W | x] using the common re-parameterization of the Be(a, b) model in terms of its mean μ = a/(a + b) and ψ = a + b, where μ = μ_x varies with x and the pdf is

$$f_W(w|{\mathit{\theta }}_Z,x)=\frac{\mathrm{\Gamma }(\psi )}{\mathrm{\Gamma }({\mu }_x\psi )\mathrm{\Gamma }((1-{\mu }_x)\psi )}{w}^{{\mu }_x\psi -1}{(1-w)}^{(1-{\mu }_x)\psi -1},\text{for}0<w<1,$$ (6)

(cf. Williams, 1982; Ferrari and Cribari-Neto, 2004), and Γ(·) denotes the gamma function. Denote the indexes of the doses in increasing order by j(x) = 1,⋯, J. We assume a saturated model for the mean of [W | x],

$${\mu }_x={\{1+\sum _{r=1}^{j(x)}{\alpha }_r\}}^{-1}$$

where α₁,⋯, α_J > 0. Our preliminary simulations showed that assuming constant ψ in the beta regression model for [W | x] results in a model for [Z | x], shown below, that is not sufficiently flexible across a range of possible dose-outcome scenarios to facilitate reliable utility-based dose-finding. To obtain a more flexible model, we explored the behavior of several parametric functions for ψ. We found that the function

$${\psi }_x={\{{\mu }_x(1-{\mu }_x)\}}^{1-2{\gamma }_1}{(2+{\gamma }_2{x}^{{\gamma }_3})}^2$$ (7)

with γ₁, γ₂ > 0 and γ₃ real-valued gives a model that does a good job of fitting a wide range of simulated data. The initial rationale for this particular functional form was to model the standard deviation as the function σ_x = {μ_x(1 − μ_x)}^ν/(2 + ζx^α), with ν > 0. To ensure the usual beta distribution parameter constraints σ_x < 0.50 and ψ_x > 0, it was necessary to modify this so that σ_x = [{μ_x(1 − μ_x)}/(1 + ψ_x)]^1/2 with ψ_x given by (7). Modeling the ESS parameter as a function of x and μ_x in this way, in addition to the more common practice of defining a regression model for the mean, is similar in spirit to the generalized beta regression model of Simas, et al. (2010).

Denote the incomplete beta function $B(w,c,d)={\int }_0^w{u}^{c-1}{(1-u)}^{d-1}dw$ for 0 < w < 1 and c, d > 0. Using the continuous distribution of [W | x] given in (6), we define the discrete distribution for [Z | x] as

$${\pi }_Z(z|x,{\mathit{\theta }}_Z)=\text{Pr}(z-0.5\le 21W-10.5\le z+0.5|x,{\mathit{\theta }}_Z)=\text{Pr}\{(z+10)/21\le W\le (z+11/21|x,{\mathit{\theta }}_Z\}=B\{\frac{z+11}{21},{\mu }_x{\psi }_x,(1-{\mu }_x){\psi }_x\}-B\{\frac{z+10}{21},{\mu }_x{\psi }_x,(1-{\mu }_x){\psi }_x\}$$ (8)

for z = −10, −9,⋯, +9, +10, where θ_Z = (α, γ) = (α₁,⋯, α_J, γ₁, γ₂, γ₃). Since J = 6 propofol doses will be studied, this model for the distribution of Z in terms of the generalized beta latent variable W expresses the probability of a GSS in terms of the incomplete beta function evaluated at arguments characterized by x, the 6 dose-response parameters α = (α₁,⋯, α₆) of μ_x, and the three parameters γ = (γ₁, γ₂, γ₃) of ψ_x. While this model for [Z | x] may seem somewhat elaborate, it must be kept in mind that Z is a sum with 21 possible values and its distribution is a function of J possible doses, so for the propofol trial a 6 × 20 = 120 dimensional distribution is represented by a 9-parameter model.

It follows from (8) that the probability of GSS = (−7 ≤ Z ≤ −3) is

$${\pi }_G(x,{\mathit{\theta }}_Z)=B\{8/21,{\mu }_x{\psi }_x,(1-{\mu }_x){\psi }_x\}-B\{3/21,{\mu }_x{\psi }_x,(1-{\mu }_x){\psi }_x\}.$$ (9)

While the distribution of W is monotone in dose by construction, it should be clear from expressions (6) – (9) that π_G(x, θ_Z) is a complex, possibly non-monotone function of dose.

2.3 Prior, Likelihood, and Posterior Computation

Collecting terms, the model parameter vector is θ = (ρ, α, γ, θ_E, θ_H), which has 20 elements. To establish a prior, we assumed ρ ~ Unif[−1, +1], and for the remaining 19 parameters, θ−ρ, we used the following pseudo-sample-based approach, similar to that of Thall and Nguyen (2012). The pseudo samples were obtained by treating the elicited means of the probabilities π_E(z, x) and π_H(z, x) and interval probabilities Pr(l ≤ Z ≤ u | x) in Table 2 as the true state of nature. For each dose x, we used these elicited probabilities to generate a pseudo-sample of 100 iid patient outcomes,

$$\mathrm{𝒟̃}(x)=\{({\mathrm{Z̃}}^i(x),{Ỹ}_E^i(x,({\mathrm{Z̃}}^i(x)),{Ỹ}_H^i(x,({\mathrm{Z̃}}^i(x)),i=1,\cdots ,100\}.$$

To generate each pseudo-sample, it first was necessary to specify π_Z(z | x) for all combinations of x and z = −10,⋯, +10. For each x, we did this by first fitting the three interval probabilities in the corresponding column of Table 2a to a beta(a_x, b_x), then partitioning [0, 1] into 21 equal subintervals and setting each π_Z(z | x) to be the fitted beta probability of the corresponding subinterval. To obtain π_E(x, z) for all 21 values of z, we linearly interpolated the rows of Table 2b, and we obtained π_H(x, z) similarly from 2c. Using these probabilities, for each i and x, we first simulated Z̃ⁱ(x) from π_Z(z | x) and then simulated ${Ỹ}_k^i(x,{\mathrm{Z̃}}^i(x))$ from π_k(x, Z̃ⁱ(x)) for k = E and H. Given the combined pseudo-sample 𝒟̃= ∪_x𝒟̃(x), and assuming a highly non-informative pseudo prior on θ−ρ, we computed a pseudo-posterior p(θ−ρ | 𝒟̃). This entire process was repeated 3000 times, and the average of the 3000 pseudo-posterior means was used as the prior mean of θ−ρ. The pseudo-sample size 100 was chosen to be large enough to provide reasonably reliable pseudo-posteriors, but small enough so that the computations could be carried out feasibly. Pseudo-sampling provides a reliable alternative to nonlinear least squares, which often fails to converge in this type of setting.

For priors, we assumed that {α₁,⋯, α₆, −θ_E,1,−θ_E,2,−θ_E,3, θ_H,1, θ_H,2, θ_H,3} were normal truncated below at 0, {γ₁, γ₂, θ_E,4, θ_H,4} were lognormal, and {γ₃, θ_E,0, θ_H,0} were normal. Given the prior means established by the pseudo-sampling method, we calibrated the prior variances to be uninformative in the sense that effective sample size (ESS, Morita et al., 2008) of the prior was 0.10. Numerical prior means and variances are given in Supplementary Table 2.

Let N denote the maximum trial sample size. Index the patients enrolled in the trial by i = 1,⋯, N, and denote the observed outcomes by O_i = (Z_i, Y_i,E, Y_i,H), and the assigned dose by x_[i] for the i^th patient. Let n = 1,⋯, N denote an interim sample size where an adaptive decision is made during the trial, and 𝒪_n = (O₁,⋯, O_n) the observed data from the first n patients. The likelihood for the first n patients in the trial is

$${ℒ}_n({𝒪}_n|\mathit{\theta })=\prod _{i=1}^{n}f({\mathbf{O}}_i|x_{[i]},\mathit{\theta })=\prod _{i=1}^n{\pi }_Z(Z_i|x_{[i]},{\mathit{\theta }}_Z){\pi }_{E,H}(Y_{i,E},Y_{i,H}|x_{[i]},Z_i,{\mathit{\theta }}_{E,H}).$$

The posterior based on this interim sample is

$$p(\mathit{\theta }|{𝒪}_n)\propto {ℒ}_n({𝒪}_n|\mathit{\theta })\text{prior}(\mathit{\theta }).$$

All posterior quantities used for decision making by the trial design were computed using Markov chain Monte Carlo with Gibbs sampling (Robert and Cassella, 1999).

3. Decision Criteria

3.1 Utilities

Denote the utility function by U(y), where y = (y_G, y_E, y_H) ∈ {0, 1}³ is an elementary outcome. The numerical utilities for the propofol trial outcomes were obtained by first fixing the scores of the best and worst possible elementary outcomes to be U(1, 1, 0) = 100 and U(0, 0, 1) = 0, and eliciting the remaining six scores as values between 100 and 0 from neonatologists familiar with the INSURE procedure. An admissible utility U(y_G, y_E, y_H) must increase in y_G and y_E and decrease in y_H. While these admissibility requirements may seem obvious, they must be kept in mind during the elicitation process. Although we used the range [0, 100] for U, in general for a given application any convenient interval may be used, depending on what the area experts find intuitively appealing.

To construct dose-finding criteria from the utility function U(y), we first define the mean utility of dose x given θ,

$$Ū(x|\mathit{\theta })=\sum _{\mathit{y}}U(\mathit{y}){\pi }_{G,E,H}(\mathit{y}|x,\mathit{\theta }),$$ (10)

where the joint distribution π_G,E,H is as given earlier. This expression says that, if one knew the parameters θ, then the mean utility (10) is what one would expect to achieve by giving an infant dose x. Since θ is not known, it must be estimated. Rather than computing a frequentist estimator θ̂ and basing decisions on Ū (x | θ̂), we will exploit our Bayesian model to compute statistical decision criteria, as follows. Let data_n denote the observed dose-outcome data from n babies at any interim point in the trial, 1 ≤ n < N. Let p(θ | data_n) denote the current posterior of θ. The posterior mean utility of dose x given data_n is

$$u(x|{\mathit{\text{data}}}_n)={\int }_{\mathit{\theta }}Ū(x|\mathit{\theta })p(\mathit{\theta }|{\mathit{\text{data}}}_n)d\mathit{\theta }.$$ (11)

In words, based on what has been learned from the observed the data from n babies, the posterior mean utility u(x | data_n) is what one would expect to achieve if the next baby were given dose x. An important point is that, with small sample sizes, some of the eight elementary events may not occur, and in this case u(x | data_n) will be based partly on the prior. Note that (11) is obtained by averaging over the distribution of [Y|x, θ] in (10) to obtain Ū (x | θ), and then averaging this mean utility over the posterior of θ. We denote by $x_n^{\mathit{\text{opt}}}$ the dose having maximum u(x | data_n) among the doses under study. For brevity, we denote $u_n^{\mathit{\text{opt}}}=u(x_n^{\mathit{\text{opt}}}|{\mathit{\text{data}}}_n)$. Subject to the restriction that an untried dose may not be skipped when escalating, the design U^opt chooses each successive cohort’s dose to maximize u(x | data_n) among all x ∈ {x₁,⋯, x₆}.

It may seem appropriate to place a probability distribution on the utility function U to reflect uncertainty about what alternative utilities others may have. If a distribution q(U) is assumed for U, using the elicited consensus utility as the mean U_q under q, then one would need to integrate over q(U) as well as π_G,E,H(y) and p(θ | data_n) to obtain u(x | data_n). This computation gives the original posterior mean utility (11), however, essentially because the trial data provide no new information about U. We will address this issue by sensitivity analyses to U, in Section 5.

3.2 Dose Acceptability Criteria

A critical issue is that a dose that is “optimal” in terms of the utility alone may be unacceptable in terms of either safety or overall success rate. To ensure that any administered dose has both an acceptably high success rate and an acceptably low adverse event rate, based on the current data, we define the following two posterior acceptability criteria. Given the fixed upper limit ${\mathrm{\pi ̅}}_H^{*}$, we say that a dose x is unsafe if

$$\mathit{\text{Pr}}\{{\mathrm{\pi ̅}}_H(x,{\mathit{\theta }}_H,{\mathit{\theta }}_Z)>{\mathrm{\pi ̅}}_H^{*}|\mathit{\text{data}}\}>p_{U,H}$$ (12)

for fixed upper limit p_U,H. Recall that the overall success event is S = (Y_G = 1 and Y_E = 1), that a GSS was achieved with the initial propofol administration and the INSURE procedure was completed with extubation within 30 minutes. Denoting π_S(x, θ) = Pr(S = 1 | x, θ), the probability of this event is given by

$${\pi }_S(x,\mathit{\theta })=\text{Pr}(Y_E=1,Y_G=1|x,\mathit{\theta })=\text{Pr}(Y_E=1\text{and}-7\le Z\le -3|x,\mathit{\theta })=\sum _{z=-7}^{-3}\text{Pr}(Y_E=1|x,Z=z,{\mathit{\theta }}_E){\pi }_Z(z|x,{\mathit{\theta }}_Z),$$

parameterized by (θ_E, θ_Z). We say that a dose x has unacceptably low overall success probability if

$$\mathit{\text{Pr}}\{{\pi }_S(x,{\mathit{\theta }}_E,{\mathit{\theta }}_Z)<{\pi }_S^{*}|\mathit{\text{data}}\}>p_{U,S}$$ (13)

for fixed upper limit p_U,S. We will refer to the subset of doses that do not satisfy either (12) or (13) as acceptable doses. We denote this subset by 𝒜_n, and we denote the modification of design U^opt restricted to 𝒜_n by U^opt + Acc.

4. Adaptive Randomization

Intuitively, it may seem that the best dose is simply the one maximizing the posterior mean utility, possibly enforcing the additional acceptability criteria given above. However, it is well known in sequential decision making that a “greedy” algorithm that always chooses each successive action by optimizing some decision criterion risks getting stuck at a suboptimal action. A greedy algorithm may get stuck at a suboptimal action due to the fact that, because it repeatedly takes the suboptimal action, it fails to take and thus obtain enough data on an optimal action to determine, statistically, that it is truly optimal. This problem is sometimes known as the “optimization versus exploration” dilemma. (cf. Robbins, 1952; Gittins, 1979; Sutton and Barto, 1998). This fact has been recognized only recently in the context of dose-finding clinical trials (Azriel, et al., 2011; Thall and Nguyen, 2012; Oron and Hoff, 2013). In the propofol trial, always choosing an “optimal” dose x by maximizing u(x | data_n) is an example of a greedy algorithm, even if x is restricted to 𝒜_n. A simple aspect of this problem is that the statistics u(x₁ | data_n),⋯, u(x_K | data_n) are actually quite variable for most values of n during the trial, and simply maximizing their means ignores this variability. This problem has both ethical and practical consequences, since maximizing the posterior mean utility for each cohort may lead to giving suboptimal doses to a substantial number of the infants in the trial, and it also may increase the risk of recommending a suboptimal dose at the end. To deal with this problem, we use adaptive randomization (AR) to improve this greedy algorithm and thus the reliability of the trial design. Our AR criterion is similar to that used by Thall and Nguyen (2012). One goal of the AR is to obtain a design that, on average, treats more patients at doses with higher actual utilities and is more likely to choose a dose with maximum or at least high utility at the end of the trial. At the same time, it must not allow an unacceptable risk for the two infants in each cohort. Thus, while the AR is implemented using probabilities proportional to the posterior mean utilities, it is restricted to the set 𝒜_n of acceptable doses. Given current data_n, the next cohort is randomized to dose x_j ∈ 𝒜_n with probability

$$p_{j,n}=\frac{u(x_j|{\mathit{\text{data}}}_n)}{{\sum }_{r=1}^{K}u(x_r|{\mathit{\text{data}}}_n)I(x_r\in {𝒜}_n)}.$$ (14)

The following algorithm is a hybrid of utility maximization and AR. It chooses doses according to U^opt + Acc, unless the current optimal dose has at least δ more patients than any other acceptable dose. In this case, it applies the AR criterion (14) to choose a dose, as follows. Denote the sample size at dose x_j after n patients have been treated by m_n(x_j), so that m_n(x₁) + ⋯ m_n(x_K) = n. Among the doses in 𝒜_n if m_n(x^opt) ≥ m_n(x_j) + δ for all x_j ≠ x^opt, then assign x_j with probability p_j,n. Otherwise, assign x^opt.

For ethical reasons, AR must be applied carefully. Once enough data have been obtained to apply AR reliably, it is ethically inappropriate to randomize patients to a dose that is unlikely to be best. Formally, we say that x is unlikely to be best if

$$\text{Pr}\{Ū(x,\mathit{\theta })={\mathit{\text{max}}}_{x\text{'}}Ū(x\text{'},\mathit{\theta })|{\mathit{\text{data}}}_n\}<p_L$$ (15)

for fixed lower limit p_L. Thus, AR is applied to the set of doses that not only are acceptable in terms of the safety and efficacy criteria (12) and (13), but that also do not satisfy (15), i.e. that are not unlikely to be best. This restriction is most useful when larger sample sizes are available, later in the trial, and has the effect of reducing the numbers of patients treated at inferior doses. We denote this hybrid algorithm by U^opt + Acc + AR_δ.

For each design U^opt, U^opt + Acc, and U^opt + Acc + AR_δ, the first cohort is treated with 1.0 mg/kg, untried doses may not be skipped when escalating, but there is no constraint on de-escalation. Acc restricts doses to 𝒜_n. For U^opt + Acc + AR_δ, doses unlikely to be best also are excluded, and the AR criterion is used only if, within this subset of doses, x^opt has at least δ more patients than any other dose. For both U^opt +Acc, and U^opt + Acc + AR_δ, if it is determined that 𝒜_n = ϕ, the trial is stopped and no dose is selected. For all three designs, if the trial is not stopped early, at the end of the trial, the dose x_select having maximum posterior mean utility, u_dataN, is selected.

While the trial will be shut down if 𝒜_n is empty, i.e. no dose is acceptable, we consider this very unlikely. If this happens, then for neonatologists performing the INSURE procedure using propofol, in practice a safe dose with HEM rate < 0.10 but a success rate lower than 0.60 would be used. This might motivate a subsequent trial to study the idea of titrating the dose in more than one administration for each infant. However, optimizing such a multi-stage procedure is a much more complex problem, and would require a very different design.

5. Simulation Study

In the simulations, the trial has maximum sample size N = 60, cohort size c = 2, and acceptability cut-offs p_U,H = p_U,S = 0.95, with p_L = 0.05 when AR_δ is used. In preliminary simulations, these design parameters were varied, along with the prior variances, to study their effects and obtain a design with desirable properties. The hybrid U^opt + Acc + AR_δ was studied for δ = 2, 4, 6, 8, and 10. Since the results were insensitive to δ in this range, only the case δ = 2 is reported.

We also included the following ad hoc non-model-based 4-stage design suggested by a Referee as a comparator. Stage 1: Randomize 24 patients to each of the 6 doses (4 per dose). Select the 4 doses with the highest mean utility Ū (x) for evaluation in stage 2. Stage 2: Randomize 16 patients to each of the 4 selected doses (4 per dose), and select the 3 doses (from all 6) with highest Ū (x) for evaluation in stage 3. Stage 3: Randomize 12 patients to each of the 3 newly selected doses (4 per dose), and select the 2 doses (from all 6) with the highest Ū (x) for evaluation in stage 4. Stage 4: Randomize 8 patients to each of the 2 remaining doses (4 per dose), and select the best dose, having highest Ū (x) across all 6 doses. This design uses 60 patients, evaluates at least 4 patients per dose, and the selected dose has information on up to 16 patients. While it interimly selects (drops) doses with higher (lower) empirical mean utilities, it does not have rules that drop doses in terms of their empirical HEM or Success rates.

We used the following criteria to assess and compare the designs. The first is the proportion of the difference between the utilities of the best and worst possible doses achieved by x_select, scaled to the domain [0, 100],

$$R_{\mathit{\text{select}}}=100\frac{u^{\mathit{\text{true}}}(x_{\mathit{\text{select}}})-u_{\mathit{\text{min}}}}{u_{\mathit{\text{max}}}-u_{\mathit{\text{min}}}}.$$

The second criterion quantifies how well a method assigns doses to patients in the trial,

$$R_{\mathit{\text{treat}}}=100\frac{\frac{1}{N}{\sum }_{i=1}^N{u}^{\mathit{\text{true}}}(x_{[i]})-u_{\mathit{\text{min}}}}{u_{\mathit{\text{max}}}-u_{\mathit{\text{min}}}},$$

where u^true(x_[i]) is the true utility of the dose given to the i^th patient. Larger value correspond to better design performance, with R_select quantifying benefit to future patients while R_treat, which may be regarded as an ethical criterion, quantifying benefit to the patients treated in the trial.

Table 3 compares the four designs, based on mean values across 3000 simulated trials under each of 9 different dose-outcome scenarios, given in Supplementary Tables 3.1 – 3.9. Scenario 1 is based on the elicited prior probabilities. The beta regression model was used to obtain all 21 true π_Z(x) values from three interval probabilities, and linear interpolation was used to obtain true π_E(x) and π_H(x). Otherwise, none of the scenarios are model-based. The scenarios assume that a larger dose will shift the Z distribution toward −10, which is reasonable given the nature of the sedative drug. Given this, the interval probabilities for Z vary widely across the scenarios. The scenarios’ true π_E(x) and π_H(x) have the same general trends as the prior in that π_E(x) decreases and π_H(x) increases with x given Z. To reflect the prior belief that Y_E and Y_H are slightly negatively correlated (Table 2), we set ρ = − 0.1 when generating the true joint distributions of each scenario. Preliminary simulation results were insensitive to the assumed true ρ value. Both U^opt and 4-Stage have no early stopping rules, so these designs always treat 60 patients. Due to the much larger number adverse HEM events of 4-Stage in Scenarios 1, 2 and 8, the fact that it treats 60 patients in Scenarios 8 and 9 where no doses are acceptable, and the much lower R_treat values across all scenarios, this design is unethical. Compared to U^opt + Acc and U^opt + Acc + AR, 4-Stage has R_select values that are slightly higher in Scenarios 1 and 2 with the price being many more occurrences of HEM, and in Scenarios 3 – 7 it has lower R_select values. Comparison of U^opt to U^opt + Acc shows the effects of including dose acceptability criteria in a sequentially adaptive utility-based design. While these two designs have similar values of R_select and R_treat for Scenarios 1 – 4, the importance of the acceptability rules is shown clearly by the other scenarios, where U^opt + Acc has greatly superior performance. Moreover, the mean of 19.2 adverse HEM events for U^opt in Scenario 8 illustrates the potential danger of using a design with a utility-based decision criterion without an early stopping rule for safety. The much higher values of R_select and R_treat for U^opt + Acc in Scenarios 5 – 7 show that it is both more reliable and more ethical in these cases compared to U^opt.

Table 3.

Comparison of alternative designs. Scenarios 8 and 9 have no acceptable dose, so R_select values are less relevant and thus have a gray background. A dose x is unacceptable if either π̅_H(x, θ) > .10 or π_S(x, θ) < .60 with posterior probability > .95.

		Scenario
Design		1	2	3	4	5	6	7	8	9
Uopt	Rselect	96	93	99	90	73	49	30	95	48
	Rtreat	96	92	98	90	64	46	21	95	42
	% None	0	0	0	0	0	0	0	0	0
	# Pats	60.0	60.0	60.0	60.0	60.0	60.0	60.0	60.0	60.0
	# HEM	4.1	2.7	2.4	2.8	2.2	2.3	2.1	19.3	2.0
	# Succ	36.7	40.8	39.6	33.0	25.7	20.2	9.2	37.1	11.0
Uopt + Acc	Rselect	95	93	99	95	93	89	88	96	99
	Rtreat	96	92	98	92	79	69	64	96	73
	% None	4	0	1	2	4	7	10	100	93
	# Pats	58.9	59.8	59.8	59.4	59.0	58.1	56.9	15.4	40.6
	# HEM	4.2	2.6	2.4	2.9	2.3	2.6	2.9	4.9	1.9
	# Succ	36.4	40.6	39.3	35.1	32.2	28.7	25.5	9.4	11.9
Uopt + Acc + AR2	Rselect	95	94	94	95	92	89	94	98	97
	Rtreat	92	84	87	87	76	71	69	94	72
	% None	4	1	1	4	5	6	7	100	95
	# Pats	59.0	59.7	59.7	59.2	58.9	58.5	57.9	15.4	39.7
	# HEM	5.7	4.5	2.8	3.8	2.6	2.9	3.0	5.0	1.9
	# Succ	36.5	39.0	36.4	35.1	32.4	30.3	28.2	9.5	11.6
4-Stage	Rselect	97	97	92	93	89	82	84	90	86
	Rtreat	83	65	73	76	66	63	59	74	69
	% None	0	0	0	0	0	0	0	0	0
	# Pats	60.0	60.0	60.0	60.0	60.0	60.0	60.0	60.0	60.0
	# HEM	8.8	8.9	3.2	5.0	2.7	2.9	2.7	22.8	2.7
	# Succ	34.5	35.4	33.3	31.9	29.8	28.4	23.1	36.4	16.8

After excluding U^opt and 4-Stage as ethically unacceptable, comparison between U^opt + Acc and U^opt + Acc + AR₂ shows the effects of including AR. Recall that AR₂ randomizes patients among acceptable doses having u(x | data) close to u(x^opt | data), to better explore the dose domain. These designs have very similar R_select values for Scenarios 1 – 6, with U^opt + Acc + AR₂ showing a slight advantage in Scenario 7. As expected, U^opt + Acc has slightly larger R_treat values and slightly smaller mean numbers of HEM events in most scenarios. Consequently, for the propofol trial, U^opt + Acc is the better of the two ethical designs, but by a small margin.

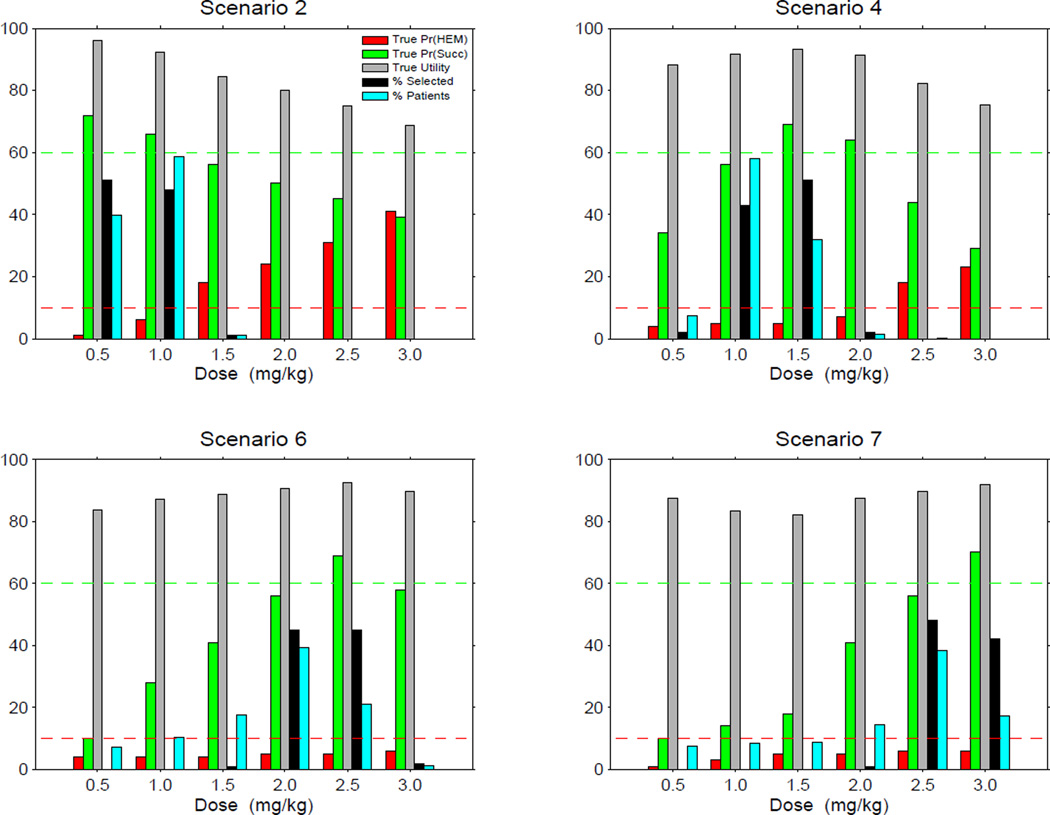
Table 4 summarizes the simulations in more detail for U^opt + Acc. In each of Scenarios 1 – 7, the selection rates, subsample sizes, and success event rates for the 6 doses all follow the u^true(x) values, and doses with comparatively low u^true(x) are selected seldom or not at all. The design is very likely to stop the trial and select no dose in both Scenario 8, where all doses are unsafe with ${\pi }_H^{\mathit{\text{true}}}(x)\ge 0.29$, and Scenario 9, where all doses have a low success probability with ${\pi }_S^{\mathit{\text{true}}}(x)\le 0.41$. In particular, U^opt + Acc does a good job of controlling the HEM event rate at very low values across all scenarios. Figure 1 illustrates properties of U^opt + Acc in four selected scenarios.

Table 4.

Simulation results using the U^opt + Acc design. A dose x is unacceptable if either π̅_H(x, θ) > .10 or π_S(x, θ) < .60 with posterior probability > .95. Utilities of unacceptable doses have a gray background. The highest utility among acceptable doses is given in boldface.

dose (mg/kg)		0.5	1.0	1.5	2.0	2.5	3.0	% none, Sum
Scenario 1	utrue	94.0	91.6	90.9	83.5	74.7	49.9
	% Sel	18	69	9	0	0	0	4
	# Pats	12.1	42.8	3.9	0.1	0.0	0.0	58.9
	# HEM	0.2	3.5	0.5	0.0	0.0	0.0	4.2
	# Succ	6.5	27.1	2.8	0.0	0.0	0.0	36.4
Scenario 2	utrue	95.9	92.3	84.3	79.9	75.0	68.7
	% Sel	51	48	1	0	0	0	0
	# Pats	23.9	35.2	0.7	0.0	0.0	0.0	59.8
	# HEM	0.3	2.2	0.1	0.0	0.0	0	2.6
	# Succ	17.2	23.0	0.4	0.0	0.0	0.0	40.6
Scenario 3	utrue	93.0	94.4	92.2	88.7	86.0	80.6
	% Sel	8	89	2	0	0	0	1
	# Pats	8.2	50.0	1.4	0.1	0.0	0.0	59.8
	# HEM	0.3	2.0	0.1	0.0	0.0	0.0	2.4
	# Succ	4.4	34.0	0.9	0.0	0.0	0.0	39.3
Scenario 4	utrue	88.2	91.7	93.2	91.3	82.1	75.3
	% Sel	2	43	51	2	0	0	2
	# Pats	4.4	34.8	19.2	0.8	0.1	0.0	59.4
	# HEM	0.2	1.6	1.0	0.1	0.0	0.0	2.9
	# Succ	1.5	19.7	13.3	0.5	0.0	0.0	35.1
Scenario 5	utrue	80.6	85.7	90.9	92.9	90.4	84.4
	% Sel	0	0	35	58	2	0	4
	# Pats	3.7	6.4	28.4	19.7	0.8	0.1	59.0
	# HEM	0.1	0.2	1.1	0.9	0.0	0.0	2.3
	# Succ	0.3	1.8	15.6	13.9	0.5	0.0	32.2
Scenario 6	utrue	83.6	87.0	88.8	90.7	92.6	89.6
	% Sel	0	0	1	45	45	2	7
	# Pats	4.4	6.3	10.6	23.5	12.6	0.7	58.1
	# HEM	0.1	0.2	0.4	1.1	0.7	0.0	2.6
	# Succ	0.4	1.8	4.3	13.1	8.7	0.4	28.7
Scenario 7	utrue	87.5	83.4	82.1	87.5	89.8	91.8
	% Sel	0	0	0	1	48	42	10
	# Pats	4.6	5.0	5.2	8.7	23.1	10.3	56.9
	# HEM	0.1	0.2	0.2	0.4	1.3	0.6	2.9
	# Succ	0.5	0.7	0.9	3.5	12.8	7.2	25.5
Scenario 8	utrue	82.1	80.5	78.5	75.2	69.7	59.9
	% Sel	0	0	0	0	0	0	100
	# Pats	7.2	7.8	0.4	0.0	0.0	0.0	15.4
	# HEM	2.1	2.6	0.1	0.0	0.0	0.0	4.9
	# Succ	4.2	4.9	0.2	0.0	0.0	0.0	9.4
Scenario 9	utrue	79.9	82.2	83.9	85.1	86.0	85.9
	% Sel	0	0	0	0	1	6	93
	# Pats	4.6	5.1	5.9	6.9	9.4	8.6	40.6
	# HEM	0.1	0.2	0.2	0.3	0.5	0.6	1.9
	# Succ	0.4	0.8	1.4	2.2	3.6	3.5	11.9

Figure 1.

Simulation results for the design U^opt + Acc using the greedy algorithm with safety and efficacy acceptability rules, under four selected scenarios. For convenience, probabilities as percentages, utilities, and selection percentages are given together in the same plot. Horizontal dashed lines show the upper limit 10% for π_H(dose) and lower limit 60% for π_S(dose).

The numerical limits π_H(x) ≤ 0.10 and π_S(x) ≥ 0.60 in the propofol trial are very demanding, and they constrain the acceptable dose set severely. This is ethically appropriate for a trial where the patients are newborn infants and, although the optimal sedative dose is not known, the INSURE procedure has been very successful. Recall that adding AR to the design is motivated by the desire to reduce the chance of getting stuck at a suboptimal dose. In other structurally similar settings, different numerical values for the dose admissibility limits p_U,H and p_U,S may produce substantively different behavior of U^opt + Acc and U^opt + Acc + AR_δ. As a hypothetical but realistic example, consider an oncology trial of an anti-cancer agent where G is a desirable early biological effect, E is tumor response, and H is toxicity. Suppose that, based on what has been seen with standard chemotherapy, p_U,H = 0.25 and p_U,S = 0.40 are appropriate numerical values for the dose acceptability criteria (12) and (13). Changing only these two design parameters to reflect this hypothetical oncology setting, we re-simulated U^opt + Acc and U^opt + Acc + AR₂ to assess the effect of including AR in the design, under Scenarios 1 – 7. Table 5 summarizes the results. In terms of both R_select and R_treat, the design U^opt + Acc performs slightly better in Scenarios 1 – 3, where the optimal dose is close to the starting dose, but U^opt + Acc + AR₂ is greatly superior in Scenarios 5 –7, where the optimal dose is far away from the starting dose. The general message is that including AR may be regarded as an insurance policy against extremely poor behavior in some cases, with the price being a small drop in R_select and R_treat in other cases.

Table 5.

Simulation study comparing U^opt + Acc and U^opt + Acc + AR₂ for a hypothetical trial where the acceptability limits π_H(x) ≤ .25 and π_S(x) ≥ 0.40 are appropriate.

		Scenario
Design		1	2	3	4	5	6	7
Uopt + Acc	Rselect	96	93	99	91	82	61	65
	Rtreat	96	92	98	90	73	53	50
	% None	0	0	0	0	0	0	2
	# Pats	60.0	60.0	60.0	60.0	60.0	60.0	59.3
	# HEM	4.1	2.7	2.4	2.8	2.2	2.5	2.8
	# Succ	36.7	40.7	39.4	33.2	29.0	22.9	21.7
Uopt + Acc + AR2	Rselect	95	93	95	96	91	84	90
	Rtreat	92	83	88	88	76	67	66
	% None	0	0	0	0	0	0	1
	# Pats	60.0	60.0	60.0	60.0	59.9	59.9	59.5
	# HEM	5.7	4.6	2.7	3.7	2.6	2.7	3.1
	# Succ	36.7	39.1	36.7	35.4	32.6	29.0	27.6

We also evaluated our design’s performance under simpler versions of the model obtained by dropping f(Z), Y_G, or both from the linear term (3). We found that dropping f(Z) results in a design that escalates far too slowly or often fails to escalate when higher doses have higher utility. Dropping Y_G, so that neither π_E(x, θ) nor π_H(x, θ) depends on Y_G, causes the design to stop early far too often in cases where Y_E or Y_H actually are associated with Y_G. As a final comparator, we used the bivariate CRM (Braun, 2002) with Success as ‘efficacy’ and HEM as ‘toxicity’, since this method is model-based but simpler than our method (Supplementary Table 8). Because the bivariate CRM requires that the probability of efficacy must increase with dose, and our elicited prior has non-monotone π_S(x), to implement it we adjusted the prior mean success probabilities to be nearly at over the last 4 doses rather than decreasing. For the one stopping rule allowed by the available bivariate CRM software, we chose the toxicity rule with upper limit 0.10. The simulation results show that the bivariate CRM performs much worse than our method in six scenarios (2 through 7), and about the same in the other three.

To evaluate robustness to the model assumptions, we perturbed the scenarios’ true probabilities in each of three ways: (1) mixing the true beta score distribution with a piecewise uniform score distribution in various proportions (Supplementary Table 5), (2) changing the assumed optimal Z scores for Pr(EXT) and Pr(HEM) (Supplementary Table 6), and (3) increasing the true risks by various amounts when GSS is not achieved (Supplementary Table 7). We found that, when the model was misspecified by these perturbations, in most cases the early stopping probability tended to increase, but the dose selection performance (both R_select and R_treat) remained relatively high.

A key issue is that the elicited neonatologists’ consensus utilities are subjective, and others may have different utilities. To address this, we carried out two sensitivity analyses. For the first, which addresses this concern by anticipating how the trial results may be interpreted by others after its completion, we evaluated the results of the trial conducted as before using the elicited consensus utility, but analyzed using each of the three alternative utilities given in Table 1. These alternative utilities numerically reflect the respective viewpoints that, compared to the consensus utility, GSS is more important, EXT is more important, or HEM is more important. Note that, for each alternative, several numerical values of U(y) differ substantially from the corresponding values of the consensus utility. For the second sensitivity analysis, we simulated the trial conducted using each alternative utility in place of the consensus utility. The results, summarized in Table 6, show that the design appears to be quite robust to changes in numerical utility values, either for trial conduct or data analysis. Thus, the trial results based on the consensus utility should be acceptable for a wide audience of other neonatologists who may have differing opinions.

Table 6.

a. Comparison of results obtained by conducting the trial using the consensus utility with the design Uopt + Acc, but analyzing the resulting data using each of the alternative utilities. Rselect values have a gray background in Scenarios 8 and 9 because these have no acceptable doses.
		Scenario
Utility Used for Analysis		1	2	3	4	5	6	7	8	9
Consensus	Rselect	95	93	99	95	93	89	88	96	99
	Rtreat	96	92	98	92	79	69	64	96	73
Alternative 1:	Rselect	87	92	95	86	90	88	85	76	98
GSS more important	Rtreat	87	90	92	77	73	66	55	75	64
Alternative 2:	Rselect	96	93	99	97	95	90	90	97	98
EXT more important	Rtreat	97	92	99	94	84	73	72	97	75
Alternative 3:	Rselect	92	93	99	98	94	90	84	93	73
HEM more important	Rtreat	93	92	99	97	81	73	68	93	73

b. Comparison of results if different alternative utilities are used to conduct the trial in place of the consensus utility, for the design Uopt + Acc. Rselect values have a gray background in Scenarios 8 and 9 because these have no acceptable doses.
		Scenario
Utility		1	2	3	4	5	6	7	8	9
Consensus	Rselect	95	93	99	95	93	89	88	96	99
	Rtreat	96	92	98	92	79	69	64	96	73
	% None	4	0	1	2	4	7	10	100	93
	# Pats	58.9	59.8	59.8	59.4	59.0	58.1	56.9	15.4	40.6
	# HEM	4.2	2.6	2.4	2.9	2.3	2.6	2.9	4.9	1.9
	# Succ	36.4	40.6	39.3	35.1	32.2	28.7	25.5	9.4	11.9
Alternative 1:	Rselect	88	89	97	89	92	90	86	72	97
GSS more important	Rtreat	87	89	92	78	75	68	55	75	64
	% None	4	1	1	2	4	6	9	99	94
	# Pats	59.1	59.8	59.7	59.4	59.0	58.3	57.2	15.4	40.3
	# HEM	4.4	2.8	2.4	2.9	2.4	2.7	2.9	4.8	1.9
	# Succ	36.8	40.4	39.3	35.5	32.6	29.4	26.0	9.4	11.8
Alternative 2:	Rselect	96	94	99	96	95	89	90	98	96
EXT more important	Rtreat	97	92	99	94	85	73	72	97	75
	% None	4	0	1	2	3	6	9	100	93
	# Pats	58.9	59.9	59.7	59.3	59.0	58.4	57.5	15.4	40.8
	# HEM	4.2	2.5	2.4	2.9	2.4	2.7	2.9	4.9	1.9
	# Succ	36.5	40.9	39.2	34.9	32.5	29.2	25.9	9.4	12.0
Alternative 3:	Rselect	93	94	99	98	93	90	84	94	74
HEM more important	Rtreat	93	92	98	97	80	73	67	93	73
	% None	4	1	1	2	3	6	9	100	94
	# Pats	59.0	59.9	59.7	59.2	59.1	58.3	57.3	15.4	40.7
	# HEM	4.1	2.2	2.4	2.8	2.3	2.6	2.9	4.8	1.9
	# Succ	36.4	41.3	39.3	34.8	32.0	28.6	25.6	9.4	11.9

6. Discussion

We have presented a Bayesian model and method for choosing sedative doses in a clinical trial involving newborn babies being treated for RDS with the INSURE procedure. The design is based on elicited utilities of three binary clinical outcome variables. The proposed method sequentially optimizes doses using posterior expected utilities, with additional restrictions to exclude doses that are likely to be either unsafe or inefficacious.

Using the utility function to reduce the three-dimensional outcome (Y_G, Y_E, Y_H) to a single quantity may be regarded as a technical device that is ethically desirable. Comparison of U^opt to U^opt + Acc clearly shows that use of the greedy utility-based algorithm per se gives a design that is ethically unacceptable, but that this can be fixed by adding dose admissibility criteria. As shown by the hypothetical example where the limits on π_U,H and π_U,S were replaced with different numerical values that might be more appropriate in an oncology trial (Table 5), in some settings using AR may be preferable.

Important caveats are that a particular utility function is setting-specific, and it may not be reasonable to attempt to include outcomes having dramatically different clinical importance in the utility function. For example, in cancer trials it may not be possible to construct a utility including both death and tumor response. This is a practical and ethical limitation of this type of utility-based methodology.

Application of a complex outcome-adaptive clinical trial design presents several important practical challenges. The first step, which has been our focus here, is to establish the design, write the necessary computer program, and obtain approval from the physicians who will treat patients enrolled in the trial. Key elements in implementation include (1) establishing a database and procedure for data entry in the clinic, (2) obtaining approval of the trial protocol by the Institutional Review Boards of all participating medical centers, and (3) implementing the design using the database and computer program as patients are enrolled, treated, and evaluated. Updating the database in real time, which is critically important for outcome-adaptive designs, is challenging since it requires research nurses or data managers to enter patient outcomes in a timely manner. The required data usually are simple, however. For example, the vector (x, Z, Y_E, Y_H) is all that is required by the propofol trial design. Computing each assigned dose is straightforward, since it requires only one run of the computer program using the updated database.

Upon completion of the trial, in addition to recommending an optimal dose, inferences from the final data will include summaries of the posterior distributions of the key outcome probabilities, including π_G(x, θ_Z), π̅_E(x, θ_E, θ_Z), π̅_H(x, θ_H, θ_Z), and the success event probability, π_S(x, θ_E, θ_Z). This will be done by cross-tabulating posterior means and 95% credible intervals (ci’s) with dose x. This table also will include the posterior means u(x | data_N) and 95% ci’s of the utilities Ū (x | θ), which provide a set of natural summary statistics for evaluating and comparing the doses. Corresponding plots of the posteriors will provide a graphical illustration of what has been learned about each of these parametric quantities. As suggested in our sensitivity analyses, the summaries of u(x | data_N) could be repeated for each of several reasonable alternative utilities, such as those in Table 1. Finally, it also will be important to include non-model-based summaries of the empirical distribution of the sedation score Z and the count of each of event G, E, H, and S for each dose.

The propofol trial design synthesizes ideas from several areas, including phase I–II dose-finding, sequential optimization, decision analysis, Bayesian statistics, and intervention in preterm newborns. For future studies in neonatal care and similar medical settings, several potential extensions and improvements are worth mentioning. More general regimes might include multiple agents, two or more different administration schedules, or more than one cycle of therapy. Use of multi-category ordinal rather than binary outcomes would provide a more refined assessment of treatment or dose effects, and thus a more informed basis for decision-making. Accounting for effects of known prognostic covariates to optimize so-called “individualized” therapies also is highly desirable, although such a design is likely to be complex and logistically difficult, since it would require rapid evaluation of the necessary covariates and adaptive computation of the dose in real time.

Designing clinical trials in children is challenging, both technically and ethically. Successful use of this type of statistical methodology in the propofol trial may serve as proof-of-concept, and possibly provide a bridge to future pediatric trials using similar approaches.