Abstract
BACKGROUND
Signaling networks are of great importance for us to understand the cell’s regulatory mechanism. The rise of large-scale genomic and proteomic data, and prior biological knowledge has paved the way for the reconstruction and discovery of novel signaling pathways in a data-driven manner. In this study, we investigate computational methods that integrate proteomics and transcriptomic data to identify signaling pathways transmitting signals in response to specific stimuli. Such methods can be applied to cancer genomic data to infer perturbed signaling pathways.
METHOD
We proposed a novel Bayesian Network (BN) framework to integrate transcriptomic data with proteomic data reflecting protein phosphorylation states for the purpose of identifying the pathways transmitting the signal of diverse stimuli in rat and human cells. We represented the proteins and genes as nodes in a BN in which edges reflect the regulatory relationship between signaling proteins. We designed an efficient inference algorithm that incorporated the prior knowledge of pathways and searched for a network structure in a data-driven manner.
RESULTS
We applied our method to infer rat and human specific networks given gene expression and proteomic datasets. We were able to effectively identify sparse signaling networks that modeled the observed transcriptomic and proteomic data. Our methods were able to identify distinct signaling pathways for rat and human cells in a data-driven manner, based on the facts that rat and human cells exhibited distinct transcriptomic and proteomics responses to a common set of stimuli. Our model performed well in the SBV IMPROVER challenge in comparison to other models addressing the same task. The capability of inferring signaling pathways in a data-driven fashion may contribute to cancer research by identifying distinct aberrations in signaling pathways underlying heterogeneous cancers subtypes.
Keywords: Bayesian Network, signaling pathways, protein phosphorylation, gene expression, species translation
Introduction
Phosphorylation of signaling proteins is one of the common mechanisms cells employ to transmit signals. The emerging proteomics technology provides us with an excellent platform to monitor the phosphorylation states of a large number of phospho-proteins under different external stimuli.1,2 Signal transduction pathways respond to external stimuli and internal environmental changes in order to maintain cellular homeostasis. During the process, many signaling pathways eventually affect the transcription of the genes involved in various biological processes. Therefore, simultaneously studying transcriptomic and proteomic responses of cells will help us to elucidate signal transduction. Unveiling cells’ complex signaling network is of great importance for us to understand the cell’s regulatory mechanisms under physiological and pathological conditions. Moreover, the disease treatment and drug development could be largely enhanced by studying to what extent the animal signaling networks can be used to explain the human signaling network.3 However, it is computationally challenging to accurately reconstruct the complete signaling networks responsible for transducing the signals and ultimately regulating gene expression,4,5 due to the lack of established methods to integrate protein phosphorylation and gene expression data.
A wealth of data is available for investigating large-scale regulatory networks, due to the rise of the high-throughput technology which enables the simultaneous genome-scale measurements. Certain technologies have been applied to utilize large-scale data in the field.4–7 One commonly used method is differential equations, which uses a set of ordinary differential equations (ODEs) to represent a dynamic system in a more quantitative and precise manner.8 However, with the increasing size of the network, the identification of model structure and estimation of parameters become very difficult, which might require network simplification or approximation.9 The information theory based model, in general, is to determine the regulatory dependency based on correlation analysis, and has a major advantage of low computational cost on large-scale networks.6,10 There are also other various methods to model and simulate large-scale signal transduction network: Boolean network which uses binary variables and simple Boolean operation functions, eg, AND, OR, NOT, to represent a discrete dynamic system;11,12 Network Component Analysis (NCA) which uses prior information to constrain the search space for pathway inference;13,14 supervised inference method, eg support vector machine (SVM), which splits the network inference into multiple classification problems.15
However, most of the approaches described above do not allow uncertainty to be included in the model. In contrast, Bayesian Network (BN) can formulate the quantitative knowledge of the signaling pathways using probabilistic graphical representation, which introduces the uncertainty to the model.16–18 A BN is a directed acyclic graph (DAG) used to represent the joint distribution of a set of variables, and with certain constraints it can represent the causal relationship among these variables.18 A BN approach is particularly suitable to represent the regulatory relationships among signaling proteins because the directed edges can be used to represent causal relationships.16,17,19,20 However, applying BN to learn signaling pathways based on large-scale genome data is also challenging in the following aspects. First, the DAG constraint of a conventional BN hinders its capability to represent the often observed feedback loops in biological systems, recent development of “loopy” inference algorithm may address such concerns.21 Second, with a large number of signaling proteins interacting and regulating each other, conventional approaches of representing probabilistic relationships among variables using conditional probability tables (CPT) becomes intractable, because the size of a CPT is exponential to the number of parents of a node. Finally, de novo learning structure based on observed data is NP-hard, which involves searching for a super exponential space of possible structures, but prior knowledge helps to constrain the searching space.19
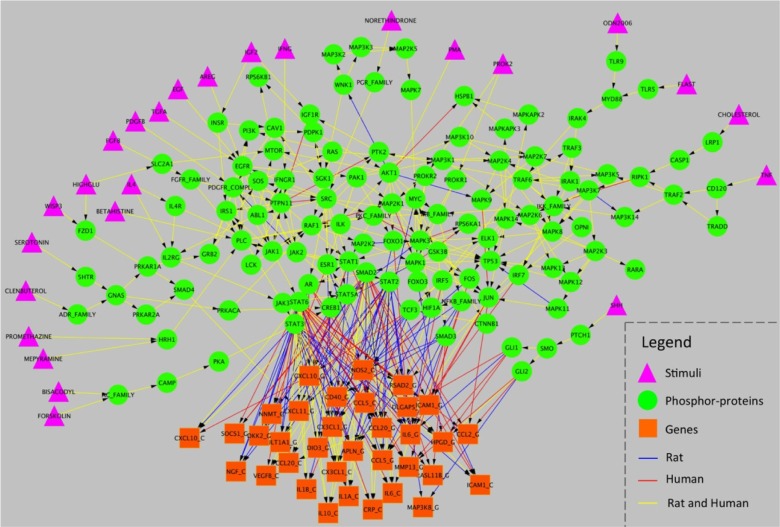
To assess the current methods in learning cell signaling network and also try to understand the differences between rat and human cell signaling networks in response to common stimuli, SBV IMPROVER organized a Species Specific Network Inference challenge (https://www.sbvimprover.com/challenge-2/sub-challenge-4-species-network-inference) based on rat and human genomic and proteomic data.22 In this challenge, a literature curated reference network with 220 nodes and 501 edges was provided as prior knowledge, from which the participants could add or remove edges. Figure 1 shows the overview of the network inference problem.
Figure 1.
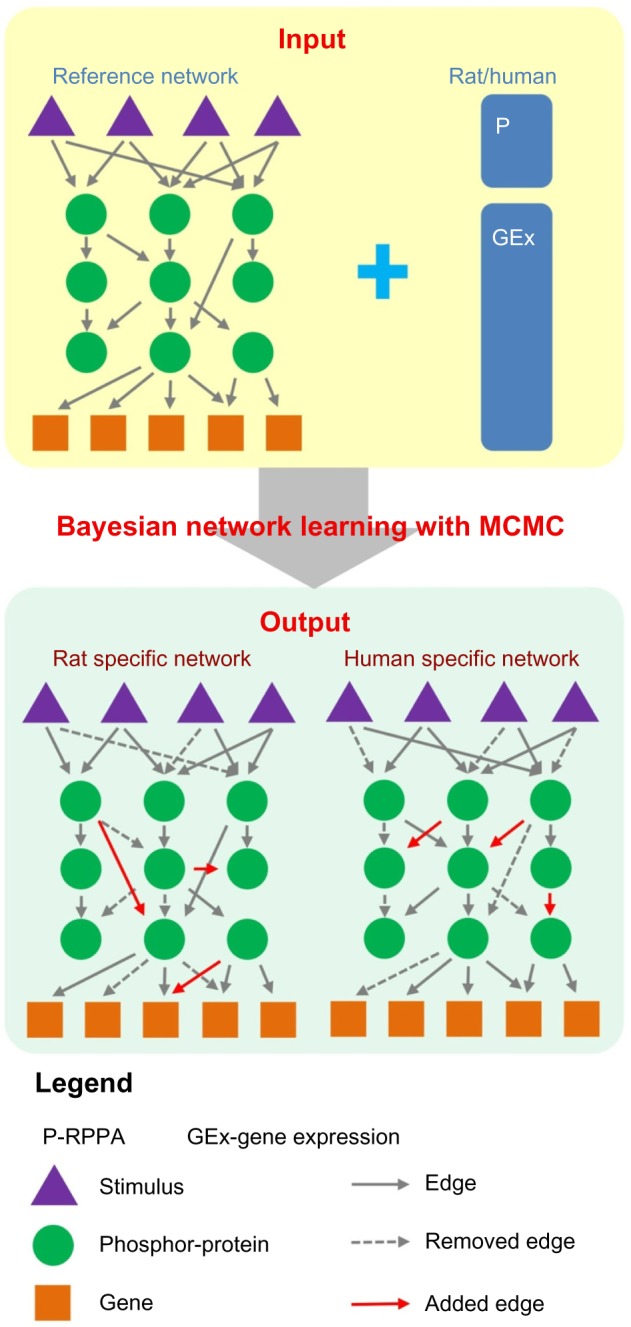
Overview of the network inference problem. The task is to predict two separate signaling networks for rat and human by adding and trimming edges from reference network by applying BN learning method to gene expression and reverse phase protein array data.
We participated in the SBV IMPROVER challenge and developed a novel BN learning approach to search for signaling pathways that model the information flow from extracellular stimuli to phospho-proteins states and further onto regulated gene expression. We adopted an approach that mimics full Bayesian framework in which we concentrated on identifying the BN that has the highest posterior probability conditioning on prior knowledge and data, rather than just fitting model parameters which often leads to the over-fitting problem. Instead of using conventional CPT, we defined conditional probabilities among variables using logistic regression, which was amenable to a large number of parents per node. We further designed a Markov chain Monte Carlo (MCMC) based inference algorithm to learn the BN structure through parameterization of conditional probabilities. When applied to SBV IMPROVER challenge data, our models were capable of identifying biologically sensible networks and performed well during the SBV challenge.23
Methods
Data collection and pre-processing
The transcriptomic and proteomic data for both rat and human were provided by SBV IMPROVER organizers.24 The phosphorylation states for 16 phospho-proteins under 26 different stimuli were measured in rat and human bronchus cells. Each stimulus experiment included triplicates and data was collected at five and 25 minutes. The SBV IMPROVER organizers provided discretized protein phosphorylation data, which was then pre-processed into a binary matrix such that a “1” in the matrix indicates a protein is phosphorylated under a treatment condition. A phospho-protein was considered phosphorylated if it was phosphorylated under either five or 25 minutes. Therefore, the protein phosphorylation data was transformed in to a 16 × 78 binary matrix, ie, 16 phospho-proteins and 78 experimental measurements, for rat and human, respectively.
Gene expression data was also measured and normalized for cells exposed to 26 stimuli (two or three replicates per stimulus) and DME controls (Dulbecco’s Modified Eagle’s Medium corresponding to standard cell culture medium). In total, the data included 13,841 genes measured under 75 stimuli conditions and 16 DME controls for rat, and 20,010 genes measured under 76 stimuli conditions and 16 DME controls for human. We then calculated the gene expression fold change as the ratio of the gene expression level under stimuli conditions over the DME controls. We define a gene is differentially expressed under a specific treatment condition, if the expression value of the gene exhibited a change of over twofold (increase or decrease). Then, we transformed the gene expression data into a 13,841 × 75 binary matrix for rat and a 20,010 × 76 binary matrix for human, such that a “1” in the matrix indicates a gene is differentially expressed under a treatment condition.
A reference network derived from literature was provided by the SBV IMPROVER as a starting point, which contains 220 nodes and 501 edges. The nodes could be classified into three categories: (1) stimuli, (2) signaling proteins which are composed of receptors, phospho-proteins, and transcription factors (TFs), and (3) targets which are composed of genes and cytokines. We further augmented the reference network as follows: (1) adding an edge from known transcription factors in the reference network, eg, SMAD2, STAT2 and STAT3, to all genes in the network; (2) adding edges between phospho-proteins if correlation of their phosphorylation states was above 0.4. The augmented reference network with 220 nodes and 817 edges was used for rat and human BN structure inference.
BN representation
A BN is a DAG to represent the joint distribution of a set of variables, which could be further factorized as a series of conditional probabilities. First, we transformed the augmented reference network into a BN, where the nodes represent the variables, eg, stimuli, phospho-proteins, TFs and genes, and directed edges represent regulatory effects from parent nodes to the children nodes. Second, the states of the stimuli, measured phospho-proteins and genes were represented as Bernoulli variables, such that 1 is the “on” state (for example, proteins being phosphorylated, or gene being differentially expressed) and 0 is the “off” state. Third, we represented the conditional probabilistic relationship between a node and its parents as a logistic function as defined in Equation (1):
| (1) |
where Xi denotes the state of node i, Pa(Xi) denotes the states of the parent nodes of node i, and β is a vector of logistic regression coefficients, with each element being associated with an edge between the node i and its parent nodes plus a bias term.
Learning structure of species-specific signaling networks
We formulated the problem of learning signaling pathways as a task of learning BN structure based on the observed gene expression and protein phosphorylation data under different stimuli. Here, we adopt a Bayesian approach toward the goal of searching for a network structure, S, which maximized the posterior probability given the observed data D:
| (2) |
| (3) |
| (4) |
where P(S|D) is the posterior probability of a given structure S and P(D|S) is the marginal likelihood of observing the data conditioning on a given structure, which involves integrating all possible values of the model parameter θ.
Learning BN structure based on observed data in our setting is difficult in the following aspects: (1) It is a NP-hard problem, due to the super exponential number of all possible network structures G with respect to the number of nodes, and exhaustive search all structure is intractable. (2) The integration in Equations (3) and (4) is often intractable. (3) The reference network contains many signaling proteins of which their activation states are unobserved; thus we need to infer their states when modeling the signal propagation in the system, from stimuli to gene.
We developed an algorithm integrating Gibbs-sampling-based belief propagation and a Monte Carlo approach to simultaneously address the items 2 and 3 in the previous paragraph (Fig. 2). Assuming that prior probability for any structure was uniformly distributed, we concentrated on computing an approximated marginal likelihood using samples obtained from Gibbs sampling and calculated the integration in Equation (4) via a Monte Carlo approach. Given a BN structure, we started N sampling chains, with each chain independently sampling the states of latent variables for all cases, updating model parameters and calculating the chain-specific likelihood of data P(D|S, θn). Then, the marginal likelihood can be approximated as follows:
| (5) |
Figure 2.
Pseudo code of learning BN structure with MCMC algorithm.
where N is the number of chains, θn denotes the parameters derived from the nth sampling chain, and P(θ) is a prior distribution over the parameters. We will further discuss how to approximate the integration in Equation (5) in later subsections.
Learning network structure and parameters simultaneously
To avoid exhaustively searching through the space of network structures which was intractable, we developed an approach to simultaneously infer network structure and parameters by taking advantage of the form of conditional probability defined in our model. We constructed an initial network including all the edges in the augmented reference network, and we represented the conditional probability of a node using a logistic function as defined in Equation (1). The logistic regression represents the conditional probability between a node and its parent in a linear space instead of the exponential space associated with CPT. A logistic regression representation further enabled us to search for the BN structure through parameterization of the conditional probability. If an element β associated with an edge from a parent node is set to zero, it is equivalent to deleting the edge from the network. We employed an elastic network approach to trim the edges using the R package “glmnet.”25 The elastic network can be used to learn regularized parameters in the framework of a generalized linear model in the following form:
| (6) |
where
| (7) |
There is a connection between regularized regression and Bayesian treatment of regression as follows: estimating model parameters with an L1 regularization is equivalent to estimating the maximum a posterior (MAP) parameters under a Laplacian prior over the parameters; estimating parameters with an L2 regularization is equivalent to estimating MAP parameters under a Gaussian prior over the parameters centering at 0. Therefore, the elastic network model in a linear regression setting can be thought of as estimating MAP parameters under a mixture of prior distributions. When the above assumptions are generalized to logistic regression under our setting, one can treat a MAP parameter vector as a sample drawn from the posterior distribution over parameters. While is not exactly drawn from the prior distribution as required by Equation (5), integrating it out using a Monte Carlo approach would approximate the marginal likelihood of the model as follows:
| (8) |
Under such a setting, our task of searching for optimal BN structure that effectively models the data is carried out by first instantiating the edges of the initial BN according to knowledge and data (augmentation step of our approach) and then trimming the edges that are not needed to explain the observed data. In this approach, we simultaneously learned the optimal structure as well as the parameters associated with the optimal structure.
Results
Overview
Learning a species-specific network is equivalent to searching for a subset of nodes and edges from the reference network, which give the best representation of the observed data for a particular species. We addressed this task by going through the following steps: (1) augmenting the initial reference network by adding edges from known TFs to potential targets and edges between phospho-proteins with strong correlations of their phosphorylation states; (2) learning the BN by utilizing the experimental data and augmented reference network, which determines the network structure through parameterization; (3) using elastic network approach to determine if an edge should be retained between the parent node and its child node. Our approach enabled us to reduce the augmented network to a very sparse network that models the observed data well, and also allowed us to avoid exploring super-exponential space of all possible structures in a polynomial time.
We tuned the α and λ parameters of “glmnet” and searched for the optimal penalty that led to the sparsest model with best performance [Equations (8) and (9)]. Figure 3A shows that by increasing α (increasing L1 penalization while decreasing L2 penalization), we tend to have sparser networks, which is to be expected. Interestingly, Figure 3B shows that the models with around 350 edges return the best marginal log likelihood for both rat and human data, whereas models with too many edges or too few edges do not fit the data well. This is a key advantage of Bayesian model selection, such that it penalizes the too complex models that tend to over-fit data and the too simple models that cannot explain data well – a characteristic commonly referred to as Occam’s razor. We selected the best models with αrat = 0.9 and αhuman = 1, for rat and human, respectively. Over half of the edges were trimmed off for both rat and human augmented reference networks. We also found that interactions between phospho-proteins in signaling pathways tended to be more translatable with few divergent points from rat to human, whereas TF–gene interactions tended to be more divergent between rat and human, which explained the difference in gene expression profiles.
Figure 3.
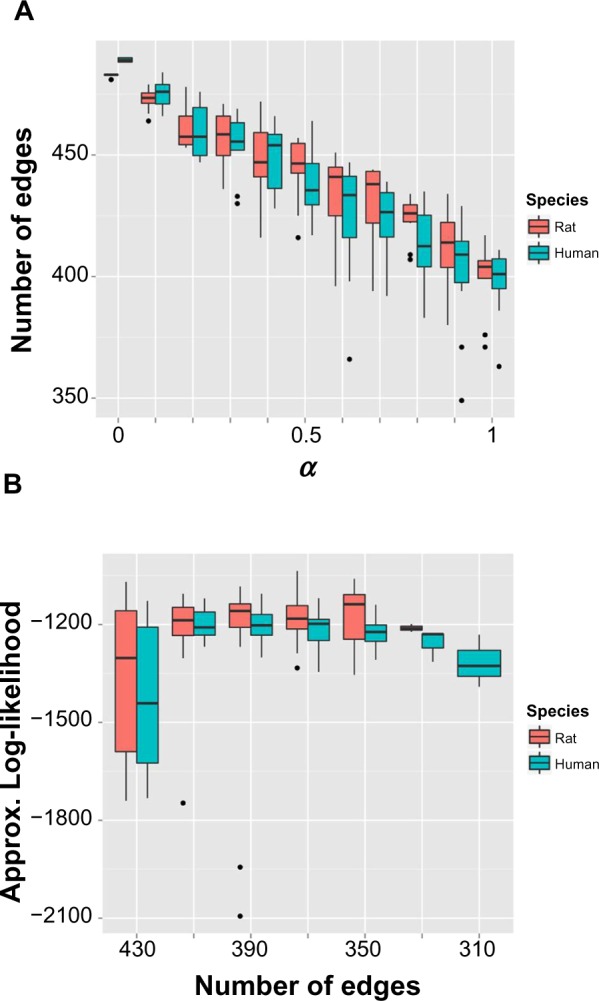
(A) Number of predicted edges against elastic network approach parameter α. (B) Approximated log-likelihood against number of edges in the predicted network.
Learning rat and human specific signaling networks
We applied our BN learning method to infer the rat and human specific signaling networks from experimental data, incorporating the augmented reference network which contains 220 nodes and 817 edges. The predicted networks are much sparser than the given the reference network, which only contains about half the edges in the reference network: the rat network is composed of 171 nodes and 366 edges, and the human network is composed of 171 nodes and 355 edges (Table 1 and Figure 4). Notably, most of the trimmed edges correspond to TF->gene interactions, ie, 38 out of 72 genes were deleted for having no incoming transcriptional signal. The result was evaluated and scored by the SBV IMPROVER Species Specific Network Inference challenge committee, and ranked as one of two best performing teams in the competition, ie, team PITT.DBMI.DREAM (https://www.sbvimprover.com/challenge-2/overview).
Table 1.
Number of nodes, edges, signaling edges, and transcriptional edges in segmented reference network, predicted rat network, predicted human network, and predicted network intersection between rat and human.
| REFNET | RAT | HUMAN | BOTH | |
|---|---|---|---|---|
| # of nodes | 220 | 171 | 171 | 162 |
| # of edges | 817 | 366 | 355 | 289 |
| # of signaling edges | 272 | 255 | 258 | 247 |
| # of transcriptional edges | 545 | 111 | 97 | 42 |
Figure 4.
The predicted rat and human signaling network.
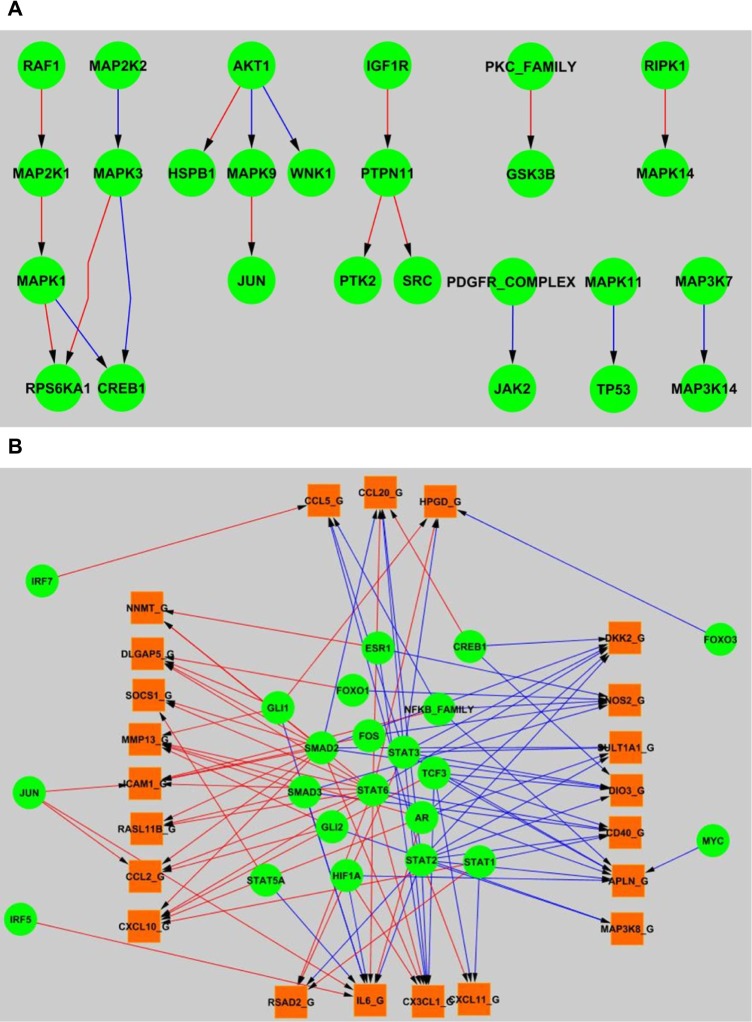
The two predicted networks inferred by our approach represent plausible signaling pathways specific to rat and human, respectively. In contrast to the original reference network, six signaling edges are not retained in either rat or human network. For example, MTOR → RPS6KB2, RPS6KB2 → RPS6, and RPS6KB2 → RPS6 are deleted due to the fact that the parameters associated with these edges cannot be learned since both of the latent variables, i.e. RPS6 and RPS6KB2, do not have any downstream observable node. We have also added three edges between AKT1 and three other proteins, ie, IKB_FAMILY, HSPB1, and MAPK9. The proposed regulations are consistent with the experimental facts: Aurora-A down-regulates IKB_FAMILY via AKT activation;26 HSPB1 phosphorylation level is mediated by AKT activity in epidermal differentiation;27 and the JNK2-mediated phosphorylation of JIP1 results in the dissociation of AKT1 from JIP1 and subsequently restores AKT1 enzyme activity.28 Moreover, a number of gene targets have been added to the networks for known TFs, ie, CREB1 (2 targets), SMAD2 (25 targets), STAT2 (23 targets), STAT3 (21 targets), and STAT6 (30 targets).29–31
Signaling network translatability between rat and human
Figure 4 shows the networks learned by our method and the comparison between rat and human. There is a significant overlap between these two networks, ie, 162 shared nodes and 289 shared edges (Table 1). The predicted network represents various cellular pathways according to the KEGG database,32 eg, MAPK signaling pathway, PI3 K-Akt signaling pathway, Jak-STAT signaling pathway, Ras signaling pathway, NF-kappa B signaling pathway, etc.
The result also shows that the interactions among phospho-proteins in signaling pathways tend to be more conserved with fewer divergent points, whereas TF–gene interactions tend to be more divergent between rat and human. Figure 5 illustrates the rat/human specific signaling edges and transcriptional edges. Notably, there are no significant difference between rat and human at protein–protein signaling transduction level. Moreover, as shown in Figure 5A, most of the species specific edges were localized to only one or two interactions within the same signal cascade. However, gene expression might be more mediated in a species-specific fashion, where the same TF is responsible for regulating the expression of different sets of genes from rat to human as illustrated in Figure 5B.
Figure 5.
(A) Rat and human specific signaling edges in the predicted network. (B) Rat and human specific transcriptional edges in the predicted network.
Discussion
Reconstruction of the signaling networks is very important for us to study cells’ regulatory mechanism, and the knowledge of correctly inferred signaling pathways can be further utilized to improve disease treatment and drug development.5,33 Animal models play an essential role during this process, and exploring the commonality and discrepancy between human and animal models can help us better understand the human signaling network and ultimately design better drugs. In this study, we developed a BN structure learning approach for a species specific network learning task with three advantages: (1) we efficiently built the reference network to confine the network searching space by incorporating prior knowledge from literature and adding edges between the nodes with statistically significant correlations; (2) we avoided searching the super exponential space of all possible structures by adopting the MCMC EM method to infer the states of latent variables and estimate parameters associated with the edges; (3) we predicted the sparsest network to best represent the observed data by employing elastic network approach to determine the edge weight and network structure.
The predicted networks showed very strong overlaps between rat and human, especially at the protein signal transduction level, which suggested that there was no entire signaling paradigm shift between rat and human. However, TF to gene interactions tended to be more divergent between rat and human, where certain TFs were predicted to have different sets of gene targets. This difference could be the key to explain the discrepancy in gene expression profiles between rat and human under a common stimulus. These findings need further careful verification which may require carrying out more thorough experimental work.
Our approach could be further extended to infer the activation states of signaling proteins given only gene expression profiles once the network structure and parameters are determined. This inference process could be very useful to learn the pathway driving forces in a patient specific fashion, because gene expression technology is readily applicable in clinical environment, particularly in cancer care, whereas proteomic analysis has not been widely used in clinical setting and is more expensive. In addition, our study provides an example to demonstrate the feasibility of inferring the signaling pathway and its state through integrating transcriptomic and proteomic data, and it may motivate more studies to apply the principles developed in this study in cancer and other disease researches.
Conclusion
We developed a BN framework for learning species-specific signaling pathways that provided the best presentations for the observed data with the sparsest network, by applying advanced statistical methods on the reference graph to infer the states of latent variables and estimate the parameters associated with the edges. The results were assessed and scored as the top performer by SBV IMPROVER Species Specific Network Inference challenge committee and also matched with experimental evidence. Our predictions that the protein signaling pathways are conserved and TF–gene interactions are divergent, could be used to explain the difference in gene expression profiles between rat and human, which needs further experimental verifications.
Acknowledgments
The authors would like to thank Drs. Gregory Cooper and Sognjian Lu for their constructive discussions during the project. The authors also would like to thank Mr. Kevin Lu for proofreading the final manuscript.
Footnotes
Author Contributions
Conceived and designed the experiments: XL, CC. Analyzed the data: LC, CC, XL. Wrote the first draft of the manuscript: CC. Contributed to the writing of the manuscript: XL, XJ. Agree with manuscript results and conclusions: XL, CC, XJ. Jointly developed the structure and arguments for the paper: XL, CC. Made critical revisions and approved final version: CC, XL, XJ. All authors reviewed and approved of the final manuscript.
ACADEMIC EDITOR: JT Efird, Editor in Chief
FUNDING: This study was partially supported by Grant Numbers R01 LM 010144 and 1 R01 LM 011155 from the National Library of Medicine, NIH.
COMPETING INTERESTS: Authors disclose no potential conflicts of interest.
This paper was subject to independent, expert peer review by a minimum of two blind peer reviewers. All editorial decisions were made by the independent academic editor. All authors have provided signed confirmation of their compliance with ethical and legal obligations including (but not limited to) use of any copyrighted material, compliance with ICMJE authorship and competing interests disclosure guidelines and, where applicable, compliance with legal and ethical guidelines on human and animal research participants. Provenance: the authors were invited to submit this paper.
REFERENCES
- 1.Sutandy FX, Qian J, Chen CS, Zhu H. Overview of protein microarrays. Current Protocols in Protein Science. 2013; Unit. 27:1. doi: 10.1002/0471140864.ps2701s72. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Fuentes M. Protein microarrays overview. Recent Pat Biotechnol. 2013;7(2):83. doi: 10.2174/1872208311307020001. [DOI] [PubMed] [Google Scholar]
- 3.Renner O, Carnero A. Mouse models to decipher the PI3 K signaling network in human cancer. Curr Mol Med. 2009;9(5):612–25. doi: 10.2174/156652409788488766. [DOI] [PubMed] [Google Scholar]
- 4.Petricka JJ, Benfey PN. Reconstructing regulatory network transitions. Trends Cell Biol. 2011;21(8):442–51. doi: 10.1016/j.tcb.2011.05.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Papin JA, Hunter T, Palsson BO, Subramaniam S. Reconstruction of cellular signalling networks and analysis of their properties. Nat Rev Mol Cell Biol. 2005;6(2):99–111. doi: 10.1038/nrm1570. [DOI] [PubMed] [Google Scholar]
- 6.Hecker M, Lambeck S, Toepfer S, van Someren E, Guthke R. Gene regulatory network inference: data integration in dynamic models-a review. Biosystems. 2009;96(1):86–103. doi: 10.1016/j.biosystems.2008.12.004. [DOI] [PubMed] [Google Scholar]
- 7.De Smet R, Marchal K. Advantages and limitations of current network inference methods. Nat Rev Microbiol. 2010;8(10):717–29. doi: 10.1038/nrmicro2419. [DOI] [PubMed] [Google Scholar]
- 8.Schwacke JH, Voit EO. Improved methods for the mathematically controlled comparison of biochemical systems. Theor Biol Med Model. 2004;1:1. doi: 10.1186/1742-4682-1-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Aldridge BB, Burke JM, Lauffenburger DA, Sorger PK. Physicochemical modelling of cell signalling pathways. Nat Cell Biol. 2006;8(11):1195–1203. doi: 10.1038/ncb1497. [DOI] [PubMed] [Google Scholar]
- 10.Margolin AA, Nemenman I, Basso K, et al. ARACNE: an algorithm for the reconstruction of gene regulatory networks in a mammalian cellular context. BMC Bioinformatics. 2006;7(suppl 1):S7. doi: 10.1186/1471-2105-7-S1-S7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Thomas R. Boolean formalization of genetic control circuits. J Theor Biol. 1973;42(3):563–85. doi: 10.1016/0022-5193(73)90247-6. [DOI] [PubMed] [Google Scholar]
- 12.Li F, Long T, Lu Y, Ouyang Q, Tang C. The yeast cell-cycle network is robustly designed. Proc Natl Acad Sci USA. 2004;101(14):4781–86. doi: 10.1073/pnas.0305937101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Liao JC, Boscolo R, Yang YL, Tran LM, Sabatti C, Roychowdhury VP. Network component analysis: reconstruction of regulatory signals in biological systems. Proc Natl Acad Sci USA. 2003;100(26):15522–27. doi: 10.1073/pnas.2136632100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Gardner TS, di Bernardo D, Lorenz D, Collins JJ. Inferring genetic networks and identifying compound mode of action via expression profiling. Science. 2003;301(5629):102–105. doi: 10.1126/science.1081900. [DOI] [PubMed] [Google Scholar]
- 15.Mordelet F, Vert JP. SIRENE: supervised inference of regulatory networks. Bioinformatics. 2008;24(16):i76–i82. doi: 10.1093/bioinformatics/btn273. [DOI] [PubMed] [Google Scholar]
- 16.Pe’er D. Bayesian network analysis of signaling networks: a primer. Sci STKE. 2005;2005(281):l4. doi: 10.1126/stke.2812005pl4. [DOI] [PubMed] [Google Scholar]
- 17.Needham CJ, Bradford JR, Bulpitt AJ, Westhead DR. Inference in Bayesian networks. Nat Biotechnol. 2006;24(1):51–53. doi: 10.1038/nbt0106-51. [DOI] [PubMed] [Google Scholar]
- 18.Sachs K, Gifford D, Jaakkola T, Sorger P, Lauffenburger DA. Bayesian network approach to cell signaling pathway modeling. Sci STKE. 2002;2002(148):e38. doi: 10.1126/stke.2002.148.pe38. [DOI] [PubMed] [Google Scholar]
- 19.Qin T, Tsoi LC, Sims KJ, Lu X, Zheng WJ. Signaling network prediction by the Ontology Fingerprint enhanced Bayesian network. BMC Syst Biol. 2012;6(suppl 3):S3. doi: 10.1186/1752-0509-6-S3-S3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Heckerman D, Meek C, Cooper G. A Bayesian approach to causal discovery. Computation, Causation, and Discovery. 1999;19:141–66. [Google Scholar]
- 21.Murphy KP, Weiss Y, Jordan MI. Loopy belief propagation for approximate inference: an empirical study; Paper presented at: Proceedings of the Fifteenth conference on Uncertainty in artificial intelligence; 1999. [Google Scholar]
- 22.Rhrissorrakrai K, Belcastro V, Bilal E, et al. Animal models as predictors of human biology: lessons learned from the sbv {IMPROVER} Species Translation Challenge. Bioinformatics. 2014 doi: 10.1093/bioinformatics/btu611. (Submitted to Bioinformatics) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Bilal E, Sakellaropoulos T, Challenge Participants, et al. A crowd-sourcing approach for the construction of species-specific cell signaling networks. Bioinformatics. 2014 doi: 10.1093/bioinformatics/btu659. (Submitted to Bioinformatics) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Poussin C, Mathis C, Alexopoulos LG, et al. The species translation challenge – a systems biology perspective on human and rat bronchial epithelial cells. Bioinformatics. 2014 doi: 10.1038/sdata.2014.9. (Submitted to Bioinformatics) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Friedman J, Hastie T, Tibshirani R. Regularization paths for generalized linear models via coordinate descent. J Stat Softw. 2010;33(1):1–22. [PMC free article] [PubMed] [Google Scholar]
- 26.Yao JE, Yan M, Guan Z, et al. Aurora-A down-regulates IkappaBalpha via Akt activation and interacts with insulin-like growth factor-1 induced phosphatidylinositol 3-kinase pathway for cancer cell survival. Mol Cancer. 2009;8:95. doi: 10.1186/1476-4598-8-95. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.O’Shaughnessy RF, Welti JC, Cooke JC, et al. AKT-dependent HspB1 (Hsp27) activity in epidermal differentiation. J Biol Chem. 2007;282(23):17297–305. doi: 10.1074/jbc.M610386200. [DOI] [PubMed] [Google Scholar]
- 28.Song JJ, Lee YJ. Dissociation of Akt1 from its negative regulator JIP1 is mediated through the ASK1-MEK-JNK signal transduction pathway during metabolic oxidative stress: a negative feedback loop. J Cell Biol. 2005;170(1):61–72. doi: 10.1083/jcb.200502070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Taylor AK, Klisak I, Mohandas T, et al. Assignment of the human gene for CREB1 to chromosome 2q32.3-q34. Genomics. 1990;7(3):416–21. doi: 10.1016/0888-7543(90)90176-u. [DOI] [PubMed] [Google Scholar]
- 30.Takenoshita S, Mogi A, Nagashima M, et al. Characterization of the MADH2/Smad2 gene, a human Mad homolog responsible for the transforming growth factor-beta and activin signal transduction pathway. Genomics. 1998;48(1):1–11. doi: 10.1006/geno.1997.5149. [DOI] [PubMed] [Google Scholar]
- 31.Pellegrini S, Dusanter-Fourt I. The structure, regulation and function of the Janus kinases (JAKs) and the signal transducers and activators of transcription (STATs) Eur J Biochem. 1997;248(3):615–33. doi: 10.1111/j.1432-1033.1997.00615.x. [DOI] [PubMed] [Google Scholar]
- 32.Kanehisa M, Goto S, Kawashima S, Okuno Y, Hattori M. The KEGG resource for deciphering the genome. Nucleic Acids Res. 2004;32(Database issue):D277–D280. doi: 10.1093/nar/gkh063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Lu KP. Pinning down cell signaling, cancer and Alzheimer’s disease. Trends Biochem Sci. 2004;29(4):200–9. doi: 10.1016/j.tibs.2004.02.002. [DOI] [PubMed] [Google Scholar]