Abstract
Background: Using multipollutant models to understand combined health effects of exposure to multiple pollutants is becoming more common. However, complex relationships between pollutants and differing degrees of exposure error across pollutants can make health effect estimates from multipollutant models difficult to interpret.
Objectives: We aimed to quantify relationships between multiple pollutants and their associated exposure errors across metrics of exposure and to use empirical values to evaluate potential attenuation of coefficients in epidemiologic models.
Methods: We used three daily exposure metrics (central-site measurements, air quality model estimates, and population exposure model estimates) for 193 ZIP codes in the Atlanta, Georgia, metropolitan area from 1999 through 2002 for PM2.5 and its components (EC and SO4), as well as O3, CO, and NOx, to construct three types of exposure error: δspatial (comparing air quality model estimates to central-site measurements), δpopulation (comparing population exposure model estimates to air quality model estimates), and δtotal (comparing population exposure model estimates to central-site measurements). We compared exposure metrics and exposure errors within and across pollutants and derived attenuation factors (ratio of observed to true coefficient for pollutant of interest) for single- and bipollutant model coefficients.
Results: Pollutant concentrations and their exposure errors were moderately to highly correlated (typically, > 0.5), especially for CO, NOx, and EC (i.e., “local” pollutants); correlations differed across exposure metrics and types of exposure error. Spatial variability was evident, with variance of exposure error for local pollutants ranging from 0.25 to 0.83 for δspatial and δtotal. The attenuation of model coefficients in single- and bipollutant epidemiologic models relative to the true value differed across types of exposure error, pollutants, and space.
Conclusions: Under a classical exposure-error framework, attenuation may be substantial for local pollutants as a result of δspatial and δtotal with true coefficients reduced by a factor typically < 0.6 (results varied for δpopulation and regional pollutants).
Citation: Dionisio KL, Baxter LK, Chang HH. 2014. An empirical assessment of exposure measurement error and effect attenuation in bipollutant epidemiologic models. Environ Health Perspect 122:1216–1224; http://dx.doi.org/10.1289/ehp.1307772
Introduction
Most epidemiologic studies of the health effects of ambient air pollution have focused on adverse effects associated with single pollutants. In reality, humans are simultaneously exposed to a complex mixture of pollutants that can vary both spatially and temporally (Dominici et al. 2010). Epidemiologic analyses that have examined multipollutant health effects have typically relied on ambient monitoring data to estimate exposures (Hoffmann et al. 2012; Tolbert et al. 2007). Measurements from federal or state ambient monitoring networks often lack spatial and temporal coverage (Goldman et al. 2010; Sarnat et al. 2010) and do not account for exposures in different microenvironments (e.g., in-vehicle and in-home exposures) where infiltration (Sarnat et al. 2006; Weisel et al. 2005) and indoor sources (Baxter et al. 2007; Meng et al. 2009) can contribute substantially. There is, therefore, a potential for exposure measurement error that can lead to effect attenuation and reduced statistical power when measurements from ambient monitors are used as the exposure estimate in an epidemiologic study.
Complex relationships may exist between exposures to various pollutants, and between the exposure error associated with each pollutant. The magnitude of the exposure error may differ across pollutants (Tolbert et al. 2007). For example, pollutants with primarily local sources [e.g., carbon monoxide (CO), nitrogen oxides (NOx), elemental carbon (EC)] exhibit significant spatial heterogeneity (Goldman et al. 2010; Sarnat et al. 2010; Strickland et al. 2013) that may not be captured by central-site (CS) ambient monitors. Exposures estimated from ambient monitors for these pollutants may be associated with more error than monitor-based estimates for pollutants that are more spatially homogeneous [e.g., fine particulate matter (PM2.5; ≤ 2.5 μm in aerodynamic diameter), sulfate (SO4), ozone (O3)]. When exposure estimates do not take into account exposure factors such as time–location–activity patterns (including time spent indoors) (Monn 2001; Setton et al. 2011), significant indoor sources [e.g., gas stoves contributing to nitrogen dioxide (NO2) exposures] (Williams et al. 2012), or housing characteristics [e.g., air exchange rate (AER), pollutant infiltration] (Sarnat JA et al. 2013), exposure error may be greater.
Previous studies have predominantly focused on quantifying and accounting for exposure error in single-pollutant models (Sarnat et al. 2010; Setton et al. 2011; Strickland et al. 2013). Zeka and Schwartz (2004) focused on a method for the analysis of health effects in multipollutant studies that is resistant to measurement error. Among other findings, Zeka and Schwartz (2004) found an association between CO and daily mortality when traditional analysis did not, suggesting that a high degree of measurement error due to spatial heterogeneity of CO concentrations may be contributing to the difference in findings. In another study, Schwartz and Coull (2003) provided alternative methods for estimating the effect of two exposures on an outcome that reduced bias at the cost of a small-to-moderate reduction in power.
The objective of the present analysis was to examine exposure errors for multiple pollutants and provide insights on the potential for bias and attenuation of effect estimates in single- and bipollutant epidemiologic models. We used this approach to examine the robustness of the association for a pollutant of interest when a second pollutant is controlled for, that is, to examine the attenuation due to measurement errors present in both pollutants. In a previous analysis, alternative exposure estimates for ambient-generated PM2.5, EC, SO4, CO, NOx, and O3 were developed, and spatiotemporal patterns for each estimate were characterized in comparison with CS monitor measurements (Dionisio et al. 2013). The exposure estimates were used in an epidemiologic study in the Atlanta, Georgia, metropolitan area, using a time-series design to examine the association between daily exposure to ambient air pollution and daily emergency department (ED) visits for asthma/wheeze during a 4-year study period (1999–2002) (Sarnat SE et al. 2013). Using a modified set of the previously generated exposure estimates, we examined the exposure error and between-pollutant relationships and quantified potential attenuation of model coefficients in single- and bipollutant models at the ZIP code level for ambient-generated PM2.5, EC, SO4, CO, NOx, and O3 in Atlanta.
Methods
Estimates of exposure. Three estimates of daily exposure to ambient PM2.5, EC, SO4, CO, NOx, and O3 were derived for 193 ZIP codes in the 20-county Atlanta metropolitan area for use in an epidemiologic analysis of cardiovascular and respiratory outcomes based on data from ED visits. Each metric builds on previous metrics, incorporating the coarser measurements and model estimates and becoming increasingly more finely resolved. The three estimation approaches, or “metrics,” for exposure to ambient pollution include a) CS: CS measurements; b) AQ: a hybrid of a statistical model for regional background and a dispersion model for the local contribution to ambient air quality; and c) PE: a stochastic population exposure model. We used the AERMOD (American Meteorological Society/Environmental Protection Agency Regulatory Model) dispersion model, version 09292, for the local contribution to the AQ metric, and the U.S. Environmental Protection Agency’s (EPA) Stochastic Human Exposure and Dose Simulation (SHEDS) model (Burke et al. 2001) for the PE metric. The contribution from indoor sources was not included in any of the approaches because of the desire to associate exposure to ambient pollution with the health outcome. All three approaches estimate exposures to ambient pollution at each ZIP code centroid in the study area. Daily estimates (8-hr maximum for O3, 24-hr average for other pollutants) for 1999–2002 were generated for the three exposure estimation approaches.
CS measurements. CS measurements for each pollutant were obtained from the Southeastern Aerosol Research and Characterization (SEARCH) network (http://www.atmospheric-research.com/studies/SEARCH/), the Assessment of Spatial Aerosol Composition in Atlanta (ASACA) network (Butler et al. 2003), and the U.S. EPA’s Air Quality System (AQS) monitoring network (http://www.epa.gov/ttn/airs/airsaqs/aqsweb/)(see Supplemental Material, Figure S1). Details regarding measurement methods, imputations for filling in missing data, and previous work using these monitors to characterize background air pollution levels have been reported previously (Dionisio et al. 2013; Metzger et al. 2004; Tolbert et al. 2000). Daily 24-hr average concentrations of PM2.5, EC, and SO4 were taken directly from monitor measurements. Hourly concentrations for CO and NOx were aggregated to 24-hr averages, and hourly concentrations for O3 were aggregated to daily 8-hr maximum concentrations.
AQ model estimates. AQ model estimates were obtained by combining local- and regional-scale model results (based on CS measurements) to account for all major atmospheric processes, including local contributions (driven by local-scale variation in pollutant emissions and meteorology) and regional contributions (background levels associated with large-scale synoptic patterns). The sum of the modeled regional background contribution and the local contribution was computed hourly to obtain total modeled ambient air concentrations at each ZIP code centroid for each pollutant being studied. To obtain estimates of the regional background contribution, we modified an approach developed to provide population-weighted daily averages of ambient pollution concentrations (Ivy et al. 2008) to provide spatially resolved hourly estimates of regional background pollution by removing local-source impacts modeled by hour of day and day of week. Local-scale pollutant contributions for PM2.5, EC, SO4, CO, and NOx at each ZIP code centroid were modeled using the AERMOD dispersion model, version 09292 (Cimorelli et al. 2005), which simulates concentrations of pollutants directly emitted into the atmosphere. Because O3 is formed by photochemical processes and has no direct emissions, O3 concentrations were not modeled with AERMOD. Similarly, the SO4 concentrations estimated from AERMOD were from direct vehicle exhaust emissions and did not include the secondary SO4 contribution due to photochemical transformations in the atmosphere. Further details on methodology and modeling of the regional contribution, local-scale contribution, and computation of the AQ metric estimates have been reported previously (Dionisio et al. 2013).
PE model estimates. We used the SHEDS model (Burke et al. 2001) to derive PE model estimates of daily population exposures to ambient pollution at each ZIP code centroid. The SHEDS model is a stochastic population exposure model that uses a probabilistic approach to estimate personal exposures for simulated individuals of a defined population based on ambient concentrations, distributions of residential AERs and particle infiltration parameters (i.e., penetration factors and deposition rates), and time spent in various microenvironments (e.g., home, office, school, vehicle) from a large database of human activity diaries. Key inputs to the model are the AQ metric estimates described above, time–location–activity data from the U.S. EPA’s Consolidated Human Activity Database (McCurdy et al. 2000), spatially varying local AERs (Sarnat JA et al. 2013), and census tract–level home-to-work commuting data (Bureau of Transportation Statistics 2000; U.S. EPA 2012). Penetration and decay parameters used in the model are specific to each pollutant; however, they do not vary spatially or temporally (see Supplemental Material, Tables S1 and S2). To derive model estimates for exposures to ambient pollution, consistent with the CS and AQ metrics, we excluded contributions from indoor source emissions for this analysis. For additional details, see Supplemental Material, “Population exposure metric.”
Statistical analyses. We computed ZIP code–level summary statistics for each exposure metric for each pollutant. Statistics included the annual mean normalized pollutant concentrations, as well as the variance across days of the normalized pollutant concentrations, for each exposure metric. To allow for comparisons across pollutants, we normalized ZIP code–specific pollutant concentrations for each exposure metric by dividing the daily pollutant concentration by the annual average CS measurement for that pollutant. We then compared the magnitude and spatial variability of normalized pollutant concentrations across pollutants and exposure metrics.
One standard approach for examining the health effects of multiple pollutants is to include each pollutant as an independent risk factor simultaneously in a single epidemiologic model (Bell et al. 2007; Tolbert et al. 2007). The correlation between the exposure estimates, the degree of exposure error for each pollutant, and the correlation of exposure errors between pollutants must all be considered in order to assess the impacts of exposure error on health risk estimates in a multipollutant model (Zeger et al. 2000; Zidek et al. 1996).
In the present analysis, exposure error, δ, was calculated as the difference between two exposure metrics. We present three types of exposure error (δspatial, δpopulation, and δtotal). The exposure error due to a lack of spatial refinement in the exposure estimate is represented by δspatial = AQ – CS because our air quality models add spatial variability to the AQ metric compared with CS measurements, which lack spatial variability because the same CS measurement was used to represent exposure in each ZIP code. Exposure error introduced when human exposure factors are not included in an exposure estimate is represented by δpopulation = PE – AQ. Our PE metric includes variability due to human exposure factors such as time–location–activity patterns of individuals, commuting patterns, and infiltration of ambient pollutants to the indoor environment. A third type of exposure error, δtotal = PE – CS, represents the combined exposure error when both spatial variability and human exposure factors are not accounted for. δTotal does not represent all potential sources of exposure error that may be present in a study; instead it represents the total exposure error that we were able to assess in this analysis. As with the pollutant concentrations, daily ZIP code–specific estimates of exposure error were normalized by dividing by the annual average CS measurement for that pollutant to allow for comparison across pollutants and types of exposure error. We also present the variance calculated across days of the normalized exposure error to aid in estimating the degree of bias and attenuation of model coefficients.
We calculated the between-pollutant Pearson correlations over time for each exposure estimation approach—and for each type of exposure error—to provide information on the collinearity of exposure estimates and exposure error that must be accounted for in a multipollutant model. Correlations were calculated for each ZIP code individually, allowing the range of correlations to be compared across the study domain.
Estimates of the level of attenuation of model coefficients for single- and bipollutant models are presented to aid in the interpretation of future epidemiologic models including two or more pollutants. The attenuation factor (λ) for a classical error, single-pollutant framework is calculated as
λ = 1/{1 + [var(δ)/var(xfine)]} [1]
βobserved = λ × βtrue, [2]
where δ is the exposure error, xfine is the exposure metric with the greater degree of refinement (i.e., increased spatial resolution or inclusion of weighting by population factors), var(xfine) is the variance across days of xfine, and β represents the model coefficients. Assuming that the related epidemiologic analysis fits a time-series model separately for each ZIP code, β represents the association between the health outcome and the daily pollutant exposure. For simplicity, we present the attenuation factor λx1 for pollutant x1 in a bipollutant model, assuming that pollutant x2 has no effect (βx2 = 0), given by the diagonal elements of
λx1 = S(S + V)–1 [3]
βobserved,x1 = λx1 × βtrue,x1, [4]
where S is the covariance of the exposure metrics with the greater degree of refinement for x1 and x2, and V is the covariance of the exposure errors for x1 and x2. For the single- and bipollutant models, an attenuation factor of λ = 1 indicates no attenuation (i.e., βobserved = βtrue), and λ = 0 (i.e., βobserved = 0) indicates null results. An attenuation factor of λ > 1 indicates bias away from the null, and λ < 0 indicates that the estimated coefficient will be in the opposite direction of the true effect. For example, the λ associated with δspatial in a single-pollutant model reflects the attenuation of model coefficients due to error from incomplete characterization of the spatial variation in the concentration of the pollutant in question.
All statistical analyses were completed in R, version 2.15.1 (R Foundation for Statistical Computing; http://www.r-project.org/). All mapping was done in ArcGIS 10 (ESRI; http://www.esri.com/software/arcgis/).
Results
This study builds on previous work in which single-pollutant epidemiologic models were used to estimate the association between daily counts of ZIP code–level ED visits and ZIP code–specific exposures using the three metrics (Sarnat JA et al. 2013; Sarnat SE et al. 2013). Related analyses also showed that the temporal variation in the AQ measure was not always more variable than temporal variation in the CS metric (Dionisio et al. 2013). The goal of the present analysis was to examine exposure error and between-pollutant relationships and how these differ by pollutant pair and exposure metric. Using the empirical covariance structures allowed us to assess potential attenuation of model coefficients in bipollutant epidemiologic models.
Summary statistics for exposure metrics. Figure 1A presents ZIP code–specific normalized exposure metrics averaged across the entire study period (see Supplemental Material, Figure S2A, for an expanded version that shows the full distributions for each metric). Distributions of pollutant concentrations differ by exposure metric—with the PE estimates being consistently equal to AQ estimates for CO or lower than AQ estimates for NOx, EC, PM2.5, SO4, and O3—due to the penetration and decay parameters used in the SHEDS model (see Supplemental Material, Tables S1 and S2). There was no spatial variability for the CS metric because the same CS measurement was used for all ZIP codes. However, when AQ or PE modeling was used, we observed considerable spatial variability [i.e., variation among the 193 ZIP code–specific estimates, as indicated in the box plots by a larger interquartile range (IQR), and a larger range from the 5th to 95th percentiles]. For all pollutants except CO, PE estimates exhibited a lower degree of spatial variability than AQ estimates. Local pollutants (CO, NOx, and EC) had relatively more spatial variability in their AQ and PE metrics than did regional pollutants (PM2.5, SO4, and O3), which was expected given the variation of local source emissions such as traffic at the ZIP code level.
Figure 1.
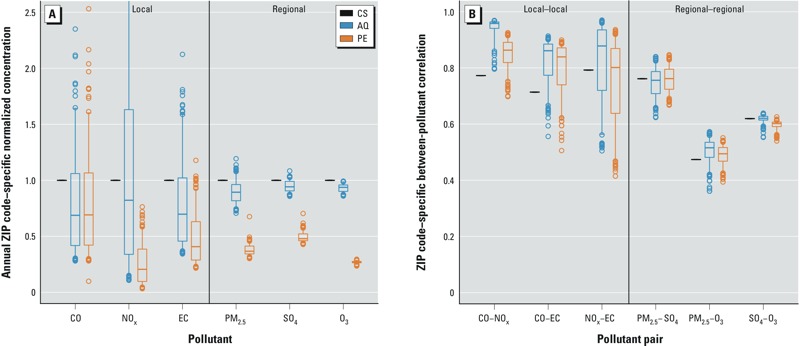
Relationships between the three ZIP code–specific exposure metrics. (A) Normalized exposure metrics for local and regional pollutants (see Supplemental Material, Figure S2A, for full extent of data and outliers). (B) Between-pollutant correlations of exposure for local–local and regional–regional pollutant pairs (see Supplemental Material, Figure S2B, for local–regional pollutant pairs). The bottoms and tops of boxes represent 25th and 75th percentiles, lines within boxes indicate the median, and the whiskers represent 5th and 95th percentiles; n = 193.
Between-pollutant correlations of exposure metrics. Box plots of pairwise Pearson correlation coefficients of daily, ZIP code–specific exposure metrics for local–local and regional–regional pollutant pairs are presented in Figure 1B. All local–local and regional–regional pollutant pairs showed moderate-to-strong positive correlations for each metric; however, correlations for regional–regional pollutant pairs tended to be lower. For the regional–regional pollutant pairs, the median correlation for each pair was consistent across the three exposure metrics. In contrast, for each local–local pollutant pair, the correlation coefficient for CS measurements was lower than the median correlation for the AQ and PE metrics. Correlations of local–regional pollutant pairs were more varied and typically weaker than local–local and regional–regional pollutant pair correlations, with the exception of correlations of CO, NOx, and EC with PM2.5 (see Supplemental Material, Figure S2B).
Spatial variability (described by the width of the box plot) was present to varying degrees for correlations within the AQ and PE metrics, with more spatial variability present for local–local pollutant correlations than for regional–regional pollutant correlations, especially for the CO–EC and NOx–EC pairs (Figure 1B). The degree of spatial variability for regional–regional pollutant pairs was similar for both the AQ and PE metrics. There was no spatial variability present for the between-pollutant correlations of exposure for the CS metric, given that the same CS measurement was used for each ZIP code.
Summary statistics for exposure error. The magnitude and spatial variability of the three types of normalized exposure error (δspatial, δpopulation, and δtotal) across pollutants are presented in Figure 2A (see Supplemental Material, Figure S3A, for the full distribution). The distribution of exposure error across ZIP codes was mostly negative (indicating that the exposure metric with a greater degree of refinement had a lower magnitude), although exposure errors were positive for a small number of ZIP codes. The magnitude of the exposure error varied by type of error, with the absolute value of exposure error greater for δpopulation and δtotal than for δspatial for regional pollutants, and with mixed results for local pollutants. With δspatial near zero for the regional pollutants (the median absolute value of δspatial across ZIP codes was < 0.12, indicating similar magnitude for CS measurements and AQ estimates), their total exposure error (δtotal) consisted mostly of exposure error due to human exposure factors (δpopulation), indicating greater differences in magnitude for AQ estimates relative to PE estimates.
Figure 2.
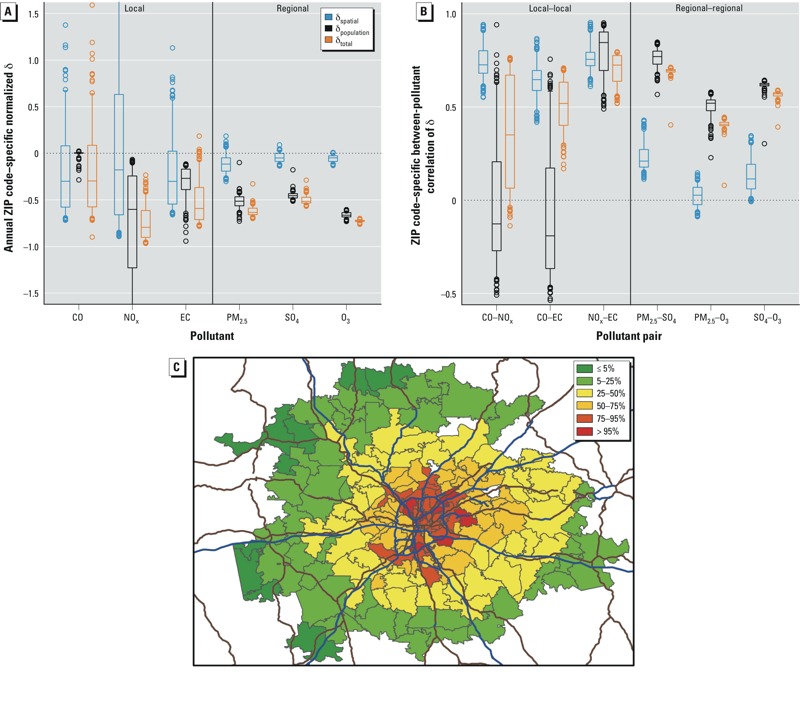
Relationships between the three types of exposure error. (A) Normalized exposure error for local and regional pollutants (see Supplemental Material, Figure S3A, for full extent of data and outliers). (B) Between-pollutant correlations of exposure error for local–local and regional–regional pollutant pairs (see Supplemental Material, Figure S3B, for local–regional pollutant pairs). The bottoms and tops of boxes represent 25th and 75th percentiles, lines within boxes indicate the median, and the whiskers represent 5th and 95th percentiles; n = 193. δspatial = AQ – CS; δpopulation = PE – AQ; and δtotal = PE – CS. (C) Map showing δspatial of NOx for ZIP codes in Atlanta metropolitan area. Blue and brown lines indicate major roads; colors indicate the percentile, where 5% = –0.85; 25% = –0.66; 50% = –0.18; 75% = 0.63; and 95% = 1.73.
To assess the potential for spatially differential exposure error, we compared the spatial variability of exposure errors across ZIP codes. With the exception of δpopulation for CO, the spatial variability of exposure error was greater for local pollutants than regional pollutants (Figure 2A,C). For local pollutants, spatial variability was present to varying degrees across all types of error [smallest range of 5th to 95th percentiles of normalized exposure error, –0.64 to –0.13 (EC, δpopulation); largest range, –0.85 to 1.73 (NOx, δspatial)], with the exception of δpopulation for CO, which was near zero because of the use of a penetration factor of 1 (i.e., assuming free flow of outdoor and indoor air) in the SHEDS model for CO (see Supplemental Material, Table S2). In contrast, regional pollutants exhibited little spatial variability across types of exposure error, and the degree of spatial variability was consistent within a pollutant and across types of error.
Between-pollutant correlations of exposure error. The collinearity of exposure error was examined based on Pearson correlations between daily exposure error for local–local and regional–regional pollutant pairs (Figure 2B; see also Supplemental Material, Figure S3B, for local–regional pairs). The correlation of exposure error was highly dependent on both pollutant pair and type of exposure error. Between-pollutant correlations of exposure error were mostly positive, although there were some ZIP codes with negative correlations, especially for CO. The correlation of exposure error due to a lack of spatial refinement (δspatial) was moderate to strong for local–local pollutant pairs (median correlation over all ZIP codes ranged from 0.65 to 0.76), and relatively weak for regional–regional pollutant pairs (median correlation ranged from 0.03 to 0.21). The correlation for δpopulation showed a near opposite trend, with weak, negative correlations of δpopulation for CO–NOx and CO–EC (–0.13 and –0.19, respectively), and moderate-to-strong positive correlations of δpopulation for NOx–EC (0.85) and the regional–regional pollutant pairs (ranged from 0.52 to 0.77). The magnitude of the correlation of total exposure error (δtotal) between local–local and regional–regional pollutant pairs varied, with median correlations of δtotal across ZIP codes ranging from 0.35 to 0.72 (Table 1, Figure 2B).
Table 1.
Parameters affecting attenuation and bias in bivariate pollutant models of pairs of local pollutants (CO, NOx, and EC) or pairs of regional pollutants (PM2.5, SO4, and O3).
| Parameter | CO–NOxa | CO–EC | NOx–EC | PM2.5–SO4 | PM2.5–O3 | SO4–O3 |
|---|---|---|---|---|---|---|
| AQ Corr(x1,x2) | 0.96 | 0.86 | 0.88 | 0.76 | 0.52 | 0.62 |
| PE Corr(x1,x2) | 0.86 | 0.84 | 0.80 | 0.76 | 0.49 | 0.60 |
| δspatial | ||||||
| Var(δ1)b | 0.25 | 0.25 | 0.83 | 0.04 | 0.04 | 0.05 |
| Var(δ2)b | 0.83 | 0.30 | 0.30 | 0.05 | 0.02 | 0.02 |
| Corr(δ1, δ2) | 0.73 | 0.65 | 0.76 | 0.21 | 0.03 | 0.11 |
| δpopulation | ||||||
| Var(δ1) | 0.00 | 0.00 | 0.32 | 0.09 | 0.09 | 0.10 |
| Var(δ2) | 0.32 | 0.05 | 0.05 | 0.10 | 0.11 | 0.11 |
| Corr(δ1, δ2) | –0.13 | 0.85 | 0.85 | 0.77 | 0.52 | 0.62 |
| δtotal | ||||||
| Var(δ1) | 0.25 | 0.80 | 0.80 | 0.12 | 0.12 | 0.16 |
| Var(δ2) | 0.80 | 0.33 | 0.33 | 0.16 | 0.16 | 0.16 |
| Corr(δ1, δ2) | 0.35 | 0.72 | 0.72 | 0.70 | 0.41 | 0.57 |
| Corr, correlation. Data are presented as medians across all ZIP codes. aThe first pollutant in each pair corresponds to x1 and the second to x2. bVar(δ) represents variance of normalized exposure error. | ||||||
Local–local and regional–regional pollutant pairs showed a moderate degree of spatial variability in the correlation of δspatial (Figure 2B). The patterns of spatial variability of the correlation of δpopulation are more varied, with local–local pollutant pairs showing a larger degree of spatial variability than regional–regional pollutant pairs (5th to 95th percentile for correlation coefficients of 0.56 to 0.93 for NOx–EC, –0.42 to 0.63 for CO–NOx, and –0.46 to 0.59 for CO–EC). Although there was a large range of correlations across ZIP codes for δpopulation for CO–NOx and CO–EC in particular, the bulk of the correlations across the study area were relatively weak (25th to 75th percentile for correlation coefficients of –0.27 to 0.21 for CO–NOx and –0.37 to 0.17 for CO–EC. As reflected in comparisons of δspatial and δpopulation, we saw greater spatial variability in the correlation of δtotal for the local–local pollutant pairs, and very little spatial variability in the correlation of δtotal for the regional–regional pairs.
Variance of exposure error. For regional pollutants (PM2.5, SO4, and O3), variance across days of the normalized exposure error had very little spatial variability (i.e., box plots of the variance of normalized exposure error are narrow) and was < 0.20 for any type of error in any ZIP code (Figure 3A). In comparison, with the exception of δpopulation for CO, variance of the exposure error, as well as spatial variability of the variance, was present for local pollutants (Figure 3; see also Supplemental Material, Figure S4, for the full distribution). For the local pollutants, the magnitude and spatial variability of the variance of normalized error differed depending on pollutant and type of error, with the variance of δspatial and δpopulation for NOx having the largest range of spatial variability, whereas the variance of exposure error for EC exhibited more modest spatial variability.
Figure 3.
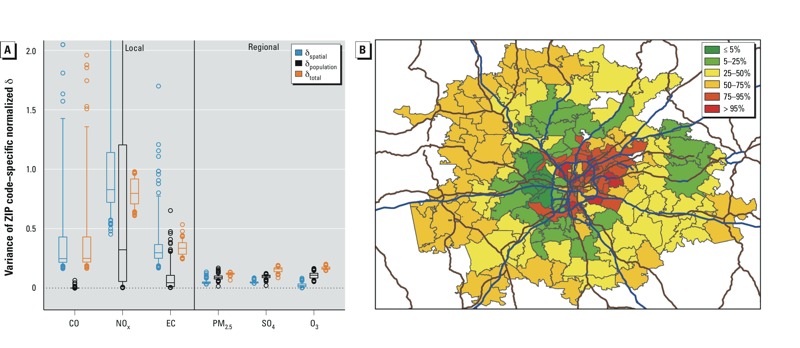
Variance of exposure error. (A) Variance of normalized exposure error (δ) for local and regional pollutants (see Supplemental Material, Figure S4, for full extent of data and outliers). The bottoms and tops of boxes represent 25th and 75th percentiles, lines within boxes indicate the median, and the whiskers represent 5th and 95th percentiles; n = 193. δspatial = AQ – CS; δpopulation = PE – AQ; and δtotal = PE – CS. (B) Map showing variance of δspatial of NOx for ZIP codes in the Atlanta metropolitan area. Blue and brown lines indicate major roads; colors represent percentiles, where 5% = 0.58; 25% = 0.72; 50% = 0.83; 75% = 1.14; and 95% = 4.14.
Attenuation of model coefficients. By compiling empirically determined parameters related to the between-pollutant relationships and their associated exposure error (Table 1), and utilizing Equation 3, we were able to quantify the potential attenuation of model coefficients in a bipollutant model. Table 1 presents the median values across all ZIP codes of the correlations over time and the variances across days for pollutant concentrations and their associated exposure errors. To calculate the attenuation factors, we used the individual ZIP code–specific values of these parameters (Figures 1B, 2B, and 3A; for the full range of parameter values across all ZIP codes, see Supplemental Material, Figures S2A, S3B, and S4).
Figure 4 presents the potential attenuation factors for single- and bipollutant epidemiologic models, based on empirical estimates of the relationships between exposure metrics and their exposure error. The attenuation factors presented for bipollutant models were based on the assumption that one pollutant has a true effect on the health outcome and the other pollutant has no effect. For δspatial, we saw a clear distinction between local and regional pollutants, with more attenuation (typically, λ < 0.6) for both single- and bipollutant models of local pollutants, and less attenuation for regional pollutants (typically, λ > 0.6) [Figure 4A; λ = 1 indicates no attenuation (i.e., βobserved = βtrue), λ = 0 indicates null results, λ > 1 indicates bias away from the null, and λ < 0 indicates that the estimated coefficient will be in the opposite direction of the true effect]. The addition of a co-pollutant appears to increase attenuation. Results for δpopulation and δtotal are more varied, with attenuation factors depending on the pollutant and co-pollutant (Figures 4B,C). For δspatial and δtotal, we observed notable spatial variability in the attenuation factors (evidenced by wider box plots) for local pollutants (except for δtotal for NOx). For δpopulation, and regional pollutants for δspatial and δtotal, the degree of spatial variability depends on the type of exposure error, pollutant, and co-pollutants.
Figure 4.
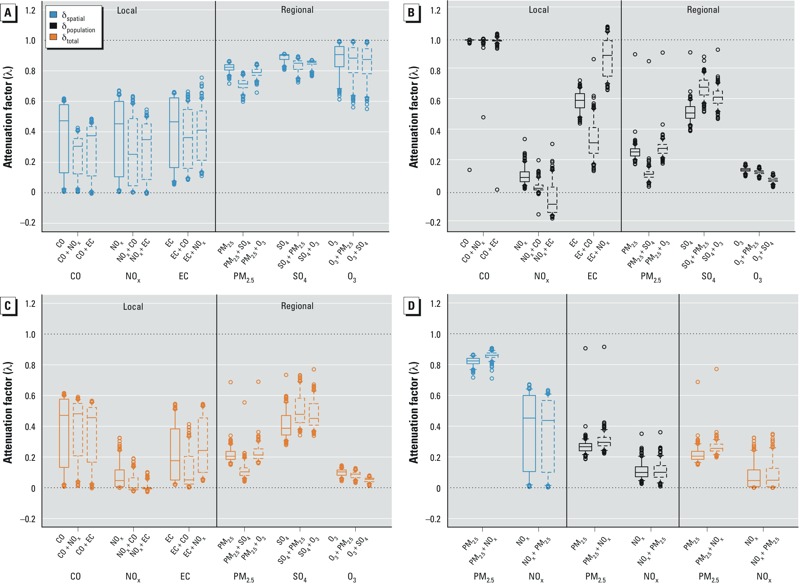
Attenuation of model coefficients in a classical-error, single-pollutant framework and in bipollutant models, assuming that one pollutant has an effect and one pollutant has no effect. (A) λ for local–local and regional–regional pollutant pairs due to δspatial. (B) λ local–local and regional–regional pollutant pairs due to δpopulation. (C) λ for local–local and regional–regional pollutant pairs due to δtotal. (D) λ due to δspatial, δpopulation, and δtotal for a local–regional pollutant example (i.e., PM2.5, PM2.5 and Nox). See Supplemental Material, Figure S5, for all local–regional pollutant pairs. The bottoms and tops of boxes represent 25th and 75th percentiles, lines within boxes indicate the median, and the whiskers represent 5th and 95th percentiles; n = 193. Solid-line boxes indicate attenuation factors for single-pollutant models, and dashed-line boxes represent attenuation factors for bipollutant models. The top row of x-axis labels indicates the pollutant effect being considered (e.g., CO), and the bottom row of x-axis labels indicates the relevant model and the presence or absence of co-pollutants (e.g., CO, CO + NOx, CO + EC). For example, for the three plots representing attenuation factors for CO, the first plot is the set of attenuation factors for CO in a single-pollutant model; the second is the attenuation factors for CO in a bipollutant model with NOx, assuming that NOx has no effect; and the third is the attenuation factors for CO in a bipollutant model with EC, assuming that EC has no effect. λ = 1 indicates no attenuation, λ = 0 indicates null results.
For comparison, the attenuation factors for a bipollutant model with one local (NOx) and one regional (PM2.5) pollutant are presented in Figure 4D, showing significant differences in the attenuation factor across types of exposure error but smaller differences between single- and bipollutant models. See Supplemental Material, Figure S5, for the attenuation factors for bipollutant models for all local–regional pollutant pairs. Results occasionally showed bias away from the null (λ > 1) for some bipollutant combinations because of the strong correlations in both pollutant concentrations and exposure errors.
Discussion
An improved understanding of the degree of exposure error among pollutants and their dependent structure is needed to properly interpret results from epidemiologic models that include multiple pollutants. By examining three different exposure metrics and three types of associated exposure measurement errors, we were able to empirically estimate bipollutant relationships and the potential for attenuation of model coefficients in related bipollutant epidemiologic models. For bipollutant models with local–local pollutant pairs, δspatial and δtotal were likely to introduce attenuation of model coefficients given the high correlations between local pollutant concentrations [corr(x1, x2] > 0.80 for all local–local pollutant pairs), unequal and nonzero variance of the exposure error for each pollutant [0.25 < var(δ) < 0.83], and moderate-to-high correlation of the exposure error for each pollutant pair [corr(δ1, δ2) > 0.52, except CO–NOx for δtotal]. For regional–regional pollutant pairs, the attenuation of model coefficients was likely to be minimal given the relatively low variance of the exposure error [var(δ) < 0.16 for all regional pollutants and types of exposure error]. The empirical quantification of the above parameters resulted in a predicted attenuation factor due to δspatial that was typically < 0.6 for single- and bipollutant models of local pollutants, with less attenuation for regional pollutant models (typically, λ > 0.6) and more varied results for δpopulation and δtotal.
The mean over all ZIP codes of AQ metric estimates that incorporated both regional background and local pollution contributions are similar in magnitude to CS measurements, although AQ metric estimates can exhibit spatial variability depending on local traffic patterns within the ZIP code, particularly for local pollutants. With the exception of CO, PE metric estimates for each pollutant were lower than their corresponding CS measurement because of the infiltration and decay parameters incorporated into the SHEDS human exposure model and the inclusion of time–activity data based on diaries that indicated that individuals spent the majority of their time indoors. PE metric estimates for CO were similar to AQ metric estimates because the penetration parameter for CO was set to 1 (i.e., assuming full penetration of CO from the outdoor to the indoor environment). Pollutant contributions from indoor sources were not included in this study; thus, the PE metric represents indoor and outdoor exposures to ambient pollution originating outdoors only.
Air quality models introduce spatial variability into AQ exposure estimates that is not captured when a single CS measurement is used for all ZIP codes in a study area. Spatial variability was much greater for pollutants with predominantly local sources (CO, NOx, and EC) compared with pollutants dominated by regional source contributions (PM2.5, SO4, and O3). This increase in spatial variability for local pollutants was mainly due to differences in traffic volume and patterns among different ZIP codes. Between-pollutant correlations were strong for local–local pollutant pairs, and moderate to strong for regional–regional pairs, reflecting the common emissions sources contributing to pollutant concentrations within each pair.
As expected, total exposure error (δtotal) for regional pollutants was made up mostly of exposure error due to human exposure factors (e.g., time–activity patterns, AER in the home), with a small contribution from unmeasured spatial variability. In contrast, for the local pollutants NOx and EC, there were substantial exposure error contributions from both human exposure factors and spatial heterogeneity in ambient concentrations. For CO, we saw a near-zero contribution from δpopulation (due to full penetration of CO indoors).
Potential impact of attenuation on epidemiologic model coefficients. In a multipollutant model, the absolute magnitude of this bias will depend on the variance of the exposure error, the correlation between exposure estimates, and the correlation between exposure errors.
The present analysis builds upon the hypothetical simulation presented by Zeger et al. (2000) of predicted bias in regression coefficients in a bipollutant epidemiologic model. In a bipollutant model, we may not be concerned with bias if two regional pollutants are included because of the near-zero (δspatial) and very low (δpopulation and δtotal) variance of exposure error for regional pollutants (Figure 3A, Table 1). However, in a bipollutant model including two local pollutants, there is the potential for bias and attenuation of model coefficients because of a higher degree of variance of exposure error. The effect in bipollutant models that include one local and one regional pollutant will vary, depending on the pollutant pair. In addition, empirically determined attenuation factors for single- and bipollutant models show that the potential for attenuation in the estimated effects can be quite substantial for many pollutants and exposure error types, in particular for local pollutants (with the exception of δpopulation for CO) (Figure 4).
In addition to the potential for bias, the results presented here show that spatial variability is present in the exposure error for local pollutants and in the between-pollutant correlations of exposure error for local–local pollutant pairs. Figure 3B shows how the variance of spatial exposure error for NOx changed across the study domain, with the variance of spatial exposure error being highest in the urban core (within and immediately surrounding the blue circular line indicating a major road), lowest in the central ring of our study domain (ring surrounding the urban core), and increasing slightly again as you extend to the western boundary of the study domain. These results highlight the importance of characterizing intraurban variations in exposure to avoid spatially varying differential exposure error. This is a particular concern when examining effect modification of air pollution health risks obtained without spatially resolved exposure estimates. For example, observed effect modification by ZIP code–level socioeconomic measures (Sarnat SE et al. 2013), which exhibit strong spatial patterns, may be due at least in part to varying degrees of attenuation bias from spatially differential exposure error.
Finally, when multiple pollutants are included simultaneously in a model of associations with health outcomes, bias away from the null may also occur. “Effect transfer” (Zidek et al. 1996) occurs when two correlated pollutants are measured with differential exposure error, and the effect of the pollutant measured with more error is transferred to the pollutant measured with less error. In this case, a pollutant without an effect on an outcome may become associated with it.
Limitations. Limitations of this study include uncertainties in the more refined exposure metric estimates (including that small area variations in pollutant concentrations may not be resolved due to sparsely distributed measurements used as inputs) and the exclusion of the influence of indoor sources. Although it is commonplace to use exposure to ambient sources as a proxy for an individual’s total exposure in an epidemiologic study, the inclusion of indoor sources would further enhance study findings.
Our findings may be generally applicable to study areas with similar source contributions (e.g., predominantly traffic-related local sources) and housing characteristics (e.g., low AERs). For any study area, the methods and models presented here may be applied if appropriate input data sets are used. With the exception of the locally derived AERs, all Atlanta-specific input data sets (e.g., CS pollutant measurements, traffic patterns, local emissions) were extracted from larger, publically available databases maintained by federal and state agencies; thus, similar input data sets for any study area could be compiled. If local AERs were not available, estimates could be made based on published distributions of AERs from various parts of the country.
Although the magnitudes of effects may differ, we expect that general conclusions from our analysis will be applicable to other geographic areas. For example, most study regions will have some pollutant concentrations dominated by regional sources that are likely to remain spatially homogeneous and some pollutant concentrations dominated by local sources that are likely to be spatially heterogeneous within the study area. Thus, we believe that our conclusions about the spatial variability of exposure error being present, and the general likelihood of bias due to measurement error for certain pollutants, are likely to apply across studies.
In calculating the attenuation factor, we assumed a classical exposure measurement error framework. We recognize this is a strong assumption, but we feel it is more appropriate than assuming a Berkson error framework because the CS does not necessarily represent “average” exposure for any ZIP code on any given day. Because exposure measurement error is likely to contain both classical and Berkson type errors, depending on the pollutants and study design, the assumption of a solely classical error framework implies limited applicability. Moreover, an assumption of our assessment of attenuation was that the effect estimate is not subject to residual confounding, the association between pollutant concentration and the health outcome is linear, and there is no effect modification between the pollutant association in a bipollutant model. Further, we have implicitly assumed that the only bias present is additive (the present analysis does not consider multiplicative bias), and this should not impact the regression slope. Last, although empirical covariance structures and exposure errors have been used to quantify potential attenuation in bipollutant models (assuming only one pollutant has an effect on the health outcome), our analysis does not address the potential for effect transfer in a bipollutant model when both pollutants have an effect on the health outcome. A simulation study including the covariance structures of data presented here is warranted to quantify the effect on model coefficients in a multipollutant model.
In addition to the role of exposure error, additional factors must be considered as researchers further investigate epidemiologic analyses that include multiple pollutants. These include the possibility of nonlinear relationships of the various pollutants with the health outcome, interaction or synergism among pollutants included in a single epidemiologic model, and the possibility of the high correlation we have seen among pollutants leading to one pollutant appearing to be associated with the health outcome in an epidemiologic model when a correlated pollutant is the true causal association. A future simulation study that examines the applicability of the classical exposure measurement error framework and the degree of effect attenuation and transfer is warranted.
Conclusions
This analysis is one of the first to quantify the effects of correlated exposure measurement error in bipollutant models (Chang et al. 2011). To our knowledge, this is the first study to look in detail at the effects of spatial variation using dispersion models and stochastic personal exposure simulators in a multipollutant context. We used empirical relationships to show the potential for bias (particularly effect attenuation) in epidemiologic model coefficients for bipollutant models [particularly for local pollutants (CO, NOx, and EC)] due to the presence of variance in the exposure error and correlation between pollutants and their errors. Further, we found evidence of the potential for spatially varying attenuation and bias due to the spatial variability present in these parameters on the ZIP code level. As researchers move toward multipollutant approaches, we must recognize the potential effects on model coefficients depending on the relationships that exist between pollutants and their errors.
Supplemental Material
Acknowledgments
We acknowledge J. Burke, V. Isakov, J. Mulholland, J. Sarnat, S. Sarnat, and H. Ozkaynak for their contributions to the development of the exposure metrics used in this analysis, and C. Stallings and L. Smith for assistance with the U.S. EPA Stochastic Human Exposure and Dose Simulation (SHEDS) modeling runs.
Footnotes
The U.S. EPA, through its Office of Research and Development, National Exposure Research Laboratory, funded and collaborated in the research described here under cooperative agreement CR-83407301-1 to Emory University, and by a U.S. EPA Clean Air Research Center grant to Emory University and the Georgia Institute of Technology (R834799). This work was also funded by grant 1R21ES022795-01A1 from the National Institutes of Health.
Although this work was reviewed by the U.S. EPA and approved for publication, it may not necessarily reflect official agency policy. The U.S. EPA does not endorse the purchase of any commercial products or services mentioned in this publication.
The authors declare they have no actual or potential competing financial interests.
References
- Baxter LK, Clougherty JE, Laden F, Levy JI. Predictors of concentrations of nitrogen dioxide, fine particulate matter, and particle constituents inside of lower socioeconomic status urban homes. J Expo Sci Environ Epidemiol. 2007;17:433–444. doi: 10.1038/sj.jes.7500532. [DOI] [PubMed] [Google Scholar]
- Bell ML, Kim JY, Dominici F.2007Potential confounding of particulate matter on the short-term association between ozone and mortality in multisite time-series studies. Environ Health Perspect 1151591–1595.; 10.1289/ehp.10108 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bureau of Transportation Statistics. Census Transportation Planning Package (CTPP) 2000. Part 3–Journey to Work. 2000. Available: http://www.transtats.bts.gov/Tables.asp?db_id=630&db_name=Census%20Transportation%20Planning%20Package%20%28CTPP%29%202000 [accessed 14 December 2004]
- Burke JM, Zufall MJ, Özkaynak H. A population exposure model for particulate matter: case study results for PM2.5 in Philadelphia, PA. J Expo Anal Environ Epidemiol. 2001;11:470–489. doi: 10.1038/sj.jea.7500188. [DOI] [PubMed] [Google Scholar]
- Butler AJ, Andrew MS, Russell AG.2003Daily sampling of PM2.5 in Atlanta: results of the first year of the Assessment of Spatial Aerosol Composition in Atlanta study. J Geogr Res 108D78415; 10.1029/2002JD002234 [DOI] [Google Scholar]
- Chang HH, Peng RD, Dominici F. Estimating the acute health effects of coarse particulate matter accounting for exposure measurement error. Biostatistics. 2011;12:637–652. doi: 10.1093/biostatistics/kxr002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cimorelli AJ, Perry SG, Venkatram A, Weil JC, Paine RJ, Wilson RB, et al. AERMOD: a dispersion model for industrial source applications. Part I: General model formulation and boundary layer characterization. J Appl Meteorol. 2005;44:682–693. [Google Scholar]
- Dionisio KL, Isakov V, Baxter LK, Sarnat JA, Sarnat SE, Burke J, et al. Development and evaluation of alternative approaches for exposure assessment of multiple air pollutants in Atlanta, Georgia. J Expo Sci Environ Epidemiol. 2013;23:581–592. doi: 10.1038/jes.2013.59. [DOI] [PubMed] [Google Scholar]
- Dominici F, Peng RD, Barr CD, Bell ML. Protecting human health from air pollution: shifting from a single-pollutant to a multipollutant approach. Epidemiology. 2010;21:187–194. doi: 10.1097/EDE.0b013e3181cc86e8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldman GT, Mulholland JA, Russell AG, Srivastava A, Strickland MJ, Klein M, et al. Ambient air pollutant measurement error: characterization and impacts in a time-series epidemiologic study in Atlanta. Environ Sci Technol. 2010;44:7692–7698. doi: 10.1021/es101386r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoffmann B, Luttmann-Gibson H, Cohen A, Zanobetti A, de Souza C, Foley C, et al. 2012Opposing effects of particle pollution, ozone, and ambient temperature on arterial blood pressure. Environ Health Perspect 120241–246.; 10.1289/ehp.1103647 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ivy D, Mulholland JA, Russell AG. Development of ambient air quality population-weighted metrics for use in time-series health studies. J Air Waste Manag Assoc. 2008;58:711–720. doi: 10.3155/1047-3289.58.5.711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCurdy T, Glen G, Smith L, Lakkadi Y. The National Exposure Research Laboratory’s Consolidated Human Activity Database. J Expo Anal Environ Epidemiol. 2000;10:566–578. doi: 10.1038/sj.jea.7500114. [DOI] [PubMed] [Google Scholar]
- Meng QY, Spector D, Colome S, Turpin B. Determinants of indoor and personal exposure to PM2.5 of indoor and outdoor origin during the RIOPA study. Atmos Environ. 2009;43:5750–5758. doi: 10.1016/j.atmosenv.2009.07.066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Metzger KB, Tolbert PE, Klein M, Peel JL, Flanders WD, Todd K, et al. Ambient air pollution and cardiovascular emergency department visits. Epidemiology. 2004;15:46–56. doi: 10.1097/01.EDE.0000101748.28283.97. [DOI] [PubMed] [Google Scholar]
- Monn C. Exposure assessment of air pollutants: a review on spatial heterogeneity and indoor/outdoor/personal exposure to suspended particulate matter, nitrogen dioxide and ozone. Atmos Environ. 2001;35:1–32. [Google Scholar]
- Sarnat JA, Sarnat SE, Flanders WD, Chang HH, Mulholland J, Baxter L, et al. Spatiotemporally-resolved air exchange rate as a modifier of acute air pollution related morbidity in Atlanta. J Expo Sci Environ Epidemiol. 2013;23:606–615. doi: 10.1038/jes.2013.32. [DOI] [PubMed] [Google Scholar]
- Sarnat SE, Coull BA, Ruiz PA, Koutrakis P, Suh HH. The influences of ambient particle composition and size on particle infiltration in Los Angeles, CA, residences. J Air Waste Manag Assoc. 2006;56:186–196. doi: 10.1080/10473289.2006.10464449. [DOI] [PubMed] [Google Scholar]
- Sarnat SE, Klein M, Sarnat JA, Flanders WD, Waller LA, Mulholland JA, et al. An examination of exposure measurement error from air pollutant spatial variability in time-series studies. J Expo Sci Environ Epidemiol. 2010;20:135–146. doi: 10.1038/jes.2009.10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sarnat SE, Sarnat JA, Mulholland J, Isakov V, Özkaynak H, Chang H, et al. Application of alternative spatiotemporal metrics of ambient air pollution exposure in a time-series epidemiological study in Atlanta. J Expo Sci Environ Epidemiol. 2013;23:593–605. doi: 10.1038/jes.2013.41. [DOI] [PubMed] [Google Scholar]
- Schwartz J, Coull BA. Control for confounding in the presence of measurement error in hierarchical models. Biostatistics. 2003;4:539–553. doi: 10.1093/biostatistics/4.4.539. [DOI] [PubMed] [Google Scholar]
- Setton E, Marshall JD, Brauer M, Lundquist KR, Hystad P, Keller P, et al. The impact of daily mobility on exposure to traffic-related air pollution and health effect estimates. J Expo Sci Environ Epidemiol. 2011;21:42–48. doi: 10.1038/jes.2010.14. [DOI] [PubMed] [Google Scholar]
- Strickland MJ, Gass KM, Goldman GT, Mulholland JA. 2013Effects of ambient air pollution measurement error on health effect estimates in time-series studies: a simulation-based analysis. J Expo Sci Environ Epidemiol; 10.1038/jes.2013.1016 [DOI] [PMC free article] [PubMed]
- Tolbert PE, Klein M, Metzger KB, Peel J, Flanders WD, Todd K, et al. Interim results of the study of particulates and health in Atlanta (SOPHIA). J Expo Sci Environ Epidemiol. 2000;10:446–460. doi: 10.1038/sj.jea.7500106. [DOI] [PubMed] [Google Scholar]
- Tolbert PE, Klein M, Peel JL, Sarnat SE, Sarnat JA. Multipollutant modeling issues in a study of ambient air quality and emergency department visits in Atlanta. J Expo Sci Environ Epidemiol. 2007;17(suppl 2):S29–S35. doi: 10.1038/sj.jes.7500625. [DOI] [PubMed] [Google Scholar]
- U.S. EPA (U.S. Environmental Protection Agency). Total Risk Integrated Methodology (TRIM) Air Pollutants Exposure Model Documentation (TRIM.Expo/APEX, version 4.5), Volume II: Technical Support Document. EPA-452/B-12-001b. Research Triangle Park, NC:U.S. EPA Office of Air Quality Planning and Standards. 2012. Available: http://www2.epa.gov/fera/apex-4-user-guides [accessed 15 October 2014]
- Weisel CP, Zhang J, Turpin BJ, Morandi MT, Colome S, Stock TH, et al. Relationships of Indoor, Outdoor, and Personal Air (RIOPA): Part 1. Collection methods and descriptive analyses. Res Rep Health Eff Inst. 2005;130(pt 1):1–107. [PubMed] [Google Scholar]
- Williams R, Jones P, Croghan C, Thornburg J, Rodes C. The influence of human and environmental exposure factors on personal NO2 exposures. J Expo Sci Environ Epidemiol. 2012;22:109–115. doi: 10.1038/jes.2011.20. [DOI] [PubMed] [Google Scholar]
- Zeger SL, Thomas D, Dominici F, Samet JM, Schwartz J, Dockery D, et al. Exposure measurement error in time-series studies of air pollution: concepts and consequences. Environ Health Perspect. 2000;108:419–426. doi: 10.1289/ehp.00108419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeka A, Schwartz J.2004Estimating the independent effects of multiple pollutants in the presence of measurement error: an application of a measurement-error-resistant technique. Environ Health Perspect 1121686–1690.; 10.1289/ehp.7286 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zidek JV, Wong H, Le ND, Burnett R. Causality, measurement error and multicollinearity in epidemiology. Environmetrics. 1996;7:441–451. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


