Heterogeneous Preferential Solvation of Water and Trifluoroethanol in Homologous Lysozymes

Abstract

Cytoplasmic osmolytes can significantly alter the thermodynamic and kinetic properties of proteins relative to those under dilute solution conditions. Spectroscopic experiments of lysozymes in cosolvents indicate that such changes may arise from the heterogeneous, site-specific hydrophobic interactions between protein surface residues and individual solvent molecules. In pursuit of an accurate and predictive model for explaining biomolecular interactions, we study the averaged structural characteristics of mixed solvents with homologous lysozyme solutes using all-atom molecular dynamics. By observing the time-averaged densities of different aqueous solutions of trifluoroethanol, we deduce trends in the heterogeneous solvent interactions over each protein’s surface, and investigate how the homology of protein structure does not necessarily translate to similarities in solvent structure and composition—even when observing identical side chains.

Introduction

The interiors of metabolizing cells have high concentrations of proteins, nucleic acids, and small molecules that can constitute more than 40% of the total cellular mass.^1,2 In some cases, the density of nonwater components in cells exceeds 400 g/L, which makes cytoplasmic crowding on the same order as that found in protein crystals.^1,3−5 Contributions to crowding effects arise not only from biomacromolecules but also a plethora of smaller osmolytes varying from sugars, such as sucrose and trehalose, to polymers, such as polysaccharides and ribonucleic acids.⁶⁻⁸ Previous studies have shown that such crowding effects from cytoplasmic osmolytes can significantly change the thermodynamic and kinetic properties of not only nucleic acids and proteins but also water molecules.^3,6,7,9−19 Furthermore, the complex interplay of chemicals in the cytoplasm remains difficult to characterize as simple cosolvent systems, such as octanol–water mixtures.^20,21 After decades of research, the molecular mechanisms and biological significance of osmolytes interacting with biomacromolecules remain an active area of study.^7,18

Water molecules interacting with hydrophobic solutes have fewer available hydrogen bonding partners relative to the bulk, which can result in significantly constrained movements and diffusion rates. When water solvates large molecules (>1 nm), the physical constraints cause large changes to its network of hydrogen bonds. These can halve the average time between hydrogen bond jumps, and slow diffusion by more than an order of magnitude.^9,19,22−35 Dynamically constrained solvent is not only a structural component to biology,^8,30,31 but its altered chemistry is also exploited by processes such as protein–ligand binding,^33,36−40 protein–protein recognition,^41,42 ice crystal inhibition,⁴³ and protein–DNA interactions.⁴⁴ It is therefore a necessity to molecular biology, especially when studying within the context of cell-like environments, to deconvolve the influence on hydration environments near proteins due to various interactions, such as van der Waals, electrostatics, and protein topology.^45,46

Previous studies of proteins interacting with cosolvents have shown that changes in transfer free energy of solvent molecules near a protein’s surface relative to the bulk, or so-called “epistructural interfacial tension”, receive electrostatic contributions from the protein’s interfacial topology.⁴⁷⁻⁴⁹ This notion has led to accurate docking predictions of small molecules on a protein’s surface using implicit-water methods such as the three-dimensional reference interaction site model (3D-RISM).^47,50 However, further evidence has shown that not all protein–ligand systems may be mapped accurately without a dynamic, explicit representation of water intermediating protein–ligand associations.^37,51 These studies have led to reassessments of such simplified models, even by coupling them to molecular-dynamics (MD) simulations to increase conformational sampling of both protein and solvent.^52,53 Owing to the complexity of liquid solvent and the rapidly fluctuating nature of protein topology, it may be premature to suggest a theoretical model short of an all-atom molecular dynamics (MD) simulation that predicts protein–solvent interactions accurately.^53,54 It may also be an equally arduous task to modify a topology-based approach, such as 3D-RISM, to represent accurate hydrophobic protein–solvent interfaces and three-body interactions for any particular protein–ligand–water system.^9,54 Thus, for this study, we turn to all-atom MD simulations as a means to investigate biomolecular interactions in mixed-solvent systems.

Previous work by King et al.⁴⁹ on systems of lysozyme and trifluoroethanol used the method of two-dimensional infrared spectroscopy (2DIR) to investigate how solvation and dehydration can differ depending on the specific location on a protein. Hen egg white lysozyme (HEWL) and human lysozyme (humLys) offer homologous protein topologies, each with one solvent-exposed histidine. Although the two proteins are 77% similar by amino acid sequence and are structurally different by only 0.54 Å root-mean-square, the histidines are located on different domains of the protein. The H15 on HEWL is located on a turn adjacent to an α-helix, and the H78 on humLys is located on a region without secondary structure. Local environments around these histidines were probed by covalently attaching a ruthenium–carbonyl vibrational chromophore. In initial studies, the vibrational lifetime of the chromophore in H₂O and D₂O was used to measure not only the presence of water but also the hindering of hydrogen bond reorientation dynamics in the nearby hydration water. It was found that different water dynamics correlate strongly with the local surface structure of the protein. The H15 probe location of HEWL is a low-curvature region solvated by orientationally constrained water, whereas the H78 site of humLys is high-curvature and unstructured, and solvated by bulk-like water. To test the connection between constrained water and the thermodynamic driving force for dehydration by an amphiphilic cosolvent trifluoroethanol (TFE), lifetime measurements were made in a series of D₂O/TFE solutions. In pure D₂O, both sites were found to be hydrated based on their sub-5 ps vibrational lifetimes, which are consistent with water-assisted relaxation.⁵⁵ Upon addition of TFE, however, the sites displayed markedly distinct responses. The lifetime of the probe at the H15 site of HEWL exhibited an order-of-magnitude slowdown in a 10% (v/v) TFE solution consistent with local dehydration, whereas the H78 labeled site of humLys showed no TFE-dependent vibrational lifetime changes at any of the experimental concentrations.

These data indicate that the local solvent compositions at the two sites are different.^32,55,56 Previous NMR and circular dichroism studies of HEWL confirm that a 10% concentration of TFE does not change the helical content nor the tertiary contacts of lysozyme, which supports the conclusion that the change in vibrational lifetime is not due to a change in protein conformation.^57,58 This result is consistent with prior observations that helical regions on proteins (such as the H15 on HEWL) are preferentially solvated by TFE more than unstructured regions (such as the H78 on humLys).⁵⁹ Additionally, this result suggests that a protein’s surface topology can modify the local dynamics, orientation, and number density of solvent molecules.

The simulations of the present study are designed to investigate these results and explore the heterogeneous nature of preferential solvation of lysozyme by TFE–water mixtures. In the current study, we used explicit solvent MD simulations to model human and hen egg white lysozymes mixed with water and different concentrations of the cosolvent trifluoroethanol. We then aligned each trajectory by lowest protein backbone-atom root-mean-square deviation (RMSD) to one common structure. We used these trajectories to compute time-averaged three-dimensional (3D) histograms of the number density of solvent relative to each protein’s structure. These values represent the spatial distribution of both the probability of finding a type of solvent atom and solvent density. Using these data, we mapped out trends of trifluoroethanol interacting with lysozyme surfaces and suggest a possible explanation for the observed phenomena in the spectroscopic experiments. Finally, we made a spatially dependent, solvent-centric comparison of homology between HEWL and humLys.

Simulations

Two homologous lysozyme systems were simulated: hen egg white lysozyme (HEWL; PDB code 3IJU) and human lysozyme (humLys; PDB code 2ZIJ). Eighteen replicas of both proteins were created, which consisted of three separate trajectories for each of six concentrations of TFE: 0, 1, 5, 10, 15, and 20% by volume fraction (v/v). Water/TFE mixtures exhibit a nonideality of less than 10 mL/L (less than 1%), so a ratio of molar fractions could be approximated by a ratio of volume fractions. Equation 1 shows how the precise number of TFE and water molecules could be calculated for a given cosolvent when assuming the solution behaves ideally.

1

V_m is the molar volume, x is the mole fraction, and N is the number of solvent molecules. The number of TFE and water molecules used in each simulation is listed in Table 1 of the Supporting Information.

Hydrogen atoms were added to the proteins using the pdb2gmx utility in the GROningen MAchine for Chemical Simulations (GROMACS).⁶⁰ All replicas were solvated in SPC/E water⁶¹ using the genbox utility in GROMACS with rectangular edges at least 20 Å from all protein atoms. Excess charge from the protein was neutralized by placing eight chloride ions per lysozyme at random locations in the solvent using the genion utility in GROMACS. The TFE structure was energy-minimized using the Gaussian 03 software package.⁶² An appropriate number of TFE molecules (Supporting Information, Table 1) were added to each replica simultaneously with the chloride ions, using the genion utility from GROMACS. The locations of the TFE molecules were randomized for each replica to enhance the sampling of solvent configurations.

All 36 systems (2 proteins × 6 TFE concentrations × 3 independent trajectories) were simulated using the GROMACS macromolecular modeling package (version 4.5.5).⁶⁰ The antechamber program from the Antechamber package (version 1.25)⁶³ was coupled with Gaussian 03 to assign partial charges and to create an Amber-like force field for TFE. Partial charges were assigned using the restrained electrostatic potential (RESP) method.⁶⁴ The remaining atoms of each replica were simulated using the AMBER99 all-atom force field.⁶⁴ Each replica was an isobaric–isothermal ensemble, and was maintained at 1 atm and 300 K using the Berendsen barostat and thermostat, respectively.⁶⁵ A time coupling constant of 1 ps was used for both pressure and temperature, and the system compressibility was set to 4.5 × 10^–5 bar. Electrostatic energies were determined using particle-mesh Ewald (PME) summations⁶⁶ with a Fourier-transform grid width of 1.2 Å and real-space Coulomb and Lennard-Jones cutoffs of 9 Å. The magnitude of the PME-shifted potential at the cutoff was set to 10^–5, and the Leapfrog Verlet integrator was used with an integration time step of 1 fs. Each replica was energy minimized using a steepest-descent algorithm for 500 steps with a tolerance of 10 kJ mol^–1 nm^–1, followed by an equilibration run for 50 ps, and finally a production run of 20 ns. Coordinates were saved every 1 ps, which yielded a total of 60,000 structures for each protein at each concentration.

Analysis and Results

Volumetric Distribution Function of Solvents

Owing to the extremely low flexibility, high stability, and highly conserved structure of the two lysozymes,^57,67 all saved structures from all simulations represent fluctuations of one lysozyme system. The calculated circular dichroism (CD) shows an ellipticity of 10.1 ± 0.8°, and the root-mean-square deviation (RMSD) of protein backbone atoms from the initial structure was 1.0 ± 0.1 Å (Figure 1 in the Supporting Information shows more detailed results of the calculated CD and RMSD). Additionally, no protein structure shows an RMSD of backbone atoms greater than 2 Å from any other structure, even between human and hen egg white lysozymes. Although concentrations of TFE were simulated that would normally denature lysozyme, it may be that the mechanism of denaturing takes place on time scales longer than the 20 ns simulated in this study. These conditions permit the calculation of high-resolution three-dimensional (3D) solvent distribution functions centered on a relatively static protein structure.

First, periodic boundary conditions are used to align the protein at the center of each box. Then, all saved structures from all simulations are aligned by least-squares fitting of protein backbone atoms to a single energy-minimized reference structure of HEWL. The reference structure is obtained from the first frame of one of the production runs of HEWL. Finally, time-averaged solvent distribution functions G(r) are calculated for each trajectory using voxelized 3D histograms with a 1 ų resolution using eq 2, as performed in previous studies.^10,68 The solvent distribution function G(r_xyz) is approximated by integrating the time-averaged solvent density ρ for a voxel of size ΔxΔyΔz. The data is then normalized for bulk density ρ_bulk, which resulted in a series of 36 maps of solvent distribution, each with a protein in the center.

2

As an artifact of the least-squares fitting of saved structures, the corners of the periodic boundary boxes rotate during simulation. As such, G(r) data at the corners is not representative of bulk solvent in the solvent distribution functions, and was removed before analysis. This left a spherical volume of solvent density with a radius of 41 Å and an edge with bulk solvent density. This radius also maintains a minimum of 18 Å between all protein atoms and the edge of the spherical volume. Radial distribution functions of solvent from protein atoms (Supporting Information, Figure 2) indicate that no significant solvent clustering occurs much more than 9 Å from the surface of the protein. Hence, interactions between the protein and the solvent, such as an enhanced solvent density, are not omitted from analyses by removing the corners. Furthermore, the edge of the data is representative of the time-averaged bulk density of water and TFE. The solvent densities at the edge of the spherical shape of the G(r) histograms are averaged to calculate the ρ_bulk of TFE and water.

Figure 3 in the Supporting Information shows the convergence of data within the G(r) histograms, revealing that protein and water densities converge within the first 1–2 ns of simulation time, and TFE density took 5–14 ns. This indicates that a 20 ns simulation is sufficient to converge the atomic densities to a consistent distribution of values. TFE, relative to water, has a slower reorientation time and a slower diffusion time; thus, G(r) functions of TFE require more sampling to converge to one set of values, especially at lower concentrations.

Local Percent of TFE by Volume

As noted in the simulation procedure, water/TFE mixtures are sufficiently ideal to translate a percent TFE by volume into a ratio of molecules to within 1% accuracy. Conversely, we can calculate the concentration of TFE v/v of a given volume from the number density of solvent molecules using eq 1. Since the solvent distribution function G(r) is the time-averaged number density of solvent molecules, we can relate it to eq 1 and find the percent TFE v/v of the solvent distribution function G(r). By converting solvent atom counts per cubic angstrom into moles per cubic centimeter, we calculate the percent TFE v/v for a single voxel. This calculation works wherever the volume in question contains solvent density from both water and TFE.

Every residue on human lysozyme shares a corresponding spherical volume with a residue on hen egg white lysozyme, except for the T43 which has no analogous residue on HEWL. These volumes can then be used to compare simulations with different solvent concentrations and different protein identities. These spheres of radius 7 Å are centered at the average center of geometry of a residue’s backbone atoms. The result is a total of 36 analogous spheres for every residue location, with each sphere consisting of 1437 voxels. This selection encompasses 86% of volume with 3 times the bulk density of TFE. Since there is no clear method for rotating and realigning the grid of one residue to another, comparisons between nonanalogous residues are not performed in this study.

Since the goal of this study is to analyze protein solvation, buried residues are excluded. Buried residues are identified by computing all solvent-accessible surface area (SASA) values for all simulations. A residue is considered buried if its average SASA is less than 17 Ų. The method of calculating SASA and the resultant values are reported in Table 2 in the Supporting Information.

As shown in Figure 1A, helical regions of the protein (green) show an enhanced concentration of TFE by up to 5.6% v/v relative to the bulk, while unstructured regions of the protein (magenta) show an enhanced concentration of water by up to 3.5% v/v relative to the bulk. By “helical”, we mean both α-helical and 3/10-helices, and by “unstructured”, we mean turns, bends, and regions without secondary structure. This result is reasonable, since helices both are richer in solvent-exposed hydrophobic residues and have been previously shown to be preferentially solvated by TFE.^58,69 Unstructured regions, on the other hand, have more hydrophilic residues, and are preferentially solvated by water. A feature of high local concentrations of TFE (such as 15 and 20% by volume) is a greater standard deviation in solvent density data among parallel simulations. As mentioned in the previous section, this may be attributed to the longer time needed for TFE solvation data to converge.

Figure 1.

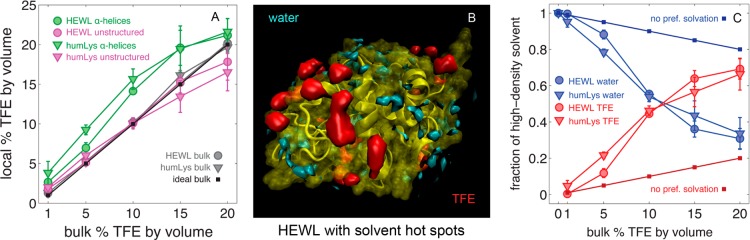
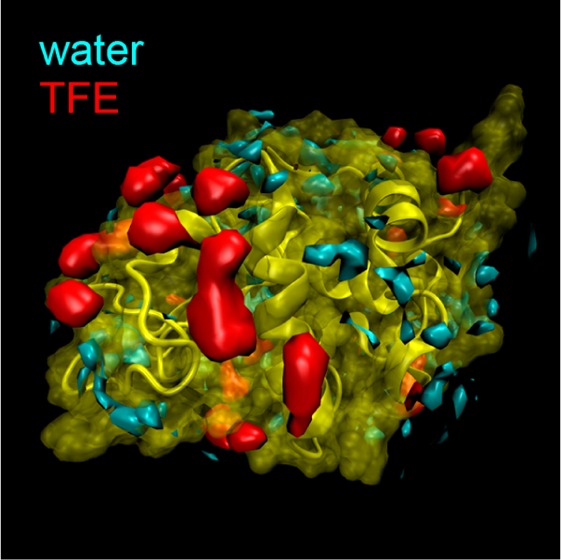
(A) Percent TFE v/v calculated for the local environment of each surface-lying residue. Shown here are the average percentage of TFE for α-helices (green) and unstructured regions of the protein (magenta). α-Helices show a local increase in TFE concentration relative to bulk solvent (gray/black), while unstructured regions show a relatively bulk-like concentration. The error bars are the standard deviation among the three parallel trajectories for each protein at each concentration. (B) HEWL is shown as a visual cue for the general distribution and location of high density hot spots. TFE (red) and water (cyan) hotspots do not overlap in this study. (C) The total volume of hot spots for water and TFE exhibit a crossover near 10% TFE, beyond which the majority of hot spots are due to TFE. The error bars are the standard deviation among the three parallel trajectories for each protein at each concentration.

What was not revealed in the data was a correlation between an individual residue’s hydrophobicity and the local concentration of TFE. As discussed later in the section “Insight into Site-Specific Dehydration near Lysozymes”, a single residue’s local concentration of TFE is most influenced by neighboring residue effects than its own hydrophobicity. Only when averaging over protein domains does a trend in TFE solvation become greater than the variance in the data.

Interestingly, the 50 residues with the highest local concentration of TFE from simulations of 15% bulk v/v TFE match more than 50% of the TFE–lysozyme crystal contacts found in X-ray studies (detailed comparison in the Supporting Information).^58,69 These data indicate the force field choices reliably capture features of lysozyme in a water/amphiphilic cosolvent mixture.

Solvent Hot Spots

Hot spots contain a high number density of one solvent type. Within these regions of space, the probability density of a solvent is similar to that of the protein backbone atoms, which effectively makes them extensions of the protein’s surface topology into the surrounding solvent. In terms of G(r) data, hot spots are voxels that have an averaged local solvent density much higher than that of the bulk. For the simulations at 10% v/v TFE, the G(r) functions show maxima over 2 and 12 times higher than the bulk density of water and TFE, respectively. Isosurfaces enclosing these high-density regions on HEWL are shown in Figure 1B. No simulation shows hot spots extending further than 5 Å from protein atoms, indicating that stationary, high-density solvent clustering does not form in the bulk solvent during the simulations, and that large perturbations in solvent density do not extend beyond 5 Å from the surface of the protein. This also suggests protein–protein interactions from opposite sides of the lysozyme did not extend through the periodic boundaries of the solvent box.

The total volume of high-density solvent for all simulations averaged to 642 ± 91 ų, which indicates that a feature of the protein–solvent interface is a conserved volume of strongly associated solute. With respect to the relative sizes of TFE and water molecules (126 and 32 ų, respectively), this space corresponds to about 5 TFEs or 20 waters. What does change among different cosolvent concentrations is the identity of solvent dominating the hot spots. Interestingly, as the bulk concentration of TFE increased, the interfacial solvent environment shows a transition from being water-dominated to being TFE-dominated at the same concentrations that are known to denature lysozyme in experiments. High-density solvent is rich with water at low concentrations of TFE in the bulk, and in 15 and 20% TFE v/v in the bulk, the high-density solvent became dominated by TFE, as shown in Figure 1C. This observation is also reflected in the standard deviation of local concentration of TFE, as noted in the previous section. Although we see no evidence that the proteins denature during the simulations, this transition may lend insight into the mechanism that unfolds the protein. Lysozyme maintains its native fold by maintaining a relatively consistent distribution of strongly associated water. It is the removal of this water that leads to a non-native packing of the protein. Experiments have shown that lysozymes denaturing thermally also experience a disruption in their hydrogen bonding network before unfolding.⁷⁰

Insight into Site-Specific Dehydration near Lysozymes

Studies of both model hydrophobic interfaces and biomolecules have provided insight into the nature of hydration water on the molecular scale. Patel et al. calculated the probability density distributions of finding water near the solute–solvent interfaces of model systems, which included hydrophobic methyl groups, hydrophilic hydroxyl groups, melittin dimers, and biphenyl dioxygenase (BphC). Despite the chemical differences, it was found that the time-averaged number densities for water at the solvent interface are independent of the hydrophobicity of the surface itself. What differs markedly is the probability of finding a very small number of water molecules near each type of surface. That is, deviations from the average number density of water, corresponding to dewetting, are much more likely in the vicinity of hydrophobic surfaces than hydrophilic ones.^34,51,71

Although the simulations of the current study do not reach the level of precision in the work done by Patel et al., with some margin of error, we can still infer the relative hydrophobicity of the two histidine sites. By counting the number of empty voxels around each histidine for each simulation, we obtain the metric shown in Figure 2C, which shows a systematic increase in the number of waterless voxels with an increase in the concentration of TFE. The probability distribution of empty voxels at various concentrations of TFE is shown in Figure 5 of the Supporting Information. The data shows that, beyond the standard deviation of the data between replicas, when the histidines are exposed to higher concentrations of TFE, one is more likely to find a vacuum-like environment around H15 of HEWL and one is more likely to find a hydrated environment around H78. By the same logic from the studies of Patel et al., we find with high confidence that H15 is more hydrophobic in an environment of 10% TFE than one of pure water. These observations may be influenced by the large difference in SASA between the residues: 55.1 and 175.1 Ų for H15 (HEWL) and H78 (humLys) respectively. Figure 2A and B shows a visual reference of the relative surface area and solvent composition. Interestingly, neither radial distribution functions nor local concentrations of TFE show any significant difference between the two histidine sites.

Figure 2.

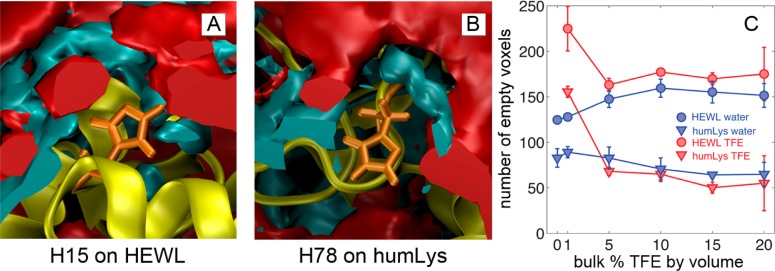
Local solvent structures near the histidines in simulations of 10% TFE v/v. (A) HEWL (yellow) with histidine 15 (orange sticks) is surrounded by TFE (red) and water (blue) isosurfaces. (B) Isosurfaces for histidine 78 on humLys. Notice that both locations are surrounded by similar ratios of both solvent types. (C) The average number of empty voxels in the local environment around each histidine at various cosolvent concentrations as calculated by integrating G(r) functions. The error bars correspond to the standard deviations of data among the three independent simulations at each concentration of TFE.

Although this particular TFE model is not properly tuned to exhibit a maximum number of evacuated voxels at the experimentally analogous 10% TFE by volume, it does support the hypothesis that TFE dehydrates the H15 location of the HEWL protein. These data suggest that a direct mechanism of locally dehydrating the surface of lysozyme causes the change in signal amplitude from the protein label. As TFE removes neighboring water molecules, it also reduces the number of water molecules that can couple to the probe. The H78 on humLys has more SASA, and consequently many opportunities for water to reach and couple with the probe.

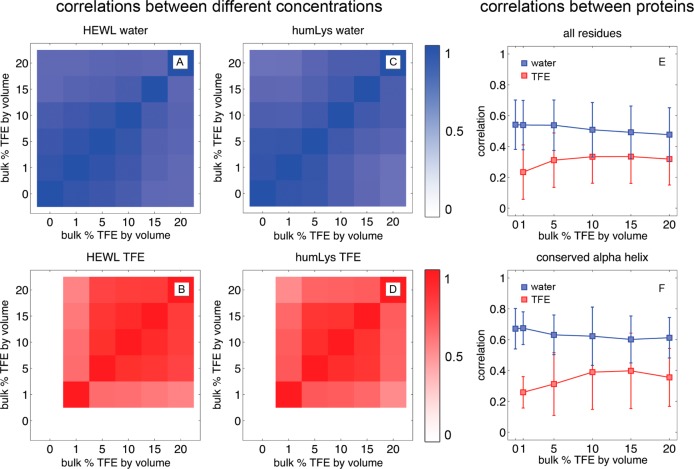
Pearson Correlation Coefficients

Since all G(r) functions are analogous 3D histograms, direct comparisons of the distribution of solvent density are made between pairs of simulations. Specifically, the local environments around each residue (detailed above as being 7 Å spherical volumes) are selected and analyzed by calculating Pearson correlation coefficients between sets of analogous voxels using eq 3.

3

Here, the solvent densities of two local environments are compared by multiplying each normalized element x from one residue’s G(r) to its corresponding analogous element y from another residue’s G(r). This process converts the shapes of two solvent densities into a value that indicates their relative similarity: 0 as noncorrelative (no spatial overlap of data), 1 as a perfect correlation (a perfect spatial overlap of data), and −1 as a perfect anticorrelation. No attempt is made in this study to remedy the antialiasing artifacts of G(r) data that occur when aligning nonanalogous volumes. Thus, no comparisons between nonanalogous locations are made (such as between two alanines on different protein domains).

Using eq 3, we investigate three aspects of protein–solvent interactions: how much simulation time is needed to converge on one solvent density distribution (comparing a residue site to itself at different times within the same simulation), what TFE and water interactions are conserved in cosolvent mixtures (comparing a site on one protein to itself in different cosolvent mixtures), and what TFE and water interactions are conserved between homologous proteins (comparing a site on HEWL to a homologous site on humLys).

When calculating the convergence of solvent density around residues within a single simulation, we find that 20 ns of simulation provides sufficient sampling. Correlations of local G(r) functions at each residue site are made between the instantaneous and time-averaged G(r) functions. Due to the low flexibility and high stability of lysozyme systems as well as the high diffusion rate of the solvents, local G(r) functions of water, the protein, and TFE converge within 2, 2, and 14 ns, respectively, and had maximum correlations of 0.89, 0.75, and 0.62, respectively (Supporting Information, Figure 3). This indicates that each trajectory not only converges to a self-consistent atomic density but also is well-correlated to the average of all densities. As such, the average G(r) function of all 60 ns of simulation at each concentration is used as a representative atomic occupancy distribution of each protein in that corresponding environment.

Comparisons between identical amino acids at different concentrations of TFE revealed that, for a single protein, there is a persistent configuration of solvent density (Figure 3A–D). Water and TFE have minimum correlations of 0.54 and 0.45, respectively, which indicates that, even when placing a lysozyme in the extremes of 1 and 20% TFE, the local solvent density retains at least a 45% overlap between any two simulations of that protein. When placed in solutions that showed better sampling for the cosolvent (such as in 5 and 10% TFE), the correlation coefficients between simulations rise even higher to 0.89 and 0.83 for water and TFE, respectively. While comparing simulation data of one protein in different concentrations of TFE, not only can representative information be gained from G(r) data between cosolvent concentrations for a protein, but also the lysozymes preferentially configure the solvent molecules on their surfaces regardless of the solvent composition. Remarkably, solvent molecules quickly find preferred configurations both when subjected to low sampling rates (such as TFE G(r) data in the 1% TFE simulations) and when experiencing lower diffusion of solvent molecules (such as in the 15 and 20% TFE simulations).

Figure 3.

For all plots, only data from solvent-exposed amino acids are considered. Panels A–D show average correlation coefficients between amino acids of one protein (HEWL or humLys) in solutions of different concentrations of TFE v/v. All correlations fall between 1 (on the diagonals) and 0.54 (at the corners) in these plots. Plots A and C are correlations of water densities at different concentrations, and plots B and D are correlations of TFE. Plot E is an average correlation of G(r) functions around each amino acid by comparing residues from HEWL to its homologue on humLys. The error bars are the standard deviation of data among the correlations of amino acids. Plot F is the same analysis as seen in plot E, except for only residues on the α-helix that has 100% conservation of residue identity. A stronger correlation is observed here, but due to neighboring effects of nonidentical amino acids, the TFE distributions remained nonhomologous between the proteins.

Next we explore what happens when imposing a hard cutoff, as defined in eq 4. This technique reduces the effects of noise on the correlation coefficient analyses, and presumably defines a more rigid shape to solvent configuration near the lysozymes.

4

G(r) functions are then converted into rigid-boundary maps of high-density solvent where any location within G(r) with more than twice the bulk value of a solvent ρ_bulk is 1, and every other space is 0. Correlation coefficients of G′(r) functions are decreased on average by 0.13 as compared to those reported in Figure 3A–D, indicating that the shapes of high-density solvent are also conserved between different bulk concentrations of TFE. This comparison also suggests there are thermodynamic minima on the protein for binding specific solvent components, and that these are maintained, at least in part, regardless of the bulk cosolvent composition.

When making comparisons between local solvent density around the two lysozymes, as shown in Figure 3E and F, TFE correlation coefficients are impacted much more than those of water. Hen egg white and human lysozymes are 77% similar and 60% identical according to a Smith–Waterman alignment.⁷² When ignoring the shape of solvent density, the Pearson correlation coefficient between the local concentrations of TFE by volume around each residue is 0.55, as calculated with eq 3. Presumably, the proteins should have similar shapes of local solvent density, and comparably high correlation coefficients. Correlation coefficients between local volumes of the two proteins, shown in Figure 3E, average to 0.51 ± 0.03 for water and 0.26 ± 0.13 for TFE. These were 0.10 (water) and 0.22 (TFE) less than the lowest correlation values from Figure 3A–D.

While HEWL-humLys sequence alignment is a good predictor of the local concentration of TFE, it is a poor predictor of the shape and orientation of solvent molecules at the protein−solvent interface. Water’s solvent density near HEWL is more similarly shaped between cosolvents of 0 and 20% TFE v/v than it is to humLys with the same concentration of TFE. The correlations of averaged TFE density between the two proteins is even lower, indicating that, although both lysozymes are similar in sequence, they have dissimilar interactions with water and TFE. Moreover, both proteins are more similar in their interaction with water than with TFE.

To ensure that noise in the G(r) functions was not falsely inflating the error of the analyses, parallel calculations were run with voxel volumes of 8 and 64 ų (2 and 4 Šof voxel side lengths). The G(r) functions with reduced resolutions changed correlation coefficients by no more than 0.11, which indicates that the observations discussed above are resolution-independent.

In order to locate the sources of dissimilar solvent interactions, correlations are segregated by secondary structure type, residue identity, residue similarity, and hydrophobicity. Unfortunately, there are no apparent correlations of the shape of G(r) data between the two types of proteins beyond the variation of the data. Of particular interest is the α-helix from residues 105 to 114 on HEWL that is entirely conserved between the two lysozymes. An illustration of solvent density at the conserved α-helix is shown in Figure 4, and their correlations are shown in Figure 3F. There is an average 0.11 and 0.03 increase in correlation for water and TFE, respectively, for this particular group, which still falls 0.17 short of the lowest correlations of that same group when comparing only one protein to itself in different cosolvents. Comparing homologous residues in the binding pockets of the proteins yields correlations that are lower than the average.

Figure 4.

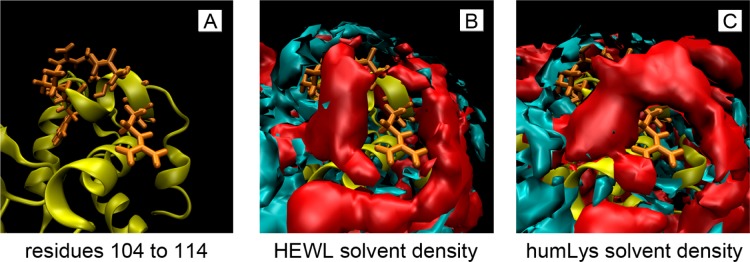
All three figures above show a reference lysozyme tertiary structure (yellow) and the residues of the α-helix that are conserved between hen egg white and human lysozymes (orange). Since this study ignores buried residues, only the surface-lying residues 107, 108, 109, 112, 113, and 114 are shown as sticks. Panel A illustrates the configuration of side chains, and panels B and C overlay the protein with solvent density averaged from the three replicas at 10% TFE. Even though this helix is completely conserved between the proteins, both in amino acid sequence and relative backbone RMSD, the averaged solvent densities of water (cyan) and TFE (red) are significantly different at this region. This difference illustrates that neighboring effects on solvent density from nonidentical residues extend over many angstroms, and that a region with conserved amino acid sequence does not necessarily indicate a region with conserved solvent interactions.

Evidentially, water and TFE interact with the specific details of protein surfaces differently. Water, being relatively small and having several axes of symmetry, resembles a more ideal solvent molecule than TFE. Its average interaction with the protein interface is conserved between HEWL and humLys as much as their amino acid sequences. TFE, being 9 times larger, having fewer axes of symmetry, and having more internal degrees of freedom (such as dihedral angles), is more sensitive to influences from neighboring residues. Although the extent of these influences is unclear, they are long-ranged enough to disrupt the solvent density near the conserved α-helix. In order to have similar solvent density at one homologous location between two proteins, it may require conserved topological features on the protein surfaces beyond the 7 Å radius used in the calculations of this study. Observing that TFE can influence water molecules as far as 8 Å away (twice the length of a TFE molecule) when in solution,⁷³ it is reasonable to expect that small differences in a protein’s surface topology can have similarly long-reaching influences on solvent interactions.

Since the two proteins are highly conserved both in enzymatic mechanisms and in physiological distribution among species,⁷⁴ the homology of solvent interactions may be unimportant to lysozyme chemical activity. Conversely, the similarity of averaged solvent interactions between two proteins may not indicate a structural homology. A well-equilibrated G(r) function of solvent density may be a poor predictor for G(r) functions of homologous systems, even with solvent molecules as small as TFE. When comparing a region of the protein with similar chemical function (and presumably similar charge distribution), such as the binding pocket, there always is a wide standard deviation of correlations between individual residues. For instance, W62 shows good correlations between the lysozymes in various cosolvents for both water and TFE, but a key catalytic residue D52 always shows a poor correlation. It may be that specific residues must maintain a certain number density of solvent interaction to maintain chemical properties (such as protein stability or catalytic reactivity). Other residues merely need to enforce electrostatic qualities in a reactive center. Even though TFE is not a target molecule for lysozyme catalysis, this study suggests that targeted binding experiments with one lysozyme may not well predict results from similar experiments with another lysozyme.

Conclusions

Inspired by our experiments of mapping site-specific solvent interactions of lysozymes, we present here an analytical approach to using molecular dynamics for characterizing local interactions of lysozyme residues with a water–TFE cosolvent. This is a process of aligning all trajectories to one homologous structure, making a time-averaged 3D G(r) function of the data, and dividing G(r) into small volumes that encapsulate high-density solvent. As such, we show a process for locating probable crystal contacts, observing preferential solvation trends, and comparing protein homology from the shape of averaged solvent density. These techniques are fully generalizable to proteins interacting with cosolvents of denaturants, small molecules, and salts.

We show that our trifluoroethanol force field mimics its basic chemical properties, such as preferentially solvating α-helices more than unstructured regions of the protein and finding crystal contacts. Additionally, we find that, at concentrations above 10% TFE, water around the protein is displaced with TFE. This is consistent with a water displacement mechanism for TFE chemically denaturing lysozymes. Using our system setup, we also found that it might be TFE displacing water hot spots on lysozyme that results in the protein denaturing. With regard to site-specific solvent dynamics, as with the ruthenium-dicarbonyl experiments on human and hen egg white lysozyme, displacing water on the surface of the protein can isolate regions of the protein from the bulk solvent and effectively shut off pathways of energy transfer from small molecule probes to the surrounding solvent.

Using a 3D G(r) function, we have a method for comparing the shape and overlap of averaged solvent density around proteins. We find that the two lysozymes conserve solvent hot spots despite being surrounded by different concentrations of TFE. We also find that homologous proteins may share similar interactions with one solvent, such as water, but not share similar interactions with another solvent, such as TFE. Larger solvent molecules with more degrees of freedom may have more pronounced effects from neighboring residues, and accordingly exhibit greater differences in average solvent interaction. Conversely, smaller solvents with several axes of symmetry, such as water, can have similar interactions with homologous proteins. What is very clear is that homologous proteins may be poor representations of one another when measuring solvent molecule interactions.

Supporting Information Available

Details and additional analyses of the molecular dynamics simulations, including tests of stability and convergence, as well as radial distribution functions, solvent density cross sections, and comparisons to previous X-ray studies. This material is available free of charge via the Internet at http://pubs.acs.org.

Author Present Address

^§ Present address: Department of Materials Science and Engineering, University of Illinois at Urbana−Champaign, Urbana, IL, USA.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States