APPLICATION OF FINITE ELEMENT MODELING TO OPTIMIZE FLAP DESIGN WITH TISSUE EXPANSION

Abstract

Background

Tissue expansion is a widely used technique to create skin flaps for the correction of sizeable defects in reconstructive plastic surgery. Major complications following the inset of expanded flaps include breakdown and uncontrolled scarring secondary to excessive tissue tension. While it is recognized that mechanical forces may significantly impact the success of defect repair with tissue expansion, a mechanical analysis of tissue stresses has not previously been attempted. Such analyses have the potential to optimize flap design pre-operatively.

Methods

We establish computer-aided design as a tool to explore stress profiles for two commonly employed flap designs, the direct advancement flap and the double back-cut flap. We advanced both flaps parallel and perpendicular to the relaxed skin tension lines to quantify the impact of tissue anisotropy on stress distribution profiles.

Results

Stress profiles were highly sensitive to flap design and orientation of relaxed skin tension lines, with stress minimized when flaps were advanced perpendicular to relaxed skin tension lines. Maximum stresses in advancement flaps occurred at the distal end of the flap, followed by the base. The double back-cut design increased stress at the lateral edges of the flap.

Conclusions

We conclude that finite element modeling may be used to effectively predict areas of increased flap tension. Performed pre-operatively, such modeling can allow for the optimization of flap design and a potential reduction in complications such as flap dehiscence or hypertrophic scarring.

Tissue expansion is a widely used technique in plastic and reconstructive surgery to create local flaps of skin for the correction of large defects and deformities.^{1, 2} A major determinant of flap complications following the inset of expanded tissue is excessive mechanical loading, or tissue tension. Tension has been shown to be a key factor in the healing and scarring processes following reconstructive surgery.⁶ Acutely, local stress concentrations may cause vascular insufficiency and localized flap necrosis.³ Chronically, local stress concentrations may induce excessive wound tension resulting in dehiscence and/or hypertrophic scarring⁷ (Fig. 1). Unfortunately, determining regional stress distributions in vivo is virtually impossible. However, computational simulations present an excellent alternative to virtually explore stress distributions during pre-operative planning. With this motivation, recent studies have simulated sutures of local flaps in idealized plane sheets of tissue using finite element analyses.^{8, 9} However, realistic three-dimensional flap geometries have not been studied to date.

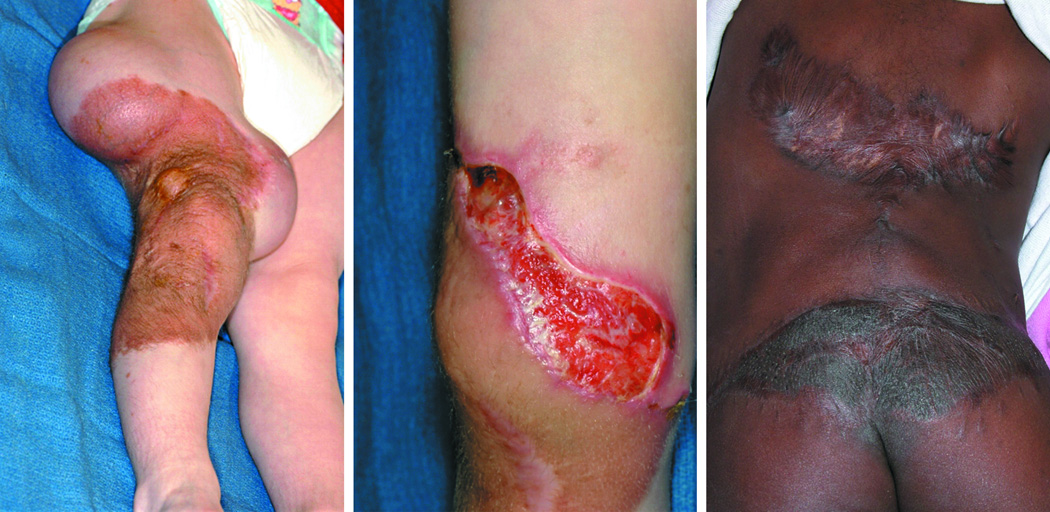
Figure 1.

Demonstration of complications of tissue expansion due to excessive tension. a) Tissue expanders inserted in thigh in preparation for of a giant pigmented nevus and resurfacing with advancement flap. b) Dehiscence of flap secondary to tension. c) Patient with scar hypertrophy and widening due to tension following expanded flap advancement for resurfacing of back following resection of a giant pigmented nevus; additional tissue expansion will be required to address residual pigmented nevus of lower back.

After tissue expansion, skin is no longer a flat sheet,¹⁰ but instead presents itself as a three-dimensional membrane that has undergone significant stretching and growth under extreme mechanical conditions.¹¹ Although the consequences of large tissue deformation on appropriate flap design are critical to repair durability, it remains a major challenge to accurately predict the mechanics of skin flap advancement. An important mechanical effect is the rotation of the relaxed skin tension lines associated with rotation of the dermal collagen fiber bundles.¹² Another challenge is the flattening of a three-dimensionally grown membrane,^{13, 14} which creates a complex stress profile that is difficult to estimate intuitively and impossible to measure experimentally. This stress profile, which not only depends on the total tissue deformation but also on the amount of skin growth, can be predicted by computational modeling.^{11, 16} In an in vivo scenario, computational modeling has the potential to reduce flap tension and to therefore optimize healing and scarring.

The goal of the present study is to explore, via finite element modeling, local stress concentrations within expanded flaps and the degree to which this may be influenced by flap design. We focus on two commonly employed flap designs, the direct advancement and double back-cut flaps.⁵ We test the hypothesis that flap stresses are highly sensitive to the location of expander placement and the direction of flap advancement with respect to lines of relaxed skin tension.

Materials and Methods

Flap design

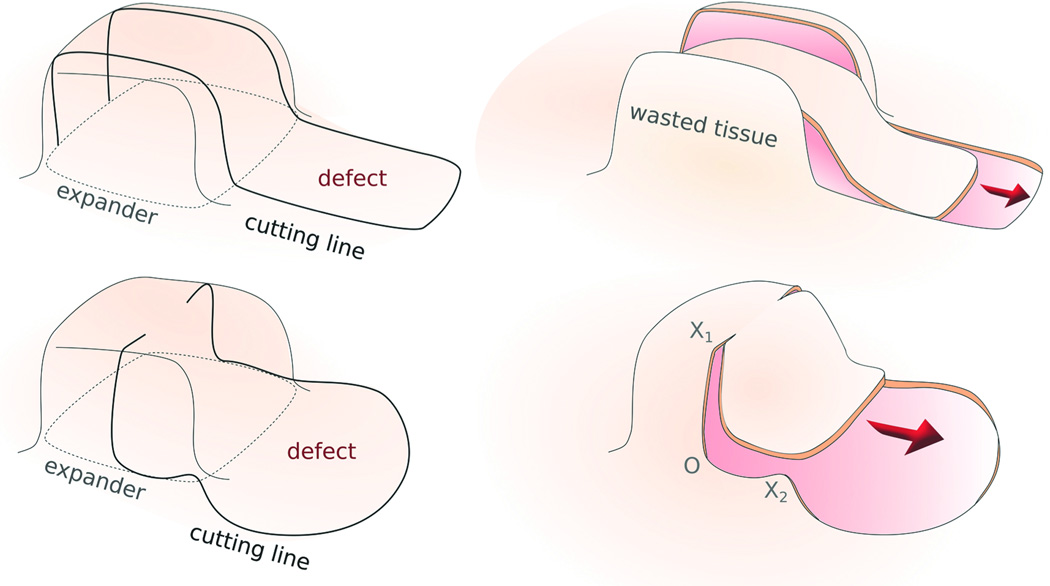
The present study evaluated the direct advancement flap and the double back-cut flap designs following tissue expansion (Fig. 2).⁵ To create a direct-advancement flap, two parallel cuts are made along the sides of the expanded skin. Extra tissue at both sides along the cuts is discarded and the resulting flap is stretched along the advancement direction to cover the defect. The direct-advancement flap is associated with a significant waste of tissue; however, the relaxed skin tension lines of the utilized skin flap remain aligned with the relaxed skin tension lines of the native skin. To create a double back-cut flap, the grown skin is first cut along the sides, from front to middle, and then perpendicular cuts are made towards the center. The flap is advanced at the front, but is rotated at the edges. The double back-cut flap allows a resourceful and more efficient tissue use; however, the relaxed skin tension lines of the flap are rotated with respect to the relaxed skin tension lines of the native skin.

Figure 2.

Two commonly used flap designs after tissue expansion. a) Direct-advancement flap. Two parallel cuts are made along the sides of the expanded skin. The extra tissue is discarded and the resulting flap is stretched to cover the defect. b) Double back-cut flap. The expanded skin is cut along the sides from the front to the middle and then perpendicular cuts towards the center are made. The flap is advanced at the front but there is rotation at the edges.

Creation of three-dimensional model

To create the complex three-dimensional geometry of expanded skin, we virtually created new skin by implanting and inflating a rectangular expander using a computational tissue expansion tool previously developed by our group.^{13, 14} Briefly, we considered an idealized skin sample and modeled skin as a flat, rectangular, thin tissue. We focused on simulating the middle layer of the skin, the dermis, since the dermal layer is the major load-carrying element due to its high collagen content.¹⁵ For the direct-advancement flap, we divided a rectangular tissue sample with dimensions 26×16×0.5cm³ into 3,328 brick-shaped elements. For the double back-cut flap, we simulated a 24×22×0.5cm³ tissue sample divided into 4,224 brick-shaped elements. Both geometries consisted of two layers of elements across the thickness. In both cases, the expanders covered an initial base area of 11×11cm². We gradually filled the expanders and allowed the skin to grow. Our computational model was inspired by the natural response of skin, in which mechanotransduction of non-physiological mechanical cues triggers a net gain in skin area until the skin re-establishes a homeostatic equilibrium state.¹⁶ Finally, we slowly decreased the pressure to deflate and remove the expanders. Our virtual tissue expansion naturally accounted for reversible, elastic deformation: upon deflation, skin retracts and the final surface is the net tissue surface available for reconstructive purposes.¹¹ However, the geometry of the newly grown skin is no longer flat, but now has the shape of a three-dimensional membrane, from which we can create the desired skin flap.

Simulation of flap design

After our virtual tissue expansion, the net skin area gain was 40.9% of the initial base surface area, which corresponded to a total area gain of 49.6 cm². We then post-processed the grown geometry to create a direct-advancement flap and a double back-cut flap. To this end, we first cut the region where the expander was placed in order to generate the flap, and then removed the defect zone adjacent to the flap.

To create the direct advancement flap, we first performed two cuts parallel to the advancement direction and then performed another cut along the base of the expanded area as illustrated in Fig. 2a. We determined the area of the defect to be removed, dividing the area gain by the width of the direct advancement flap. We excised the defect by removing elements in the finite element mesh. This resulted in a rectangular hole of 54 cm² that had to be resurfaced.

To create the double back-cut flap, we first cut along the sides from the front to the middle of the expanded region and then performed perpendicular cuts towards the center. Finally, we cut along the base of the expanded region to create the flap as illustrated in Figure 2b. The flap was advanced at the front, which induced a rotation at the edges. We considered the same advancement distance as for the direct advancement flap, but now excised a total area of 80 cm². The additional area that could be covered by the double back-cut flap resulted from the semi-circular regions excised at the sides as shown in Figure 2b. We advanced both flaps through wire connectors between nodes,¹⁷ and pulled these nodes together to closely mimic the clinical procedure, in which two opposite skin edges are joined by means of suture at discrete locations.

To monitor the mechanical forces acting on the flap throughout the advancement procedure, we calculated the von Mises stress distribution in the affected skin region. Tissue stresses are an important indicator for local tissue damage and long-term repair durability. Here, we used a transversely isotropic material model for skin, which explicitly accounts for the characteristic tissue microstructure with dermal collagen fiber bundles as the major load-bearing constituents.¹⁸ This allowed us to explore the stress profiles upon flap advancement parallel and perpendicular to the relaxed skin tension lines, which we assumed to be aligned with the collagen fiber bundles. For the model parameters, we selected an extracellular matrix stiffness of 0.0511MPa, a fiber stiffness of 0.015MPa, an exponential fiber stiffness of 0.0418, and a fiber dispersion of 0.05. These parameters were adopted from the literature from recent ex vivo biaxial tests of pig skin.¹²

In summary, we modeled the region of interest as a three-dimensional, expanded region and an adjacent flat, unexpanded region. We virtually excised a defect from the unexpanded region and created the flap from the expanded region. We gradually pulled on the flap to cover the region from where the defect was removed. We performed the computational analysis using the Finite Element program Abaqus. In addition to the geometry of the expanded and unexpanded regions, the Finite Element method requires a mathematical model to describe the characteristics of the tissue and its response to deformation. We selected a well-established tissue model that accounts for the different stiffness of skin along and perpendicular to the relaxed skin tension lines. The computational analysis generates stress profiles throughout the tissue sample. Stress profiles characterize the mechanical state of tension at every location, and are a well-known engineering indicator for zones of risk due to potential tissue damage.

Results

Direct advancement flap

Figures 3 and 4 show the von Mises stress contours of the direct advancement flap at four distinct time points during the procedure with the advancement direction oriented parallel and perpendicular to the relaxed skin tension lines, respectively. The direct comparison of both figures documents the significant influence of the flap orientation, which affects the peak stresses, the stress profiles, and the geometries of the resurfaced zone. When the flap is advanced parallel to the relaxed skin tension lines (Fig. 3) maximum stresses of 2.00 MPa and more occur at the base and at the distal end of the flap. When the flap is advanced perpendicular to the relaxed skin tension lines (Fig. 4) maximum stresses of 0.75 MPa occur in the same regions; however, the overall stress distribution is a lot more homogeneous and stresses are of a much smaller magnitude.

Figure 3.

Direct-advancement flap oriented parallel to relaxed skin tension lines. Consecutive time frames show the evolution of the stress distribution in skin as the flap is pulled over the defect. Maximum stresses of 2.00MPa occur at the base and at the distal end of the flap. Arrow: Direction of flap advancement. Solid lines: Direction of relaxed skin tension lines.

Figure 4.

Direct-advancement flap oriented perpendicular to relaxed skin tension lines. Consecutive time frames show the stress distribution in skin as the flap is pulled over the defect. Maximum stresses of 0.75MPa occur at the base and at the distal end of the flap. Arrow: Direction of flap advancement. Solid lines: Direction of relaxed skin tension lines.

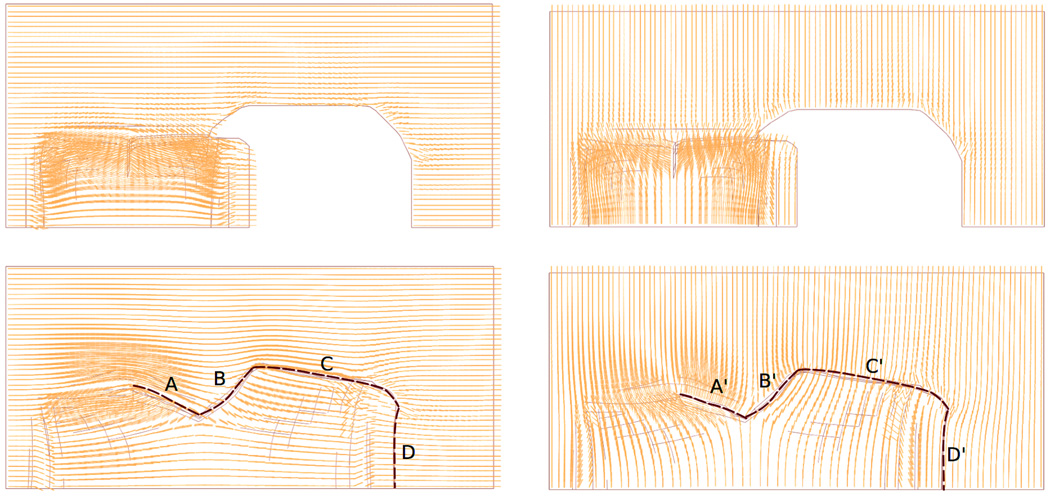
Figure 5 illustrates collagen fiber orientation when performing the direct advancement flap. For illustrative purposes, we highlight the suture regions as dashed black lines. For a flap advancement parallel to the relaxed skin tension lines in Figure 5a, collagen fibers run parallel to the suture lines in region A and perpendicular to the suture lines in region B. For a flap advancement perpendicular to the relaxed skin tension lines in Figure 5b, collagen fibers run perpendicular to the suture lines in region A’ and parallel to the suture lines in region B’. In both cases, the fibers maintain their initial orientations and rotate only marginally upon flap advancement.

Figure 5.

Collagen fiber orientations for direct-advancement flap oriented a) parallel and b) perpendicular to relaxed skin tension lines. Dashed lines highlight the suture regions. Collagen fibers maintained their initial orientations and rotated only marginally upon flap advancement.

Double back-cut flap

Figures 6 and 7 show the von Mises stress contours of the double back-cut flap at four distinct time points during the procedure with the advancement direction oriented parallel and perpendicular to the relaxed skin tension lines, respectively. In general, maximum stress values for the double back-cut flap are slightly lower in magnitude than those for the direct advancement flap. When the flap is advanced parallel to the relaxed skin tension lines (Fig. 6) maximum stresses of 1.50 MPa occur at the base and at the distal end of the flap, located in similar regions as for the direct advancement flap. However, now, there are additional high stress regions of 1.50MPa at both lateral sides where the tissue was rotated. When the flap is advanced perpendicular to the relaxed skin tension lines (Fig. 7) the stress contours are entirely different from the parallel orientation in Figure 6. In this case, maximum stresses of 1.50MPa are locally concentrated at all four corners of the resurfaced region while the base and the distal end experience stresses of only 0.75 MPa.

Figure 6.

Double back-cut flap oriented parallel to relaxed skin tension lines.. Consecutive time frames of the stress distribution in skin as the direct-advancement flap is pulled over the defect. Maximum stresses of 1.50MPa occur at the base and at the distal end of the flap. Additional stress concentrations of 1.50MPa occur at the lateral sides, in regions where the tissue is rotated. Arrow: Direction of flap advancement. Solid lines: Direction of relaxed skin tension lines.

Figure 7.

Double back-cut flap oriented perpendicular to relaxed skin tension lines. Consecutive time frames show the stress distribution in skin as the flap is pulled over the defect. Maximum stresses of 1.50MPa are locally concentrated at all four corners of the resurfaced region, while the base and the distal end experience stresses of only 0.75MPa. Arrow: Direction of flap advancement. Solid lines: Direction of relaxed skin tension lines.

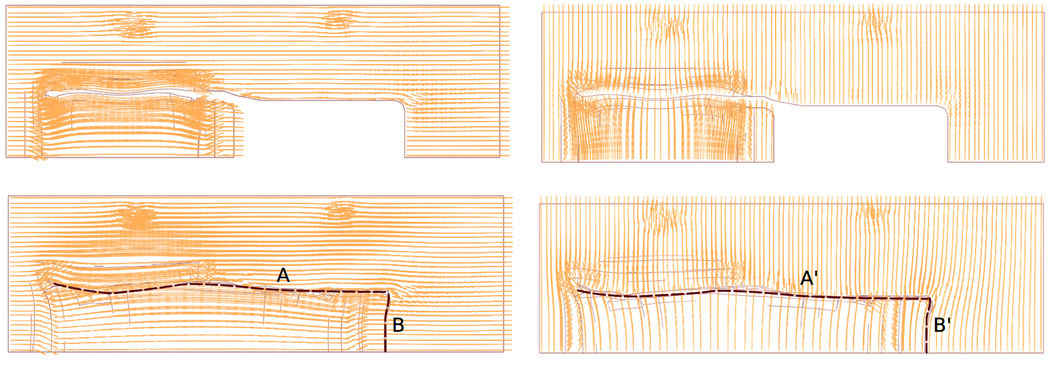
Figure 8 illustrates the collagen fiber orientation when performing the double back-cut flap. For illustrative purposes, we highlight the suture regions as dashed black lines. The collagen fiber orientation maps demonstrate that the double back-cut flap involves both advancement and rotation. As a result of the rotation, different fiber orientations meet at the suture lines. For the advancement parallel to the relaxed skin tension lines in Figure 8a, collagen fibers run parallel to the suture lines in region C, and perpendicular to the suture lines in regions A, B and D. For the advancement perpendicular to the relaxed skin tension lines in Figure 8b, the orientation is opposite and collagen fibers run perpendicular to the suture lines in region C’, and parallel to the suture lines in regions A’, B’ and D’.

Figure 8.

Collagen fiber orientations for double back-cut flap oriented a) parallel and b) perpendicular to relaxed skin tension lines. Dashed lines highlight the suture regions. Different fiber orientations meet at the suture lines because of collagen fibers rotation.

Discussion

Excessive skin tension is a major contributor to complications following the inset of tissue expanded flaps. In this analysis, we have studied the involved mechanical forces to address the fundamental question: Can mechanics be used to inform flap design? Our studies reveal three major findings, which have critical clinical implications.

First, we find that elevated stresses at the base of the flap are inherent to all flap designs, while stress concentrations at the distal end and at the sides of the flap are flap-specific: the direct advancement flap induces high stress concentrations at its distal end (Fig. 3). The double back-cut flap induces slightly lower stress concentrations at its distal end; however, it induces additional regions of high stresses at the lateral sides (Fig. 6).

Second, we find that stress profiles are highly sensitive to the orientation of the relaxed skin tension lines. Advancing the flap parallel to the direction of the relaxed skin tension lines creates stress maxima of 2.00 MPa and 1.50 MPa at the distal end (Figs. 3 and 6). Advancing the flap perpendicular to the direction of the relaxed skin tension lines creates stress maxima of 0.75 MPa and 0.75 MPa at the distal end (Figs. 4 and 7). As a useful byproduct of the simulation, we explored changes in orientation of the relaxed skin tension lines. For the direct advancement flap, the relaxed skin tension line orientation remains virtually unchanged (Fig. 5). For double back-cut flap, however, after flap advancement, relaxed skin tension lines with different orientations meet at the same suture lines (Fig. 8). Flap-induced rotation of the relaxed skin tension lines might have a critical impact on improved healing and reduced scar formation. Our findings suggest that a surgeon who is not limited by anatomic zones or local geometries can minimize stresses by placing the expander such that the flap is advanced perpendicular to the relaxed skin tension lines. Overall, our simulations support our hypothesis that stresses in the flap are highly sensitive to the location of expander placement and the direction of flap advancement with respect to the relaxed skin tension lines.

Third, we have shown that stress profiles are sensitive to the chosen flap design. The direct advancement technique mainly affects the base and the distal end, while all other regions are stressed homogeneously to the same level (Figs. 3 and 6). The double back-cut technique equally affects the base and the distal end, but also adds critical zones at the lateral sides (Figs. 4 and 7). Although we used the same expander size in all four cases, the defect region covered by the double back-cut flap is significantly larger than the region covered by the direct advancement flap. Taken together, these analyses do not support a single uniform recommendation in favor of one flap design over the other. Rather, they underline the critical need to consider each individual case on a patient-specific basis. The design of a successful flap is a complex procedure, which is highly sensitive to the balance of mechanical forces. Computational simulation, as we have shown here, offers a powerful tool to account for patient-specific geometries and local anatomies on an individual basis. A detailed knowledge of regional stress distributions might help the surgeon to identify regions of high stress that require special care or to select regions of low stress for safe suture placement.

Although this study provides mechanistic insight into the design of skin flaps in reconstructive surgery, it is not free of limitations. First, the underlying technology, the finite element method, is inherently ill conditioned and overestimates the absolute stress values at corners or sharp cuts. Thus, unrealistic large stresses result at singular points of the finite element mesh. Second, the truly quantitative comparison of tissue stresses requires a precise knowledge about the material properties of human skin. Here we have used parameters, which had been fit to pig skin experiments ex vivo. Unfortunately, most of the published material parameters of human skin are associated with isotropic material models that do not account for relaxed skin tension lines and collagen fiber orientations. More experimental efforts are needed to determine the appropriate parameters for anisotropic models of human skin suitable for large deformations. Third, for direct comparison, we have only analyzed a single flap size. In future studies, we will conduct systematic parameter analyses to identify optimal flap widths and lengths to minimize tissue stress. Last, as a first proof of principle, we have only compared the performance of two specific flap designs advanced on a flat geometry. However, the inherent versatility of the finite element method conceptually allows us to analyze various different flap designs, and to expand the analysis to characteristic anatomic regions in the body such as the forehead, the scalp, the torso, or the upper and lower extremities.

Overall, we believe that computational modeling is a powerful tool to guide individualized flap design with the common goal to minimize tissue stresses, accelerate healing, minimize scarring, and optimize tissue use. Mechanistic finite element analyses allow the surgeon to account for personalized anatomies and patient-specific geometries for individualized flap design. Today, the application of finite element analyses in plastic and reconstructive surgery is still in its infancy. Once this technology has advanced to a reliable, predictive tool, it could be tremendously helpful to integrate computer-aided pre-surgical planning in the daily surgical routine.