External Vibration Multi-directional Ultrasound Shearwave Elastography (EVMUSE): Application in Liver Fibrosis Staging

Abstract

Shear wave speed can be used to assess tissue elasticity, which is associated with tissue health. Ultrasound shear wave elastography techniques based on measuring the propagation speed of the shear waves induced by acoustic radiation force are becoming promising alternatives to biopsy in liver fibrosis staging. However, shear waves generated by such methods are typically very weak. Therefore, the penetration may become problematic, especially for overweight or obese patients. In this study, we developed a new method called External Vibration Multi-directional Ultrasound Shearwave Elastography (EVMUSE), in which external vibration from a loudspeaker was used to generate a multi-directional shear wave field. A directional filter was then applied to separate the complex shear wave field into several shear wave fields propagating in different directions. A two-dimensional (2D) shear wave speed map was reconstructed from each individual shear wave field, and a final 2D shear wave speed map was constructed by compounding these individual wave speed maps. The method was validated using two homogeneous phantoms and one multi-purpose tissue-mimicking phantom. Ten patients undergoing liver Magnetic Resonance Elastography (MRE) were also studied with EVMUSE to compare results between the two methods. Phantom results showed EVMUSE was able to quantify tissue elasticity accurately with good penetration. In vivo EVMUSE results were well correlated with MRE results, indicating the promise of using EVMUSE for liver fibrosis staging.

I. INTRODUCTION

Liver fibrosis and cirrhosis are the result of chronic liver injury, and affect hundreds of millions of patients worldwide [1]. Staging of liver fibrosis is crucial for treatment decision making and follow-up. Liver biopsy is currently considered as the gold standard for liver fibrosis staging and diagnosis [2]. However, it is an invasive procedure, and is also subject to sampling error and interpretation variability [3].

The state of tissue health is found to be associated with tissue elasticity, which can be noninvasively and quantitatively estimated by inducing shear waves into the tissue and measuring shear wave propagation speed, c_s, in the tissue [4]. Many techniques based on c_s measurement or on the direct estimation of material properties from shear wave propagation have been applied for noninvasive liver fibrosis staging. In particular, Magnetic Resonance Elastography (MRE) has outstanding performance for liver fibrosis staging [5, 6]. It can quantify tissue elasticity over a relatively large area of the liver, and therefore does not suffer from sampling or interpretation variability as does liver biopsy. However, MRE is not widely available and the associated cost is relatively high, thus its clinical use is limited to a few large medical centers.

Techniques such as Acoustic Radiation Force Impulse (ARFI) shear wave imaging [7, 8] and supersonic shear imaging (SSI) [9, 10] use acoustic radiation force (ARF) to produce shear waves and are capable of providing a two-dimensional (2D) quantitative elasticity imaging of in vivo liver tissue. However, the shear waves generated by ARF are typically very weak (motion amplitudes on the order of micrometers), limiting the penetration of these methods, which may become problematic in overweight or obese patients. In a recent study, SSI failed to obtain reliable measurements in 15% of the subjects [11]. The Body Mass Index (BMI) of subjects in the successful group and failed group was 22.3 ± 3.7 and 29.7 ± 3.3, respectively. In another study of 321 patients, ARFI shear wave imaging failed in 49% of patients with BMI greater than 30 [12]. The prevalence of adult obesity (defined by BMI ≥ 30) in the United States is over one third of the population and keeps increasing [13]. It is estimated that by 2025, there will be about 25 million nonalcoholic steatohepatitis (NASH) patients in America, who are commonly obese and in need of fibrosis staging [14]. Therefore, shear wave penetration is becoming a non-trivial limitation for these ARF-based methods.

External mechanical vibration can produce shear waves with higher amplitude for more reliable shear wave speed estimates in deeper tissues. Fibroscan (or transient elastography) uses a piston-like vibrator to generate a transient longitudinally polarized shear wave on the axis of the vibrator inside the liver, and measures the liver elasticity based on the shear wave propagation speed [15]. It has been widely applied for studying liver fibrosis [16, 17]. Recently Tzschatzsch et al. proposed a method called time-harmonic elastography (THE) to study liver elasticity and viscosity using continuous vibrations at a range of frequencies [18]. However, both methods provide only one-dimensional localized elasticity information and lack imaging guidance for its measurements.

Multiple vibrations using one or more vibration sources can fill the field of view (FOV) with propagating shear waves from which a 2D elasticity image could be calculated [19, 20]. Shear waves generated by such methods often have complicated patterns with unknown propagation directions due to reflection, diffraction and other phenomena, making it difficult for conventional time-of-flight methods [7, 21] to measure c_s. A 2D c_s estimator has been proposed to improve the accuracy of c_s estimation in sonoelastographic shear velocity imaging [20, 22]. Such a method requires consistent shear wave propagation direction, which is often difficult to obtain in in vivo applications. A time reversal approach also has been proposed for elasticity imaging based on correlations of a diffuse wave field [23], which is, however, also difficult to obtain in vivo.

In this study, we propose a new method called External Vibration Multi-direction Ultrasound Shearwave Elastography (EVMUSE) to assess liver fibrosis. EVMUSE uses the external mechanical vibration from a loudspeaker to create a multi-directional shear wave field. Such a wave field does not have to be diffuse, and there is no restriction on the direction, location, and occurrence of the shear waves propagating in the image plane. EVMUSE uses directional filtering to separate shear waves moving in different directions. For each direction, a 2D c_s map is calculated based on the local 2D shear wave speed estimation method. The final c_s map is constructed by compounding the c_s maps calculated from all the directions. EVMUSE was validated using two tissue-mimicking homogeneous phantoms and one multi-purpose phantom. Ten patients undergoing liver MRE were also studied with the EVMUSE method and the results were compared between the two methods.

II. METHOD

A. Experimental Setup

As illustrated in Fig. 1, a single loudspeaker (Pioneer SW-8, Pioneer Electronics Inc., Japan) was embedded as a part of the examination bed, with the diaphragm exposed and facing upward. This setup is similar to that used in the time-harmonic elastography study reported by Tzschatzsch, et al. [24]. During the experiment, the subject was laid supine with the back (lower rib cage) coupled with the loudspeaker and right arm abducted, giving the transducer access to the available intercostal acoustic windows.

Fig. 1.

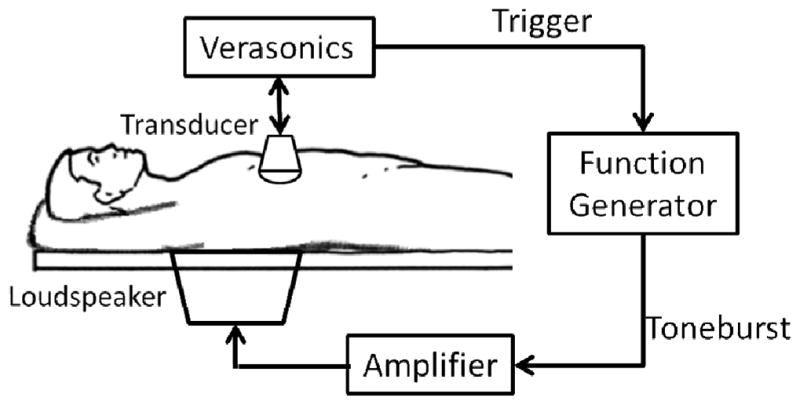
Illustration of the experimental setup. The embedded loudspeaker is driven by an amplifier controlled by a function generator. The Verasonics ultrasound system sends out a trigger signal to activate the vibration, and then acquires the B-mode image and records the motion.

A Verasonics ultrasound system with a C5-2v curved array transducer (Verasonics Inc., Redmond, WA) was programmed to have both B-mode imaging and shear wave motion detection capabilities. Under the guidance of the B-mode imaging, the transducer can be adjusted to locate the region of interest (ROI). By hitting a button, the system immediately sends a trigger signal to a function generator (Agilent 33250A, Agilent Technologies, Inc., Santa Clara, CA) to activate the loudspeaker after the signal is amplified (Crown XLS202, Crown Audio, Inc., Elkhart, IN), and then quickly switches to the high frame rate imaging mode [25] for shear wave motion detection. Once triggered, the function generator sends out a 50 Hz tone burst with a duration of 100 ms and an amplitude of 1.2 V to the speaker via the amplifier (voltage gain: 30 dB). The frequency and duration were selected such that the speaker had a high amplitude response while being capable of delivering sufficient shear wave motion into the liver.

Because the transducer was in rigid contact with the subject (between the ribs), transducer motion induced by speaker vibration can introduce artifacts in the shear wave motion tracking. Therefore, in this study the high frame rate motion detection did not start until 10 ms after the termination of the vibration, at which time the propagating shear waves were still present in the ROI while the transducer motion was negligible. The motion detection lasted for 200 ms with 0.5 mm spatial resolution and 3-angle (−2°, 0°, and 2°) spatial compounding [25] at a frame rate of 1 kHz.

B. Directional Filter

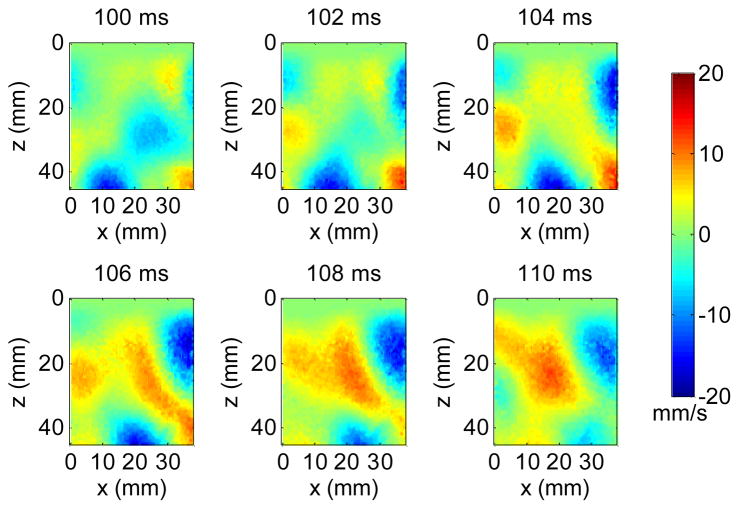
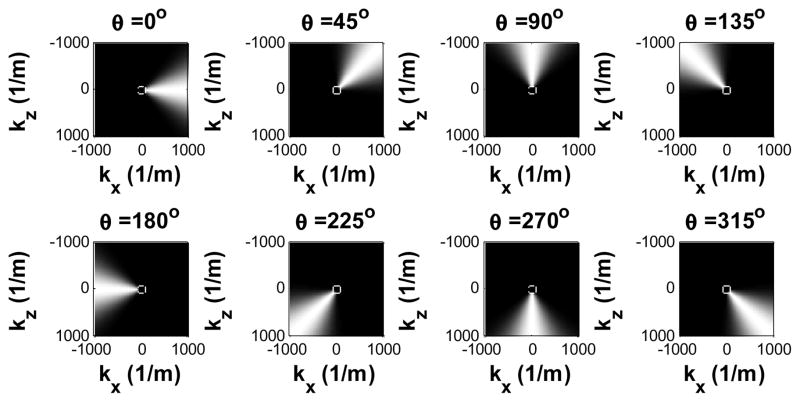
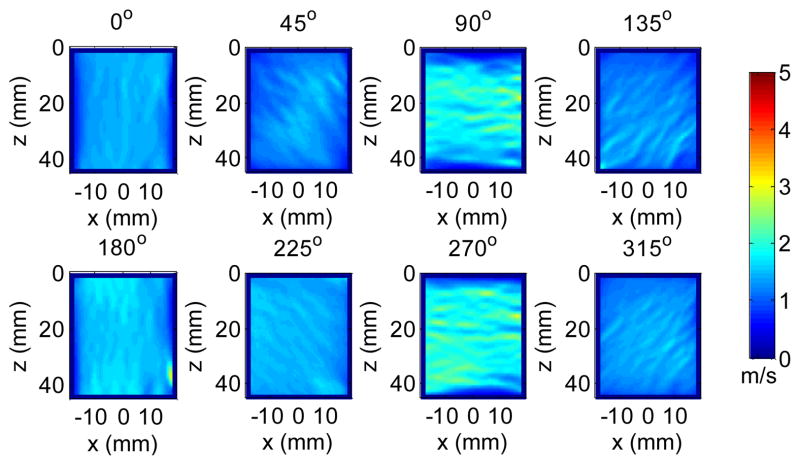
Shear wave particle velocity in the axial (z) direction was calculated from the recorded in-phase/quadrature (IQ) signals based on 2D autocorrelation [26]. Fig. 2 shows snapshots from a movie of a typical multi-directional shear wave field in a phantom generated by the loudspeaker. Because the vibration is transmitted from the loudspeaker to the phantom through a large coupling area, multiple shear waves may occur at different locations and propagate in different directions at any given time. Therefore, they have to be separated in order for conventional time-of-flight shear wave speed estimation [7, 21] to work. To isolate the shear waves propagating in different directions, the spatiotemporal (x, z, t) motion signals were first converted to the spatiotemporal-frequency (k_x, k_z, f_t) domain, or k-f domain, using a three-dimensional (3D) Fourier transform. Tukey windows were applied to the spatiotemporal signals to create a smooth transition from the FOV to surrounding zeros, minimizing the edge effects due to the Fourier transform. Directional filters were then applied by multiplying the directional filter response with the signals in the k-f domain [27]. Fig. 3 shows the directional filter response in 8 directions. For each direction, shear waves propagating within an angular range near the primary direction can pass through whereas shear waves moving in other directions were suppressed.

Fig. 2.

Snapshots from a movie of a shear wave field generated by the loudspeaker in a phantom. The number above each snapshot indicates the elapsed time since the data acquisition started.

Fig. 3.

Eight directional filters from 0° to 315° separated by 45° steps. The cutoff region at the center indicates the speed limit of 5m/s evaluated at f_t = 400 Hz.

Both compressional waves [28] and out-of-plane shear waves (for geometric reasons; see [29]) appear as high speed waves which are present as low spatial frequency components in the k-f domain. Given an upper speed limit c_h at a temporal frequency f_t, a spatial frequency limit k_l = f_t/c_h can be imposed upon the directional filter to suppress waves with propagation speeds higher than c_h, by removing spatial frequency components lower than k_l as indicated by the regions inside the white circle at the center of the directional filter response in Fig. 3. According to the relation between k_l and f_t, the radius of the removed region increases with the temporal frequency f_t. A 6^th-order Butterworth high-pass filter was designed to apply smooth transitions for k_l to avoid Gibbs ringing effects. According to a review of 1,377 patients with liver diseases studied by MRE, the highest measured c_s was 4.3 m/s for cirrhotic liver [30]. Therefore, a speed limit of 5 m/s was applied in this study, and Fig. 3 shows the corresponding directional filter response at f_t = 400 Hz.

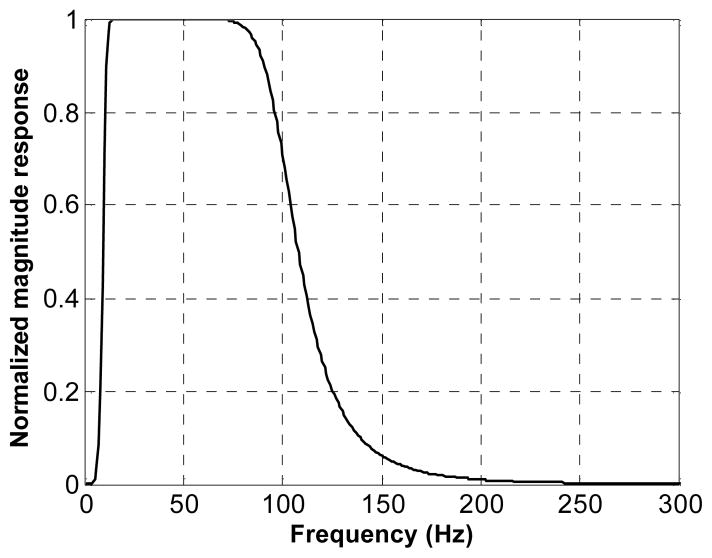
Besides the spatial high-pass filtering, another 6^th-order Butterworth band-pass filter was applied in the temporal frequency direction to remove low frequency drift and high frequency noise, as shown in Fig. 4. Given the vibration frequency of 50 Hz, the cut-off frequencies of the filter were set at 10 Hz and 100 Hz, respectively.

Fig. 4.

Normalized magnitude response of the temporal band-pass filter. The cut-off frequencies are 10 Hz and 100 Hz, respectively.

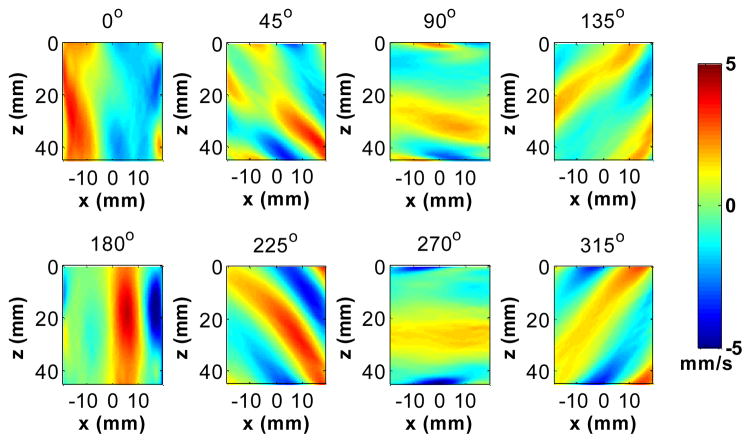
After the directional filtering, the resulting shear wave signals in different directions were converted back to the spatiotemporal domain using an inverse 3D Fourier transform. Fig. 5 shows snapshots at 106 ms (after the data acquisition started) of the shear wave movie after applying the 8 directional filters and the high-pass spatial frequency filter (Fig. 3) and the temporal filter (Fig. 4) to the multi-direction wave field (Fig. 2).

Fig. 5.

A snapshot from a movie of the shear waves after applying the directional filters in Fig. 3 to the shear wave field shown in Fig. 2 (at 106 ms after the data acquisition started).

C. 2D Shear Wave Speed Estimation

After directional filtering, shear waves propagating in different directions were separately processed using a 2D shear wave speed estimation method. Data filtered by each directional filter mainly contain waves propagating in that direction, which can be at an oblique angle to the lateral and axial coordinates (x, z) of the ultrasound detection data grid. Similar to the method introduced in [20, 22], cross-correlation was applied to calculate the time delays between the temporal signal at one pixel and the signals from two other pixels a certain distance away in the x and z directions, respectively. As illustrated in Fig. 6, consider a plane shear wave (indicated by the long dashed lines) moving at a constant speed of c_s with an angle of θ with respect to the x axis. The time delays are measured between the origin o and two locations x and z, both with a distance of r from o. There is a tradeoff for the selection of r, since a shorter distance would result in higher resolution and lower signal decorrelation, but also a larger percentage error for time delay estimation [31]. In this study, r was empirically set at 4 mm (8 pixels). The time for the shear wave to travel from o to x is Δt_x, and the time for the shear wave to propagate from o to z is Δt_z. Based on geometry, it follows that rcosθ = c_s · Δt_x and rsinθ = c_s · Δt_z. Therefore $c_s=\frac{r}{\sqrt{\mathrm{\Delta }{t}_x^2+\mathrm{\Delta }{t}_z^2}}$. To improve the estimation accuracy, the temporal signals were upsampled 10 times and parabolic interpolation was applied to locate the sub-pixel correlation peaks [32, 33]. Normalized correlation coefficients (CC) [34] were also calculated in both the x and z directions to control the quality of c_s estimation. Because there were two CCs for each pixel from shear wave estimation along x and z directions, respectively, the lower value of the two was selected to represent the CC for that pixel to be conservative.

Fig. 6.

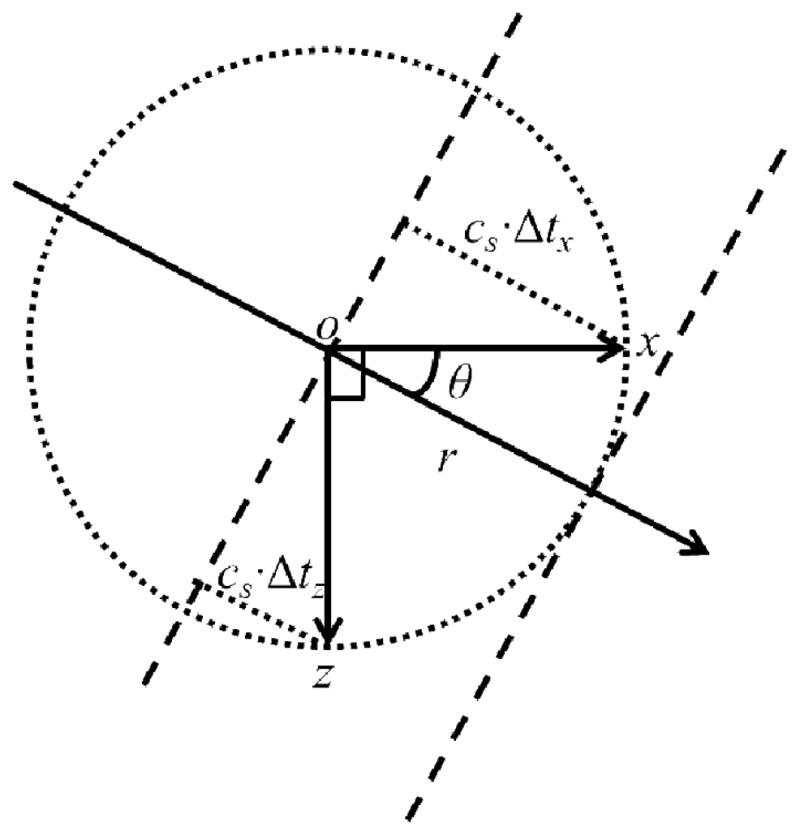
Illustration of the principle of the 2D c_s estimation.

To further improve the robustness of the measurement, the value of c_s at one pixel (c̄_s) was determined by averaging with estimates from the surrounding pixels. Both inverse distance weighting (IDW) [35] and correlation coefficient weighting (CCW) were applied to calculate the average speed as described in Eq. (1) [22]:

$$\begin{array}{l}{\overline{c}}_s(0,0)=\frac{{\displaystyle \sum _{x=-N}^N}{\displaystyle \sum _{z=-N}^N}{c}_s(x,z)·cc{(x,z)}^2/r(x,z)}{{\displaystyle \sum _{x=-N}^N}{\displaystyle \sum _{z=-N}^N}cc{(x,z)}^2/r(x,z)},\\ r(x,z)=\{\begin{array}{c}\sqrt{x^2+z^2}\left(x^2+z^2\ne 0\right)\\ 0.1\left(x^2+z^2=0\right)\end{array}\end{array}$$ (1)

where c_s(x, z) is the speed measured at a location with a CC of cc(x, z) and a distance of r(x, z) (unit: pixel) away from the center pixel (0, 0). N determines the range of the pixels involved in the averaging (also the spatial resolution of the c_s image), which were each 4 pixels away from the center pixel in the x and z directions in this study, resulting an image resolution of 4 mm (8 pixels) in x and z. The above process was applied to each imaging pixel of Fig. 5 to form a 2D c_s image in each direction as shown in Fig. 7.

Fig. 7.

Estimated c_s in eight directions from the shear waves in Fig. 5 using 2D cross-correlation and spatial averaging. The mean and standard deviation for each direction was 1.46 ± 0.05, 1.40 ± 0.10, 1.89 ± 0.21, 1.32 ± 0.09, 1.61 ±0.05, 1.48 ± 0.03, 1.94 ± 0.16, 1.44 ± 0.06 m/s for angles 0–315°, respectively.

D. Shear Wave Speed Image Compounding

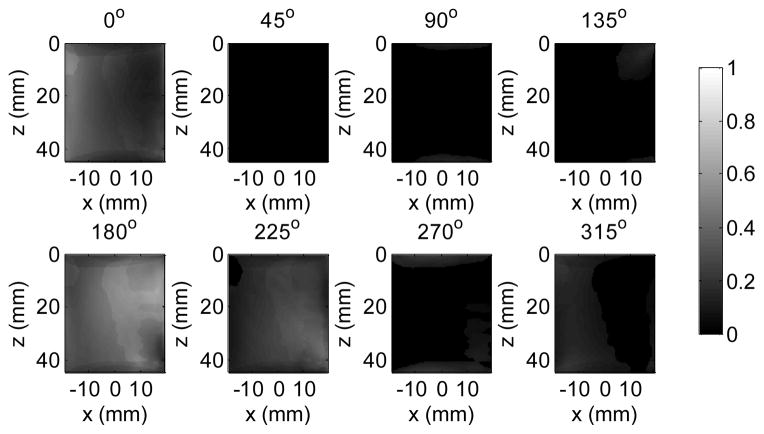
After the 2D c_s maps from each of the directions are calculated, they can be compounded into a final image by averaging the measured c_s in each direction. In some cases, especially for in vivo measurement, the shear wave field may mostly propagate in one or two directions instead of in many directions. The c_s results should be more reliable in directions where there are strong shear waves. Therefore, in this study the final c_s value at each pixel was calculated as a weighted average of the c_s results in different directions, using the shear wave energy for that direction as the weight. The shear wave energy at each pixel in each direction was calculated by summation of the corresponding squared temporal signal, and normalized by the aggregation of the shear wave energy over different directions, such that the weights in different directions from each pixel always add up to 1 [22] as shown in Fig. 8. The c_s images from Fig. 7 can be compounded into a final image as shown in Fig. 9, using the energy weights from Fig. 8.

Fig. 8.

Energy weight calculated from the shear wave signals in each direction in Fig. 5 after directional filtering. For each pixel, the sum of the weights from eight directions is always one.

Fig. 9.

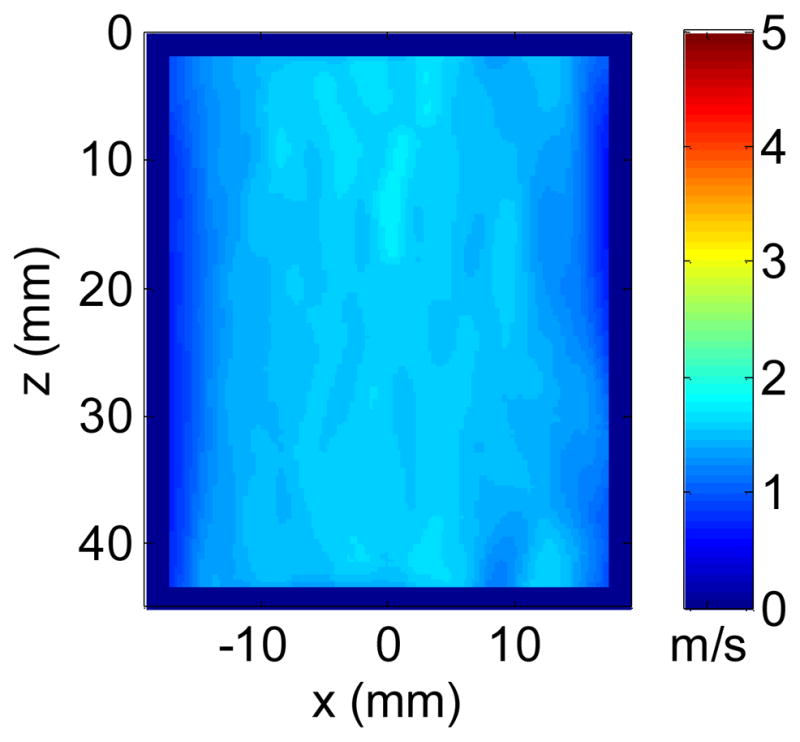
Final c_s image using energy weighted compounding from Fig. 7. The mean and standard deviation of the final image was 1.59 ± 0.05 m/s.

E. Phantom Study

Two homogeneous elasticity phantoms (Phantoms 1 and 2; CIRS Inc., Norfolk, VA) calibrated with SSI using the Aixplorer scanner (SuperSonic Imagine, Aix-en-Provence, France) were studied using EVMUSE. Each phantom was placed on the examination bed with the bottom coupled with the loudspeaker. The C5-2v transducer was held by hand perpendicularly to the surface of the phantom with minimum pressure. Five EVMUSE measurements were taken for each phantom at 5 random locations on the phantom. For each measurement, a 2D c_s image was constructed and a mean value was calculated from all the pixels of the image. For comparison, five SSI images were acquired at 5 random locations on the phantom using a curved array transducer SC6-1 and the Aixplorer [36]. The SSI images were analyzed offline, and a mean Young’s modulus (E) was measured from a round ROI with 2 cm diameter centered at 3 cm depth in each of the SSI images, from which a mean c_s value was calculated based on $E\approx 3\mu =3\rho c_s^2$ [36], where ρ is the mass density of the medium (assumed to be 1000 kg/m³) and μ is the shear modulus.

To demonstrate the penetration of the proposed method, a multi-purpose phantom (Model 040GSE; CIRS Inc., Norfolk, VA) was studied using EVMUSE. The maximum depth of the measured phantom section was 16 cm with attenuation coefficient of 0.7 dB/cm/MHz. One EVMUSE measurement was taken with an ROI reaching the depth of 14 cm using the C5-2v transducer. For comparison, one SSI measurement was taken using the Aixplorer and SC6-1 with an ROI centered at 6.5 cm depth, where measurements failed at the bottom half of the ROI due to the penetration limitations. Five more SSI measurements were taken using the Aixplorer and the SC6-1 with the ROI centered at 3 cm depth where elasticity of the phantom was reliably measured, and the results were used as validation for EVMUSE measurement at deeper depth.

F. In Vivo Liver Study

Ten patients (8 women and 2 men; age range: 30–77 years; BMI: 19.4–34.0) undergoing clinically indicated liver MRE exams participated in the study. Among the 10 patients, 4 patients had primary sclerosing cholangitis, 3 patients had chronic hepatitis C, and one patient each had chronic hepatitis B, NASH, and hemochromatosis. Five patients were overweight with BMI between 25 and 30, and two patients were obese with BMI over 30. The study was approved by the institutional review board (IRB) of the Mayo Clinic and written consent was obtained from each subject.

During the experiment, the subject was laid supine on the examination bed with the back coupled with the loudspeaker and right arm abducted. For each measurement, a sonographer (26 years of experience) positioned the transducer using B-mode imaging to locate a relatively large liver region free of major vessels through intercostal spaces. Then the subject was instructed to suspend breathing while the operator pressed the button to activate the loudspeaker followed by shear wave motion detection and data recording. For each subject, 15 measurements were obtained through 3 intercostal spaces (between ribs 9 and 10, 8 and 9, 7 and 8) with 5 repetitions for each intercostal space.

Nine subjects underwent MRE on the same day of their EVMUSE study. One subject had the MRE exam one day before the EVMUSE study. The MRE exams were performed using a 1.5T MRI scanner (GE Healthcare, Milwaukee, WI), with a pneumatic driver attached to the subject’s abdomen to provide a harmonic mechanical vibration at 60 Hz. Standard MRE exam acquired images of wave propagation in the liver were analyzed by physicians following the standardized clinical routine [37].

III. RESULTS

A. Phantom Study

Fig. 10 shows representative 2D c_s images measured from the two homogeneous phantoms superimposed over their B-mode images. The edges of the c_s images were 1 cm away from the edges of the FOV to avoid possible edge effects due to the Fourier transform in the directional filters. For each measurement, a mean value was calculated from the entire c_s image. The measured c_s averaged over 5 measurements were 1.18 ± 0.04 m/s and 2.08 ± 0.05 m/s for Phantom 1 and 2, respectively, compared to 1.18 ± 0.01 m/s and 2.04 ± 0.01 m/s, respectively using SSI. The penetration of EVMUSE in both phantoms was over 7 cm.

Fig. 10.

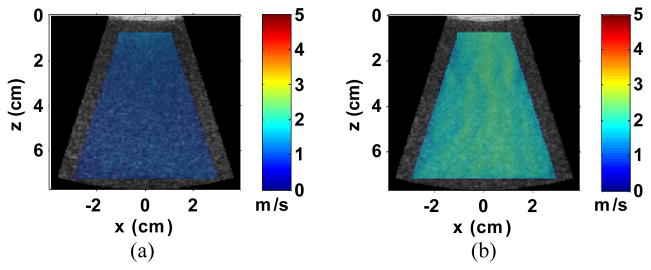
Representative c_s images of Phantoms 1 (a) and 2 (b) superimposed over their corresponding B-mode images.

Fig. 11(a) shows the 2D c_s image measured from the multi-purpose phantom using EVMUSE. The image was superimposed over a B-mode image in order to compare with the SSI image shown in Fig. 11(b). The ROI of the EVMUSE image was centered at 12.5 cm depth (11–14 cm) with measured c_s averaged over the ROI of 2.60 ± 0.15 m/s. The ROI of the SSI image was centered at 6.5 cm depth. No elasticity result could be acquired from the lower part of the ROI due to the attenuation. For the other five SSI measurements at 3 cm depth, the c_s averaged over different measurements was 2.60 ± 0.01 m/s, which was comparable to the single EVMUSE measurement result. Note that the standard deviation for EVMUSE was calculated from the c_s at different pixels within the ROI, whereas the standard deviation for SSI was from the mean c_s of different measurements.

Fig. 11.

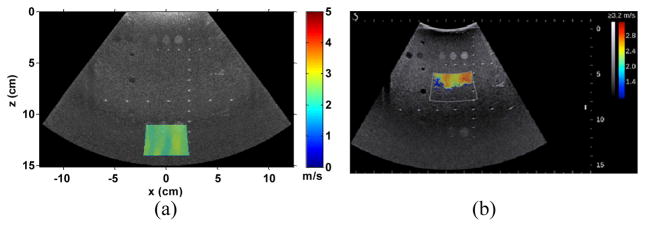
(a) 2D c_s image of the multi-purpose phantom superimposed over its B-mode image. The ROI of the image was centered at 12.5 cm with measured average c_s over the ROI of 2.60 ± 0.15 m/s; (b) SSI image of the same phantom with ROI centered at 6.5 cm depth.

B. In Vivo Liver Study

EVMUSE data from the 10 patients were processed using the proposed method. For each measurement, a 2D c_s image was calculated. Fig. 12(a) shows a representative c_s image superimposed over the B-mode image from one measurement of one patient (BMI: 26.4). The EVMUSE ROI of in vivo liver reached around 7 cm. A mean value was computed over a trapezoidal ROI, the edges of which were 1 cm away from the liver capsule, the left, right, and bottom edges of the FOV, respectively. The ROI was set to cover a large area of the liver, while also avoiding possible edge effects.

Fig. 12.

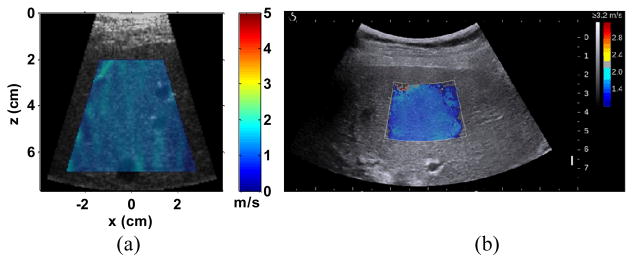
(a) Representative c_s image of the in vivo liver superimposed over its corresponding B-mode images from one patient (patient No. 6). The measured c_s within the colored region of the image was 1.48 ± 0.07 m/s. (b) Representative SSI image of the same patient. The measured c_s based on the offline analysis described in the phantom study was 1.46 m/s. The mean shear modulus of the patient measured by MRE was 2.3 kPa which corresponds to a c_s of 1.52 m/s.

Among the 10 patients, 5 patients were also examined by SSI on the same day of the EVMUSE study following similar protocol (15 measurements through 3 different intercostal spaces). A representative SSI image of the same patient is shown in Fig. 12(b).

Fig. 13 shows representative measurement results from a patient with obesity (BMI: 32.3) using EVMUSE and SSI. For EVMUSE, relatively uniform c_s image was obtained, whereas SSI failed to give uniform measurement within the ROI.

Fig. 13.

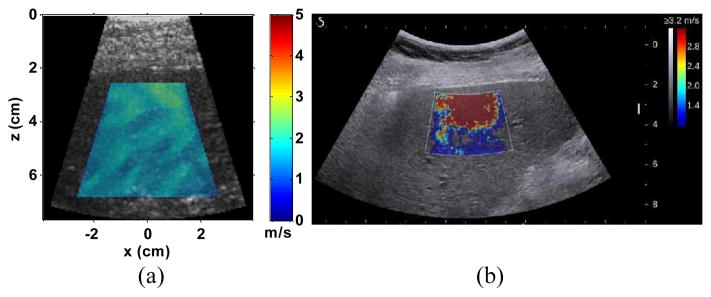
(a) Representative c_s image of the in vivo liver superimposed over its corresponding B-mode images from one obese patient (patient No. 8). The measured c_s within the colored region of the image was 1.80 ± 0.22 m/s; (b) Representative SSI image of the liver from the same patient using the Aixplorer, which failed to give a reliable elasticity map. The mean shear modulus of the patient measured by MRE was 3.9 kPa, which corresponds to a c_s of 1.97 m/s.

For each patient, a median value was calculated from the 15 mean values from the EVMUSE measurements as that patient’s result. The interquartile ratio, defined as the ratio between the interquartile range (from the first quartile to the third quartile) and the median value, was also calculated to evaluate the reliability of the results [12, 38]. The interquartile ratios for the EVMUSE results are listed in Table 1. All of the ratios using EVMUSE were below the 30% boundary, within which the results are regarded as reliable [38]. The ratios of the SSI measurements from the 5 patients are also listed in Table 1. The interquartile ratios of the EVMUSE and SSI measurements for the patient shown in Fig. 12 were 10.1% and 10.8%, respectively, whereas the ratios for the patient shown in Fig. 13 were 15.6% and 74.4%, respectively. Data in Table I suggest that EVMUSE may be able to give more consistent results within each patient.

TABLE I.

INTERQUARTILE RATIOS OF EVMUSE AND SSI RESULTS

Patient No.	BMI	EVMUSE Ratio (%)	SSI Ratio (%)
1	26.9	8.0
2	28.4	22.8
3	27.4	9.8
4	34.0	17.1
5	22.7	8.0	5.0
6	26.4	10.1	10.8
7	19.4	13.5
8	32.3	15.6	74.4
9	24.2	19.8	69.0
10	23.5	9.1	84.1

To compare with MRE results, c_s results of EVMUSE were converted to shear modulus μ based on $\mathrm{\mu }=\mathrm{\rho }{c}_s^2$ [4], where ρ is the mass density of the medium (assumed to be 1000 kg/m³). EVMUSE results from the 10 patients were plotted against MRE results as shown in Fig. 14. The Pearson product-moment correlation coefficient between the MRE and ultrasound results was 0.86 (95% confidence interval: 0.71–0.98) with p < 0.001, indicating the correlation was significant.

Fig. 14.

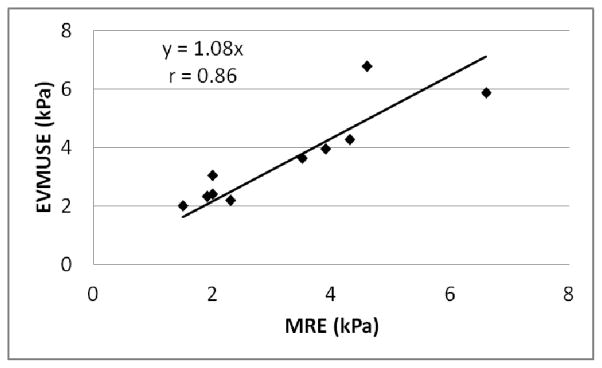
EVMUSE results from the 10 patients plotted against the MRE results. The Pearson product-moment correlation coefficient r was 0.86 with p < 0.001, indicating the correlation was significant.

IV. DISCUSSION

In this study, we developed a new method called EVMUSE to assess liver fibrosis. A loudspeaker was used to generate a multi-directional shear wave field inside the liver. Directional filtering and a 2D shear velocity estimator were used to construct 2D c_s images of the liver from which the elasticity of the liver was calculated. Phantom and in vivo liver studies showed EVMUSE had sufficient penetration, accurate elasticity measurement, and good correlation with liver elasticity results measured by MRE.

A single loudspeaker was used as the vibration source in this study. As the transcostal vibration was delivered into the liver, the ribs functioned as multiple shear wave sources according to the Huygens principle [39], generating multi-directional shear waves which can fill up the FOV and enable c_s measurement everywhere. Such a configuration requires minimum setup effort, and also leaves the subject’s lateral intercostal gaps open for the transducer to access. However, the portability of the setup may be an issue, because a specially designed bed is required. Multiple electromagnetic or pneumatic actuators could also be used to generate a multi-directional shear wave field [40]. Such configurations may be more portable and flexible for multi-directional shear wave production. However, it would take more effort to attach the actuators to the body and to minimize their interference with the ultrasound transducer.

To minimize the transducer vibration, shear wave motion detection was conducted after the vibration stopped. Such an approach is not the most efficient, as the larger motion during the vibration is not used to estimate c_s. Also, when the external vibration stopped, the remaining vibration of the tissue may follow its own resonant frequency. Therefore, it was difficult to compare c_s at the same shear wave frequency among all the patients. Future study will be conducted to mitigate the effect of transducer motion so that shear wave motion detection could be done during the vibration.

The frequency of the shear waves produced by mechanical vibration is generally lower than those generated by ultrasound radiation force, resulting in larger spatial wavelength of the shear waves and consequently lower spatial resolution of the c_s images. Since liver fibrosis is generally a diffuse disease, the impact of lower image resolution for liver fibrosis staging is limited.

In this study, directional filters in eight directions were designed to adequately cover all directions of the shear wave field. In principle more directions might improve the quality of the c_s images, because the filters would align better with the shear waves. However, more directions would require more computation. Therefore, the number of the directions is a tradeoff between the c_s image quality and the computational load. Future investigation would be needed to evaluate the relationship between directional filter design and image quality.

Shear wave energy was used to weight c_s values in different directions when compounding them into a final image. If the shear waves are diffuse, then the c_s measured in each direction contribute to the final compounded image. If the shear waves are not diffuse, such an image compounding method emphasizes the estimation results from the direction(s) where the shear waves are strongest. This may not be optimal for imaging inclusions, because without multi-directional shear compounding [22, 36], the resulting c_s image may not have good delineation of the inclusions. Therefore, such an approach may work better for homogeneous media such as liver.

The out-of-plane and compressional waves were suppressed by setting a speed limit in the directional filter, which is possible for most clinical applications, as the physiological range of shear wave speed values is usually known. However, the remaining out-of-plane waves can still introduce an overestimation bias to the c_s measurement. The choice of speed limit is likely application dependent and this is a limitation of the method. Adopting multiple vibration sources and arranging them in the image plane of the transducer may minimize the out-of-plane waves. 3D ultrasound imaging [41] may help mitigate the bias caused by out-of-plane waves. More studies are needed to effectively suppress the generation of or contribution from out-of-plane waves.

In this study, both MRE and EVMUSE calculated shear modulus μ from the c_s based on $\mathrm{\mu }=\mathrm{\rho }{c}_s^2$, where viscosity was ignored. However, liver tissue is viscoelastic [42], and the measured c_s should increase with shear wave frequency because of the dispersion effect [43]. Compared to the 60 Hz shear wave frequency in MRE, the center frequency of the shear waves after 50 Hz vibration in EVMUSE is probably lower, which should result in a lower measured μ than MRE. However, the EVMUSE results are probably biased high by the remaining out-of-plane waves, which we believe is the reason for a slope slightly greater than 1.0 in Fig. 12. MRE can either minimize the out-of-plane waves by selecting the optimal image plane in the 3D space [44], or correctly process 3D waves by acquiring true 3D data. Nevertheless, the good correlation still indicates EVMUSE has promising performance in fibrosis staging, despite the differences of the absolute values between EVMUSE and MRE results.

The MRE results of the ten patients participating in the study ranged from 1.5 kPa to 6.6 kPa. The clinical cut-points for MRE routinely used at our institute to classify normal and cirrhotic livers are shear modulus μ_MRE < 2.5 kPa and μ_MRE > 5.0 kPa, respectively. Therefore, the ten patients involved in this study should cover such range. According to a review of 1,377 patients with liver diseases studied by MRE, the shear moduli measured in the liver ranged from 1.1 kPa to 18.8 kPa [30]. Therefore, more patients will be needed to fully evaluate the performance of EVMUSE in liver fibrosis staging.

Among the ten patients, one patient had a relatively low BMI of 22.7 and an abnormal back curvature, such that the coupling between the back and the loudspeaker was not ideal. Also the patient had difficulty keeping still during the EVMUSE experiment. The corresponding result of this patient appears to be an outlier in Fig. 12 (the data point with highest EVMUSE value), without which the correlation coefficient r would be 0.98 (95% confidence interval: 0.95–1.00).

The penetration advantage of EVMUSE over radiation force methods was demonstrated by the multi-purpose phantom study. To further investigate the penetration capability of EVMUSE, we measured a volunteer without any history of liver disease who had a BMI of 40 using EVMUSE and SSI. The representative c_s image of EVMUSE and SSI elasticity image are shown in Figs. 15(a) and (b), respectively. The ROIs of both EVMUSE and SSI images were centered at 9.5 cm depth (8–11 cm). EVMUSE was still able to measure the c_s at over 11 cm depth, whereas SSI failed to make such measurements. The measured c_s by EVMUSE in the colored region of Fig. 15(a) was 1.38 ± 0.19 m/s. We do not have MRE results in the subject. The c_s of 1.38 m/s corresponds to a shear modulus of 1.9 kPa, which is within the range of normal liver stiffness [6].

Fig. 15.

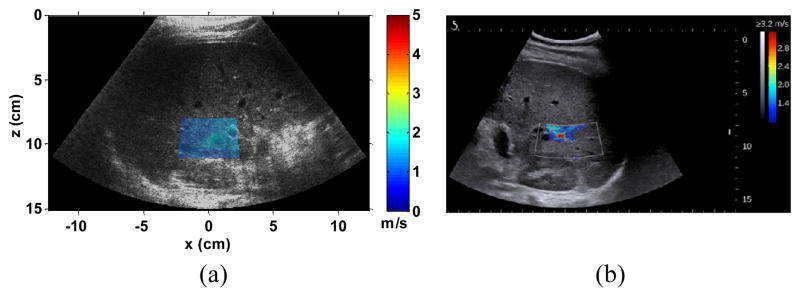
(a) Representative c_s image of the in vivo liver superimposed over its corresponding B-mode images from one subject with a BMI of 40 and without any history of liver disease. The ROI was centered at 9.5 cm with measured c_s within the ROI of 1.38 ± 0.19 m/s. (b) Representative SSI image of the same subject with the ROI centered at 9.5 cm, where it failed to make the measurement.

In this study, the motion was monitored for 200 ms. The CC values should increase with the motion detection time duration, because more shear wave events can be recorded, making cross-correlation results more reliable. However, a longer recording time would not work for measuring rapid stiffness change, for example in contracting muscles. Multiple vibration sources may be advantageous over a single source for such applications, because they could simultaneously generate as many shear waves coming from many directions as possible.

The c_s image compounding method in this study assumes the medium is isotropic, meaning the c_s is the same in all the directions. However, the proposed method potentially could be used to study anisotropic media by measuring c_s in various directions.

V. CONCLUSION

In this study, EVMUSE was developed for liver fibrosis staging by measuring the c_s from a multi-directional shear wave field in the liver. Results showed the proposed method is capable of measuring tissue elasticity accurately, as validated by SSI in phantom studies, and the in vivo measurements in patients with liver disease correlate well with MRE results. EVMUSE was demonstrated to have better penetration than the radiation force based method, and thus has potential for non-invasive staging of liver fibrosis in obese patients.