Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2015 Nov 7.
Published in final edited form as: Phys Med Biol. 2014 Oct 16;59(21):6595–6606. doi: 10.1088/0031-9155/59/21/6595

A Unifying Probabilistic Bayesian Approach to Derive Electron Density from MRI for Radiation Therapy Treatment Planning

Madhu Sudhan Reddy Gudur 1, Wendy Hara 1, Quynh-Thu Le 1, Lei Wang 1, Lei Xing 1, Ruijiang Li 1,*
PMCID: PMC4216734  NIHMSID: NIHMS636783  PMID: 25321341

Abstract

MRI significantly improves the accuracy and reliability of target delineation in radiation therapy for certain tumors due to its superior soft tissue contrast compared to CT. A treatment planning process with MRI as the sole imaging modality will eliminate systematic CT/MRI co-registration errors, reduce cost and radiation exposure, and simplify clinical workflow. However, MRI lacks the key electron density information necessary for accurate dose calculation and generating reference images for patient setup. The purpose of this work is to develop a unifying method to derive electron density from standard T1-weighted MRI. We propose to combine both intensity and geometry information into a unifying probabilistic Bayesian framework for electron density mapping. For each voxel, we compute two conditional probability density functions (PDFs) of electron density given its: (1) T1-weighted MRI intensity, and (2) geometry in a reference anatomy, obtained by deformable image registration between the MRI of the atlas and test patient. The two conditional PDFs containing intensity and geometry information are combined into a unifying posterior PDF, whose mean value corresponds to the optimal electron density value under the mean-square error criterion. We evaluated the algorithm's accuracy of electron density mapping and its ability to detect bone in the head for 8 patients, using an additional patient as the atlas or template. Mean absolute HU error between the estimated and true CT, as well as ROC's for bone detection (HU>200) were calculated. The performance was compared with a global intensity approach based on T1 and no density correction (set whole head to water). The proposed technique significantly reduced the errors in electron density estimation, with a mean absolute HU error of 126, compared with 139 for deformable registration (p=2×10-4), 283 for the intensity approach (p=2×10-6) and 282 without density correction (p=5×10-6). For 90% sensitivity in bone detection, the proposed method achieved a specificity of 86%, compared with 80%, 11% and 10% using deformable registration, intensity and without density correction, respectively. Notably, the Bayesian approach was more robust against anatomical differences between patients, with a specificity of 62% in the worst case (patient), compared to 30% specificity in registration-based approach. In conclusion, the proposed unifying Bayesian method provides accurate electron density estimation and bone detection from MRI of the head with highly heterogeneous anatomy.

Introduction

Magnetic resonance imaging (MRI) provides a number of advantages over computed tomography (CT) for radiation therapy treatment planning. Due to its superior soft tissue contrast, MRI significantly improves the accuracy and reliability of target delineation in many disease sites. Typically, MRI is used as an adjunct and often fused with CT for radiation treatment planning (Khoo 2006, van der Heide et al 2012). However, this suffers from the inherent CT/MR co-registration errors, which persist throughout the treatment process. A treatment planning process with MRI as the sole imaging modality will eliminate such systematic errors, and also bring additional benefits, such as reduced cost, simplified clinical workflow, as well as lower radiation exposure (Devic 2012). However, MRI lacks the key electron density information, which is necessary for accurate dose calculation and generating reference images for patient setup.

Methods to derive electron density information from MRI have been investigated (Lambert et al 2011, Dowling et al 2012, Hsu et al 2013). The simplest approach for mapping electron density is uniform mapping, i.e., to set entire patient to uniform electron density (usually water). This approach cannot generate useful reference images and leads to erroneous radiation dose calculation in nonhomogeneous tissues, and thus is unacceptable for MRI-based treatment planning. An improved approach is bulk density assignment based on manual or automatic tissue segmentation of MRI, which assigns a uniform density to a segmented region (Lambert et al 2011, Lee et al 2003, Chen et al 2007). The main drawback of this approach is the inter-observer inconsistency and auto-segmentation errors (Weltens et al 2001, Mazzara et al 2004, Isambert et al 2008).

Recently, more sophisticated methods for mapping electron density using MRI have been proposed. They can be broadly divided into two groups: geometry-based (Dowling et al 2012, Stanescu et al 2008) and intensity-based (Catana et al 2010, Keereman et al 2010, Korhonen et al 2014, Kapanen and Tenhunen 2013, Hsu et al 2013) methods. The geometry-based approach relies on deformable image registration to a sample patient or atlas with known tissue label or electron density (typically derived from CT). This approach suffers from the inherent registration errors due to inter-patient anatomical differences. On the other hand, the intensity-based approach aims to characterize tissue properties directly based on the MR image intensity. However, due to the lack of a one-to-one correspondence or relation between electron density and MR image intensity, this approach often leads to ambiguous results. In particular, the differentiation of bone from air has been challenging because of their similar and short T2 characteristics (both appear dark on MRI). More recent studies have used newer MR sequences such as the ultra-short echo time (UTE) sequence to visualize bony anatomy (Berker et al 2012, Catana et al 2010, Keereman et al 2010). However, the currently available image quality of UTE imaging is still far from satisfactory. For instance, blood vessels appear dark on UTE images, and thus may be confused with bone (Hsu et al 2013). Moreover, the non-standard MR sequence also adds considerable scan time (∼6 min) to the existing patient simulation workflow, which may introduce more patient motion and discomfort. More reliable methods are needed to map electron density using standard sequences in MRI.

The purpose of this work is to develop a unifying method to derive electron density from standard T1-weighted MRI. Here, we propose to combine both intensity and geometry information into a unifying probabilistic Bayesian framework for electron density mapping. For each voxel, we compute two conditional probability density functions (PDFs) of electron density given its: (1) T1-weighted MRI intensity, and (2) geometry in a reference anatomy, obtained by deformable image registration between the MRI of the atlas and test patient. The two conditional PDFs containing intensity and geometry information are combined into a unifying posterior PDF, whose mean value gives the electron density. We evaluated the algorithm's accuracy of electron density mapping and its ability to detect bone in the head and skullbase.

Methods and materials

Image Acquisition

We retrospectively analyzed the MRI and CT data acquired during radiation treatment planning of 9 consecutively treated primary brain tumor patients in 2013. The main patient selection criterion was that the MRI was acquired with same 3D sequence, had fine spatial resolution and covered the whole head. MRI was acquired using a large-bore 3T MR scanner (Discovery MR750, GE Medical Systems, Milwaukee, Wisconsin, USA). Standard T1-weighted MRI images were acquired using the magnetization-prepared rapid gradient echo sequence, with TE/TR/TI = 13/950/0 ms, flip angle = 90°, and voxel size ≈ 1.09 × 1.09 × 2 mm3 CT was acquired with a Discovery CT scanner (GE Medical Systems, Milwaukee, Wisconsin, USA), with a voxel size ≈ 0.6 × 0.6 × 1.25 mm3.

Image Processing

The MRI data were first resampled to match the resolution of CT for subsequent analysis. For each patient, all MR and CT images were rigidly coregistered using Elastix software (Klein et al 2010) with localized mutual information as a similarity measure. Since we are only interested in patient anatomy, a binary mask of the patient head was generated by segmenting the CT images with a HU value of -500 on the outermost regions of the head, followed by morphological erosion with a 5 voxel spherical kernel to eliminate any objects that are not physically part of the patient. Registration of MR images across patients consisted of a rigid registration followed by a B-spline deformable image registration. The transformation matrix obtained during this registration process was used on the CT images to generate the deformable template CT, or the geometry map as we refer in this paper.

Bayesian Approach for Electron Density Mapping

We propose a unifying approach to combine both MR image intensity and geometry information in a Bayesian framework. Briefly, we learn the appropriate probability distributions of the electron density of a certain voxel, given its T1-weighted MR image intensity and geometry (or position in a reference anatomy), using an atlas or template patient with matched pairs of CT/MRI. The information gained from geometry through atlas registration and intensity values of T1-weighted MRI is encoded in a conditional probability density function. The Bayesian formalism is used to derive the posterior probability density function, which is a probability distribution of unknown electron density on a continuous scale conditional on known relevant information such as MRI intensity and its geometry or position. Figure 1 summarizes the major steps involved in the proposed Bayesian approach.

Figure 1.

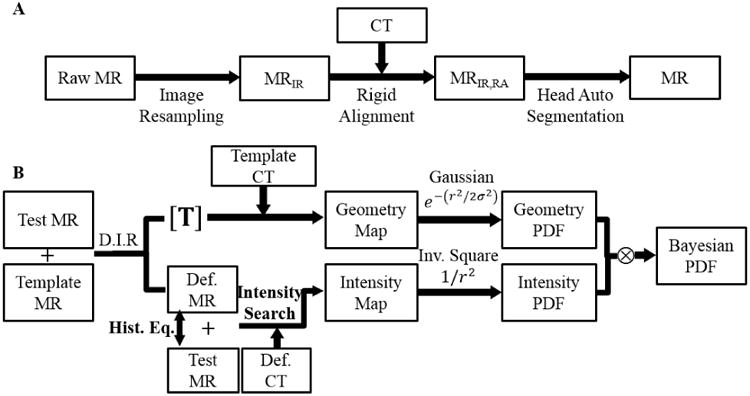
Figure 1

Open in a new tab

(A) Pre-processing steps of MR images for each patient. (B) Schematic flow of the proposed Bayesian approach for estimating electron density. (Abbreviations: D.I.R: Deformable Image Registration, Def. MR: Deformed Template MR, Def. CT: Deformed Template CT, Hist. Eq.: Histogram Equalization)

In the proposed method using Bayesian theorem, the posterior probability density function (PDF) of a voxel having an electron density value of x, given the corresponding MRI intensity y, and its geometry or position z in a reference anatomy (established through deformable image registration with MRI of an atlas patient) is formulated as:

p(x|y,z)=p(x)p(y|x)p(z|x)p(y,z)∝p(x|y)p(x|z) (1)

In deriving the above equation, we have assumed statistical independence of the MRI intensity y, and geometry z, as well as a uniform prior probability distribution. Through this formulation, we are able to keep all the important information gained from geometry and intensity, and at the same time greatly simplify subsequent calculations. To estimate the PDFs in practice, the nonparametric kernel density estimation method (Bowman and Azzalini 1997) was used.

For computing the conditional PDF of electron density given the MRI intensity at a particular voxel, we first equalized the histogram of local intensities in deformed template and test MRI to account for any differences in the range of MRI values due to differences in MR sequences during image acquisition. For each voxel in the test MRI, we found those voxels in the deformed template MRI with similar intensity values (using a 5% threshold). The mean intensities of the corresponding voxels in deformed template CT were used as the intensity map. Then, the conditional PDF of electron density given the MRI intensity was calculated with the kernel density estimation, weighted by the inverse square of the distance between the test voxel and the matching voxels with similar intensity values in the deformed template MRI.

To compute the conditional PDF of electron density at a voxel given the reference geometry or position, we chose all the voxels within 6 × 6 × 6 mm3 volume around it and constructed a PDF from their corresponding deformed template CT with Gaussian function as its kernel density weighting function. The standard deviation of the Gaussian function was 3 mm.

Finally, we apply the Bayesian theorem to obtain the posterior PDF for the electron density value of a voxel, by multiplying the above two conditional PDFs. The estimated electron density value is obtained by calculating the mean of the posterior probability density function: x̂ = E[x|y0, z0], which is optimal under the mean square-error criterion. The above process is repeated for every voxel in the MRI volume.

Validation and Evaluations

We randomly chose one out of 9 patients as the atlas or template patient. The above Bayesian approach was used to generate the synthetic CT images for the remaining 8 patients. These synthetic CT images were compared with the real x-ray CT for validation. We calculated the mean absolute HU error within the patient head. To evaluate the ability of the Bayesian approach in identifying bone, receiver operating characteristic (ROC) analysis was performed on all 8 test patients. True bone was defined in true CT scans of each patient with HU > 200 that included voxels with low density bone or voxels in which bone is mixed with other tissues. Intensity thresholds were applied to the synthetic CT images to label bone versus non-bone regions. Similarly, air was identified by applying an HU threshold below -400. Any voxel with HU between -400 and 200 was defined as soft tissue. ROC curves were generated for thresholds across the range of CT image intensities. Since bony anatomy is used as one clinical endpoint of image-guided setup, detection of bone was discussed more than air and soft tissue. Area under the ROC was calculated, along with specificity and accuracy at 90% sensitivity level in detection of bone.

Comparison with existing approaches

To demonstrate the advantages of the proposed Bayesian approach, we compare it with conventional approaches using the either geometry or intensity alone. For the geometry approach, the template patient CT was deformed to generate geometry map, using the transformation matrix obtained from deformable registration between the template and test MRI. For the intensity approach, the mean CT intensities of the voxels with matching MRI intensity were used as the intensity map (see Fig. 1). Paired t-test between the Bayesian and existing approaches was carried out to assess its statistical performance in quantitative HU values and bone detection.

Results

Axial views of MR and CT images of the template and one test patient are shown in Fig. 2, in which the MRI data of each patient was aligned with their CT through rigid transformation. Several structural differences can be noticed between these two patients. Figure 3 shows the true CT image of the test patient and estimated synthetic CT images using different approaches. The difference images clearly demonstrate the superior accuracy in electron density estimation using the Bayesian approach. The registration method has some gross misalignment of bony anatomy, due to anatomical differences between the template and test patient (arrow in Fig. 3B1). Although many of the structural details are preserved with the intensity method, the estimated electron density value has a relatively large bias, which is higher for air and lower for bone. Since both of these structures share similar MRI intensity values, the intensity approach cannot differentiate them. On the other hand, the Bayesian method is able to effectively integrate the two pieces of information to give more accurate estimates of electron density. In the last row of Fig. 3, three voxels (D, E and F) from three regions in this axial plane were chosen to illustrate the performance of different approaches in details. At voxel D, the geometry approach fails while intensity succeeds. The combination of these two PDFs in the Bayesian approach also succeeds in identifying the voxel correctly as air. At voxel E, geometry succeeds, intensity fails while the Bayesian approach still succeeds. At voxel F, all three approaches estimate CT intensity correctly.

Figure 2.

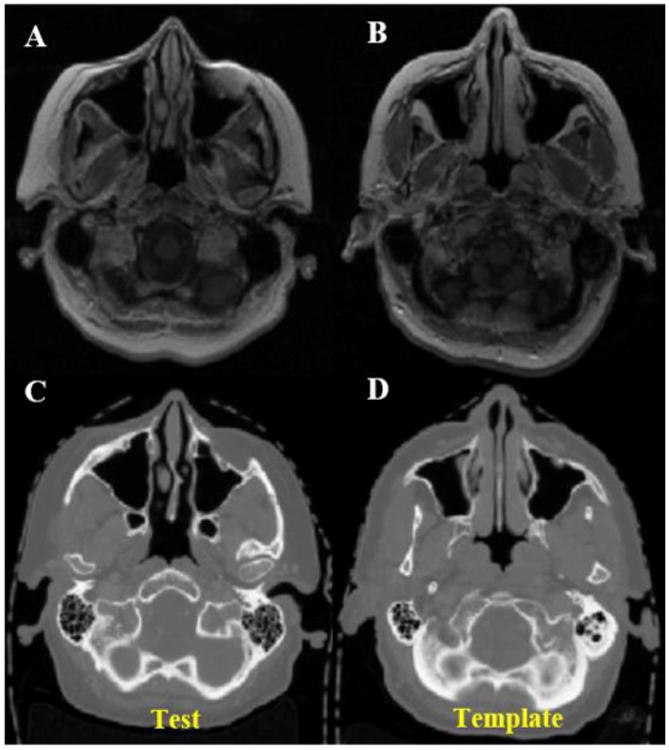
Figure 2

Open in a new tab

Axial views of MR (A, B) and CT (C, D) scans of test and template patients. Anatomical differences between the patients are noticeable.

Figure 3.

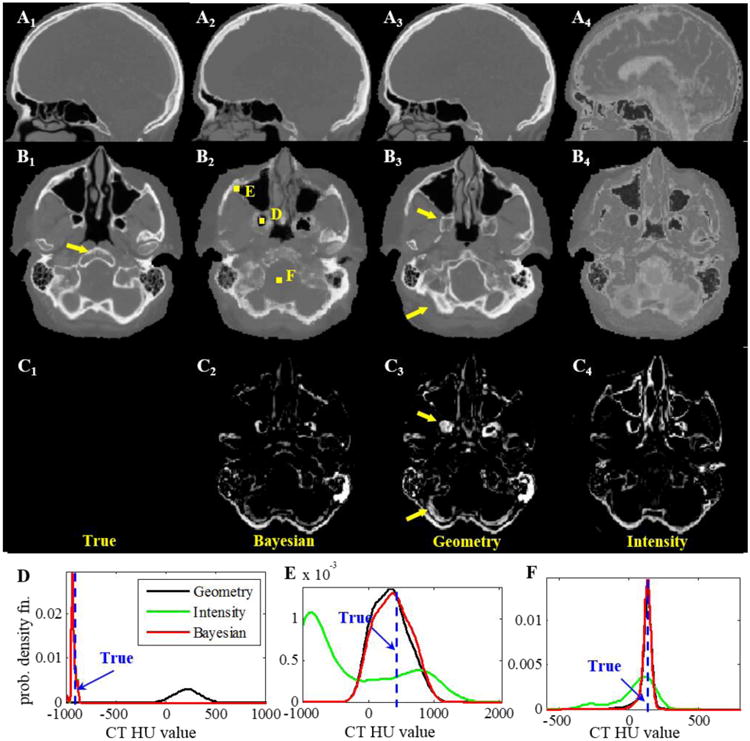
Figure 3

Open in a new tab

(Ai=1-4) Sagittal and (Bi=1-4) axial CT images of true scan, and synthetic CT using the Bayesian, geometry and intensity approaches for the test patient shown in Fig. 2. The difference images of the axial views with true scan are shown in Ci=1-4. Arrows point to the regions where the geometry approach failed to identify the correct tissue. PDFs at voxels (D, E) where the proposed Bayesian approach correctly identified the electron density (true value in dashed vertical line); but (D) geometry and (E) intensity gave the wrong estimations. (F) PDFs at a voxel where all 3 approaches had correct estimations.

As shown in Fig.4, the geometry approach can capture the gross anatomy, but also distorts the structural details when there are large anatomical variations between patients (indicated by arrow 1). On the other hand, the intensity approach may better preserve the tissue structural details, but has a large bias in electron density estimation due to the degeneracy in the MRI intensity, especially for bone and air (arrow 2). Combining both pieces of information using the Bayesian approach leads to improved estimation of electron density.

Figure 4.

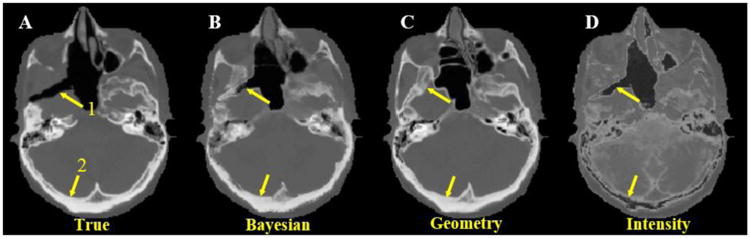
Figure 4

Open in a new tab

Axial view of true CT scan (A) and synthetic CT's by Bayesian (B), geometry (C) and intensity (D) approaches. Arrow 1 indicates an air region where the geometry approach erroneously detects bone. Arrow 2 indicates bony anatomy where the intensity approach detects air instead. In both regions, the proposed Bayesian approach correctly identifies the true electron density.

The mean ROC curves for bone, air and soft tissue detection are shown in Fig. 5. Table 1 presents the mean absolute HU errors against the true CT for all 8 test patients using different methods, as well as the area under ROC, specificity and accuracy at 90% sensitivity for bone detection. In general, the Bayesian approach outperformed all other approaches by any measure. Paired t-test between Bayesian and geometry method for mean absolute HU error of 8 test patients was significantly different with p = 2×10-4. Area under ROC, specificity and accuracy at 90% sensitivity for bone detection showed statistically significant differences with p = 4×10-4, 0.02 and 0.03 respectively. On average, the Bayesian approach achieved improvements of 5% or more for bone detection in specificity and accuracy compared with the geometry method. Of note, in the worst case (patient), Bayesian approach still achieved a specificity of 62%, while for the geometry approach, the specificity was merely 30%. Area under ROC for air detection was also significantly higher (p = 3×10-4) with Bayesian approach compared to geometry method (88.0±4.4 vs 83.1±3.2). No significant improvement was observed in soft tissue detection with Bayesian compared to geometry (84.1±5.5 vs 83.9±3.5).

Figure 5.

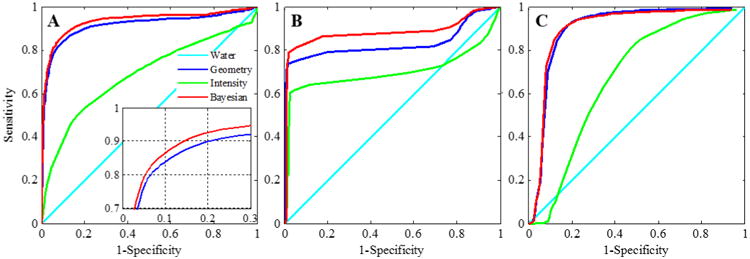
Figure 5

Open in a new tab

Receiver operating characteristics (ROC) of water, geometry, intensity and Bayesian approaches for detection of (A) Bone, (B) Air and (C) Soft Tissue. Inset shows close-up of the curves for geometry and Bayesian approaches.

Table 1.

Performance of electron density estimation using different approaches for 8 patients.

Mean Abs. HU Error Area Under ROC (%) Specificity (%) Accuracy (%)
@ 90% Sensitivity
Bayesian 126±25 93.0±2.5 86.0 86.6
Geometry 139±27 91.3±3.2 79.6 81.7
Intensity 283±17 68.5±9.3 11.2 28.1
Water 282±45 50±0.0 10 10
Open in a new tab

Figure 6 shows the sagittal and coronal views of synthetic CT as well as the digitally reconstructed radiograph (DRRs) using the Bayesian approach, compared with those obtained from the real CT. The shape and extent of skull can be clearly visualized in both DRRs. In overall they match very well qualitatively, although subtle differences exist between the two.

Figure 6.

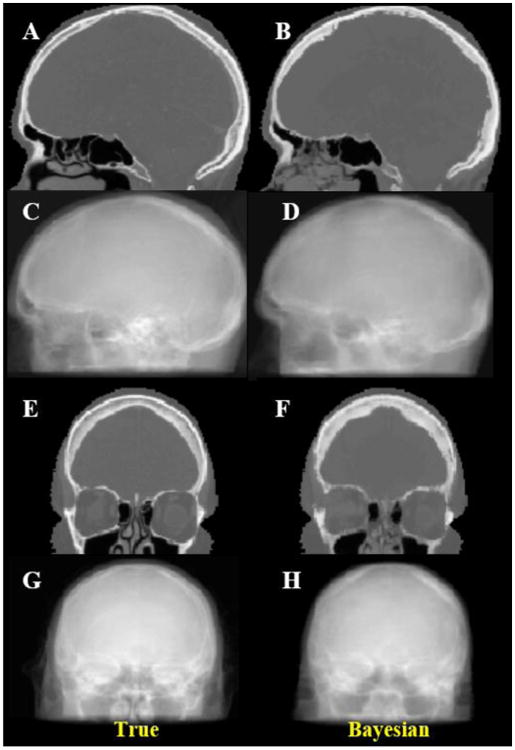
Figure 6

Open in a new tab

Sagittal (top half) and coronal (bottom half) views of true (left) CT scan and Bayesian estimated synthetic CT (right) and DRR images in two orthogonal views.

As a preliminary assessment of the effect of estimated electron density on dose distributions, we calculated the 3D dose distributions for the same volumetric modulated arc therapy (VMAT) treatment plan, using real CT and synthetic CT derived from the Bayesian approach, shown in Fig. 7. There were no visibly detectable differences between the 2 dose distributions, indicating the usefulness of the approach for the purpose of radiation dose calculation.

Figure 7.

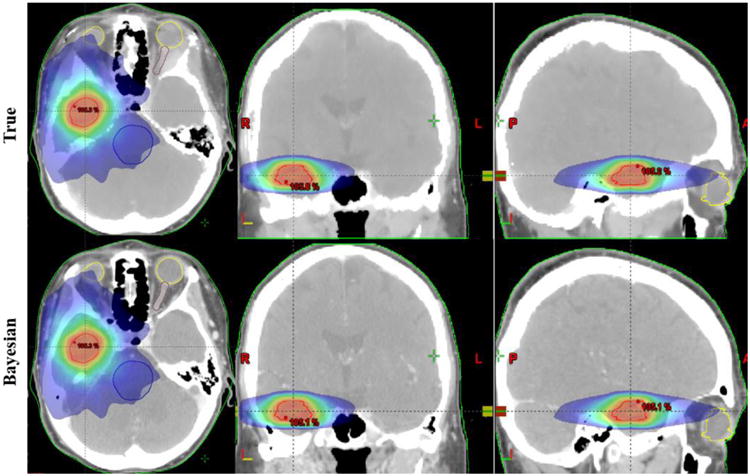
Figure 7

Open in a new tab

3D dose distributions in the axial, coronal and sagittal views, calculated based on the same treatment plan, using real CT and synthetic CT derived from the Bayesian approach.

Discussion

The proposed Bayesian method is novel in several aspects. First and foremost, it combines the disparate information given by MR image intensity and geometry in a unifying framework. Conventional approaches rely on either intensity or geometry alone, each with its respective weaknesses. Second, most conventional intensity approaches attempted to derive a one-to-one global mapping between electron density and MR image intensity, which may not exist after all. In contrast, we work with each voxel individually on a local basis, which greatly simplifies the mapping and also improves specificity. Third, distinct from previous studies based on a deterministic approach, we adopt a probabilistic approach which explicitly recognizes the various sources of uncertainties (such as deformable registration and MR intensity variations), and naturally incorporates them into a coherent Bayesian framework.

The proposed formalism is quite general and can be extended to include multiple MRI sequences. Even with a single conventional T1-weighted MR image, we can already achieve similar accuracy with existing approaches based on multiple MRI sequences. For example, in a previous study, a Gaussian mixture regression model on multiple MRI sequences (T1, T2-weighted and UTE) (Johansson et al 2011) in generating synthetic CT showed a mean absolute HU error of 137 for 5 patients, compared with a slightly smaller error of 126 for 8 patients in the current study. In another study, multiple MRI sequences, including UTE sequence, was used to generate synthetic CT images, based on fuzzy c-means clustering (Hsu et al 2013). The method, which is a form of intensity based approach, had good qualitative similarities with real CT scans. Thus inclusion of MRI with multiple sequences is expected to further improve the performance of our Bayesian approach.

The accuracy of the proposed technique is influenced by a number of factors, such as the potential geometric distortion of MRI, streak artifacts in CT, patient motion during scanning, and uncertainties in image registration. Reducing various artifacts in both MRI and CT (Wang et al 2013, Zhang et al 2011), and limiting patient motion are effective ways to improve the accuracy of the electron density mapping. Also, the differentiation of air from bone in the Bayesian model was dependent on the spread of geometry PDF, which is controlled by varying the standard deviation of the Gaussian kernel that is used as a weighting function in the geometry map. A large spread smears out the tissue interfaces and loses structural details, whereas a small spread results in the dominance of geometry PDF and loss of information from the intensity. In this study, the parameters for determining the spread were heuristically selected to give a good performance overall. In principle, more intelligently selected parameters, e.g., through adaptive weighting in various anatomical regions, may lead to better performance.

Conclusion

We have developed a unifying Bayesian method to derive electron density from standard T1-weighted MRI. By combining both intensity and geometry information into a unifying probabilistic Bayesian framework, we are able to achieve accurate electron density estimation and bone detection from MRI of the head with highly heterogeneous anatomy. This paves the way for accurate dose calculation and generating reference images for patient setup in MRI-based treatment planning.

Acknowledgments

This work was supported partially by funding from the National Institutes of Health (grant no. 5K99CA166186)

References

  1. Berker Y, Franke J, Salomon A, Palmowski M, Donker HCW, Temur Y, Mottaghy FM, Kuhl C, Izquierdo-Garcia D, Fayad ZA, Kiessling F, Schulz V. MRI-Based Attenuation Correction for Hybrid PET/MRI Systems: A 4-Class Tissue Segmentation Technique Using a Combined Ultrashort-Echo-Time/Dixon MRI Sequence. J Nucl Med. 2012;53:796–804. doi: 10.2967/jnumed.111.092577. [DOI] [PubMed] [Google Scholar]
  2. Bowman AW, Azzalini A. Applied Smoothing Techniques for Data Analysis: The Kernel Approach with S-Plus Illustrations: The Kernel Approach with S-Plus Illustrations. Oxford University Press; 1997. [Google Scholar]
  3. Catana C, van der Kouwe A, Benner T, Michel CJ, Hamm M, Fenchel M, Fischl B, Rosen B, Schmand M, Sorensen AG. Toward Implementing an MRI-Based PET Attenuation-Correction Method for Neurologic Studies on the MR-PET Brain Prototype. J Nucl Med. 2010;51:1431–8. doi: 10.2967/jnumed.109.069112. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Chen L, Nguyen TB, Jones É, Chen Z, Luo W, Wang L, Price RA, Jr, Pollack A, Ma CMC. Magnetic Resonance–Based Treatment Planning for Prostate Intensity-Modulated Radiotherapy: Creation of Digitally Reconstructed Radiographs. Int J Radiat Oncol. 2007;68:903–11. doi: 10.1016/j.ijrobp.2007.02.033. [DOI] [PubMed] [Google Scholar]
  5. Devic S. MRI simulation for radiotherapy treatment planning. Med Phys. 2012;39:6701–11. doi: 10.1118/1.4758068. [DOI] [PubMed] [Google Scholar]
  6. Dowling JA, Lambert J, Parker J, Salvado O, Fripp J, Capp A, Wratten C, Denham JW, Greer PB. An Atlas-Based Electron Density Mapping Method for Magnetic Resonance Imaging (MRI)-Alone Treatment Planning and Adaptive MRI-Based Prostate Radiation Therapy. Int J Radiat Oncol. 2012;83:e5–e11. doi: 10.1016/j.ijrobp.2011.11.056. [DOI] [PubMed] [Google Scholar]
  7. Van der Heide UA, Houweling AC, Groenendaal G, Beets-Tan RGH, Lambin P. Functional MRI for radiotherapy dose painting. Magn Reson Imaging. 2012;30:1216–23. doi: 10.1016/j.mri.2012.04.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Hsu SH, Cao Y, Huang K, Feng M, Balter JM. Investigation of a method for generating synthetic CT models from MRI scans of the head and neck for radiation therapy. Phys Med Biol. 2013;58:8419. doi: 10.1088/0031-9155/58/23/8419. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Isambert A, Dhermain F, Bidault F, Commowick O, Bondiau PY, Malandain G, Lefkopoulos D. Evaluation of an atlas-based automatic segmentation software for the delineation of brain organs at risk in a radiation therapy clinical context. Radiother Oncol. 2008;87:93–9. doi: 10.1016/j.radonc.2007.11.030. [DOI] [PubMed] [Google Scholar]
  10. Johansson A, Karlsson M, Nyholm T. CT substitute derived from MRI sequences with ultrashort echo time. Med Phys. 2011;38:2708–14. doi: 10.1118/1.3578928. [DOI] [PubMed] [Google Scholar]
  11. Kapanen M, Tenhunen M. T1/T2*-weighted MRI provides clinically relevant pseudo-CT density data for the pelvic bones in MRI-only based radiotherapy treatment planning. Acta Oncol. 2013;52:612–8. doi: 10.3109/0284186X.2012.692883. [DOI] [PubMed] [Google Scholar]
  12. Keereman V, Fierens Y, Broux T, Deene YD, Lonneux M, Vandenberghe S. MRI-Based Attenuation Correction for PET/MRI Using Ultrashort Echo Time Sequences. J Nucl Med. 2010;51:812–8. doi: 10.2967/jnumed.109.065425. [DOI] [PubMed] [Google Scholar]
  13. Khoo VS. New developments in MRI for target volume delineation in radiotherapy. Br J Radiol. 2006;79:S2–S15. doi: 10.1259/bjr/41321492. [DOI] [PubMed] [Google Scholar]
  14. Klein S, Staring M, Murphy K, Viergever MA, Pluim JPW. elastix: A Toolbox for Intensity-Based Medical Image Registration. IEEE Trans Med Imaging. 2010;29:196–205. doi: 10.1109/TMI.2009.2035616. [DOI] [PubMed] [Google Scholar]
  15. Korhonen J, Kapanen M, Keyriläinen J, Seppälä T, Tenhunen M. A dual model HU conversion from MRI intensity values within and outside of bone segment for MRI-based radiotherapy treatment planning of prostate cancer. Med Phys. 2014;41:011704. doi: 10.1118/1.4842575. [DOI] [PubMed] [Google Scholar]
  16. Lambert J, Greer PB, Menk F, Patterson J, Parker J, Dahl K, Gupta S, Capp A, Wratten C, Tang C, Kumar M, Dowling J, Hauville S, Hughes C, Fisher K, Lau P, Denham JW, Salvado O. MRI-guided prostate radiation therapy planning: Investigation of dosimetric accuracy of MRI-based dose planning. Radiother Oncol. 2011;98:330–4. doi: 10.1016/j.radonc.2011.01.012. [DOI] [PubMed] [Google Scholar]
  17. Lee YK, Bollet M, Charles-Edwards G, Flower MA, Leach MO, McNair H, Moore E, Rowbottom C, Webb S. Radiotherapy treatment planning of prostate cancer using magnetic resonance imaging alone. Radiother Oncol. 2003;66:203–16. doi: 10.1016/s0167-8140(02)00440-1. [DOI] [PubMed] [Google Scholar]
  18. Mazzara GP, Velthuizen RP, Pearlman JL, Greenberg HM, Wagner H. Brain tumor target volume determination for radiation treatment planning through automated MRI segmentation. Int J Radiat Oncol. 2004;59:300–12. doi: 10.1016/j.ijrobp.2004.01.026. [DOI] [PubMed] [Google Scholar]
  19. Stanescu T, Jans HS, Pervez N, Stavrev P, Fallone BG. A study on the magnetic resonance imaging (MRI)-based radiation treatment planning of intracranial lesions. Phys Med Biol. 2008;53:3579. doi: 10.1088/0031-9155/53/13/013. [DOI] [PubMed] [Google Scholar]
  20. Wang H, Balter J, Cao Y. Patient-induced susceptibility effect on geometric distortion of clinical brain MRI for radiation treatment planning on a 3T scanner. Phys Med Biol. 2013;58:465. doi: 10.1088/0031-9155/58/3/465. [DOI] [PubMed] [Google Scholar]
  21. Weltens C, Menten J, Feron M, Bellon E, Demaerel P, Maes F, Van den Bogaert W, van der Schueren E. Interobserver variations in gross tumor volume delineation of brain tumors on computed tomography and impact of magnetic resonance imaging. Radiother Oncol. 2001;60:49–59. doi: 10.1016/s0167-8140(01)00371-1. [DOI] [PubMed] [Google Scholar]
  22. Zhang X, Wang J, Xing L. Metal artifact reduction in x-ray computed tomography (CT) by constrained optimization. Med Phys. 2011;38:701–11. doi: 10.1118/1.3533711. [DOI] [PMC free article] [PubMed] [Google Scholar]

RESOURCES