Simulating Cancer Growth with Multiscale Agent-Based Modeling

Abstract

There have been many techniques developed in recent years to in silico model a variety of cancer behaviors. Agent-based modeling is a specific discrete-based hybrid modeling approach that allows simulating the role of diversity in cell populations as well as within each individual cell; it has therefore become a powerful modeling method widely used by computational cancer researchers. Many aspects of tumor morphology including phenotype-changing mutations, the adaptation to microenvironment, the process of angiogenesis, the influence of extracellular matrix, reactions to chemotherapy or surgical intervention, the effects of oxygen and nutrient availability, and metastasis and invasion of healthy tissues have been incorporated and investigated in agent-based models. In this review, we introduce some of the most recent agent-based models that have provided insight into the understanding of cancer growth and invasion, spanning multiple biological scales in time and space, and we further describe several experimentally testable hypotheses generated by those models. We also discuss some of the current challenges of multiscale agent-based cancer models.

1. Introduction

Increasingly, cancer is understood as a large family of diseases characterized by invasive, uncontrolled cell growth. Genetic mutations are considered to be the initial cause of the abnormal growth of cells, hence the main area of focus has been in investigating the genes involved and the intrinsic cellular processes they affect and regulate throughout tumorigenesis [1]. However, recent research has shown that cancer cells not only influence the microenvironment around them for their benefit, but also engage the stroma and other non-cancer cells to allow for tumor metastasis [2]. This is a complex, bidirectional interactive process, which cannot be easily understood by using conventional wet-lab experiments alone, whether in vitro or in vivo or both. Mathematical models and computation simulations can help overcome these limitations by offering the ability to monitor in real-time, albeit in silico, tumor growth, cellular distribution and movement, and to observe the genetic mutations that lead to aggressive growth and metastasis [3].

Current computational cancer modeling approaches can be divided into three categories: discrete, continuum, and hybrid, i.e., the combination of both (interested readers should refer to [4-9] for in depth discussions on this topic). Briefly, discrete models employ experimentally-derived, computationally-coded rules to define the step-wise or discrete interactions between individual cells and provide insight on tumor microstructure, cell proliferation and death rates, and cell densities. Continuum models represent the tumor as a continuum and give information about the overall tumor morphology and nutrient distribution while neglecting the influences of individual cells in the environment. Hybrid modeling combines aspects of both discrete and continuum modeling to provide a more complete description of the tumor environment. Because discrete and continuum domains are often inescapably linked, directly influencing one another from the viewpoint of an in vivo system, the hybrid modeling approach has become the more desirable choice for many computational cancer researchers [4].

Agent-based modeling (ABM) is a discrete-based hybrid modeling approach, offering many advantages over other methods of studying cancer development [10]. For example, ABM enables the modeler to control the likelihood of genetic mutations and to know which mutations are occurring; this, in turn, allows for simple determination of which cellular phenotypic changes have the largest influence on tumor behavior. There are several types of ABM techniques that have been widely used in cancer research, including lattice-based, lattice-free, Cellular Potts, lattice-gas, and subcellular element modeling methods (detailed discussion of each ABM technique is beyond the scope of this review; see [11] for a thorough review). Each technique has its advantages and disadvantages, and a particular technique may be favored over another depending on the specific cancer problem(s) being tackled. This implies that researchers should choose an ABM technique solely dependent on their research needs. It is also worth noting that, in the past ten years, a number of ABM simulation packages have been developed and applied to cancer research. Major open source package examples include CompuCell3D (http://www.compucell3d.org/), Chaste (http://www.cs.ox.ac.uk/chaste/), Repast (http://repast.sourceforge.net/), and NetLogo (http://ccl.northwestern.edu/netlogo/), among others (see [12, 13] for excellent reviews). These packages have facilitated the overall process of developing an agent-based cancer model and also enabled computational oncologists to focus their time and energy more on the specific cancer problems of interest.

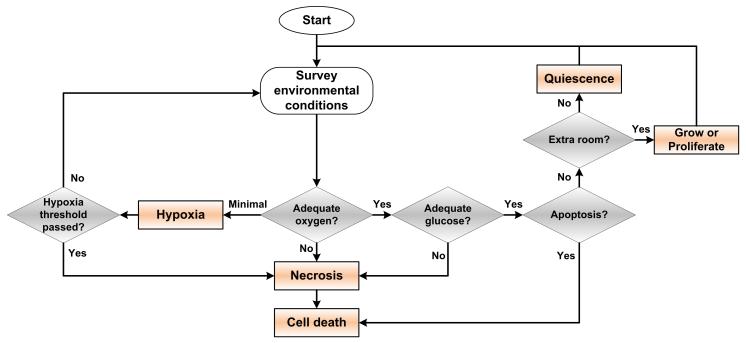
In an agent-based model, each cell is often represented as an agent. The agents have rules that they must follow in the course of a simulation, both for their independent behavior and for interactions between other agents. A description of a simple ABM with minimal rules is described as follows: Agents may receive signals and input from the environment and their neighboring agents, provide output to the environment and their neighbors, and make ‘decisions’ based on the input from around them and their internal, sub-cellular decision making rules. An agent may grow, proliferate, enter a quiescent state, or undergo apoptosis or necrosis in response to surrounding environmental conditions. Cellular proliferation often requires enough room to grow or divide into (a typical assumption for simplifying the development of an ABM), and sufficient nutrients available to maintain cell viability. If nutrients are sufficient to sustain the cell but there is not enough room to divide into, the cell enters into a quiescent state. In conditions where nutrient or oxygen levels are not high enough to maintain cellular viability, cells enter into a hypoxic state. If sufficient oxygen supply is restored, the cell will return to a healthy state; if not, it will undergo apoptosis after a defined length of time. Figure 1 illustrates a flowchart of this simple oxygen-dependent cellular phenotype decision process. More accurate descriptions of the tumor environment and behaviors can be achieved through the additional modeling of more phenotypic factors.

Figure 1.

Flowchart of a simple oxygen-dependent cellular phenotypic decision process.

Recent ABM work has seen the introduction of more complex descriptions of cellular agents, pushing the technical frontier of modeling and mathematical descriptions of cancer behavior towards a more complete understanding [14]. Most agent-based models are computationally intensive because of the (temporal-spatial) fine-resolution they operate on. Currently in the quantitative cancer research field, agent-based models often include components and/or simulate processes that occur at two or more spatial or temporal scales, thus rendering them multiscale models. A multiscale ABM is particularly suitable for exploring the diversity of cellular and molecular dynamic features exhibited at the single cell level, and for quantifying the relationship between the molecular properties of individual cancer cells, microenvironmental conditions, and the overall tumor morphology. In fact, in many cases, cancer simulations should not be limited to a specific biological scale, because cancer is an emergent collective phenomenon [15], dependent on the dynamic interactions of cancer cells and the changing heterogeneous microenvironment [16, 17]. More importantly, cancer development, invasion, and metastasis processes indeed occur across a large scale range, from the molecular and micro-scale with factors such as signaling molecules and cellular competition, to the macro-scale with environmental factors including tissue oxygen concentration and mechanical stresses on the growing tumor, i.e., spanning multiple spatial and temporal scales biologically [4]. In this review, we focus our discussion on multiscale ABM, especially on how this approach has been used to help advance different areas of cancer research towards new experimentally testable hypotheses. Some agent-based models are not specifically labeled with the ‘multiscale’ term; however, since they simulate or predict cancer behavior across different spatial and/or temporal scales, we still introduce them here, but our discussion is limited to the introduction of the most recent, representative multiscale ABM works in the literature. Interested readers can refer to other in depth reviews to have a more comprehensive understanding of ABM and its potential in cancer research [4, 5, 11, 18].

2. Overview of multiscale ABM methods

2.1. Scale ranges

A multiscale cancer ABM attempts to integrate across many spatiotemporal scales (from atomic to molecular, cellular, multicellular, organ, up to multi-organ systems) to provide a more complete and accurate representation of a variety of phenomena including cancer initiation, growth, invasion, and metastasis [4]. We only briefly describe the general methods for modeling cancer behavior on the molecular, microscopic (cellular/multicellular), and macroscopic (organ) scales.

Molecular scale modeling involves modeling the bulk average values of molecular interactions. This can include averaged receptor-ligand interactions, oxygen and nutrient concentration effects on cells, and cell-cell signaling molecule concentrations. Signaling molecules trigger cascades that cause changes in cell behavior, and oxygen and nutrient concentrations can allow cells to remain healthy or become hypoxic when they are reduced. These molecular interactions are commonly the smallest scale modeled in agent-based cancer models, and are usually represented using ordinary differential equations (ODEs) to describe the rate at which they are consumed or produced.

Microscopic scale interactions occur between cells. Cells must coexist in their environment, and both their movement and proliferative expansion is limited by their proximity to neighbors. It is at the micro-scale where cancer modeling allows for a mutation of healthy cells into cancerous phenotypes. Micro-scale modeling can be done using ABM (where each cell is modeled individually) or by describing local conditions using partial differential equations (PDEs) to calculate local environmental changes. Agents have rules that define interactions with their environment and other agents, depending on the availability of resources necessary for their survival, such as oxygen and glucose. Agents can interact with each other, influence their microenvironment, undergo taxis and mitosis, enter quiescence or die from hypoxia or apoptosis. Determination of agent behavior is based on the local environmental conditions and molecular signaling, and the biological rules posed on the agents by the modelers.

Macroscopic scale modeling involves factors that encompass the entire tumor tissue, hence spanning across the scale of many agents. Diffusion of nutrient, oxygen, and signaling molecules such as hormones, tumor tissue pH, and chemotherapy drug distribution over the entire tumor can be computed and provided as feedback to the microenvironment. Tumor morphology and vascularization are also sometimes modeled on the macro-scale, providing information on the extent of metastasis and nutrient availability. Distribution of molecular availability across the model is computed using PDEs, which can include terms to account for interactions on the micro-scale such as cellular consumption of available resources. Macro-scale models can provide information to a micro-scale model such as agent-based models, or they can treat the tumor as a continuum and simply ignore the interaction effects of individual cells. This is often used to model general patterns of growth, including the total cell number, and to determine the onset of metastasis [19]. Here, continuum modeling is acceptable because as scales become larger cellular responses can be treated as gradients in response to substrate gradients.

Scale ranges tend to correlate with time ranges, with molecular scale reactions happening over microseconds and nanometers, while macro-scale interactions can take days to years and happen over millimeters to centimeters. Because the range of interactions spans many orders of magnitude, reactions from the smallest scales can often be assumed to be at steady state relative to large-scale reactions. This eliminates the need to solve, e.g., the ODEs associated with molecular interactions, reducing computational loading and allowing for more detailed modeling of interactions at the larger scales. Instead, smaller reactions are implicitly included within the larger scales, cells undergo cellular respiration and all other normal processes, but the molecular machinery behind this is not explicitly solved for in the model. More importantly, this makes larger models (i.e., up to larger sized tumor tissues) with more agents computationally feasible.

2.2. Hybrid modeling

In hybrid ABM, only the most important micro-scale effects are modeled, while effects that can be approximated using continuum descriptions are described using PDEs and solved across the entire tumor rather than at each agent individually. Parameters including oxygen diffusion, nutrient diffusion, and hormonal distribution are often modeled through diffusion from molecularly rich regions (i.e. sources) such as vascularization or the edge of the tumor. It is often only necessary to discretize part of the tumor region [20]. Discrete modeling is necessary when parameters, including the effect of mutation-induced, more aggressive phenotypes on metastasis or cell and extracellular matrix (ECM) interaction, are to be studied. It is well established in oncology research [21, 22] that changes on the cellular level lead to tumor growth and metastasis, thus discrete modeling is crucial for providing a virtual test-bed that can recreate this multi-step process at least in part. By hybridizing a discrete model into a continuum environment, a more complete description of the tumor morphology is achieved, resulting in higher accuracy of model predictions while achieving lower computational costs to run simulations [23].

Advances in computer hardware are bridging the gap between continuum and discrete modeling in computational costs, reducing computation times and allowing for the incorporation of more agents in hybrid models. For example, parallel computing based on the use of graphics processing unit (GPU) can significantly reduce simulation run times. A thread is a small, independent task that can be executed through a core in a processor chip, and only one thread can be executed through a core at a time; chips with multiple cores can run threads in parallel, with a different thread running in each core simultaneously. GPU utilization allows for orders of magnitude more threads, although this comes at the cost of rewriting code to run on the GPU. An example of using GPU processing with a Fermi GeForce GTX 480 (480 cores) for simulating glioblastoma progression has been provided in a recent ABM work [24], where a 30-fold increase in processing speed has been reported. Massive parallelization of computations comes with large increase in simulation speed, but at the cost of more difficult debugging. In brief, coding for minimized runtimes and maximum model complexity is a difficult skill, and must be balanced in time dedicated to coding and maintenance time vs. time saved to run the simulations.

3. ABM applications

3.1. Molecular signaling

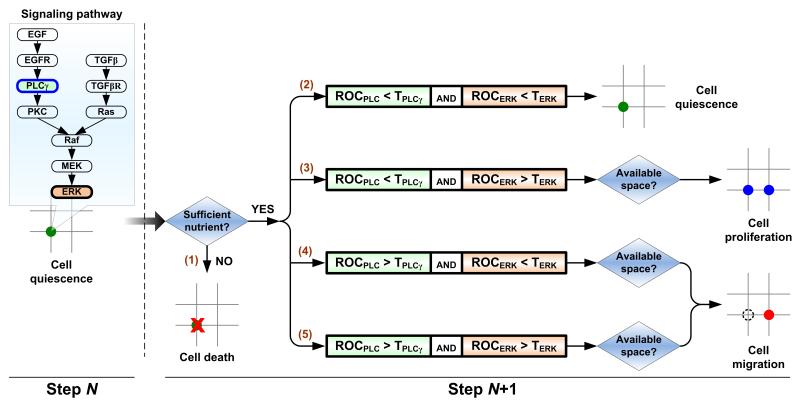
Molecular signaling plays a crucial role in tumor development, and as such it has been included in ABM to study in silico how signaling molecules influence carcinogenesis. Wang and Deisboeck et al. explored the role of EGFR (epidermal growth factor receptor) and ERK (extracellular signal-regulated kinase) pathways in non-small cell lung cancer (NSCLC). In their modeling approach, each agent is equipped with a self-maintained signaling network. As a simulation progresses, cells in distinct locations experience different external microenvironments, which in turn influences internal signaling network dynamics, potentially changing the cell’s phenotype. They found that in a rich epidermal growth factor (EGF) environment, this EGFR-ERK pathway gave rise to a more migratory cell phenotype than a proliferative one [25]. Later, the group added transforming growth factor beta (TGFβ) to the signaling milieu and examined how a combined stimulus of EGF and TGFβ affects the resulting tumor outcome [26]. This cross-talk pathway was described using a system of 26 ODEs solved simultaneously to determine signaling molecule concentrations at each time step for each individual cell. The model found that increasing EGF results in a more invasive phenotype, while increasing EGF concentration together with TGFβ concentration further increased the agents’ sensitivity to changes in the environment that could trigger invasiveness. They also presented a method to link molecular and microscopic scales: an experimentally supported molecularly-driven cellular phenotypic decision algorithm that determines cell phenotypic transitions upon molecular changes. Figure 2 depicts a brief schematic of this cellular phenotype decision algorithm. Recently, Wang and Deisboeck et al. also investigated, through a combined multiscale ABM and cross-scale target evaluation approach, which components of the implemented EGFR pathway in a NSCLC model are most crucial for the signaling cascade, and hence would have the highest therapeutic effect if targeted directly [27-31]; they found that ERK proved to be the highest ranked molecular target. In addition, other groups have used this type of ABM to examine the effects of EGFR targeted therapy in brain cancer [32].

Figure 2.

Cellular phenotypic decision algorithm. Decisions are made dependent of the molecular dynamics of PLCγ and ERK, two downstream signaling molecules of EGFR, for scenarios (2)-(5). Experimental studies have shown that the transient acceleration of accumulating PLCγ levels leads to cell migration [91], while that of ERK leads to cell replication [92]. Therefore, in our model, the rate of change of PLCγ determines the cellular migration decision, and the rate of change of ERK dictates the cellular proliferation fate. Beginning with a quiescent cancer cell at step N, its phenotype at step N+1 is determined as follows: (1) cell death if the on-site glucose level is insufficient; dependent on the molecular dynamics of PLCγ and ERK, (2) the cell will remain quiescent if the rate of change of both PLCγ and ERK remain below their corresponding thresholds; (3) the cell will proliferate (and a new cell will then occupy an adjacent free location) if only the rate of change of ERK exceeds its threshold; (4-5) the cell will migrate to the adjacent free location that has the greatest cue weight if the rate of change of PLCγ (regardless of ERK) exceeds its threshold.

3.2. Cellular metabolism

Cancer cells have a tendency to enter glycolytic metabolism, which results in faster oxygen depletion in the tumor environment and an accumulation of H⁺ in the tumor. It is still subject to debate whether this happens in all tumors [33], but favoring glycolytic metabolism is known to occur in most types of cancer [34]. Accumulation of H⁺ lowers the pH in the tumor; H⁺ leaves the tumor through diffusion to the vasculature and is then removed with other cellular waste products, or it infiltrates into the surrounding tissues. In turn, lowering pH in surrounding tissue can acidify the ECM and lead to collagen degradation, and has been shown to increase tumor invasiveness into the acidified regions [35]. The effect of lowered pH on the tumor environment has been examined using hybrid ABM, where cellular apoptosis due to pH decrease is determined by rules incorporated into the agents [36]. Agents can also evolve an acid resistant phenotype. The model agrees with the experimentally-derived theory that cancer cells are driven to glycolytic metabolism because of a lack of oxygen, and glycolytic cells will eventually dominate the environment, although there will be less total cells due to cell death caused by the hostile, acidic environment.

Gatenby et al. have extensively studied the effects of glycolytic metabolism in the presence of hyperplasia and increased acid resistance in cells through a hybrid ABM [37, 38]. Cellular response to oxygen and glucose levels was represented as a function of ATP production from the available resources, and a cell can die if it becomes ATP deficient below a threshold, H⁺ levels become too high, or if it detaches from the basement membrane and is not hyperplastic. They demonstrated that the progression to glycolytic metabolism is starting with hyperplastic growth away from the basement membrane and oxygen supply, resulting in selective advantages in cells with higher ability to adapt to changes in glucose and oxygen supply, as well as pH. Low oxygen supply favors a transition to anaerobic metabolism, which leads to higher glucose consumption and increased H⁺ levels. This results in decreased pH in the tumor environment, transitioning to a selective pressure that favors acid-resistant phenotypes. This glycolytic, acid resistant phenotype possesses an advantage over healthy cells as it creates an acidic local environment, damaging the healthy cells but not the acid resistant cells, and can lead to proliferation and an invasive phenotype. Using a combined experimental and ABM approach, they have also investigated the progress of tumor resistance to chemotherapy (both phenotypically and environmentally) [39], and concluded that the optimal therapy must look beyond the specificity and immediate cytotoxicity of a chemotherapeutic drug.

This phenotypic evolution was also observed by Gerlee and Anderson, who saw similar behavior in a somewhat different model [40]. Their model also included the effects of ECM density on tumor progression while neglecting the effects of basement membrane attachment. They found that dense ECM makes the transition to a glycolytic phenotype more favorable, and propose that the dense ECM prevents cells from moving out of the oxygen-poor region, resulting in a stronger selective force for the glycolytic phenotype. In fact, this model appears to suggest the mechanical constraint from ECM may play a critical role in this phenotypic transition. They also demonstrate that oxygen concentration plays an important role in tumor morphology, where high oxygen concentration results in smooth morphology and low oxygen concentration resulting in ‘fingering’ morphologies. The fingering morphology is thought to be a result of cells gaining an advantage by moving away from the nutrient and oxygen starved center region of the tumor and towards nutrient and oxygen sources.

3.3. Mutation-induced phenotypic changes

Cancerous cells have many phenotypic behaviors divergent from healthy cells [41]. In ABM, the decision of which phenotypic state to enter at each time step is based on rules programmed into the agents. These rules rely on inputs from the environment at both micro- and macro-scales, and are represented as numerical values in the model. Oxygen levels are known to be much lower in tumors than healthy tissues, with levels dropping as low as 5%-30% in the necrotic center [42]. Cells enter hypoxia when oxygen levels drop below a defined threshold, and will enter necrosis if they remain at that level for too long, or they can return to being healthy if oxygen levels return to normal prior to the onset of necrosis. The decision to enter mitosis is based on if the cell is mature enough to divide and if there is room for its progeny or daughter cells. Often, agents experience environmental stimulation and signaling with conflicting behavioral responses; these interactions can be dealt with by implementing a hierarchal decision chain or a neural network logic system. Using hybrid ABM, Gerlee and Anderson have investigated how the evolutionary dynamics of tumor growth respond to the microenvironment, using the output of an intracellular neural network to determine cell phenotype [40, 43, 44]. An important contribution from their work is that they developed an approach to deliberately circumvent the considerable complexity of the multiscale tumor system. That is, instead of defining the mapping from environment to phenotype, they used an evolutionary algorithm to evolve mappings that give rise to the resulting growth rate and tumor morphology (branched or compact). Aruajo et al. studied how the unequal division of chromosomes can lead to cancer phenotype in cells [45]. They found in their simulations that uneven segregation of chromosomes gave rise to a group of cells that contained an abnormal number of chromosomes and exhibited an increase in growth.

3.4. Angiogenesis

Angiogenesis is the process of new vascularization growing from existing vessels, and is a critical step in tumors progressing from benign to malignancy. Competition for nutrients has been established to drive the natural selection of more aggressive phenotypes, while vascularization provides the primary route for long-range metastasis to occur [46]. Angiogenesis also provides more resources to the tumor, allowing growth beyond the maximum size as limited by diffusion in avascular regions. Vasculature surrounding the tumor tissue is sensitive to tumor angiogenic factors (TAF) released by the tumor tissue that propel the endothelial cells to initiate growth towards the tumor cells [47]. This property of induction of tumor vasculature movement in response to TAF was investigated by Anderson and Chaplain using a 2D hybrid model of angiogenesis back in 1998 [48]. This was deemed the seminal work in modeling tumor-induced angiogenesis. In particular, the discrete modeling part, derived from a discretized form of the continuum modeling part, allowed for a closer examination of how individual endothelial cells located at the tip of the capillary sprouts gave rise to a variety of branching patterns, anastomosis (formation of loops), formation of “brush border” effect (increase in capillary sprouts near the tumor), and the overall dendritic constitution of a capillary network. Recent work in ABM modeling has provided additional insight into the biology of angiogenesis and its effects on tumor morphology and metastasis. Sun et al. examined the progression of brain tumors under tyrosine kinase inhibitors (TKI) treatments in a model that took into account the effects of angiogenesis and EGFR pathways [32]. They observed that angiogenesis seems to play a dual role in maintaining the tumor cells: the immense vascularization plays a positive role in controlling the growth of tumor cells as a higher amount of TKI can be delivered through the vessels, thus inhibiting the growth of tumor cells; but at the same time, more vascularization also means that tumors have greater access to oxygen and nutrients that helps them to thrive in the long run. Olsen and Siegelmann have recently developed a 3D agent-based model to study tumor growth and angiogenesis on three scales, i.e., molecular, cellular, and tissue scales, in different types of cancers [49]. Even with a new, simplified abstraction of the complex tumor growth environment, the model was still able to produce similar results to previous angiogenesis models.

Frieboes, Cristini, and Lowengrub et al. have recently developed a series of hybrid vascularized tumor growth models which include an agent-based model for tumor cells that is coupled directly to a continuum model by balancing the exchanges of mass and momentum between the discrete and continuum representations of tumor tissue [50-52]. Angiogenesis in these models was described also using a continuum-discrete representation that accounts for chemotaxis of vascular endothelial cells in response to vascular endothelial growth factor (VEGF, a tumor angiogenic regulator), haptotaxis, vessel branching, looping and anastomoses, and cell substrates released from functional vessels. When cells are in regions with sufficient nutrients, their proliferation is up-regulated and motility is down-regulated. When their density exceeds a critical threshold, they are converted back to the continuum, and then tumor microsatellites form around the neovasculature. This approach is more advanced than many other hybrid approaches, but overall the model is still phenomenological in that the functional relationships between the parameters and variables used at the continuum level involve quantities that are not directly measured at the cellular scale.

3.5. Microenvironment

ECM is known to play an important role in carcinogenesis and metastasis. Transition to the carcinogenic phenotype is a complex process, involving changes in focal adhesion kinase, integrin composition and expression, as well as degradation of ECM through the production of specific enzymes [53]. Using a hybrid model, Anderson demonstrated that although cell-cell interactions were important at the early phase of tumor penetration into healthy tissue, ultimately it was the cell-matrix interactions that governed the subsequent growth and invasiveness of the tumor cells [54]. Many tumors grow in tissues containing dense cellular packing and ECM, while others develop in very different environments, each requiring distinct modeling representations of their environment. ABM has also been used to predict tumor sizes of ductal carcinoma in situ (DCIS), based on patient histopathology data [55]. A follow-up study improved the patient-specific calibration method, and made better quantitative predictions of individual patient’s tumor growth [56]. Chapa et al. used an agent-based model to study the long-term transition of normal mammary epithelium cells into carcinogenic cells over a period of 40 years of simulated time [57]. This required integrating extensive rules based on peer-reviewed mechanisms, at the cellular and molecular levels, in the pathogenesis of ductal epithelial breast cells. The model was able to replicate in vivo cellular dynamics seen during the menstrual cycle, pregnancy and cancer. Consequently, it has the potential to serve as a platform to study breast cancer dynamics over long periods of time.

To provide insights into the influence of the environmental changes on cellular phenotypic selection, Anderson et al. [58] allowed for 100 possible different phenotypes in their hybrid model, each equally likely to occur due to genetic mutations. They found that only a few phenotypes dominated in the natural selection process. When resources are plentiful, cells do not gain a selective advantage by out-competing their neighbors; whereas when resources are reduced below the level necessary for all cells in the tumor to remain viable, cells must compete to survive. Also, a reduced resource concentration drives stronger competition and can result in more extreme spatial formations or ‘fingering’ behavior, while plentiful resources result in little competition and natural selection, resorting in more uniform phenotypic distribution in the tumor environment, and therefore a smoother tumor surface profile as there is no need for cellular competition over resources. In the model, the boundary conditions for the PDEs that are used to solve for resource gradients at the macro-scale are easily modified at the blood-tumor interfaces, representing any reasonable resource availability the modeler would like to examine.

Mechanical loading on cells due to ECM irregularity and the corresponding cytoskeletal loading variation have been shown to have an impact on gene expression and cell signaling, and can result in increased cellular proliferation. The effect of these mechanical forces on driving cellular proliferation towards tumorogenesis and cellular behavioral viability was examined using ABM by Werfel et al. [2]. In this model, cell growth and apoptosis were determined by external forces experienced by the cell, where tension forces increased the likelihood of cellular proliferation and compression increased the likelihood of apoptosis. This model demonstrated the biologically observed behavior that a genetic change is not necessary for cancerous behavior in cells, and that some cancer cells transplanted into a healthy tissue environment can revert back to a healthy, normal phenotype. As such, genetic modifications are not necessary for uncontrolled growth, but they can increase proliferative behavior and can lead to increased genetic modifications, often resulting in progression to a more aggressive or even a metastatic phenotype. This model provides interesting insights into how gene overexpression, as opposed to genetic mutation, can play a role in carcinogenesis, and how environmental variability can contribute to self-determined cellular behavior.

3.6. Metastasis

Metastasis is one defining feature of cancer, and is a leading cause of death in most cancer patients [59]. Metastasis of cancer cells is a complex process that begins with loss of adhesion to neighboring cells and unrestrained cell division, and can occur where one cell leads the movement of a group of cells [60]. Wynn et al. studied this movement of cells using an ABM approach. They discovered that the leader cell and the cells following it display a directed movement, which was enhanced when the leader cell preserved cellular contact with the followers. Interestingly, this finding is consistent with a recent forward-looking discussion on the interactions of cancer cell populations [61] and a more recent experimental report on collective invasion through cell-cell interactions in breast cancer [62]. All these lines of work suggest a novel cancer therapeutic strategy: in order to have a better controlled tumor system, rather than targeting random cancer cells within the main tumor mass, one could try to first slow down or even redirect the leading cohort of mobile cells away from physiologically critical or surgically not readily accessible tissue areas.

3.7. Cancer stem cells

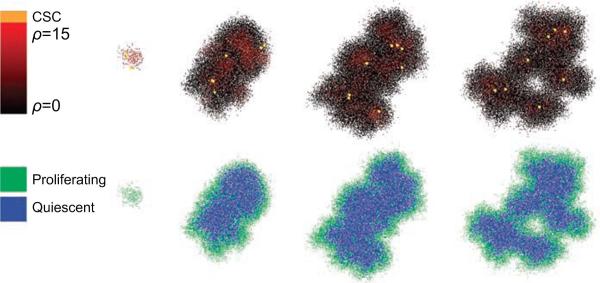
Cancer stem cells (CSCs) are a minor population of tumor cells that possess a cancerous genotype as well as the capability of stem cells to differentiate into many types of cells. They are immortal and can divide asymmetrically, i.e., one being a progenitor cell and the other remaining a stem cell. CSCs are resistant to chemotherapy, and are therefore thought of as a potential cause of tumor recurrence and metastasis after therapy [63]. Recently, the role of CSCs in resistance to chemotherapy has been investigated experimentally in more detail [64, 65]. Biava et al. developed an agent-based model incorporating different conditions that can give rise to CSCs and examined the relationship between these conditions and cancer progression [66]. This model can be used by physicians to predict the optimal dosage size and frequency of chemotherapy that will be most effective in treating CSCs. Enderling et al. also developed a series of ABMs of tumor growth comprised of cancer cells with limited replicative potential, unlimited replicative potential, and CSCs [67-69]. Their simulations showed that tumors formed without unlimited replicative potential cancer cells will inevitably die out; hence, CSCs are necessary for tumor initiation and continued malignant growth. Figure 3 shows an example of a simulated metastatic tumor growth with cancer stems cells. One important finding from their research is that spontaneous cell death due to different forms of cancer therapies can surely reduce the number of cancer cells in the short-run, but will facilitate tumor progression by releasing CSCs to the remaining tumor in the long-run. This finding has clear implications for the clinical setting. For example, the phenomenon of accelerated recurrence following chemotherapeutics and radiation can be explained by the proliferation of remaining residual CSCs (i.e., those CSCs that are not killed by the initial therapeutic regimen).

Figure 3.

Cancer stem cells (CSCs) involved metastatic tumor morphologic evolution at different time points. Spatial distributions of proliferation capacity and proliferation/quiescence state within the growing tumor are shown. ρ: proliferation capacity. Reproduced with permission from [68].

3.8. Cancer treatment

The effects of surgical and radiation treatments commonly used to treat carcinomas have also been explored using ABM. Surgical tumor excision leaves a fluid-filled wound where the tumor was excised, which any residual cancer cells missed during the operation can exploit to facilitate local regrowth and eventually, distant metastasis. The fluid region of an operated tissue provides lower mechanical resistance to metastatic cells and can induce higher nutrient gradients during the healing process. The complex interaction between mechanical forces, chemoattractants, and ECM components is still not fully understood and continues to be studied in vitro [70]. ABM modeling has provided valuable insights into metastasis in surgical wounds. Enderling et al. studied tumor recurrence after surgical excision and found that any remaining cells should often result in tumor recurrence and further progression along the mutation pathway, but that treatment with adjuvant radiation has a high chance of killing any remaining cancerous cells [71]. This demonstrates in silico the advantage of adjuvant radiation treatment over traditional radiation treatment methods and, more generally, the importance of radiation treatment after surgical excision to ensure all carcinogenic cells are eradicated. Mukhopadhyay et al. also used ABM to study effects of ionizing radiation on human mammary epithelial cells (HMEC) and have verified the model through independent in vitro experiments [72]. However, using this integrated system, they found that ionizing radiation may increase malignancy of HMEC.

The effects of chemotherapeutic treatment and hypoxia on the tumor microenvironment were investigated using hybrid multiscale ABM by Powathil and Chaplain et al. [73]. By including the cell cycle stages in the model, they were able to look at the effects of cell cycle dependent chemotherapy agents in cell-kill treatments, as well as the effects of hypoxia on cell cycle arrest. Many modern chemotherapy drugs act through the interruption of a specific phase in the cell division cycle, but hypoxia can induce quiescence, resulting in reduced cellular division and inhibition of effective treatment using these drugs. This model incorporated a six-variable approach developed by Tyson and Novak [74, 75], using ODEs to calculate the concentration profile of five key mammalian proteins and the cell mass throughout the cell cycle. It was determined that oxygen diffusion limitations result in heterogeneity in HIF-1 α (a hypoxia inducing factor), leading to heterogeneity in cell cycle distribution and thus heterogeneity in successful cell-kill treatment. Non-hypoxic cells within the drug diffusion limit responded better to treatment, resulting in redistribution of oxygen and hypoxic regions upon cell death. This complex redistribution of spatial dynamics within the tumor suggests an optimized timing between treatments. A better understanding of these dynamics should help advance chemotherapy towards patient-specific treatment.

3.9. Immune response

Recently, ABM has been employed to study immune responses against a number of different tumors, improving the efficacy of anti-cancer vaccines. This is currently a dynamic research area partly because performing in silico experiments not only helps to relieve the cost in terms of time and money, but also provides a platform to acquire difficult to measure responses in vivo [76]. ABM has been used to study anti-cancer vaccines that would prime the immune system of humans, specifically cytotoxic T lymphocytes (CTL), against newly forming tumors even before a clinical diagnosis has occurred [77]. A hybrid agent-based model has been developed that has the ability to recreate wet-lab experiments and predict the minimum number of such vaccinations required for prevention of lung metastases in vivo [78]. The same group had earlier developed an agent-based model called SimTriplex which elucidated the immune response elicited by the anti-cancer vaccine Triplex [79]. ABM has also proved its efficacy in studying immune responses for conditions for which no known animal model exists. Through in silico experiments, Pappalardo et al. have demonstrated the importance of CD137, selectively expressed on the surface of tumor endothelial cells [80], with the infiltration of CTLs into the tumors dependent on this molecule [81]. Some groups have also focused on improving existing agent-based models to incorporate more detailed immune responses in order to recreate and eventually to better understand a phenomenon that occurs in vivo. For instance, to recreate in silico the response of a peptide vaccine in cancer immunotherapy, Preissner et al. have developed a series of agent-based models taking into account real amino acid sequences of immune receptors and their ligands, thereby increasing the capability of such a computational model to predict real life events [82-84].

4. Discussion and current challenges

As described above, multiscale ABM is now widely used in the field of quantitative cancer research. However, given their extensive computational demand ~ a serious shortcoming of ABM ~ agent-based models should be developed as complex as necessary yet as simple as possible with the help of experimental and/or clinical data. There are many challenges researchers may face in pursuing and applying this type of integrated experimental and systems modeling approach in their research, ranging from access to relevant biomedical data to the development of data standards that foster transparency and facilitate exchange of input data and results [85]. In the following, we focus on discussing two of these challenges with the hope of helping researchers to better design and refine their modeling strategy; if interested, the reader can refer to reviews elsewhere (e.g., [4]) to have a more detailed understanding of the challenges involved.

4.1. Choice of variables for model inclusion

In designing biomedical experiments, interactions between experimental parameters should be considered. This is also true in in silico modeling, as interactions between variables included in models can lead to deceptive conclusions if the results are not analyzed correctly [86]. Often modelers leave out some variables that could be included in order to focus on the variables that are thought to have the most influence on tumor growth and metastasis. Conveniently, this also helps to reduce computational loading, allowing for more trials to be run with the model in the same timeframe, possessing less and sometimes scarce high-performance computing resources. However, to mitigate the risk of bias, choosing model variables must be performed in an evidence-based manner, either from available proven data (or models) or through independent experiments. Also note that some factors/variables may overlap in their functions in a model. For example, decreasing the cellular rate of oxygen consumption has the same (and thus potentially additive) effect as increasing the concentration of oxygen available to the tumor through diffusion. It is known that the limiting factors on tumor growth are oxygen and nutrient diffusion, so it is common to only include these two chemical gradients at the beginning. When more experimental data are available to use, the model can then be extended to include more variables to describe the new data.

4.2. Advanced multiscale modeling techniques

In fact, while rendering models to be predictive is often if not always difficult, functionally and appropriately linking biological processes that occur at different scales adds another layer to this complexity because multiscale models need to quantify the parameters and relationships on and across scales [4]. As such, the field of cancer modeling desperately needs the development of new, highly innovative multiscale modeling methods. Other than the heterogeneous multiscale method [87] and the equation-free approach [88] that have been discussed elsewhere, Lowengrub et al. have been developing a new theoretical upscaling framework based on dynamic density functional theory (DDFT) [89] to analyze and quantify the complexity associated with correlations in heterogeneous tumor tissues. In contrast to the standard mean-field approximations commonly used in current hybrid tumor models, the DDFT can capture multiple sources of nonlinearity both in the equations and from the spatiotemporal heterogeneity of soft tissue and its mechanics. Thus, the DDFT framework has the potential to provide a natural way to account for elasticity in soft heterogeneous tissues, such as tumors. As a first attempt focusing on only one cell species, Lowengrub et al. extended DDFT to tumor growth by incorporating cell density correlations and birth-death processes (i.e., cell proliferation and death) into the traditional DDFT framework to link cell- and tissue-scale tumor behavior [90]. While already promising, this DDFT-based multiscale approach will need to account for different cell species and lineages as well as for molecular signaling as an immediate next step, and should be further tested and validated against experiments in vivo.