Evidence from mathematical modeling that carbonic anhydrase II and IV enhance CO₂ fluxes across Xenopus oocyte plasma membranes

Abstract

Exposing an oocyte to CO₂/HCO₃⁻ causes intracellular pH (pH_i) to decline and extracellular-surface pH (pH_S) to rise to a peak and decay. The two companion papers showed that oocytes injected with cytosolic carbonic anhydrase II (CA II) or expressing surface CA IV exhibit increased maximal rate of pH_i change (dpH_i/dt)_max, increased maximal pH_S changes (ΔpH_S), and decreased time constants for pH_i decline and pH_S decay. Here we investigate these results using refinements of an earlier mathematical model of CO₂ influx into a spherical cell. Refinements include 1) reduced cytosolic water content, 2) reduced cytosolic diffusion constants, 3) refined CA II activity, 4) layer of intracellular vesicles, 5) reduced membrane CO₂ permeability, 6) microvilli, 7) refined CA IV activity, 8) a vitelline membrane, and 9) a new simulation protocol for delivering and removing the bulk extracellular CO₂/HCO₃⁻ solution. We show how these features affect the simulated pH_i and pH_S transients and use the refined model with the experimental data for 1.5% CO₂/10 mM HCO₃⁻ (pH_o = 7.5) to find parameter values that approximate ΔpH_S, the time to peak pH_S, the time delay to the start of the pH_i change, (dpH_i/dt)_max, and the change in steady-state pH_i. We validate the revised model against data collected as we vary levels of CO₂/HCO₃⁻ or of extracellular HEPES buffer. The model confirms the hypothesis that CA II and CA IV enhance transmembrane CO₂ fluxes by maximizing CO₂ gradients across the plasma membrane, and it predicts that the pH effects of simultaneously implementing intracellular and extracellular-surface CA are supra-additive.

in the two companion papers, we studied the effects of the cytosolic enzyme carbonic anhydrase II (CA II) and of the GPI-linked extracellular CA IV on enhancing CO₂ fluxes across the plasma membrane (14, 15). We assessed these fluxes by using pH microelectrodes to measure simultaneously intracellular (pH_i) and surface pH (pH_S) as we added or removed extracellular CO₂/HCO₃⁻. For pH_i measurements, the two key quantities that reflect the CO₂ flux were the maximal rate of pH_i change (dpH_i/dt)_max—negative for CO₂ influx and positive for CO₂ efflux—and the time constant for pH_i decline (τ_pHi). For pH_S measurements, the two key quantities that reflect the CO₂ flux were the maximal change in pH_S (ΔpH_S)—the pH_S spike, positive for CO₂ influx and negative for CO₂ efflux—and the time constant for the decay of pH_S from its most extreme value (τ_pHS). We found that both CA II and CA IV increase the flux of CO₂ across the plasma membrane by maximizing transmembrane CO₂ gradients. We reasoned that (dpH_i/dt)_max and ΔpH_S provide intuitive information on the effects of each of these enzymes on CO₂ fluxes only when the measurements are “trans” to (i.e., on the opposite side of the membrane from) the added enzyme. When we assess cytosolic CA II, ΔpH_S (i.e., measured “trans” to CA II) can reveal the effects of CA II in enhancing CO₂ fluxes, whereas (dpH_i/dt)_max would reflect changes in CA II activity even without a change in CO₂ flux. However, we found that the GPI-linked CA IV is present not only on the extracellular surface but also in an equivalent of a cytosol-accessible compartment. Thus, for CA IV as expressed in oocytes, both pH_i and pH_S electrodes are “cis” (i.e., on the same side of the membrane as the CA IV) and “trans” to the CA IV. Nevertheless, we reasoned that decreases in τ_pHi and τ_pHS provide intuitive information on the effects of CA IV on CO₂ fluxes.

In the preceding two papers, we used mathematical simulations to help us understand how CA II (14) or CA IV (15) influences CO₂-induced pH_i and pH_S transients when we alter the experimental protocol. These protocol changes included raising levels of CO₂ in the bulk extracellular fluid (BECF), increasing the depth of penetration of the pH_i microelectrode, and varying the concentration of the extracellular HEPES buffer. The purpose of the present paper is to describe underpinnings of the mathematical model that we exploited in the two companion papers.¹

Several investigators have used mathematical models to study CO₂ movements across the cell membrane. In 1976, Boron and De Weer developed a compartmental model that predicted for the first time the pH_i time course² caused by the passive flux of CO₂, and the passive flux of HCO₃⁻ as well as the active extrusion of H⁺, across the plasma membrane (5). In the same year, Gros and coworkers (11) developed a model of facilitated CO₂ diffusion in phosphate solutions. They used the model to predict the steady-state fluxes and concentrations of the solutes of interest, concluding that CA promotes the diffusion of HCO₃⁻ and protonated phosphate in the same direction as CO₂, as well as the diffusion of deprotonated phosphate in the opposite direction, thereby facilitating CO₂ diffusion (11). In 2000, Geers and Gros (10) employed a compartmental model to describe the diffusion of CO₂ and lactic acid from skeletal muscle to erythrocytes as blood moves along a capillary. Spitzer and coworkers (23) studied the role of intracellular CA in regulating H⁺ diffusion in rabbit ventricular myocytes with the aid of a two-dimensional model of diffusion of intracellular H⁺ from a constant source. They employed the model to estimate the apparent intracellular H⁺ diffusion coefficient, finding that CA increases the mobility of H⁺ by a factor of ∼6. More recently, Swietach and colleagues (24, 25) developed reaction-diffusion spatio-temporal models to study the role of the cancer-associated extracellular CA IX enzyme in three-dimensional tumor cell growths. These authors concluded that CA IX plays a key role in spatially regulating pH_i and extracellular pH by facilitating CO₂ removal. Note that none of these models considers 1) the diffusion of CO₂ through the cytosol or 2) a multitude of buffers.

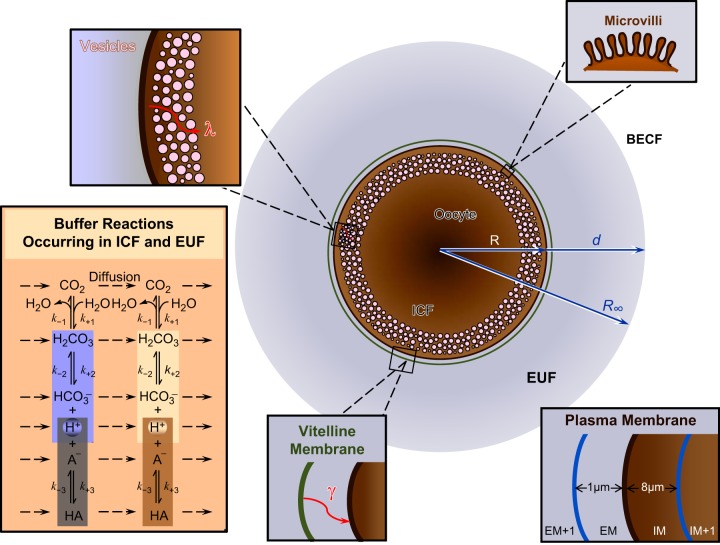
In this third and final paper of this series, we extend the reaction-diffusion mathematical model of CO₂ influx into a Xenopus oocyte, introduced in Somersalo et al. (22). The model assumes that the oocyte is a perfectly symmetric sphere, surrounded by the extracellular unconvected fluid (EUF), which in turn is surrounded by the BECF. In both EUF and intracellular fluid (ICF), the model includes the CO₂/HCO₃⁻ buffer pair as well as a multitude of non-CO₂/HCO₃⁻ buffer pairs. The model (as presently implemented) permits only the movement of CO₂ across the cell membrane. Although valuable and capable of making important theoretical predictions, this model, in its original state, cannot quantitatively reproduce some of the salient features of the measured pH_i and pH_S transients in the two accompanying papers on CA II and CA IV. Therefore, our goal in the present study is to refine the model by Somersalo et al. to create an enhanced version (Fig. 1) that is better able to simulate our oocyte experiments. We introduce nine new features (identified as 1–9 in the legend to Fig. 1), which we explain in detail in materials and methods.

Fig. 1.

Main features of the revised mathematical model. Following the approach of Somersalo et al. (22), we assume that the oocyte is a perfectly symmetric sphere of radius R, surrounded by a thin layer of extracellular unconvected fluid (EUF) of thickness d. The EUF is in turn surrounded by the bulk extracellular fluid (BECF), which is an infinite reservoir for all solutes. Within the BECF, convection could occur (though it is not included in the present model), but no reaction or diffusion. Solutes can diffuse between the BECF and EUF. In both the intracellular fluid (ICF) and EUF, reaction and diffusion occur, but no convection. The buffer reactions occurring in the ICF and EUF (illustrated in the inset in the bottom left corner) are: the CO₂/HCO₃⁻ buffer reactions (including the slow conversion of CO₂ into H₂CO₃ and vice versa) and a single non-CO₂/HCO₃⁻ buffer (HA/A⁻). New features of the model include (starting from the inside of the cell and moving outward): 1) reduced water content of cytosol, 2) reduced cytosolic diffusion constants, 3) refined CA II activity, 4) layer of intracellular vesicles (magnification in top left corner), 5) reduced membrane CO₂ permeability, 6) microvilli (magnification in top right corner), 7) refined CA IV activity, 8) vitelline membrane (magnification on lower edge), and 9) a new simulation protocol for the delivery and removal of the bulk extracellular CO₂/HCO₃⁻ solution. The inset in the bottom right corner explains the spatial discretization for the numerical solution near the plasma membrane (PM). EM, extracellular surface of the PM; IM, intracellular surface of the PM.

In the present paper, we first show how introducing these nine new features affects the pH_i and pH_S trajectories caused by the application (or withdrawal) of 1.5% CO₂/10 mM HCO₃⁻ to an oocyte. We then use this more refined model of the oocyte and of its surrounding environment, with all nine new features, to illustrate how we arrive at parameter values that can approximate the measured ΔpH_S, the time to peak pH_S, the experimentally observed time delay to the start of the pH_i change, (dpH_i/dt)_max, and the steady-state change in pH_i (ΔpH_i) caused by the equilibration of CO₂ across the cell membrane. We validate the revised model against physiological data as we work with increased CO₂/HCO₃⁻ levels, or expose oocytes to CO₂/HCO₃⁻ in the presence of varying levels of extracellular HEPES buffer. The model confirms the hypothesis that CA II and CA IV enhance CO₂ fluxes across the plasma membrane by increasing transmembrane CO₂ gradients. Finally, the model predicts that the effects on (dpH_i/dt)_max and ΔpH_S of simultaneously implementing intracellular CA and extracellular-surface CA are supra-additive. That is, the pH effects of the two CA activities are substantially larger than the sum of the two individual effects.

MATERIALS AND METHODS

Assumptions Used in Creating the Model

Here we briefly summarize the main features and assumptions of the mathematical model without reporting the details, which are extensively explained in ref. 22, on its numerical implementation. The key components of the model are summarized in Fig. 1. Following the approach of Somersalo et al. (22), we assume that the oocyte is a perfectly symmetric sphere of radius R, fixed at the center of a spherical volume of radius R_∞. The oocyte is surrounded by a thin layer of unconvected (i.e., unstirred) fluid of thickness d (d = R_∞ − R), the EUF, which in turn is surrounded by the bulk extracellular fluid, the BECF. In both the ICF and EUF, reactions and diffusion occur. The BECF, which represents the bath solution that flows around an oocyte in a physiological experiment, is an infinite reservoir of uniform, preequilibrated solution. Because it is uniform, net diffusion does not occur. Because the BECF is preequilibrated, net reactions do not occur. However, diffusion does occur at the interface between the BECF and EUF.

The buffer reactions considered in this model are 1) the CO₂/HCO₃⁻ buffer reactions, including the slow conversion of CO₂ into H₂CO₃ and vice versa; and 2) a single mobile non-CO₂/HCO₃⁻ buffer, indicated by HA/A⁻ in the bottom left inset in Fig. 1. Thus, HA/A⁻ represents the HEPES buffer (H-HEPES ⇌ H⁺ + HEPES⁻⁾ that we use in the physiological experiments described in the two companion papers. The intracellular non-CO₂/HCO₃⁻ buffer mimics the sum of all intrinsic buffers (i.e., intracellular buffers that do not readily cross the plasma membrane; refs. 2, 6) that are present in the ICF of the oocyte. The properties of this hypothetical single intrinsic buffer, intrinsic buffering power (β_I), pK, and total concentration [TA], are chosen following ref. 6 and will be described in more detail in the results.

Because, in the physiological experiments, CO₂ is the only solute that moves across the plasma membrane (i.e., the oocyte behaves as an open system only for CO₂), the model allows only CO₂ to cross the plasma membrane. Because CO₂ is electrically neutral (and thus expected to be insensitive to membrane potential, V_m), we do not implement V_m in the present model.

The new features of the present model are:

1) Water content.

We now assume that the aqueous portion of the oocyte (i.e., the volume fraction, V_f) occupies not 100% but only 40% of the total oocyte volume (29).

2) Cytoplasm.

We now assume that the viscosity and steric hindrance of the cytoplasm reduce diffusion coefficient of all solutes, specifically by a factor of two (26, 29).

3) Cytosolic CA activity.

We explore a range of values to approximate the electrophysiological data.

4) A layer of intracellular vesicles beneath the plasma membrane (Fig. 1).

This layer can explain in part the observed time delay between the initiation of the pH_S spike and the decline of the pH_i. We implement the presence of intracellular vesicles (12), which impose geometrical constraints on the diffusion path of each solute, by reducing the mobility of each solute in that layer by the same tortuosity factor λ. That is, we introduce an effective diffusion coefficient D^* = D/λ² for each solute in the layer (17, 18).

5) A reduction in the diffusion constant of the cell membrane for CO₂ (D_M,CO2).

We now assume that the oocyte plasma membrane offers resistances to the movement of CO₂. That is, unlike the original implementation in ref. 22, we no longer assume that the plasma membrane behaves as a thin film of pure water with a high D_M,CO2.

6) Folds and microvilli at the plasma membrane (Fig. 1).

We implement these features by multiplying the CO₂ membrane permeability by a surface amplification factor (28).

7) Extracellular-surface CA activity.

We explore a range of values to approximate the electrophysiological data.

8) The vitelline membrane, which surrounds the plasma membrane (Fig. 1), and is not removed during the physiological experiments in the accompanying papers.

Introducing this membrane helps to approximate ΔpH_S. We implement the vitelline membrane, which represents an additional barrier to the diffusion of all solutes, by reducing the mobility of each solute in the region (see Fig. 1, bottom right inset) immediately adjacent to the extracellular surface of the membrane (EM) by the same tortuosity factor γ. That is, we introduce an effective diffusion coefficient D^* = D/γ² in the EM region.

9) Simulation protocol to mimic delivery of CO₂/HCO₃⁻ to and removal from the BECF.

This protocol can explain the time that it takes for the pH_S transient to reach its peak (t_p). To mimic the change of solutions in electrophysiological experiments, we implement parallel, exponential changes in [CO₂], [H₂CO₃], and [HCO₃⁻].

Buffer Reactions, Chemical Equilibria, and Carbonic- Anhydrase Activity

The buffer reactions with the corresponding equilibrium constants (K_ℓ, ℓ = 1, 2, 3) and rate constants (k_ℓ, ℓ = ± 1, 2, 3) are:

1) The CO₂ hydration/dehydration reaction:

$${\text{CO}}_2+{\text{H}}_2\text{O}\underset{k_{-1}}{\overset{k_{+1}}{\rightleftharpoons }}{\text{H}}_2{\text{CO}}_3,\hspace{0.17em}\hspace{0.17em}{K}_1=\frac{[{\text{H}}_2{\text{CO}}_3]}{[{\text{CO}}_2]}=\frac{k_{+1}}{k_{-1}}$$ (1)

2) The carbonic acid dissociation reaction:

$${\text{H}}_{\text{2}}{\text{CO}}_3\underset{k_{-2}}{\overset{k_{+2}}{\rightleftharpoons }}{\text{HCO}}_{\text{3}}^{-}+{\text{H}}^{+},\hspace{0.17em}\hspace{0.17em}{K}_2=\frac{[{\text{HCO}}_{\text{3}}^{-}][{\text{H}}^{+}]}{[{\text{H}}_{\text{2}}{\text{CO}}_3]}=\frac{k_{+2}}{k_{-2}}$$ (2)

and

3) The dissociation reaction for the single non-CO₂/HCO₃⁻ buffer:

$$\text{HA}\underset{k_{-3}}{\overset{k_{+3}}{\rightleftharpoons }}{\text{A}}^{-}+{\text{H}}^{+},\hspace{0.17em}\hspace{0.17em}{K}_3=\frac{[{\text{A}}^{-}][{\text{H}}^{+}]}{[\text{HA}]}=\frac{k_{+3}}{k_{-3}}$$ (3)

Reaction 1 is very slow unless bypassed by a CA enzyme. We simulate the catalytic action of a CA enzyme—CA-like activity—by multiplying the rate constants of reaction 1, k₊₁ and k₋₁, by the same acceleration factor A, which could vary in space and time. In the present study, we do not allow A to vary with time. We assume that A_i (the factor A for intracellular/cytosolic CA activity that mimics CA II) amplifies the rate constants k₊₁ and k₋₁ everywhere inside the oocyte. However, we assume that A_S (the factor A for surface CA activity that mimics the subset of CA IV present on the outer surface of the cell) amplifies the rate constants k₊₁ and k₋₁ only in the EM region.

Reactions 2 and 3 are extremely rapid, limited only by diffusion. We ensure instantaneous equilibrium of reactions 2 and 3 by choosing the rate constants in such a way that, in the time scale of diffusion and reaction, each reaction occurs instantaneously (22).

The values of the equilibrium constants and rate constants used in the simulations are those reported in Table 1 of ref. 22.

Governing Equations

With the assumption of spherical radial symmetry, the concentration C of each solute s, C_s, depends only on the radial distance r from the center of the oocyte. Because the two processes affecting C_s are chemical reactions and diffusion, we model the change of C_s in time and space according to the reaction-diffusion equation (22):

The first term on the right-hand side describes diffusion according to Fick's second law of diffusion, whereas the second term describes the chemical reactions among the solutes. D_s(r) is the diffusion coefficient of solute s as a function of r; S_s,ℓ are the stoichiometry coefficients that can take the value +1, −1, or 0, depending on whether the ℓ-th reaction produces, consumes, or does not involve solute s; and Φ_ℓ are the reaction fluxes modeled according to the law of mass action (22). For the reactions occurring in the ICF, the reaction term is divided by V_f, to reflect that, in the ICF, solutes are restricted to a smaller water volume than the entire oocyte volume (18, 27).

In addition to Eq. 4, we postulate a set of boundary and initial conditions. At the center of the oocyte we posit a Neumann boundary condition:

$$\frac{\partial C_s}{\partial r}(t,0)=0$$ (5)

which states that the flux of solute s at the center of the oocyte is zero.

At the plasma membrane, we assign the transmission boundary conditions:

$$D_s(R+)\frac{\partial }{\partial r}{C}_s(t,R+)=D_s(R-)\frac{\partial }{\partial r}{C}_s(t,R-)$$ (6)

which establish continuity of Fick's diffusive fluxes of solute s across the plasma membrane, and

$$D_s(R\pm )\frac{\partial }{\partial r}{C}_s(t,R\pm )=SA\cdot P_{\text{M},s}\cdot \left[C_s(t,R+)-C_s(t,R-)\right]$$ (7)

which is a statement of Fick's law for diffusion across the plasma membrane.

In Eqs. 6 and 7, C_s(t, R±) denotes the concentration of solute s in the aqueous phase adjacent to the intracellular (−) or extracellular (+) side of the plasma membrane. SA denotes the surface amplification factor, accounting for the presence of folds and microvilli and P_M,s is the true permeability of the membrane to solute s (7, 22).

At R = R_∞ we assign the Dirichlet boundary condition:

$$C_s(t,R_{\infty })=C_{s,\text{BECF}}$$ (8)

which specifies the concentration of solute s in the BECF, C_s,_BECF. C_s,_BECF can be constant or time dependent. More specifically,

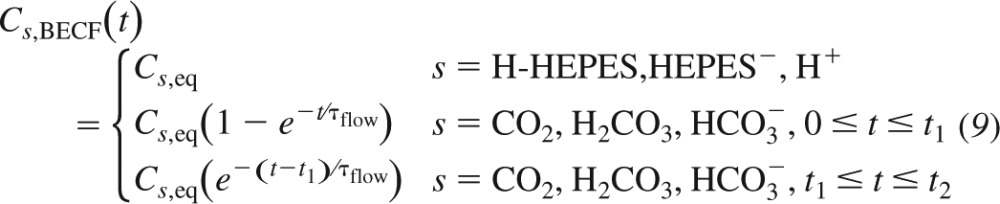Here C_s,eq is the concentration of solute s in a solution equilibrated at pH = 7.50, τ_flow is the time constant of the exponential function that we use to simulate the delivery, from time t = 0 to time t = t₁, and removal, from time t = t₁ to time t = t₂, of a solution containing CO₂/HCO₃⁻ (pH = 7.50). In the results, we will discuss how the new choice of C_s,BECF affects the results of our numerical experiments.

Finally, we assign the initial condition C_s(0, r) = C_s(r), which specifies the radially dependent concentration of solute s at time zero, that is, when we start the experiment.

Numerical Approach

We solve the resulting system of reaction-diffusion equations using the method of lines (MOL). The MOL consists of two steps: first we discretize in the radial direction using an appropriate finite-difference scheme and then we use a stiff ode solver (the MATLAB ode15s, in our case) to find the numerical solution of the resulting time-dependent system of ordinary differential equations. The details of the numerical implementation, which we perform in MATLAB, are described in ref. 22.

RESULTS

Key Quantities for Describing pH_i and pH_S Transients in Physiological experiments

Exposing an oocyte to a solution containing 1.5% CO₂/10 mM HCO₃⁻ causes pH_i to fall monotonically and pH_S to rise to a peak and then decay. Figure 2 schematically illustrates such transients of pH_i (in red) and pH_S (in green) and some of the experimentally measurable quantities that characterize these transients. For pH_i, these quantities include:

• t_d: the time delay between the initiation of the pH_S spike and the initiation of the pH_i change

• (dpH_i/dt)_max: the maximal rate of intracellular acidification caused by the CO₂ influx (a negative number)

• τ_pHi: the time constant of the pH_i decline

• ΔpH_i: the difference between the initial pH_i (in the absence of CO₂) and the final pH_i (after complete equilibration of CO₂)

For pH_S, the key quantities include:

• t_p: the time to peak (time that it takes for pH_S to reach its maximal value)

• ΔpH_S: the difference between the maximal height of the pH_S trajectory (in the presence of CO₂) and the initial pH_S (in the absence of CO₂), which in physiological experiments is very similar to pH_BECF

• τ_pHS: the time constant of the decay phase of pH_S

We can use the same quantities, but with opposite signs, to describe pH_i and pH_S transients during CO₂ removal.

Fig. 2.

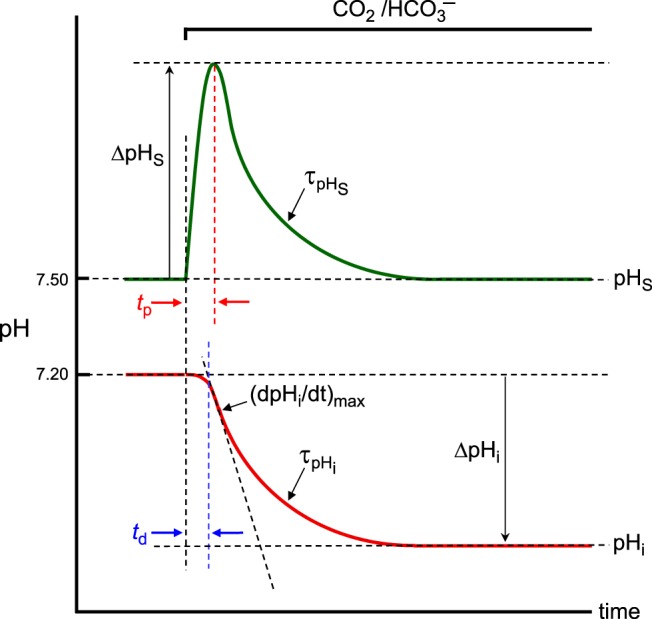
Summary of the key quantities of interest for describing intracellular-pH (pH_i) and surface pH (pH_S) transients in our physiological experiments during the addition of CO₂/HCO₃⁻. This figure schematically illustrates the transients of pH_i (in red) and pH_S (in green) and some of the experimentally measurable key quantities as we expose an oocyte to a CO₂/HCO₃⁻ solution. For pH_i, key quantities are time delay (t_d), the maximal rate of pH_i descent [(dpH_i/dt)_max], time constant for pH_i decay (τ_pHi), and the difference between initial and final pH_i (ΔpH_i). For pH_S, key quantities are time to peak (t_p), maximal height of the pH_S trajectory (ΔpH_S), and the time constant for pH_S decay (τ_pHS).

In the two companion papers we observed that injecting oocytes with recombinant human CA II increases the magnitudes of (dpH_i/dt)_max and ΔpH_S caused by switching from a BECF lacking CO₂/HCO₃⁻ to one containing CO₂/HCO₃⁻, or vice versa. Moreover, CA II causes τ_pHi and τ_pHS to become smaller (i.e., faster). Following a similar pattern, expressing CA IV, which appears on the outer surface of the plasma membrane but also in an equivalent of a cytosol-accessible compartment, increases the magnitude of (dpH_i/dt)_max and ΔpH_S and causes τ_pHi and τ_pHS to become smaller (faster) as we switch the BECF to one (or from one) containing CO₂/HCO₃⁻. Moreover, we observed that the expression of CA IV produces more extreme changes in these key quantities than does the injection of CA II.

In the following two sections we explain how we choose parameter values—τ_flow, tortuosity factors (λ and γ), and acceleration factors (A_i and A_S)—to approximate the physiological data (mean value ± SD), as described by the above key quantities, when we switch the BECF to one containing 1.5% CO₂/10 mM HCO₃⁻. In the next section, we explore the dependence of (dpH_i/dt)_max and ΔpH_S on A_i and A_S. In the last section, we validate the model by exploring the effects of altering the [CO₂]_o/[HCO₃⁻]_o or [HEPES]_o.

Standard Features of an In Silico Oocyte Experiment

In our numerical experiments we consider three types of oocytes: “control”, “CA II,” and “CA IV” oocytes.

A “control” oocyte is one not injected with, or expressing, a heterologous protein. Thus, such an oocyte would have been injected with Tris (rather than CA II + Tris) in the first paper in this series (14) or H₂O (rather than cRNA encoding CA IV + H₂O) in the second paper (15). In our numerical experiments, we will not distinguish between Tris- and H₂O-injected oocytes. Indeed, in the previous two papers, we observed that Tris and H₂O-injected oocytes behave similarly; the quantities shown in Fig. 2 are not significantly different between the two types of oocytes. For consistency, we will use the physiological data from Tris oocytes, from the first paper (14), to set up the properties of our in silico “control” oocyte in all of our simulations.

A “CA II” oocyte in our physiological experiments is one injected with recombinant human CA II protein and, from a modeling prospective, has the same features as a “control” oocyte (see below) but higher CA-like activity (A_i) throughout the ICF.

A “CA IV” oocyte in our physiological experiments is one expressing human CA IV on the outer surface of the plasma membrane as well as in an equivalent of a cytosol-accessible compartment. From a modeling prospective, a “CA IV” oocyte has the same features as a “control” oocyte (see below) but higher CA-like activity (A_S) in the EM region (Fig. 1, bottom right inset), and a slightly higher CA-like activity (A_i) throughout the ICF.

Features of a “typical” oocyte.

Based on the assumptions of our model, each oocyte type (“control”, “CA II”, “CA IV”) has the following features:

1) Only 40% of the oocyte total volume (we assume that an average oocyte has a radius R = 0.13/2 = 0.065 cm) is water (29). For implementation of this feature, see Governing Equations in materials and methods. The model predicts that as V_f decreases, reaction rates and the magnitudes of both (dpH_i/dt)_max and ΔpH_S modestly increase. For example, starting with an in silico control oocyte, decreasing V_f from 60% to 40% (the control value) to 20% causes the predicted (dpH_i/dt)_max to increase from 0.0011 to 0.0012 to 0.0015 pH s⁻¹ and causes ΔpH_S to increase from 0.027 to 0.031 to 0.036.

2) The ICF contains a single non-CO₂/HCO₃⁻ buffer (HA/A⁻), the properties of which we choose so that the mathematical model predicts a fall in ΔpH_i that matches the overall mean values for the physiological data.

3) The mobility of each solute (CO₂, H₂CO₃, HCO₃⁻, H⁺, HA, A⁻) in the ICF is ½ the mobility in pure water (26, 29).³

4) Intracellular CA-like activity (A_i) is present everywhere inside the oocyte. For a “control” oocyte, A_i = 5, and this value is higher in “CA II” and “CA IV” oocytes.

5) A layer of intracellular vesicles begins ∼10 μm beneath the plasma membrane and extends an additional ∼25 μm into the oocyte (12). As we will explain later, we choose the tortuosity factor, λ, to be ∼3.16 (i.e., 1/ λ² = 0.10) in this layer of the cytosol.

6) The true permeability of the plasma membrane to CO₂ is P_M,CO2 = P_water,CO2/10,000 = 34.2/10,000 = 0.00342 cm/s. That is, we assume that the diffusion coefficient of CO₂ within the plasma membrane, D_M,CO2, is 1/10,000 of the diffusion coefficient of CO₂ within a film of water of the same thickness, h_M = 5 nm, as the plasma membrane (1). We choose the value 10,000 based on the conclusion that the oocyte P_M,CO2 would have to be ∼1/1,000 of the value of ∼3 cm/s reported for the P_M,CO2 of artificial bilayer in Missner et al. experiments (4, 13).

7) The plasma membrane has folds and microvilli that amplify its surface by ninefold (28).

8) Extracellular CA-like activity (A_S) is present in the EM region. For a “control” oocyte, A_S = 150, and this value is higher in “CA IV” oocytes.

9) A vitelline membrane surrounds the oocyte. As we will explain later, we choose the tortuosity factor, γ, to be ∼5.77 (i.e., 1/γ² = 0.03) in the EM region (Fig. 1, bottom right inset).

Simulation of a physiological experiment.

To simulate the peculiarities of our experimental system, we assume that

1) The EUF has a thickness d of 10 μm (9).

2) The EUF and BECF have the properties of pure water. Thus each solute (CO₂, H₂CO₃, HCO₃⁻, H⁺, H⁺-HEPES, HEPES⁻) has the same mobility as in pure water.³

3) Before the beginning of an experiment

• The BECF and EUF both contain H⁺-HEPES/HEPES⁻ (pK = 7.50) at a total concentration of 5 mM in a standard experiment (pH_BECF = 7.50). The concentrations of CO₂, H₂CO₃, and HCO₃⁻ are all zero. This assumption mimics the composition of the ND96 solution (which contains other solutes not pertinent to the present model). In our simulations, we will refer to this simplified ND96 solution as “ND96”.

• In the ICF, the concentrations of CO₂, H₂CO₃, and HCO₃⁻ are all zero. The initial pH_i corresponds to the mean value of the initial pH_i for the physiological data for each oocyte type (i.e., “control”, “CA II”, “CA IV”) and experimental protocol (i.e., 1.5% CO₂/10 mM HCO₃⁻ vs. 5% CO₂/33 mM HCO₃⁻ vs. 10% CO₂/66 mM HCO₃⁻).^4,5,6

4) As the experiment begins at time t = 0, we simulate the delivery of CO₂/HCO₃⁻ at pH 7.50 by raising exponentially, with a time constant τ_flow of 4 s, the concentrations of CO₂, H₂CO₃, and HCO₃⁻ in the BECF from zero to the values in an equilibrated CO₂/HCO₃⁻ solution (see Eq. 9).

Parameter Estimation Using the Physiological Data on the Addition of 1.5% CO₂/10 mM HCO₃⁻

We approached the estimation of parameters in an iterative process. Here we present these parameters in an order that reflects, first, the relative certainty of our knowledge (i.e., intracellular buffering power, time course of switching BECF composition) and, second, the importance of the parameters for establishing realistic time courses for pH_i and pH_S (i.e., layer of intracellular vesicles, vitelline membrane, CA activities).

ΔpH_i: choosing the intracellular buffering parameters.

The magnitude of the change in steady-state pH_i (ΔpH_i) produced by exposing a cell to a solution containing equilibrated CO₂/HCO₃⁻ depends on the initial pH_i, [CO₂]_o, and intrinsic buffering power, β_I (2, 19). Using the mean values for the initial (pH_i,1) and final pH_i (pH_i,2) measured in the physiological experiments for each combination of oocyte type and [CO₂]_o, and the concepts described previously (6), we determine the properties of the single intracellular non-CO₂/HCO₃⁻ so that the mathematical model correctly predicts a ΔpH_i = (pH_i,2 − pH_i,1). Specifically, 1) we assume that the pK of the HA/A⁻ buffer is halfway between pH_i,1 and pH_i,2; 2) we calculate β_I over the interval (pH_i,1, pH_i,2) using the Davenport diagram (3, 8); and 3) knowing pK and β_I, we calculate the total amount of intracellular non-CO₂/HCO₃⁻ buffer, [TA]_i, using the equation introduced in ref. 22:

$${\left[\text{TA}\right]}_{\text{i}}=\frac{{\beta }_{\text{I}}\cdot \left({\text{pH}}_{\text{i,2}}-{\text{pH}}_{\text{i,1}}\right)}{\text{Z}}$$

where

$$Z=\frac{1}{1+{10}^{{\text{pH}}_{\text{i,1}}}\text{K}}-\frac{1}{1+{10}^{{\text{pH}}_{\text{i,2}}}\text{K}}\hspace{0.17em}\text{and}\hspace{0.17em}\text{K}={10}^{-\text{p}K}$$

Indeed, when we use the computed value of [TA]_i in simulations, the model predicts ΔpH_i = (pH_i,2 − pH_i,1) values that agree with the physiological data.

Time to peak pH_S: choosing the protocol for simulating the switch in BECF composition.

In our physiological experiments at 1.5% CO₂/10 mM HCO₃⁻/pH 7.50, the time to peak is ∼11.2 ± 3.7 s (means ± SD) for “control” oocytes (see Table 3 in the first paper in this series; ref. 14), ∼7.6 ± 2.7 s for “CA II” oocytes (see Table 3 in the first paper; ref. 14), and ∼6.5 ± 0.8 s for “CA IV” oocytes (not reported in the second paper; ref. 15).

We observe that, to simulate a pH_S trajectory with a t_p close to the physiological data, we had to simulate the initiation of the experiment using an approach substantially different from that used by Somersalo et al. (22), in which: 1) At the outset of the simulation, the BECF and EUF both contain 1.5% CO₂/10 mM HCO₃⁻/pH 7.50 plus 5 mM HEPES at a pH of 7.50. 2) The simulation starts at time t = 0, as the CO₂ begins to diffuse into the cell. Figure 3A shows results of initiating the simulations using the protocol of Somersalo et al. with a “control” oocyte. We observe that the pH_S trajectory has a nonrealistic shape, with a t_p (∼0.4 s) that is more than an order of magnitude smaller that the physiologically observed value. Moreover, after pH_S reaches its maximum, it initially falls off quite rapidly before continuing with a slower decline.

Fig. 3.

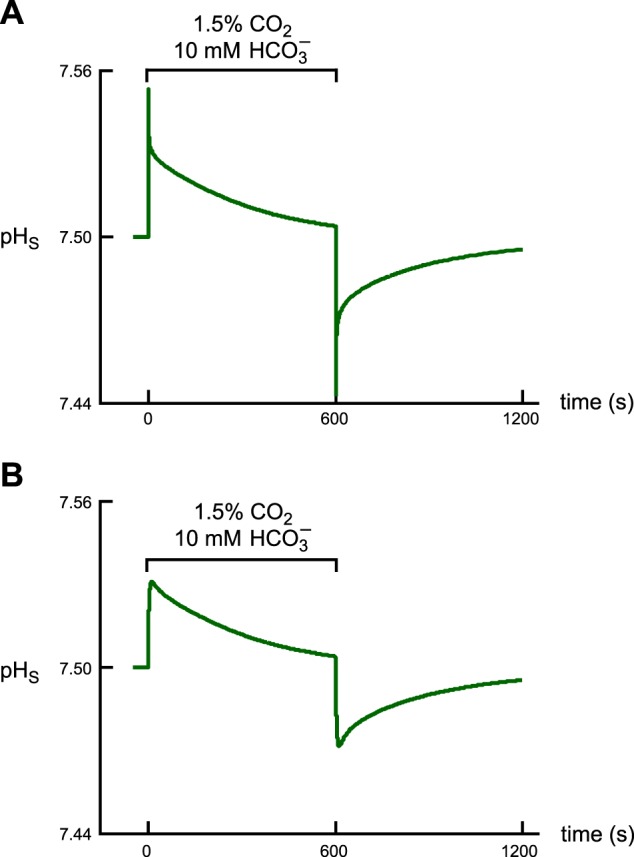
Effect of the new experimental protocol on the shape of the pH_S trajectory and on the time to peak. A: pH_S trajectory predicted by the model when using the protocol of Somersalo et al. (22). In using this original protocol, we assume that, at the outset of the simulation, the CO₂/HCO₃⁻ is already at the plasma membrane. B: pH_S trajectory predicted by the model when using the revised protocol. Here we assume that the oocyte is initially superfused with the CO₂/HCO₃⁻-free ND96 solution until we switch the bulk solution to one containing CO₂/HCO₃⁻ and allow the CO₂ and HCO₃⁻ to diffuse to the cell surface.

Figure 3B shows results of initiating simulations using our revised protocol, which is mathematically described by Eq. 9. In this new approach: 1) Before the beginning of a simulation, the BECF and EUF both contain 5 mM HEPES (pH_BECF = 7.50) but no CO₂, H₂CO₃, or HCO₃⁻. This condition reflects the situation in a physiological experiment, in which the oocyte is exposed to the “ND96” solution until the switch to bulk solution containing CO₂/HCO₃⁻. 2) As the simulation begins, the concentrations of CO₂, H₂CO₃, and HCO₃⁻ in the BECF rise exponentially. It is only after the CO₂ diffuses through the EUF that the CO₂ can begin diffusing through the cell membrane and enter the ICF. Figure 3B shows that our revised protocol, with τ_flow = 4 s, produces a pH_S trajectory that is far more realistic, with a t_p of ∼12.6 s. This value is very close to the physiological mean ± SD (∼11.2 ± 3.7). Regarding “CA II” and “CA IV” oocytes exposed to 1.5% CO₂/10 mM HCO₃⁻, the model predicts a t_p of ∼10 s for “CA II” oocytes (physiological mean ± SD ∼ 7.6 ± 2.7), and ∼8 s for “CA IV” oocytes (physiological mean ± SD ∼6.5 ± 0.8). These simulated t_p values are systematically somewhat larger than the physiologically observed mean values. On the other hand, if we reduce τ_flow to match the t_p values better, other aspects of the simulation (e.g., time delay) are negatively impacted.

Time delay and (dpH_i/dt)_max: simulating the effect of intracellular vesicles.

In the physiological experiments reported in the first paper of this series (14), we observed a pH_i time delay (averaged for CA II and Tris experiments) of ∼9 s for CO₂ addition. We explained this delay as reflecting: 1) the depth of impalement of the pH_i electrode and 2) the resistance offered to CO₂ diffusion by a relatively superficial portion of the oocyte's cytoplasm that contains vesicles (12). In the first paper (see Figs. 15–17 in ref. 14) we used our revised mathematical model to illustrate how the time delay increases with the depth of impalement. In the present paper, we show how the time delay increases as we implement a layer of intracellular vesicles, beginning ∼10 μm beneath the plasma membrane and extending an additional ∼25 μm into the oocyte (12), with increasingly larger values of the tortuosity factor λ.

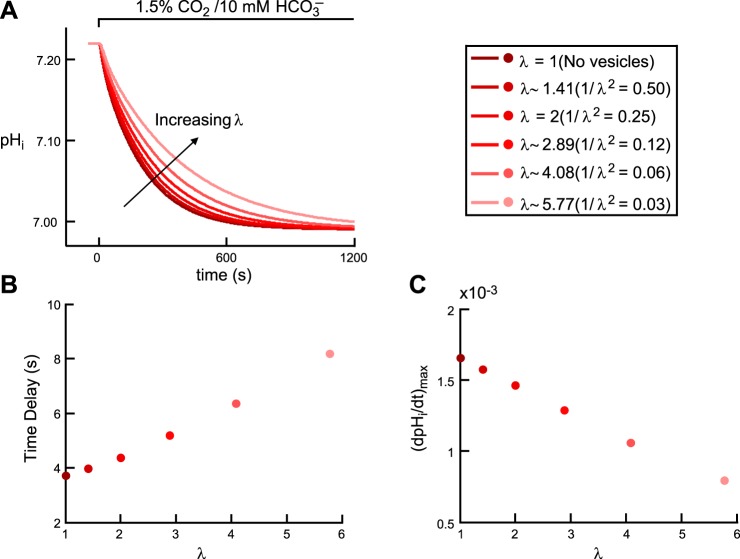
Figure 4 shows the effects of implementing such a layer of vesicles on the simulated pH_i time course (Fig. 4A), time delay (Fig. 4B), and (dpH_i/dt)_max (Fig. 4C).

Fig. 4.

Effect of intracellular vesicles on the pH_i transient during the addition of CO₂/HCO₃⁻. A: pH_i trajectories, at a depth of ∼50 μm. The six simulations correspond to six increasing values of the tortuosity factor λ. B: time delay as a function of λ. The six colored dots correspond to the six simulations in A. C: maximal rate of pH_i change (negative direction) as a function of λ. The six colored dots correspond to the six simulations reported in A.

As the tortuosity factor λ increases from 1 (i.e., no vesicles) to ∼5.77 (i.e., as 1/λ² decreases from 1 to 0.03), pH_i, computed at a depth of ∼50 μm into the oocyte, declines more slowly (Fig. 4A), the time delay rises from 3.73 to 8.18 s (Fig. 4B), and (dpH_i/dt)_max falls from 0.0017 to 0.0008 pH U/s (Fig. 4C). The magnitude of (dpH_i/dt)_max falls because, as λ rises (i.e., we reduce the mobility of solutes in the band corresponding to vesicles), the flux of CO₂ across the plasma membrane decreases (CO₂ builds up in the regions near the inner side of the plasma membrane), causing CO₂ to enter into the cell more slowly, as also indicated by the slower pH_i decline (Fig. 4A) and larger time delay (Fig. 4B).

What would the tortuosity factor have to be, in a band 10 to 25 μm below the oocyte surface, to achieve a delay of ∼9 s in simulations of CO₂ addition in “control” experiments at a reasonable electrode depth of 50 μm? If we use a λ of ∼6.32 (i.e., multiply the diffusion constants for all solutes by 1/λ² = 0.025) in the aforementioned vesicle band, we can account for a pH_i delay of ∼9 s. However, such a high λ produces excessive slowing of pH_i and pH_S transients (not shown). In fact, the events inside (and outside) the oocyte become so slow that it becomes impossible to reproduce the features of pH_i (faster pH_i decay) and pH_S (higher ΔpH_S) transients when implementing larger intracellular and extracellular values for CA-like activity, that is, to mimic a “CA II” and a “CA IV” oocyte. Therefore, in our “typical” oocyte, we compromise by using a λ of ∼3.16 (i.e., 1/ λ² = 0.10), which has the effect of reducing the pH_i delay from ∼9 s to ∼5.5 s for CO₂ addition in a “control” oocyte. As addressed in the second paper of this series (15), we believe that, in addition to vesicles, other factors, including the asymmetry of [CO₂]_BECF around the oocyte (not part of the present model), contribute to the pH_i delay.

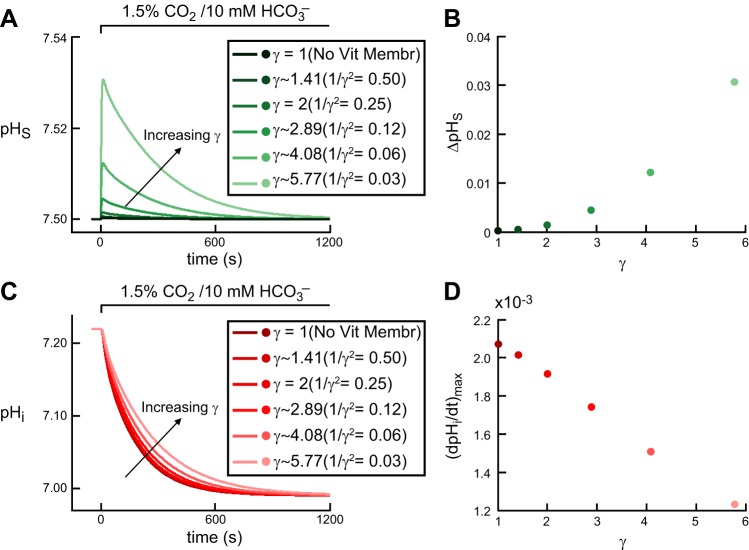
ΔpH_S: simulating the effect of vitelline membrane.

In Fig. 5, A and B, we show the effects on pH_S of implementing the vitelline membrane in a “control” oocyte, that is, the effects on pH_S of reducing the mobility of all solutes in the region immediately adjacent to the extracellular surface of the plasma membrane. The reason for implementing this vitelline membrane is that ΔpH_S approaches zero when this membrane is not present (Fig. 5, A and B). The first electrophysiologically meaningful effect on ΔpH_S occurs when we increase γ from 2 to ∼2.89 (i.e., reduce 1/γ² from 0.25 to 0.12). However, a γ of 2.89 predicts a ΔpH_S of ∼0.005, which is much less than the physiological value of 0.046 ± 0.016 for a “control” oocyte. Further increases in γ cause further increases in ΔpH_S. For γ ∼5.77 (i.e., 1/γ² = 0.03) the model predicts a ΔpH_S close to the physiological data. We also note that as we increase γ, the pH_S decay from the peak to the equilibrium state is slower.

Fig. 5.

Effect of vitelline membrane on pH_i and pH_S transients during the addition of CO₂/HCO₃⁻. A: pH_S trajectories. The six simulations correspond to six increasing values of the tortuosity factor γ. B: maximal height of the pH_S spike (positive direction) as a function of γ. The six colored dots correspond to the six simulations in A. C: pH_i trajectories, at a depth of ∼50 μm, corresponding to the simulations in A. D: maximal rate of pH_i change (negative direction) as a function of γ. The six colored dots correspond to the six simulations in A.

It is also informative to see the effects of introducing the vitelline membrane on the pH_i trajectory. Figure 5, C and D, shows that, as we increase γ, the decay of pH_i to the equilibrium state is slower and (dpH_i/dt)_max is smaller. Consistent with the analysis in Fig. 5,A and B, a γ of ∼5.77 (i.e., 1/γ² = 0.03) predicts a (dpH_i/dt)_max of −0.0012 pH U/s, which is in good agreement with the physiological data for a “control” oocyte.

The reason that increasing γ raises the magnitude of ΔpH_S (Fig. 5,A and B) is that, by implementing the vitelline membrane, we reduce the contribution of diffusion and emphasize the contribution of reaction in replacing the lost CO₂ in the EM region (for chemistry, see Fig. 1 in the first paper in this series; ref. 14).

The reason that increasing γ lowers the magnitude of (dpH_i/dt)_max is that reducing diffusion in the EM layer causes the flux of CO₂ from the EM+1 region to the EM region to fall, thereby reducing [CO₂] at the outer surface of the plasma membrane and causing CO₂ to enter into the cell more slowly, as also indicated by the slower pH_i decline and larger time delay.

“Control”, “CA II”, and “CA IV” oocytes.

The new protocol to simulate the delivery and removal of CO₂/HCO₃⁻ solution from/to the BECF, the implementation of the intracellular vesicles, and the implementation of the vitelline membrane allow us to find values for τ_flow, λ, and γ that produce simulations that approximate a “control” oocyte exposed to 1.5% CO₂/10 mM HCO₃⁻/pH 7.50. These parameter values are not unique to a “control” oocyte but also apply to “CA II” and “CA IV” oocytes. In other words, these values approximate the intrinsic properties of our in silico oocyte, independently of the injection or expression of a CA enzyme. To reproduce the pH_i and pH_S transients of “CA II” and “CA IV” oocytes, we need to find appropriate values for A_i and A_S for each oocyte type.

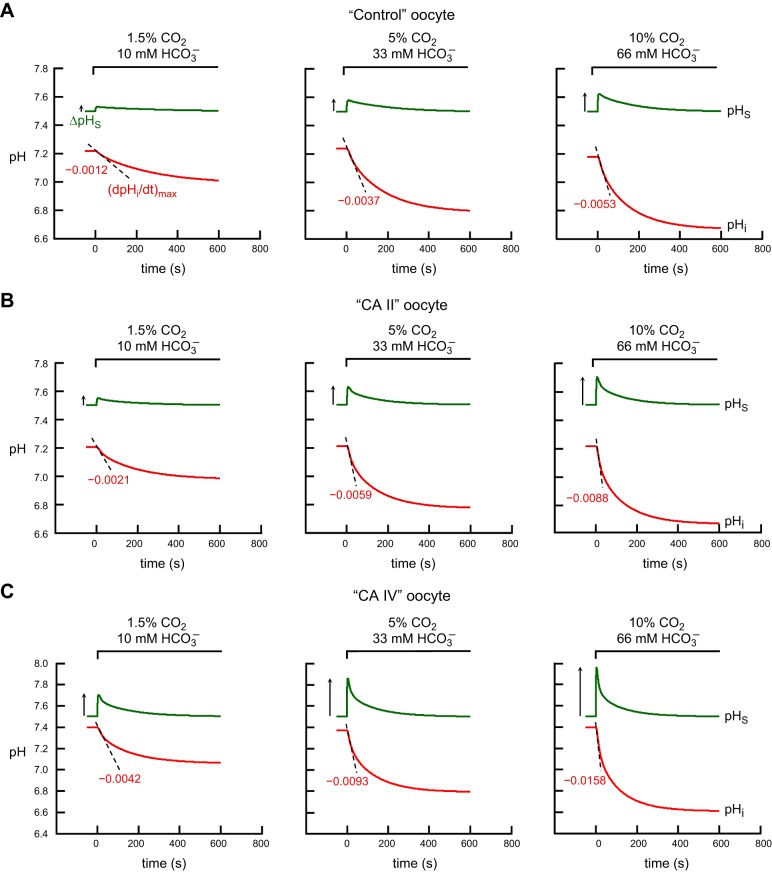
Figure 6 shows the results of simulations that best agree with the physiological data for “control” (Fig. 6A), “CA II” (Fig. 6B), and “CA IV” (Fig. 6C) oocytes. We used:

• “Control” oocyte: A_i = 5 and A_S = 150

• “CA II” oocyte: A_i = 1,000 and A_S = 150

• “CA IV” oocyte: A_i = 40 and A_S = 10,000.

Note that, for a “CA IV” oocyte, we had to increase intracellular CA II activity by a small amount (A_i = 40 vs. A_i = 5) to achieve quantitative agreement with the physiological data (see Fig. 7). The reason is that, for A_i = 5, the model predicts values for (dpH_i/dt)_max and ΔpH_S for CO₂ addition [i.e., (dpH_i/dt)_max = 0.0022 pH U/s and ΔpH_S = 0.1015] that are much smaller than the physiological data for “CA IV” oocytes [i.e., (dpH_i/dt)_max = 0.0042 ± 0.0018 pH U/s and ΔpH_S = 0.2488 ± 0.0669 (means ± SD)]. However, it is important to point out that, even when we used an A_i of 5 in a “CA IV” oocyte, an A_S of 10,000 is able to produce increases in (dpH_i/dt)_max and ΔpH_S, but not as substantial as when A_i = 40.

Fig. 6.

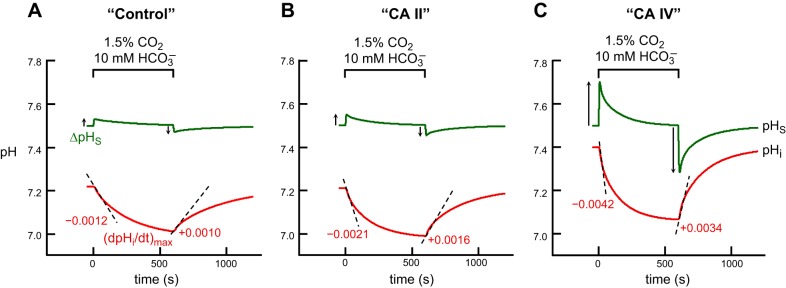
Simulations of pH_i and pH_S transients for the addition and removal 1.5% CO₂/10 mM HCO₃⁻ in 5 mM HEPES. A: “control” oocyte“. B: ”CA II“ oocyte. C: ”CA IV“ oocyte. The pH_i transients, calculated at a depth of ∼50 μm into the oocyte, are represented by the red lower trajectories, and pH_S, by the green upper trajectories. At the indicated time, we switched the extracellular solution from CO₂/HCO₃⁻-free ”ND96“ to 1.5% CO₂/HCO₃⁻ (see Eq. 9). The dashed black lines through the initial portions of the pH_i transients for CO₂ application and removal represent the maximal rates of pH_i change (negative or positive direction), as predicted by the model. The upward and downward arrows near the pH_S records represent maximal changes in pH_S (positive or negative direction).

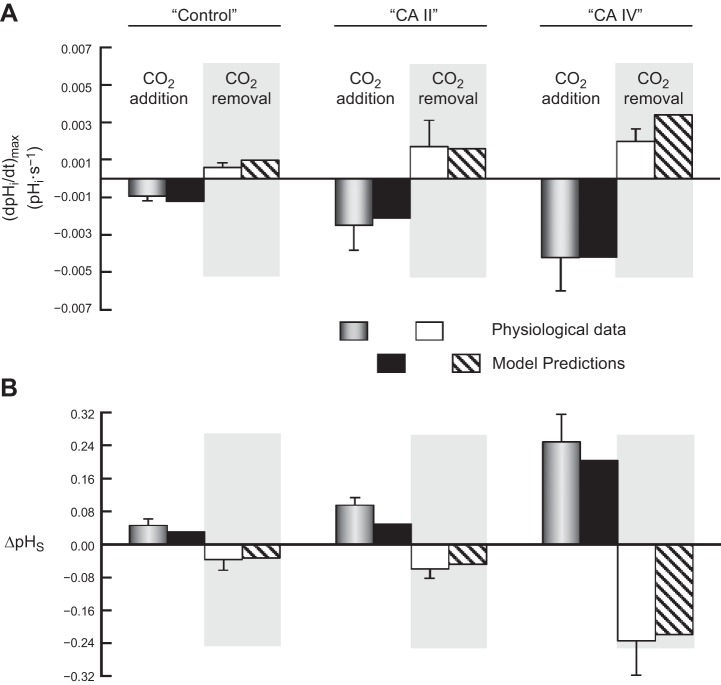
Fig. 7.

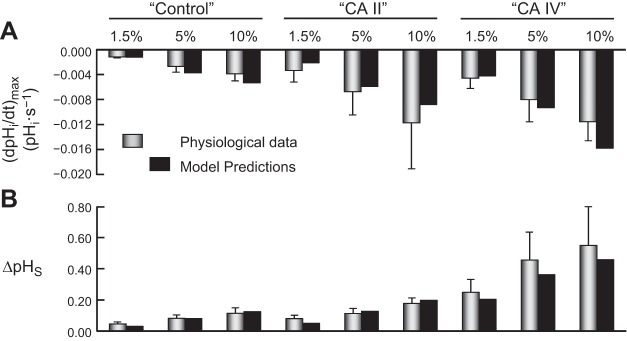
Comparison of the physiological data with predictions of the mathematical model for the addition and removal of extracellular 1.5% CO₂/10 mM HCO₃⁻. A: maximal rates of pH_i change (negative or positive direction) produced by the addition or removal of extracellular CO₂/HCO₃⁻. B: maximal changes in pH_S (positive or negative direction) caused by the addition or removal of extracellular CO₂/HCO₃⁻. The physiological data come from Fig. 2 of the first paper in this series (14) and Fig. 3 of second paper (15). Note that here we report the means ± standard deviation (and not SE, as in the previous two papers). The data for model predictions come from Fig. 6 of the present paper.

Figure 7 shows a comparison between the physiological data (means ± SD) and the predictions of the mathematical model for all three oocyte types, for both CO₂ addition and removal.

In agreement with the physiological data, the model predicts that, for both CO₂ addition and removal, increasing only cytosolic CA activity (i.e., “CA II” oocyte) increases the magnitude of (dpH_i/dt)_max and ΔpH_S, as well as the time it takes for pH_i and pH_S to reach equilibration. The model also predicts that increasing extracellular-surface plus cytosolic CA activity (i.e., “CA IV” oocyte) increases these same parameter values. Moreover, consistent with the physiological data, the model predicts that “CA IV” is more effective than “CA II” in enhancing the magnitudes of (dpH_i/dt)_max and ΔpH_S.

Dependence of (dpH_i/dt)_max and ΔpH_S on A_i and A_S

Because A_i and A_S play critically important roles in the simulations of the physiological (dpH_i/dt)_max and ΔpH_S data, we investigated how the predicted values for these two pH parameters change as we systematically vary A_i and A_S. Here we perform simulations for all possible combinations of A_i values of 5, 20, 40, 100, 1,000, and 10,000 with A_S values of 150, 1,000, 5,000, 10,000, 25,000, and 50,000. We assume that the oocyte has the intracellular composition (i.e., initial pH_i and ΔpH_i) of a “CA IV” oocyte,⁶ and that we switch from a CO₂/HCO₃⁻-free bulk solution to one containing 1.5% CO₂/10 mM HCO₃⁻.

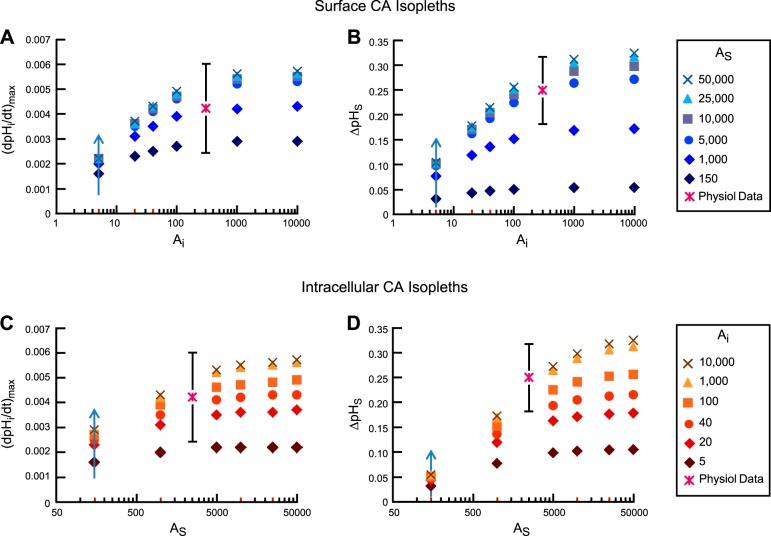
Figure 8 shows the values predicted by the model for (dpH_i/dt)_max (Fig. 8A) and ΔpH_S (Fig. 8B) as a function of A_i for six surface CA isopleths (i.e., A_S is held constant for each set of symbols). Figure 8, C and D, shows the same predicted values, but as a function of A_S for six intracellular CA isopleths. In each panel we identify with a “star” the physiological value of (dpH_i/dt)_max or ΔpH_S as mean ± standard deviation; the position of the “star” along the x-axis is arbitrary.

Fig. 8.

Dependence of (dpH_i/dt)_max and ΔpH_S on A_i and A_S. A: dependence of (dpH_i/dt)_max on A_i, for several fixed values of A_S (i.e., each set of symbols is a surface CA isopleth). B: dependence of ΔpH_S on A_i, for several fixed values of A_S (i.e., surface CA isopleths). C: dependence of (dpH_i/dt)_max on A_S, for several fixed values of A_i (i.e., intracellular CA isopleths). D: dependence of ΔpH_S on A_S, for several fixed values of A_i (i.e., intracellular CA isopleths). In these simulations, we assume that a hypothetical oocyte with the intracellular composition (i.e., initial pH_i and ΔpH_i) of a ”CA IV“ oocyte is exposed to a bulk solution containing 1.5% CO₂/10 mM HCO₃⁻. The physiological data are plotted on the ordinate as mean ± standard deviation; the position of these points along the abscissa is arbitrary.

Focusing first on the surface CA isopleths (Fig. 8, A and B), we observe that for A_i = 5 (background value for a “control” oocyte), increasing A_S from 150 to 50,000 (following the upward arrow at A_i = 5) produces only a 40% increase in (dpH_i/dt)_max and ∼3.3-fold increase in ΔpH_S. Moreover, the (dpH_i/dt)_max and ΔpH_S values predicted by these combinations of A_i (i.e., 5) and A_S (i.e., 150–50,000) are far from the mean values measured in our physiological experiments. Thus, as noted above, to simulate a “CA IV” oocyte, we must increase not only A_S but also A_i. We choose A_i = 40 because, together with A_S = 10,000, it matches the observed (dpH_i/dt)_max and is only slightly below the observed mean for ΔpH_S. Moreover, because our current model does a better job of reproducing the pH_i than the pH_S data, as also indicated by the t₆₃ values predicted by the model for pH_i (see Fig. 13 in the first paper of this series, ref. 14, and Fig. 21 in second paper, ref. 15), we gave more weight to the pH_i data in choosing the above parameter values.

Fig. 13.

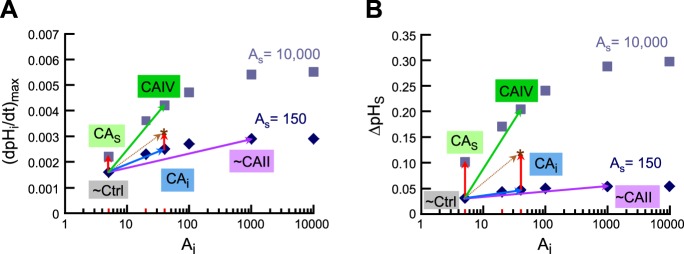
Supra-additivity of simultaneous implementation of intracellular (i.e., cytosolic) and extracellular-surface CA activity. A: dependence of (dpH_i/dt)_max on A_i, for two fixed values of A_S (i.e., surface CA isopleths), a replot of selected data from Fig. 8A. B: dependence of ΔpH_S on A_i, for two fixed values of A_S (i.e., surface CA isopleths), a replot of selected data from Fig. 8B. In all simulations for this figure, we assume that a hypothetical oocyte with the intracellular composition (i.e., initial pH_i and ΔpH_i) of a “CA IV” oocyte is exposed to a bulk solution containing 1.5% CO₂/10 mM HCO₃⁻. The points labeled “∼Ctrl” represent our hypothetical oocyte but with the CA properties of a “control” oocyte (i.e., A_i = 5, on the 150 A_S isopleth). The points labeled “∼CAII” represent our hypothetical oocyte but with the CA properties of a “CA II” oocyte (i.e., A_i = 1,000, on the 150 A_S isopleth). These points (lavender vectors) approximate the physiologically observed (dpH_i/dt)_max and ΔpH_S values for oocytes injected with CA II. The points labeled “CA_S” represent a hypothetical oocyte but in which we raise A_S to 10,000 but leave A_i = 5. These points (red vectors on left side of panels) represent (dpH_i/dt)_max and ΔpH_S values that are far smaller than those physiologically observed with oocytes expressing CA IV. The points labeled “CA_i” represent a hypothetical oocyte but in which we raise A_i to 40 but leave A_S = 150. These points (blue vectors) represent (dpH_i/dt)_max and ΔpH_S values that are far smaller than those physiologically observed with oocytes expressing CA IV. The sum of the red and blue vectors produce the brown vectors, which indicate the effects of simply adding CA_i and CA_o. Note that the asterisks (at the head of the brown vectors) represent (dpH_i/dt)_max and ΔpH_S values that are still much smaller than those physiologically observed with oocytes expressing CA IV. Finally, the points labeled “CAIV” represent the combination of simultaneously raising A_S from 150 to 10,000 and raising A_i from 5 to 40 in our simulations (green vectors). These points do indeed approximate the physiologically observed (dpH_i/dt)_max and ΔpH_S values of oocytes expressing CA IV.

As A_i increases along the x-axis, each surface CA isopleth, both in the (dpH_i/dt)_max plot (Fig. 8A) and in the ΔpH_S plot (Fig. 8B), at first increases and then tends to plateau at A_i values above ∼1,000. For any A_S isopleth, (dpH_i/dt)_max and ΔpH_S rise very little as we increase A_i from 1,000 to 10,000.

Focusing now on the intracellular CA isopleths (Fig. 8, C and D), we observe that for A_S = 150 (background value for a “control” oocyte), increasing A_i from 5 to 10,000 (following the upward arrow at A_S = 150) causes (dpH_i/dt)_max and ΔpH_S to increase by only ∼2-fold. As A_S increases along the x-axis, each intracellular CA isopleth, for both (dpH_i/dt)_max and ΔpH_S, increases but eventually tends to plateau. For any A_i isopleth, (dpH_i/dt)_max and ΔpH_S increase relatively little as we raise A_S from 10,000 to 50,000.

In summary, the mathematical model shows that simulating the physiological pH data requires that A_i and A_S be sufficiently high, but that the predictions for (dpH_i/dt)_max and ΔpH_S are not very sensitive to increases in A_i beyond ∼1,000 or to A_S beyond ∼10,000.

Model Validation

The purpose of these simulations is not to explain the physiological principles, which we have already addressed in the first two papers in this series, but to validate the mathematical model.

Effect of increasing extracellular CO₂/HCO₃⁻ levels.

Figure 9 shows the predictions of the mathematical model for “control” (Fig. 9A), “CA II” (Fig. 9B), and “CA IV” (Fig. 9C) oocytes as they are each exposed to increasing levels of extracellular CO₂/HCO₃⁻−1.5% CO₂/10 HCO₃⁻ mM, 5% CO₂/33 HCO₃⁻ mM, and 10% CO₂/66 HCO₃⁻ mM (virtually identical [CO₂]/[HCO₃⁻] ratios to fix pH_BECF at ∼7.50). In these simulations we used the same parameter values for τ_flow, λ, γ, A_i and A_S that we used to simulate the pH_i and pH_S transients illustrated in Fig. 6. Note that the three simulations corresponding to 1.5% CO₂/10 HCO₃⁻ mM in Fig. 9 (left) are the same as those illustrated in Fig. 6, A–C.

Fig. 9.

Simulations of pH_i and pH_S transients for the addition of graded levels of extracellular CO₂/HCO₃⁻ in 5 mM HEPES. A: ”control“ oocyte”. B: “CA II” oocyte. C: “CA IV” oocyte. The pH_i transients, calculated at a depth of ∼50 μm, are represented by the red lower trajectories, and pH_S, by the green upper trajectories. At the indicated time, we switched the extracellular solution from CO₂/HCO₃⁻-free “ND96” to 1) 1.5% CO₂/10 mM HCO₃⁻ (left), or 2) 5% CO₂/33 mM HCO₃⁻ (center), or 3) 10% CO₂/66 mM HCO₃⁻ (right). The dashed black lines through the initial portions of the pH_i transients for CO₂ application represent the maximal rates of pH_i change (negative direction) predicted by the model. The upward arrow near the pH_S records represent maximal changes in pH_S (positive direction).

Figure 10 compares the predictions of the mathematical model (based on parameter values developed for 1.5% CO₂), shown in Fig. 9, with the physiological data for (dpH_i/dt)_max (Fig. 10A) and ΔpH_S (Fig. 10B). The good agreement of the simulations with the physiological data for the 5% CO₂ and 10% CO₂ data validates the model.

Fig. 10.

Comparison of the physiological data with predictions of the mathematical model for the addition of graded levels of extracellular CO₂/HCO₃⁻. A: maximal rates of pH_i change (negative direction) produced by the addition of extracellular CO₂/HCO₃⁻. B: maximal changes in pH_S (positive direction) caused by the addition of extracellular CO₂/HCO₃⁻. The physiological data are taken from Fig. 10 of the first paper in this series (14) and Fig. 10 of the second paper (15). Note that here we report the means ± standard deviation (and not SE, as in the previous two papers). The data for model predictions come from Fig. 9 of the present paper.

For pH_i, the model predicts that increasing [CO₂]_BECF from 1.5% to 5% to 10%, in the ratios 1/∼3.3/∼6.6, causes a progressive increase in the magnitude of (dpH_i/dt)_max, in agreement with the physiological data (Fig. 10A). Moreover, comparing “control” vs. “CA II” vs. “CA IV” oocytes at a given CO₂ level, we see that, at each CO₂ level, the simulated (dpH_i/dt)_max is greatest for “CA IV” oocyte and smallest for “control” oocyte.

For pH_S, the model predicts that increasing [CO₂]_BECF from 1.5% to 5% to 10%, in the ratios 1/∼3.3/∼6.6, causes a progressive increase in ΔpH_S in agreement with the physiological data (Fig. 10B). Moreover, comparing “control” vs. “CA II” vs. “CA IV” oocytes at a given CO₂ level, we see that ΔpH_S is greatest for “CA IV” oocyte and smallest for “control” oocyte.

Effect of increasing extracellular HEPES levels.

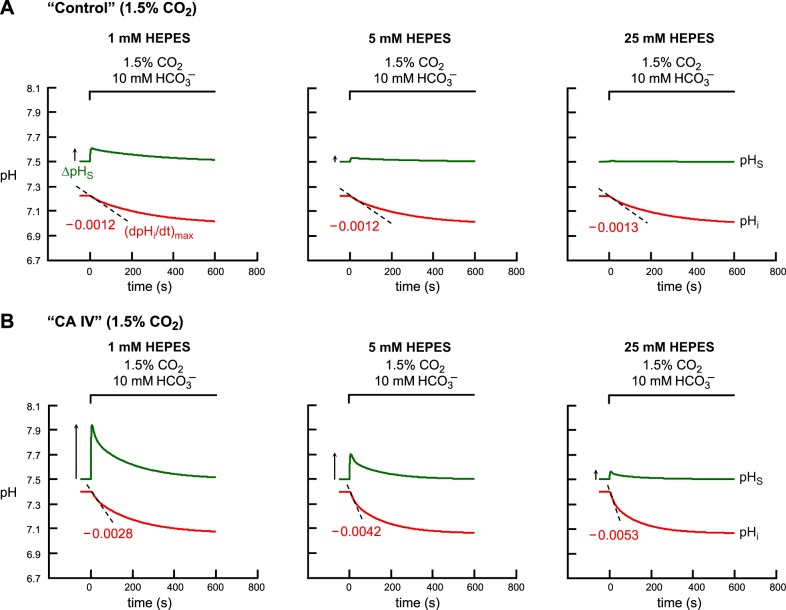
Again, for purposes of model validation, Fig. 11 shows the predictions of the mathematical model for “control” (Fig. 11A) and “CA IV” (Fig. 11B) oocytes as they are exposed to 1) 1.5% CO₂/10 mM HCO₃⁻ at pH 7.50 + 1 mM HEPES, or 2) CO₂/HCO₃⁻ + 5 mM HEPES, or 3) CO₂/HCO₃⁻ + 25 mM HEPES. In these simulations we used the same parameter values for τ_flow, λ, γ, A_i, and A_S that we used to simulate the pH_i and pH_S transients illustrated in Fig. 6, where [HEPES]_o is 5 mM. Here, for model validation, we change the experimental protocol by varying the levels of extracellular HEPES.

Fig. 11.

Simulations of pH_i and pH_S transients for the addition of extracellular 1.5% CO₂/10 mM HCO₃⁻, with graded increases in levels of extracellular HEPES. A: “control” oocyte. B: “CA IV” oocyte. The pH_i transients, calculated at a depth of ∼50 μm, are represented by the red lower trajectories, and pH_S, by the green upper trajectories. At the indicated time, we switched the extracellular solution from CO₂/HCO₃⁻-free “ND96” to: 1) CO₂/HCO₃⁻ + 1 mM HEPES, or 2) CO₂/HCO₃⁻ + 5 mM HEPES, or 3) CO₂/HCO₃⁻ + 25 mM HEPES. The dashed black lines through the initial portions of the pH_i transients for CO₂ application represent the maximal rates of pH_i change (negative direction) predicted by the model. The upward arrows near the pH_S records represent maximal changes in pH_S (positive direction).

For a “control” oocyte, the model predicts that raising [HEPES]_o from 1 to 5 to 25 mM causes minimal changes in (dpH_i/dt)_max (Fig. 11A in the present paper and Fig. 23D in the second paper in this series, ref. 15). However, as expected because of the increased extracellular buffering power, the graded increase in [HEPES]_o causes substantial decreases in ΔpH_S (Fig. 12A in the present paper and Fig. 23E in ref. 15). Finally, the model predicts that graded increases in [HEPES]_o have little effect on t₆₃ (i.e., the time required to fall by ∼63%) for pH_S (Fig. 23F in ref. 15).

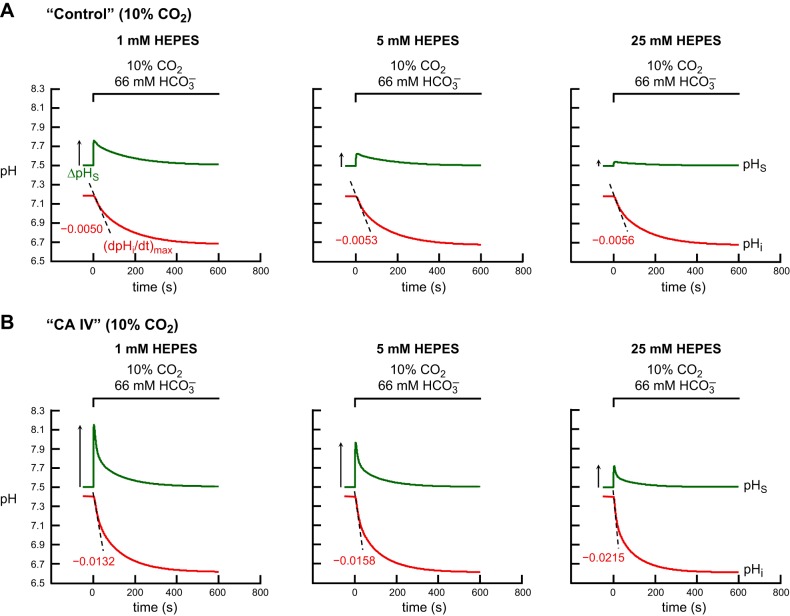
Fig. 12.

Simulations of pH_i and pH_S transients for the addition of extracellular 10% CO₂/66 mM HCO₃⁻, with graded increases in levels of extracellular HEPES. A: “control” oocyte. B: “CA IV” oocyte. This figure differs from Fig. 11 in that, here, the CO₂/HCO₃⁻ levels are ∼6.6-fold higher. The pH_i transients, calculated at a depth of ∼50 μm, are represented by the red lower trajectories, and pH_S, by the green upper trajectories. At the indicated time, we switched the extracellular solution from CO₂/HCO₃⁻-free “ND96” to 1) CO₂/HCO₃⁻ + 1 mM HEPES, or 2) CO₂/HCO₃⁻ + 5 mM HEPES, or 3) CO₂/HCO₃⁻ + 25 mM HEPES. The dashed black lines through the initial portions of the pH_i transients for CO₂ application represent the maximal rates of pH_i change (negative direction) predicted by the model. The upward arrows near the pH_S records represent maximal changes in pH_S (positive direction).

For a “CA IV” oocyte, the model predicts that raising [HEPES]_o from 1 to 5 to 25 mM causes pH_i to decay faster (Fig. 11B in the present paper and Fig. 23A in ref. 15) and greatly reduces ΔpH_S (Fig. 11B in the present paper and Fig. 23B in ref. 15). The increase in [HEPES]_o also causes t₆₃ to fall modestly (Fig. 23C in ref. 15).

The simulations in Fig. 12 are identical to those in Fig. 11 except that in Fig. 12 we work with 10% CO₂/66 mM HCO₃⁻. As we have already seen at 1.5% CO₂ for a “control” oocyte (Fig. 11A), the model predicts that, at 10% CO₂, raising [HEPES]_o from 1 to 5 to 25 mM produces a minimal enhancement of (dpH_i/dt)_max (Fig. 12A in the present paper and Fig. 24D in ref. 15). The model also predicts that raising [HEPES]_o markedly reduces ΔpH_S (Fig. 12A in the present paper and Fig. 24E in ref. 15), and has little effect on t₆₃ for pH_S (Fig. 24F in ref. 15).

Finally, for a “CA IV” oocyte exposed to 10% CO₂/66 mM HCO₃⁻, the model predicts that raising [HEPES]_o from 1 to 5 to 25 mM produces very large increases in the magnitude of (dpH_i/dt)_max (Fig. 12B in the present paper and Fig. 24A in ref. 15) and large decreases in ΔpH_S (Fig. 12B in the present paper and Fig. 24B in ref. 15). Moreover, t₆₃ for pH_S decreases modestly (Fig. 24C in ref. 15).

Note that the simulation trends that we observe in Figs. 11 and 12 for a range of [HEPES]_o values, based on parameter values developed for 5 mM HEPES, parallel the physiological data presented in the second paper in this series (15), and thereby validate the model.

DISCUSSION

Overview

When CO₂ is the only acid-base-related solute that moves across the plasma membrane, as is essentially the case in our physiological experiments, the model predicts that a CO₂ influx (or efflux) will cause a sustained fall (rise) in pH_i, but a transient rise (fall) in pH_S, followed by a relaxation. In fact, the predicted time course of the pH_S relaxation is approximately proportional to the negative derivative of the time course of pH_i. As CO₂ moves across the plasma membrane, it perturbs the equilibria of all buffer pairs, both CO₂/HCO₃⁻ and non-CO₂/HCO₃⁻ buffers, in both the intra- and extracellular fluids. The perturbations occur because these buffers all compete for a common pool of H⁺. Aside from the reaction CO₂ + H₂O ⇌ H₂CO₃, all others occur virtually instantaneously, being limited only by diffusion of buffer components. Because the CO₂/H₂CO₃ interconversion is slow, the nature of the participation by CO₂/HCO₃⁻ in buffering depends not just on diffusion but on the activity and location of CAs. In a compartment delimited by a membrane traversable only by CO₂, that is, a compartment that behaves as a closed system to all solutes other than CO₂, the CO₂/HCO₃⁻ buffer system will eventually exert its full buffering power, even in the absence of catalysis. Thus, we see that ΔpH_i is unaffected by the presence of CAs. However, in the EUF, where buffer components exchange freely with the BECF, and thus are only transiently available, the ability of the CO₂/HCO₃⁻ buffer pair to influence pH, and thus influence other reactions in the EUF, depends on the diffusion of CO₂ and HCO₃⁻ as well as the rates of the reactions that allow CO₂/HCO₃⁻ interconversion.

In the preceding two papers, we used electrophysiological approaches to study the effects of the cytosolic CA II and of the GPI-linked extracellular CA IV on accelerating transmembrane CO₂ fluxes. Moreover, we investigated the effects of CA II and CA IV on the CO₂-induced pH_i and pH_S transients when we: 1) raised the concentration of CO₂ in the BECF; 2) increased the depth of penetration of the pH_i microelectrode; 3) changed the concentration of HEPES in the BECF.

To understand the complex interconnected acid-base events triggered by the movement of CO₂ in or out of the cell, in the presence of CA II or CA IV—events so complex that their interpretation is not easily amenable to intuition—we used a previously published mathematical model (22) that we appropriately modified for the present study by introducing the nine new features 1 through 9, as indicated in Fig. 1 and its legend.

The revised mathematical model has proven to be very useful in providing new insights into the complex reaction and diffusion events underlying the pH_i and pH_S transients measured in physiological experiments in the first two papers in this series.

Major New Features of the Mathematical Model

Here we discuss a subset of the nine new features 1–9 in Fig. 1 legend, in the order that we present them in results: 9, 4, 8, 3, and 7.

Protocol for simulating the switch in BECF composition.

In physiological experiments, exposing an oocyte to a CO₂/HCO₃⁻ solution initiates an influx of CO₂ that causes pH_S to rise to a peak and then decay with a trajectory like the one schematically illustrated in Fig. 2. When we initiate a simulation using the protocol of Somersalo et al. (22), which assumes that, at the outset of the simulation, the CO₂/HCO₃⁻ solution is already at the plasma membrane, the initial portion of the pH_S trajectory exhibits a quite unrealistic needle-like shape (Fig. 3A). We reasoned that this inconsistency between the simulation and the physiological data must be related to the assumption that, at the beginning of the simulation, the CO₂/HCO₃⁻ solution is already in both BECF and EUF, and therefore immediately ready to diffuse into the ICF.

Our revised approach reflects the situation in a physiological experiment, in which the oocyte is initially superfused with the ND96 solution until we switch the bulk solution to one containing CO₂/HCO₃⁻. Indeed, Fig. 3B shows that our revised protocol produces a pH_S trajectory with a far more realistic shape and a time to peak very close to the physiological data. The results obtained with the revised protocol suggest that t_p reflects in part the time required for levels of the CO₂, H₂CO₃, and HCO₃⁻ to rise in the BECF, and in part the time required for the buffer components to diffuse throughout the EUF and enter the ICF. In our revised simulation protocol we assumed that the concentrations of CO₂, H₂CO₃, and HCO₃⁻ in the BECF rise exponentially, from zero to the values of an equilibrated solution at pH = 7.50, with a time constant τ_flow = 4 s. This τ_flow reflects the mixing of old and new solutions in the tubing (between the switches and the chamber) and the turnover of solution in the chamber. Recall that in the first paper in this series (14), we observed that the time constant for switching the solution in the chamber is ∼1.7 s. The difference between the measured τ of ∼1.7 s and the τ_flow of 4 s required to simulate a realistic t_p could reflect: 1) the special properties of the volume beneath the pH_S electrode and 2) the asymmetry of [CO₂] over the surface of the oocyte. Supporting 2), Fig. 18 in the second paper (15) shows that t_p is longer for the electrode positioned at the downstream side of the oocyte than the one positioned at the equator. Note that the present model considers neither 1) nor 2).

Intracellular vesicles.

In the physiological experiments, we consistently observe a time delay between the initiation of the pH_S spike and the start of the pH_i decline. Therefore, we used our revised mathematical model to investigate the dependence of the time delay on the presence of a layer of intracellular vesicles beneath the plasma membrane by implementing a tortuosity factor λ. The model predicts that increasing λ causes the simulated pH_i trajectory to decline more slowly (Fig. 4A), the time delay to increase (Fig. 4B), and the magnitude of (dpH_i/dt)_max to decrease (Fig. 4C). These results are consistent with the hypothesis that intracellular vesicles are, in part, responsible for the observed time delay. By offering resistance to diffusion of solutes (and in particular to CO₂), the vesicle layer presumably causes CO₂ to enter into the oocyte more slowly, thereby producing pH_i changes that occur later in time.

Vitelline membrane and pH_S electrode.

The implementation of the vitelline membrane is important to simulate pH_S transients that are large enough to approximate physiological values (Fig. 5A). When CO₂ enters (or leaves) the cell, diffusion and reaction are the two processes that compete to replenish (or deplete) CO₂ in the EM region. ΔpH_S is an index of the amount of protons that are consumed through the reaction HCO₃⁻ + H⁺ → CO₂ + H₂O (or produced through the opposite reaction, CO₂ + H₂O → HCO₃⁻ + H⁺) to replenish (or deplete) CO₂ during influx (or efflux). An extremely small ΔpH_S, which is what our simulation predicts without a vitelline membrane, indicates that the vast majority of the CO₂ is replenished (or depleted) via diffusion.

We implement the vitelline membrane by reducing the mobility of all solutes in the EM region by the same tortuosity factor γ. This approach reduces the contribution of diffusion and enhances that of reaction in the EM region. After examining the predictions of the model with increasing values of γ, we decided to use a value of γ ∼5.77 to set up the properties of a “typical” oocyte. However, we do not believe that the vitelline membrane by itself could offer such a high resistance to the diffusion of solutes. Instead, we hypothesize that the reason that the pH_S transients are so large is that the presence of the pH_S electrode creates a special environment, between the outer surface of the cell membrane and the flat surface of the electrode, where diffusion is largely reduced and reaction is enhanced. Thus, our current implementation of the vitelline membrane is a temporizing maneuver to mimic, as far as the pH_S time course is concerned, the presence of the pH_S electrode near the oocyte surface.

Because of the assumption of spherical symmetry, the vitelline membrane is implemented everywhere around the oocyte, whereas the pH_S electrode covers only a very tiny portion of the oocyte surface. Thus, choosing a large value for γ, while helpful to simulate ΔpH_S, tends to slow changes in pH_i. In our present implementation, to produce a realistically fast pH_i trajectory, we have compensated for the large γ by reducing λ (the resistance due to the layer of vesicles). The result, as noted in the previous section, is an unrealistically short t_d. Using a future model that could properly account for the volume beneath the pH_S electrode, we could reduce γ (resistance due to vitelline membrane) and replace it with an increased λ (resistance to due to layer of vesicles). The result would be more realistic values for both ΔpH_S and t_d.

CA II and CA IV.

In the present paper, our goal was to develop a mathematical model capable of reproducing the salient features of the physiological transients measured for pH_i [i.e., t_d, τ_pHi, (dpH_i/dt)_max, ΔpH_i] and for pH_S (i.e., t_p, ΔpH_S, τ_pHS) as we expose each oocyte type (“control”, “CA II,” and “CA IV”) to an extracellular solution containing or lacking CO₂/HCO₃⁻.

We began by focusing on the intrinsic properties of our in silico oocyte (i.e., in the absence of added CA). As described in results (see Standard Features of an In Silico Oocyte Experiment), we estimated reasonable parameter values for a “control” oocyte⁴—τ_flow = 4 s, λ ∼ 3.16, γ ∼ 5.77, A_i = 5, and A_S = 150—using physiological data obtained as we switched oocytes from a CO₂/HCO₃⁻-free solution to one containing 1.5% CO₂/10 mM HCO₃⁻/pH 7.50. Figure 13, A and B, is a replot of the CA II and CA IV analyses from Fig. 8, A and B, where the starting point for all simulations was a hypothetical oocyte with the composition of a CA IV oocyte.⁶ The point labeled “∼Ctrl” represents such a hypothetical oocyte with the CA properties of a “control” oocyte (i.e., A_i = 5, on the 150 A_S isopleth).

Our next step was to estimate reasonable parameters for “CA II” oocytes. Because injecting an oocyte with CA II ought to affect only the intracellular CA activity, we fixed A_S to the “control” value of 150, and estimated that A_i would have to be ∼1,000 to reproduce the pH_i and pH_S transients for an oocyte exposed to 1.5% CO₂/10 mM HCO₃⁻/pH 7.50. In Fig. 13, A and B, we represent this condition by the point labeled “∼CAII” (lavender vector).

Finally, we estimated parameters for an oocyte expressing CA IV. Our first thought was to fix A_i to the “control” value of 5, and then to estimate A_S. However, as pointed out in results, it is impossible to achieve reasonable values for (dpH_i/dt)_max or ΔpH_S if we leave A_i at 5. In Fig. 13, A and B, the point labeled “CA_S” represents a condition in which we raise A_S to 10,000 but leave A_i at 5 (red vector). In fact, inspection of Fig. 8, A and B, reveals that, at a fixed A_i of 5, raising A_S to even 50,000 has virtually no additional effect. To achieve reasonable increments in (dpH_i/dt)_max and ΔpH_S, we must also raise A_i by a small amount. As shown by the point labeled “CAIV” in Fig. 13, A and B, the combination of raising A_S from 150 to 10,000 (∼67-fold) and raising A_i from 5 to 40 (8-fold, but by an absolute amount that is rather small) is sufficient to approximately replicate, in our simulation, the physiologically observed (dpH_i/dt)_max and ΔpH_S values (green vector).

A question that arises is whether one can simulate the effects of CA IV expression by reversing the fold increases: raising A_i by 67-fold (from 5 to 335) and raising A_S by only 8-fold (from 150 to 1,200). Inspection of Fig. 8 reveals that this combination adequately predicts the (dpH_i/dt)_max data for CA IV oocytes (Fig. 8A) but produces ΔpH_S values that fall far below the physiological data (Fig. 8B). In fact, following the 1,000 A_S isopleth in Fig. 8B, the ΔpH_S effect of A_i saturates at ∼1,000. Thus, although a small increment in A_i is necessary to model the effects of CA IV expression, a much larger increment in A_S (e.g., to ∼5,000 in Fig. 8B) is also necessary.

The foregoing analysis reveals an important concept that we will call supra-additivity. If we raise A_S from 150 to 10,000 at a fixed A_i of 5, the effect on the two pH parameters is small (red vectors to the left in both Fig. 13, A and B). Conversely, if we raise A_i from 5 to 40 at a fixed A_S of 150, the effect on the two pH_i parameters is also small (blue vectors in Fig. 13, A and B). However, raising A_i and A_S simultaneously produces pH effects (green vectors) that are substantially larger than the sum of the two individual effects (brown vectors)—supra-additivity. The explanation for this effect is that adequate CA activity must be present on both sides of the membrane to optimize the CO₂ flux: CA on one side of the membrane helps to replenish CO₂ that has departed, and CA on the other side of the membrane helps dispose of newly arriving CO₂.

Is it reasonable that the expression of CA IV should increase cytosolic CA activity from 5 to 40? The preliminary immunohistochemistry work of Nakhoul et al. (16) on oocytes expressing CA IV has shown that CA IV is distributed both near the plasma membrane and near the intracellular vesicles. Recently, Schneider et al. (21) used a mass spectrometry approach to measure CA activity in oocytes expressing CA IV, with measurements on intact oocytes representing the extracellular activity of the CA IV, and measurements on lysed oocytes representing total (i.e., extracellular + intracellular) CA activity. These authors concluded that only ∼24% of the total CA activity is on the extracellular surface of the oocyte, and that ∼76% is in intracellular vesicles. Let us consider two scenarios:

• If extracellular CA IV activity is confined to a shell 1 μm thick (as it is in our simulations) immediately adjacent to the cell membrane, then this shell would represent ∼1% of the H₂O in an oocyte of radius 650 μm (assuming that an oocyte is 40% H₂O; ref. 29). Thus, if A_i = 40 and A_S = 10,000, then only ∼25% of total CA activity would be in the cytosol. If ∼76% of total oocyte CA IV is located in intracellular vesicles, then, to be consistent with our simulations, only about one-third could be available to catalyze cytosolic reactions.

• On the other hand, if extracellular CA IV is confined to a shell only 0.1 μm thick (A_S = 10,000), then we calculate that ∼78% of total CA activity would be in the cytosol, a figure virtually identical to the estimate of Schneider et al. (21). In this scenario, to be consistent with our simulations, virtually all vesicular CA IV would have to be available to catalyze cytosolic reactions with ∼100% efficiency.

Regardless of whether we consider the shell width to be 1 μm or 0.1 μm, it is clear that, because of the large discrepancy between cytosolic H₂O and the H₂O in which surface CA IV is distributed, cytosolic CA IV activity could be extremely low (e.g., A_i = 40) compared with cell-surface CA IV activity (e.g., A_S = 10,000) even if the vast majority of total CA IV protein were intracellular.

In summary, our simulations show that a small increase in cytosolic CA activity, representing a large amount of total CA IV protein, is necessary to account for the full-blown effects of CA IV as expressed in oocytes.

Conclusions and Future Directions

We have extended and improved the reaction-diffusion mathematical model of CO₂ influx into a Xenopus oocyte, presented in ref. 22. Enhancements to the model include the nine changes 1 through 9 in the legend of Fig. 1, which allow us to produce more realistic simulations of a Xenopus oocyte and of our experimental setup, capable of reproducing the salient features of our physiological experiments in the two companion papers. Because in our physiological experiments we do not have access to such parameters as CO₂ concentrations, we can use the output of the model to calculate these parameters (e.g., CO₂ fluxes across the plasma membrane for each oocyte type). The model supports the hypothesis that the cytosolic enzyme CA II and the GPI-linked extracellular CA IV enhance CO₂ fluxes across the plasma membrane by increasing transmembrane CO₂ gradients.

This revised version of the model is a major step forward towards simulating the measured pH_i and pH_S transients as we expose an oocyte to an extracellular solution containing or lacking CO₂/HCO₃⁻. However, as pointed out in the present paper and the two companion papers, the revised model has difficulties quantitatively reproducing certain aspects of the physiological experiments. These discrepancies between the physiological data and the model predictions are due to elements missing in the present reaction-diffusion model: 1) the special environment between the pH_S electrode and membrane and 2) the convective flow of BECF around the oocyte. Implementation of the pH_S electrode will allow us to reduce the resistance of the vitelline membrane and thereby produce more realistic simulations of both the measured pH_i and pH_S. Addressing the asymmetry issues will provide better agreement between τ_pHi and τ_pHS.

The revised model provides estimates of CA activity on the oocyte surface and in the cytosol. The model also will make it possible to produce rough estimates of the permeability of the oocyte membrane to CO₂, which will be invaluable for gas-channel research. Improved models that address the pH_S electrode and convective flow would improve each of these estimates, as well as our understanding of the complex acid-base chemistry that occurs on the surface and within living cells.

GRANTS

The work of R. Occhipinti was supported by a fellowship from the American Heart Association (11POST7670015). The work of R. Musa-Aziz was also supported by a fellowship from the American Heart Association (0625891T) and by Fundação de Amparo a Pesquisa do Estado de São Paulo (FAPESP no. 08/128663). W. F. Boron gratefully acknowledges the support of the Myers/Scarpa endowed chair. This work was supported by grants from the Office of Naval Research (N00014-05-1-0345, N00014-08-1-0532, and N00014-11-1-0889) and the National Institutes of Health (NS-18400 and DK-81567) to W. F. Boron.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

R.O., R.M.A., and W.F.B. conception and design of research; R.O. performed experiments; R.O. analyzed data; R.O., R.M.A., and W.F.B. interpreted results of experiments; R.O. prepared figures; R.O. and W.F.B. drafted manuscript; R.O., R.M.A., and W.F.B. edited and revised manuscript; R.O., R.M.A., and W.F.B. approved final version of manuscript.