Evidence from simultaneous intracellular- and surface-pH transients that carbonic anhydrase II enhances CO₂ fluxes across Xenopus oocyte plasma membranes

Abstract

The α-carbonic anhydrases (CAs) are zinc-containing enzymes that catalyze the interconversion of CO₂ and HCO₃⁻. Here, we focus on human CA II (CA II), a ubiquitous cytoplasmic enzyme. In the second paper in this series, we examine CA IV at the extracellular surface. After microinjecting recombinant CA II in a Tris solution (or just Tris) into oocytes, we expose oocytes to 1.5% CO₂/10 mM HCO₃⁻/pH 7.50 while using microelectrodes to monitor intracellular pH (pH_i) and surface pH (pH_S). CO₂ influx causes the familiar sustained pH_i fall as well as a transient pH_S rise; CO₂ efflux does the opposite. Both during CO₂ addition and removal, CA II increases the magnitudes of the maximal rate of pH_i change, (dpH_i/dt)_max, and the maximal change in pH_S, ΔpH_S. Preincubating oocytes with the inhibitor ethoxzolamide eliminates the effects of CA II. Compared with pH_S, pH_i begins to change only after a delay of ∼9 s and its relaxation has a larger (i.e., slower) time constant (τ_pHi > τ_pHS). Simultaneous measurements with two pH_i electrodes, one superficial and one deep, suggest that impalement depth contributes to pH_i delay and higher τ_pHi. Using higher CO₂/HCO₃⁻ levels, i.e., 5%/33 mM HCO₃⁻ or 10%/66 mM HCO₃⁻, increases (dpH_i/dt)_max and ΔpH_S, though not in proportion to the increase in [CO₂]. A reaction-diffusion mathematical model (described in the third paper in this series) accounts for the above general features and supports the conclusion that cytosolic CA—consuming entering CO₂ or replenishing exiting CO₂—increases CO₂ fluxes across the cell membrane.

the α-carbonic anhydrases (CAs) are a family of zinc-containing enzymes that catalyze the interconversion of CO₂ and HCO₃⁻. Of the 15 human CAs (32, 37, 68), 12 are known to be active (54) in catalyzing the reaction CO₂ + H₂O ⇌ HCO₃⁻ + H⁺, thereby bypassing the slow CO₂-hydration/dehydration reactions involving H₂CO₃. Three CAs—CA VIII (34, 64), CA X (50), and CA XI (23)—lack at least one of the three conserved histidine residues that coordinate Zn²⁺ in other CAs. Because Zn²⁺ is required for carbonic-anhydrase activity, and because the three His residues are required for high-affinity binding of Zn²⁺, it is reasonable to suggest that CA VIII, X, and XI are not catalytically active. Indeed, Sjöblom et al. (63) restored the CA activity of CA VIII by making two simultaneous point mutations: converting an Arg residue to the His that is conserved in catalytically active α-CAs, and converting a Glu residue to a conserved Gln.

Although CA VIII, X, and XI do not have clear physiological roles, the catalytically active CAs are major players in a variety of physiological processes that involve CO₂ and HCO₃⁻ transport across cell membranes. These processes include CO₂ carriage by erythrocytes (42), HCO₃⁻ transport across epithelia (11, 21, 36, 53, 54), fluid transport across epithelia (2, 18, 35, 40, 53, 62), transient changes in extracellular pH in the brain (12), and the speed of certain intracellular pH transients (58, 71). For a particular animal species, the enzymatically active α-CAs differ in catalytic activity, affinity for CO₂, inhibitor sensitivity, and expression pattern (32, 54, 65). Deficiency of CA II is associated with osteopetrosis, renal-tubular acidosis, and cerebral calcification (65). Moreover, CA blockers are used clinically to treat glaucoma (2, 6, 39, 60), metabolic and respiratory alkalosis (3–6), and acute mountain sickness (4, 6, 55, 69, 74), and are also weak diuretics (4–6).

In 1973, Gutknecht and Tosteson (30) explored factors that influence the diffusion of salicylic acid across an artificial lipid bilayer. They concluded that the reaction HA ⇌ H⁺ + A⁻ (where A⁻ is the salicylate anion) in the unstirred layers near the membrane, as well as the presence of non-salicylate buffers, plays a major role in enhancing HA flux across the membrane. They also predicted that non-CO₂/HCO₃⁻ buffers would accelerate the flux of CO₂. However, in 1977, Gutknecht et al. (29) reported that non-CO₂/HCO₃⁻ buffers (phosphate, HEPES, Tris) enhance CO₂ fluxes across lipid bilayers—measured using ¹⁴C-labeled CO₂—only in the presence of mobile CA.

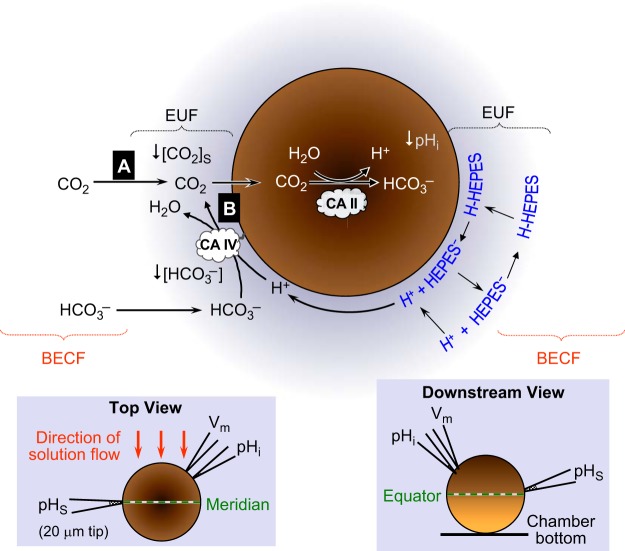
The purpose of the present study, summarized in this paper and its two companions (46, 49), is to elucidate the influence of CAs and non-CO₂/HCO₃⁻ buffers on CO₂ fluxes across the plasma membranes of living cells.¹ In 1984, De Hemptinne and Huguenin (31) used a miniaturized electrode, with a glass sensor, to monitor the pH at the extracellular surface (pH_S) of rat soleus muscle as they applied CO₂/HCO₃⁻. They observed a transient rise in pH_S that, as they pointed out, presumably reflected the influx of CO₂, which would promote the following reaction at the extracellular surface of the cell: H⁺ + HCO₃⁻ → CO₂ + H₂O. We and our collaborators used an adaptation of this pH_S approach to study the role of aquaporins and rhesus proteins as CO₂ channels (14, 22, 24–26, 45). In the present study, we chose to use this adapted pH_S approach, as well as simultaneous measurements of intracellular pH (pH_i), to assess the CO₂ fluxes across the membranes of Xenopus oocytes. In this first paper, we examine the effect of microinjecting oocytes with the soluble enzyme CA II. We chose to work with CA II because it is ubiquitous and has the highest enzymatic activity of all CAs (reviewed in ref. 54). In the second paper (46), we examine the effect of expressing CA IV (GPI-linked to the extracellular cell surface), with and without CA II in the bulk extracellular fluid (BECF). Early exploratory work by Nakhoul et al. (48) on the heterologous expression of CA IV in oocytes motivated portions of this project. In the third paper (49), we extend the three-dimensional reaction-diffusion model of Somersalo et al. (66) to assist in the interpretation of our pH_i and pH_S data in the other two papers. This model, an an extension of the single-compartment approach developed by Boron and De Weer (9), treats the oocyte as a spherical symmetric cell, with simultaneous reaction and diffusion processes occurring in both the extracellular unconvected fluid (EUF, an extension of the unstirred-layer concept) and the intracellular fluid (ICF). The model accounts for the slow equilibration CO₂ + H₂O ⇌ H₂CO₃, effective acceleration of this reaction by CA II and CA IV, and competing equilibria from a multitude of non-CO₂/HCO₃⁻ buffers in both EUF and ICF.

Our basic experimental protocol was to expose an oocyte—importantly, an oocyte not expressing any HCO₃⁻ transporters—to a solution containing 1.5% CO₂/10 mM HCO₃⁻/pH 7.50 (Fig. 1). The CO₂ influx causes the familiar fall in pH_i (for review, see ref. 58), which intracellular CA ought to accelerate, as first observed by Thomas (71). The influx of CO₂ should also reduce [CO₂]_S. The depleted CO₂ at the cell surface is replenished by 1) diffusion from the BECF and 2) the reaction HCO₃⁻ + H⁺ → CO₂ + H₂O at the cell surface. Because this reaction consumes H⁺, pH_S rises, as observed by De Hemptinne and Huguenin (31) and by Saarikoski and Kaila (59). The reaction also depletes HCO₃⁻ at the cell surface, and we would expect that the diffusion of H⁺ and HCO₃⁻ from the BECF would replenish the depleted H⁺ and HCO₃⁻ at the cell surface. If an extracellular buffer, such as HEPES, is present, it would undergo the reaction H-HEPES → H⁺ + HEPES⁻ at the cell surface and thereby reduce the magnitude of the pH_S increase. However, according to the experiments of Gutknecht et al. (29), this HEPES reaction should substantially raise [CO₂]_S (and thus enhance the influx of CO₂) in the presence of mobile extracellular CA.² Over time, as [CO₂]_i approaches [CO₂]_S, and as [CO₂]_S approaches [CO₂]_BECF, all of these fluxes and reactions slow and the system reaches equilibrium.

Fig. 1.

Model of an oocyte exposed to CO₂/HCO₃⁻. The main part of the figure illustrates the diffusion and reaction events as CO₂ enters an oocyte. The black arrows with sharp heads indicate solute diffusion in the extracellular unconvected fluid (EUF) and intracellular fluid. The black arrows with dull heads indicate reactions. The left inset is a schematic top view of the oocyte in the chamber, as seen through the microscope. The orange arrows indicate the direction of convective flow of the bulk extracellular fluid (BECF). The right inset is a schematic view of the oocyte along the axis of convective flow, looking downstream. The darker half of the oocyte, oriented upward, is the animal pole. CA II, carbonic anhydrase II; pH_i, intracellular pH; pH_S, surface pH.

In this first paper, we find that applying 1.5% CO₂/10 mM HCO₃⁻ (at a fixed pH of 7.50) does indeed cause pH_S to rise transiently and then decay with an exponential time course. pH_i also falls with an exponential time course, but more slowly, reflecting the depth of the penetration of the pH_i electrode into the cell as well as the asymmetry of [CO₂]_S as BECF flows past the oocyte. Injecting CA II into the oocyte not only accelerates the decline in pH_i but also increases the height and the rate of decay of the pH_S spike. The CA II inhibitor ethoxzolamide (EZA) blocks all of the effects of CA II. Our pH_S data imply that, by speeding the conversion of incoming CO₂ to HCO₃⁻ + H⁺, intracellular CA II keeps [CO₂]_i relatively low and thus enhances the gradient driving CO₂ influx. In turn, this increased CO₂ influx enhances the fall in [CO₂]_S, and thus accentuates the pH_S spike. A mathematical model, which is discussed in the third paper in this series (49), supports this hypothesis.

MATERIALS AND METHODS

Preparation of Xenopus Oocytes

We isolated stage V-VI oocytes from Xenopus laevis using standard techniques (27). Briefly, we anesthetized animals in 0.2% MS-222 (ethyl 3-aminobenzoate methanesulfonate, Sigma-Aldrich, St. Louis, MO) and removed ovarian lobes, which we placed in a 0-Ca solution (98 mM NaCl, 2 mM KCl, 1 mM MgCl2, 5 mM HEPES, pH 7.50). After washing the oocytes 5× in the 0-Ca solution, we dissociated and defolliculated them by enzymatic digestion, using 2 mg/ml type IA collagenase (Sigma-Aldrich) in the 0-Ca solution. We selected stage V-VI oocytes and kept them at 18°C in sterile-filtered OR3 medium, each 2 liters of which contained one pack of powdered Leibovitz L-15 media with l-glutamine (GIBCO-BRL), 100 ml of 10,000 U/ml penicillin, 10,000 U/ml streptomycin solution (Sigma-Aldrich), and 5 mM HEPES titrated to pH 7.50, and osmolality adjusted to 195 mosmol/kgH₂O. One day after their isolation, we injected the oocytes with 50 nl of H₂O as a control for the injection of cRNA encoding CA IV in the accompanying paper (46). Three days after this H₂O injection, we injected the oocytes with 50 nl of fluid, either Tris buffer (50 mM titrated to pH 7.5 with HCl) or Tris buffer containing 6 ng/nl of recombinant human CA II protein (i.e., 300 ng/oocyte ≅ 10 pmol, for a final [CA II]_i of ∼30 μM, ∼50% higher than the level in red blood cells). Dr. Peter Piermarini kindly prepared the CA II, as described previously (38, 52), using an approach similar to that described by others (70), and assessing protein purity by polyacrylamide gel electrophoresis (PAGE) and MALDI mass spectrometry (SynPep, Dublin, CA). After the Tris or CA II injection, we incubated the oocytes overnight at 18°C in the sterile-filtered OR3 medium described above. The protocols for housing and handling of Xenopus laevis were approved by the Institutional Animal Care and Use Committee of Case Western Reserve and Yale Universities.

Solutions

Table 1 summarizes the composition of the solutions. The ND96 solution is nominally CO₂/HCO₃⁻ free. The CO₂/HCO₃⁻ solutions were bubbled vigorously with the appropriate gas mixture (balance O₂) for ∼30 min.

Table 1.

Solutions

		1.5% CO2/10 mM HCO3−			5% CO2/33 mM HCO3−			10% CO2/66 mM HCO3−
			HEPES			HEPES			HEPES
Component	ND96	1	5	25	1	5	25	1	5	25
	Sol. 1	Sol. 2	Sol. 3	Sol. 4	Sol. 5	Sol. 6	Sol. 7	Sol. 8	Sol. 9	Sol. 10
NaCl, mM*	96	88	86	76	65	63	53	32	30	20
KCl, mM	2	2	2	2	2	2	2	2	2	2
MgCl2, mM	1	1	1	1	1	1	1	1	1	1
CaCl2, mM	1.8	1.8	1.8	1.8	1.8	1.8	1.8	1.8	1.8	1.8
HEPES, mM*	5	1	5	25	1	5	25	1	5	25
HCO3−, mM	0	10	10	10	33	33	33	66	66	66
pH	7.5	7.5	7.5	7.5	7.5	7.5	7.5	7.5	7.5	7.5
Osmolality, mosmol/kgH2O	≅195	≅195	≅195	≅195	≅195	≅195	≅195	≅195	≅195	≅195

^*We titrated HEPES free acid (pK 7.5) to pH 7.5 with NaOH (so that, theoretically, we have incremented H-HEPES, HEPES⁻, and Na⁺ concentrations by equal amounts) and then secondarily adjusted [NaCl], as indicated in this table, to achieve a final osmolality of ∼195 mosmol/kgH₂O.

We dissolved the CA II inhibitor EZA (Sigma-Aldrich) in 0.05 N NaOH, to prepare a stock solution with a final concentration of 50 mM. We achieved a final EZA concentration of 400 μM by diluting this stock 1:125 in ND96, and adjusted the pH to 7.50 with 5 N HCl.

Electrophysiological Measurements

Figure 8B in Ref. 44 provides a detailed view of the arrangement of the chamber, oocyte, and electrodes.

Fig. 8.

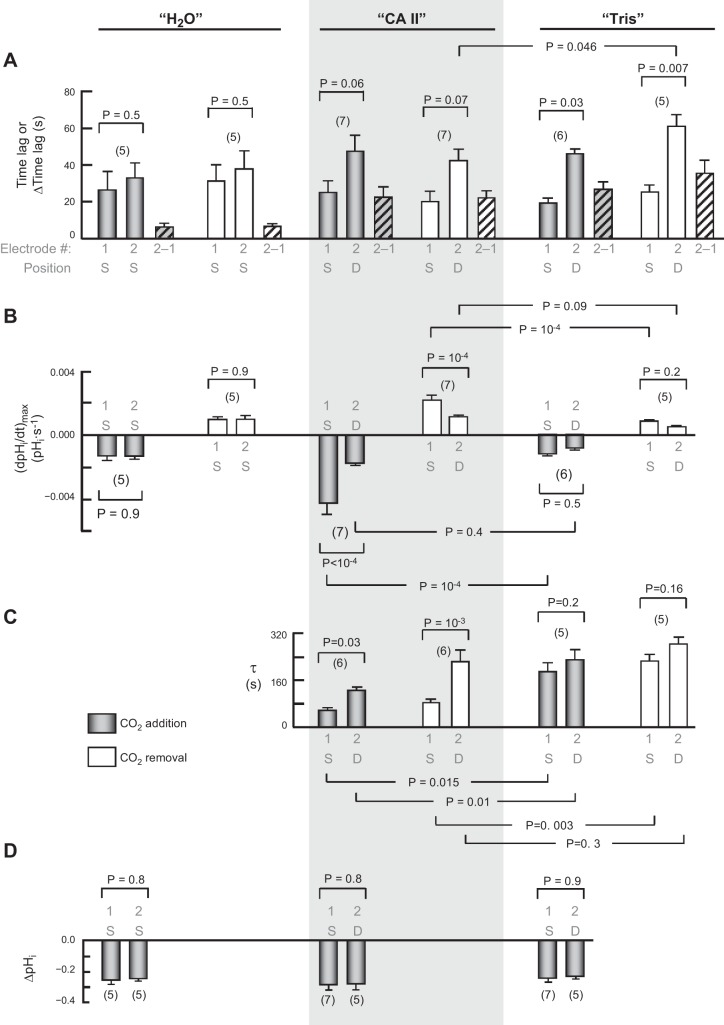
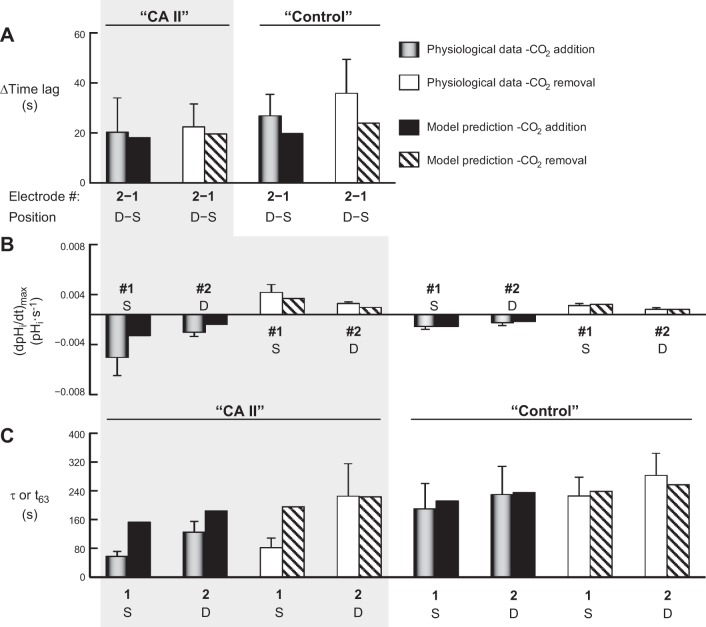
Summary of dual pH_i-electrode impalements. This figure summarizes results from a larger number of experiments, such as those in Fig. 7. We injected all oocytes with H₂O on day 0. Those for which this was the only injection are labeled “H₂O.” We impaled these oocytes superficially (S) with two pH_i microelectrodes, electrode no. 1 positioned by a manual manipulator (the one that held pH_i electrodes in other protocols), and electrode no. 2 positioned by a motorized manipulator (the one that held pH_S electrodes in other protocols). For other oocytes, we followed the injection of water on day 0 with the injection on day 3 with either “CA II” in Tris buffer, or only “Tris.” We impaled these oocytes superficially with pH_i microelectrode no. 1, and deep (D) with electrode no. 2. A: time lags between initiation of the transients for pH_i electrodes no. 1 and no. 2. The hatched bars represent the oocyte-by-oocyte difference between electrodes no. 2 and no. 1. An ANOVA for the six differences in time lags between electrode no. 2 and electrode no. 1 (six hatched bars) had an overall P value of 0.0003. The two “H₂O” values were significantly different from the others. B: maximal rates of pH_i change (negative or positive direction) produced by the extracellular solution switch. C: time constants (τ) for pH_i changes. D: changes in steady-state pH_i induced by the addition of CO₂/HCO₃⁻. Values are means ± SE, with nos. of oocytes in parentheses. We performed a one-way ANOVA, followed by a Student-Newman-Keuls (SNK) analysis (P shown for individual comparisons). The initial pH_i values for “H₂O”, “CA II”, and “Tris” oocytes in the ND96 (i.e., CO₂/HCO₃⁻-free) solution were not significantly different from one another, both for electrode no. 1 and electrode no. 2 (overall ANOVA, P = 0.81).

Chamber.

We placed an oocyte in a plastic perfusion chamber with a channel 3 mm wide × 30 mm long. A glass coverslip formed the bottom of the chamber. Solutions were placed in 140-ml plastic syringes (Sherwood Medical, St. Louis, MO) and delivered to the chamber using syringe pumps (Harvard Apparatus, South Natick, MA). Solutions were carried to the chamber via Tygon tubing (Ryan Herco Products, Burbank, CA; Formulation R3603-3; OD 4.8 mm/ID 1.6 mm) and flowed from one end of the 30-mm channel to the other. In initial experiments for the data set summarized below in Fig. 3, the solution flowed at 2 ml/min, and in later experiments, 3 ml/min. As noted in results, it does not appear that this change had a significant effect. For all other data sets in this paper, solutions flowed at 3 ml/min. We switched among solutions with pneumatically operated valves (Clippard Instrument Laboratory, Cincinnati, OH). All experiments were performed at room temperature (∼22°C), and in all experiments, the oocyte was initially superfused with the ND96 solution.

Fig. 3.

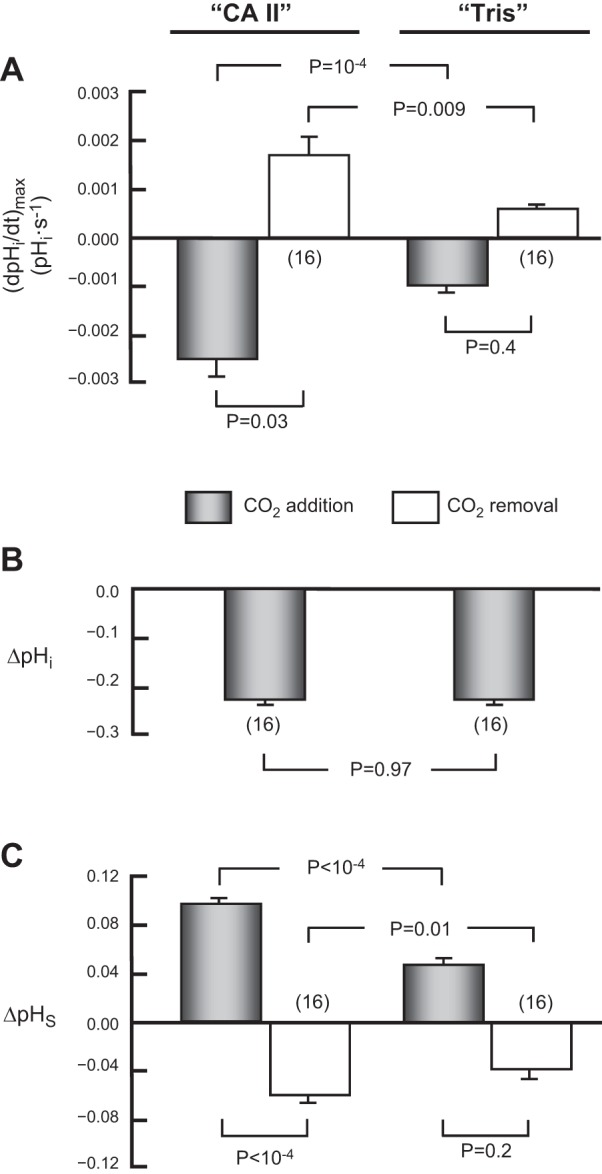
Summary of effects of CA II on pH_i and pH_S. This figure summarizes results from a larger number of experiments, such as those in Fig. 2, on oocytes injected with CA II in Tris buffer, or only Tris buffer. In each case, we switched the extracellular solution from ND96 to 1.5% CO₂/10 mM HCO₃⁻ (gray bars) and vice versa (white bars). A: maximal rates of pH_i change (negative or positive direction) produced by the extracellular solution switch. B: changes in steady-state pH_i, induced by the addition of CO₂/HCO₃⁻. C: maximal changes in pH_S (positive or negative direction) caused by the extracellular solution switch. This summary includes all oocytes injected with CA II (and exposed to 1.5% CO₂ in 5 mM HEPES) in the present study, as well as their day-matched Tris-injected controls. Values are means ± SE, with nos. of oocytes in parentheses. We performed a one-way ANOVA (overall P values: P < 10⁻⁴ in A, and P < 10⁻⁴ in C), followed by a Student-Newman-Keuls (SNK) analysis (P shown for individual comparisons). We performed a paired t-test in B. The mean initial pH_i for “CA II” oocytes in the CO₂/HCO₃⁻-free ND96 solution was 7.21 ± 0.05 (n = 16). This mean is not significantly different from that for “Tris” oocytes, 7.22 ± 0.03 (n = 16; P = 0.93).⁸

Measurement of intracellular pH.

In a typical experiment, we impaled the oocyte (with the dark animal pole facing upward) with two microelectrodes (Fig. 1, left and right insets), one for sensing membrane potential (V_m, amplified by a model OC-725 two-electrode Oocyte Clamp, Warner Instruments, Hamden, CT) and the other for sensing pH_i (amplified by a model FD223 high-impedance electrometer, World Precision Instruments, Sarasota, FL). We fabricated and used the electrodes as described previously (56, 57, 61). We used a horizontal microelectrode puller (model P-97, Sutter Instrument, Novato, CA) to produce microelectrodes from thin-walled borosilicate glass (part no. G200TF-4, 2.0 mm OD ×1.56 mm ID, Warner Instruments). We filled the V_m electrodes with 3 M KCl; these had resistances of ∼0.6 MΩ. The pH_i electrodes were identical but we filled them with a liquid, pH-sensitive membrane (Hydrogen Ionophore I, mixture B, Fluka Chemical, Ronkonkoma, NY).

The extracellular reference for the V_m electrode was the virtual ground created by the Warner OC-725 Oocyte Clamp. The I_SENSE connection was attached to a microelectrode holder (model 64-1010, Warner Instruments), which contained a Ag/AgCl half-cell that served as a bridge to a broken-tipped glass microelectrode filled with 3 M KCl (∼0.1 MΩ), and positioned so that its tip was close to the oocyte. The I_OUT connection was attached to a platinum wire that rested in a reservoir at the end of the chamber's channel (i.e., downstream from the oocyte). The circuit ground of the OC-725 (i.e., the virtual ground of the BECF or bath), and indeed the circuit grounds of all electronic components, was connected to a brass plate (i.e., “system ground”), which was in turn connected to earth.

We obtained the voltage due to pH_i by electronically subtracting the signal of the V_m electrode from that of the pH_i electrode. We obtained V_m by electronically subtracting the system ground of the OC-725 from the signal of the V_m electrode. The device that performed the subtractions (Yale University Subtraction Amplifier, V3.1) also appropriately scaled the voltages for the inputs of an analog-to-digital converter within a Windows-based computer. We simultaneously acquired all electrical data, initially, once every 2,000 ms, later once every 1,000 ms, and finally once every 500 ms, and analyzed it using software written in-house. As noted in the discussion, these differences do not appear to affect our data. We obtained the slope of the intracellular pH electrodes by calibrating pH standards at pH 6.0 and 8.0 (model SB 104-1 and SB 112-1, respectively, Fisher Scientific, Fair Lawn, NJ). An additional single-point calibration was obtained in the ND96 solution (pH 7.50) in the bath before impaling the oocyte. Oocytes had a spontaneous V_m at least as negative as −40 mV.

Measurement of surface pH.

In addition to the electrodes described above, in a typical experiment we measured pH_S using a liquid-ion-exchange pH electrode (Fig. 1, left and right insets) with an outer tip diameter of 20 μm (amplified by a FD223 electrometer, WPI). We pulled these pipettes from standard-wall borosilicate tubing (part no. G200F-4, 2.0 mm OD ×1.16 mm ID, Warner Instruments) and used a microforge to break off and fire polish the tips as one would for a giant-patch pipette (33). During experiments, we attach the pH_S electrode to an ultra-fine computer-controlled micromanipulator with digital position display (model MPC-200 system, Sutter Instrument).

A typical experiment begins with the pH_S electrode tip in the bath—in the “home” position, ∼300 μm from the oocyte surface—to calibrate the electrode at pH 7.50 in ND96 solution (Table 1). After that, we move the flat tip of the pH_S electrode to the oocyte's surface—the “zero” position—near the equator (i.e., between the animal and vegetal poles, halfway between top and bottom), and ∼5° behind the meridian perpendicular to the axis of flow (i.e., slightly in the “shadow” of the flowing extracellular solution), as illustrated in the left inset of Fig. 1. Finally, we further advance the electrode tip ∼40 μm until we observe a slight dimple in the membrane. The creation of this small dimple produces a microenvironment between the pH_S electrode tip and the oocyte membrane and has two effects: 1) maximizing the pH_S change and 2) ensuring a consistent and reproducible electrode placement, in the radial direction, on the oocyte membrane for each experiment, and thus minimizing variability from experiment to experiment. During the experiment, we periodically withdraw the electrode to its “home” position for recalibration in the flowing BECF solution at pH 7.50. In the figures, we indicate these movements of the pH_S electrode in the radial direction by “Surface” and “BECF” in the step chart.

The external reference for the pH_S electrode was a very long, broken-tipped (∼10 μm ID) glass micropipette that we pulled from the above from thin-walled borosilicate tubing on a rotating micropipette puller (model 51.511, Stoelting, Chicago, IL), filled with 3 M KCl, and bridged with a calomel half-cell to the input of a model 750 electrometer (WPI). pH_S was obtained by subtracting the calomel signal from the pH_S signal. As for the pH_i electrodes, we obtained the slope of the pH_S electrodes by calibrating pH standards at pH 6.0 and 8.0. In preliminary experiments, we found that the slope of the electrodes was the same in ND96 vs. CO₂/HCO₃⁻.

Dual measurement of intracellular pH.

In some experiments, we replaced the above pH_S microelectrode with a second sharp pH_i microelectrode (designated electrode no. 2), which we moved using the same Sutter 200 micromanipulator that otherwise carried the pH_S electrode.

Rate of bath solution change.

In mock experiments, we used pH_i and pH_S electrodes (sampling 1 per 500 ms) to monitor the pH of the bath (flowing at 3 ml/min) as we switched from a pH-7.5 to a pH-8.0 solution. We found that the time constant (τ) for the reported time course of pH was 1.76 ± 0.13 s (n = 3) for pH_i and 1.70 ± 0.35 s (n = 4) for pH_S. Because these τ figures include the response time of the electrodes, ∼1.7 s is the maximum τ for switching the solution in the chamber.

Analysis of pH Data

Intracellular pH.

Applying extracellular CO₂/HCO₃⁻ causes a fall in the measured pH_i that at first begins slowly (presumably reflecting the finite time required for [CO₂]_BECF to rise to its maximal value, the depth of penetration of the electrode into the cell, and the asymmetry of [CO₂]_S over the oocyte surface) and then accelerates to the maximal rate of decline—(dpH_i/dt)_max. The rate of pH_i decline then slows and gradually falls to zero. For example, in CA II experiments such as that in Fig. 2A below (summarized in Fig. 3 below), the fall in pH_i accelerated for an average of 9 ± 1 s (n = 16) before reaching the period of steepest decline. By inspection, we determined the time interval (which lasted an average of 39 ± 4 s, n = 16) during which pH_i declined most steeply and used software written in-house to perform a linear least-square curve fit to compute (dpH_i/dt)_max.

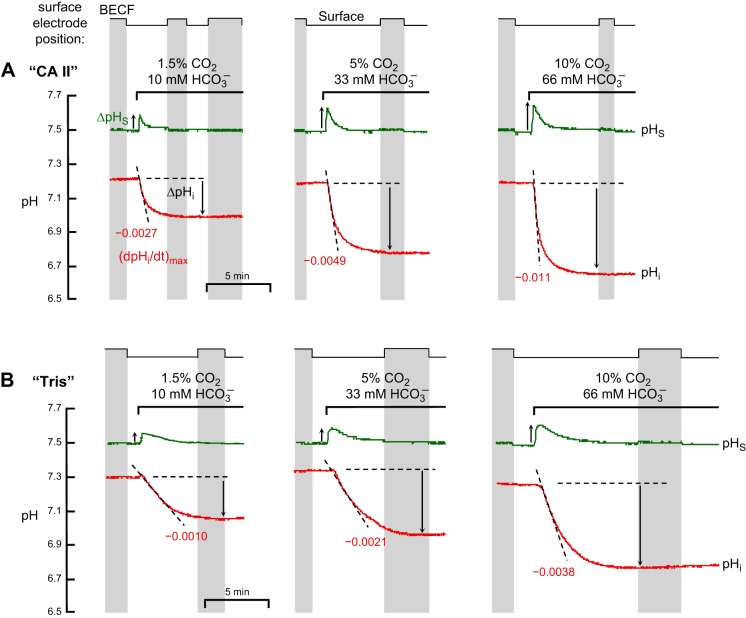
Fig. 2.

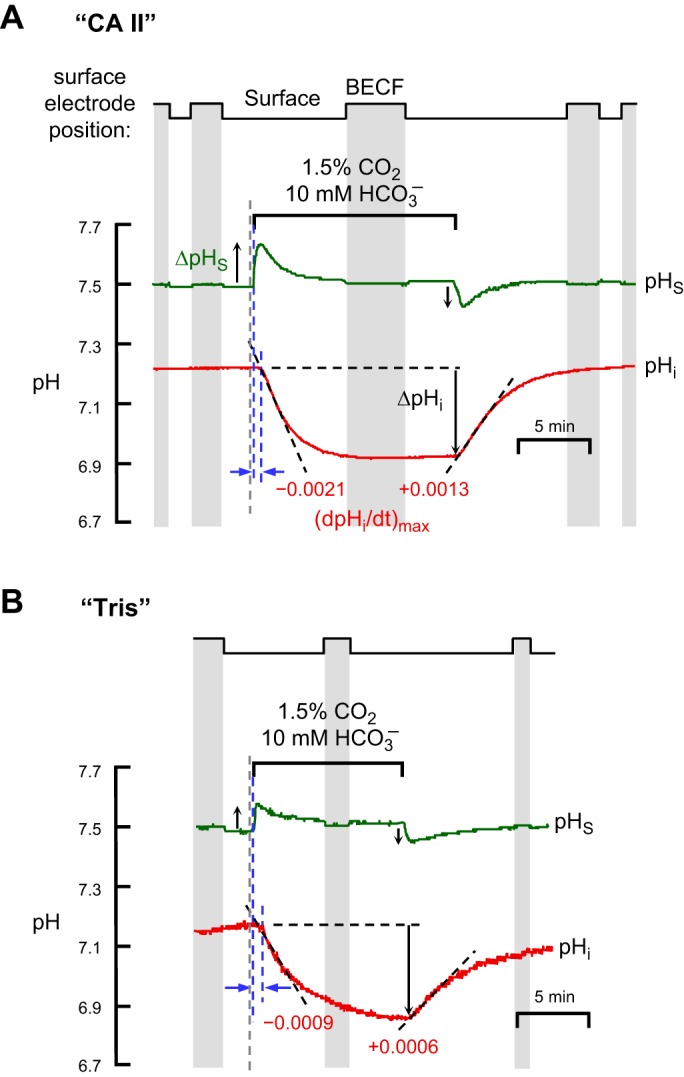
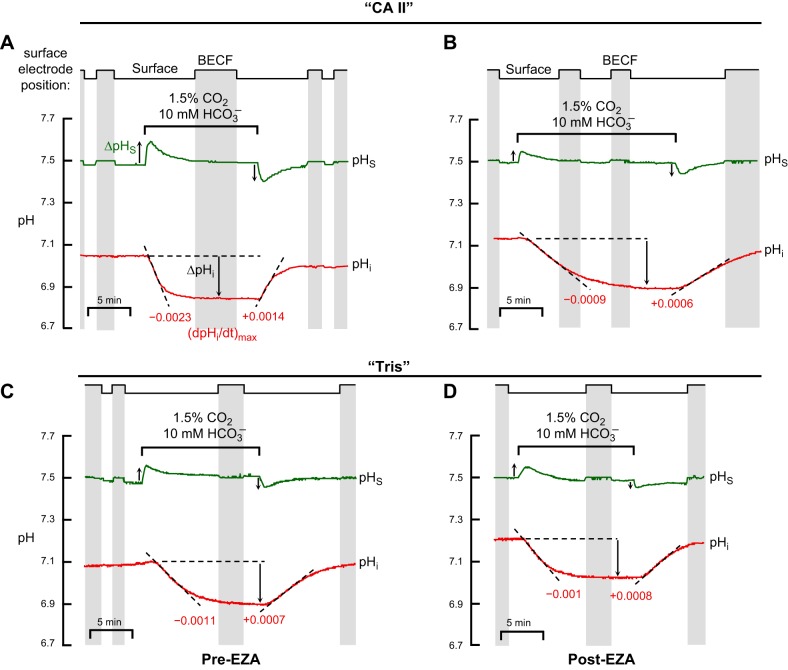
Representative experiments showing effects of CA II on pH_i and pH_S changes evoked by application and removal of CO₂/HCO₃⁻. A: oocytes injected with recombinant human CA II dissolved in Tris buffer. B: oocytes injected only with Tris buffer. Both in “CA II” or “Tris” oocytes, the pH_i trace is represented by the red lower record, and pH_S, by the green upper record. At the indicated times, we switched the extracellular solution from ND96 to 1.5% CO₂/10 mM HCO₃⁻/pH 7.50 (Table 1) and then back again. In this example, the extracellular solution flowed at 2 ml/min and the sampling rate was 1 per 1,000 ms. The vertical gray bands represent periods during which the pH_S electrode was withdrawn to the BECF for calibration. At other times the pH_S electrode was dimpling ∼40 μm into the oocyte surface. The gray, dashed vertical lines represent the times that the computer switched the valves to initiate a change of solutions. The left and right blue, dashed vertical lines (see results) represent the initiation of the pH_S and pH_i transients, respectively. The dashed black lines through the initial portions of the pH_i records for CO₂ application and removal represent best linear fits for maximal rates of pH_i change (negative or positive direction). The downward vertical arrows near the pH_i records represent the CO₂-induced changes in steady-state pH_i. The upward and downward arrows near the pH_S records represent maximal changes in pH_S (positive or negative direction).

In a subset of experiments, we used a nonlinear least-squares approach to obtain the best fit of a single-exponential function to the pH_i vs. time record.

Intrinsic intracellular buffering power.

We computed the intrinsic intracellular buffering power [β_I, mM·(pH unit)⁻¹] from the magnitude of the change in steady-state pH_i produced by exposing the cells to a solution containing 1.5% CO₂/10 mM HCO₃⁻. Because the amount of intracellular H⁺ generated by the influx of CO₂ is virtually the same as the resulting rise in intracellular [HCO₃⁻] (see ref. 58),

$${\beta }_{\text{I}}=-\frac{\Delta {\left[{\text{HCO}}_3^{-}\right]}_{\text{i}}}{\Delta {\text{pH}}_{\text{i}}}$$ (1)

The initial [HCO₃⁻]_i is assumed to be zero, and the final [HCO₃⁻]_i is computed from the steady-state pH_i and the Henderson-Hasselbalch equation. ΔpH_i is the magnitude of the fall in steady-state pH_i caused by the exposure to CO₂/HCO₃⁻.

Surface pH.

Applying extracellular CO₂/HCO₃⁻ causes pH_S to rise rapidly and then decline. We determined the maximum size of the pH_S transient (i.e., the “spike height” or ΔpH_S) as follows. The initial pH_S, before application of CO₂/HCO₃⁻ (i.e., with the oocyte in ND96 solution, Table 1), was computed by comparing the “pH_S” voltage reading obtained with the electrode tip at the oocyte surface with the “pH_S” voltage reading obtained with the electrode tip in the BECF (assumed to have a pH of 7.50). The peak pH_S during the CO₂/HCO₃⁻ exposure was computed by comparing the “pH_S” voltage reading obtained with the electrode tip at the oocyte surface (at a time corresponding to the highest pH_S) with the “pH_S” voltage reading obtained a few minutes later (after pH_S declined to ∼7.50) when we temporarily withdrew the electrode tip to the BECF (assumed to have a pH of 7.50). ΔpH_S was the difference between the peak pH_S in CO₂/HCO₃⁻ and the pH_S measured in ND96, just before the switch to CO₂/HCO₃⁻.

We used a similar approach to determine the maximum magnitude of the pH_S transient (i.e., an acidification) that occurred when we removed extracellular CO₂/HCO₃⁻.

In some experiments, we used a nonlinear least-squares approach to obtain the best fit of a single-exponential function to the pH_S vs. time record.

Statistics

Data are reported as means ± SE unless stated otherwise. To compare the difference between two means, Student's t-tests (two tails) was performed. To compare more than two means, one-way ANOVA Multiple Comparison was performed, followed by a Student-Newman-Keuls (SNK) analysis, using KaleidaGraph (version 4, Synergy Software). P < 0.05 was considered significant.

RESULTS

Effect of Injected CA II on pH_i and pH_S Changes

Protocol.

Figure 2 shows a pair of experiments in which we examined the effects of CA II on the pH_i and pH_S transients caused by applying and then removing 1.5% CO₂/10 mM HCO₃⁻ at a constant pH_BECF of 7.50. Our protocol to evaluate the effects of injected CA II was the same as previously employed by Lu et al. (38), except that in the present study we monitored pH_S in addition to pH_i. 1) Our first step was to inject H₂O into all Xenopus oocytes (day 0/step a); we did this as a control for experiments in the second paper in this series (46), in which, on day 0, we injected cRNA encoding CA IV. 2) After waiting 3 days, we randomly divided the oocytes into two groups (day 3/step b). We injected each oocyte in one group with 300 ng (or ∼10⁻¹¹ mol) of recombinant human CA II protein dissolved in Tris buffer (“CA II” group), and injected each oocyte in the other group with just the Tris buffer (“Tris” group). 3) One day later, we did our pH measurements (day 4/step c), such as those shown in Fig. 2.

The step chart at the top of Fig. 2, A and B, shows whether the extracellular pH electrode was in the BECF (gray background) or at the cell surface, dimpling ∼40 μm into the oocyte surface (white background).

pH_i changes.

An exposure to 1.5% CO₂/10 mM HCO₃⁻, causes pH_i to decrease much faster in a “CA II” oocyte (Fig. 2A, lower record) than in a “Tris” oocyte (Fig. 2B, lower record). We would expect these results, even if CA II did not increase the CO₂ influx, simply because the enzyme catalyzes the conversion of incoming intracellular CO₂ to produce HCO₃⁻ plus the intracellular H⁺ that the pH_i electrode senses (see Fig. 1). We define the maximal rate of pH_i change as (dpH_i/dt)_max; it is negative for CO₂ influx and positive for CO₂ efflux. As indicated by the two gray bars in Fig. 3A, which summarizes data for a larger series of experiments, the CO₂-induced maximal intracellular acidification rate, (dpH_i/dt)_max, is 2.5-fold greater in the presence of CA II than in its absence. However, as shown in Fig. 2 and summarized by Fig. 3B, CA II had no effect on the CO₂-induced change in steady-state pH_i (ΔpH_i). The most straightforward explanation for this result is that CA II affected neither the intrinsic buffering power of the oocyte (β_I) nor the total net entry of CO₂ into the cytosol.

pH_S changes.

The upper records in Fig. 2, A and B, show that applying of CO₂/HCO₃⁻ causes a transient rise in pH_S, as previously reported (22, 31). We define the maximal pH_S change as ΔpH_S; it is positive for CO₂ influx and negative for CO₂ efflux. Note that intracellular CA II markedly increases ΔpH_S, which, as outlined in Fig. 1, reflects the maximal rate of CO₂ entry into the cell. The gray bars in Fig. 3C show that CA II increases the mean ΔpH_S by approximately twofold. Thus, these pH_S data show that CA II speeds the influx of CO₂. CA II presumably produces this effect by keeping [CO₂]_i—especially at the inner surface of the membrane, but throughout the cytosol—relatively low during the initial part of the experiment.

Reversibility.

As shown in Fig. 2, A and B, and summarized in Fig. 3, A and C, removing CO₂/HCO₃⁻ causes pH_i and pH_S changes that are opposite in direction of those evoked by applying CO₂/HCO₃⁻. However, at least in the case of “CA II” oocytes, the magnitudes of (dpH_i/dt)_max and ΔpH_S are smaller for CO₂ removal than for CO₂ addition. We will revisit this subject in Fig. 6 below and consider the basis for the differences, in the context of the mathematical model, in the discussion (see section “Asymmetry of pH Changes Upon Addition vs. Removal of CO₂”).

Fig. 6.

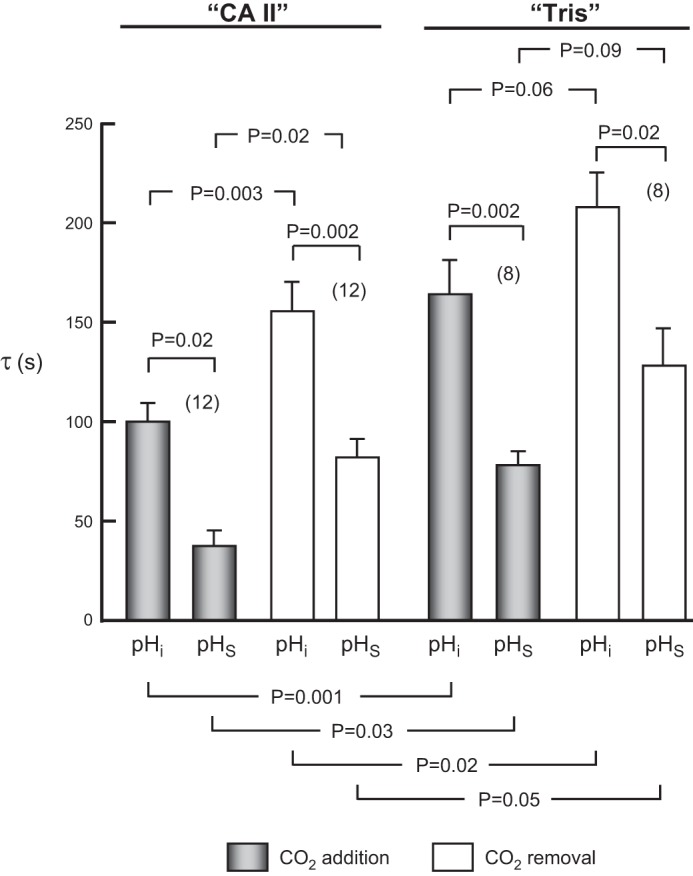
Summary of time constants (τ) for pH_i and pH_S changes for a larger number of experiments, such as those in Fig. 2, on oocytes injected with CA II in Tris buffer, or only Tris. Values are means ± SE, with nos. of oocytes in parentheses. We performed a one-way ANOVA followed by a Student-Newman-Keuls (SNK) analysis (P shown for individual comparisons).

Effect of Blocking CA II With EZA

If our hypothesis is correct, then the effects that we observed with CA II ought to be blocked by an inhibitor of CA II. In a subset of the experiments summarized above in Fig. 3, we followed the CO₂/HCO₃⁻ exposure (as in Fig. 2) by 1) a ∼3-h treatment with 400 μM ethoxzolamide (EZA, a permeant CA II inhibitor) and three washes, and then 2) a second exposure to CO₂/HCO₃⁻. Figure 4 shows a representative pair of such experiments, one on a “CA II” oocyte (Fig. 4A/Pre-EZA and Fig. 4B/Post-3h EZA), and the other on a “Tris” oocyte (Fig. 4C/Pre-EZA and Fig. 4D/Post-3 h EZA), similar to the protocol introduced by Lu et al. (38).

Fig. 4.

Representative experiments showing effects of ethoxzolamide (EZA) EZA on pH_i and pH_S. A: oocyte injected with recombinant human CA II dissolved in Tris buffer, assayed before treatment with EZA (Pre-EZA). B: “CA II” oocyte, assayed after a 3-h treatment with EZA (Post-EZA). C: oocyte injected only with Tris buffer, assayed before treatment with EZA. D: “Tris” oocyte, assayed after a 3-h treatment with EZA. For both CA II and Tris experiments, the Pre-EZA and Post-EZA pH_i and pH_S records were obtained from the same oocytes. Between the two CO₂/HCO₃⁻ exposures, the oocytes were exposed for 3 h to the ND96 solution (Table 1) supplemented with 400 μM EZA, followed by 3 washes in ND96, and incubation in ND96 (30 min to 3 h). We noticed no effect of the variable duration of the post-EZA incubation. The extracellular solutions were ND96 and, during the indicated time, 1.5% CO₂/10 mM HCO₃⁻/pH 7.50. In both experiments, the solution flowed at 2 ml/min and the sampling rate was 1 per 1,000 ms. The vertical gray bands represent periods during which the pH_S electrode was withdrawn to the BECF for calibration. The dashed black lines through the initial portions of the pH_i records for CO₂ application and removal represent best linear fits for maximal rates of pH_i change (negative or positive direction). The downward vertical arrows represent CO₂-induced change in steady-state pH_i. The upward and downward vertical arrows near the pH_S records represent the maximal CO₂-induced changes in pH_S (positive or negative direction).

pH_i changes.

As hypothesized, the CA II blocker EZA markedly slows the CO₂-induced maximal acidification rate in the “CA II” oocyte (Fig. 4, A vs. B, lower records), but not in the “Tris” oocyte (Fig. 4, C vs. D, lower records). The four bars in Fig. 5A summarize the (dpH_i/dt)_max values-corresponding to the application of CO₂/HCO₃⁻-for a larger number of experiments like those shown in the lower records of Fig. 4A–D. These data show that, in “CA II” oocytes, EZA reduces the magnitude of (dpH_i/dt)_max to a value indistinguishable from that in “Tris” oocytes, with or without EZA. As expected, Fig. 5B shows that EZA does not significantly affect the CO₂-induced change in steady-state pH_i in either “CA II” or “Tris” oocytes.

Fig. 5.

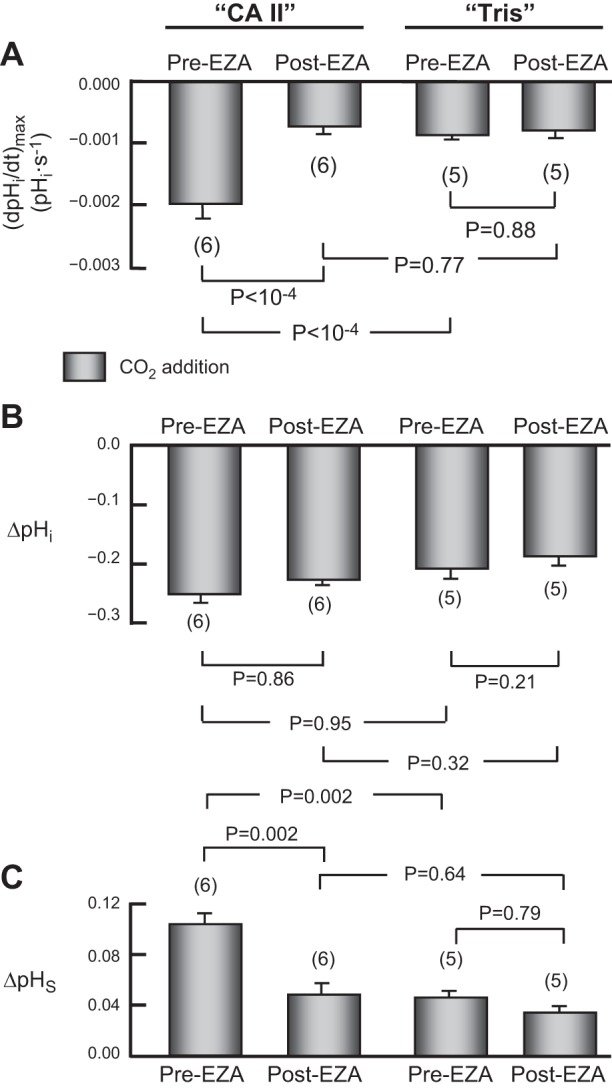
Summary of the effects of EZA on pH_i and pH_S. This figure summarizes data relating to CO₂ addition from a larger number of experiments, such as those in Fig. 4, on oocytes injected with CA II in Tris buffer, or only Tris buffer. After an assay during which we switched the extracellular solution from ND96 to 1.5% CO₂/10 mM HCO₃⁻, in the absence of EZA (Pre-EZA), we exposed the same oocyte to 400 μM EZA for 3 h, and then repeated the assay (Post-EZA). A: maximal rates of pH_i change (negative direction) produced by the extracellular solution switch. B: changes in steady-state pH_i produced by the switch to CO₂/HCO₃⁻. C: maximal changes in pH_S (positive direction) produced by the extracellular solution switch. Values are means ± SE, with nos. of oocytes in parentheses. We performed a one-way ANOVA (overall P values: P < 10⁻⁴ in A, P = 0.38 in B, and P = 0.0012 in C), followed by a Student-Newman- Keuls (SNK) analysis (P shown for individual comparisons). The mean initial pH_i for “CA II” oocytes in the CO₂/HCO₃⁻-free ND96 solution was 7.13 ± 0.11 (n = 6), which is not significantly different from the mean value for “Tris” oocytes, 7.05 ± 0.07 (n = 5; P = 0.93). For both “CA II” and “Tris” oocytes, EZA had no effect on the initial pH_i.

pH_S changes.

EZA markedly blunts the pH_S transients in the “CA II” oocyte (Fig. 4A vs. B, upper records) but does not reduce the size of the already blunted pH_S transients in the “Tris” oocyte (Fig. 4, C vs. D, upper records). Finally, Fig. 5C shows that, in “CA II” oocytes, EZA reduces the CO₂-induced ΔpH_S to a value not significantly different from that in “Tris” oocytes, with or without EZA.

Figure 5 does not show the data summary for (dpH_i/dt)_max, ΔpH_i, and ΔpH_S for the CO₂-removal phase of the experiment. However, the effects of EZA on these three parameters during CO₂ removal were similar to the effects during CO₂ addition. Also not shown are two sham experiments on CA II oocytes and one on a Tris oocyte, in which we followed the first CO₂/HCO₃⁻ exposure by a treatment in ND96 without EZA, followed by washes and a second exposure to CO₂/HCO₃⁻. We saw no obvious difference, in either the pH_i or pH_S changes, between first and second exposures to CO₂/HCO₃⁻. Thus, the differences between pre-EZA and post-EZA values in Fig. 4 and Fig. 5 are due to EZA and not the time course of the experiment.

Analysis of Time Constants for pH_i and pH_S Changes

According to the model in Fig. 1, after a step increase in [CO₂]_BECF, the rate of pH_i decline should fall over time as the rate of CO₂ entry falls. Similarly, after reaching its maximal value, the change in pH_S—another manifestation of this same CO₂ entry—should fall over time as the rate of CO₂ entry falls. Thus, we might expect that the time courses of both the decrease in pH_i and the decay in pH_S from its peak value should follow approximately exponential time courses with similar time constants. For each experiment summarized in Fig. 3, we used whenever possible a nonlinear least-squares approach to obtain four sets of best-fit parameters for a single-exponential function, one each for pH_i and pH_S, both for the addition and removal of CO₂/HCO₃⁻.³

CA II vs. Tris.

As far as the pH_i time course is concerned, because CA II increased the magnitude of (dpH_i/dt)_max when we applied CO₂ (Fig. 3A, gray bars), we expected that it also would decrease the time constant (τ) for the CO₂-induced pH_i decline. This was indeed the case (compare pH_i bars 1 vs. 5 in Fig. 6).

As far as the pH_S time course is concerned, the initial rate of CO₂ entry is greater for “CA II” than for “Tris” oocytes, as evidenced by the greater ΔpH_S in Fig. 3C (gray bars). However, the net number of CO₂ molecules entering the cytosol is the same for “CA II” and “Tris” oocytes, as evidenced by the identical magnitudes of the CO₂-induced ΔpH_i (Fig. 3B, gray bars). Thus, CO₂ entry across the plasma membrane should come to completion earlier in “CA II” oocytes, which should therefore have a smaller τ for pH_S, as was indeed the case (compare pH_S bars 2 vs. 6 in Fig. 6).

With the removal of CO₂, we also observed, as expected, that the τ for pH_i was smaller (i.e., faster) for “CA II” than for “Tris” oocytes (compare bars 3 vs. 7 in Fig. 6). Similarly, the τ for pH_S was smaller (faster) for “CA II” oocytes (compare bars 4 vs. 8 in Fig. 6).

CO₂ addition vs. CO₂ removal.

For pH_i, the τ values for CO₂ addition—oocyte by oocyte—were almost invariably smaller (faster) than their counterparts for CO₂ removal for “CA II” oocytes (compare bars 1 vs. 3 in Fig. 6) and for “Tris” oocytes (compare bars 5 vs. 7 in Fig. 6). However, in an ANOVA, the differences reached statistical significance only for the CA II data.

For pH_S, like pH_i, the mean τ values—oocyte by oocyte—were again invariably smaller (faster) for CO₂ addition than for CO₂ removal for “CA II” (compare bars 2 vs. 4 in Fig. 6) and for “Tris” (compare bars 6 vs. 8 in Fig. 6). Again, the difference reached statistical significance in an ANOVA only for the CA II data. These trends for τ are antiparallel to the trends that we noted above for (dpH_i/dt)_max (Fig. 3A) and ΔpH_S (Fig. 3C). In the discussion, we will examine these issues in the context of the mathematical model.

pH_i vs. pH_S.

Another unexpected observation was that the τ values for the pH_S transients—oocyte by oocyte—were consistently less than those of the corresponding pH_i transients, both for “CA II” and “Tris” oocytes, and both for CO₂ application and removal (compare bars 1 vs. 2, 3 vs. 4, 5 vs. 6, and 7 vs. 8 in Fig. 6). As we will see in the section after the next, and as confirmed by our mathematical model, the slower time course of pH_i vs. pH_S probably reflects, at least in part, delays due to the depth of penetration of the pH_i electrode. In addition, the asymmetry of [CO₂]_BECF around the oocyte probably makes a contribution (see discussion).

Analysis of Time Delay For pH_i Changes

Time delay is the time difference between the initiation of the CO₂-induced acidification rate upswing in pH_S (see next section) and the initiation of the fall in pH_i. To estimate the time of the initiation of the pH_i decline, we obtained two linear fits of pH_i time courses: 1) baseline pH_i vs. time (i.e., before the addition of CO₂/HCO₃⁻) and 2) the maximal rate of pH_i decline (see materials and methods). The time of initiation (indicated by the right blue, dashed vertical line in Fig. 2A) is the time at the intersection of the two linear fits.

We observed, with both the application and removal of CO₂, and for both “CA II” and “Tris” oocytes, that the initiation of the pH_S spike preceded the initiation of the pH_i change for every oocyte. Table 2 summarizes the delays between the initiation of the pH_S spike and the initiation of the corresponding pH_i change (i.e., the time between the two vertical blue, dashed lines in Fig. 2A). This delay is not significantly different among the four conditions in Table 2. As we will see in the next section, this delay reflects, to some extent, the depth of impalement of the pH_i electrode. Our mathematical model (see discussion) confirms this depth effect and predicts that other factors, such as the tortuosity factor for the diffusion of intracellular solutes, also could influence the delay.

Table 2.

Delay between initiation of pH_S and pH_i transients

	Delay, s
	“CA II”		“Tris”
	CO2 Addition	CO2 Removal	CO2 Addition	CO2 Removal
Initiation of pHS spike to initiation of pHi change*	11.2 ± 1.9 (9)	12.0 ± 2.6 (9)	7.2 ± 1.1 (6)	14.0 ± 1.8 (6)

Values are means ± SE (no. of experiments).

^*Differences among values in this row are not significant based on an ANOVA (P = 0.18). pH_S, surface pH; pH_i, intracellular pH; CA II, carbonic anhydrase II; Tris, control group injected with Tris buffer.

Analysis of Time to Peak For pH_S Changes

Time to peak is the time difference between the initiation of the CO₂-induced acidification rate upswing in pH_S and the peak of the pH_S spike. To determine the time of the initiation of the CO₂-induced acidification rate upswing, we obtained two linear fits of pH_S time courses: 1) baseline pH_S vs. time (i.e., before the addition of CO₂/HCO₃⁻) and 2) the linear phase of the CO₂-induced acidification rate pH_S increase. The time of initiation (indicated by the left blue, dashed vertical line in Fig. 2A) is the time at the intersection of the two linear fits. We determined the peak of the pH_S spike by inspection of an Excel file. Table 3 summarizes the time to peak for a large number of experiments. Differences among values in the columns are not significant based on an ANOVA either for “CA II” (P = 0.09) or for “Tris” (P = 0.6). On the other hand, differences between “CA II” and “Tris” oocytes were statistically significant for each CO₂/HCO₃⁻combination. Our mathematical model (see third paper in this series; ref. 49) suggests that time to peak reflects in part the time required for the CO₂/HCO₃⁻buffer components to rise in the BECF, and in part the time required for the buffer components to diffuse throughout the EUF and enter the ICF.

Table 3.

Time to peak pH_S in “CA II” or “Tris” oocytes

	Time, s
Condition	“CA II”	“Tris”	P Value
1.5% CO2/10 mM HCO3−	7.6 ± 0.9 (9)	11.2 ± 1.5 (6)	P = 0.05
5% CO2/33 mM HCO3−	5.3 ± 0.3 (7)	12.3 ± 2.3 (6)	P = 0.006
10% CO2/66 mM HCO3−	7.0 ± 0.6 (7)	14.0 ± 1.9 (6	P = 0.007

Values are means ± SE (no. of experiments).

Experiments With Dual-pH_i Microelectrodes: Depth of Impalement

To elucidate the differences in τ values between pH_i and pH_S, as well as the delays between the initiation of the pH_i and pH_S transients, we performed three series of experiments in which we impaled the oocyte with two pH_i electrodes. Note that we did not obtain pH_S records in these experiments.

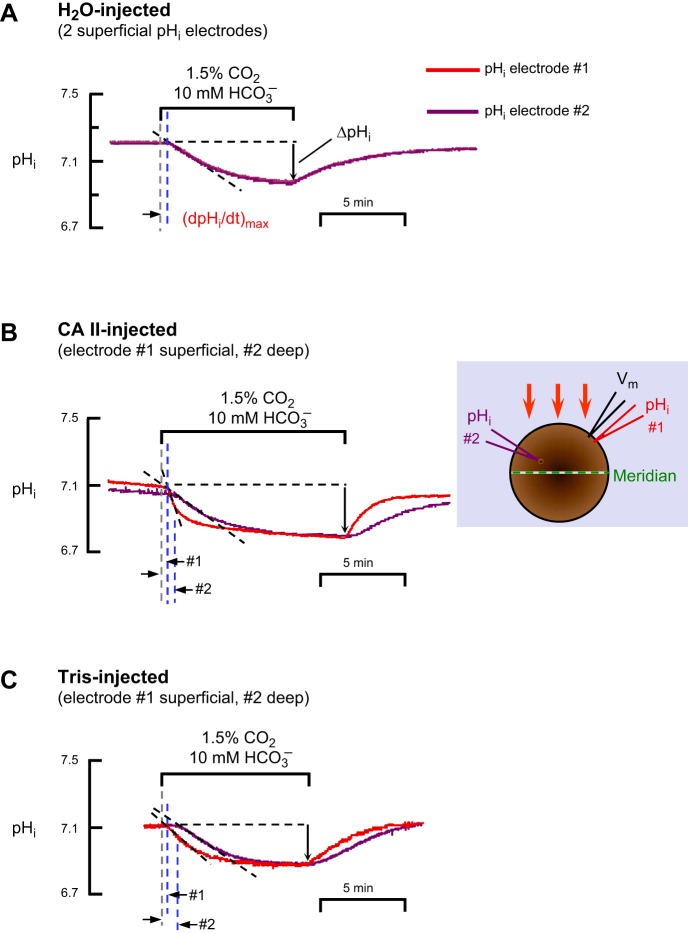
In the first series of experiments, as a control, we inserted both pH_i microelectrodes (referred to as electrode no. 1 and electrode no. 2) as superficially as possible into H₂O-injected oocytes.⁴ After impaling with the V_m electrode, we inserted pH_i electrode no. no. 1, as we would insert the lone pH_i electrode in a standard experiment (Fig. 1): we advanced the pH_i microelectrode with a manual manipulator, observed a small dimple on the oocyte surface, tapped the table, and observed the voltage deflection indicating a successful impalement. We mounted pH_i electrode #2 on motorized manipulator, which held the pH_S electrode in a standard experiment (Fig. 1), and regarded, as “0”, the position where the electrode tip was at the oocyte surface. We advanced electrode no. 2, observed a dimple, and continued to advance the electrode slowly, a total of ∼40 μm from the “0” position, until we observed the appropriate voltage deflection. As shown in Fig. 7A, one of seven similar experiments, when we apply and then remove CO₂/HCO₃⁻, the pH_i records from the two superficially placed electrodes were virtually identical.

Fig. 7.

Representative experiments with dual pH_i-electrode impalements of Xenopus oocytes. A: oocyte injected with H₂O on day 0. B: oocyte injected with recombinant human CA II dissolved in Tris buffer on day 3. The inset is a schematic top view of the oocyte, showing the arrangement of microelectrodes; the orange arrows show the direction of convective flow. C: oocyte injected only with Tris buffer on day 3. The extracellular solutions were ND96 (Table 1) and, during the indicated time, 1.5% CO₂/10 mM HCO₃⁻/pH 7.50. For all three oocytes, the solution flowed at 3 ml/min and the sampling rate was 1 per 500 ms. The pH_i record from electrode no. 1 (superficial) is in red, and the pH_i record from electrode no. 2 (deep) is in purple. The gray, dashed vertical lines represent the times that the computer switched the valves to initiate a change of solutions. The left and right blue, dashed vertical lines represent the initiation of the transients for pH_i electrodes no. 1 and no. 2, respectively. The dashed black lines through the initial portions of the pH_i records for CO₂ application represent best linear fits for maximal rates of pH_i change (negative direction). The downward vertical arrows represent the CO₂-induced change in steady-state pH_i.

In the second set of experiments, we performed a superficial impalement with electrode no. 1 and used the motorized manipulator to drive electrode no. 2 increasingly deeper into “CA II” oocytes (Fig. 7B) or “Tris” oocytes (Fig. 7C). In reviewing the initial data on “Tris” oocytes, we noticed that for two impalements to an apparent depth of 250–300 μm beyond the “0” position, the CO₂-induced steady-state ΔpH_i was indistinguishable from that detected by the superficially placed pH_i electrode no. 1 (data not shown). However, for a single impalement to an apparent depth of 540 μm, the ΔpH_i value was ∼25% less than that of a simultaneous superficial impalement. Therefore, in all subsequent experiments we chose ∼300 μm beyond the “0” position to be the standard depth of the no. 2 or “deep” electrode.

Figure 7B shows one of seven experiments on “CA II” oocytes in which electrode no. 1 was superficial and electrode no. 2 was at an apparent depth of ∼300 μm. Figure 7C shows one of six such experiments on “Tris” oocytes.

The three vertical regions in Fig. 8, i.e., H₂O, CA II, and Tris, summarize the salient features of the three protocols illustrated in Fig. 7, A–C. In Fig. 8A, each cluster of three bars summarizes the data for CO₂ addition (gray or gray hatched) or for CO₂ removal (white or white hatched). The leftmost bar in each cluster is the time lag⁵ between the change of the computer-actuated valve (to switch extracellular solutions) and initiation of the change sensed by pH_i electrode no. 1. The middle bar is the comparable time lag for pH_i electrode no. 2. The rightmost (hatched) bar is the mean difference in the time lags between pH_i electrodes no. 2 and no. 1. For H₂O-injected oocytes, we observe no statistically significant difference between the time lags detected by superficial electrode no. 1 vs. superficial electrode no. 2. For both the “CA II” oocytes and the “Tris” oocytes, the no. 2–no. 1 differences in time lags are substantially larger than for “H₂O” oocytes, reflecting the deeper impalement with electrode no. 2. Note that the no. 2–no. 1 differences are the same for “CA II” vs. “Tris”, and CO₂ addition vs. removal.

Figure 8B summarizes the (dpH_i/dt)_max data. Note that for the “H₂O” oocytes, the (dpH_i/dt)_max values are identical for superficial electrode no. 1 and superficial electrode no. 2. For the “CA II” (but not “Tris”) oocytes, the pH_i changes are significantly faster for superficial vs. the deep electrodes. Comparing “CA II” vs. “Tris” oocytes, we see that CA II accelerates the pH_i changes recorded by superficial but not by the deep electrodes. The mathematical model confirms this pattern (see discussion).

The (dpH_i/dt)_max values in Fig. 8B reflect linear fits to the region of steepest CO₂-induced descent in the pH_i vs. time plot. In parallel, we also used a nonlinear least-squares approach to obtain the best-fit parameters for a single-exponential function, beginning at the point of steepest descent of the pH_i vs. time plot. Figure 8C summarizes the mean time τ values from these exponential fits. The pattern of rate constants (i.e., 1/τ values) is similar to the pattern for (dpH_i/dt)_max data in Fig. 8B: the rate constants for pH_i change are significantly faster for superficial vs. the deep electrodes for “CA II” oocytes (but not for “Tris” oocytes).

Figure 8D summarizes the ΔpH_i data and shows that neither the presence of CA II nor the depth of impalement (to ∼300 μm) has a significant effect.

Effect of Increasing Extracellular CO₂/HCO₃⁻ Levels

The preceding data, all obtained with 1.5% CO₂, are consistent with the hypothesis that the maximal increase in pH_S that occurs during an exposure to CO₂/HCO₃⁻—under a particular set of experimental conditions⁶—is a semiquantitative index of the rate of CO₂ entry into the cell. If this hypothesis is true, then the maximal ΔpH_S ought to increase when we raise [CO₂], [CO₂]_BECF, and [HCO₃⁻]_BECF at a fixed pH_BECF. Figure 9 shows experiments in which we pulsed a “CA II” oocyte (Fig. 9A) and a “Tris” oocyte (Fig. 9B) with increasing levels of extracellular CO₂/HCO₃⁻—1.5%/10 mM, 5%/33 mM, and 10%/66 mM—always using the same ratio of [CO₂]/[HCO₃⁻] to keep pH_BECF at 7.50. Figure 10 summarizes a larger series of experiments similar to those in Fig. 9.

Fig. 9.

Representative experiments showing the effect of graded increases in extracellular CO₂/HCO₃⁻ levels on pH_i and pH_S. A: oocyte injected with recombinant human CA II in Tris buffer. B: oocyte injected only with Tris buffer. A and B each represent an experiment on single oocytes. The pH_i trace is represented by the red lower record, and pH_S, by the green upper record. At the indicated times, we switched the extracellular solution (Table 1) from 1) ND96 to 1.5% CO₂/10 mM HCO₃⁻ (left), or 2) ND96 to 5% CO₂/33 mM HCO₃⁻ (center), or 3) ND96 to 10% CO₂/66 mM HCO₃⁻ (right). After the first two CO₂/HCO₃⁻ exposures, we restored the ND96 solution (not shown). For both oocytes, the solution flowed at 3 ml/min and the sampling rate was 1 per 500 ms. The vertical gray bands represent periods during which the pH_S electrodes were withdrawn to the BECF for calibration. The dashed black lines through the initial portions of the pH_i records for CO₂ application represent best linear fits for maximal rates of pH_i change (negative direction). The downward vertical arrows represent CO₂-induced changes in steady-state pH_i. The upward vertical arrows represent the maximal excursion of pH_S (positive direction).

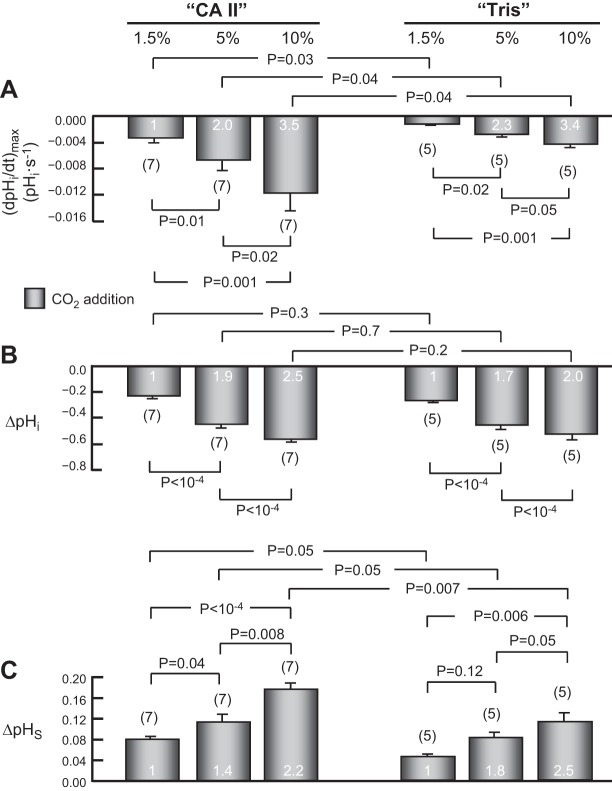
Fig. 10.

Summary of effects of graded increases of extracellular CO₂/HCO₃⁻ levels on pH_i and pH_S. This figure summarizes results from a larger number of experiments, such as those in Fig. 9, on oocytes injected with CA II in Tris buffer, or only Tris buffer. A: maximal rates of pH_i change (negative direction) produced by the introduction of extracellular CO₂/HCO₃⁻. B: changes in steady-state pH_i induced by the addition of CO₂/HCO₃⁻. C: maximal changes in pH_S (positive direction) caused by the addition of CO₂/HCO₃⁻. Values are means ± SE, with nos. of oocytes in parentheses. The white numerals are the ratios of mean values, relative to the value at 1.5% CO₂. We performed a one-way ANOVA followed by a Student-Newman-Keuls (SNK) analysis (P shown for individual comparisons). The initial pH_i values for “CA II” or “Tris” oocytes in the ND96 (i.e., CO₂/HCO₃⁻-free) solution were not significantly different (overall ANOVA, P = 0.84).

pH_i changes.

Comparing 1.5% vs. 5% vs. 10% CO₂, either for “CA II” or “Tris” oocytes, we see that graded increases in [CO₂]_BECF cause pH_i to decrease faster (Fig. 10A) and to a greater extent (Fig. 10B). Increasing [CO₂]_BECF from 1.5% to 5% to 10%—in the ratios 1/∼3.3/∼6.6—increases the magnitude of (dpH_i/dt)_max in the ratios 1/∼2.0/∼3.5 for “CA II” oocytes and in virtually the same ratios (i.e., 1/∼2.3/∼3.4) for “Tris” oocytes (Fig. 10A, white numerals). These results are generally in agreement with the predictions of the mathematical model (see discussion).

Comparing “CA II” vs. “Tris” oocytes at a given CO₂ level, we see that even though the steady-state ΔpH_i is the same (Fig. 10B), the (dpH_i/dt)_max is significantly greater in “CA II” oocytes (Fig. 10A). These results are consistent with the 1.5%-CO₂ data presented above in Fig. 3, A and B. However, because the pH_i electrode is “cis” (i.e., “on the same side”) to the added CA II, and because this enzyme speeds the production of H⁺ from incoming CO₂, these (dpH_i/dt)_max data per se do not provide intuitive insight into the effect of CA II on the CO₂ influx.

From the magnitude of the CO₂-induced decreases in steady-state ΔpH_i, we can compute the intrinsic intracellular buffering power (β_I). As summarized in Table 4, the β_I values that we computed were very similar, whether we raised [CO₂]_BECF to 1.5%, 5%, or to 10%. An ANOVA indicated no significant difference among the values. Thus, β_I must be virtually constant over the entire pH_i range of our experiments (10). In addition, the ΔpH_i data (Fig. 10B) reveal that, as expected, incremental increases in [CO₂]_BECF lead to incremental increase in the total net influx of CO₂ integrated over the period of the CO₂ exposure.

Table 4.

Nominal intrinsic intracellular buffering power (β)*

Buffering Power (β)	“CA II”	“Tris”
1.5% CO2/10 mM HCO3−	14 ± 1 (7)	14 ± 1 (5)
5% CO2/33 mM HCO3−	15 ± 1 (7)	17 ± 3 (5)
10% CO2/66 mM HCO3−	17 ± 2 (7)	15 ± 4 (5)

Values are means ± SE (no. of experiments).

^*We computed β from the change in steady-state pH_i caused by the addition of CO₂/HCO₃⁻, in oocytes injected with CA II protein or in others injected just with Tris buffer. Differences among values are not significant based on an ANOVA (P = 0.67).

pH_S changes.

Comparing 1.5% vs. 5% vs. 10% CO₂, either for “CA II” or “Tris” oocytes, we see that graded increases in [CO₂]_BECF (in the ratios 1/∼3.3/∼6.6) cause ΔpH_S to rise in the ratios 1/∼1.4/∼2.2 for “CA II” oocytes and 1/1.8/2.5 for “Tris” oocytes (Fig. 10C). These results are in general qualitative agreement with the predictions of the mathematical model.

Comparing “CA II” vs. “Tris” oocytes at a given CO₂ level, we see that ΔpH_S is significantly greater in “CA II” than in “Tris” oocytes, consistent with the 1.5%-CO₂ data presented above in Fig. 3C. Because the pH_S electrode is “trans” to the added CA II enzyme, we can conclude, on the basis of intuition alone, that the increments in ΔpH_S caused by CA II must reflect increases in CO₂ influx across the plasma membrane. Figure 10C shows that intracellular CA II, over a wide range of CO₂ levels, enhances the influx of CO₂.

DISCUSSION

Previous investigators had used extracellular electrodes to monitor transient changes in pH caused by the addition of CO₂/HCO₃⁻to the fluid surrounding skeletal muscle fibers (31) or lamprey neurons (15). We have adapted their approach to track pH_S as CO₂ crosses the cell membrane of Xenopus oocytes. Previously, in the absence of exogenous CA, we used ΔpH_S during CO₂/HCO₃⁻ applications to assess the role of heterologously expressed channel proteins in enhancing the influx of CO₂ into oocytes (14, 22, 24–26, 45). According to Fick's law, this increased flux could be due to an increase in CO₂ permeability or to an increase in the CO₂ transmembrane gradient. Inasmuch as aquaporin 1 (AQP1) (45) and the rhesus proteins (26) have no apparent CA-like activity, they increase ΔpH_S by raising CO₂ permeability (i.e., acting as gas channels). Nevertheless, even in gas-channel studies, the CO₂ gradient is important. Indeed, in the work of Nakhoul et al. (47) on oocytes with intact vitelline membranes, the ability of AQP1 to increase CO₂-induced (dpH_i/dt)_max did not become statistically significant until those authors injected CA II. Cooper and Boron (16) detected a statistically significant effect of AQP1 on CO₂-induced (dpH_i/dt)_max in the absence of injected CA II, but only after removing the vitelline membrane, which reduces the extracellular unconvected layer. Both CA II injection and devitellinization presumably acted by increasing the transmembrane CO₂ gradient.

The purpose of the present study was to better understand how transmembrane CO₂ gradients, at a fixed permeability, affect CO₂ fluxes. Specifically, we ask: 1) how CA II influences CO₂ fluxes across the cell membrane (done by monitoring pH_S) and 2) how CO₂/HCO₃⁻ levels influence CO₂-induced pH_S transients. A key element in our approach was to monitor simultaneously both pH_i and pH_S. It is very likely that our pH_S electrode creates a special environment—an enhancement of the natural extracellular unconvected fluid—between the outer surface of the cell membrane and the flat surface of the electrode. However, this special environment almost certainly communicates by diffusion with the surrounding EUF. Otherwise, we could not detect the pH_S transients that we observe with the introduction or removal of extracellular CO₂/HCO₃⁻.

We find that cytosolic CA II accelerates the transient CO₂ influx produced by raising [CO₂]_BECF as well as the transient CO₂ efflux produced by lowering [CO₂]_BECF. The evidence for this acceleration is threefold: 1) a marked increase in the magnitude of maximal CO₂-induced pH_S changes, 2) a marked decrease in the τ for the pH_i change following application (or removal) of CO₂/HCO₃⁻, and 3) a marked decrease in the τ for the relaxation of pH_S from its maximum (or minimum) following application (or removal) of CO₂/HCO₃⁻. To our knowledge, ours is the first use of τ_pHi or τ_pHS to infer an increase in the flux of an acid-base-related species.

Some of our observations were predictable: 1) increasing the depth of penetration by the pH_i electrode lengthens the time lag and increases time constant of measured pH_i changes and 2) increasing [CO₂]_BECF/[HCO₃⁻]_BECF levels increases the rate and magnitude of the decrease in pH_i and increases the magnitude of pH_S trajectories.

In addition, we made three unanticipated observations: 1) the time constants for pH_i changes are greater than those for pH_S changes, 2) following a change in [CO₂]_BECF, pH_i begins to change many seconds after pH_S begins to change, and 3) during removal of CO₂/HCO₃⁻ from “CA II” oocytes, the magnitudes of both the rate of pH_i change and the pH_S transient are smaller than those observed during the application of CO₂/HCO₃⁻.

To improve our understanding of the above seven issues, we extended a mathematical model of a spherical cell and of its surrounding environment (66) that allows one to simulate the effects of introducing (or removing) CO₂/HCO₃⁻ to (or from) the BECF. The third paper in this series introduces extensions to the model of Somersalo et al. (66) that make it more realistic for oocytes. In the following sections, we present predictions of the extended model that are germane to the analysis and discussion of the CA II data in the present paper. The parameter values for the simulations are those of the “standard oocyte,” as defined in the third paper (49).

Effect of CA II on CO₂ Fluxes

Importance of trans-side pH measurements.

Even if the injection of CA II did not enhance CO₂ influx per se, we would expect the enzyme to increase (dpH_i/dt)_max because CA II, which is “cis” to the pH_i electrode, catalyzes the overall intracellular reaction CO₂ + H₂O → HCO₃⁻ + H⁺. For example, preliminary work of Nakhoul et al. (48) showed that injecting CA II into Xenopus oocytes increases CO₂-induced (dpH_i/dt)_max. However, this result, like the (dpH_i/dt)_max data in the present study, does not prove that CA II enhances CO₂ influx. We can apply the same blanket statement about speeding pH_i changes to any process that, in the presence of a CO₂/HCO₃⁻ buffer, produces or consumes H⁺ (or OH⁻). This principle explains at least in part why others, working with cells expressing the Cl-HCO₃ exchanger AE1, observed that the extracellular removal or re-addition of Cl⁻ produces larger and faster pH_i changes in the presence of active CA II (67). Although (dpH_i/dt)_max provides little intuitive insight on the effect of CA II on fluxes, a new contribution of the present paper is that the time constant for the pH_i trajectory does provide such intuitive insight, as discussed below (section titled “Effects of CA II on time constants for pH_i and pH_S”).

In principle, we also could use an intracellular CO₂ electrode to assess the effect of intracellular CA II on CO₂ fluxes. However, a more practical alternative is to monitor pH at the extracellular surface, that is, on the side “trans” to the added CA II.

Effects of CA II on ΔpH_S.

The fundamental observation in this paper is that introducing CA II into an oocyte increases the magnitude of ΔpH_S, both with CO₂ application or withdrawal (Fig. 2 and Fig. 3C). According to both the cartoon in Fig. 1 and the mathematical model, the higher ΔpH_S magnitude in oocytes injected with CA II only could have been the result of three effects: 1) a reduced buffering power in the EUF, 2) a greater extracellular CA activity, or 3) a greater maximal CO₂ influx (independent of extracellular CA activity). We know of no reason why the injection of CA II should have reduced β_EUF. We can rule out an increase in extracellular EZA-sensitive CA activity because loading an oocyte with EZA, which entailed an EZA pretreatment followed by three washes (so that extracellular EZA was not present during the pH_S assay), completely reverses the effects of CA II on pH_i and pH_S (Figs. 4 and 5). Thus, we are left with the third possibility: CA II must increase the ΔpH_S magnitude by increasing the maximal CO₂ flux, presumably as outlined in Fig. 1 and confirmed by our mathematical model.

The mathematical model predicts that, during the initial phase of CO₂ influx⁷ (Fig. 11A, hatched area), cytosolic CA should decrease [CO₂] at the intracellular surface of the membrane ([CO₂]_IM), thereby providing a larger gradient for CO₂ influx, which should secondarily lead to a fall in [CO₂] at the extracellular surface ([CO₂]_EM; Fig. 11B). However, two processes replenish CO₂ at the outer membrane surface: 1) diffusion of CO₂ from the BECF (which has no effect on pH_S) and 2) the reactions HCO₃⁻ + H⁺ → H₂CO₃ → CO₂ + H₂O at the outer surface of the membrane (which raise pH_S). As a result, ([CO₂]_EM) is less than it otherwise would have been. Nevertheless, the net effect is that, during the initial phase of CO₂ influx, CA II increases the CO₂ gradient (Δ[CO₂]_PM; Fig. 11C), thus causing a greater transient increase in pH_S.

Fig. 11.

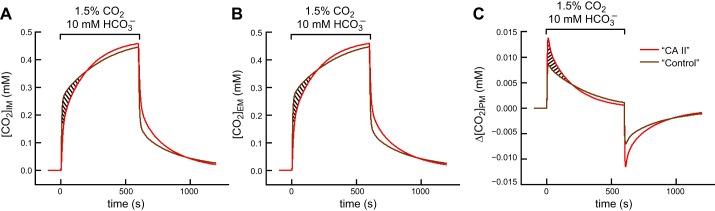
Predictions of the mathematical model for concentration-time profiles of CO₂ for a “CA II” oocyte (red curves) and a “Control” or “Tris” oocyte (brown curves). A: [CO₂] at the intracellular surface of the plasma membrane (IM). B: [CO₂] at the extracellular surface of the plasma membrane (EM). C: gradient of CO₂ across the plasma membrane (PM), the result of subtracting values in B from corresponding values in A. The hatched areas in A and B identify the initial phase of CO₂ influx, during which the model predicts that cytosolic CA decreases [CO₂] at the inner and outer surfaces of the plasma membrane. However, the dominant effect is at the inner membrane, so that CA provides a larger gradient for CO₂ influx, as indicated by the hatched area in C. Details of the mathematical model are presented in the third paper in this series (49).

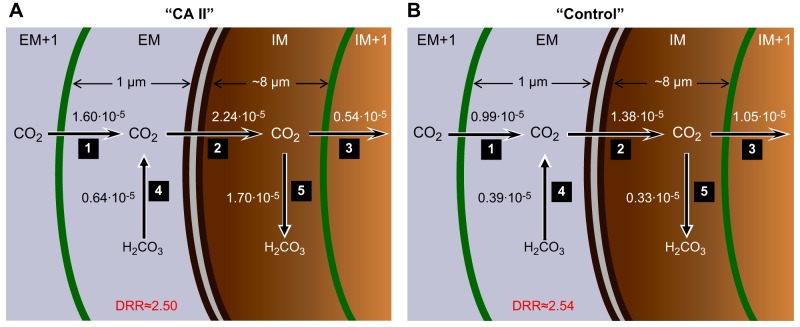
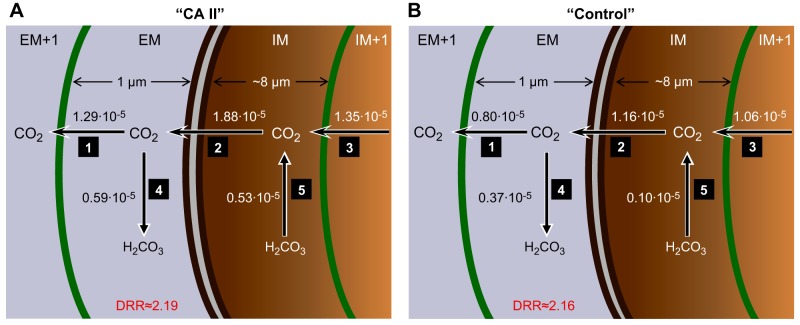
Figure 12 summarizes the effect of CA II on the predicted maximal CO₂ diffusion and reaction rates near the membrane. Note that the model predicts that the diffusion/reaction ratio (DRR) for replenishing CO₂ at the extracellular surface of the membrane is ∼2.5, regardless of whether cytosolic CA II is present (Fig. 12). As mentioned in the previous paragraph, the model predicts that the maximal transmembrane flux is higher in the presence of cytosolic CA II (compare arrow no. 2 of A vs. B) because the CA II in the IM region rapidly consumes incoming CO₂ (compare arrow no. 5 of A vs. B). As a result of this rapid CO₂ consumption, [CO₂]_IM is relatively low, accounting for the paradoxical decrease in CO₂ flux from the IM region to the IM+1 region (compare arrow no. 3 of A vs. B).

Fig. 12.

Predictions of the mathematical model for maximal CO₂ diffusion and reaction fluxes near the plasma membrane during addition of 1.5% CO₂/10 mM HCO₃⁻. A: “CA II” oocyte. B: “Control” or “Tris” oocyte. The parallel dark brown curves identify the plasma membrane (PM). The green curves to the left and right of the PM represent the spatial discretizations for the numerical solutions. The numbers near the arrows 1 through 5 indicate the maximal diffusive fluxes (sharp arrowheads) and reaction fluxes (dull arrowheads) in units of μmol/s. These maximal fluxes occur within ∼1 s of each other. The diffusion/reaction ratio (DRR) is the quotient of flux no. 1/flux no. 4. Details of the mathematical model are presented in the third paper in this series (49).

Effects of CA II on time constants for pH_i and pH_S.

CA II has no effect on the total net amount of CO₂ entering or leaving the cell, as evidenced by the lack of an effect on the CO₂-induced fall in steady-state ΔpH_i (Fig. 3B). However, as we saw above, because we observe that CA II causes a larger maximal ΔpH_S, we can conclude that CA II must increase the maximal CO₂ flux. Therefore, CA II should reduce the total time necessary for CO₂ to complete its equilibration across the plasma membrane, and thus reduce both the τ for the change in pH_i and the τ for the decay of pH_S from its peak. Indeed, this is what we observe under all experimental conditions (Fig. 6). Moreover, the mathematical model predicts this same trend for “CA II” vs. “control” (Fig. 13).

Fig. 13.

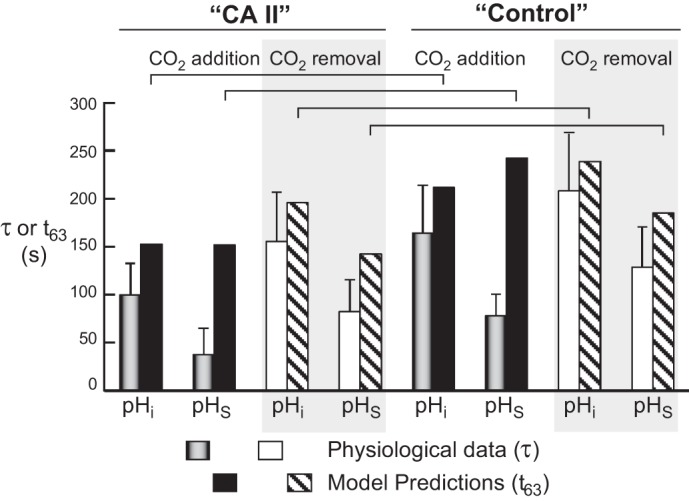
Comparison of physiological τ data with t₆₃ data predicted by the mathematical model. The physiological data are taken from Fig. 6; note that here we report the means ± standard deviation (and not SE, as in Fig. 6). An apparent inconsistency arises when we compare pH_S data from physiological experiments (time constant, τ) and simulations (time to 63% of completion, t₆₃) for CO₂ addition, under both CA II and control conditions. The inconsistency probably arises, in part, because of the multiexponential decay of the simulated pH trajectory, the special nature of the pH_S trajectory beneath the pH_S electrode, and the asymmetry of pH_S over the oocyte surface. Details of the mathematical model are presented in the third paper in this series (49).

In our physiological experiments, both under “control” (“Tris”) and CA II conditions, we consistently see that the τ that describes the CO₂-induced fall in pH_i (τ_pHi) is much larger (i.e., slower) than the τ that describes the decay of pH_S (τ_pHS). As described in the second paper in this series (46), this τ_pHi–τ_pHS difference probably reflects an asymmetrical [CO₂]_EUF over the surface of the oocyte. We suspect that pH_S actually decays with more than one exponential, and that our τ_pHS values reflect only the large, rapid relaxation of pH_S, and not the much smaller and slower decay that necessarily parallels the diffusion of CO₂ to the center of the cell.

An apparent inconsistency between the model and the physiological data arises when we compare pH_i and pH_S data during CO₂ addition, both under “CA II” and “control” conditions (Fig. 13). Note that we report the modeling data as t₆₃, i.e., the time required for pH_S to fall by 1 − (1/e) or ∼63%, to provide a simple measure of pH decay. However, because both computed pH trajectories, particularly pH_S, approximate multiexponential decays, the t₆₃ parameter is an imperfect reflection of the simulated pH trajectories. The simulation, of course, would benefit from further refinements. Finally, as noted above, the physiological data are probably influenced by [CO₂]_EUF asymmetries over the oocyte surface.

Evidence that oocytes have modest endogenous CA-like activity.

As described by Somersalo et al. (66), if oocytes totally lacked CA activity, then the addition of CO₂/HCO₃⁻ would elicit a rapid rise of pH_S, followed by an extremely rapid but partial decay of pH_S, and then by a very slow pH_S decay to pH_BECF. Simulating a more natural pH_S trajectory (e.g., Fig. 2A) requires assuming that the oocyte has modest CA activity both on the extracellular surface and in the cytoplasm. However, this endogenous intracellular CA activity must be insensitive to EZA because both Lu et al. (33) and we found that pretreating “Tris” oocytes with 400 μM EZA has no effect on a CO₂-induced (dpH_i/dt)_max (Fig. 4C vs. D, Fig. 5A), even though this pretreatment completely blocks the sizeable effects of injected CA II protein. Note that Dahl et al. (17) report the presence of endogenous CA II protein in Xenopus oocytes and demonstrate that injected acetazolamide (ACZ) causes a slight but statistically significant decrease in the rate of pH_i rise elicited by removing extracellular Cl⁻. Thus, it is possible that modest, endogenous CA II activity—sensitive to ACZ but not EZA-contributed to CO₂—induced pH_i (and to a lesser extent, pH_S) transients in our experiments.

In the second paper in this series (46), we find that ACZ has no effect on ΔpH_S in H₂O-injected control oocytes. Thus, we can conclude that the modest, endogenous CA activity on the oocyte surface must be ACZ insensitive.

Likely effects of HCO₃⁻ transport on pH_S.

In his experiments on lamprey neurons, Chesler (15) found that applying CO₂/HCO₃⁻ did not cause a transient increase in pH_S, but a decrease. Importantly, these neurons, unlike the oocytes in our experiments, had a powerful transport mechanism for the uptake of HCO₃⁻ (or an equivalent species, such as CO̿₃). Such a HCO₃⁻-uptake mechanism, by itself, would have caused pH_S to decrease. We suggest that, in Chesler's experiments, the tendency of HCO₃⁻ influx to lower pH_S outweighed the tendency of CO₂ influx to raise pH_S.

Effect of Varying CO₂/HCO₃⁻ Levels

Effect on pH_i.

In Figs. 9 and 10, we saw that, as we increase [CO₂]_BECF from 1.5% to 5% to 10% (ratios: 1/∼3.3/∼6.6), (dpH_i/dt)_max increases in smaller ratios (1/2.0–2.3/3.4–3.5), regardless of whether CA II is present.

The mathematical model predicts that, as [CO₂]_BECF increases, the maximal CO₂ influx (which occurs at ∼9–12 s into the simulation) across the plasma membrane (arrow no. 2 in Fig. 12) should increase in the ratios 1/∼3.0–3.2/∼5.6–6.2 (Table 5, column “2”), which is only slightly less than the ratios of [CO₂]_BECF values. This small discrepancy almost certainly reflects the effect of CO₂ diffusing across the EUF, inasmuch as the discrepancy nearly vanishes when we preequilibrate CO₂/HCO₃⁻ throughout the EUF and then begin the simulations by suddenly allowing the CO₂ to cross the membrane at time 0.

Table 5.

Parameter ratios from simulations at 1.5%, 5%, and 10% CO₂

	Predicted Ratios
[CO2]BECF	(dpHi/dt)max	ΔpHS	1	2	3	4	5	(d[H+]IM/dt)max	(dpHIM/dt)max
“CA II”
1.5% (1)	1	1	1	1	1	1	1	1	1
5% (∼3.3)	2.8	2.5	3.2	3.0	3.6	2.5	2.9	3.2	2.9
10% (∼6.6)	4.2	3.9	6.3	5.6	7.5	3.9	5.2	5.1	4.3
“Control” (Tris)
1.5% (1)	1	1	1	1	1	1	1	1	1
5% (∼3.3)	3.1	2.6	3.5	3.2	3.2	2.6	3.2	3.2	3.0
10% (∼6.6)	4.4	4.1	7.0	6.2	6.2	4.0	6.0	5.3	4.3

Ratios predicted by the mathematical model for “CA II” oocyte and “Control” (Tris) oocyte at the three different experimental conditions (i.e., 1.5% CO₂, 5% CO₂, and 10% CO₂). The numerals at the top of the columns refer to the numbered arrows in Fig. 12, A (CA II) and B (Control). BECF, bulk extracellular fluid; (dpH_i/dt)_max, maximal rate of pH_i change; (d[H⁺]_IM/dt)_max, maximum rate of change of [H⁺] in intracellular surface of the membrane.

Returning to the standard mathematical model, in which CO₂ and HCO₃⁻ must diffuse across the EUF at the beginning of the simulation, we find that the maximal CO₂ fluxes into the region adjacent to the extracellular surface of the membrane (EM) from the adjacent extracellular region (EM+1; arrow no. 1 in Fig. 12) increase in the ratios 1/3.2–3.5/6.3–7.0 (Table 5, column “1”). Similarly, the maximal CO₂ fluxes from the region adjacent to the intracellular surface of the membrane (IM) to the adjacent intracellular region (IM+1; arrow no. 3 in Fig. 12) increase in similar ratios, 1/3.2–3.6/6.2–7.5 (Table 5, column “3”). Thus, we can conclude that CO₂ diffusion near the membrane is not responsible for the relatively small ratios that we observe for (dpH_i/dt)_max in our physiological experiments.

When we examine the maximal fluxes through the reaction CO₂ + H₂O → H₂CO₃ in the IM region (arrow no. 5 in Fig. 12), we see that they increase in the ratios 1/2.9–3.2/5.2–6.0 (Table 5, column “5”). Because the ratios of CO₂ diffusive fluxes (arrow nos. 1, 2, and 3) are near ideal, this small decrease in the ratios for the reaction flux (arrow no. 5) must be due to a rise in [H₂CO₃]_IM, which in turn is likely due to an accumulation of H⁺ in “IM.”

When we examine the maximum rate of change of [H⁺] in “IM,” we see that the (d[H⁺]_IM/dt)_max rises in the ratios 1/3.1–3.2/5.1–5.3 [Table 5, “(d[H⁺]_IM/dt)_max” column], indicating a decrease in ratios at 10% CO₂. Finally, when we examine (dpH_IM/dt)_max, the model predicts ratios of 1/2.9–3.0/4.3 [Table 5, “(dpH_IM/dt)_max” column], indicating an effect of converting rates of [H⁺] change to rates of pH change at 10% CO₂. These (dpH_IM/dt)_max ratios in the “IM” region are virtually identical to those predicted at a depth of 50 μm, 1/∼2.8–3.1/∼4.2–4.4, regardless of the presence of CA II [see Table 5, “(dpH_i/dt)_max” column]. Indeed, we find that although the absolute magnitudes of (dpH_i/dt)_max decrease with increasing depth, the ratios of the (dpH_i/dt)_max values are not appreciably depth sensitive.

The (dpH_i/dt)_max values that we observed in our physiological experiments were smaller yet than those predicted by the model for a depth of 50 μm (compare Fig. 10 and Table 5). One explanation for this discrepancy is that we obtained physiological (dpH_i/dt)_max values in Fig. 10 not precisely at 10 s, but between ∼10 and ∼40 s into the electrophysiological experiments (during which time pH_i was falling at an approximately steady rate). Indeed, the model predicts that the ratio of dpH_i/dt values at 40 s into the simulation will be ∼10–26% less than those taken at 10 s. In fact, the dpH_i/dt ratios predicted by the model at 50 μm and 40 s (not shown) are now rather close to those reported in Fig. 10A.

Effect on pH_S.

In Figs. 9 and 10, we saw that, as we increase [CO₂]_BECF from 1.5% to 5% to 10% (1/∼3.3/∼6.6), ΔpH_S increases in smaller ratios (1/1.4–1.8/2.2–2.5), regardless of whether CA II is present. In fact, these ratios are about 1/3 less than the (dpH_i/dt)_max ratios obtained in physiological experiments, and discussed above.

We have already seen in the previous section that the mathematical model predicts that, as [CO₂]_BECF increases, the maximal CO₂ fluxes from “EM+1” to “EM” to “IM” to “IM+1” increase in nearly the same ratio as [CO₂]_BECF (Table 5, columns “1”, “2”, and “3”). However, when we examine the fluxes through the reaction H₂CO₃ → CO₂ + H₂O in “EM” region (arrow no. 4 in Fig. 12), we see that they increase in the ratios 1/2.5–2.6/3.9–4.0 (Table 5, column “4”), which are virtually identical to those for the predicted ΔpH_S values, 1/∼2.5–2.6/∼3.9–4.1.

Even in the case of the mathematical model, the ratios of ΔpH_S are somewhat smaller (∼7%) than the ratios of (dpH_i/dt)_max. However, in the case of the physiological data, the ΔpH_S ratios can be as much as 37% smaller than the (dpH_i/dt)_max ratios. We think that the explanation for this larger discrepancy lies with the pH_S electrode and the special environment it creates between the electrode tip and the oocyte membrane. When we introduce CO₂/HCO₃⁻ into the BECF, CO₂ and HCO₃⁻ diffuse from the BECF to the EUF that surrounds the electrode tip. As CO₂ and HCO₃⁻ diffuse into the space between the electrode and membrane, a portion of the CO₂ that has entered the space diffuses into the cell, lowering the local [CO₂] and thus raising the local [HCO₃⁻]/[CO₂] ratio in the electrode/membrane space. As CO₂ and HCO₃⁻ diffuse even deeper into the space between the electrode and membrane, and as more CO₂ enters the cell, the local [HCO₃⁻]/[CO₂] ratio increases even further. Thus, on a relative scale, [CO₂] should rise more slowly than [HCO₃⁻] near the center of the pH_S electrode, promoting the reactions HCO₃⁻ + H⁺ → H₂CO₃ → CO₂ + H₂O, and thus tending to amplify the ΔpH_S value reported by the pH_S electrode. However, as we proportionally raise [CO₂]_BECF and [HCO₃⁻]_BECF, the rate of the preceding reactions does not go up in the same proportions, either because of the special environment beneath the pH_S electrode (which is not in our model) or because the native carbonic-anhydrase activity at the extracellular surface of the oocyte (which we did model) begins to saturate (19) with respect to local [HCO₃⁻] (which we did not model). A combination of these factors puts a brake on the formation of CO₂ and therefore the consumption of H⁺. Testing this prediction will require more sophisticated models of the interface between the electrode and cell membrane.

Asymmetry of pH Changes Upon Addition vs. Removal of CO₂

In oocytes injected with CA II, CO₂ addition, compared with CO₂ removal, produced the following: 1) initial (dpH_i/dt)_max values whose magnitudes were greater and pH_i trajectories whose time constants were smaller (faster) and 2) pH_S spikes whose magnitudes were greater and that decayed with smaller τ values. In Tris-injected oocytes, we observed similar trends, but the differences did not reach statistical significance.

Effect on pH_i.

Figure 3A shows that, in “CA II” oocytes, the magnitude of (dpH_i/dt)_max is only about two-thirds as great during CO₂ removal (white bar) as during CO₂ addition (gray bar). Figure 6 shows that the τ values for pH_i are similarly larger (slower) for CO₂ removal vs. addition. As far as we are aware, previous authors over the past four decades have not explicitly noted such differences in pH_i data between CO₂ addition and removal. However, in examining pH_i-vs.-time records in the literature, both in studies in which one of us was a coauthor (9, 10, 28, 51, 57, 72, 73) as well as studies of others (1, 8, 20, 41, 43, 71), we find many examples in which the magnitude of (dpH_i/dt)_max was 40–170% greater for CO₂ addition vs. CO₂ removal.

One reason for the CO₂-on/off disparity is clear from the first-generation mathematical model developed by Boron and De Weer (9), which ignores diffusion. That is, when CO₂ first enters the cell following addition of extracellular CO₂, pH_i is relatively high (i.e., further away from the pK), so that a relatively high fraction (“1-α” in the Boron-De Weer model) of incoming CO₂ will undergo the reaction CO₂ + H₂O → HCO₃⁻ + H⁺.

$$1-\alpha =\frac{{\left[{\text{HCO}}_3^{-}\right]}_{\text{i}}}{{\left[{\text{HCO}}_3^{-}\right]}_{\text{i}}+{\left[{\text{CO}}_2\right]}_{\text{i}}}=\frac{1}{1+{10}^{\text{p}K-{\text{pH}}_{\text{i}}}}$$ (2)

Thus, during the initial moments of the CO₂ exposure, when pH_i is relatively high (e.g., ∼7.22 in Fig. 2A), the influx of a bolus of CO₂ generates a relatively large amount of H⁺, causing the cell to acidify relatively rapidly. Eventually, CO₂ equilibrates between the extra- and intracellular fluid, and, if the effects of pH_i regulation have been small, pH_i is now lower than before CO₂ was added (e.g., ∼6.93 in Fig. 2A). Upon the subsequent removal of extracellular CO₂, the exit of CO₂ leads to a depletion of cytosolic CO₂, which is partially replenished via the net reaction HCO₃⁻ + H⁺ → CO₂ + H₂O. However, because pH_i (and thus “1-α”) is now relatively low, the previous reaction replenishes a relatively small fraction of the exiting CO₂, and thus consumes a relatively small amount of H⁺. Thus, assuming that β_I is the same under both conditions, we expect the initial maximal rate of pH_i rise with CO₂ removal to be less than the initial maximal rate of pH_i fall with CO₂ addition. In our experiments in which we added 1.5% CO₂, the mean initial pH_i was ∼7.22 (1-α ≅ 0.929). Just before subsequently removing this 1.5% CO₂, the mean steady-state pH_i was ∼6.98 (1-α ≅ 0.884). Thus, the Boron-De Weer model predicts a slowing of the initial pH_i trajectory for CO₂ removal vs. addition of only [(0.929/0.884) − 1] or ∼5%. In fact, our physiological data reveal a slowing of ∼1/3.

Our present mathematical model predicts (dpH_i/dt)_max magnitudes that are 17–19% less for CO₂ removal vs. addition (see Table 6). The model also predicts t₆₃ values for pH_i that are larger (slower) for CO₂ removal vs. addition, both for “CA II” and “control” oocytes (Fig. 13), in agreement with the experimental results (Fig. 6). As to the mechanism, the model predicts a maximal CO₂ efflux during CO₂ removal (arrow no. 2 in Fig. 14) that is ∼16% less than the influx during CO₂ addition (arrow no. 2 in Fig. 12). The difference in predictions between the Boron-De Weer model (∼5% asymmetry) and the present model must be due to the inherent asymmetry of the oocyte vs. its surroundings (discussed below) and diffusion. Indeed, increasing the width of the EUF from 10 μm to 100 μm causes the discrepancy of (dpH_i/dt)_max magnitudes between CO₂ removal vs. addition to increase by ∼30%. Nevertheless, the present model cannot adequately account for the reduction of (dpH_i/dt)_max magnitude for CO₂ removal vs. addition observed in our physiological experiments, and in the experiments of others. One possibility, discussed in the second paper in this series (46), is that convective flow over the oocyte creates asymmetries of [CO₂] at the oocyte surface. Another possibility is that β_I could be greater at low pH_i (during the first moments of CO₂ efflux) than at high pH_i (during the first moments of CO₂ influx), as has indeed been observed in some cell types (7, 10, 13).

Table 6.

Simulations of CO₂ addition vs. removal

	“CA II”		“Control” (Tris)
	(dpHi/dt)max	ΔpHS	(dpHi/dt)max	ΔpHS
CO2 Addition	0.0021	0.0501	0.0012	0.0307
CO2 Removal	0.0017	0.0481	0.0010	0.0324

Predictions of the mathematical model for (dpH_i/dt)_max and ΔpH_S for CO₂ addition and removal at 1.5% CO₂.

Fig. 14.

Predictions of the mathematical model for maximal CO₂ diffusion and reaction fluxes near the plasma membrane during removal of 1.5% CO₂/10 mM HCO₃⁻. A: “CA II” oocyte. B: “Control” or “Tris” oocyte. The parallel dark brown curves identify the plasma membrane (PM). The green curves to the left and right of the PM represent the spatial discretizations for the numerical solutions. The numbers near the arrows 1 through 5 indicate the maximal diffusive fluxes (sharp arrowheads) and reaction fluxes (dull arrowheads) in units of μmol/s. These maximal fluxes occur within ∼1 s of each other. The diffusion/reaction ratio (DRR) is the quotient of flux no. 1/flux no. 4. Details of the mathematical model are presented in the third paper in this series (49).

Effect on pH_S.

Figure 3C shows that, in the presence of CA II, the magnitude of ΔpH_S with CO₂ removal (white bar) is only ∼40% as great as that for CO₂ addition (gray bar). In the absence of CA II, the magnitudes of ΔpH_S are not statistically significant different between CO₂ addition vs. removal. Figure 6 shows that the τ values for pH_S are smaller (faster) for CO₂ addition vs. removal, both in the presence and absence of CA II.

A small part of the explanation for the pH_S asymmetries between CO₂ removal and addition comes from the mathematical model. The DRR is modestly smaller during CO₂ efflux (Fig. 14A) than CO₂ influx (Fig. 12A), indicating that the reaction is more important during efflux. However, because the maximal transmembrane CO₂ flux is smaller during efflux (arrow no. 2 in Fig. 14A) than influx (arrow no. 2 in Fig. 12A), the overall effect is a decrease in reaction rate. Thus, in the presence of CA II, the reaction CO₂ + H₂O → H₂CO₃ during CO₂ removal (arrow no. 4 in Fig. 14A) is ∼8% slower than the opposite reaction H₂CO₃ → CO₂ + H₂O during CO₂ addition (arrow no. 4 in Fig. 12A). As summarized in Table 6, this asymmetry in reaction rates translates to an even smaller asymmetry of ΔpH_S magnitude (∼4%) between CO₂ efflux vs. influx, only about 1/10th of the observed asymmetry of 40%.

What, then, is the explanation for the remaining ∼90% of the pH_S asymmetry with CO₂ addition vs. removal? We suggest that two elements are essential: 1) The special environment between the pH_S electrode and the oocyte membrane, which our present model does not include. Our present model simulates pH over the vast majority of the oocyte surface, whereas the pH_S electrodes reports pH_S only beneath the electrode tip. 2) The relatively low CA activity on the outer surface of the native oocyte plasma membrane. Indeed, as reported in the second paper in the series (46), and as confirmed by the model, we find that expressing CA IV on the cell surface eliminates the CO₂ off/on asymmetry for ΔpH_S.

How do these two elements conspire to produce the large pH_S asymmetry? CO₂ efflux is not the mirror image of CO₂ influx. During the first instants of influx, CO₂ diffuses from an infinite reservoir to a cell (a blind alley) that is CO₂ free, whereas during the first instants of efflux, CO₂ diffuses from the cell into the EM region that still contains considerable CO₂. Indeed, we already saw that the maximal efflux (arrow no. 2 in Fig. 14A) is smaller than the maximal influx (arrow no. 2 in Fig. 12A). We suggest that during CO₂ efflux, particularly beneath the pH_S electrode, CO₂ builds up near the outer surface of the cell membrane and reduces the local transmembrane flux, thereby reducing the reaction CO₂ + H₂O → HCO₃⁻ + H⁺ at the cell surface, and thus the magnitude of the transient fall in pH_S. In oocytes expressing CA IV, the enzyme consumes enough of the exiting CO₂ to maintain a low [CO₂] beneath the electrode, thereby maintaining a gradient for CO₂ efflux. Figures 20 and 22 in the second paper of this series (46) support this explanation.

Effect of Electrode Depth on CO₂-Induced pH_i Changes

Even though we inserted the pH_i electrode as superficially as possible, we hypothesize that two unexpected findings in the present study, namely, 1) the delay between the onsets of the pH_S and pH_i changes (see Table 2) and 2) the larger (slower) τ values for the pH_i vs. the pH_S changes (see Fig. 6), reflect the depth of impalement of the pH_i electrode. To test this hypothesis, we performed experiments with dual pH_i electrodes, one superficial and one deep.

Effects on pH_i delay.

The delay between an extracellular solution change and a pH_i response, which almost certainly occurred in previous oocyte studies from our laboratory and other laboratories, is not easy to recognize without a parallel indicator of the BECF solution change, pH_S in the present study.

Figure 7 and Fig. 8A show that, starting from the “0” position (i.e., outer surface of cell), advancing a second pH_i microelectrode (electrode no. 2) to a total depth of ∼300 μm deeper into the oocyte increases the time lag (i.e., pH_i delay)—with or without CA II, with application or removal of CO₂. We do not know the precise depths of the tips of either electrode no. 1 (advanced ∼40 μm beyond the “0” position) or no. 2 because the electrode tips could drag the plasma membrane deeper into the oocyte. Thus, the actual depth beneath the local plasma membrane could be less than the apparent depth. Nevertheless, it is reasonable to conclude from Figs. 7 and 8A that an increased depth of impalement exaggerates delay.

The mathematical model makes the following predictions for the application of CO₂: 1) Immediately beneath the cell membrane, pH should begin to fall virtually instantaneously. 2) At progressively greater depths, pH should remain relatively stable for a progressively longer time period before beginning the transition to a near-linear phase of decline, as simulated for several electrode depths in Fig. 15.

Fig. 15.

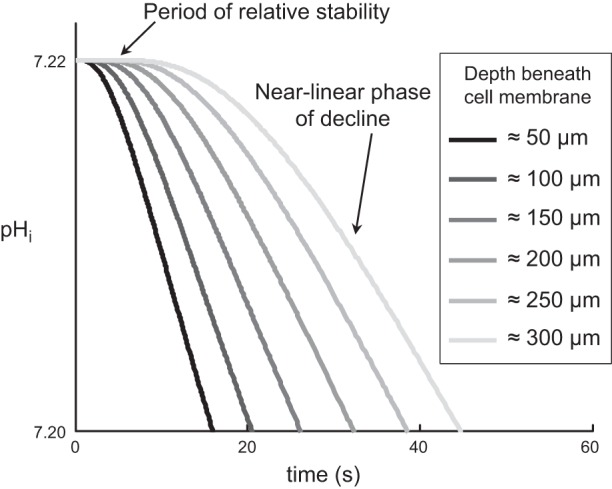
Predictions of the mathematical model for different depths of impalement, during the application of 1.5% CO₂/10 mM HCO₃⁻ to a “Control” or “Tris” oocyte. We report pH_i trajectories for the first 60 s for six depths (∼50, 100, 150, 200, 250, and 300 μm) for a hypothetical oocyte having a radius of 650 μm. At progressively greater depths, pH_i remains relatively stable for progressively longer time periods before beginning the transition to a near-linear phase of decline. Details of the mathematical model are presented in the third paper in this series (49).

How deep would the electrode tip have to be to account for a delay (averaged for CA II and Tris experiments) of ∼9 s for CO₂ addition (see Table 2)? In addressing this question using the mathematical simulations, we initially omit the implementation of vesicles beneath the oocyte membrane (present for the simulation in Fig. 15) by reducing the tortuosity factor (λ) beneath the membrane from ∼3.16 (representing our “standard oocyte”) to 1. This implementation of the model (λ = 1) predicts that the electrode tip would have to be ∼150–200 μm beneath the cell membrane. This figure is unreasonably deep, considering that in the experiment of Fig. 7A we advanced pH_i electrode no. 2 only ∼40 μm beyond the “0” position. Therefore, we suspected that a relatively superficial portion of the oocyte's cytoplasm offers considerable resistance to the diffusion of CO₂ and other solutes. Indeed, light micrographs of oocytes show a layer of vesicles, beginning ∼10 μm below the plasma membrane and extending an additional ∼25 μm into the oocyte (38). In the mathematical model, implementing such a band by reducing the diffusion of all solutes by the same tortuosity factor (λ∼6.32) can by itself account for the observed delay of ∼9 s for CO₂ addition at a more realistic depth of 50 μm into the oocyte. In the third paper in this series (49), we will explain how we came to choose a λ of ∼3.16 for our standard oocyte.

Figure 16 (a simulation of Fig. 7) shows the predicted pH_i trajectories for “CA II” and “control” oocytes at depths of ∼50 μm and ∼300 μm (assuming a λ of ∼3.16). Figure 17A shows a comparison of the physiological data and mathematical predictions for the difference between pH_i time lags at depths of ∼300 μm and ∼50 μm. The model confirms that the time lag (and thus the delay) increases with the depth of impalement—with or without CA II, with application or removal of CO₂.

Fig. 16.

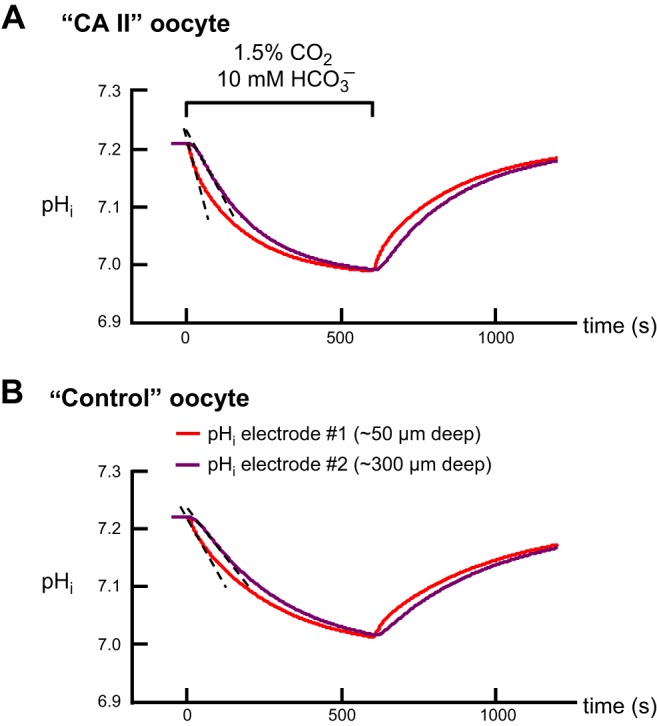
Predictions of the mathematical model for pH_i trajectories at depths of ∼50 μm and ∼300 μm. A: simulations for a “CA II” oocyte. B: simulations for a “Control” or “Tris” oocyte. In these simulations, which are comparable to the physiological experiments in Fig. 7, the tortuosity factor (λ) used to simulate a layer of intracellular vesicles is ∼3.16. Details of the mathematical model are presented in the third paper in this series (49).

Fig. 17.

Comparison of predictions of the model, at depths of ∼50 μm (S, Superficial) and ∼300 μm (D, Deep), and the physiological data. A: difference (Deep-Superficial) between pH_i time lags. B: (dpH_i/dt)_max values. C: time constants from physiological experiments or time to 63% of completion (i.e., t₆₃) for simulations. The gray background identifies data for “CA II” oocytes; the absence of background color identifies “Control” or “Tris” oocytes. The physiological data are taken from Fig. 8; note that here we report means ± standard deviation (and not SE, as in Fig. 8).

Effects on (dpH_i/dt)_max and τ.

The second unexpected finding that, we hypothesize, reflects the depth of impalement is that, both for application and withdrawal of CO₂, τ is always larger (slower) for pH_i than for pH_S (Fig. 6). Compared with electrode no. 1 (∼40 μm beyond the “0” position), electrode no. 2 (∼300 μm beyond the “0” position) reports a significantly smaller (dpH_i/dt)_max magnitude and larger τ (Fig. 7 and Fig. 8, B and C) in “CA II” oocytes, both for application and removal of CO₂. The effects of depth did not reach statistical significance in an ANOVA for “Tris” oocytes. Viewed differently, CA II significantly speeds the CO₂-induced pH_i changes reported by the superficial electrode, but the effects of CA II did not reach statistical significance for the deeper electrodes.

As summarized in Fig. 17B (comparable to Fig. 8B), the mathematical model is in good agreement with the physiological (dpH_i/dt)_max data except for CO₂ addition in the presence of CA II, where the difference is slightly more than one standard deviation. In fact, for this condition, the model (for an electrode depth of 50 μm) agrees very well with the (dpH_i/dt)_max data for CO₂ addition/CA II averaged over the entire study (Fig. 3A). The reason for the difference in mean values in Fig. 3A vs. Fig. 8B is probably that the superficial electrode no. 1 was less deep for the data summarized in Fig. 8B.

As summarized in Fig. 17C (comparable to Fig. 8C), the mathematical model agrees well with all of the control τ data and with the CA II data for the deep electrode. However, the physiological τ values for the superficial electrode no. 1 in CA II experiments are much smaller (faster) than predicted by the model for an electrode depth of 50 μm. Again, this difference probably reflects a relatively shallow electrode depth for the subset of oocytes summarized in Fig. 8C vs. the overall data summarized in Fig. 6. Indeed, the agreement between the model and the physiological τ data is much better for the data in Fig. 6.

Conclusions

Injected CA II increases the magnitude of the pH_S spike—a semiquantitative index of peak, transmembrane CO₂ flux—both during CO₂ addition and removal, and EZA reverses these effects. The mathematical model predicts that CA II maintains a relatively low [CO₂]_i during CO₂ influx, and a relatively high [CO₂]_i during efflux, thereby maximizing CO₂ gradients, and thus CO₂ fluxes and magnitudes of (dpH_i/dt)_max.

The time constant for the decay of pH_i is larger (slower) than that of pH_S, reflecting in part the depth of the tip of the pH_i electrode, even during “superficial” impalements.

The ΔpH_S magnitude increases with [CO₂]_BECF, but less than proportionally.

As an index of peak CO₂ flux, ΔpH_S approach offers the practical advantage of requiring a relatively simple and reproducible measurement. Moreover, ΔpH_S measurements provide intuitive insights into 1) the effects of cytosolic CA on CO₂ fluxes and 2) reaction-diffusion events involving acids and bases at the outer surface of the membrane, near many membrane proteins. Although ΔpH_S is presently only a semiquantitative index of the absolute maximal CO₂ flux (or permeability), it is nonetheless invaluable for assessing CO₂ permeability through channels. More sophisticated mathematical models could in principle extract CO₂ permeabilities from ΔpH_S data. In principle, one could use pH-sensitive fluorescent dyes, confined to the extra- or intracellular cell surface. We predict that the dye-derived pH_S values from isolated cells would be smaller than electrode-derived pH_S values because of the special environment created beneath the electrode. Nevertheless, this special environment may provide insight into events in narrow extracellular spaces.

The traditional approach of determining the maximal CO₂ flux from the maximal slope of the pH_i vs. time record has the disadvantage of requiring that one use a curve-fitting procedure with several (time, pH_i) points. The fitted (dpH_i/dt)_max value depends on one's judgment of the region to be fitted and the depth of pH_i-electrode impalement. In the case of pH_i measurements based on cytosolic fluorescent dyes, (dpH_i/dt)_max values represent a mean over the volume of observation. In either case, (dpH_i/dt)_max provides limited intuitive insight into CA II activity because the measurement is “cis” to the enzyme.

Measurements of pH_i are intrinsically valuable for assessing transporter-mediated acid-base fluxes as well as intracellular buffering power. Thus, the combination of pH_i and pH_S approaches provides a depth of insight that is not possible from either modality alone.

GRANTS

R. Musa-Aziz was supported, for a part of this project, by a fellowship from the American Heart Association (0625891T) and by Fundação de Amparo a Pesquisa do Estado de São Paulo (FAPESP no. 08/128663). R. Occhipinti was supported by a fellowship from the American Heart Association (11POST7670015). W. F. Boron gratefully acknowledges the support of the Myers/Scarpa endowed chair. This work was supported by National Institutes of Health Grants NS-18400 and DK-81567 as well as Office of Naval Research Grants N00014-05-1-0345, N00014-08-1-0532, and N00014-11-1-0889 to W. F. Boron.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

R.M.A., R.O., and W.F.B. conception and design of research; R.M.A. and R.O. performed experiments; R.M.A. and R.O. analyzed data; R.M.A., R.O., and W.F.B. interpreted results of experiments; R.M.A. and R.O. prepared figures; R.M.A. and W.F.B. drafted manuscript; R.M.A., R.O., and W.F.B. edited and revised manuscript; R.M.A., R.O., and W.F.B. approved final version of manuscript.