Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2015 Sep 1.
Published in final edited form as: Psychol Sci. 2014 Jun 27;25(9):1712–1721. doi: 10.1177/0956797614538458

Young Children Bet On Their Numerical Skills: Metacognition in the Numerical Domain

Vy A Vo 1, Rosa Li 2, Nate Kornell 3, Alexandre Pouget 4, Jessica F Cantlon 5
PMCID: PMC4217213  NIHMSID: NIHMS596427  PMID: 24973137

Abstract

Metacognition, the ability to assess one’s own knowledge, has been targeted as a critical learning mechanism in mathematics education. Yet, the early childhood origins of metacognition have proven difficult to study. Using a novel nonverbal task and a comprehensive set of metacognitive measures, we provide the strongest evidence to date that young children are metacognitive. We show that children as young as 5 years make metacognitive “bets” on their numerical discriminations in a wagering task. However, contrary to previous reports from adults, children’s metacognition proved to be domain-specific: children’s metacognition in the numerical domain was unrelated to their metacognition in another domain (emotion discrimination). Moreover, children’s metacognitive ability in only the numerical domain predicted their school-based mathematics knowledge. The data provide novel evidence that metacognition is a fundamental, domain-dependent cognitive ability in children. The findings have implications for theories of uncertainty and reveal new avenues for training metacognition in children.

Metacognition has been targeted as an important learning mechanism in the STEM disciplines, particularly mathematics (Kuhn, 2000; Schoenfeld, 1992). Education research has shown that those with poor metacognitive abilities tend to overestimate their knowledge, study less, and consequently learn less (Dunlosky & Rawson, 2011; Metcalfe & Kornell, 2007). Creating interventions that explicitly teach metacognitive strategies is an active area of investigation (de Bruin & van Gog, 2012; Son, 2010). Moreover, models of mathematics learning that include assessments of metacognitive monitoring and self-regulation better predict children’s mathematical competence in the classroom (Schoenfeld, 2006). However, it is currently unclear how metacognitive skills emerge in development or what factors influence their developmental trajectory. The vast majority of developmental research on metacognition has been with older children between the ages of 8 and 18 years because children younger than 7 or 8 often fail metacognitive tasks (Flavell, 1979; Reyna, 1996). Thus it is unclear what types of interventions would be effective for training metacognition to improve young children’s learning within the domain of mathematics and beyond.

A long history of metacognition research in adults, especially with memory tasks, has shown that humans can access and rate their internal uncertainty (Nelson & Narens, 1990). In a typical metacognition paradigm, subjects study a list of words or facts and estimate the likelihood that they will recall individual list items at a later time. Adults are typically above-chance at predicting their future recall of the list items, and thus are capable of assessing the strength of their own knowledge (Dunlosky & Bjork, 2008). An open question is to what extent metacognition is available to young children (< 8 years old). The existing data from older children and adolescents show that uncertainty monitoring improves with age (Koriat & Shitzer-Reichert, 2002; Lyons & Ghetti, 2010; Sussan & Son, 2007). However, data on the development of metacognitive skills during early childhood are generally sparse and sometimes conflicting (Balcomb & Gerken, 2008; Schneider, 2008). Several studies rely on measures used to assess metacognition in adults, such as verbal measures of metacognitive strategies, which could be ineffective for measuring metacognitive ability in young children (Garner & Alexander, 1989; Reyna, 1996). In this study, we begin to fill the void in the study of early childhood metacognition using a novel non-verbal metacognition task.

We also investigate whether the relationship between metacognitive skill and learning in young children is content-specific. Studies of adult metacognition, wherein subjects rate their own knowledge across different domains, support a domain-general model of metacognitive processes (Schraw, Dunkle, Bendixen, & Roedel, 1995). A domain-general model of metacognition predicts that an individual with poor uncertainty monitoring for one domain (e.g., solving subtraction problems) will also have poor uncertainty monitoring for another domain (e.g., recognizing faces). Such cross-domain correlations in metacognitive sensitivity have been observed in adults. For example, adults who are good at estimating their knowledge of major American cities also tend to be good at estimating their knowledge of mathematical probabilities (Schraw et al., 1995; but see Kelemen, Frost, & Weaver, 2000). Additionally, adults do not show a metacognitive benefit for domains in which they have a high level of knowledge or expertise such as music or physics, suggesting that metacognitive ability does not co-vary with domain knowledge (Glenberg & Epstein, 1987). The prior data indicate that adult metacognition is a general skill that is correlated across content domains and is not bound to domain knowledge. If metacognition is also domain-general in young children, this would imply that metacognitive interventions in any domain (e.g., math, reading, science) will improve metacognitive ability across all domains. Alternatively, some researchers have suggested that metacognitive abilities could be domain-specific early in development and only generalize across domains as children mature (Lyons & Ghetti, 2010; Pressley, Borkowski, & Schneider, 1987; Schraw et al., 1995; Veenman & Spaans, 2005). We test these hypotheses by comparing the metacognitive abilities of 5 to 8-year-olds from two distinct cognitive judgment types: numerical judgments and emotional valence judgments. We then investigate the relationship between children’s metacognitive abilities and standardized measures of mathematical learning and general intelligence.

Beyond revealing the origins of metacognition, tests of metacognition in children have implications for theories of the representation of uncertainty. Recent theories of cognitive and neural representations propose that internal uncertainty is inherently encoded in perceptual representations (Knill & Pouget, 2004; Pouget, Beck, Ma, & Latham, 2013). These theories argue that by encoding information probabilistically, the brain automatically represents both the intensity of a stimulus along a perceptual dimension and the uncertainty associated with that internal estimate of stimulus intensity (Ma, Beck, Latham, & Pouget, 2006). There is evidence that the cognitive and neural computations underlying confidence judgments, such as those tested in the current study, are derived from probabilistic representations of perceptual variables (Beck et al., 2008; Kiani & Shadlen, 2009). It is unknown whether young children represent their uncertainty during perceptual discriminations and use uncertainty to guide their postdecisional confidence judgments. Evidence that young children are capable of accurately judging both the perceptual intensity of a stimulus and their uncertainty about that judgment would be consistent with a central claim from theories of probabilistic representation—that representations of uncertainty are fundamental.

Method

We asked 5- to 8-year-olds to make a basic numerosity discrimination (“Which set is larger?”), immediately followed by a retrospective wager on the accuracy of that judgment (“How sure are you?”). Children earned or lost virtual tokens depending on both their accuracy and the value of their bet. In the same session, children also made confidence judgments after perceptually comparing the valence of a facial expression. This allowed us to directly compare children’s metacognitive abilities in the ‘number’ and ‘emotion’ domains while keeping task demands constant. Separately, we administered a risk assessment to control for individual biases that might influence the children’s confidence wagers. Finally, we administered standardized IQ tests to examine the relationship between metacognition and mathematics development (c.f. Kelemen, Winningham, & Weaver, 2007).

Participants

We aimed to recruit 45 to 50 subjects (ages 5 to 8), distributed approximately evenly across three age groups. We did not include three participants who exclusively chose one bet option during the entire task because we could not calculate their metacognitive scores. The general assessment is that these subjects were not motivated to participate or follow task instructions. Data for the remaining 45 children (M = 6y7m) are reported here (5 to 6 year-olds: n = 18, M = 5y6m, range = 5y – 6y1m; 6 to 7 year-olds: n = 13, M = 6y6m, range = 6y1m–7y1m; 7 to 8 year-olds: n = 14, M =7y11m, range = 7y1m–8y11m).

Six children exclusively chose the high bet for either the number task or the emotion task. Some metacognitive measures are invalid for that behavior. Those six subjects could not be included in a subset of the statistics that required a full dataset for each subject (e.g., paired t-tests, PCA).

Behavioral Measures

Children completed a baseline risk preference assessment, the metacognitive wagering task for both stimulus types, and lastly, standardized intelligence tests. Children were rewarded with tokens in all tasks, and exchanged them for prizes. Although they were told their prizes would be commensurate with the amount they earned in the wagering tasks, all children received similarly valued prizes.

Baseline risk assessment

Children completed a version of the “Cups Task” which we used to calculate their baseline risk preferences (Levin, Weller, Pederson, & Harshman, 2007; see Supplemental Material).

Metacognition task

Children were familiarized with the metacognitive wagering paradigm prior to testing (see Supplemental Material). The task presented children with a binary discrimination task (“Which picture has more dots?” or “Which person is happier?”) on a touchscreen computer. Immediately following their decision, children made a confidence judgment by placing a wager on their accuracy (Figure 1). Children completed at least 30 trials in each of the number and emotion conditions.

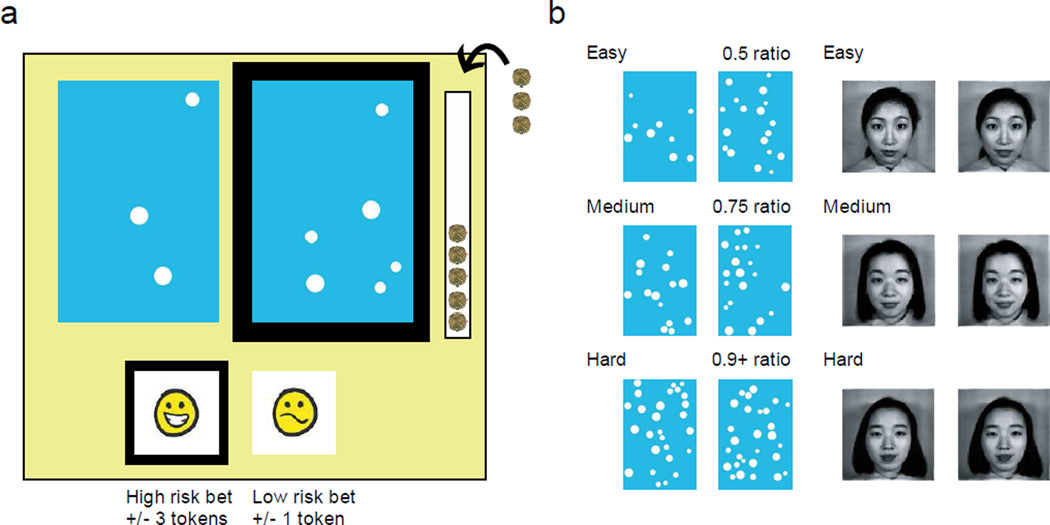
Figure 1.

Figure 1

Open in a new tab

(a) Children first made a judgment on either number or emotion stimuli. A black box appeared around their selection, and the bet icons appeared below while the stimuli remained on the screen. Children then made a confidence judgment by wagering on their discrimination accuracy. A smiley icon indicated a high bet (high confidence) and a squiggle icon indicated a low bet (low confidence). Children then gained or lost tokens in the bank based on their accuracy and bet selection. (b) Examples of number and emotion stimuli at each difficulty level.

Number condition

Two sets of dots, randomly placed and heterogeneous in size, were presented on each trial in quantities from 3 to 31. Each pair of dot arrays was classified as an easy, medium, or hard judgment based on the numerical ratio of the pair (1:2 ratio, 4:5 ratio, and a 9:10 or greater ratio, respectively). If children performed greater than 80% on the numerical judgments within the first ten trials, perceptual discrimination difficulty was increased to include more medium or hard judgments so that children were motivated to use both high and low bets throughout the session.

Emotional valence control condition

Two pictures of a single individual with different intensities in their emotional expression were presented on each trial. In order to systematically vary the intensity of the expression, a photograph of a neutral expression was morphed with a happy expression from the same individual in 120 steps using Morph Age Express 4.1.1 (c.f. Kelly & Metcalfe, 2011). The photographs of three females were taken from the Yale Face Database (Belhumeur, Hespanha, & Kriegman, 1997). Easy, medium, and hard trials were classified based on the distance between the two morphs (average distance of 48, 16, and 8 morphs, respectively). Discrimination difficulty was calibrated for each subject in the same manner as for the numerical condition.

Measures of metacognition

We calculated three measures for each child: phi, gamma, and A’ROC (described in Results). The data were inspected for outliers (> 2 SD of the mean). One data point (A’ROC, number task) for one subject was the sole outlier, and was excluded.

Intelligence and ability tests

Children also completed the Test of Early Mathematical Ability 3 (TEMA-3) and the Kaufman Brief Intelligence Test 2 (KBIT-2) to measure their mathematical, verbal, and nonverbal IQ (Ginsburg & Baroody, 2003; Kaufman & Kaufman, 2004).

Results

First, we test children’s overall metacognitive sensitivity. Then, we test the domain-specificity of children’s metacognition using multiple measures of metacognitive sensitivity (phi, gamma, and A’ROC). Finally, we examine the correlation between children’s metacognitive sensitivity and education in the domain of mathematics.

Metacognitive sensitivity

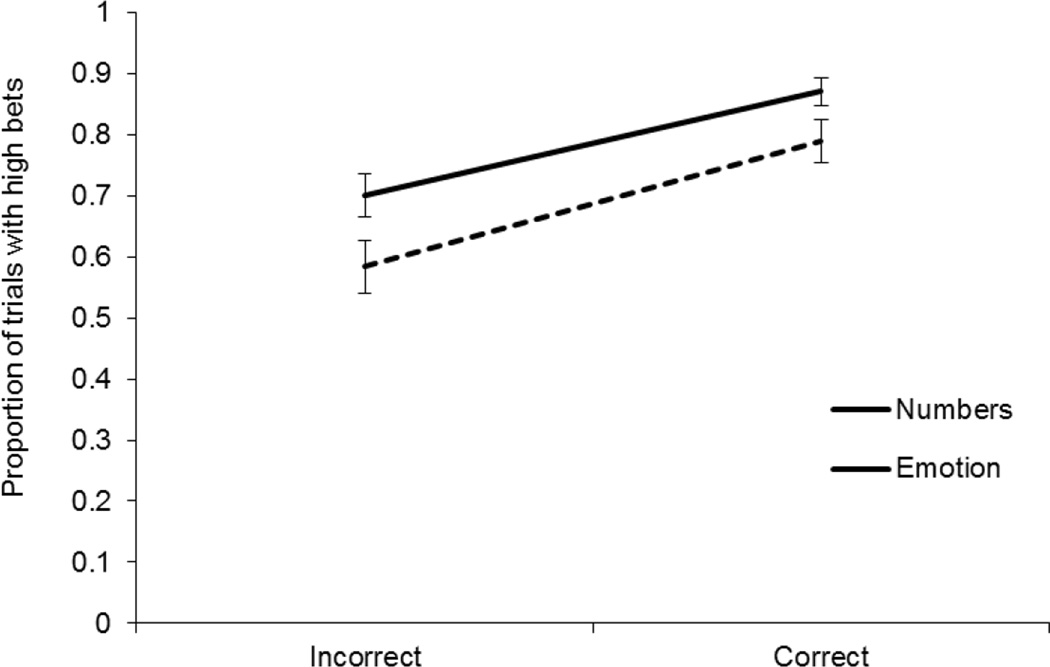
Children placed appropriate bets on the accuracy of their discrimination judgments. Discrimination accuracy was significantly above chance on both tasks (number: M = 0.80, t(44) = 21.50, p < .001; emotion: M = 0.77, t(44) = 24.63, p < .001). We found that children generally bet appropriately: they placed high-risk bets more often on correct trials than incorrect trials (Figure 2).

Figure 2.

Figure 2

Open in a new tab

Children made significantly more high bets following correct trials than incorrect trials (number: t(88) = −4.08, p < .001; emotion: t(88) = −3.76, p < .001).

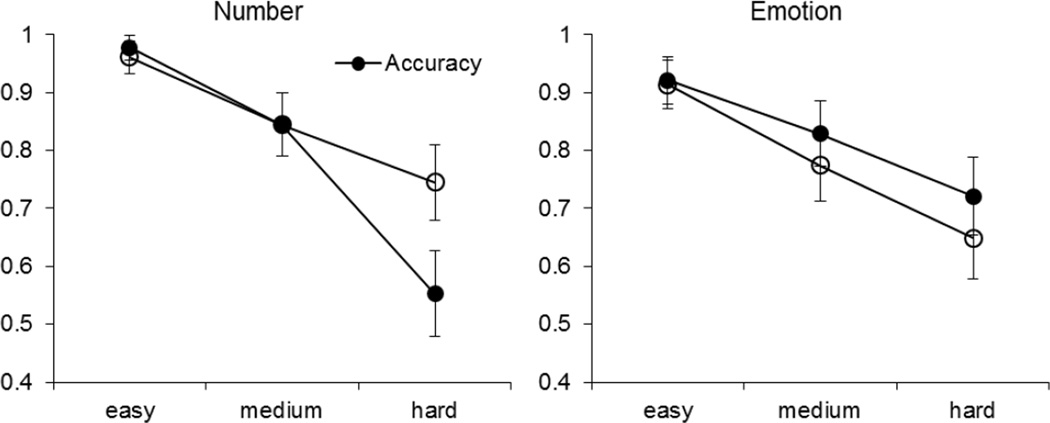
In addition, the proportion of high-risk bets decreased as difficulty increased (Figure 3).

Figure 3.

Figure 3

Open in a new tab

Accuracy and the proportion of high bets decreased with increasing difficulty for both conditions (main effect of difficulty across conditions: accuracy, F(2, 42) = 274.51, p < .001;risk, F(2, 42) = 30.30, p < .001).

Phi correlation

To measure metacognitive sensitivity, we calculated the phi correlation between task accuracy (correct or incorrect responses) and confidence judgments (high or low bets) for each child (c.f. Kornell, Son, & Terrace, 2007). Phi is also reducible to Pearson’s r. Phi correlations that are significantly greater than zero reflect a pattern of successful predictions about the accuracy of their judgments1. Phi coefficients were significantly greater than zero in both the number and emotion conditions for all age groups (Table 1).

Table 1.

Tests of Metacognitive Sensitivity by Age Group and Condition.

Phi Gamma A′ROC
Mean t df p Mean t df p Mean t df p
Number
  5 – 6 y.o. 0.13 2.33 16 .03 0.20 1.23 16 .24 0.64 2.93 13 .01
  6 – 7 y.o. 0.22 4.82 10 <.001 0.52 4.67 10 <.001 0.68 4.32 10 <.001
  7 + y.o. 0.35 7.55 12 <.001 0.74 13.75 12 <.001 0.78 14.82 12 <.001
  All subjects 0.22 6.84 40 <.001 0.46 5.55 40 <.001 0.68 6.36 38 <.001
Emotion
  5 – 6 y.o. 0.12 2.83 16 .01 0.26 1.53 16 .15 0.68 5.41 13 <.001
  6 – 7 y.o. 0.29 3.26 11 .008 0.41 1.86 11 .09 0.75 5.22 9 <.001
  7 + y.o. 0.30 7.39 13 <.001 0.66 14.39 13 <.001 0.77 13.32 13 <.001
  All subjects 0.22 6.53 42 <.001 0.43 4.62 42 <.001 0.73 11.75 37 <.001
Open in a new tab

Note. All tests are two-tailed, against chance (0 for phi and gamma; 0.5 for A′ROC).

Effects of age

Prior research with older children has reported that metacognitive sensitivity increases with age. We conducted a repeated measures two-way ANOVA of age group by experimental condition on phi. We found a main effect of age group, F(2, 36) = 9.73, p < .001, but no effect of condition, F(1, 36) = 0.02, p = .90, and no interaction, F(2, 36) = 0.32, p = .73. Metacognitive sensitivity on both the number and emotion conditions generally increases with age among 5- to 8-year-olds.

Control analyses

Children’s metacognitive sensitivity was unaffected by their baseline risk preferences and response time cues.

Risk preferences

Children’s baseline risk preferences were not correlated with phi for either condition (Table 2). This indicates that children’s metacognitive judgments were not dominated by generic risk-seeking or risk aversive behaviors.

Table 2.

Correlations Between Metacognitive Sensitivity (phi, gamma, A’ROC) and Risk Preference for Each Task.

Risk preference score
r p df
Phi
  number .03 .86 39
  emotion .13 .42 41
Gamma
  number .01 .93 39
  emotion .05 .74 41
A’ROC
  number .19 .27 36
  emotion .22 .19 36
Open in a new tab
Response time

According to some models of decision-making, the elapsed time to make a perceptual judgment is a critical internal parameter for estimating uncertainty (Kiani & Shadlen, 2009). However, others have argued that confidence judgments can be confounded by response time in wagering tasks where the appropriate bet can be predicted by the “public cue” of one’s own response time (Hampton, 2009; Koriat & Ackerman, 2010). That is, subjects could base their confidence judgments on the external observation of their own response time, rather than by an internal monitoring mechanism.2

To test whether response time was a critical predictor of children’s confidence judgments, we calculated phi as a partial correlation of accuracy and risk that controlled for discrimination response time. The phi correlation remained significant for both conditions (number: M = 0.21, t(40) = 6.26, p < .001; emotion: M = 0.17, t(42) = 4.80, p < .001), suggesting that children’s confidence judgments depended on an internal representation of uncertainty that is independent of response time (as predicted by uncertainty models developed in Beck et al., 2008).

Domain-specificity of metacognition

To test whether metacognitive knowledge follows a domain-general or domain-specific trajectory during early childhood, we compared several measures of metacognitive sensitivity across the number and emotion domains: confidence bias, phi, gamma, and A’ROC. Prior studies of metacognition have used only one or two of these measures, though each one may have its own flaws (Fleming & Dolan, 2012; Masson & Rotello, 2009; Nelson, 1984).

Confidence bias

We calculated a measure of confidence judgment bias by taking each child’s average confidence judgment (high or low) minus the child’s average task accuracy (confidence bias: number M = +0.05 ± .046, emotion M = −0.08 ± .076). Biases differed significantly between the number and emotion domains (t(38) = −3.45, p = .001), with children exhibiting marginal overconfidence in their numerical judgments and underconfidence in their emotion judgments (one-sample t-tests: t(38) = 1.92, p = .059; t(38) = −2.10, p = .04; see Supplemental Material for further tests). However, bias effects are known to be influenced by differences in task accuracy, so the true degree of children’s overestimation or underestimation is unclear (Schraw & Roedel, 1994).

Phi coefficient

The phi coefficient, as described above, represents each subject’s correlation between their discrimination accuracy and their risk choices. We tested whether children’s phi coefficients were correlated between the number and emotion conditions. Children’s phi values were not correlated between the two domains, suggesting that children’s metacognitive sensitivity is not uniform across different judgment types (Table 3).

Table 3.

Correlations of the Three Measures of Metacognitive Sensitivity (phi, gamma, A’ROC) Across Domains.

Number vs. emotion
r df p
Phi −.12 37 .91
Gamma .08 37 .64
A’ROC .04 30 .84
Open in a new tab

Gamma coefficient

The gamma coefficient is a non-parametric measure of correlation that is calculated by taking the difference between concordances (e.g., high bets on correct items) and discordances (e.g., high bets on incorrect items) and dividing by the total number of trials, bounding the score between 1 and -1 (Nelson, 1984). Gamma was significantly above zero for both conditions and most age groups, although the youngest children showed large variance in their scores (Table 1). However, the lack of a gamma effect in young children should be viewed cautiously due to systematic biases in the gamma measure (Masson & Rotello, 2009).

As with phi, gamma was not statistically predicted by the child’s baseline risk preference (Table 2). Gamma also was not correlated between the number and emotion domains (Table 3).

A′ROC

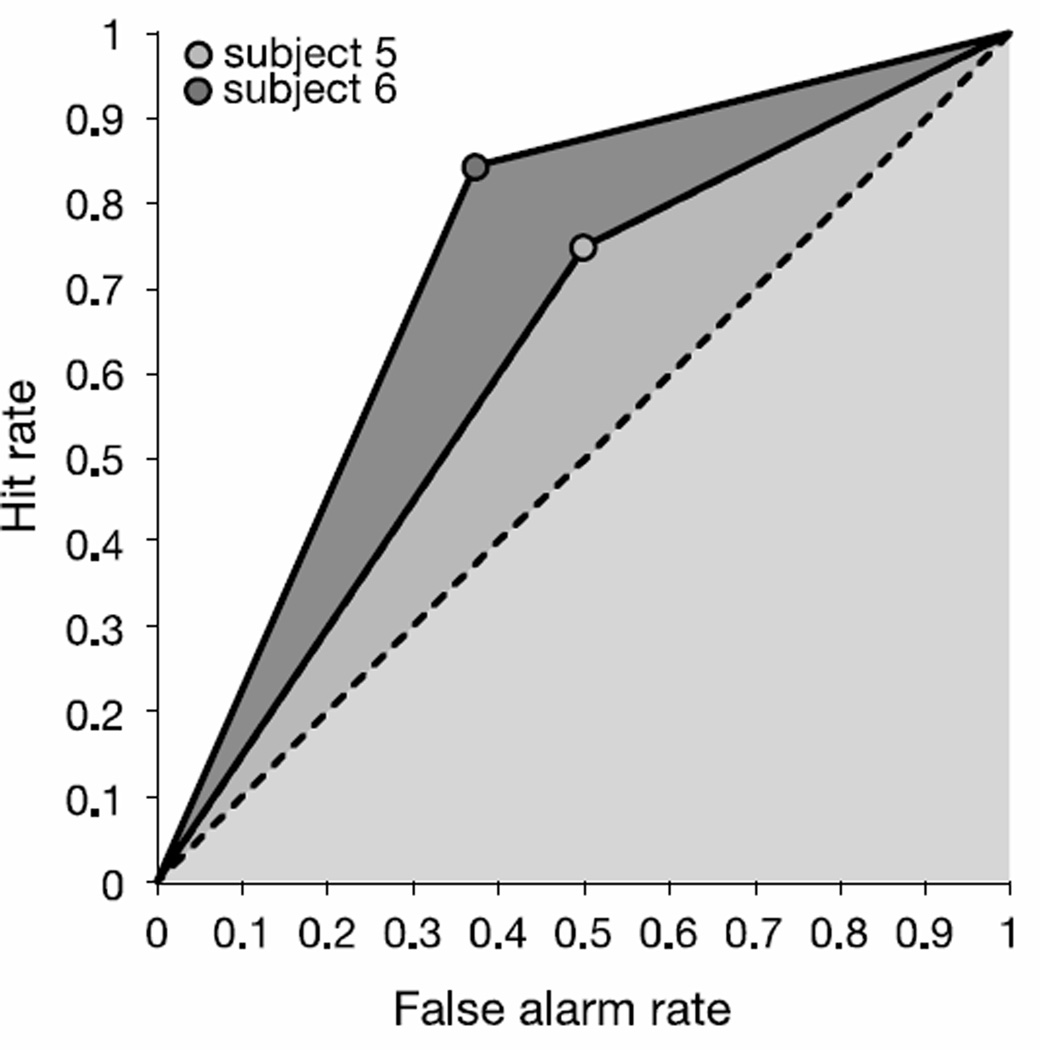
We calculated a non-parametric measure of metacognitive sensitivity from signal detection theory: the estimated area under the receiver operation characteristic (ROC) curve, or A′ROC (Galvin, Podd, Drga, & Whitmore, 2003; Kornbrot, 2006). The ROC function plots the hit rate (high bets on correct trials or low bets on incorrect trials, or ‘concordances’) against the false alarm rate (low bets on correct trials and high bets on incorrect trials, or ‘discordances’), such that equivalence between the two represents no metacognitive sensitivity (A′ROC = 0.5, see Figure 4).

Figure 4.

Figure 4

Open in a new tab

Example receiver operating characteristic (ROC) functions using data from the emotion condition. The dashed diagonal line represents cases where the hit rate is equal to the false alarm rate, or when the subject exhibited no metacognitive sensitivity. Any deviations towards the upper left indicate sensitivity above chance. Here subject 5 has a smaller area under their curve, and is therefore less metacognitively sensitive than subject 6.

The area under the ROC curve, A′ROC, was significantly greater than chance for both conditions and all age groups, indicating that even the youngest children showed significant metacognitive sensitivity (Table 1). A′ROC was not significantly influenced by baseline risk preferences (Table 2). And as with phi and gamma, A′ROC was not correlated between the number and emotion domains (Table 3).

Summary analyses across measures of metacognition

The results from phi, gamma, and A′ROC broadly indicate that individual differences in metacognitive ability are not correlated across content domains during early childhood. To test whether this was the broad pattern across all measures, we performed a canonical correlation analysis (CCA) (Hair, Anderson, Tatham, & Black, 1998).

CCA finds the maximal correlation between a linear combination of one set of variables (in this case, number-related metacognition measures) and a linear combination of another set (emotion-related measures). The full CCA model indicated that there is no significant linear relationship between the two domains (Wilks Λ = .759, R2 c = .431, F(9, 63.43) = 0.846, p = .58). This supports the conclusion that metacognitive ability is domain-specific in children.

We next used principal components analysis (PCA) to obtain a summary score of metacognitive sensitivity for each subject. PCA plots the data in an n-dimensional space (n = number of input variables) and determines which of the n dimensions, or components, account for most of the variance in the data (Hair et al., 1998).

We performed a PCA across the measures of metacognitive sensitivity (phi, gamma, and A’ROC) for both domains, resulting in six input variables. Both the Kaiser criterion and the scree plot indicated that two components accounted for most of the variance in the data (Table 4). The loads, which quantify the strength of the relationship between the component and each input variable, were varimax rotated to improve the interpretability of the solution. The metacognitive measures clustered together by domain. All number measures loaded highly on component 1, whereas all emotion measures loaded highly on component 2 (Table 4). These results are consistent with the conclusion that children’s performance segregates by content domain, rather than by measurement type. We then used the individual PCA scores for each component as a summary measure of number-related or emotion-related metacognition to test the relationship between metacognitive sensitivity and children’s cognitive development.

Table 4.

Loadings of Each Metacognition Measure on the PCA Components.

Component 1 Component 2
N = 32 N = 32
Number phi .968*** .026
Number gamma .984*** .019
Number A′ROC .987*** −.026
Emotion phi −.153 .923***
Emotion gamma .109 .951***
Emotion A′ROC .062 .991***
Eigenvalue 2.93 2.73
Variance explained 49% 46%
Open in a new tab

Note. Loadings are reported for the varimax rotated solution.

***

p < .005.

PCA was performed on the correlation matrix to make the scales equivalent across variables.

Metacognition and education

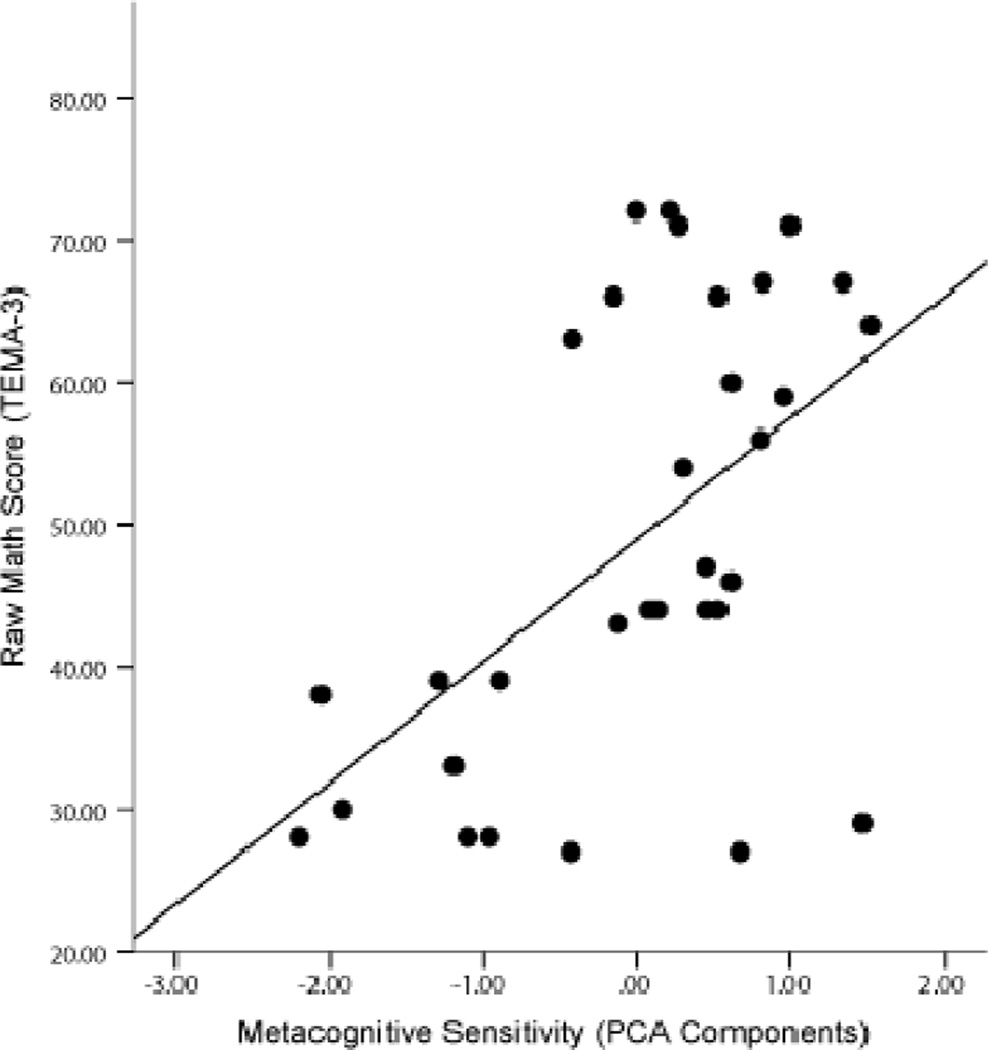
To investigate the possible link between domain-specific metacognition and cognitive development, we correlated children’s metacognitive scores from the PCA with their standardized test scores. Metacognitive sensitivity on numerical judgments, but not emotion judgments, correlated with children’s mathematics test scores on the TEMA (Figure 5). Since children’s mathematics ability is not related to metacognitive sensitivity for both conditions, the effect is not likely explained by a generic age or competence effect.

Figure 5.

Figure 5

Open in a new tab

Metacognitive sensitivity on the number task was significantly related to math ability (r(30) = .54, p = .001). A correlation was not observed for the emotion condition (emotion: r(30) = .26, p = .17). The abscissa represents scores from a PCA performed on three different measures of metacognition (phi, gamma, and A′ROC) from the numerical condition.

No measure of metacognition was significantly correlated with general intelligence scores as measured by the KBIT-2 (emotion r(30) = .11, p = .55, number r(30) = .13, p = .46). This is further evidence of the domain-specificity of metacognition in that children’s numerical metacognition is uniquely related to their numerical and mathematical skills.

Discussion

Our data provide novel evidence that 1) young children are capable of reporting their uncertainty in a nonverbal metacognitive task; 2) uncertainty monitoring in early childhood is not a global ability that matures uniformly across content domains, but instead develops along domain-specific trajectories; 3) children’s domain-specific metacognition for numerical discrimination predicts their formal education achievement in mathematics.

Young children monitor their internal uncertainty

Several prior studies have reported that young children fail metacognitive tasks (Flavell, Green, & Eleanor, 2000; Flavell, 1979; Miller & Bigi, 1989; Myers & Paris, 1978; for review, Garner & Alexander, 1989; Reyna, 1996). However, we show with a nonverbal wagering task that young children are capable of uncertainty monitoring for a basic perceptual discrimination task. That is, young children were metacognitively sensitive across age groups, stimulus types, and multiple metacognitive measures (phi, gamma, A′ROC). This robust relationship between discrimination accuracy and confidence judgments on a trial-by-trial basis provides strong evidence that young children can access and track an internal estimate of their uncertainty.

Uncertainty monitoring is domain-specific in early childhood

We found no correlation between children’s metacognitive abilities in the number and emotion domains across multiple measures of metacognitive sensitivity. This was confirmed by canonical correlation analysis and principal components analysis (PCA). This suggests that metacognitive skill does not globally mature across content domains.

Furthermore, we found that generic metacognitive skill cannot predict formal mathematical ability—only numerical metacognition, not emotion-related metacognition, correlated with scores on a standardized math test. Whether numerical metacognition drives the development of mathematical ability, or whether mathematical ability drives the development of numerical metacognition remains to be determined. Nonetheless, these results imply that metacognition develops along domain-specific trajectories, such that children’s metacognitive abilities depend on information content and domain knowledge.

Our results support the hypothesis that metacognition transitions from a domain-specific process to a domain-general mechanism over development. A previous study with older children suggests that metacognitive abilities begin to show correlations among different content domains during adolescence (Veenman & Spaans, 2005). By adulthood, metacognition seems to be largely domain-general and independent of domain knowledge (Glenberg & Epstein, 1987; Schraw et al., 1995). These data are broadly consistent with the theory that content-specific learning strategies (and therefore, metacognitive abilities) develop as knowledge increases in a domain (Pressley et al., 1987; Reyna, 1996). Global abilities emerge when children can generalize knowledge structures and learning procedures across domains (Lyons & Ghetti, 2010; Schneider, 2008).

Implications for education

Our study shows that children can report their uncertainty nonverbally by at least age 5. This suggests that nonverbal paradigms, such as wagering, could be used in metacognitive interventions with preschool children. Yet, although children were generally metacognitive in our task, their metacognitive judgments were still imperfect. Children made several errors in their metacognitive “bets”, and on average these errors were biased toward higher wagers (‘overconfidence’) for numerical judgments and lower wagers for emotion judgments (‘underconfidence’; see Supplemental Material for discussion). Moreover, as described above, children’s metacognitive skill was domain-specific and related to their formal domain knowledge. Overall our data suggest that young children can show different metacognitive skills and biases for different stimulus types. In this case, generic interventions to improve children’s metacognitive accuracy might be less effective than training specific metacognitive strategies that depend on the content of the learning materials.

We predict that early in development the types of metacognitive errors that children make in one domain would not transfer to another domain. Characterizing these errors could be informative for educators to develop specific intervention techniques (Borkowski, 1992; Carr & Biddlecomb, 1998; Kuhn, 2000).

Children’s internal uncertainty may be represented probabilistically

Questions remain as to the precise nature of the representations that allow children to monitor their uncertainty. There are currently few formal models of metacognitive processes for children or adults (Koriat & Ackerman, 2010; Nelson & Narens, 1990). One possibility, suggested by probabilistic models of representation, is that humans inherently encode uncertainty in their perceptual representations (Knill & Pouget, 2004; Pouget et al., 2013). If this is true, then even young children should show evidence of representing the uncertainty associated with their perceptual judgments. Our data show that they do.

The probabilistic theory of representation proposes that the representation of uncertainty is a fundamental component of the cognitive architecture (Beck et al., 2008; Kiani & Shadlen, 2009; Ma et al., 2006; Pouget et al., 2013). Our finding that young children accurately report their uncertainty is consistent with the proposal that the representation of uncertainty is a fundamental ability. Developmental changes between childhood and adulthood have not yet been studied with this framework. Yet, probabilistic theories could provide new insights into the nature of fundamental mechanisms by which uncertainty is represented and those by which uncertainty is consciously accessed and reported.

Conclusion

We conclude that young children ‘know what they know’ in making basic perceptual judgments. Young children can accurately report their uncertainty nonverbally, by at least age 5. Yet, children’s metacognitive abilities continue to develop into childhood and adolescence, and even adults are far from perfect (Dunlosky & Bjork, 2008). Our data suggest that metacognitive abilities develop in tandem with domain-specific changes in children’s knowledge. The links we observed between children’s metacognitive sensitivity and formal mathematical abilities indicate that early interventions on children’s metacognitive strategies could have far-reaching effects on their education.

Supplementary Material

Supplementary data

Acknowledgements

We are grateful to Brad Mahon, Jeff Beck, the Aslin Lab, and the CAOs Lab, especially Gina Gerhardt, Laura Ackerman, and Sydney Robinson. This work was funded by NSF REESE 1109366 to A.P. & J.F.C. and NIH R01 HD064636 to J.F.C.

Contributor Information

Vy A. Vo, Department of Brain and Cognitive Sciences, University of Rochester

Rosa Li, Department of Brain and Cognitive Sciences, University of Rochester.

Nate Kornell, Department of Psychology, Williams College.

Alexandre Pouget, Department of Brain and Cognitive Sciences, University of Rochester and Department of Basic Neuroscience, University of Geneva.

Jessica F. Cantlon, Department of Brain and Cognitive Sciences, University of Rochester

References

  1. Balcomb FK, Gerken L. Three-year-old children can access their own memory to guide responses on a visual matching task. Developmental Science. 2008;11(5):750–760. doi: 10.1111/j.1467-7687.2008.00725.x. [DOI] [PubMed] [Google Scholar]
  2. Beck JM, Ma WJ, Kiani R, Hanks T, Churchland AK, Roitman J, Pouget A. Probabilistic population codes for Bayesian decision making. Neuron. 2008;60(6):1142–1152. doi: 10.1016/j.neuron.2008.09.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Belhumeur PN, Hespanha JP, Kriegman DJ. Eigenfaces vs. Fisherfaces: Recognition using class specific linear projection. IEEE Transactions on Pattern Analysis and Machine Intelligence. 1997;19(7):711–720. [Google Scholar]
  4. Borkowski JG. Metacognitive theory: A framework for teaching literacy, writing, and math skills. Journal of Learning Disabilities. 1992;25(4):253–257. doi: 10.1177/002221949202500406. [DOI] [PubMed] [Google Scholar]
  5. Carr M, Biddlecomb B. Metacognition in mathematics from a constructivist perspective. In: Hacker DJ, Dunlosky J, Graesser AC, editors. Metacognition in Educational Theory and Practice. Mahwah, NJ: Lawrence Erlbaum Associates Publishers; 1998. pp. 69–91. [Google Scholar]
  6. De Bruin ABH, van Gog T. Improving self-monitoring and self-regulation: From cognitive psychology to the classroom. Learning and Instruction. 2012;22(4):245–252. [Google Scholar]
  7. Dunlosky J, Bjork RA. The Integrated Nature of Metamemory and Memory. In: Dunlosky J, Bjork RA, editors. Handbook of Metamemory and Memory. Hillsdale, NJ: Psychology Press; 2008. pp. 11–28. [Google Scholar]
  8. Dunlosky J, Rawson KA. Overconfidence produces underachievement: Inaccurate self evaluations undermine students’ learning and retention. Learning and Instruction. 2011;22(4):271–280. [Google Scholar]
  9. Flavell JH. Metacognition and cognitive monitoring: A new area of cognitive-developmental inquiry. American Psychologist. 1979;34(10) [Google Scholar]
  10. Flavell JH, Green FL, Eleanor R. Development of children ’ s awareness of their own thoughts. Journal of Cognition and Development. 2000;1:97–112. [Google Scholar]
  11. Fleming SM, Dolan RJ. The neural basis of metacognitive ability. Philosophical Transactions of the Royal Society B: Biological Sciences. 2012;367(1594):1338–1349. doi: 10.1098/rstb.2011.0417. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Galvin SJ, Podd JV, Drga V, Whitmore J. Type 2 tasks in the theory of signal detectability: Discrimination between correct and incorrect decisions. Psychonomic Bulletin & Review. 2003;10(4):843–876. doi: 10.3758/bf03196546. Retrieved from http://www.ncbi.nlm.nih.gov/pubmed/15000533. [DOI] [PubMed] [Google Scholar]
  13. Garner R, Alexander PA. Metacognition: Answered and unanswered questions. Educational Psychologist. 1989;24(2):143–158. [Google Scholar]
  14. Ginsburg HP, Baroody AJ. Test of Early Mathematical Ability. 3rd ed. Austin, TX: PRO_ED, Inc.; 2003. [Google Scholar]
  15. Glenberg AM, Epstein W. Inexpert calibration of comprehension. Memory & Cognition. 1987;15(1):84–93. doi: 10.3758/bf03197714. Retrieved from http://www.ncbi.nlm.nih.gov/pubmed/3821493. [DOI] [PubMed] [Google Scholar]
  16. Hair JF, Anderson RE, Tatham RL, Black WC. Multivariate Data Analysis. 5th ed. Pearson Education, Inc.; 1998. [Google Scholar]
  17. Hampton RR. Multiple demonstrations of metacognition in nonhumans: Converging evidence or multiple mechanisms? Comparative Cognition & Behavior Reviews. 2009;4:17–28. doi: 10.3819/ccbr.2009.40002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Kaufman AS, Kaufman NL. Kaufman Brief Intelligence Test. 2nd ed. NCS Pearson; 2004. [Google Scholar]
  19. Kelemen WL, Frost PJ, Weaver CA. Individual differences in metacognition: Evidence against a general metacognitive ability. Memory & Cognition. 2000;28(1):92–107. doi: 10.3758/bf03211579. Retrieved from http://www.ncbi.nlm.nih.gov/pubmed/10714142. [DOI] [PubMed] [Google Scholar]
  20. Kelemen WL, Winningham RG, Weaver CA. Repeated testing sessions and scholastic aptitude in college students’ metacognitive accuracy. European Journal of Cognitive Psychology. 2007;19(4/5):689–717. [Google Scholar]
  21. Kelly KJ, Metcalfe J. Metacognition of emotional face recognition. Emotion. 2011;11(4):896–906. doi: 10.1037/a0023746. [DOI] [PubMed] [Google Scholar]
  22. Kiani R, Shadlen MN. Representation of confidence associated with a decision by neurons in the parietal cortex. Science (New York, N.Y.) 2009;324(5928):759–764. doi: 10.1126/science.1169405. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Knill DC, Pouget A. The Bayesian brain: The role of uncertainty in neural coding and computation. Trends in Neurosciences. 2004;27(12):712–719. doi: 10.1016/j.tins.2004.10.007. [DOI] [PubMed] [Google Scholar]
  24. Koriat A, Ackerman R. Choice latency as a cue for children’s subjective confidence in the correctness of their answers. Developmental Science. 2010;13(3):441–453. doi: 10.1111/j.1467-7687.2009.00907.x. [DOI] [PubMed] [Google Scholar]
  25. Koriat A, Shitzer-Reichert R. Metacognitive judgments and their accuracy: Insights from the processes underlying judgments of learning in children. In: Chambres P, Izaute M, Marescaux P-J, editors. Metacognition: Processes, Function, and Use. Kluwer Academic Publishers; 2002. pp. 1–17. [Google Scholar]
  26. Kornbrot DE. Signal detection theory, the approach of choice: Model-based and distribution-free measures and evaluation. Perception & Psychophysics. 2006;68(3):393–414. doi: 10.3758/bf03193685. Retrieved from http://www.ncbi.nlm.nih.gov/pubmed/16900832. [DOI] [PubMed] [Google Scholar]
  27. Kornell N, Son LK, Terrace HS. Transfer of metacognitive skills and hint seeking in monkeys. Psychological Science. 2007;18(1):64–71. doi: 10.1111/j.1467-9280.2007.01850.x. [DOI] [PubMed] [Google Scholar]
  28. Kuhn D. Metacognitive development. Current Directions in Psychological Science. 2000;9(5):178–181. [Google Scholar]
  29. Levin IP, Weller JA, Pederson AA, Harshman LA. Age-related differences in adaptive decision making: sensitivity to expected value in risky choice. Judgment and Decision Making. 2007;2(4):225–233. [Google Scholar]
  30. Lyons KE, Ghetti S. Metacognitive development in early childhood: New questions about old assumptions. In: Efklides A, Misailidi P, editors. Trends and Prospects in Metacognition Research. Boston, MA: Springer US; 2010. pp. 259–278. [Google Scholar]
  31. Ma WJ, Beck JM, Latham PE, Pouget A. Bayesian inference with probabilistic population codes. Nature Neuroscience. 2006;9(11):1432–1438. doi: 10.1038/nn1790. [DOI] [PubMed] [Google Scholar]
  32. Masson MEJ, Rotello CM. Sources of bias in the Goodman-Kruskal gamma coefficient measure of association: implications for studies of metacognitive processes. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2009;35(2):509–527. doi: 10.1037/a0014876. [DOI] [PubMed] [Google Scholar]
  33. Metcalfe J, Kornell N. Principles of cognitive science in education: The effects of generation, errors, and feedback. Psychonomic Bulletin & Review. 2007;14(2):225–229. doi: 10.3758/bf03194056. Retrieved from http://www.ncbi.nlm.nih.gov/pubmed/17694905. [DOI] [PubMed] [Google Scholar]
  34. Miller PH, Bigi L. The development of children’s understanding of attention. Merrill-Palmer Quarterly of Behavior and Development. 1989;25(4):235–250. [Google Scholar]
  35. Myers MI, Paris SG. Children’s metacognitive knowledge about reading. Journal of Educational Psychology. 1978;70(5):680–690. [Google Scholar]
  36. Nelson TO. A comparison of current measures of the accuracy of feeling-of-knowing predictions. Psychological Bulletin. 1984;95(1):109–133. Retrieved from http://www.ncbi.nlm.nih.gov/pubmed/6544431. [PubMed] [Google Scholar]
  37. Nelson TO, Narens L. Metamemory: A theoretical framework and new findings. The Psychology of Learning and Motivation. 1990;26:125–173. [Google Scholar]
  38. Pouget A, Beck JM, Ma WJ, Latham PE. Probabilistic brains: knowns and unknowns. Nature Neuroscience. 2013;16(9):1170–1178. doi: 10.1038/nn.3495. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Pressley M, Borkowski JG, Schneider W. Cognitive strategies: Good strategy users coordinate metacognition and knowledge. Annals of Child Development, Vol. 4. 1987;4:89–129. [Google Scholar]
  40. Reyna VF. Conceptions of memory development with implications for reasoning and decision making. Annals of Child Development. 1996;12:87–118. [Google Scholar]
  41. Schneider W. The development of metacognitive knowledge in children and adolescents: Major trends and implications for education. Mind, Brain, and Education. 2008;2(3):114–121. [Google Scholar]
  42. Schoenfeld AH. Learning to think mathematically: Problem solving, metacognition, and sense-making in mathematics. In: Grouws DA, editor. Handbook for Research on Mathematics Teaching and Learning. Macmillan Publishing Co, Inc.; 1992. pp. 334–370. [Google Scholar]
  43. Schoenfeld AH. Alexander PA, Winne PH, editors. Mathematics teaching and learning. Handbook of Educational Psychology. 2006:479–510. [Google Scholar]
  44. Schraw G, Dunkle ME, Bendixen LD, Roedel TD. Does a general monitoring skill exist? Journal of Educational Psychology. 1995;87(3):433–444. [Google Scholar]
  45. Schraw G, Roedel TD. Test difficulty and judgment bias. Memory & Cognition. 1994;22(1):63–69. doi: 10.3758/bf03202762. Retrieved from http://www.ncbi.nlm.nih.gov/pubmed/8035686. [DOI] [PubMed] [Google Scholar]
  46. Son LK. Metacognitive control and the spacing effect. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2010;36(1):255–262. doi: 10.1037/a0017892. [DOI] [PubMed] [Google Scholar]
  47. Sussan D, Son LK. The training of metacognitive monitoring in children. Columbia Undergraduate Science Journal. 2007;2(1):98–109. [Google Scholar]
  48. Veenman MVJ, Spaans MA. Relation between intellectual and metacognitive skills: Age and task differences. Learning and Individual Differences. 2005;15(2):159–176. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary data
NIHMS596427-supplement-Supplementary_data.doc (41.5KB, doc)

RESOURCES