Interplay between partner and ligand facilitates the folding and binding of an intrinsically disordered protein

Significance

Specific protein–protein interactions are abundant in, and essential for, cellular life. In contrast to the well-studied docking of two already folded proteins, it has been recently established that many proteins are disordered and unfolded in the absence of their partner protein, but appear folded once bound. Must these initially disordered proteins transiently fold in isolation before binding their partners? We examine a small disordered protein and find that interactions with its (already structured) partner protein are what cause the relatively unstructured protein to fold. Thus, the requirement for one protein to fold is not an obstacle for reliable, fast association between two proteins. This result offers some explanation for the abundance of similar protein–protein interactions throughout biology.

Abstract

Protein–protein interactions are at the heart of regulatory and signaling processes in the cell. In many interactions, one or both proteins are disordered before association. However, this disorder in the unbound state does not prevent many of these proteins folding to a well-defined, ordered structure in the bound state. Here we examine a typical system, where a small disordered protein (PUMA, p53 upregulated modulator of apoptosis) folds to an α-helix when bound to a groove on the surface of a folded protein (MCL-1, induced myeloid leukemia cell differentiation protein). We follow the association of these proteins using rapid-mixing stopped flow, and examine how the kinetic behavior is perturbed by denaturant and carefully chosen mutations. We demonstrate the utility of methods developed for the study of monomeric protein folding, including β-Tanford values, Leffler α, Φ-value analysis, and coarse-grained simulations, and propose a self-consistent mechanism for binding. Folding of the disordered protein before binding does not appear to be required and few, if any, specific interactions are required to commit to association. The majority of PUMA folding occurs after the transition state, in the presence of MCL-1. We also examine the role of the side chains of folded MCL-1 that make up the binding groove and find that many favor equilibrium binding but, surprisingly, inhibit the association process.

For many proteins, correct folding to a specific 3D structure is essential for their function inside the cell; once folded, some of these have the appropriate shape and accessible chemical groups to interact specifically with, and bind to, another protein (1). However, for a number of protein–protein interactions, folding and binding do not appear to be separate, sequential events (2, 3). Many intrinsically disordered proteins (IDPs) will appear largely unfolded in isolation, only forming a specific structure when bound to an appropriate partner protein and undergoing coupled folding and binding (4–6). Such reactions are abundant in signaling and regulatory processes (7, 8). Protein folding does not simply provide correctly shaped building blocks for the cell; it can play an intimate role in molecular recognition.

Over the past decade, bioinformatics studies have revealed that protein disorder (7, 9), and coupled folding and binding (10), are widespread in biology. Many structures of bound, folded IDPs have been solved and have shown the wide range of topologies that can be formed (11). Biophysical techniques (12), NMR in particular (13), can characterize isolated IDPs in detail. Despite this progress, the number of studies examining kinetics and the mechanisms of binding remains relatively small (14–21) given that the most commonly observed function of IDPs is in coupled folding and binding reactions (22).

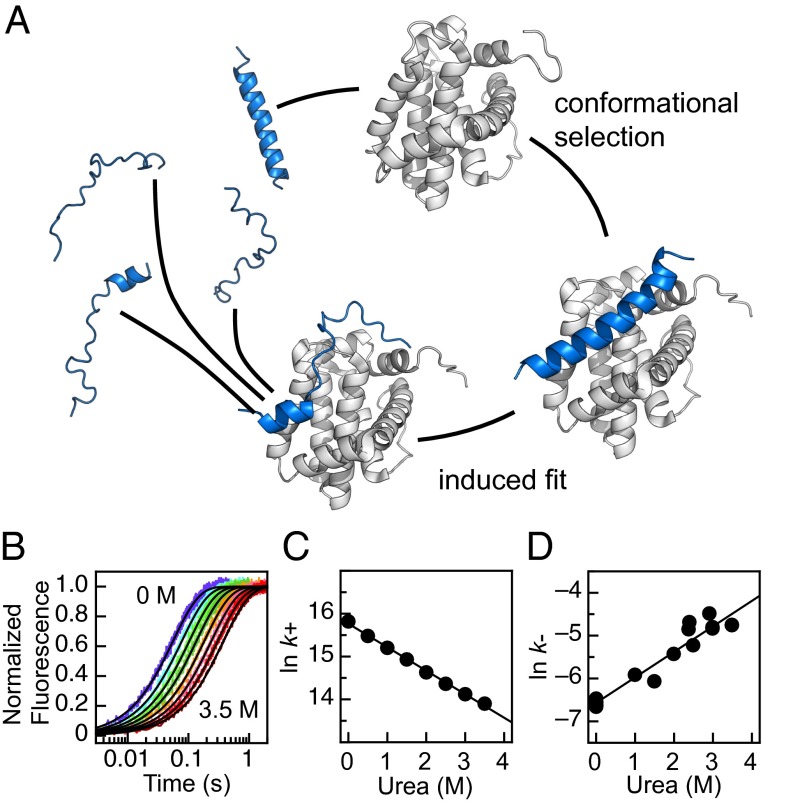
To describe coupled folding and binding, two extreme mechanisms are often discussed, focusing on whether an IDP needs to fold before interacting productively with its binding partner. In isolation an IDP could, perhaps only transiently, occupy a conformation that resembles the bound state. In the pure conformational selection mechanism, the IDP must be in this conformation at the start of the eventually successful encounter with the partner protein (23, 24) (Fig. 1A). Arguments in support of this mechanism largely come from NMR studies that have successfully detected these lowly populated, folded states in unbound IDPs (25–27). In the contrasting induced-fit mechanism, there is no requirement for the IDP to fold in isolation (28). Instead, the potentially transient interactions with the partner protein lead to the folding of the IDP (Fig. 1A). Complex mixtures of these two extreme mechanisms can also be imagined: e.g., perhaps only a proportion of the IDP needs to fold before the encounter, i.e., conformational selection followed by induced fit of the remaining peptide chain (29). To add to the potential complexity, flux through different pathways could occur simultaneously, and may depend on the concentrations of protein involved (23, 30). Further, confirming the degree of induced fit and conformational selection is only one aspect of the binding mechanism. There remain a large number of mechanistic possibilities beyond the state of the IDP prior to successful encounters.

Fig. 1.

PUMA–MCL-1 binding. (A) Cartoon of binding mechanisms. IDP PUMA (blue) can undergo coupled folding and binding with structured MCL-1 (white) to form a single, contiguous α-helix. Structures based on PDB 2ROC (39) and 1WSX (58). Unbound PUMA and encounter complex built using Chimera (University of California, San Francisco). Figure prepared using PyMol. (B) Representative fluorescence stopped-flow traces for binding. Increasing the concentration of urea from 0 to 3.5 M (in 0.5-M increments) slows association. (C) The urea dependence of the natural log of the association rate constant (k+) for the wild-type PUMA peptide used in this study. (D) The urea dependence of the dissociation rate constant (k−). k− was determined by preforming the PUMA–MCL-1 complex at micromolar concentrations and manually diluting to nanomolar concentrations to induce dissociation. The resulting kinetic trace was fit to a reversible model, fixing k+ from the association experiments (41). Gradient of the linear fits corresponds to the m values discussed in the main text. A, B, and C adapted from ref. 37.

It is largely agreed that most protein folding (and unfolding) reactions are limited by the requirement to populate a high-energy transition state (31). Kinetic, time-resolved experiments, in combination with site-directed mutagenesis and Φ-value analysis (32), have been applied successfully to describe these transition states (33, 34). With carefully chosen mutations, the distribution of Φ values (classically between 0 and 1) offers an average picture of the interactions formed at this critical stage of the folding reaction, at residue-level resolution. This picture, in conjunction with other evidence, can offer invaluable insights into the mechanisms of folding (35, 36).

We have previously reported the kinetics of a model coupled folding and binding reaction (37, 38); the BH3 motif of PUMA (an IDP) can associate with the structured protein MCL-1 and fold to a single contiguous α-helix (39). The solvent and temperature dependence of the association reaction suggested that this reaction is limited by a free energy barrier, or transition state (TS) (37). Here we systematically make structurally conservative mutations to the IDP and the partner protein, apply Φ-value analysis, and describe the transition state for binding. Molecular dynamics simulations using a coarse-grained, topology-based model of the binding process are consistent with our experimental results. We bring together all available evidence to propose a mechanism of binding.

Results

The IDP System.

We have previously shown that a peptide construct of PUMA (similar to that found in the NMR structure, with mutation M144I) self-associates at concentrations >2 μM (37), but that the mutant M144A does not (38); thus, in all these studies, we use this peptide as the pseudo wild-type into which other substitutions are made. This PUMA–MCL-1 system behaves in an apparent two-state manner so that the equilibrium dissociation constant, K_d, can be determined from the ratio of the association and dissociation rate constants (K_d = k−/k+). Because PUMA binds so tightly (K_d = 0.181 ± 0.017 nM) (38), ITC data are unreliable, but we have shown for a destabilized mutant of PUMA, that the K_d determined from ITC and that determined from kinetics are the same within error (38).

Position of the Transition State.

In the study of monomeric protein-folding, the position of the TS along one reaction coordinate can be estimated using the denaturant dependence of folding and unfolding rate constants (40). A similar approach was applied to the folding and binding of PUMA–MCL-1. Stopped flow was used to rapidly mix solutions of the proteins, the change in intrinsic fluorescence was followed, and the resulting trace fit to determine the rate constant for association (k+) (37, 38). Increasing concentrations of the denaturant urea resulted in slower association [lower k+, even when taking viscosity into account (37)] (Fig. 1 B and C). Similar to the barrier-limited folding of monomeric proteins, and unlike a purely diffusion-limited reaction (37), ln(k+) decreased linearly with concentration of urea, with a gradient referred to as an m value, m₊ = −0.55 ± 0.01 M⁻¹ (37, 41) (Fig. 1C).

Dissociation was accelerated in the presence of urea and ln(k−), where k− is the rate constant for dissociation, was also linear with concentration of denaturant, m₋ = 0.60 ± 0.04 M⁻¹ (Fig. 1D). The magnitude of these m values can be used to estimate the position of the TS, with respect to burial of solvent accessible surface area, by calculating a β Tanford (β_T) value (40, 41) (Eq. 1). For the association of PUMA and MCL-1, β_T = 0.48 ± 0.02, which is lower than the values generally seen in monomeric protein-folding, which are typically in the range 0.6–0.95 (42), suggesting that this TS is comparatively early.

Selection of Mutations in the PUMA IDP.

To apply Φ-value analysis, it is important to make structurally conservative mutations (32). To probe side-chain interactions at the protein–protein interface, the five large hydrophobic residues of PUMA, which make up the majority of the protein–protein interface with MCL-1, were mutated to the smaller residue alanine (with one exception, W133F) (SI Appendix, Fig. S1A). To probe helix formation, solvent-exposed PUMA residues were first mutated to alanine and subsequently mutated to glycine. The alanine mutant could then be used as an appropriate pseudo wild-type during analysis. These alanine–glycine (Ala–Gly) scanning mutations have been shown to specifically destabilize helical secondary structure (43, 44) and have been used to probe helix formation in protein folding (45) and coupled folding and binding reactions (15, 18, 20). Eight positions along the solvent-exposed side of PUMA were subjected to Ala–Gly scanning (SI Appendix, Fig. S2A).

Mutation Has Small Effects on Residual Helicity.

Circular dichroism (CD) has previously been used to show that wild-type PUMA peptide has ∼20% helical content in the absence of its binding partner (38). CD was used to estimate this residual helicity for the mutant PUMA peptides. Mutations to alanine (and W133F) led to either no change or a small increase in the residual helicity (SI Appendix, Figs. S3 and S4). As expected, mutations to glycine, in every case, led to a drop in overall helicity compared with the corresponding alanine mutant.

Binding of Mutant IDPs.

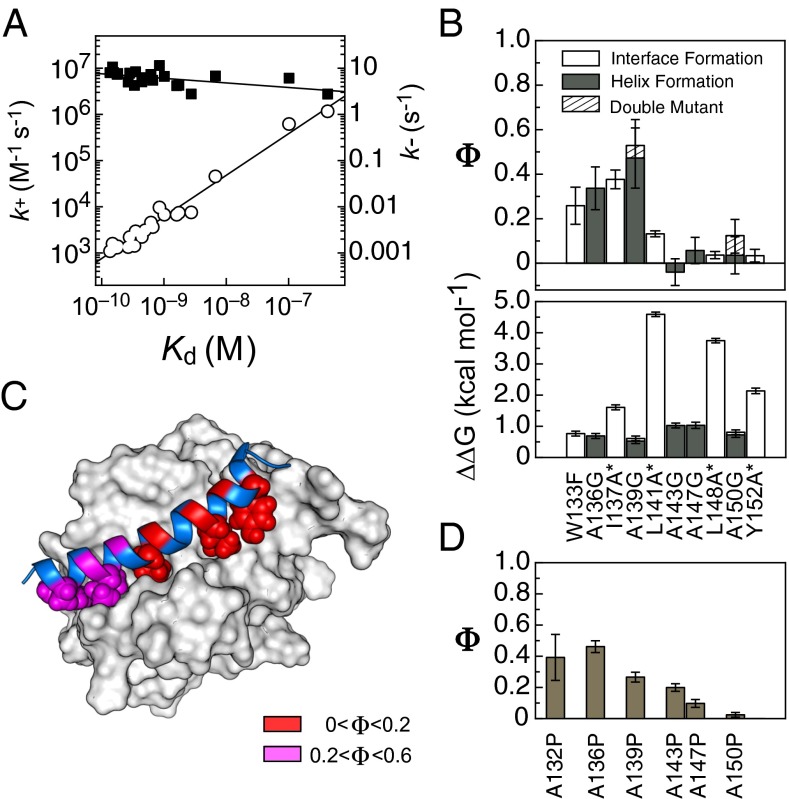
The rate constants for mutant PUMA peptides binding wild-type MCL-1 (k+, k−) (SI Appendix, Figs. S1 B and C and S2 B and C) and the equilibrium dissociation constant (K_d = k−/k+) were calculated in each case (SI Appendix, Table S1). Ala–Gly mutations were uniformly destabilizing across the center of the PUMA binding site (SI Appendix, Fig. S5), and the changes in free energy of binding (∆∆G), ∼1 kcal⋅mol⁻¹, are similar to equivalent mutations destabilizing (the folding of) α-helical monomeric proteins (43). Hydrophobic to alanine mutations were significantly more destabilizing than the Ala–Gly mutations (SI Appendix, Fig. S5 and Fig. 2B). Again, the change in free energies, 2–5 kcal⋅mol⁻¹, are similar to what would be expected if these mutations were probing the folding of a monomeric protein (45). The most destabilizing mutation (L141A) removes a leucine that is highly conserved in BH3 motifs (46).

Fig. 2.

Mutants of the IDP PUMA. (A) Linear free-energy plot showing k+ (■) and k− (○) against K_d for every PUMA mutant binding wild-type MCL-1. Most of the variation in K_d comes from the increase in k−, not the reduction in k+. (B) Φ values (Upper) and binding destabilization, ∆∆G (Lower), for mutations reporting on interface formation (large hydrophobic to smaller, open bars) and helix formation (solvent exposed alanine to glycine, closed bars). Asterisks indicate mutations with ∆∆G > 1.67 kcal⋅mol⁻¹ (see SI Appendix, Methods, for discussion on errors and Φ values). The Φ values produced from the double-mutant (A139G + A150G) are shown as dashed bars. (C) Heat map of the above Φ values plotted onto the bound structure. PUMA cartoon shown in blue, MCL-1 surface shown in white, wild-type hydrophobic residues shown as spheres, and positions of Ala–Gly mutations shown on the PUMA cartoon. (D) Φ values for the highly disruptive, nonconservative alanine-to-proline mutations (38) largely agree with those of the conservative mutations in B.

Kinetic Effects of IDP Mutation.

Inspection of the mutant and wild-type rate constants reveals that the destabilization caused by mutation occurs almost entirely through increased k−, not reduced k+ (SI Appendix, Table S1); this is best shown by a linear free energy relationship (LFER) plot (Fig. 2A). The k− varies over many orders of magnitude, whereas k+ is largely unaffected by mutation. If ln(k+) is assumed to be proportional to the free-energy penalty to reach the TS, and ln(K_d) is proportional to the free energy of binding, then the gradient of ln(k+) vs. ln(K_d) is analogous to the Leffler α value used in protein-folding studies to estimate global structure formation in the TS (47). Leffler α values may produce an underestimate of the true global structure formation (47); however, for PUMA binding MCL-1, α is very low (0.10 ± 0.04) and suggests that the TS is early, structurally.

Φ Values for IDP Mutations.

LFER plots and Leffler α values hide the detail that can be obtained by examining the effect each individual mutation has on the binding kinetics. The kinetic rate constants were used to calculate Φ values (Eq. 2) for the binding of mutant PUMA and MCL-1. Only Φ values with a SD lower than 0.2 were analyzed further, which corresponded to ∆∆G_D-N > 0.38 kcal⋅mol⁻¹ (1.6 kJ⋅mol⁻¹; SI Appendix, Fig. S6).

Generally, Φ values were low, with a notable absence of any high (>0.6) values (Fig. 2B). Importantly, there is a nonrandom distribution of Φ across the IDP, the N-terminal region shows fractional (0.2–0.6) Φ values, whereas the entire C-terminal half of the peptide produced Φ = 0 (Fig. 2 B and C). Additionally, those mutations designed to probe interface formation showed the same distribution of Φ values, both in pattern and magnitude, as those designed to probe helix formation (Fig. 2 B and C).

To confirm the accuracy of these Φ values, and to test for any movement of the TS upon destabilization of the complex (e.g., Hammond effects) and effects of altering residual helicity, a PUMA double-mutant (A139G + A150G) was produced. The Φ value for the A139G mutation was, within error, identical for the same mutation made to the A150G peptide, and vice versa (Fig. 2B), which suggests that the TS does not experience significant structural changes as the complex is destabilized or as the position of residual helical content is changed in the free IDP. We note that this behavior is in contrast to similar mutations made to probe the dimerization of two unstructured GCN4-p1 peptides to form an α-helical bundle (48).

Glycine, as well as disfavoring helix formation, has the potential to change the mechanism of binding as the lack of a side chain allows a larger range of sterically accessible backbone torsional angles. In a previous study, the same solvent-accessible residues were mutated to proline (38). Similar to glycine, the residue proline disfavors helix formation but, in contrast, restricts the torsional angles available. The Φ values for the Ala–Gly and Ala–Pro mutations show similar distributions (Fig. 2D), suggesting that helix formation is being probed in both cases and that the mechanism is not changed significantly by restricting or opening up the backbone angles accessible to one residue.

Selection of MCL-1 Protein Mutations.

Across the PUMA binding interface, 13 residues (hydrophobic, charged, and polar) of MCL-1 were individually mutated to the smaller residue alanine (SI Appendix, Fig. S7 A and B). Given the high stability of wild-type MCL-1 (∆G = 12.9 ± 0.8 kcal⋅mol⁻¹), all these MCL-1 surface mutants can reasonably be expected to remain folded throughout all experiments (37, 49).

Truncation of Wild-Type Residues Can Accelerate Association.

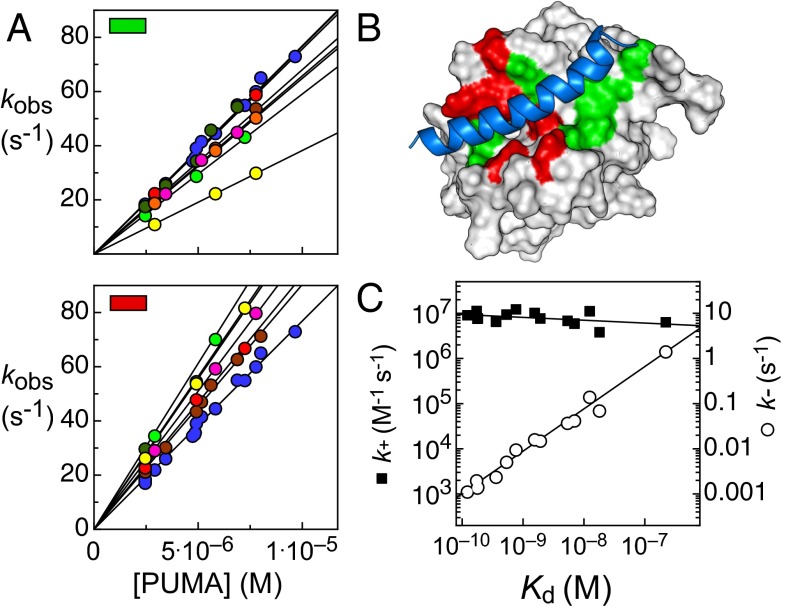
Association experiments were carried out with identical wild-type PUMA solutions, with PUMA in excess to set up pseudo first-order conditions. Unexpectedly, given that all mutations were chosen to remove native interactions with the bound PUMA peptide, around half of the mutant MCL-1 proteins bound the IDP faster than the wild-type protein (Fig. 3A). Interestingly, these mutations are spatially grouped on the binding interface (Fig. 3B).

Fig. 3.

Mutants of the protein MCL-1. (A) Observed rate constants (k_obs) for wild-type PUMA binding mutant MCL-1 under pseudo first-order conditions with PUMA in excess. Gradient of this plot corresponds to k+. (Upper) MCL-1 alanine mutations that lead to slower association, V197 (light green), V201 (brown), L216 (red), V230 (dark green), R244 (magenta), F300 (yellow), and V302 (orange). (Lower) MCL-1 mutations that lead to fast association. H205 (light green), M212 (brown), H233 (dark green), V234 (magenta), D237 (yellow), and T247 (red). (B) PUMA (blue) bound to MCL-1 (white), with the wild-type residues that inhibit association (red) and all others mutated (green) highlighted. (C) LFER plot showing k+ (■) and k− (○) against K_d for wild-type PUMA mutant binding mutant MCL-1. Similar to when PUMA is mutated (Fig. 2A), most of the variation in K_d comes from the increase in k−, not the reduction in k+.

Despite the unusual association kinetic behavior, at equilibrium essentially all mutant MCL-1 proteins bound PUMA weaker than the wild type (SI Appendix, Fig. S8), which suggests that favorable wild-type interactions in the bound complex are, as expected, removed by the alanine mutations.

A LFER plot show that, similar to the PUMA mutations, the effect on k+ is small compared with the orders of magnitude changes in k− (Fig. 3C). The Leffler α from the fit is low (0.06 ± 0.04) and similar to that of the PUMA mutations (0.01 ± 0.04). Binding Φ values were calculated for all MCL-1 mutations and, generally, Φ values were low (SI Appendix, Fig. S8). However, because many mutants had both larger k+ and larger K_d than the wild type, a number of nonclassical, negative Φ values were produced, making their distribution difficult to interpret.

Simulation Results.

When combined with experimental data, molecular dynamics simulation is a powerful tool for providing insights into the mechanistic details of coupled folding and binding processes (50). Coarse-grained, topology-based models have been particularly helpful because their computational efficiency allows for extensive sampling of protein energy landscapes; for this reason, they have been frequently used in the study of protein folding and binding (51). In this study we have used a coarse-grained Gō model (52) constructed using data from the NMR structure and calibrated according to experimental measurements of the PUMA residual helicity, MCL-1 melting temperature, and PUMA-MCL-1 binding affinity (see SI Appendix for details).

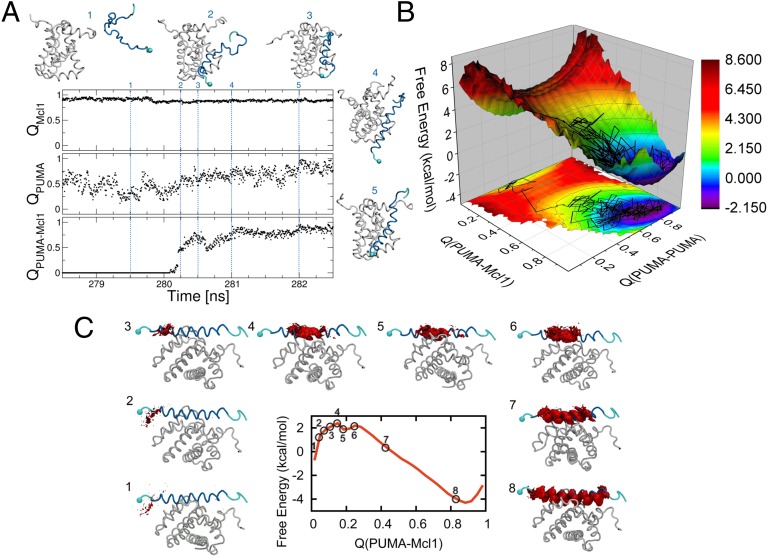
In a set of equilibrium simulations started from the unbound state, we find that folding of PUMA, monitored using the fraction of native (helical) contacts (Q_PUMA), only occurs upon binding to its partner (Fig. 4A). The average value of Q_PUMA in the unbound state (∼0.5), in fact, corresponds to a fraction of helical content of ∼0.3, consistent with the experimental results from CD (SI Appendix, Fig. S4).

Fig. 4.

Results of the simulations. (A) Time series from a binding trajectory from equilibrium molecular dynamics simulation performed with a coarse-grained Gō model, projected in the fraction of native intramolecular contacts (Q_PUMA and Q_MCL1) and intermolecular contacts (Q_PUMA–MCL1). We show snapshots at different time-points during the simulation, with MCL-1 being shown in white and PUMA in blue, with the N terminus marked with a sphere. At 280.25 ns, binding occurs (see jump in Q_PUMA–MCL1), resulting also in an increase of the fraction of intra-PUMA contacts (Q_PUMA). (B) PMF calculated from umbrella sampling simulations, using restraints at different windows of Q_PUMA–MCL1, and projected also on Q_PUMA. The plot shows a single binding barrier, with an early transition state at Q_PUMA–MCL1 ∼ 0.2. On top of the PMF we overlay the trajectory from the equilibrium run from A. (C) Free-energy surface calculated from umbrella sampling simulations, with corresponding plots of the native PUMA–MCL-1 structure showing the PUMA residues (in red) forming contacts with MCL-1 within each window of the umbrella sampling simulation.

To obtain more detailed insight on the nature of the TS for binding, we have also run biased simulations, restraining the simulation at different values of the progress coordinate. Free-energy surfaces [potentials of mean force (PMFs)] were calculated along the fraction of native intra- and intermolecular contacts (Fig. 4B and C); these indicate that the TS occurs early in the binding process, with Q_PUMA–MCL1 ∼0.2. In Fig. 4B we show the free-energy surface as a function of both PUMA–MCL-1 binding and PUMA folding, and it reveals a broad saddle point at the binding TS, indicating that PUMA does not occupy a single specific structure at the TS. Using the data at each of the restrained simulations for Q_PUMA–MCL1, we analyze the nature of the contacts formed along the binding pathway (Fig. 4C). We find that the initial contacts form preferably at the N terminus of PUMA, with C-terminal contacts only formed after the TS, in agreement with the results from the Φ-value analysis.

Discussion

We have previously shown that association is relatively fast (37) and assisted by favorable, long-range electrostatic interactions. In this context it is interesting that the structurally conservative nonpolar-to-nonpolar mutations made here have a small but detectable influence on the association rate constant. Thus, the largely separate dynamics of whole-chain diffusion and of folding apparently both contribute to the observed reaction rate and neither can be considered entirely rate-limiting; this is further evidence that reaction is not entirely diffusion limited (37), and that some form of energetic barrier due to folding exists. The low β_T, low Leffler α, and the lack of high Φ values suggest that the transition state is early, with little structural resemblance to the bound state. Although the proteins are in contact at the TS, the IDP is highly unstructured and the protein–protein interface is largely unformed. The independent simulations support this picture of the TS.

Mutations to the C-terminal region of PUMA uniformly gave Φ = 0, implying that helix formation and side-chain contact with MCL-1, though important for the strength of binding overall, are not present in the rate-limiting TS. In contrast, mutations to the N-terminal region of PUMA gave low, but nonzero, Φ values. Thus, the only residues of the IDP that interact significantly with MCL-1 in the TS are in this region and only this part of the IDP has embryonic helical structure (above that which was already present in the unbound state). It is interesting to note that the most destabilizing mutants at the interface, corresponding to the “hotspots” for this interaction (53), are not part of this region. Because the MCL-1 Φ values do not mirror the distribution of the PUMA Φ values, the side-chain interactions made by PUMA are not necessarily those present in the final bound structure. The simulations suggest that some native PUMA–MCL-1 interactions need to form before PUMA starts to form stable, native helical structure (Fig. 4A), but we have to note that nonnative interactions are not specifically considered in the simplified, but computationally efficient, model we have used.

This TS picture offers a key snapshot of the folding and binding process; it shows that the vast majority of PUMA folding occurs after the TS, while loosely bound to MCL-1, in a presumably energetically downhill process. An important corollary of this unstructured TS is that the IDP must significantly unfold before escaping the bound complex.

Some helicity has developed in the TS; is this also induced by contact with the partner protein, or are these helical conformations selected from the unbound IDP ensemble? Introduction of proline residues, essentially removing helicity in this region of unbound PUMA, did not abolish binding and, importantly, led to only modest reductions in k+ (38), which suggests that induced fit predominates during the initial stages of the binding mechanism.

No mechanism can be proved; mechanisms can only be ruled out. When considering all information available it is difficult (at these nanomolar-to-micromolar concentrations) (23, 30) to propose, or even support, a mechanism where association is limited by the selection of a lowly populated, helical PUMA conformation, formed in the absence of MCL-1. Though conformational selection may play a larger role in more structurally complex systems (27), for the particular case of a short, disordered motif binding an already folded protein, this study adds to the mounting experimental evidence for induced-fit mechanisms (14, 16–19, 54). However, interestingly, the degree of structure formed at the TSs varies significantly among the small number of systems studied (16–18).

Though the binding of PUMA appears to be induced fit, this still leaves open many possibilities for the later stages of the binding mechanism. As hinted at by the polarized structure of the TS, it is possible that the N-terminal half of PUMA binds and folds at its subsite, followed by a separate step where the remainder of the helix forms—an example of the dock-and-coalesce model proposed by Zhou et al. (55). However, there are potentially many ways for the largely unstructured TS described here to develop into the final bound and folded complex.

Perhaps the most surprising result is that many wild-type MCL-1 residues, though favoring binding overall, actually inhibit the association reaction. Describing the mechanism of interface formation only as a monotonic increase in native interactions is clearly inappropriate, and explains the complex distribution of Φ values observed. How can this be explained? Inspection of the Protein Data Bank (PDB) structures indicate that there are a number of small, but perhaps significant, structural changes between bound and unbound forms of MCL-1. Backbone movements are required to open the PUMA binding groove and accept the whole helix (SI Appendix, Fig. S9). In particular, for those residues that slow down association, side-chain rotations are also required to allow docking of the PUMA helix (red; Fig. 3B and SI Appendix, Fig. S9). To probe the possibility that PUMA folding cannot occur before there is an opening of the binding groove, we have undertaken a principal component analysis (PCA) of the NMR ensemble of the unbound MCL-1 (PDB ID code: 1wsx); this allows us to resolve dynamical modes from the ensemble of NMR structures (56). These modes have been shown to be a good predictor of functional collective motions of proteins (57). As one of the principal components, we find an opening movement involving the two helices that in the PUMA-bound structure form the binding groove (SI Appendix, Fig. S10 and Movie S1). The results from the mutations and the PCA analysis of the unbound MCL-1 structures suggest that the dynamics of folded MCL-1, either the side-chain rotations or backbone motions, or both, must be considered in the description of this binding mechanism. Clearly, there is interplay between the conformations of MCL-1 and the mostly unfolded PUMA as the binding TS is crossed—truncation of some of the side chains on the binding surface could open up MCL-1 to allow PUMA to have access to the early binding site or change the timescales of the backbone motions described above.

Conclusions

The BH3 motif of PUMA has been extensively mutated in this and a previous study (38). No single mutation had a significant effect on the magnitude of the association rate constant (all k_on∼10⁶ M⁻¹⋅s⁻¹). Furthermore, many of the residues of wild-type MCL-1 actually slow association. Few, if any, specific interactions between the proteins are required to commit to binding, and little folding of the IDP before binding appears to be required. In this system, the major effect of truncating an interface-forming side chain or reducing IDP helix propensity (which could be considered as increasing disorder propensity) is to allow for easier escape from the bound complex. Evidence from both experiment and simulations supports a mechanism of folding and binding involving induced fit (of the IDP). Importantly, these results show that a structured partner protein cannot be considered a static template during these coupled folding and binding reactions.

Methods

Protein expression and purification was carried out as described previously (37, 38). PUMA mutant R154G could not be produced because this mutation introduced an unwanted Factor Xa cleavage site, used during peptide purification. All circular dichroism and kinetic experiments were carried out as described in SI Appendix. Briefly, association was carried out with pseudo first-order conditions using at least 10-fold excess of wild-type/mutant PUMA. All experiments were carried out at 25 °C, in 50 mM sodium phosphate (pH 7.0). For most mutants, the dissociation rate constant was determined by preforming the MCL-1–PUMA complex and adding an outcompeting peptide (38), the fit k− was then used to calculate K_d (K_d = k−/k+). For four of the weakest-binding MCL-1 mutants, the binding to the outcompeting peptide was too weak to measure the dissociation rate constant using this approach. Fortunately, binding was sufficiently weak for VP-ITC (MicroCal) to be used to determine the K_d, from which k− could be calculated (using the appropriate k+ from stopped flow). All data fitting and plots were made using ProFit (QuantumSoft).

β_T was calculated according to (40, 41)

$${\mathrm{\beta }}_{\text{T}}=\frac{m_{+}}{m_{+}-m_{-}}$$ [1]

where m₊ is the fit gradient of ln(k+) [and m₋, ln(k−)] against the concentration of urea.

Errors in the kinetic rate constants from the pseudo first-order experiments were assessed as described in SI Appendix and SI Appendix, Fig. S11.

The Φ values were calculated using (16–18, 32)

$$\mathrm{\Phi }=\frac{\mathrm{l}\mathrm{n}\left(\frac{k_{+}^{wild-type}}{k_{+}^{mut}}\right)}{\mathrm{l}\mathrm{n}\left(\frac{K_d^{mut}}{K_{\text{d}}^{wild-type}}\right)},$$ [2]

where k₊^wild-type is the association rate constant for the wild-type PUMA–MCL-1 interaction, and k₊^mut is the rate constant for the mutant PUMA–MCL-1 interacting with the wild-type protein. K_d^wild-type and K_d^mut are the equilibrium binding constants for the wild-type and mutant proteins, respectively.

Molecular simulations of the binding of PUMA to MCL-1 were carried out using a simple topology-based model. Equilibrium simulations were first used to observe binding events in real time. Then, extensive sampling at the barrier region and accurate determination of free-energy surfaces was carried out using restrained simulations. See full details in SI Appendix.