An animal-to-human scaling law for blast-induced traumatic brain injury risk assessment

Significance

A physics-based animal-to-human scaling law for the effects of a blast wave on brain tissue is proposed. This scaling law, or transfer function, enables the translation of animal-based assessments of injury to the human, thus effectively enabling the derivation of human injury criteria based on animal tests. This is critical both in the diagnosis of traumatic brain injury as well as in the design of blast-protective helmets.

Abstract

Despite recent efforts to understand blast effects on the human brain, there are still no widely accepted injury criteria for humans. Recent animal studies have resulted in important advances in the understanding of brain injury due to intense dynamic loads. However, the applicability of animal brain injury results to humans remains uncertain. Here, we use advanced computational models to derive a scaling law relating blast wave intensity to the mechanical response of brain tissue across species. Detailed simulations of blast effects on the brain are conducted for different mammals using image-based biofidelic models. The intensity of the stress waves computed for different external blast conditions is compared across species. It is found that mass scaling, which successfully estimates blast tolerance of the thorax, fails to capture the brain mechanical response to blast across mammals. Instead, we show that an appropriate scaling variable must account for the mass of protective tissues relative to the brain, as well as their acoustic impedance. Peak stresses transmitted to the brain tissue by the blast are then shown to be a power function of the scaling parameter for a range of blast conditions relevant to TBI. In particular, it is found that human brain vulnerability to blast is higher than for any other mammalian species, which is in distinct contrast to previously proposed scaling laws based on body or brain mass. An application of the scaling law to recent experiments on rabbits furnishes the first physics-based injury estimate for blast-induced TBI in humans.

The pervasive use of improvised explosive devices (IEDs) in the recent conflicts in Iraq and Afghanistan has resulted in a vast number of injuries attributed to blasts, with a particularly high prevalence of blast-induced traumatic brain injury (bTBI) (1–10). bTBI has also been linked to chronic traumatic encephalopathy (11). One of the main knowledge gaps in blast TBI research is how to relate blast exposure levels to the risk of brain injury, what is commonly referred to as brain injury criteria (9). This is of critical importance both in the diagnosis of bTBI as well as in the design of helmets and other blast-protective devices (12).

Ideally, brain injury criteria should be elucidated from the specific injury mechanisms that are operative in humans, the metrics of blast intensity responsible for driving these mechanisms, and the threshold values associated with different injury levels. However, in the case of blast-related neurotrauma these human brain injury mechanisms remain controversial or unknown. As a consequence, past attempts to develop blast injury criteria have relied on animal studies, which have provided valuable information on the mechanisms and severity of injury resulting from blast loads for the specific species studied (e.g., refs. 13–17). However, the applicability of animal injury assessments to humans is usually mired by the absence of adequate scaling criteria across species. Notable exceptions include blast injury to the lung, where scaling laws based on animal body mass have been shown to scale across more than one animal species and therefore have furnished widely accepted blast lung injury criteria for humans (18–20).

Scaling laws based on body mass (9, 21) or brain mass (22) have also been proposed for describing blast effects on the brain. However, and as recognized in those references, mass scaling suffers from the serious limitation of neglecting the significant anatomical differences across the heads of different mammals. In particular, one of the main issues with the body or brain mass scaling approach is that it does not account for the role of protective structures surrounding the brain (bone, flesh, and skin). One of the questionable consequences of those mass-scaling laws is their prediction of higher injury risk for species with smaller bodies and brains, which is in direct opposition to previous studies of the effects of impact loading on birds (23). Mass scaling also implies that the human brain is more protected against blast neurotrauma than, for instance, that of a pig or a mouse, a rather counter intuitive result considering how large and unprotected the human brain is compared with those of other mammalian species.

In order to develop an adequate scaling law for blast neurotrauma it is imperative to establish a physics-based connection between the intensity of the external threat and the intensity of the internal mechanical effects on the brain tissue across species. Toward this end, advanced computer simulations have provided detailed assessments of intracranial stresses resulting from blast exposure of the human head with high spatial and temporal resolution (12, 24–28). In this paper we use advanced simulations of blast effects on mammalian head models for the purpose of establishing the sought connection between blast characteristics and their intracranial mechanical effects for different species. To this end, we simulated the intracranial stress field resulting from different blast conditions (peak incident overpressure and positive phase duration) for three mammalian species: mouse, pig, and human. The detailed dynamic stress fields provided by the simulations enable the identification of the mechanisms responsible for momentum and energy transfer from the blast wave into the brain tissue, accounting for morphological features and differences among mammals, and thus naturally suggest the combination of physical parameters that define the scaling law. Specifically, a comparison of the dynamic stress fields across species suggests an important role played by the protective structures surrounding the brain tissue in mitigating the magnitude of the stresses transmitted into the brain.

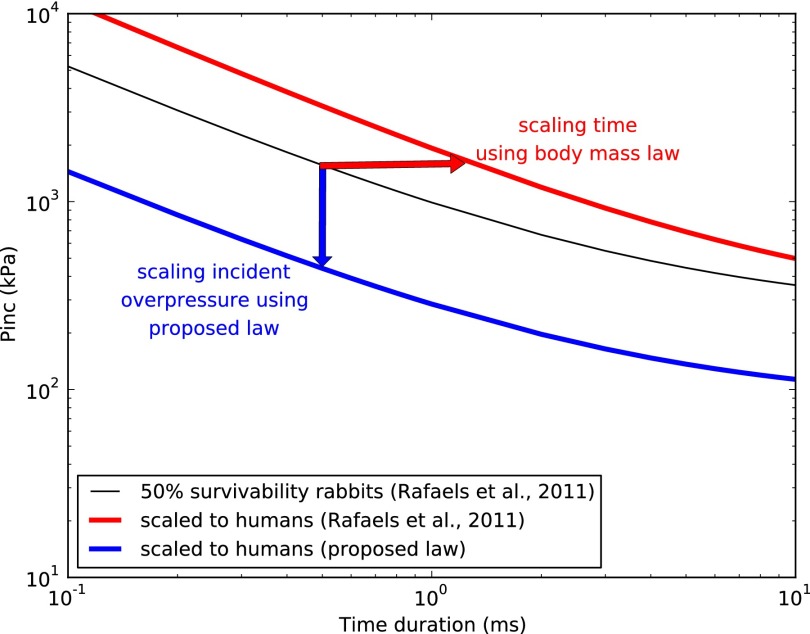
Based on this observation, we identified a scaling parameter and functional form of the scaling law that captures the cross-species variations of peak intracranial pressures observed in simulations. The scaling law is the first to be obtained from an analysis of the physical mechanisms of stress wave transmission into the brain tissue. It can be used to translate animal injury criteria obtained using animal testing to humans. As a proof of concept, we applied the scaling law to translate recent data on brain injury survivability risk for rabbits to humans (20) and obtained a risk curve for humans (see Fig. 7). Significant work is required to validate this result by applying the scaling law to additional animal test data. However, the human blast brain injury risk curve obtained constitutes the first physics-based criterion for the assessment of blast-induced TBI in humans.

Fig. 7.

Brain injury risk criteria for human derived from rabbit test data using previous body mass scaling (21) and our proposed scaling law accounting for tissue properties and basic animal morphological features. The figure shows plots of incident overpressure vs. time duration in log-log scale. The red horizontal arrow emphasizes the fact that in the case of mass scaling the scaling variable is the abscissa (time duration), whereas in the new approach (blue vertical arrow) the scaling variable is the ordinate (blast incident overpressure).

Results

Interspecies Scaling Law for Intracranial Pressures Resulting from Blast.

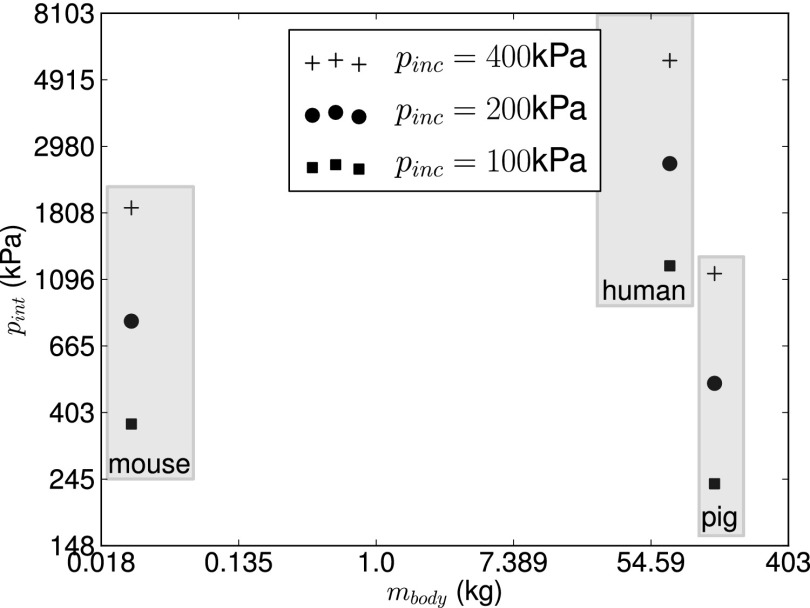
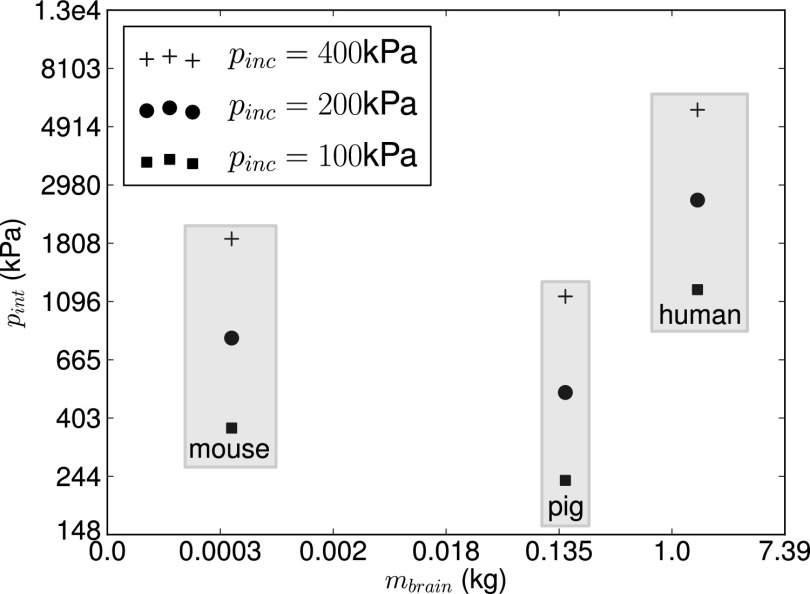
Simulations of blast waves interacting with the head of a mouse, a pig, and a human were conducted for different blast conditions relevant to mild TBI using imaged-based biofidelic computational models (Fig. 1). The computational framework described in ref. 12 was used in the simulations. Peak incident shock overpressures of 100, 200, and 400 kPa with a fixed shock positive phase duration of 3 ms were considered. As is commonly done in blast injury biomechanics (13–15, 17), the peak intracranial pressure was chosen as a characteristic metric of blast intensity transmitted to the brain tissue. Intracranial pressure can also be measured in animal tests in either in vitro or in vivo conditions (16), thus facilitating model validation. Peak intracranial pressure values furnished by our simulations are given in Table 1 and plotted in Fig. 2 as a function of species body mass. The body mass of each species was estimated from the biofidelic model using brain-to-body mass ratios obtained from ref. 29. It can be clearly seen that intracranial pressure does not correlate with animal body mass. In particular, it is observed that the human experiences the largest intracranial pressure among the three species and for all of the three blast intensities considered, despite its much higher body mass compared with the mouse and similar mass compared with the pig. When the results are replotted as a function of animal brain mass (Fig. 3) the correlation is even worse. This suggests that recently proposed blast injury criteria based on either body and brain mass scaling (9, 21, 22, 30) do not capture blast effects on the brain. The limitations of body and brain mass scaling were recognized in refs. 9 and 21, where it was suggested that an adequate scaling law should capture morphological differences of the head across species.

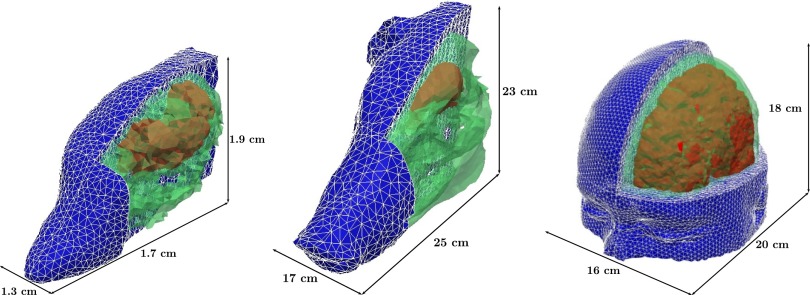
Fig. 1.

Image-based finite element models of the head of mouse, pig, and human (not to scale) used in simulations, depicting the relevant tissue structures: skull (green), brain (red), and flesh (blue).

Table 1.

Computed peak intracranial pressure for each species

	Time duration
Blast condition/species	2 ms	3 ms			4 ms
pinc, kPa	200	100	200	400	200
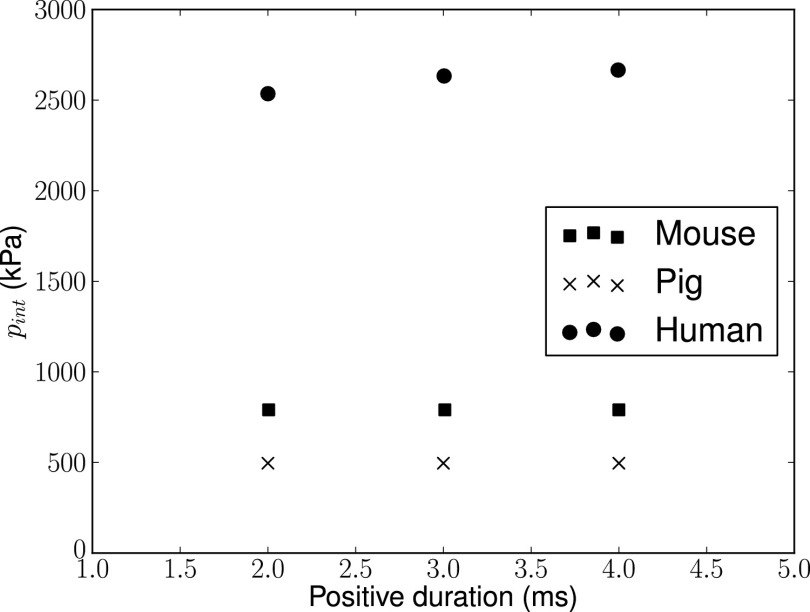
Mouse	796.6	375.8	800.5	1,849	800.7
Pig	497.5	237.9	502.3	1,133	506.4
Human	2,526	1,219	2,618	5,671	2,658

Fig. 2.

Intracranial peak overpressure vs. species body mass (m_body) for different incident blast overpressures.

Fig. 3.

Intracranial peak overpressure vs. species brain mass (m_brain) for different incident blast overpressures.

Identification of Scaling Variable: The Blast Brain Vulnerability Parameter.

Our simulation results (Fig. 4) show that the structural characteristics of the skull and other protective structures play an important role in the intensity of the stress waves transmitted to the brain tissue. More specifically, these results show that the peak intracranial pressure decreases with increases of skull thickness and increases with brain mass (Table 1). The derivation of an adequate scaling parameter must be based on an identification of the dominant physical process of interest, the fundamental parameters describing it, and the use of dimensional analysis. In our case, the transfer of mechanical energy from the blast wave to the brain tissue is dominated by stress wave propagation. Although the air blast wave is in the supersonic nonlinear wave propagation regime, the stress waves transmitted to the tissue are clearly in the subsonic or acoustic regime. The fundamental parameter determining the transmission and reflection of stress waves in a heterogeneous elastic medium is the acoustic impedance Z = ρc, where ρ is the mass density and c the wave speed. It is then expected, from dimensional considerations, that blast effects on the brain can only scale across species with the ratio of acoustic impedance of the tissues $Z_1/Z_2$, or equivalently, the acoustic transmission coefficient $4Z_1{Z}_2/{\left(Z_1+Z_2\right)}^2$ at tissue interfaces, if no other parameter influences the physical response. However, it is clear that to account for anatomical differences across species the relative dimensions (e.g., volume) of brain and surrounding protective tissues need to enter the scaling parameter as well. If we assume that the individual tissues participate in the transmission of stress wave intensity in direct proportion to their volume, a reasonable hypothesis to a first order of approximation, then we can deduce that the scaling parameter must be a function only of ${\rho }_{skull}{c}_{skull}{V}_{skull}^s/{\rho }_{brain}{c}_{brain}{V}_{brain}^s=c_{skull}{m}_{skull}^s/c_{brain}{m}_{brain}^s$ and $c_{flesh}{m}_{flesh}^s/c_{brain}{m}_{brain}^s=c_{flesh}{m}_{flesh}^s/c_{brain}{m}_{brain}^s$, where $V_{tissue}^s,m_{tissue}^s$ stand for the volume and mass of a given tissue in species s, respectively, and where we have assumed that tissue properties do not change across species. A final simplification can be achieved by assuming a mass-weighted role of all of the protective tissues surrounding the brain or alternatively a linear dependence of the scaling parameter on the two nondimensional parameters above, leading to the following form of the scaling parameter:

$${\eta }^s=\frac{c_{brain}{m}_{brain}^s}{c_{skull}{m}_{skull}^s+c_{flesh}{m}_{flesh}^s}.$$ [1]

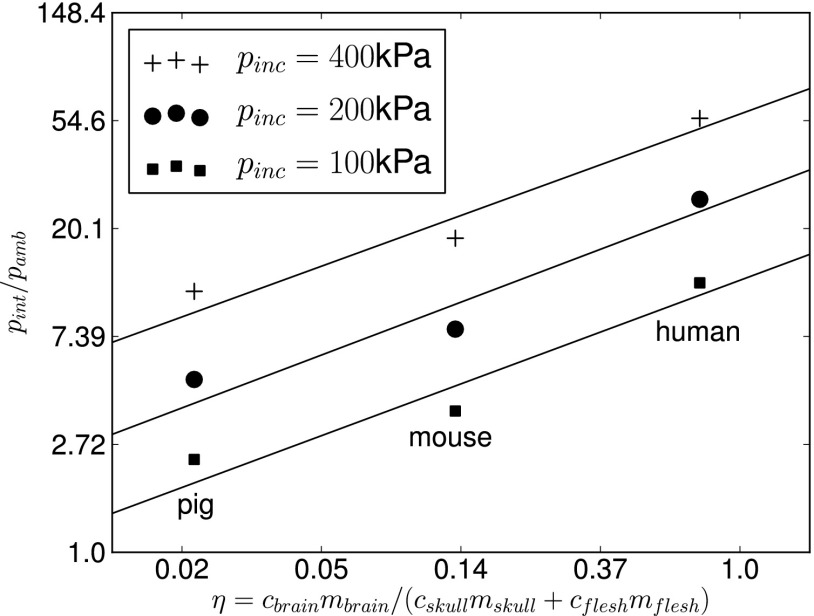
In soft tissues (brain and flesh), where the shear response can be neglected at least for the purpose of stress wave propagation, the wave celerity corresponds essentially to the speed of sound computed from the Newton–Laplace equation $c=\sqrt{K/\rho }$, where K is the bulk modulus of the tissue. For the skull, the wave celerity of interest is that of the longitudinal stress waves $c=\sqrt{\lambda +2\mu /\rho }$, where λ and μ are the Lamé elastic constants of the bone tissue. We will refer to η^s as the brain blast vulnerability parameter corresponding to species s. The value of η^s for the three species considered was computed by multiplying the volumes of the different structures computed from the geometry of the biofidelic models, the tissue density values used in simulations, and the celerities computed directly from the mechanical properties of the tissues used in simulations (Table 2). It is clear that according to this definition of blast vulnerability, the human head (η^human = 0.75) is the most vulnerable, followed by the rat (η^mouse = 0.13) and then the pig (η^pig = 0.02). This is a direct consequence of the massive brain relative to its surrounding protective structures in the human compared with other mammalian species. Fig. 5 shows log-log plots of the peak intracranial pressures obtained from blast simulations in terms of the proposed blast vulnerability parameter η^s. The strong linear correlation observed for three different blast conditions $\left(R_{100kPa}^2=0.95,R_{200kPa}^2=0.97,\mathrm{and}\hspace{0.17em}{R}_{400kPa}^2=0.97\right)$ suggests that the peak intracranial pressure p_int depends on the blast vulnerability parameter via a power scaling relation of the form

$$\frac{p_{int}^s}{p_{amb}}=\beta \times {\left({\eta }^s\right)}^{\alpha },$$ [2]

where the intracranial pressure has been normalized with the ambient pressure p_amb, β(p_inc) is a nondimensional function encapsulating the influence of external blast intensity, and α is the power-law exponent. By computing the linear regressions for each blast intensity (Fig. 5) it is found that the dependence of the function β on the normalized blast incident overpressure represents a linear vertical shift in the log of the scaling relation, whereas the slope (power-law exponent α) is invariable. The combined dependence of p_int on the arguments (p_inc, η^s) can then be fitted by the expression

$$\frac{p_{int}\left(p_{inc},{\eta }^s\right)}{p_{amb}}=\left(A\times \frac{p_{inc}}{p_{amb}}-B\right)\times {\left({\eta }^s\right)}^{\alpha },$$ [3]

where A = 15.3, B = 3.13, and α = 0.48 are fitting parameters. We have also assessed the influence of the duration of the positive phase of the blast wave by conducting additional simulations for time durations of of 2, 3, and 4 ms for the case of 200-kPa peak incident overpressure. We confirmed (Fig. 6) that the peak normalized intracranial pressure has a negligible dependence on this characteristic of the blast wave for all species considered, as expected, and, thus does not affect the scaling law. However, it is expected that blast duration will affect risk of injury, as is the case in blast lung injuries (18–20).

Fig. 4.

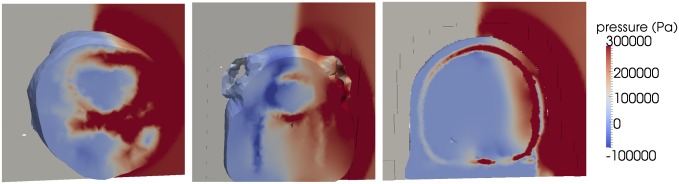
Snapshot of pressure field within the head tissues of mouse, pig, and human at t = 0.34 ms for a blast of 2 ms with an incident overpressure of 200 kPa, illustrating the differences in stress wave transmission across species resulting from the influence of head protective structures.

Table 2.

Mass of brain and protective structures (skull and flesh), tissue longitudinal stress wave celerity, and value of the proposed blast scaling variable for different species considered

Species	Mbody, kg	Mbrain, g	cbrain, ms−1	Mskull, g	cskull, ms−1	Mflesh, g	cflesh, ms−1	η
Mouse	0.028	0.410	1,549	0.740	2,295	1.876	1,778	0.13
Pig	138.2	151.3	1,549	948.9	2,295	4,186	1,778	0.02
Human	72.97	1,573	1,549	705.6	2,295	918.1	1,778	0.75

Fig. 5.

Log-log plots of normalized computed peak overpressure vs. η = c_brainm_brain/(c_skullm_skull + c_skinm_skin) for different incident blast overpressures and corresponding linear regressions.

Fig. 6.

Intracranial overpressure vs. time duration of the positive phase of the blast wave for peak incident overpressure p_inc = 200 kPa across mammalian species.

Blast-Induced Brain Injury Risk Criterion Scaled to Humans.

The animal-to-human transfer function, Eq. 3, can be used to scale animal testing results and thus estimate injury risk in humans. Here, we outline the procedure involved and apply it to a previous experimental assessment of brain injury owing to blast in rabbits (21). Given an experimental threshold value of normalized incident blast overpressure $p_{inc}^s/p_{amb}$ resulting in injury for a given species s, the scaling law, Eq. 3, gives the corresponding peak normalized intracranial pressure predicted by the model for that species. Assuming that this threshold value of normalized intracranial pressure is indicative of injurious levels of blast intensity and invariant across species, an estimate of the incident normalized blast overpressure causing the same injury level in the human $p_{inc}^h$ can be obtained by equating the right-hand side of Eq. 3 to the same equation applied to the human:

$$\left(A\times \frac{p_{inc}^h}{p_{amb}}-B\right)\times {\left({\eta }^h\right)}^{\alpha }=\left(A\times \frac{p_{inc}^s}{p_{amb}}-B\right)\times {\left({\eta }^s\right)}^{\alpha }$$ [4]

and then solving for $p_{inc}^h$. The following transfer function is obtained:

$$\frac{p_{inc}^h}{p_{amb}}=\overline{\mathcal{T}}\left(\frac{p_{inc}^s}{p_{amb}}\right)=\frac{p_{inc}^s}{p_{amb}}{\left(\frac{{\eta }^s}{{\eta }^h}\right)}^{\alpha }+\frac{B}{A}\left[1-{\left(\frac{{\eta }^s}{{\eta }^h}\right)}^{\alpha }\right].$$ [5]

We illustrate this procedure by applying it to the 50% survivability risk function from blast exposure to the head in rabbits recently proposed in ref. 21:

$$p_{inc}^r=P^{\mathrm{\ast }}\times \left(1+a\mathrm{\Delta }{t}^{-b}\right),$$ [6]

where P* = 250 kPa and a = 2.95 and b = 0.83 are experiment-fitting constants (see also ref. 19). Replacing Eq. 6 in Eq. 5, we obtain

$$\frac{p_{inc}^h}{p_{amb}}=\overline{\mathcal{T}}\left(\frac{p_{inc}^r}{p_{amb}}\right)=\frac{P^{\mathrm{\ast }}\times \left(1+a\mathrm{\Delta }{t}^{-b}\right)}{p_{amb}}{\left(\frac{{\eta }^r}{{\eta }^h}\right)}^{\alpha }+\frac{A}{B}\left[1-{\left(\frac{{\eta }^r}{{\eta }^h}\right)}^{\alpha }\right].$$ [7]

Fig. 7 shows plots of the original risk function for rabbits, Eq. 6, the scaled function for humans, Eq. 7 with parameter values summarized in Table 3, and the previously proposed scaled function based on body mass.

Table 3.

Scaling law fitting parameters and parameters in rabbit 50% blast survivability criterion from ref. 21

Pamb	α	A	B	a	b	P*	ηr
101 kPa	0.48	15.3	3.13	2.95	0.83	250 kPa	0.05†

^†Obtained from ref. 55.

Discussion

Previous animal-to-human scaling laws for blast effects on the brain have been based on mass scaling that did not take into account the physical mechanisms that determine brain response to blast or differences in properties of soft tissues of the head or the major anatomical differences, particularly of the skull. In this paper, we have shown via advanced simulations that blast-induced intracranial overpressure does not scale with either animal body or brain mass across species. Instead, dimensional arguments in wave propagation (the dominant energy transfer mechanism from the blast wave to the tissue) as well as a direct observation of the simulation results suggest that a more relevant scaling parameter must consider the relative acoustic impedance and mass of the brain and the surrounding protective structures. Consequently, a blast brain vulnerability parameter taking into account these considerations is proposed and shown to provide a strong (power-law) correlation for intracranial overpressure owing to blast across species. In stark contrast to previously proposed scaling laws, the proposed transfer function results in lowest brain blast vulnerability for highly protected small-brain species, such as the pig, and highest vulnerability for the human owing to its larger brain and thinner protective structures. Further improvements of the proposed scaling law should consider blast orientation (31) and additional morphological features including the ratio of gray matter to white matter and the level of brain gyrencephaly (9).

As a proof of concept, we applied our animal-to-human transfer function to scale recent brain injury results for rabbits to the human and compared the results to the predictions based on mass scaling. It was found that the newly proposed scaling results in a much lower human brain tolerance to blast than previously believed. By way of example, for a blast positive phase duration of 0.5 ms, the blast incident pressure threshold for 50% survivability in rabbits has been experimentally estimated at 1.5 MPa (21) (Fig. 7). Mass scaling leads to 106% higher human tolerance, whereas the proposed scaling predicts a value 72% lower. Further validation against additional animal experimental data is required before a conclusive human injury risk criterion can be obtained. However, from a practical perspective, a validated risk function could be extremely useful to support medical diagnosis and reduce the large proportion of blast-induced TBIs that are commonly left unidentified (32) both in the military and in the civilian population. In addition, a validated human injury risk would be of critical importance for guiding the design of blast-protective helmets and face shields.

Materials and Methods

Computational Framework for Simulating Blast Waves Interacting with the Head.

The simulations in this work were conducted using an extension of the Virtual Test Facility (VTF) (33, 34), a computational framework for large-scale simulation of coupled fluid–structure interaction problems on massively parallel computers. The VTF was extended to simulate air blast waves in previous work, where an advanced model of the human head was used to demonstrate the propagation of stress waves inside the brain tissue from blast waves (24). The simulations were conducted on US Department of Defense supercomputers. The blast wave is modeled before impact on the target following a semianalytical solution of the point-source blast problem (spherical waves) based on a procedure outlined in ref. 35. The advantage of this approach is that it provides a full-field description of the blast wave flow field at any time after detonation without having to model the detonation process and the propagation of the blast wave until it reaches the target. The blast conditions are defined by the type, the mass, and the spatial location of the explosive source with respect to the target head position.

Image-Based Biofidelic Head Models for Mouse, Pig and Human.

Biofidelic finite element (FE) models of the three species (mouse, pig, and human) were used in simulations to describe the response of mammal heads to the blast conditions considered. The computational model for the pig head was obtained in two steps using the same procedure outlined in ref. 24 for reconstruction of a human head model from magnetic resonance (MR) images: (i) image reconstruction from computed tomography images (Virtual Pig Project, The Ohio State University) using a marching cube algorithm in Amira (36) and (ii) computational mesh generation using an octree meshing algorithm in the commercial software ANSYS ICEM/CFD (37). For simplicity, three tissue types were differentiated in the image segmentation of the pig head: brain, skull, and soft tissue and skull (Fig. 1). The mouse head model was extracted from the publicly available finite element model of a complete mouse (38). The mouse head model contained seven different structures: brain, skull, skin, lacrimal glands, masseter muscle, eyes, and sinus. For the human, the full head model presented in ref. 24 was used. This model was obtained by segmentation of MR images from the Montreal Neurological Institute using the procedure explained in ref. 24 and contained 11 phases: the cerebral spinal fluid (CSF), the eyes, the muscle, the air sinus, the flesh, the venous sinus, the ventricle, the glia, the external sinus, the brain, and the skull. The FE meshes for the mouse, pig, and human contained, respectively, 36,720, 91,778, and 743,341 quadratic tetrahedral elements.

Material Models and Properties.

The mechanical response of the various tissues was modeled using constitutive models with the ability to describe the propagation and interaction of stress waves inside the different mammalian heads resulting from the incident blast. For the brain tissue, the viscoelastic model developed in ref. 39 was used for all three species considered. The model parameters correspond to in vitro properties for the pig (Tables 4–6).

Table 4.

Viscoelastic model parameters for mammalian brain

ρ, kg/m3	K, MPa	G0, kPa	n	σ0,Pa	λL	μ0, Pa	m, kPa⋅s	G∞, Pa
1,000	10	6.0	0.3	2.0 ×103	1.03	1.0 ×104	1.0 ×103	2.0 ×103

Table 6.

Viscoelastic model parameters with Tait equation of state for other human, pig, and other mouse soft tissues

Materials	ρ, kg/m3	K, MPa	G, kPa	κ, kPa⋅s	μv, kPa⋅s	Γ0
Human
CSF	1,040	2,190	0.438	1.0	1.0	6.15
Eyes	1,040	2,190	22.5	1.0	1.0	6.15
Muscle	1,100	0.135	14.0	1.0	1.0	6.15
Air sinus	1,040	2,190	0.438	1.0	1.0	6.15
Skin/fat	1,100	3,479	5.88 × 105	1.0	1.0	6.15
Venous sinus	1,040	2,190	0.438	1.0	1.0	6.15
Ventricle	1,040	2,190	0.438	1.0	1.0	6.15
Pig	1,100	3,479	5.88 × 105	1.0	1.0	6.15
Mouse
Skin	1,100	3,479	5.88 × 105	1.0	1.0	6.15
Muscle	1,100	0.135	14.0	1.0	1.0	6.15
Lacrimal gland	1,040	2,190	0.438	1.0	1.0	6.15
Eyes	1,040	2,190	22.5	1.0	1.0	6.15
Sinus	1,040	2,190	0.438	1.0	1.0	6.15

Table 5.

Viscoelastic model parameters with Mie–Gruneisen equation of state for mammalian skull

ρ, kg/m3	K, MPa	G, GPa	C0	s
1,412	3,890	2.7	1,850	0.94

The mechanical response of the other tissues was described using a viscoelastic model with a deviatoric viscosity and an equation of state for the pressure response following ref. 12. For completeness, we briefly summarize the main ingredients of the models. The Mie–Gruneisen equation of state was adopted for the skull:

$$p=\frac{{\rho }_0{C}_0^2\left(1-J\right)}{{\left[1-s\left(1-J\right)\right]}^2},$$ [8]

where J is the local deformation gradient and s and C₀ are the material parameters. Also, a Tait equation of state, which is commonly used to model fluids under large pressure variations, was used to describe the volumetric response of other soft tissues:

$$p=B\left[J^{-\left({\mathrm{\Gamma }}_0+1\right)}-1\right],$$ [9]

where B = K/(Γ₀ + 1) and Γ₀ are material parameters. The elastic part of the deviatoric response was computed using a neo-Hookean model in which the strain energy is written as follows:

$$W\left(C\right)=\frac{\mu }{2}\left(I_1-3\right),$$ [10]

where μ is the shear modulus and I₁ is the first invariant of the right Cauchy–Green deformation tensor. Finally, the rheological tissue response was described using a linear viscosity model. The final form of the Cauchy stress components is given by

$${\sigma }_{ij}={\sigma }_{ij}^{e,vol}+{\sigma }_{ij}^{e,dev}+2{\mu }_v{d}_{ij}^{dev}+\kappa d_{ii}{\delta }_{ij},$$ [11]

where d_ij are the components of the rate of deformation tensor and μ_v and κ are the deviatoric and the volumetric viscosity parameters, respectively. The material parameters adopted in simulations were obtained from the literature for the skull (25, 40–42), for the CSF (25, 40–52), and for the skin (42, 46, 48–50, 53–54). For the pig and mouse head the brain and the skull were assigned the same model parameters as used for the human (12), whereas the eyes and soft tissue response were modeled using a viscoelastic model with a Tait equation of state. Tables 4–6 present the material constitutive parameters for each tissue component and for the three species considered.