Reputation and impact in academic careers

Significance

Over a scientist’s career, a reputation is developed, a standing within a research community, based largely upon the quantity and quality of his/her publications. Here, we develop a framework for quantifying the influence author reputation has on a publication’s future impact. We find author reputation plays a key role in driving a paper’s citation count early in its citation life cycle, before a tipping point, after which reputation has much less influence relative to the paper’s citation count. In science, perceived quality, and decisions made based on those perceptions, is increasingly linked to citation counts. Shedding light on the complex mechanisms driving these quantitative measures facilitates not only better evaluation of scientific outputs but also a more transparent evaluation of the scientists producing them.

Abstract

Reputation is an important social construct in science, which enables informed quality assessments of both publications and careers of scientists in the absence of complete systemic information. However, the relation between reputation and career growth of an individual remains poorly understood, despite recent proliferation of quantitative research evaluation methods. Here, we develop an original framework for measuring how a publication’s citation rate Δc depends on the reputation of its central author i, in addition to its net citation count c. To estimate the strength of the reputation effect, we perform a longitudinal analysis on the careers of 450 highly cited scientists, using the total citations C_i of each scientist as his/her reputation measure. We find a citation crossover c_×, which distinguishes the strength of the reputation effect. For publications with c < c_×, the author’s reputation is found to dominate the annual citation rate. Hence, a new publication may gain a significant early advantage corresponding to roughly a 66% increase in the citation rate for each tenfold increase in C_i. However, the reputation effect becomes negligible for highly cited publications meaning that, for c ≥ c_×, the citation rate measures scientific impact more transparently. In addition, we have developed a stochastic reputation model, which is found to reproduce numerous statistical observations for real careers, thus providing insight into the microscopic mechanisms underlying cumulative advantage in science.

Citation counts are widely used to judge the impact of both scientists and their publications (1–4). Although it is recognized that many factors outside the pure merit of the research or the authors influence such counts, little effort has been devoted to identifying and quantifying the role of the author-specific factors. Recent investigations have begun to study the impact the individual scientists have through collaboration and reputation spillovers (5, 6), two integrative features of scientific careers that contribute to cumulative advantage (7–9). However, the majority of citation models avoid author-specific effects, mainly due to the difficulty in acquiring comprehensive disambiguated career data (10–13). As the measures are becoming increasingly common in evaluation scenarios throughout science, it is crucial to better understand what the citation measures actually represent in the context of scientists’ careers. Moreover, how does reputation affect a scientist’s access to key resources, the incentives to publish quality over quantity, and other key decisions along the career path (14–18)? In addition, what role does reputation play in the mentor-matching process within academic institutions, in the effectiveness of single/double blinding in peer review, and in the reward system of science (14, 15, 19)?

It is against this background that we have developed a quantitative framework with the goal of isolating the effect of author reputation upon citation dynamics. Specifically, by controlling for time- and author-specific factors, we quantify the role of author reputation on the citation life cycle of individual publications at the micro level. We use a longitudinal career dataset from Thomson Reuters Web of Science comprising 450 highly cited scientists, 83,693 articles, and 7,577,084 citations tracked over 387,103 publication years. Dataset [A] refers to 100 top-cited physicists, [B] to another set of 100 highly prolific physicists, [C] to 100 assistant professors in physics, [D] to 100 top-cited cell biologists, and [E] to 50 top-cited pure mathematicians (for further data elaboration, see SI Appendix). For each central scientist i, we analyze the scientific production measured by the number $n_i\left(t\right)$ of publications published in year t, the cumulative number of citations $c_{i,p}\left(t\right)$ received by publication p, and our quantitative reputation measure defined here as the net citations aggregated across all publications $C_i\left(t\right)={\displaystyle {\sum }_p{c}_{i,p}\left(t\right)}$.

We begin with a description of our reputation model, followed by an empirical analysis of career trajectories, establishing $C_i$ as a good quantitative measure of reputation. We then establish quantitative benchmarks from the citation distribution within individual publication portfolios and also quantify features of the citation life cycle, both of which are crucial components of our reputation effect model. Combining several empirical features of our analysis, we then investigate the role of the reputation effect, showing that author reputation accounts for a significant fraction of the citation rate of young publications, thus providing a testable mechanism underlying cumulative advantage in science (7–9). We conclude by developing a stochastic Monte Carlo (MC) reputation model, one which matches the microscopic and macroscopic citation dynamics.

Results

Reputation Signaling.

Academic career growth is a complex process emerging from the institutional, social, and cognitive aspects of science. Conceptually, each career i is embedded in two fundamental networks that are interconnected: the nodes in the first network represent scientists and in the second network represent publications. The links within the first network represent collaborations between scientists, and within the second network they represent citations between publications; the cross-links represent the associations between individuals and their publications.

Because these networks are dynamic, it is difficult to fully understand for any given individual, let alone the entire system, the complex information contained by all associations. As a result, scientific reputation has emerged as a key signaling mechanism to address the dilemma of excessive information that arises, for example, in the task of evaluating, comparing, and ranking publication profiles in academic competitions. Reputation signals can flow between scientists, $j\rightleftarrows k$; between publications, $p\rightleftarrows q$; and between a publication and a scientist, $p\rightleftarrows i$. The focus of our analysis is on this latter dependency, $i\to p$, whereby author reputation can impact the citation rate of his/her publications, generating subsequent reputation feedback, $p\to i$.

Reputation plays an important role as a signal of trustworthiness and quality, a role that addresses directly the “agency problem” characterizing the reward system in science (14). Moreover, reputation signaling in scientific networks is used to overcome information asymmetries between scientists and other academic agents; in this role, it will become increasingly important as the rate of science publication grows and scientists have less time to absorb relevant advancements (14, 19–21). With little time to read every paper on a given topic, this trustworthiness signal is anecdotally consistent with the common practice of perusing the author names when preliminarily evaluating the relevance of a newly found publication. In the past, an author’s identity and associated reputation was mainly linked to reference lists and personal interactions. Nowadays, an author’s reputation is becoming increasingly visible through searchable publication databases, laboratory websites, press, and other media, in addition to citations.

We measure the author reputation by $C_i\left(t\right)$, which measures not only the number of times his/her $N_i\left(t\right)$ publications have been referenced (an indication of overall scientific impact) but also the number of appearances of his/her name in the literature, thereby providing a name association visibility. What $C_i$ does not account for is intrinsic research quality, e.g., the quality ratio $C_i/N_i$ is broadly distributed across scientists. Because quantitative proxies for quality are limited to citation counts, it is presently difficult to distill the role played by quality in assessing overall scientific impact.

By analyzing the top scientists, we reduce the compound reputation effect occurring when two or more scientists of comparable reputation are coauthors on a publication, a scenario where it may be difficult to estimate the differential impact of these scientists on the citation rate. Due to data limitations requiring author name disambiguation and career data for all coauthors j, we assume that a majority of the reputation signal is attributable to the central scientist i by the following approximation: $C\left(t\right)\approx {\displaystyle {\sum }_j{C}_j\left(t\right)\approx C_i\left(t\right)}$. Also, by analyzing top-cited cohorts, we can establish an upper bound to the strength of the reputation effect. We note that $C_i$ possibly discounts the role of mentor reputation effects early in the career (22). Nevertheless, by analyzing top scientists, the signaling advantage received early in their careers by associating with prestigious mentors/coauthors should be negligible over the long run (20).

To measure the role of author reputation vis-à-vis publication impact, we use a regression model that correlates the increase in the number of citations $\mathrm{\Delta }{c}_{i,p}\left(t+1\right)$ for a given paper p in year $t+1$ using three explanatory variables: (i) the role played by the net number of citations $c_p\left(t\right)$ accrued up to paper age ${\tau }_p$ quantified by the power-law regression parameter π, (ii) the role of publication age and the obsolescence of knowledge quantified by the exponential regression parameter $\overline{\tau }$; and (iii) the role of author reputation $C_i\left(t\right)$ quantified by the power-law regression parameter ρ.

Together, these three features are (i) the publication citation effect ${\mathrm{\Pi }}_p\left(t\right)\equiv {\left[c_p\left(t\right)\right]}^{\pi }$, (ii) the life cycle effect $A_p\left(\tau \right)\equiv \exp \left[-{\tau }_p/\overline{\tau }\right]$, and (iii) the author reputation effect $R_i\left(t\right)\equiv {\left[C_i\left(t\right)\right]}^{\rho }$. We perform a multivariate regression to estimate the π, $\overline{\tau }$, and ρ values that parameterize the citation model,

$$\mathrm{\Delta }{c}_{i,p}\left(t+1\right)\equiv \eta \times {\mathrm{\Pi }}_p\left(t\right)\times A_p\left(\tau \right)\times R_i\left(t\right),$$ [1]

with the multiplicative log-normal noise term η. In SI Appendix, we perform an additional fixed-effects regression using year as well as author variables to better control for the overall growth in scientific output across time. To fully justify our reputation effect model, in what follows we first account for two key features: measures for cumulative career reputation and obsolescence features of the citation life cycle.

Patterns of Growth for Longitudinal Reputation Measures.

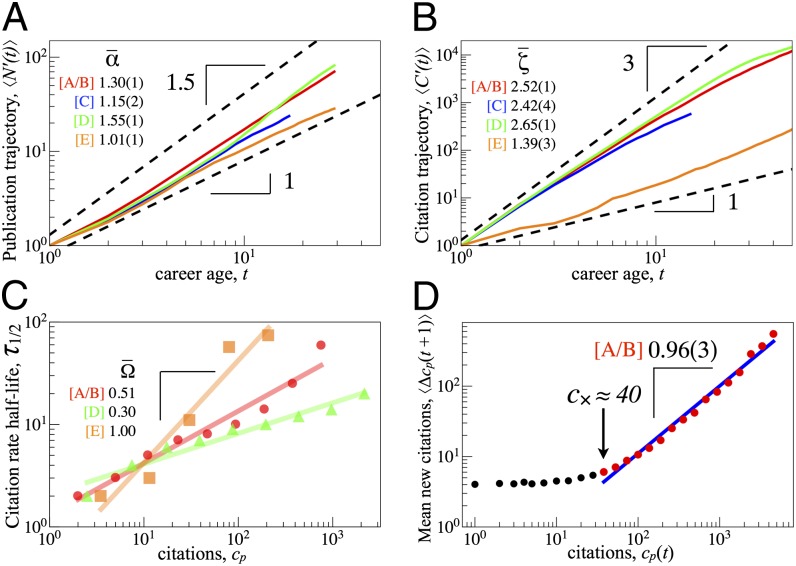
In this section, we investigate the patterns of cumulative publication and citation growth across the career. A striking statistical patterns observed for top scientists is the faster than linear growth in time, both in cumulative publication number $N_i\left(t\right)\equiv {\displaystyle {\sum }_{t^{\prime }=1}^t{n}_i\left(t^{\prime }\right)}$ and in cumulative citation count $C_i\left(t\right)\equiv {\displaystyle {\sum }_{p=1}^{N_i\left(t\right)}{c}_{i,p}\left(t\right)}$ for a large part of a scientist’s “growth phase,” which we find to be $\approx 30$ y after their first publication. Fig. 1 A and B shows the characteristic growth trajectories $\langle N^{\prime }\left(t\right)\rangle \sim t^{\overline{\alpha }}$ and $\langle C^{\prime }\left(t\right)\rangle \sim t^{\overline{\zeta }}$, calculated by an appropriate average over individual $N_i\left(t\right)$ and $C_i\left(t\right)$, respectively. To facilitate visual comparison, we use arbitrary normalized ordinate units so that each curve starts from the same point, $\langle N^{\prime }\left(1\right)\rangle =\langle C^{\prime }\left(1\right)\rangle \equiv 1$. The growth trajectories are characterized by superlinear algebraic growth, with $\overline{\alpha }\mathrm{\gtrsim }1$ and $\overline{\zeta }>\overline{\alpha }$ (values shown in Fig. 1). Individual exponents ${\alpha }_i$ and ${\zeta }_i$ are also calculated for the $N_i\left(t\right)$ and $C_i\left(t\right)$ of each author (in addition to multiple other quantitative measures; SI Appendix, Tables S1–S9). We averaged both ${\alpha }_i$ and ${\zeta }_i$ within each dataset, confirming that $\langle {\alpha }_i\rangle \cong \overline{\alpha }$ and $\langle {\zeta }_i\rangle \cong \overline{\zeta }$, confirming that the aggregate patterns hold for the individual scale. In SI Appendix, we control for the exponential growth in scientific publication rates, which can contribute to the longitudinal growth in $C_i\left(t\right)$. We define “deflated” citation counts $\mathrm{\Delta }{c}_{i,p}^D\left(t\right)\equiv \mathrm{\Delta }{c}_{i,p}\left(t\right)/D\left(t\right)$, which are normalized by the number of publications $D\left(t\right)$ within a given discipline (because a new publication can cite an old publication only once). For each discipline, we observe a 5% exponential growth in $D\left(t\right)$ over the last half century. After deflating each $C_i\left(t\right)$, the net affect is only to reduce the estimated ${\zeta }_i$ values by roughly 15%, meaning that the growth exponents ${\zeta }_i\mathrm{\gtrsim }2$ reflect significant growth above the underlying baseline growth trend in science.

Fig. 1.

Quantifying cumulative reputation measures and citation dynamics. (A and B) Growth trajectories of the cumulative publications $N\prime \left(t\right)$ and citations $C\prime \left(t\right)$, appropriately rescaled to start from unity in each ordinate. The characteristic $\overline{\alpha }$ and $\overline{\zeta }$ exponents shown in each legend are calculated over the growth phase of the career. The mathematicians [E] have distinct career trajectories, with $\overline{\alpha }\approx 1$ because collaboration spillovers via division of labor likely play a smaller role in publication rate growth. See SI Appendix, Tables S1–S9, for ${\alpha }_i$ and ${\zeta }_i$ values calculated for individual careers. (C) Relation between ${\tau }_{1/2}$ and cumulative citations $c_p$. (D) PA dynamics with $\pi \approx 1$ break down for $c<c_{\times }$. The reputation effect provides a citation boost above the baseline PA citation rate attributable to $c_p\left(t\right)$ only.

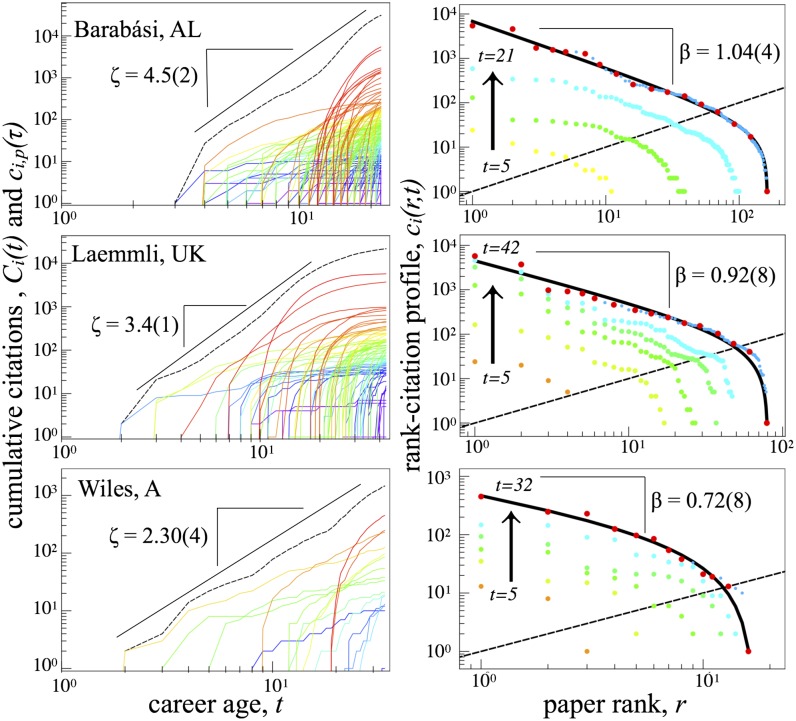
Hence, we use $C_i\left(t\right)$ as a quantitative measure of reputation owing to the fact that the time dependence is readily quantified by a single parameter ${\zeta }_i$. We also use the power-law scaling of $C_i\left(t\right)$ as a benchmark for the stochastic career model we develop in the final section. Fig. 2 shows two additional empirical benchmarks: (i) the microscopic citation dynamics of individual publications comprising the publication portfolio, and (ii) the rank-citation profile, which is the Zipf distribution of the publications ranked in decreasing order of rank r, $c_i\left(1\right)\ge c_i\left(2\right)\ge \dots \ge c_i\left(N_i\right)$. We confirm that the individual curves $c_i\left(r\right)$ belong to the class of the discrete generalized β distributions (DGBDs), which in the general form reads $c\left(r\right)\propto r^{-\beta }{\left(N+1-r\right)}^{\gamma }$ (4). We validate the DGBD fits using the ${\chi }^2$ test (SI Appendix).

Fig. 2.

Quantitative patterns in the growth and size-distribution of the publication portfolio for scientists from 3 disciplines. (Left) $c_{i,p}\left(t\right)$ for each author’s most cited papers (colored according to net citations in 2010) along with $C_i\left(t\right)\sim t^{{\zeta }_i}$ (dashed black curve). (Right) The evolution of each author’s rank-citation profile using snapshots taken at 5-y intervals. The darkest blue data points represent the most recent $c_i\left(r,t\right)$, and the subset of red data points indicate the logarithmically spaced data values used to fit the empirical data to our benchmark DGBD rank-citation distribution model (4) (solid black curve; SI Appendix). The intersection of $c_i\left(r,t\right)$ with the dashed black line corresponds to the author’s h-index $h_i\left(t\right)$.

Variability in the Citation Life Cycle.

Important scientific discoveries can cause paradigm shifts and significantly boost the reputation of scientists associated with the discovery (23). To measure the reputation effect, one must also account for obsolescence features of scientific knowledge. It is also important to account for the variations in scientific impact, because most publications report results that are not seminal breakthroughs, but, rather, report incremental advances that are likely to have relatively short-term relevance.

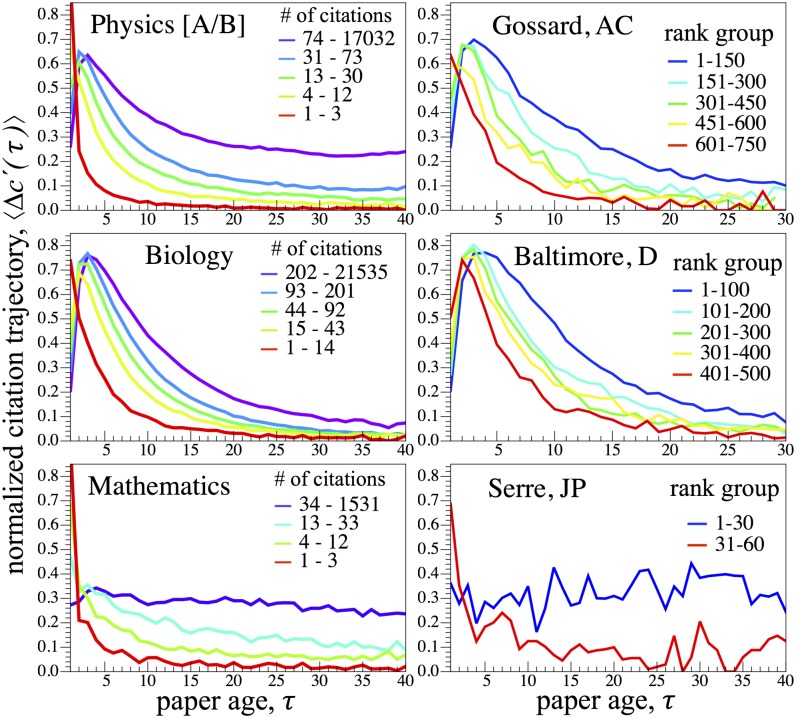
In this section, we analyze the dynamics of the citation trajectory $\mathrm{\Delta }{c}_p\left(\tau \right)$, the number of new citations received in publication year τ, where τ is the number of years since the publication was first cited. We analyze $\mathrm{\Delta }{c}_p\left(\tau \right)$ at two levels of aggregation: (i) for each discipline, we calculate an averaged $\mathrm{\Delta }{c}_p\left(\tau \right)$ by collecting publications with similar total citation counts $c_p$. To achieve a scaled trajectory that is better suited for averaging, we normalize each individual $\mathrm{\Delta }{c}_p\left(\tau \right)$ by its peak citation value, $\mathrm{\Delta }{c\prime }_p\left(\tau \right)\equiv \mathrm{\Delta }{c}_p\left(\tau \right)/\text{Max}\left[\mathrm{\Delta }{c}_p\left(\tau \right)\right]$. In Fig. 3, the panels on the Left show the characteristic citation trajectory of publications belonging to each of the top 5 quintiles of each disciplinary citation distribution. Each curve represents the average trajectory $\langle \mathrm{\Delta }{c}^{\prime }\left(\tau \right)\rangle \equiv N_q^{-1}{\displaystyle {\sum }_p\mathrm{\Delta }{c\prime }_p\left(\tau \right)}$ calculated from the $N_q$ publications in quintile q. (ii) For each career i, we calculate $\langle \mathrm{\Delta }{c\prime }_i\left(\tau \right)\rangle$ by averaging over groups of ranked citation sets within his/her publication portfolio. The panels on the Right of Fig. 3 show that, even within prestigious careers, there is significant variation in the citation life cycle.

Fig. 3.

The citation life cycle reflects both the intrinsic pace of discovery and the obsolescence rate of new knowledge, two features that are discipline dependent. (Left) For each of three disciplines, the averaged citation trajectory $\langle \mathrm{\Delta }{c}^{\prime }\left(\tau \right)\rangle$ is calculated for papers in the nth quintile with the corresponding citation range indicated in each legend. For example, for physicists in dataset [A], the top 20% of papers have between 74 and 17,032 citations, and the papers in percentile 21–40 have between 31 and 73 citations. (Right) $\langle \mathrm{\Delta }{c}^{\prime }\left(\tau \right)\rangle$ calculated for rank-ordered groups of papers (listed in each legend) for three authors chosen from each discipline.

At both levels of aggregation, the impact life cycle typically peaks before publication age $\tau \approx 5$ y. Counterexamples likely correspond to publications that receive a delayed secondary attention, e.g., receiving subsequent experimental validation of a previous theoretical prediction, and vice versa. We define the half-life ${\tau }_{1/2}$ as the time to reach half the peak citation rate, $\Delta c^{\prime }\left({\tau }_{1/2}\right)=1/2$ in the decay phase. Papers in the theoretical domains of mathematics and physics can exhibit ${\tau }_{1/2}>40$ y. Remarkably, some mathematics publications even have ${\tau }_{1/2}$ that span nearly the entire data sample duration of 100 y, reflecting the indisputable and foundational nature of progress by proof. This is in contrast to top-cited cell biology publications, whereby for even the top 20% of most cited works, the value ${\tau }_{1/2}\approx 10$ y. This relatively short decay timescale likely arises from the large scale of research output in biomedical fields, which leads to a significantly higher discovery rate, and likewise, a relatively faster obsolescence rate.

The relation between the decay timescale $\overline{\tau }$ and $c_p$ provides insight into the knowledge diffusion rate. Fig. 1C shows an approximate scaling relation ${\tau }_{1/2}\sim c_p^{\overline{\Omega }}$ when grouping publications into logarithmically spaced $c_p$ bins. Physics and biology differ mainly for the highly cited publications with $c_p\mathrm{\gtrsim }40$, whereas mathematics shows larger variation in ${\tau }_{1/2}$ per citation. The $\overline{\Omega }$ value provides an approximate relation between citations and time. In mathematics, ${\tau }_{1/2}\propto c_p$, indicating that the impact is distributed roughly uniformly across time. However, for biology publications, the sublinear relation with $\overline{\Omega }\approx 0.30$ indicates that for two publications, one with twice the citation impact as the other, the more cited publication gained twice the number of citations over a time period ${\tau }_{1/2}$ that was less than twice as large as the ${\tau }_{1/2}$ of the less-cited publication. The differences in $\overline{\Omega }$ are possibly related to discipline-dependent bursts in technological advancement, funding initiatives (15), and other social aspects of science that are related to nonlinearities in scientific advancement.

Baseline Citation Model.

To provide an initial test for basic mechanistic differences between the citation dynamics of highly cited publications and less-cited publications, in this subsection we analyze the relation between $\mathrm{\Delta }{c}_p\left(t+1\right)$ and $c_p\left(t\right)$ representing the standard baseline preferential attachment (PA) model (corresponding to the limit $\overline{\tau }\to \infty$ and $\rho =0$). Grouping together papers by $c_p\left(t\right)$ (using logarithmic bins), we calculate for each group the mean number of new citations in the following year, $\langle \mathrm{\Delta }{c}_p\left(t+1\right)\rangle$. Fig. 1D shows the empirical relation for physicists in datasets [A/B], indicating that publications with citations above a gradual but substantial citation crossover value $c_{\times }$ obey a distinct scaling law that matches approximately linear ($\pi \approx 1$) PA dynamics (see SI Appendix, Fig. S8, for other disciplines). However, below $c_{\times }$, the citation rates are in excess of the citation rate expected from linear PA alone, reflecting the citation premium that can be achieved via reputation.

Quantifying the Role of the Reputation Effect.

By analyzing the publications of highly cited scientists, we have shown that the basic citation dynamics above and below the citation crossover value $c_{\times }$ vary considerably. In this subsection, we investigate the role played by the reputation effect for publications with $c_p\left(\tau \right)\ge c_{\times }$ compared with publications with $c_p\left(\tau \right)<c_{\times }$. Based upon the assessment of the growth dynamics (SI Appendix, Figs. S8 and S9), we choose the crossover values $c_{\times }\equiv 40$ [A/B], $c_{\times }\equiv 10$ [C], $c_{\times }\equiv 100$ [D], and $c_{\times }\equiv 20$ [E]. Our results are not strongly dependent on reasonable variations around our choice of $c_{\times }$. Table 1 shows the ${\pi }_i$, $\overline{{\tau }_i}$, and ${\rho }_i$ estimates, above and below $c_{\times }$, for the individual careers highlighted in Figs. 1 and 3.

Table 1.

Best-fit parameters for each effect (±SEs), both for individuals and the average values (±SD) within each dataset

	$c\left(t-1\right)<c_{\times }$			$c\left(t-1\right)\ge c_{\times }$
Name	${\pi }_i$ (paper)	${\overline{\tau }}_i$ (life cycle)	${\rho }_i$ (reputation)	${\pi }_i$ (paper)	${\overline{\tau }}_i$ (life cycle)	${\rho }_i$ (reputation)
Gossard, A. C.	0.34 ± 0.027	4.92 ± 0.261	0.25 ± 0.008	0.80 ± 0.048	4.73 ± 0.184	0.09 ± 0.024
Barabási, A. L.	0.42 ± 0.036	3.00 ± 0.155	0.29 ± 0.010	1.06 ± 0.016	3.65 ± 0.111	0.01 ± 0.011
Average ± SD [A]	0.43 ± 0.14	5.67 ± 2.52	0.22 ± 0.06	0.96 ± 0.19	8.93 ± 4.09	−0.07 ± 0.11
Baltimore, D.	0.32 ± 0.018	4.64 ± 0.148	0.28 ± 0.006	0.62 ± 0.047	5.92 ± 0.250	0.15 ± 0.026
Laemmli, U. K.	0.54 ± 0.036	5.09 ± 0.297	0.21 ± 0.014	1.09 ± 0.025	6.40 ± 0.255	−0.12 ± 0.019
Average ± SD [D]	0.40 ± 0.14	6.64 ± 6.24	0.26 ± 0.05	0.99 ± 0.22	9.55 ± 26.30	−0.06 ± 0.14
Serre, J. P.	0.33 ± 0.095	15.90 ± 3.724	0.14 ± 0.026	0.66 ± 0.065	20.50 ± 3.862	−0.03 ± 0.039
Wiles, A.	0.56 ± 0.208	5.23 ± 1.187	0.24 ± 0.052	0.70 ± 0.059	9.04 ± 0.633	0.10 ± 0.042
Average ± SD [E]	0.27 ± 0.17	30.60 ± 56.80	0.14 ± 0.07	0.54 ± 0.25	21.40 ± 54.30	0.01 ± 0.11

For statistical significances, see SI Appendix, Tables S10–S22.

Our main result is a robust pattern of role switching by author- and publication-specific effects, specifically,

$$\rho \left(c<c_{\times }\right)>\rho \left(c\ge c_{\times }\right)\hspace{1em}\text{and}\hspace{1em}\pi \left(c<c_{\times }\right)<\pi \left(c\ge c_{\times }\right).$$ [2]

For example, for the aggregate dataset [A/B] representing prolific physicists, we estimate the values $\rho \left(c<40\right)\approx 0.2$, $\rho \left(c\ge 40\right)\approx 0$, $\pi \left(c<40\right)\approx 0.4$, and $\pi \left(c\ge 40\right)\approx 1$. To emphasize the role of reputation on new publications, consider two scientists separated by a factor of 10 in their cumulative citations, $C_1\left(t\right)=10C_2\left(t\right)$. All other things being equal, the citation premium attributable to reputation alone for publications in the reputation regime $\left(c<c_{\times }\right)$ is $\mathrm{\Delta }{c}_1\left(t\right)/\mathrm{\Delta }{c}_2\left(t\right)={10}^{\rho }\approx 1.66$ (using the value $\rho =0.22$ for dataset [A]). Hence, there is a 66% increase in the citation rate for each 10-fold increase in $C_i\left(t\right)$, which integrated over a career can provide significant positive feedback. A pattern that emerges independent of discipline is $\rho \left(c\ge c_{\times }\right)\approx 0$, meaning that reputation only plays a significant role for $c<c_{\times }$. In SI Appendix, section S6, we test the robustness of this result by implementing a fixed-effects regression, the result of which reaffirms the distinct roles of π and ρ above and below $c_{\times }$. Hence, these two inequalities in Eq. 2 indicate that publications are initially boosted by author reputation to a citation “tipping point” $c_{i,p}\approx c_{\times }$, above which the citation rate is sustained in large by publication reputation. These findings show how microscopic reputation mechanisms contribute to cumulative “rich-get-richer” processes in science (7, 9).

Simulating Synthetic MC Careers with the Reputation Model.

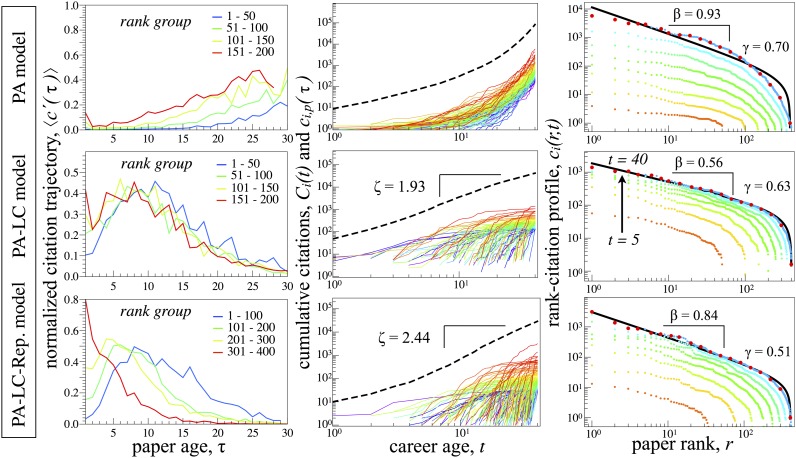
Here, we discuss three variants of a MC career growth model that simulates the dynamics of $\mathrm{\Delta }{c}_{i,p}\left(t+1\right)$ for each publication p in each time period t of the career of synthetic author i. With each variant, we introduce progressively a new feature of publication citation trajectories. (i) We begin with a basic linear PA model whereby $\mathrm{\Delta }{c}_{i,p}\left(t+1\right)\propto c_{i,p}\left(t\right)$. Model ii (PA-LC) includes a life-cycle (LC) obsolescence effect, $A_p\left(\tau \right)$. Fig. 4 compares models i and ii, which do not incorporate author specific factors, with the reputation model iii given by Eq. 1. The PA model fails to reproduce the characteristic trajectories of real publications, because there is a clear first-mover advantage (24) for the first publications published in the career, as well as non–power-law growth of $C_i\left(t\right)$.

Fig. 4.

Comparison of three MC career models against empirical benchmarks demonstrated in Figs. 1–3 and SI Appendix, Figs. S1–S3. For each model, we show $\langle \mathrm{\Delta }{c}^{\prime }\left(\tau \right)\rangle$ for the top four groups of ranked papers, the evolution of $c_{i,p}\left(\tau \right)$ and $C_i\left(t\right)$ (dashed black curve), and the evolution of the rank-citation profile $c_i\left(r\right)$ at 5-period intervals. The best-fit DGBD β and γ parameters are also useful as quantitative benchmarks. For each model, we evolve the system over $T\equiv 40$ periods, each period representative of a year. See SI Appendix for further elaboration of the model parameters used in the MC simulation.

We use quantitative patterns demonstrated for real careers in Figs. 2 and 3 as empirical benchmarks to distinguish models ii and iii. We confirm that the reputation model iii satisfies the empirical benchmark characteristics in all three graphical categories (Fig. 4). We also confirm for the model iii, but not for the model ii, that there is a distinction between $\langle \mathrm{\Delta }{c}^{\prime }\left({\tau }_p\right)\rangle$ for different rank sets. Furthermore, for model iii, we quantitatively confirm that $C\left(t\right)\sim t^{\zeta }$ with $2\mathrm{\lesssim }\zeta \mathrm{\lesssim }3$. For sufficiently large t, we also confirm that $c\left(r,t\right)$ belongs to the class of DGBD distributions, with β values within the range of values observed empirically. In SI Appendix, we further demonstrate how the model can be used to estimate properties of “average” careers for a given MC parameter set. For example, SI Appendix, Fig. S11, shows excellent agreement between the reputation model’s prediction and empirical data when estimating the fraction $f_{\ge c_x}$ of publications with $c_p\ge c_{\times }$ for a given career age t. Empirically, we observe saturation $f_{\ge c_x}\approx$ 0.20–0.30 for large t.

Discussion

Social networks in science are characterized by heterogeneous structure (25) that provides opportunities for intellectual and social capital investment (26) and influences scientists’ research strategies (21). Identifying patterns of career growth is becoming increasingly important, largely due to the widespread emergence of quantitative evaluation processes and recent efforts to develop quantitative models of career development. However, difficulties in accounting for complex social mechanisms, in addition to nonlinearities and nonstationarities in the career growth process, highlight the case for caution in the development of predictive career models (16, 17). Without a better understanding of the institutional features and scientific norms that affect scientific careers, along the variable path from apprentice to group leader and mentor, there is a possibility to misuse quantitative career metrics in the career evaluation process.

Toward the goal of better understanding career growth, with potential policy implications for the quantitative career evaluation process, we have analyzed the effect of reputation on the microlevel processes underlying the dynamics of a scientist’s research impact. We used a regression model for the citation rate $\mathrm{\Delta }{c}_{i,p}$, which accounts for the role of publication impact (π), the role of knowledge obsolescence ($\overline{\tau }$), and the role of author reputation (ρ). Interestingly, we find that the reputation parameter $\rho \left(c\ge c_{\times }\right)\approx 0$, meaning that in the long run the reputation effect makes a negligible contribution to the citation rate of papers with large $c_p$. However, we identify caveats concerning the way publications can become highly cited. By analyzing the variation of ρ and π for publications above and below a citation threshold $c_{\times }$, we identify the advantageous role that author reputation plays in the citation dynamics of new publications, finding that future publications can gain roughly a 66% increase in $\mathrm{\Delta }c$ for each 10-fold increase in reputation $C_i$. We note that it is also likely that both institutional affiliation and journal reputation also play a role in the citation dynamics; however, disentangling the interaction between the multiple reputation sources will likely be challenging and remains an open avenue for investigation.

In the process of analyzing the effect of reputation on career growth, it was necessary to also quantify two essential features of our model, namely patterns of cumulative productivity and impact across the career, and patterns of obsolescence in the citation life cycle of individual publications. For prolific scientists, we have identified a robust pattern of growth for two cumulative reputation measures, $N_i\left(t\right)$ and $C_i\left(t\right)$, each of which are quantifiable by a single scaling parameter, ${\alpha }_i$ and ${\zeta }_i$, respectively. These regularities suggest that underlying social processes sustain career growth via reinforcing coevolution of scientific collaboration and publication (6, 27–29). We also introduced a citation deflator index to control for the increased supply of citations arising from the exponential 5% growth (per year) in the total publication output. Analyzing the growth of “deflated” citation trajectories, $C_i^D\left(t\right)$, we observed ${\zeta }_i\mathrm{\gtrsim }2$ values which confirms that the observed career growth is significantly above the baseline inflation rate of science. We note that in using nondecreasing cumulative reputation measure $C_i\left(t\right)$, we have overlooked the possibility that reputation can significantly decrease, as occurs when a scientist is associated with invalidated and/or fraudulent science. Indeed, recent evidence indicates that the retraction of a publication can have a negative impact on the potential growth of $C_i$ (30). As a robustness check, we also used the annual citation rate $\mathrm{\Delta }{C}_i\left(t\right)$ as an additional (noncumulative) reputation measure, one that is more amenable to controlling for secular growth trends. We applied a multivariate fixed effects regression using $\mathrm{\Delta }{C}_i\left(t\right)$ as the reputation measure (SI Appendix, section S6), which reconfirms the role of reputation in citation dynamics.

Our analysis tracks the evolution of each scientist’s publication portfolio across the career, suitably illustrated by the rank-citation profile $c_i\left(r\right)$, which highlights the skewed distribution of $c_{i,p}$, even within a career. Arising from the power-law features of $c_i\left(r\right)$ (4), we emphasize the disproportionate fraction of a scientist’s total citations $C_i$ owed to the $c_i(r=1)$ citations coming from his/her highest-cited publication. For example, the average and SD of the ratio $c_i\left(1\right)/C_i$ is $0.15\pm 0.13$ for the physicists, $0.09\pm 0.08$ for the biologists, and $0.16\pm 0.08$ for the mathematicians we analyzed, which emphasizes the potentially large reputation boost that can follow from just a single high-impact publication. With rapidly increasing numbers of journals accompanied by the opportunity for rapid publication, the reputation effect provides an incentive to aim for quality over quantity in the publication process, reinforcing a research strategy that is beneficial for science and scientists.

It is also important to consider the role of reputation in light of the increasing orientation of science around team endeavors characterized by multiple levels of hierarchy and division of labor (31). Because it is difficult to evaluate and assign credit to individual contributions in a team setting, there may be an increase in the role and strength of the reputation in overcoming the problem associated with asymmetric and incomplete information. In addition to the collaboration network, reputation also plays a key role in numerous other scientific inputs (money, labor, knowledge, etc.) that inevitably affect the overall quantity and quality of scientific outputs. It will become increasingly important to understand the relation between these inputs and outputs to efficiently allocate scientific resources (6, 15, 18).

In light of individual careers, an institutional setting based on quantitative appraisal that neglects these complex relations may inadvertently go against the goal of sustaining the careers of talented and diligent young academics (6). For example, our finding of a crossover behavior around $c_{\times }$ shows how young scientists lacking reputation can be negatively affected by social stratification in science. The appealing competitive advantage gained by working with a prestigious mentor may be countered by the possibility that it may not be the ideal mentor–advisee match. Despite having analyzed cohorts of highly cited scientists, our results have broad implications across the scientific population when one considers the numerous careers that interact with top scientists via collaboration or mentorship.

In excess, the reputation effect may also negatively affect science, especially considering how online visibility has become a relatively new reputation platform in an increasingly competitive environment. As such, strategies of self-promotion may emerge as scientists try to “game” with reputation systems. In such scenarios, it may be hard to disentangle fair from foul play. For example, it may be difficult to distinguish self-citation strategies aimed at boosting $C_i$ from the natural tendency for scientists who are crossing disciplinary borders to self-cite with the intention to send credibility signals (32). Reputation will also become increasingly important in light of preferential treatment in search queries, e.g., Google Scholar, which provide query results ordered according to citation measures. These systemic search and retrieval features may further strengthen association of reputation between publications and authors. In all, our results should motivate future research to inspire institutional and funding body evaluation schemes to appropriately account for the roles that reputation and social context play in science. For example, our results can be used in support of the double-blind review system, which by reducing the role of reputation, is perceived to have advantages due to its objectivity and fairness (33). We conclude with a general note that the data deluge brought forth during the past decade is fueling extensive efforts in the computational social sciences (34) to identify and study the so-called “social atom” (35). Because our methodology is general, we speculate that other social networks characterized by trust and partial/asymmetric information are also based on similar reputation mechanisms. Indeed, it is likely that agent-based reputation mechanisms will play an increasing role in society due to the omnipresence of online recommender systems governed by reputation dynamics operating as a general diffusive contagion phenomena (36).