Combating Unmeasured Confounding in Cross-Sectional Studies: Evaluating Instrumental-Variable and Heckman Selection Models

Abstract

Unmeasured confounding is the principal threat to unbiased estimation of treatment “effects” (i.e., regression parameters for binary regressors) in nonexperimental research. It refers to unmeasured characteristics of individuals that lead them both to be in a particular “treatment” category and to register higher or lower values than others on a response variable. In this article, I introduce readers to 2 econometric techniques designed to control the problem, with a particular emphasis on the Heckman selection model (HSM). Both techniques can be used with only cross-sectional data. Using a Monte Carlo experiment, I compare the performance of instrumental-variable regression (IVR) and HSM to that of ordinary least squares (OLS) under conditions with treatment and unmeasured confounding both present and absent. I find HSM generally to outperform IVR with respect to mean-square-error of treatment estimates, as well as power for detecting either a treatment effect or unobserved confounding. However, both HSM and IVR require a large sample to be fully effective. The use of HSM and IVR in tandem with OLS to untangle unobserved confounding bias in cross-sectional data is further demonstrated with an empirical application. Using data from the 2006–2010 General Social Survey (National Opinion Research Center, 2014), I examine the association between being married and subjective well-being.

Unmeasured confounding is an ever-present threat to causal inference in nonexperimental research. (The problem goes by several names depending on discipline, e.g., unmeasured heterogeneity, selection bias, endogeneity, and so forth.; in this article, these terms are used interchangeably with unmeasured confounding.) Unmeasured confounding refers to unmeasured characteristics of individuals that lead them both to be in a particular “treatment” category and to register higher or lower values than others on a response variable (Wooldridge, 2003). For example, those who cohabit before marrying have been found to perceive their marriages as more unstable than those who have not (DeMaris & MacDonald, 1993). One reason may be that those who have more reservations about the prospective spouse are both more likely to cohabit first and more likely to register ambiguity about the permanence of their marriage afterward. Another example is peer delinquency, which has been found to be strongly predictive of one's own delinquency (Mears, Ploeger, & Warr, 1998; Warr, 1993). This may simply reflect that those with poor impulse control or little regard for the law are both more likely to choose delinquent friends and more likely to engage in delinquent acts.

The only way to ensure that all sources of unmeasured confounding are controlled in research is to randomly assign cases to “treatment” levels (Rosenbaum & Rubin, 1983; Schafer & Kang, 2008. I use treatment here only as a generic term for a binary explanatory variable, not to imply an experimental manipulation.)As this is either impractical or unethical in many instances, researchers must rely on statistical modeling to eliminate unmeasured confounds. A popular approach is to use fixed-effects regression modeling (Allison, 2005, 2009). This strategy presupposes the existence of an unmeasured selection factor in the cross-sectional model of a regressor's effect on a response. With more than one wave of data for the same respondents, the unmeasured confound can be elided from the model via a differencing process (see, for example, Allison, 2005, 2009; Wooldridge, 2002, for an explication of this approach). Although this technique is elegant, it requires panel data, which are more expensive and time-consuming to collect than cross-sectional samples. (See, however, Antonovics & Town, 2004; Gager, Sanchez, & DeMaris, 2009, for examples of fixed-effects regression using cross-sectional data on siblings.) Some data sets that are rich in social measures, including such national data sets as the General Social Survey (GSS; National Opinion Research Center, 2014), the American Community Survey (U.S. Department of Commerce, Economic and Statistics Administration, U.S. Census Bureau, 2013), and the survey of Violence and Threats of Violence Against Women and Men in the United States 1994–1996 (Tjaden & Thoennes, 1999), are thereby automatically excluded.

In this article, I therefore consider the performance of two econometric techniques designed to eliminate unmeasured-confounding bias in cross-sectional data analysis: instrumental-variable regression (hereinafter, IVR) and the Heckman selection model (hereinafter, HSM). In what follows, I present a “model” of unmeasured confounding in cross-sectional analysis to illustrate the nature of the problem. I then discuss IVR and HSM as remedies and report the results of a Monte Carlo study of the efficacy of IVR and HSM in eliminating the problem. I also examine the statistical power of these techniques to discover whether unmeasured confounding is influencing the analyses. Subsequently, I illustrate the utility of IVR and HSM with an empirical application from the GSS. Triangulating these methods with ordinary least squares regression (hereinafter, OLS), I examine the effect of marital status on subjective well-being. The estimation of causal effects is a primary goal of most research in the social and behavioral sciences (Allison, 2009; Davis, 1985; Rubin, 1974). Although the IVR and HSM approaches are typically couched in the context of causal inferences, one's estimates need not necessarily be given a causal interpretation. These techniques can also be used simply to facilitate unbiased estimation of a partial regression coefficient for a binary regressor in one's model when there are measured and unmeasured confounders.

Explication of IVR and HSM

Unmeasured Confounding and Cross-Sectional Data

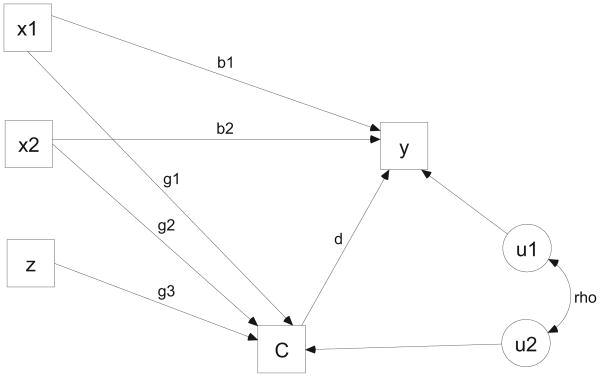
In this section of the article, I consider the operation of unmeasured confounding in cross-sectional analyses. Let Y_i be a continuous response variable and $C_i^{\ast }$ be an unmeasured propensity for assignment to the treatment (vs. the control) condition for the ith case; C_i be a binary variable coded 1 if the case is exposed to the treatment condition and 0 otherwise; X_i1, X_i2, and Z_i be measured covariates; and a_i, ε_i, and υ_i be unmeasured random variables. For ease of presentation and subsequent simulation (discussed later), I assume that X_i1, and X_i2 are uncorrelated, although this requirement is not necessary. On the other hand, Z_i , the “instrument” in the model for $C_i^{\ast }$ must (as explained later) be uncorrelated with both X_i1, and X_i2. I further assume that X_i1, X_i2, and Z_i are exogenous, that is, uncorrelated with a_i , ε_i, and υ_i. I also assume that a_i , ε_i, and υ_i are uncorrelated with each other and have zero means. Let q be a threshold value such that if $C_i^{\ast }>q$, then C_i = 1; otherwise C_i = 0. The value of q determines the relative distribution of cases into categories of C_i. A model for the impact of unmeasured confounding is as follows:

$$C_i^{\ast }={\mathrm{\alpha }}_1+g_1{X}_{i1}+g_2{X}_{i2}+g_3{Z}_i+{\mathrm{\zeta }}_1{a}_i+{\mathrm{\epsilon }}_i,$$ (1)

$$Y_i={\mathrm{\alpha }}_2+b_1{X}_{i1}+b_2{X}_{i2}+d{C}_i+{\mathrm{\zeta }}_2{a}_i+{\mathrm{\upsilon }}_i.$$ (2)

The term a_i is the unmeasured characteristic. Since a_i is unobserved, it is not included in the estimation model for Y_i and is therefore part of the equation error. When that model is estimated by OLS, treatment condition C_i is correlated with the error term, which is ζ₂a_i + υ_i. The reason for this correlation is that C_i is a function of a_i (via a_i's influence on $C_i^{\ast }$), and therefore it is correlated with ζ₂a_i. When a regressor is correlated with the error term in the same equation, it is said to be endogenous. An omitted regressor is the usual cause of endogeneity but is not the only reason for it. Endogeneity can also be caused by measurement error in regressors or by simultaneity (i.e., the response and the regressor mutually affect each other; Wooldridge, 2002). However, I focus only on the omitted-regressor issue in this article, and therefore, the test for an unmeasured confound is referred to as a test for endogeneity. It is also the case that the error terms in the equations for $C_i^{\ast }$ and for Y_i , which are ζ₁a_i + ε_i and ζ₂a_i + υ_i, respectively, are correlated by virtue of their common dependence on a_i. I refer to that correlation as “ρ (rho),” throughout this article. It is instructive to examine this correlation:

$$\rho =\frac{cov({\mathrm{\zeta }}_1{a}_i+{\mathrm{\epsilon }}_i,{\mathrm{\zeta }}_2{a}_i+{\mathrm{\upsilon }}_i)}{\sqrt{V({\mathrm{\zeta }}_1{a}_i+{\mathrm{\epsilon }}_i)V({\mathrm{\zeta }}_2{a}_i+{\mathrm{\upsilon }}_i)}}=\frac{{\mathrm{\zeta }}_1{\mathrm{\zeta }}_2{\mathrm{\sigma }}_a^2}{\sqrt{({\mathrm{\zeta }}_1^2{\mathrm{\sigma }}_a^2+{\mathrm{\sigma }}_{\mathrm{\epsilon }}^2)({\mathrm{\zeta }}_2^2{\mathrm{\sigma }}_a^2+{\mathrm{\sigma }}_{\mathrm{\upsilon }}^2)}}.$$

Here it is clear that ρ is a function of the effects of the unobserved regressor on both the probability of being exposed to treatment and the response to that treatment. Because of the endogeneity problem, the estimate of d arrived at by OLS is biased and inconsistent for d (Wooldridge, 2002, 2003; also, see the development of the HSM later). In fact, in the absence of an actual treatment effect, the endogeneity problem can make it appear as though there is a treatment effect in the model for Y_i . Figure 1 depicts the model represented by Equations 1 and 2. (In the figure, u1 = ζ₂a_i + υ_i and u2 = ζ₁a_i + ε_i.)

Figure 1.

Unmeasured confounding in cross-sectional data.

IVR and HSM Models

The IVR model employs one or more additional variables as instruments for the endogenous regressor, C_i. The variable Z_i, in Equation 1 is an example. The requirements for an instrument are as follows (Bound, Jaeger, & Baker, 1995; Hernán & Robins, 2006; Wooldridge, 2002). First, it must have a causal effect on the treatment, C_i. Second, it must affect Y_i only through its effect on C_i. That is, it has no direct effect on Y_i , conditional on treatment and other covariates; this is known as the “exclusion restriction” (Hernán & Robins, 2006, p. 360). Third, it does not share common causes with the outcome variable, Y_i ; that is, Z_i is “exogenous” in the equation for Y_i (Wooldridge, 2002, p. 82). These conditions are all depicted in the model shown in Equations 1 and 2 and Figure 1. The ideal instrument is, moreover, uncorrelated with any other regressors in the model as well as with any other unmeasured factors that affect Y_i (Wooldridge, 2003). The best example of the ideal instrument is random assignment to treatment levels (Angrist & Pischke, 2009). As it is random, it is by definition uncorrelated with any other possible regressors or unmeasured variables. It is strongly predictive of actual treatment received (although, due to noncompliance and other irregularities, may not be perfectly correlated with it). And its only influence on the response is indirect, via the potential effect of the treatment itself. Some studies in which IVR has been used have been able to show approximately random influences on treatment assignment that come close to fulfilling these conditions. For example, Angrist (1990) used draft eligibility based on the random sequence number from the Vietnam-era draft lottery as an instrument for veteran status in examining the effect of veteran status on earnings. Lochner and Moretti (2004) used changes over time in the number of years of compulsory education mandated by states as an instrument for the effect of schooling on criminal activity. Nevertheless, much of the time, an instrument that is akin to random assignment is difficult to discover. Instead, we may have to settle for a surrogate that we hope approximates the conditions that have been outlined.

IVR is typically accomplished using two-stage least squares (2SLS). In the first stage, the binary treatment indicator, C_i , is regressed on the instruments and other covariates using OLS regression. Then, the fitted value for C_i , Ĉ_i , is generated using that same equation. In the second stage, Y_i is regressed on Ĉ_i and the other covariates (but not Z_i) to get a consistent estimate of the effect of C_i. Because Z_i and the other covariates are uncorrelated with ζ₂a_i + υ_i, Ĉ_i—a linear function of the other covariates and Z_i—is also uncorrelated with ζ₂a_i + υ_i, and the endogeneity problem has been eliminated. The resulting estimate of d, d̂, should then be consistent for d.

The HSM was originally proposed by Heckman (1978) and is to be distinguished from his incidentally truncated version of the model, which is referred to as the Heckit procedure (Heckman, 1979; Wooldridge, 2002). The latter adjusts for sample selection (i.e., nonrandom exclusion of cases based on missingness on Y_i). The HSM, instead, adjusts for nonrandom selection into the treatment group. The HSM assumes the following variation on Equations 1 and 2:

$$C_i^{\ast }={\mathrm{\alpha }}_1+g_1{X}_{i1}+g_2{X}_{i2}+g_3{Z}_i+{\mathrm{\omega }}_{i1},$$ (3)

$$Y_i={\mathrm{\alpha }}_2+b_1{X}_{i1}+b_2{X}_{i2}+d{C}_i+{\mathrm{\omega }}_{i2}.$$ (4)

Here ω_i1 = ζ₁a_i + ε_i and ω_i2 = ζ₂a_i + υ_i, whereas C_i = 1 if $C_i^{\ast }>0$, and 0 otherwise. HSM further assumes that ω_i1 and ω_i2 are jointly distributed as bivariate normal, with 0 means and correlation ρ. This is a critical assumption for identification of the model; its violation may lead to serious bias in the estimate of a treatment effect. The variance of ω_i2 is allowed to be a free parameter, while the variance of ω_i1 is constrained to equal 1 for estimation purposes (Greene, 2003). Z_i in Equation 3, referred to hereinafter as the unique regressor, is an additional covariate that only causes assignment to the treatment condition but not Y_i.

Because of the joint distribution of the error terms, the expectation of Y_i conditional on C_i equaling 1 is

$$\mathrm{E}(Y_i|C_i=1,X_{i1},X_{i2},Z_i)={\mathrm{\alpha }}_2+b_1{X}_{i1}+b_2{X}_{i2}+d+\mathrm{\rho }{\mathrm{\sigma }}_2(\frac{\mathrm{\phi }({\mathrm{\alpha }}_1+g_1{X}_{i1}+g_2{X}_{i2}+g_3{Z}_i)}{\mathrm{\Phi }({\mathrm{\alpha }}_1+g_1{X}_{i1}+g_2{X}_{i2}+g_3{Z}_i)})$$ (5)

where σ₂ is the standard deviation of ω_i2, ϕ(.) is the standard normal density function, and Φ(.) is the standard normal distribution function. That is, compared with the control group, the conditional mean of Y_i for those in the treatment group is shifted by d plus an additional term. That term (the last term in Equation 5), called the inverse Mills ratio (IMR), is a nonlinear function of the set of regressors for $C_i^{\ast }$. Attempts to estimate Equation 5 via OLS result in an inconsistent estimate of d, due to the omission of this term. Notice that the coefficient of this term is a function of ρ, the correlation between ω_i1 and ω_i2. And as shown previously, ρ is a function of the effects of unmeasured heterogeneity on both treatment and response. Therefore, incorporation of ρ into the equation for Y_i controls for the unmeasured heterogeneity. HSM estimates the treatment effect by including the IMR in the likelihood function for the data and employing maximum-likelihood estimation to arrive at a consistent estimate of d. Alternatively, Equation 5 can be estimated via a two-step procedure. First a probit model is employed to estimate Equation 3 using C_i as the binary response. Then, an estimate of the IMR is computed using the probit coefficients, and Equation 5 is estimated after adding the IMR as an extra regressor (Greene, 2003; Maddala, 1983).

Differences Between IVR and HSM

IVR solves the endogeneity problem by eliminating it: Ĉ_i, the instrument employed as C_i's surrogate in the substantive model, is no longer endogenous. HSM, on the other hand, solves the problem by employing the IMR to control for endogeneity in the substantive equation. This control is accomplished via the inclusion of ρ in its regression coefficient. In IVR, the instrument is a surrogate for the treatment indicator in the substantive equation. On the other hand, in HSM, the treatment indicator is included in the substantive equation. Additionally, HSM makes the strong assumption of bivariate normality for the joint distribution of the errors in the equations for $C_i^{\ast }$ and Y_i . IVR imposes only the less restrictive assumption that both errors are independent realizations of a random variable with zero mean and finite variance (Greene, 2003; Wooldridge, 2002).

Perhaps the most important difference is in the necessity for Z_i in Equation 1 versus Equation 3. In IVR, the instrument must have a causal effect on C_i. IVR uses a linear combination of the substantive-model covariates plus an additional instrumental variable as a proxy for treatment. Should the instrumental variable have no partial effect on C_i controlling for the other covariates, Ĉ_i will be more or less exactly collinear with the covariates in the substantive model. Extreme multicollinearity will then render the estimates of Equation 2 nonviable. In HSM, Z_i , has a different role. Its primary function is to provide a unique regressor in the equation for C_i to ensure that Equation 5 is identified other than through the nonlinear transformation effected by the IMR. If the same regressor set is used for Equation 3 as for Equation 4, then identification may become an issue. Wooldridge (2002) pointed out that if the right-hand-side of the model for C_i exhibits little variation in the sample, the IMR can be well approximated by a linear function of the regressor set. If the regressor set is the same in selection and substantive equations, this can result in substantial collinearity between the IMR and the covariates in the substantive equation. However, Nawata (2004) has shown that HSM's “cousin,” the Heckit model, performs reasonably well even when the regressor set is identical for the selection and substantive equations, provided that maximum-likelihood estimation is employed.

Tests for Endogeneity

Associated with IVR is the Hausman test for endogeneity (Hausman, 1978, 1983). The test is based on a comparison of the OLS and IVR estimates of the coefficients in Equation 2. If C_i is uncorrelated with the error term in that equation, then the OLS and 2SLS estimates should differ only by sampling error in large samples. As the original form of the statistic is unwieldy, Hausman (1983) recommended a regression-based version that is asymptotically equivalent. If C_i is endogenous, then the error terms in the regression models for C_i and for Y_i will be correlated, with p denoting that correlation (see Wooldridge, 2002, for the relevant mathematical development). What is required is a test for whether ρ is nonzero. To accomplish this, one simply saves the residual term from the first-stage regression for C_i in the 2SLS procedure. This term is then included in a regression of Y_i on the original C_i (not Ĉ_i) and the other covariates in Equation 2. The coefficient of this term, β̂, is the estimated unstandardized regression coefficient for the regression of ε_i (from Equation 1) on υ_i (from Equation 2). The usual OLS t statistic for this coefficient is the test in question (Hausman, 1983; Wooldridge, 2002). Note that β̂, not being itself a correlation coefficient, is not constrained to fall in the [−1, 1] interval. A similar test is available in the HSM model, with the same rationale: endogeneity implies a nonzero value of ρ. As an estimate of ρ is available via the maximization of the likelihood function, dividing ρ̂ by its standard error provides a t test for the presence of endogeneity.

Monte Carlo Results for IVR and HSM

Prior Simulation Results

Several Monte Carlo studies of the HSM and Heckit models, as well as the IVR, have been heretofore conducted. As the mathematics and distributional assumptions for HSM and Heckit are identical, they are both discussed in this review. Stolzenberg and Relles (1990, 1997) conducted simulations of the Heckit model. They found that, on average, Heckit performed no better than OLS, worsening estimates as often as improving them. Nevertheless, the technique appeared to consistently reduce estimator bias when substantive- and selection-model errors were highly correlated, and the regressors in the substantive equation were highly correlated with those in the selection equation. Alluded to earlier, Nawata's (2004) study compared two-step and maximum-likelihood estimation (MLE) of Heckit and found the MLE version to perform well in all conditions. Moreover, it proved superior to the two-step alternative, especially with small N or identical regressor variables in both equations. Both Angrist (1991) and Staiger and Stock (1997) undertook small Monte Carlo studies of instrumental-variables techniques (Angrist's involved bivariate probit instead of linear regression, however). They found that IVR was generally robust to nonnormality of errors and performed reasonably well even in moderate-sized samples. Nevertheless, IVR estimates were particularly poor when the instruments were only weakly correlated with the endogenous regressor. In this case, large sample size did not improve the situation (Staiger & Stock, 1997). Both Bhattacharya, Goldman, and McCaffrey (2006) and Chiburis, Das, and Lokshin (2012) employed Monte Carlo experiments to examine instrumental-variable and Heckman-selection techniques for a binary response variable. They found the Heckman model (applied as a bivariate probit regression) estimated via maximum likelihood to be generally superior to all other choices. However, all models exhibited biased estimation of treatment effects under conditions of nonnormal equation errors, especially when combined with a low probability of assignment to the treatment group. Chiburis et al. (2012) recommended presenting both linear instrumental-variable and bivariate probit estimates whenever there are covariates in the model besides treatment (or its proxy). They also recommended employing confidence intervals via bootstrapping for the treatment-effect estimate with sample sizes below 10,000 (Chiburis et al., 2012).

The Current Simulation

A simulation was conducted in the current study primarily to examine how IVR and HSM would perform under ideal conditions, as well as under conditions in which important assumptions were violated. Only a few prior simulations (previously reviewed) have been conducted in which IVR and HSM were evaluated together. Moreover, very few additionally have examined the performance of the test of endogeneity associated with each technique. The current simulation was based on the theoretical model portrayed in Equations 1 and 2. It seemed critical to examine a number of conditions that might affect the ability of IVR and HSM to produce viable estimates of the treatment effect. First, the variables X_i1, X_i2, Z_i, and a_i were all created as normal random variables with mean 0 and variance 1, while α₁ and α₂ were fixed at .5 and −2, respectively. Second, I manipulated the parameters q, d, g₃, ζ₁, and ζ₂, along with the distributions of ε_i and υ_i, in Equations 1 and 2 in order to vary the treatment and error distributions, as well as the selection, instrument/unique regressor, and treatment effects. (The parameters g₁, g₂, b₁, and b₂ were fixed at 1.7, −2.3, 1, and 2, respectively, for all simulation conditions.) Finally, I varied the sample size in each simulation condition.

The distribution into the treatment condition (C_i = 1) was varied, as it has been shown to have a meaningful effect on the power of tests for d (Chiburis et al., 2012). I chose two values for the percentage of cases in the treatment condition: 50% and 15% (how this was accomplished is discussed later).

Next, I chose two different distributions for the pair of error terms, ε_i and υ_i, to examine how normality (an assumption of the HSM) versus nonnormality of errors would affect estimates. The performance of the Heckman model, in particular, has been found to be seriously degraded in the presence of nonnormal errors (Bhattacharya et al., 2006). The error distributions were chosen to be either standard normal or exponential. Standard normal errors are symmetric and have mean zero and variance 1. Exponential errors are right-skewed with a variance that exceeds the mean. In the estimation process, the equation errors would be ζ₁a_i + ε_i and ζ₂a_i + υ_i. With ε_i and υ_i both specified as standard normal, ζ₁a_i + ε_i and ζ₂a_i + υ_i would also each be normally distributed, by theorem (Hoel, Port, & Stone, 1971). In order to create markedly nonnormal errors, I gave ε_i an exponential distribution with mean 2 and variance 4, but gave υ_i an exponential distribution with mean −2 and variance 4. Both error terms were then centered so that they had means of zero. The resulting distributions for ζ₁a_i + ε_i and ζ₂a_i + υ_i were skewed, but in opposite directions, with ζ₁a_i + ε_i right-skewed (skew = 1.37 in a random sample of 500 observations) and ζ₂a_i + υ_i left-skewed (skew = −1.14 in a random sample of 500 observations).

Selection bias (i.e., confounding) was chosen to be either present or absent. For it being present, ζ₁ was set at .75 and ζ₂ at 1.5. For it being absent, both ζ₁ and ζ₂ were set to 0. The instrument effect/unique regressor effect was chosen to be either present, by setting g₃ to 1.75, or absent, by setting g₃ to 0. Similarly, the treatment effect was chosen to be either present, setting d to 1.25, or absent, setting d to 0. To judge the effect sizes of these parameters, we can draw on Cohen's (1988) formulation for the standardized effect size, defined as the difference in mean response for treatment vs. control conditions divided by the standard deviation of the response. In a similar vein, dividing the parameter values by the standard deviation of either $C_i^{\ast }$ (3.578; see online supplemental materials) or Y_i (3.132; see online supplemental materials) results in standardized effect sizes of .21 for ζ₁, .48 for ζ_2, .49 for g₃, and .40 for d. According to Cohen's classification scheme, these all fall somewhere between small and medium effect sizes. Finally, three sample sizes were chosen to reflect small, medium, and large samples: 50, 250, and 2,000.

It should be noted that the settings for the error distributions, in combination with those for selection effects, resulted in three theoretical, or “population,” values for ρ: 0 with no selection, .5 with selection and normal errors, and .21 with selection and nonnormal errors (see the online supplemental materials for the derivation of the two latter values). The error distributions also determined the values chosen for q to render a 50–50, versus a 15–85 split on the percentage of cases falling into each treatment level. For normally distributed errors, because $C_i^{\ast }$ is a linear combination of normal random variables, it, too, has a normal distribution, by theorem (Hoel et al., 1971). A 50–50 split was achieved by setting q to .5, the mean of $C_i^{\ast }$. A 15–85 split was achieved by setting q to 1.036 (the 85th percentile of a standard normal distribution) standard deviations above the mean of $C_i^{\ast }$. The standard deviation of $C_i^{\ast }$ varied depending on whether instrument/unique regressor and/or unmeasured confounding was present. For example, when they were both present, the theoretical standard deviation of $C_i^{\ast }$ was 3.578 (see the online supplemental material for the derivation of this value; the accuracy of these settings was verified with 2,000 random observations.) For the nonnormal-errors conditions, cutoffs for q were constructed empirically, as the cumulative distribution function in this case is not readily available. Hence, using an N of 2,000, I examined the sample distribution of $C_i^{\ast }$ under the various simulation conditions and chose cutoffs based on averaging the 50th (for a 50–50 split) or the 85th (for a 15–85 split) percentile over eight replications of the distribution.

There are several limitations of the current simulation that should be kept in mind. First, the models employed in the simulation are particularly pristine. Model covariates, as well as the instrument/unique regressor and the unmeasured confound, are all normally distributed. The instrument/unique regressor, and the covariates are all uncorrelated with each other and exogenous to the equation errors. The model R²s are quite high relative to values commonly observed in psychological research: .88 for the selection model and .67 for the substantive equation (see the online supplemental material for these computations). Similarly, the treatment, selection, and instrument/unique regressor effects, when present, are reasonably strong. Real-world empirical analyses are not typically characterized by such favorable conditions. However, the key point of the simulation is to reveal how these techniques perform when their assumptions are met versus when they are egregiously violated.

The various parameter combinations of the simulation resulted in two treatment distributions × two error distributions × two selection conditions × two instrument/unique regressor conditions × two treatment conditions × three sample sizes = 96 different simulation conditions. For each simulation condition, I drew 2,000 samples, a number of replications that is typical for Monte Carlo studies (Fan, Felsovalyi, Sivo, & Keenan, 2002). I then estimated Equation 2 via OLS, IVR, and HSM in each one, while also testing for endogeneity with the tests embedded in IVR and HSM. Maximum-likelihood estimation was used instead of the two-step procedure throughout for estimation of the HSM model, due to its superior performance in prior simulations (Bhattacharya et al., 2006; Chiburis et al., 2012; Nawata, 2004). SAS Version 9.1 was used throughout, with PROC REG, PROC SYSLIN and PROC QLIM employed to test, respectively, OLS, IVR, and HSM models. (SAS code for SYSLIN and QLIM, as well as for the IVR test of endogeneity, is shown in the online supplemental material.).

Criteria for Evaluating the Estimates and Tests

The 2,000 replications of each simulation condition provided an estimate of the sampling distribution of d̂ under OLS, IVR, and HSM. They also enabled estimation of the power of the tests for endogeneity under IVR and HSM. Estimates of d were evaluated by examining three different criteria over the 2,000 replications: the mean of d̂, the mean-square error (MSE) of d̂, and the power of the test for the treatment effect. The mean of d̂ affords an assessment of the degree to which it is characterized by bias; the closer this mean is to d, the less biased it is. Although unbiased estimators are desirable, the more important criterion in many contexts is MSE. The MSE for d̂ is defined as E(d̂ – d)² (Bickel & Doksum, 1977). MSE equals the average square distance between the estimator and the parameter it is meant to estimate and thus reflects how close the estimator is, on average, to the actual parameter. An unbiased estimator merely assures that, over repeated samples from the same population, the estimator is, on average, equal to the parameter. On the other hand, a small MSE suggests that, in any given sample, the estimator is close to the actual parameter value. MSE is equal to the variance of an estimator plus the square of its bias (Bickel & Doksum, 1977). For consistent estimators, MSE converges to zero as the sample size increases without bound. Smaller values of MSE indicate a more accurate estimate in any given sample.

The power of a test is the probability that it will lead to rejection of the null hypothesis under the condition that the parameter equals a particular value (Bickel & Doksum, 1977). Power values of .80 or higher are considered desirable when the null hypothesis is false (Cohen, 1988). When the null hypothesis is true, power is synonymous with the alpha level for the test, which is nominally .05 (Bickel & Doksum, 1977), p. 167). For a particular test of the treatment effect or test of endogeneity, power was figured as the proportion of the 2,000 tests having a p value less than or equal to .05. I refer to this proportion as the rejection rate. Several of the HSM tests with N = 50 produced estimates of zero for the standard error of ρ̂. In that case, the test of endogeneity was a missing value. In such cases, the test was considered nonsignificant. This was exclusively a small-sample problem. It was at its worst under the condition of treatment and unique regressor effects but no unmeasured confounding, 15% in the treatment group, normal errors, and N = 50. In this scenario, fully 78% of the tests of endogeneity were missing. However, the problem cleared up with greater sample size, such that at most .65% of tests were missing at N = 250 and none were missing at N = 2,000.

Outcome of the Simulation

To conserve space, I show only the MSE and power results below, as the bias of the treatment estimator is incorporated into the MSE measure. (The bias results, in the form of figures displaying treatment-estimate means, are available in the online supplement to this article.) Figures 2 through 4 present trellis plots of the MSE results for the conditions in which a treatment effect is actually present (figures for the conditions in which the treatment effect is absent are virtually identical to these and so are not shown here but are available in the online supplemental material). Each figure depicts the MSE values for—from left to right—OLS, IVR, and HSM estimates of the treatment effect under particular conditions of the simulation. Each “cell” of the trellis plot shows the MSE values for a particular simulation condition defined by treatment and error distributions as well as the presence or absence of the confound and the instrument. The first row of the column headings indicates distribution into treatment categories as being either symmetric (i.e., a 50–50 split; “Sym T”) or asymmetric (i.e., a 15–85 split; “Asym T”), and equation errors as being either normal (“Norm E”) or exponential (“Exp E”). The second-row heading indicates conditions in which the instrument is absent (“Inst A”; its coefficient is set to zero in the equation for $C_i^{\ast }$ or present (“Inst P”; its coefficient is set to 1.75 in the equation for $C_i^{\ast }$). It also indicates whether the confound (a_i) is absent (“Cnfd A”; both ζ₁ and ζ₂ set to 0) or present (“Cnfd P”; ζ₁ set at .75 and ζ₂ at 1.5). Thus the top row of figures represents the worst case simulation conditions where the treatment and error distributions were asymmetric, and the bottom row represents the ideal case where the treatment and error distributions were symmetric. MSE values greater than 2 were recoded to 2 in all figures. This was done to prevent large MSEs from distorting the scale of the plots.

Figure 2.

Simulation results for N = 50 with treatment effect present. Sym T = symmetric treatment condition; Asym T = asymmetric treatment condition; Norm E = normal errors; Exp E = exponential errors; Cnfd P = confound present; Cnfd A = confound absent; Inst P = instrument present; Inst A = instrument absent; MSE = mean square error; OLS = ordinary least squares; IVR = instrumental-variable regression; HSM = Heckman selection model.

Figure 4.

Simulation results for N = 2,000 with treatment effect present. Sym T = symmetric treatment condition; Asym T = asymmetric treatment condition; Norm E = normal errors; Exp E = exponential errors; Cnfd P = confound present; Cnfd A = confound absent; Inst P = instrument present; Inst A = instrument absent; MSE = mean square error; OLS = ordinary least squares; IVR = instrumental-variable regression; HSM = Heckman selection model.

Mean Square Error

Figure 2 shows MSE values for a sample size of 50. The most important conditions are those in which the confound is present and are shown in the third and fourth columns of the plot. MSEs are uniformly high in all conditions in these columns. The best performance from all three estimators is found in the bottom-rightmost plot, representing ideal conditions: an effective instrument, a symmetric treatment distribution, and normally distributed errors. Even here, however, MSE values are greater than 1 for all three estimators. OLS outperforms IVR, whose MSE is close to 2. HSM affords no improvement over OLS. In fact, OLS outperforms both IVR and HSM in all other conditions of the simulation at this sample size, as is readily gleaned from the plots.

Figure 3 presents plots for a sample size of 250. The third and fourth columns show that HSM, under some conditions, affords some advantage over the OLS estimator. In the bottom rightmost cell of the figure, illustrating ideal conditions, HSM shows a clear advantage over OLS in MSE values. IVR is also superior to OLS here, although not as good as HSM. In fact, HSM is superior to OLS in all conditions of the fourth column except the topmost. The latter is that in which both asymmetry of treatment distribution and nonnormality of equation errors are present. There OLS is clearly superior to the other estimators. When the instrument is absent (third column of the figure), HSM outperforms OLS in the two conditions involving normal errors; otherwise, OLS is superior to HSM. The degradation in the performance of IVR under instrument ineffectiveness comes as no surprise.

Figure 3.

Simulation results for N = 250 with treatment effect present. Sym T = symmetric treatment condition, Asym T = asymmetric treatment condition; Norm E = normal errors; Exp E = exponential errors; Cnfd P = confound present; Cnfd A = confound absent; Inst P = instrument present; Inst A = instrument absent; MSE = mean square error; OLS = ordinary least squares; IVR = instrumental-variable regression; HSM = Heckman selection model.

Figure 4 shows MSE plots for a sample size of 2,000. Here we begin to see a pronounced advantage of using IVR and HSM when there is an effective instrument. The fourth column of Figure 4 shows that both IVR and HSM improve on OLS regardless of treatment or error distributions. However, under asymmetry of treatment distribution and error nonnormality, IVR and HSM are only slightly better than OLS. Otherwise, IVR and HSM have substantially smaller MSEs than the OLS estimator, with HSM slightly superior to IVR in all conditions. The third column shows the effect of unmeasured heterogeneity on estimators when the instrument is ineffective. Without an instrument, the performance of IVR is especially poor. The HSM estimator, on the other hand, has a smaller MSE than OLS in all conditions except that in which asymmetry of treatment and nonnormal errors are both operating. It is also noteworthy that, at this sample size, even without unobserved heterogeneity (the first two columns), the HSM estimator is virtually as accurate as OLS provided that errors are normally distributed.

Statistical Power

Figures 5 through 10 present plots of power values for tests of the treatment effect based on OLS, IVR, and HSM estimators (labeled OLS, IVR, and HSM, respectively), as well as for tests of endogeneity based on IVR and HSM (labeled IVE and HME, respectively). From left to right, the bars represent the values for OLS, IVR, HSM, IVE, and HME. Column headings indicating treatment conditions are identical to those in Figures 2–4. Two additional horizontal bars on the plots are drawn to indicate the criterion values of .80 and .05, as discussed earlier. Figures 5,7, and 9 show power values when there is a treatment effect present, while Figures 6, 8, and 10 show comparable values (i.e., power values for detecting the unmeasured confound, rejection rates for the null hypothesis of no treatment effect) when there is no treatment effect present.

Figure 5.

Simulation results for N = 50 with treatment effect present. Sym T = symmetric treatment condition; Asym T = asymmetric treatment condition; Norm E = normal errors; Exp E = exponential errors; Cnfd P = confound present; Cnfd A = confound absent; Inst P = instrument present; Inst A = instrument absent; MSE = mean square error; OLS = ordinary least squares; IVR = instrumental-variable regression; HSM = Heckman selection model; IVE = endogeneity based on IVR; HME = endogeneity based on HSM.

Figure 10.

Simulation results for N = 2,000 with treatment effect absent. Sym T = symmetric treatment condition, Asym T = asymmetric treatment condition, Norm E = normal errors, Exp E = exponential errors, Cnfd P = confound present, Cnfd A = confound absent, Inst P = instrument present, Inst A = instrument absent. MSE = mean square error; MSE = mean square error; OLS = ordinary least squares; IVR = instrumental-variable regression; HSM = Heckman selection model; IVE = endogeneity based on IVR; HME = endogeneity based on HSM.

Figure 7.

Simulation results for N = 250 with treatment effect present. Sym T = symmetric treatment condition, Asym T = asymmetric treatment condition, Norm E = normal errors, Exp E = exponential errors, Cnfd P = confound present, Cnfd A = confound absent, Inst P = instrument present, Inst A = instrument absent. MSE = mean square error; OLS = ordinary least squares; IVR = instrumental-variable regression; HSM = Heckman selection model; IVE = endogeneity based on IVR; HME = endogeneity based on HSM.

Figure 9.

Simulation results for N = 2,000 with treatment effect present. Sym T = symmetric treatment condition, Asym T = asymmetric treatment condition, Norm E = normal errors, Exp E = exponential errors, Cnfd P = confound present, Cnfd A = confound absent, Inst P = instrument present, Inst A = instrument absent. MSE = mean square error; MSE = mean square error; OLS = ordinary least squares; IVR = instrumental-variable regression; HSM = Heckman selection model; IVE = endogeneity based on IVR; HME = endogeneity based on HSM.

Figure 6.

Simulation results for N = 50 with treatment effect absent. Sym T = symmetric treatment condition, Asym T = asymmetric treatment condition, Norm E = normal errors, Exp E = exponential errors, Cnfd P = confound present, Cnfd A = confound absent, Inst P = instrument present, Inst A = instrument absent. MSE = mean square error, OLS = ordinary least squares; IVR = instrumental-variable regression; HSM = Heckman selection model; IVE = endogeneity based on IVR; HME = endogeneity based on HSM.

Figure 8.

Simulation results for N = 250 with treatment effect absent. Sym T = symmetric treatment condition, Asym T = asymmetric treatment condition, Norm E = normal errors, Exp E = exponential errors, Cnfd P = confound present, Cnfd A = confound absent, Inst P = instrument present, Inst A = instrument absent. MSE = mean square error; OLS = ordinary least squares; IVR = instrumental-variable regression; HSM = Heckman selection model; IVE = endogeneity based on IVR; HME = endogeneity based on HSM.

Figures 5 and 6 present results for a sample size of 50. The third and fourth columns of Figure 5 show the key conditions: cases in which both a treatment effect and an unmeasured confound are operating. The first thing to notice is that power for detecting unmeasured heterogeneity is uniformly low. Neither of the tests of endogeneity reaches even the .50 value, let alone the criterion of .80, although HSM's test has greater power than that of IVR. Similarly, power values for the test of a treatment effect in columns 3 and 4 suggest that, although HSM has substantially more power than IVR, neither technique reaches the .80 criterion. HSM comes closest, at a value of about .60 for the conditions in which error distributions are normal, whether the instrument is present or not. Figure 6 shows the situation in which no treatment effect is actually present. Columns 3 and 4 of the figure again reveal the key results. Power is uniformly low (<.50) for detecting endogeneity in any case. On the other hand, the rejection rate for tests of the treatment effect should be held at .05. In this regard, IVR is superior to HSM: its Type I error rates for the test of a treatment effect are lower than those of HSM in all conditions of the simulation.

Figures 7 and 8 present results for N = 250. Tests for endogeneity are clearly better at this sample size, as a glance at the third and fourth columns of Figure 7 shows. Thus, when both treatment effect and unmeasured confound are present, the test in HSM has power >.80 for detecting endogeneity in the ideal case of symmetric treatment distribution and normal errors (bottom rightmost cell of the figure). Otherwise power approaches .70 for the Heckman endogeneity test as long as the errors are normally distributed, with or without an instrument present. However, the IVR's test of endogeneity never reaches even this level of power. With an effective instrument, symmetric treatment distribution, and normally distributed errors, HSM also turns in adequate power for a test of the treatment effect, as is seen in the bottom rightmost cell of the figure. Otherwise, the performance of IVR and HSM with respect to power for detecting a treatment effect in the presence of a confound at this sample size is not particularly impressive. Figure 8 shows what happens when there is no actual treatment effect. In column 4 of the plot, once again HSM's test of endogeneity has adequate power only with a symmetric treatment distribution and normal errors. The power of IVR's test of endogeneity, however, is never adequate. On the other hand, columns 3 and 4 reveal, once again, that IVR is better than HSM at holding down the rejection rate of the test for a treatment effect to approximately the .05 level when the treatment effect is nil.

Figures 9 and 10 show that IVR and HSM turn in improved performance with respect to power with a large enough sample size, in this case, an N of 2,000. As column 4 of Figure 9 shows, power for detecting an unmeasured confound is adequate for both IVR and HSM provided there is an instrument present and asymmetric treatment is not combined with nonnormal errors. As in other cases, power in the Heckman procedure is generally superior to its counterpart from IVR. In the ideal condition (bottom rightmost cell) in which distribution into treatment is symmetric and errors are normal, both IVR and HSM have power values of 1.00 for detecting endogeneity. The third column of the figure makes it clear that, even with an ineffective instrument, HSM has good power to detect endogeneity when the errors are normal. Power values are 1.00 regardless of the treatment distribution. Tests for the treatment effect have good power in most conditions provided the instrument is effective (column 4). However, when treatment skew is combined with nonnormal errors, only HSM's power for detecting a treatment effect approaches adequacy. When the instrument is not effective (column 3), only HSM has good power to detect a treatment effect. But this only holds when treatment skew is not combined with nonnormal errors. Finally, Figure 10 depicts power results when there is no actual treatment effect. Columns 3 and 4 show that the Heckman approach has good power to detect endogeneity provided the error distributions are normal. If there is an effective instrument, HME is also good at detecting endogeneity with nonnormal errors provided that the treatment distribution is not also skewed. The test of endogeneity provided by IVR is only adequate with an effective instrument and only in the ideal scenario of symmetric treatment distribution and normal errors. As before, however, the IVR is superior to the HSM at keeping the rejection rate for the test of a treatment effect down to approximately the .05 level. This is particularly noticeable in the first and third rows of the third and fourth column figures, that is, conditions in which the error distributions are nonnormal.

In sum, both techniques introduced here should be considered large-sample techniques. As the figures show, the performance of IVR and HSM was uniformly poor with an N of 50 and only somewhat better with an N of 250. Only with an N of 2,000 did the techniques really show clear advantages over OLS with respect to either MSE or power. And my results are consistent with other simulations (Bhattacharya et al., 2006; Chiburis et al., 2012) in showing the superiority of HSM over IVR. It outperformed IVR with respect to both MSE and power except when there was no treatment effect. In that case, IVR was superior in keeping the rejection rate for the test of a treatment effect close to the .05 level. On the other hand, when error nonnormality was combined with a skewed distribution of the treatment variable, neither technique performed well.

Of the two, the HSM should nevertheless be given more weight in both the detection of endogeneity and in the test for a treatment effect in the presence of endogeneity, based on these simulation results. However, the HSM should be used with caution. Many methodologists would not recommend using any procedure based on power that did not also control Type I error. As was evident, with smaller sample sizes or in conditions in which equation errors were markedly nonnormal, HSM was noticeably deficient in this regard. This finding suggests that use of the Heckman procedure comes at a potentially higher danger of rejecting a true null hypothesis than is desirable. Next, I illustrate how to apply these techniques to a substantive research problem.

An Empirical Application Using the GSS

Research Question

To illustrate the application of IVR and HSM, I used data from the General Social Survey (GSS). This is a national probability-sample survey of U.S. noninstitutionalized adults that has been conducted approximately every other year since 1972. Each year's sample is an independently sampled cross-section of the population (although a panel component was added in 2008). Triangulating IVR and HSM with OLS, I hoped to demonstrate how researchers can utilize these techniques to discern whether unmeasured heterogeneity is confounding their analyses. The research question here is the extent to which marriage affects psychological well-being.

Does marriage lead to greater psychological well-being, compared with being unmarried? This issue has been investigated in countless studies (Brown 2000; Brown, Bulanda, & Lee, 2005; Frech & Williams, 2007; Gove, Hughes, & Style, 1983; Horwitz, White, & Howell-White, 1996; Kim & McKenry, 2002; Lamb, Lee, & DeMaris, 2003; Marks, 1996; Simon, 2002; Zimmermann & Easterlin, 2006). There are reasons to suspect that it does. Marriage entails what Cherlin (2009, p. 138) refers to as “enforceable trust.” It involves a public commitment to enter into a potentially lifelong, caring relationship with one's partner. As it is a legally enforceable commitment, it requires substantially more effort to sunder than, say, a cohabiting relationship. Therefore, the married can be relatively secure in their spouse's obligation to support them both financially and emotionally in times of need. They also have regular access to a confidant, a companion, and a sexual partner. All of these elements may contribute to a feeling of subjective well-being (Horwitz et al., 1996; Kim & McKenry, 2002; Marks, 1996). On the other hand, any apparent marriage effect on well-being could well be the result of selection bias. In particular, those who are initially more psychologically healthy may be more attractive marriage partners than others. Therefore, preexisting subjective well-being may facilitate both getting and staying married, along with subsequent well-being (Horwitz et al., 1996; Lamb et al., 2003; Simon, 2002).

The association between marital status and psychological well-being is well documented. Cross-sectional studies typically find that the married are happier, more satisfied with life, and in better mental health than the unmarried (e.g., Brown et al., 2005; Gove et al., 1983). Longitudinal studies are further able to show that becoming married is associated with a reduction in depressive symptomatology or an increase in happiness (Frech & Williams, 2007; Horwitz et al., 1996; Kim & McKenry, 2002; Lamb et al., 2003; Simon, 2002; Zimmermann & Easterlin, 2006). Moreover, loss of the spouse is associated with an increase in depression and alcohol problems (Simon, 2002) or a decrease in life satisfaction (Zimmermann & Easterlin, 2006). Some researchers have found that the marriage advantage is stronger for men (Gove et al., 1983). However, others have found that both sexes benefit equally from entry into marriage, and both suffer equally from exiting marriage (Horwitz et al., 1996; Simon, 2002). Although some evidence for the selection of the psychologically better adjusted into marriage has been uncovered, it does not typically account for the entire marriage advantage (Horwitz et al., 1996; Simon, 2002). Other studies have found no evidence for a selection of the psychologically healthier into marriage (Kim & McKenry, 2002; Lamb et al., 2003; Zimmermann & Easterlin, 2006). And at least one study found an inverted selection effect for women, based on enduring personal characteristics measured in their teen years. In Marks' (1996) analysis of the Wisconsin Longitudinal Study, separated/ divorced and never-married women in later years of the survey were more intelligent and open to new experience than married women.

Current Example

To investigate the effect of marital status on well-being, I used data from the 2006, 2008, and 2010 GSS. I limited the sample to respondents who were married, never married, divorced, or separated. I excluded widowed individuals, as others have done (Simon, 2002; Zimmermann & Easterlin, 2006) because arguments about selection into marriage have emphasized unmeasured characteristics leading to the ability to get and stay married (e.g., Horwitz et al., 1996). As widowhood is a nonvoluntary transition out of marriage, such a selection process would not apply to the widowed. In all likelihood, any effect of marriage on well-being would be underestimated in this study because many of those identified as never married or divorced/separated are cohabiting unmarried with an intimate partner. However, studies have shown that cohabitation does not provide the same level of psychological benefits that marriage does (Brown, 2000; Brown et al., 2005; Lamb et al., 2003; but see Zimmermann & Easterlin, 2006, who found no difference between the cohabitation vs. marriage advantage in mental health in a German sample). Therefore, it makes sense to distinguish the legally married from everyone else. I further employed listwise deletion to address missing data by excluding any respondents who were missing on any of the study variables. A total of 2,621 respondents were available in the final sample.

The outcome variable was the sum of three items from the GSS tapping well-being. The first was “Taken all together, how would you say things are these days—would you say that you are very happy, pretty happy, or not too happy?” Responses of very, pretty, and not too happy were coded 1, 2, and 3, respectively. The second question was “In general, do you find life exciting, pretty routine, or dull?” Responses of exciting, pretty routine, and dull were coded 1, 2, and 3, respectively. The third question was “Would you say your own health, in general is excellent, good, fair, or poor?” Responses of excellent, good, fair, and poor were coded from 1 to 4, respectively. Because these items were in different metrics, they were standardized first, and then summed, with higher scores reflecting greater subjective life distress. Cronbach's alpha for the scale was .52.

The “treatment” indicator is a dummy variable for being married versus being unmarried. As the simulation showed, IVR and HSM produced the best results under a symmetric treatment distribution. In the present case, 51% of respondents were currently married and 49% were not. This qualifies as an approximately symmetric distribution. If the treatment variable is originally binary, there may be little the analyst can do to correct excessive skew. But if the treatment originally has several treatment conditions, the analyst may be able to collapse categories to achieve a more symmetric treatment indicator. Optimum results in the simulation also obtained when the errors in Equations 1 and 2 were normally distributed. The error distribution in the equation for the unmeasured propensity for assignment to treatment (Equation 1) cannot be examined. However, the error distribution for the substantive model can be examined (see later discussion). And to ensure that such distribution is approximately normal, the analyst can first check the distribution of the outcome variable. The life distress scale was somewhat right-skewed, with a skewness coefficient of .31. Greater symmetry could be achieved by transforming the scale. As the metric of the scale is arbitrary, any monotonic transformation could be used. I chose to utilize a transformation from the family of power transformations (Hoaglin, Mosteller, & Tukey, 1983). After experimenting with a few transformations, I found that raising (life distress + 3.5) to the power of .85 provided a good approximation to symmetry (skew coefficient = .02). Because the metric of life distress is not particularly meaningful in its original form, that the coefficient for the treatment effect in the transformed version also has no interpretable metric is not particularly consequential. Transforming the response variable inevitably implies a transformation of the associated model. As a result, coefficients for the regression of the transformed response may not lend themselves to ready interpretation. If preserving the original metric is especially important, transformation may not be an option. See Cook and Weisberg (1999), however, for additional suggestions regarding transformations to achieve normality.

Control variables for the analysis included age, education (in years of schooling completed), a dummy variable for female gender, income (ordinally scaled from 1 for under $1,000 to 25 for $150,000 or over), and dummy variables for being Black or of another race (with White as the reference group). I examined the GSS in the hopes of finding a good instrumental variable for marital status. Recall that the ideal instrument would be a regressor that has an effect on the substantive outcome only via its effect on treatment status, and otherwise has no effect on the outcome controlling for treatment status. It should also be uncorrelated with any other covariate in the analysis, as well as uncorrelated with the equation error. The search for an ideal instrumental variable proved fruitless; no random events that might influence marital status were available in the data set. However, a unique predictor of marital status was also required for the HSM, and it did not have to meet such stringent requirements. I therefore decided to use for both purposes the variable parent absence. This was based on the question “Were you living with both your own mother and father around the time you were 16? IF NO: With whom were you living around that time?” Parent absence was coded 0 if the respondent answered “own mother and father” and 1 if the respondent gave any other response. Thirty-three percent of respondents were not living with both biological parents, and of these, 80% were living with either their father or their mother (with or without a stepparent). Most parent absence was probably the result of a divorce or separation. In all likelihood, exposure to marital dissolution at this stage of respondents' development negatively impacted their view of marriage. They should therefore be less likely to marry, compared with those growing up in an intact home.

Table 1 presents the results of OLS, IVR, and HSM models applied to the data. As Wooldridge (2003) noted, the requirement that the instrument (or unique predictor of treatment for the HSM model) be a predictor of treatment is easily checked. Model 1 shows the OLS estimates for the regression of being married on model covariates and parent absence. As is evident, net of the other covariates, parental absence is associated with a significantly lower likelihood of being married (p = .002). The size of this effect can be calculated, as demonstrated earlier, by dividing it by the standard deviation of the response, which is the square root of 0.51 × 0.49, or 0.50. The effect size for parental absence is therefore −0.06/0.50 = −0.12. In Cohen's parlance, this is a small effect, and, in fact, considerably smaller than the effect size of .49 for the instrument in the simulation. Nevertheless, the requirement in question is satisfied. However, as Morgan and Winship (2007) made clear, the exclusion restriction is not empirically testable. Despite that, it is worth investigating whether the instrumental variable is a predictor of the outcome when treatment is controlled. As the instrument is also used in the HSM as a unique predictor of treatment status, it is desirable that it does not also belong in the substantive model. Otherwise, that model is misspecified by its exclusion. Model 2 shows the OLS estimates for the regression of life distress on marital status and model covariates, as well as parent absence. It appears that parent absence can safely be excluded from this model, as its effect is not significant (p > .2).

Table 1. Regression Estimates (and Standard Errors) for Models of Marital Status and Life Distress.

Explanatory variable	Model 1a	Model 2b	Model 3b	Model 4c	Model 5d
Intercept	0.17**	4.26***	4.32***	4.46***	4.43***
(SE)	(0.06)	(0.18)	(0.17)	(0.22)	(0.19)
Married		−0.57***	−0.58***	−1.75†	−1.51*
(SE)		(0.06)	(0.06)	(1.06)	(0.60)
Age	0.01***	0.01***	0.01***	0.02*	0.02***
(SE)	(0.00)e	(0.00)e	(0.00)e	(0.01)	(0.00)e
Education	−0.00***e	−0.10***	−0.11***	−0.11***	−0.11***
(SE)	(0.00)e	(0.01)	(0.01)	(0.01)	(0.01)
Female	−0.01	0.01	0.01	0.00e	0.01
(SE)	(0.02)	(0.06)	(0.06)	(0.07)	(0.06)
Income	0.01***	−0.02***	−0.02***	−0.01	−0.01
(SE)	(0.00)e	(0.01)	(0.01)	(0.01)	(0.01)
Black	−0.21***	0.17†	0.19*	−0.08	−0.02
(SE)	(0.03)	(0.09)	(0.09)	(0.25)	(0.16)
Other race	0.01	0.14	0.14	0.16	0.15
(SE)	(0.03)	(0.09)	(0.09)	(0.10)	(0.10)
Parent absence	−0.06***	0.08
(SE)	(0.02)	(0.06)
Endogeneity IVR (β̂)				1.18
(SE)				(0.99)
Endogeneity HSM (ρ̂)					0.38†
(SE)					(0.22)
R2	0.09	0.10	0.10	0.07

Note. N = 2,621 respondents. SE = standard error; IVR = instrumental-variable regression; HSM = Heckman selection model.

^aOrdinary least squares (OLS) regression for being married.

^bOLS regression for life distress.

^cInstrumental-variable regression for life distress.

^dHeckman selection model for life distress.

^eCoefficient is less than .005 in absolute value.

^†p < .10.

^*p < .05.

^**p < .01.

^***p < .001.

Model 3 presents the OLS results for the substantive model, regressing life distress on marital status and controls. Being married (the “treatment”) is associated with a significantly lower level of life distress, compared with being unmarried, consistent with past research. And this effect is invariant with respect to gender. A test for the interaction of being married with gender (not shown) proved to be nonsignificant (p> .3); moreover the effect of being married was negative and significant among both women and men (also not shown). At this point, one should examine the equation errors to see whether they are approximately normal. Figure 11 shows the residuals from this model. According to the Cramer-von Mises or Anderson-Darling tests for normality provided in PROC UNIVARIATE in SAS (not shown; see D'Agostino & Stephens, 1986), the distribution is significantly nonnormal. Nevertheless, the plot suggests a reasonably symmetric distribution (skewness = −.06; not shown) that approximates a normal shape. Therefore, the performance of IVR and HSM may not be too seriously degraded.

Figure 11.

Residuals from ordinary least squares (OLS) regression of life distress on model predictors.

Model 4 presents the IVR regression for life distress. The endogeneity test is nonsignificant (p > .2), suggesting that unmeasured heterogeneity is not at work. The positive sign of β̂ indicates that if it were present, it would be opposite to expectation: those who are more likely to marry are also those who are potentially more distressed. Controlling for any unmeasured heterogeneity, the married are marginally less distressed than others. Model 5 shows the HSM estimates. In this case, there is more evidence of unmeasured confounding, as ρ̂ is marginally significant (p < .09). Again, and consistent with other research (Marks, 1996), its positive sign suggests inverted selectivity: those more likely to marry are also more prone to life distress. Controlling for the unmeasured heterogeneity, being married is significantly associated with a lower average level of distress (p < .02). That there is a marriage advantage net of control variables for selection into marriage is consistent with most prior research (Brown 2000; Brown et al., 2005; Frech & Williams, 2007; Gove et al., 1983; Horwitz et al., 1996; Kim & McKenry, 2002; Lamb et al., 2003; Marks, 1996; Simon, 2002; Zimmerman & Easterlin, 2006).

Causal Inference: Issues and Controversies

The current findings agree with much previous research in suggesting that being married is associated with greater subjective well-being. We could simply leave it at that. That is, we can be content with demonstrating a partial association between marriage and subjective well-being, net of measured covariates as well as unmeasured confounding. And we can leave it to others to ferret out whether the effect of marriage is actually causal, as opposed to just an association that might yet be accounted for by some other factor. We could also say that our results are consistent with marriage having a causal effect on subjective well-being. However, the estimation of causal effects is a primary goal of most research in the social and behavioral sciences (Allison, 2009; Angrist & Pischke, 2009; Davis, 1985; Rubin, 1974). Therefore, we might wish to declare that −0.58 (Model 3 in Table 1) or −1.51 (Model 5 in Table 1) is an estimate of the causal effect of marriage on subjective well-being. This much stronger statement would be both controversial and unwarranted, for several reasons. First, consider what is meant by a “causal effect.”

Rubin's causal paradigm is commonly accepted across the sciences as the reigning definition of a causal effect (Angrist & Pischke, 2009; Morgan & Winship, 2007; Rubin, 2010; Schafer & Kang, 2008). In words, it is the difference, for a given individual, of that person's response under the treatment condition versus that same person's response under the control condition. As a person can only be in one or the other condition, a causal effect is unobservable, as is the average causal effect (ACE), which is the average of all such causal effects for the population of interest (Rubin, 2010; Schafer & Kang, 2008). Unbiased estimation of the ACE is possible, however, under some stringent conditions. First, the stable unit treatment value condition requires that there be no hidden versions of treatments. That is, there is only one version of the treatment that is uniformly applied to all units (Rubin, 2010). Additionally, the condition stipulates that there must be no interference between treatments. This means that any given person's response to the treatment or control condition is unaffected by the treatment/control condition received by any other unit (Rubin, 2010). For the treatment of marriage, these conditions would appear to be satisfied. Second, the strong ignorability condition requires that the mechanism through which people are assigned to treatment or control conditions is independent of the potential responses to these conditions, given measured covariates (Rubin, 2010; Schafer & Kang, 2008). That is, there is no unmeasured propensity for those who would respond more or less favorably to treatment to be assigned to the treatment, as opposed to the control, condition. In addition to including important covariates, addressing unmeasured confounding—via, say the IVR or HSM—is a strategy for attempting to ensure strong ignorability. In the current application, IVR and HSM produced no evidence for selection of the psychologically healthier people into marriage. The marginal evidence found for selection of the psychologically less healthy into marriage, on the other hand, would, if anything, only suppress a marriage advantage.

Unfortunately, there are still several reasons for caution in attributing a causal interpretation to the “marriage advantage” in the present application. First, as we have seen through simulation results, IVR and HSM are very susceptible to the failure of their assumptions. The “instrument” used here is not equivalent to random assignment, for example. The error term in the substantive equation is not really normally distributed. The tenability of joint normality for the equation errors of the selection and substantive models in HSM is even more in question. However, even were the assumptions for IVR and HSM met, there are several other reasons for caution. First, the causal priority of marital status over subjective well-being must be tenable. That getting married would bring about an improvement in well-being is at least theoretically reasonable. This argument is strengthened to the extent that mechanisms can be found that help to bring about the effect (Morgan & Winship, 2007; Shadish, Cook, & Campbell, 2002). For example, marriage supposedly results in a greater household income and the availability of a confidant and supportive mate. It also confers greater benefits than unmarried cohabitation because it is perceived as a more permanent arrangement (Horwitz et al., 1996). Studies have found evidence that having greater household income and the availability of a confidant account for some portion of the marriage advantage (Marks, 1996). And others have found that cohabitors' greater relationship instability accounts for their disadvantage vis a` vis married couples in depressive symptomatology (Brown, 2000). Nevertheless, reverse causation must be ruled out: subjective well-being should not be the cause of marital status. It is highly unlikely that current perceptions of happiness or health status cause current marital status. However, one could argue that preexisting happiness or health status does, because it affects one's attractiveness as a marital partner. Yet, this is the social selection argument that I was not able to find any evidence for using IVR and HSM. And the lack of support for such selectivity has been echoed by several other studies (Kim & McKenry, 2002; Lamb et al., 2003; Marks, 1996; Zimmermann & Easterlin, 2006).

If the causal priority of marital status over well-being is established, and if there is little evidence for unmeasured heterogeneity, what other limitations remain? There are two important ones. First, there is considerable measurement error in the response variable, life distress. Only slightly over half the variance in this measure is attributable to a stable trait. Although measurement error in the response does not necessarily bias the treatment effect estimate, it has other repercussions. In order to estimate the causal impact of marriage on well-being, we require a reliable and valid measure of psychological well-being. The poor reliability of the life distress measure used in this demonstration is a drawback in that regard.

Second, the use of listwise deletion to address missing-data problems has resulted in a very select sample. Excluding widows and widowers, there were a total of 7,854 respondents in the 2006–2010 years of the GSS. Only a third of those respondents were included in the current analysis. If the included respondents are a random subset of the 7,854, then the data would be missing completely at random, or MCAR, and the treatment estimate arrived at using listwise deletion would be unbiased (Allison, 2002). However, it is unlikely that the missing data are MCAR. If the probability of missingness on any variables is a function of the other observed measures included in the analysis, but not of the missing values themselves, then the data are said to be missing at random, or MAR (Allison, 2002; Fitzmaurice, Laird, & Ware, 2004). If this situation obtains, replacing missing data using multiple imputation would result in unbiased estimates of regression effects. Listwise deletion is robust to violation of MAR for the independent variables (see Allison's, 2002, for proof of this) but not for the dependent variable. Hence, if missing data on the response are only MAR, but not MCAR, then the treatment estimate based on listwise deletion is biased (Allison, 2002). In the worst case, if MAR is violated, such as when the probability of being missing is a function of the missing values themselves, then the missing data are said to be not missing at random, or NMAR (Fitzmaurice et al., 2004). This would obtain if, say, the likelihood of being missing on the life distress measure is greater for those who are more distressed. In that case, the missing-data mechanism itself must be modeled in order to achieve a good estimate of the treatment effect. Although there are techniques for modeling the missing-data mechanism, for example by employing the Heckit procedure (Greene, 2003; Heckman, 1979), they have not been employed here.

Conclusion

In this article, I have attempted to evaluate the efficacy of IVR and HSM methods to counteract unmeasured confounding in cross-sectional studies. Via simulation, I have shown that the methods can indeed provide good estimates of a treatment effect in the presence of unmeasured confounding when their assumptions are met. However, they can also go seriously awry when those assumptions are violated. I have also demonstrated how these techniques can be triangulated with OLS to detect and control for endogeneity in an actual substantive application. Of the two approaches presented here, HSM is clearly to be preferred over IVR. It outperformed IVR in the simulation with respect to both power and MSE in all conditions except when no treatment effect was present, and the sample was moderate or large. In these cases, IVR was superior at holding the rejection rate down to the nominal alpha level for the test of a treatment effect. I recommend that HSM be used as the primary technique, with IVR estimated for comparison purposes. Whether the regression estimate of the “treatment effect” is to be given a causal interpretation is up to the individual researcher. In most cases, when the treatment has not been randomly assigned, such an inference would be unwarranted. However, to provide an unbiased estimate of a partial association or to marshal evidence that is consistent with a causal effect of the treatment variable is nevertheless a contribution to knowledge. Despite the limitations of cross-sectional data in this enterprise, IVR and HSM can provide psychological researchers with additional tools for this purpose.