Validity Concerns with Multiplying Ordinal Items Defined by Binned Counts: An Application to a Quantity-Frequency Measure of Alcohol Use

Abstract

Social and behavioral scientists often measure constructs that are truly discrete counts by collapsing (or binning) the counts into a smaller number of ordinal responses. While prior quantitative research has identified a series of concerns with similar binning procedures, there has been a lack of study on the consequences of multiplying these ordinal items to create a desired index. This measurement strategy is incorporated in many research applications, but it is particularly salient in the study of substance use where the product of ordinal quantity (number of drinks) and frequency (number of days) items is used to create an index of total consumption. In the current study, we demonstrate both analytically and empirically that this multiplicative procedure can introduce serious threats to construct validity. These threats, in turn, directly impact the ability to accurately measure alcohol consumption.

Social science researchers often measure constructs representing an overall total value by multiplying individual quantity and frequency items. This multiplicative measurement strategy is present in a wide array of research applications. For example, in the study of gambling, total monetary expenditure has been estimated by multiplying the number of days gambled by the number of dollars spent per session and total time expenditure has been estimated by multiplying the number of days gambled by the number of hours per session (Dickerson, Baron, Hong, & Cottrell, 1996). In a more complicated example, Pecknold, Luthe, and Munjack (1993) measured a “panic factor” as the product of the number of panic attacks times the average duration of the attacks times the average intensity of the attacks.

Researchers also frequently measure constructs that are truly discrete counts by binning the counts into a smaller number of ordinal responses. This is particularly evident in the study of substance use. For example, leading funding agencies such as the National Institute on Alcohol Abuse and Alcoholism (NIAAA, 2003) recommend that the quantity and frequency of substance use be measured with collapsed counts. Further, substance use researchers routinely utilize the product of these ordinal quantity and frequency items to assess total levels of use and to test empirical theory.

This measurement strategy remains widely used in practice despite extensive quantitative research demonstrating that coarse categorization (or collapsing) alone can lead to negative consequences such as reduced effect size and power, loss of information on individual differences, and the possible introduction of spurious effects (e.g., Cohen, 1983; MacCallum, Zhang, Preacher, & Rucker, 2002; Taylor, West, & Aiken, 2006). While these consequences are important and can arise when collapsing counts into ordinal categories, here we focus on a unique set of concerns. More specifically, whereas prior research has addressed the costs of coarsely categorizing underlying continuous variables, our intent is to demonstrate the risks associated with multiplying two coarsely categorized underlying count, not continuous, variables. Although we motivate our work with the study of substance use, our conclusions apply to similar applications in which counts are binned into ordinal categories and multiplied.

To begin, consider a quantity-frequency (QF) measure of alcohol use for an individual who drank four times in the past month (frequency) and drank three drinks on each occasion (quantity) resulting in a total alcohol consumption of 12 drinks (Q × F = 3 × 4 = 12). Although this measurement strategy is potentially appropriate for open-ended count data (e.g., a participant freely reports any integer count value), for expediency and automation researchers often collect what are truly counts of quantity and frequency using participant reports on pre-defined ranges of collapsed counts (e.g., 1–3, 4–6, etc.). As we will demonstrate, this strategy can directly lead to significant threats to the construct validity of QF measures including overestimation actual alcohol consumption, inability to capture individuals’ relative ranks, and non-monotonic QF estimates that are not invariant across covariates. Our goal is to examine and demonstrate all of these threats in detail.

A central component to empirically testing any theory is construct validity. Construct validity refers to the degree to which a measure aligns with the theoretical construct of interest (Shadish, Cook, & Campbell, 2002). In alcohol research, construct validity pertains to the extent to which numerical alcohol consumption measures produce accurate and meaningful estimates of alcohol consumption. Understanding how various validity threats arise in the measurement of alcohol consumption is not obvious because measures are typically face valid (e.g., they appear to produce valid estimates; Shadish, et al., 2002). However, we will show that face validity does not necessitate construct validity and commonly used alcohol consumption measures can routinely produce invalid estimates.

Table 1 displays quantity (Q) and frequency (F) items that are reflective of those often used in practice. A typical QF measure estimates alcohol consumption by multiplying the mid-values of the selected quantity and frequency response categories (Dawson, 2003). For example, based on the measures in Table 1, if a person drank eight times in the past 30 days and usually had three drinks each occasion, their QF estimate would be 26.25 (Q_mid × F_mid = 3.5 × 7.5 = 26.25).

Table 1.

Quantity and frequency items and corresponding mid-values

Items	Mid-values
During the past 30 days, on how many days did you drink one or more drinks of an alcoholic beverage?” (F)
20 to 30 days	25
10 to 19 days	14.5
6 to 9 days	7.5
3 to 5 days	4
1 to 2 days	1.5
0 days	0
“On days that you drank during the past 30 days, how many drinks did you usually have?” (Q)
12 or more drinks	13
9 to 11 drinks	10
7 to 8 drinks	7.5
5 to 6 drinks	5.5
3 to 4 drinks	3.5
2 drinks	2
1 drink	1
0 drinks	0

Previous research has identified both strengths and weaknesses of total alcohol consumption measures (see Greenfield & Kerr, 2008 for a review). Studies have demonstrated that QF measures can underestimate consumption and inaccurately represent patterns of drinking, yet these measures remain widely used in practice because of their parsimony and minimal participant burden (Greenfield, 1986; Midanik, 1994; Rehm et al., 1999). Despite an extensive literature using comparative approaches to evaluate alcohol consumption measures (i.e., comparing QF measures to other modes of assessment), the potential consequences of multiplying mid-values of ordinal quantity and frequency items to estimate alcohol consumption has not been thoroughly investigated. This is our goal here.

In the current study, we first analytically demonstrate how multiplying ordinal quantity and frequency items can produce invalid estimates of alcohol consumption even under optimal circumstances. We then empirically show that the outlined validity threats arise in real data. Importantly, many of the issues highlighted in our study generalize to other measures reliant on the product of two ordinal items representing binned counts. We intentionally avoid fitting statistical models to the QF data. Instead, we focus on the properties of the QF measure itself. Our work is organized around four key issues.

1. Overestimation of Alcohol Consumption

It is straightforward to mathematically demonstrate that multiplying ordinal quantity and frequency items can overestimate alcohol consumption. This overestimation will occur when the category mid-values represent upwardly biased measures of central tendency. By definition, quantity and frequency measures are scaled as discrete counts (1 drink, 2 drinks, etc.). Typically, counts are assumed to follow either a Poisson or negative binomial (NB) distribution (Hilbe, 2011). The NB distribution extends the Poisson distribution by adding an additional dispersion parameter. The probability mass function for the negative binomial distribution is:

$$P(Y=y)=\frac{\mathrm{\Gamma }(y+{\alpha }^{-1})}{\mathrm{\Gamma }({\alpha }^{-1})\mathrm{\Gamma }(y+1)}{(\alpha \mu )}^y{(1+\alpha \mu )}^{-(y+{\alpha }^{-1})},y=0,1,2,\dots$$ (1)

where Γ is the gamma function, μ is the mean, and α is the dispersion parameter. The variance of the negative binomial distribution is μ(1 + αμ). The NB dispersion parameter allows the mean and variance of the distribution to differ (the equality of which is a stringent restriction of the Poisson). As a result, the NB distribution is usually more consistent with the characteristics of data collected in the social and behavioral sciences, including alcohol use.

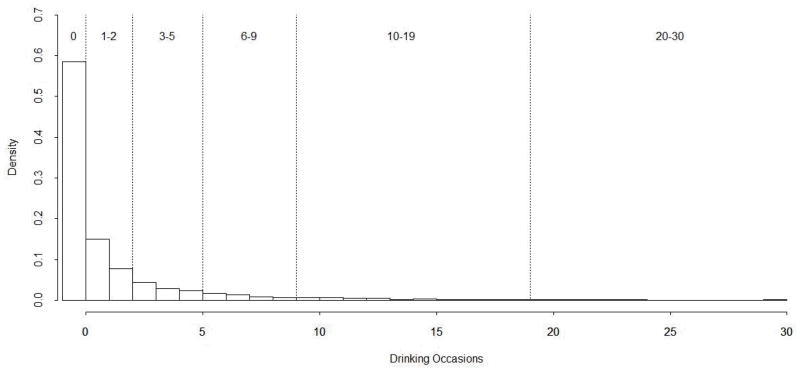
At lower mean levels of alcohol use (as is typical in alcohol research, especially with children and adolescents), these count distributions are commonly positively skewed. Figure 1 displays n=5,000 artificially simulated responses randomly drawn from a NB distribution that are reflective of alcohol frequency data often obtained in practice. The vertical lines in Figure 1 represent the cut-points for the ordinal categories of the frequency item in Table 1 and the numbers above designate the ranges of binned counts. Within each ordinal category there is a positively skewed distribution of counts. Thus, category mid-values will be greater than any standard measure of central tendency (e.g., mode, median, mean) and systematically overestimate the frequency of alcohol use. This issue also applies to quantity of use, which tends to be positively correlated with frequency. Thus, the multiplication of upwardly biased quantity and frequency mid-values results in measures of total alcohol consumption that are routinely overestimated.

Figure 1.

Artificially simulated alcohol frequency data. The vertical lines represent cut-points for the ordinal categories defined by the Frequency item in Table 1.

2. Shifts in Relative Ranks of Alcohol Consumption

All statistical models must assume that the relative ranking of measures is valid across individuals. However, multiplying ordinal quantity and frequency items commonly produces shifts in individuals’ relative ranks of total alcohol consumption. In other words, individuals who consume more alcohol can receive smaller QF estimates than individuals with less consumption. Consider a simple scenario in which we know the exact number of drinks each of two individuals consumed over a 30 day period. Person A drank ten times in the past 30 days (F) and consumed three drinks each time (Q) resulting in 30 drinks (Q × F = 3 × 10 = 30). Person B reported drinking nine times (F) and consuming four drinks each time (Q) resulting in 36 drinks (Q × F = 4 × 9 = 36). Clearly, person B consumed a larger number of drinks than person A over the same period of time. However, if we were to estimate alcohol consumption using the QF measure in Table 1, we would obtain a rank reversal for these two individuals. That is, person A would receive a higher QF estimate than person B (person A’s QF estimate = 3.5 × 14.5 = 50.75; person B’s QF estimate = 3.5 × 7.5 = 26.25) even though person B consumed more drinks.

The ubiquity of relative rank reversals is salient in Figure 2 which depicts the ranges of possible actual consumption that fall within given QF estimates using the quantity and frequency items from Table 1¹. The horizontal axis represents actual consumption and the vertical axis represents the corresponding ordinal QF estimates. The staggered horizontal lines denote the possible ranges of actual consumption that fall within the specific QF estimates. Overlapping horizontal lines at specific levels of actual consumption (e.g., a vertical line could be drawn on the plot that intersect more than one horizontal line) signify points at which individuals can reverse relative ranks. For instance, the horizontal lines for QF estimates of 15 and 30 overlap indicating that it is possible for person A to drink less than person B, but obtain a QF estimate over twice as large. Indeed, this threat is very likely to happen when using mid-values of ordinal items to estimate alcohol consumption.

Figure 2.

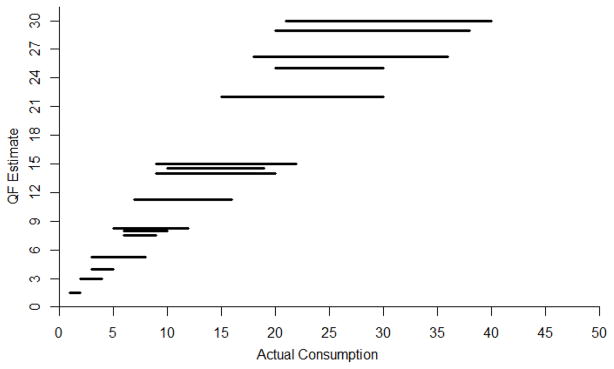
Overlapping distributions of actual alcohol consumption across QF estimates. The horizontal axis represents actual consumption and the vertical axis represents the corresponding ordinal QF estimates. The staggered horizontal lines denote the ranges of actual consumption that can fall within the QF estimates. For simplicity, only QF estimates ≤ 30 are displayed.

3. Non-Monotonic QF Estimates

All statistical models must assume that numerical estimates of alcohol consumption are monotonically ordered such that an estimate of two drinks is greater than one, three drinks greater than two, and so on. However, logically extending what we know about shifts in individuals’ relative ranks, we can also show that consumption measures based on ordinal quantity and frequency items may not meet this assumption. It is important to note that the threat of shifts in individuals’ relative ranks is distinct from the threat of non-monotonic QF estimates. In order to have non-monotonically ordered QF estimates, there must be shifts in individual ranks. However, shifts in individuals’ relative ranks do not require non-monotonically ordered QF estimates.

For example, assume that every participant with a QF estimate of 50.75 has the same actual consumption as person A (Q × F = 3 × 10 = 30) and every participant with a QF estimate of 26.25 has the same actual consumption as person B (Q × F = 4 × 9 = 36). This situation actually results in non-monotonically ordered categories because a QF estimate of 26.25 represents a greater amount of actual alcohol consumption than a QF estimate of 50.75 (actual consumption: 36 drinks vs. 30 drinks). Another way to view this relationship is that individuals actually consuming 30 drinks are overestimated by 20.75 drinks using QF (QF estimate − actual consumption = 50.75 − 30 = 20.75) whereas individuals consuming 36 drinks are actually underestimated by 9.75 drinks using QF (QF estimate − actual consumption = 26.25 − 36 = −9.75). Although this is a purposefully extreme example, it clearly demonstrates that QF measures can potentially lead to shifts in ranks at the level of the individual and the broader level of the QF estimates themselves.

4. Unequal Measurement of Alcohol Use across Covariates

All statistical models must assume that measures of alcohol consumption are psychometrically equivalent across the covariates under study. In other words, measurement is invariant across individuals, and any observed group differences are due solely to mean shifts in the true value of the dependent variable. For example, a QF estimate of 14 should represent the same underlying amount of alcohol use for both males and females, and not indicate some different magnitude of the construct despite the same numerical value. Without this assumption, valid inferences cannot be drawn from models because it is unknown if differences exist in the population or if they are instead an artifact of failed measurement invariance. This threat to validity can easily arise in practice.

We can demonstrate measurement invariance as a function of gender. Suppose that every female who obtains a QF estimate of 14 drank three times in the past 30 days and three drinks per occasion. This reflects that all females with this estimate consumed nine drinks. Further suppose that all males with a QF estimate of 14 drank five times in the past 30 days with four drinks per occasion. This, in turn, reflects that all males with this score consumed 20 drinks. This example highlights that, although males and females have same QF estimate (i.e., QF estimate = 3.5 × 4 = 14) their actual alcohol consumption is markedly different (females=9 drinks and males=20 drinks). While this is again an intentionally extreme example, this phenomenon could easily arise in practice as men are consistently shown to drink at higher levels than women (WHO, 2011). This threat to validity can exist as a function of categorical (e.g., gender, ethnicity) or continuous (e.g., age, SES) covariates.

In sum, we have shown that QF estimates may overestimate the true level of alcohol use, lead to switches in the relative rank order in individuals’ alcohol consumption, produce non-monotonically ordered estimates of consumption, and result in estimates that are not invariant across covariates. We expect these threats to construct validity to arise in real empirical data. We next evaluate this expectation using data from the 2010 National Survey on Drug Use and Health (USDHHS, 2012).

Method

The National Survey on Drug Use and Health (NSDUH) is a nationwide survey funded by the Substance Abuse and Mental Health Services Administration (SAMHSA) that annually interviews around 70,000 adolescents and adults. The NSDUH aims to monitor trends, consequences, levels, and patterns of substance use and abuse. A key feature of these data is that open-ended quantity and frequency alcohol use items were administered. The questions of interest here were: “During the past 30 days, on how many days did you drink one or more drinks of an alcoholic beverage?” (F) and “On days that you drank during the past 30 days, how many drinks did you usually have?” (Q). Responses to the frequency item ranged from 0–30 days and responses to the quantity item ranged from 0–20 drinks. Participants reporting a quantity greater than 20 were omitted due to validity concerns (n=39, .5% of the eligible subsample used for analyses). We then binned the responses to the open-ended quantity and frequency items into categories according to the quantity and frequency items in Table 1 to create ordinal items reflective of those typically used in practice. QF estimates were calculated from the mid-values of the ordinal alcohol items, which is the standard method used in practice (Dawson, 2003)².

We compared QF estimates to actual consumption, which was calculated from open-ended quantity and frequency counts. By doing so, we assumed that quantity and frequency of use are perfectly valid and reliable measures and actual consumption measures individuals’ true total consumption over the past 30 days. Importantly, although restrictive, this assumption does not undermine our demonstration. Instead, it demonstrates that even in the best case scenario of perfect participant report, validity concerns still arise because of the multiplication of ordinal items with underlying counts³. Further, there is no reason to believe that introducing unreliability in participant reporting would improve the performance of ordinal QF estimates.

We extracted a subsample of 18–20 year olds for our empirical demonstrations. We omitted participants missing quantity or frequency items because the consumption estimates could not be calculated. Our final sample consisted of 7,213 18–20 year old participants (35.4% 18 year olds, 32.9% 19 year olds, and 31.7% 20 year olds) that were 49% male and 40.3% minority.

Results

Overestimation of Alcohol Consumption

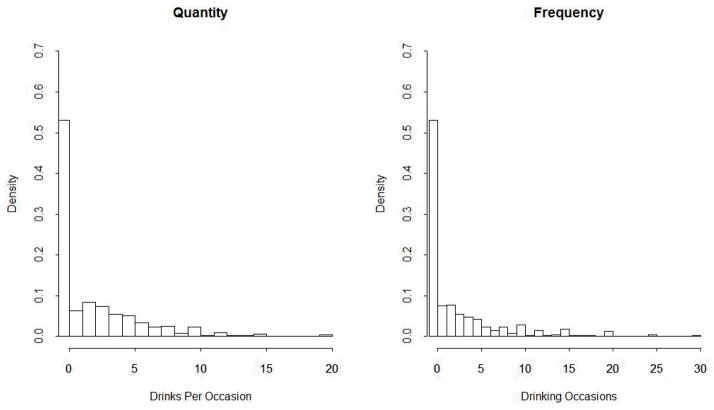
First, we investigated whether QF estimates overestimated actual consumption in the empirical data. Figure 3 shows that the distributions of the NSDUH quantity and frequency items were clearly positively skewed. As we expected, this skew resulted in inaccurate estimates of actual alcohol consumption. Figure 4 illustrates how this overestimation occurred with these data. The top left frame of Figure 4 displays the underlying counts for the number of drinks per occasion for the third ordinal quantity category from Table 1 (e.g., “3 to 4 drinks”) for individuals with a QF estimate of 50.75. The top right frame of Figure 4 shows the underlying counts for the number of drinking occasions for the fifth ordinal frequency category from Table 1 (“10–19 days”) for individuals with a QF estimate of 50.75. Clearly, the mid-values, Q_mid=3.5 and F_mid=14.5, were not an accurate measure of central tendency for these data and, consequently, overestimated the majority of the underlying quantity and frequency counts. Thus, multiplying these upwardly biased mid-values overestimated total alcohol consumption. For instance, multiplying the modal quantity and frequency counts, which is 3 for quantity and 10 for frequency, produces an actual consumption of 30. Indeed, a substantial number of individuals’ QF estimates were greater than their actual consumption (78.7%). The bottom frame of Figure 4 also shows that the QF estimate of 50.75 (Q_mid × F_mid = 3.5 × 14.5) often overestimated actual consumption. More specifically, for the QF estimate of 50.75, the mean and median of the underlying actual consumption were 43.38 and 45, respectively.

Figure 3.

Distribution of NSDUH quantity and frequency items. The quantity counts ranged from 0–20 drinks and the frequency counts ranged from 0–30 days.

Figure 4.

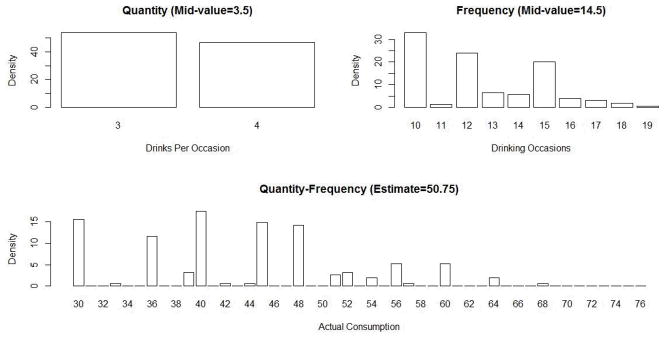
Distributions of quantity, frequency, and actual consumption for the QF estimate of 50.75. The top left frame displays the underlying counts for the ordinal quantity category “3–4 drinks”. The top right frame shows the underlying counts for the ordinal frequency category “10–19 days”. The bottom frame shows the underlying actual consumption for the QF estimate of 50.75.

Table 2 reports the means, standard deviations, and medians for the actual consumption that underlie each QF estimate. This table shows that QF estimates were often larger than the mean level of actual consumption. Importantly, the most extreme cases of overestimation occurred in highly populated QF estimates (e.g., the estimates with the larger sample sizes) such as 22, 26.25, 50.75, and 79.75. This suggested that a large proportion of actual consumption is overestimated by the QF measure.

Table 2.

Descriptive statistics for the actual consumption that underlie QF estimates

Ordinal QF	Actual Consumption				Ordinal QF minus Mean	Ordinal QF	Actual Consumption				Ordinal QF minus Mean
	N	Mean	SD	Median			N	Mean	SD	Median
0.00	3825	0.00	0.00	0.0	0.00	40.00	73	40.05	8.59	40.0	−0.05
1.50	295	1.43	0.50	1.0	0.07	41.25	114	38.38	6.74	40.0	2.87
3.00	245	2.91	1.00	2.0	0.09	50.00	23	46.17	7.70	40.0	3.83
4.00	99	3.73	0.82	3.0	0.27	50.75	155	43.38	9.12	45.0	7.37
5.25	282	5.25	1.86	6.0	0.00	52.00	54	57.20	16.43	60.0	−5.20
8.00	200	7.86	1.61	8.0	0.14	56.25	78	54.00	8.85	56.0	2.25
8.25	137	8.36	2.90	10.0	−0.11	75.00	40	70.93	10.43	70.0	4.07
11.25	71	12.13	3.93	14.0	−0.88	79.75	146	68.34	15.20	62.5	11.41
14.00	310	13.54	3.30	12.0	0.46	87.50	34	78.06	19.74	77.5	9.44
14.50	32	12.56	2.50	12.0	1.94	97.50	35	104.51	23.73	96.0	−7.01
15.00	104	14.58	3.60	14.0	0.42	108.75	75	90.55	17.69	84.0	18.20
19.50	32	22.66	8.47	24.0	−3.16	137.50	38	129.39	27.83	120.0	8.11
22.00	189	20.96	4.75	20.0	1.04	145.00	60	129.43	27.32	120.5	15.57
26.25	147	25.12	5.50	24.0	1.13	188.50	50	194.32	57.82	180.0	−5.82
29.00	70	25.63	5.50	24.0	3.37	250.00	24	237.50	42.43	237.5	12.50
30.00	109	29.48	6.56	28.0	0.52

Note: Ordinal QF estimates with N greater than 20 are shown. The “Ordinal QF minus Mean” column represents the difference between the Ordinal QF estimate and the mean of Actual Consumption.

Shifts in Relative Ranks of Alcohol Consumption

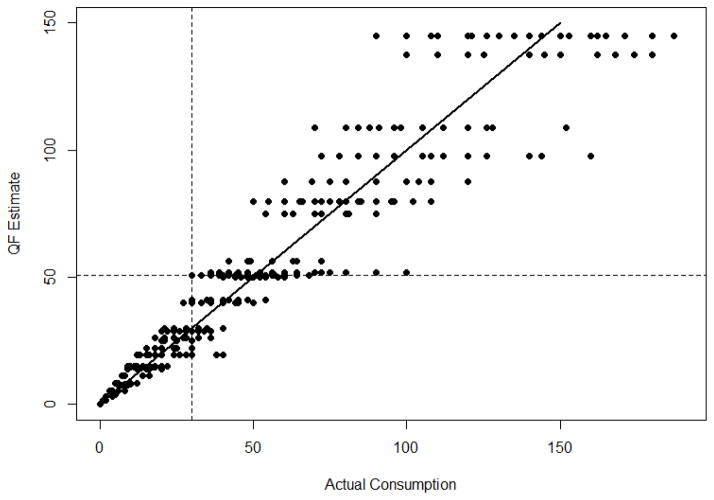
Figure 5 plots QF estimates based on the ordinal items against actual consumption. This illustrates that individuals routinely shifted relative ranks in the empirical data. The dots falling on the dashed vertical line represent the range of QF estimates obtained in the data for an actual consumption of 30 drinks. That is, each dot represents a different QF estimate stemming from precisely the same number of drinks actually consumed. The dots falling on the horizontal dashed line represent the range of actual consumption for a QF estimate of 50.75. That is, for a given QF estimate of 50.75, each dot represents a different number of drinks actually consumed. Therefore, the point where the lines meet represents individuals who consumed 30 drinks and obtained a QF estimate of 50.75. Shifts in relative ranks are cases where individuals that consume more alcohol receive smaller QF estimates relative to individuals with less consumption. Figure 5 explicates specific shifts in relative ranks such that any dot in the lower right quadrant represents individuals who had more actual consumption but lower QF estimates than those with a QF estimate of 50.75 and actual consumption of 30 drinks. This confirmed that shifts in relative ranks occur in the NSDUH data.

Figure 5.

Scatterplot of QF estimates by actual consumption. The dots falling on the dashed vertical line represent the range of QF estimates obtained in the data for an actual consumption of 30 drinks. The dots falling on the horizontal dashed line represent the range of actual consumption for a QF estimate of 50.75. Diagonal line designates where QF estimates equal actual consumption.

Figure 5 also illustrates the overall imprecision of QF estimates. If QF estimates perfectly measured actual consumption, all of the data points would fall on the diagonal line. Conversely, QF estimates that overestimated actual consumption fall above the diagonal line and QF estimates that underestimate fall under the line diagonal line. Clearly, there are numerous data points off the diagonal line. This illustrates imprecision in QF estimates caused by the multiplication of ordinal items with underlying counts.

Non-Monotonic QF Estimates

Results also showed that QF estimates were not monotonically ordered in the NSDUH data. Referring again to Table 2, we found multiple cases in which smaller QF estimates had larger mean or median actual consumption than larger QF estimates. For example, the average actual consumption for the QF estimate of 19.5 was greater than the QF estimate of 22, the QF estimate of 52 was greater than the QF estimate of 56.25, and so on. In sum, the NSDUH data corroborated the concern that smaller QF estimates can, on average, represent greater alcohol consumption compared to larger QF estimates. Again, even though this concern about whether QF estimates are ordered is related to individual shifts in relative ranks, this is a unique threat to validity. It is possible to have individual-level shifts in ranks, but have monotonically ordered QF estimates.

Unequal Estimates of Alcohol Use across Covariates

Our fourth concern was that QF estimates can be unequal as a function of covariates. In the NSDUH data, for many of the QF estimates, the average underlying alcohol consumption was similar for males and females. However, Table 3 shows QF estimates in which the average actual alcohol consumption levels for males and females differ by more than half of a drink. For example, males’ average actual consumption for a QF estimate of 30 was 2.9 drinks larger than females’ average consumption. Similarly, for the QF estimate of 50.75, males’ average alcohol consumption was 2.04 drinks larger than females’ average consumption. This means that, given these same QF estimates, males consumed more alcohol than females. Although these gender differences were usually such that males drank more than females, there were some QF estimates where females’ average consumption was larger than males’ consumption. This concern can directly undermine the validity of any formal inferential tests of gender differences in alcohol consumption.

Table 3.

Gender differences in actual consumption within QF estimates

Ordinal QF	Males			Females			Mean Difference
	Actual Consumption			Actual Consumption
	N	Mean	SD	N	Mean	SD
22.00	105	20.61	4.65	84	21.40	4.87	−0.79
29.00	31	25.94	5.57	39	25.38	5.51	0.56
30.00	81	30.22	6.75	28	27.32	5.54	2.90
40.00	48	39.71	8.77	25	40.72	8.38	−1.01
41.25	69	38.88	6.93	45	37.60	6.45	1.28
50.75	82	44.34	8.93	73	42.30	9.27	2.04
56.25	55	53.82	9.32	23	54.43	7.79	−0.61
79.75	87	69.62	15.91	59	66.44	14.02	3.18

Note: QF estimates shown have a gender mean difference greater than |.5| and N greater than 15 for each gender. The “Mean Difference” column represents the difference between the mean actual consumption of males compared to females.

Discussion

We have shown both analytically and empirically the potential risks of multiplying ordinal items that consist of binned counts. We demonstrated that this measurement strategy poses unique risks beyond those identified in previous quantitative work on coarse categorization (e.g., MacCallum et al., 2002; Taylor et al., 2006). Our study focused specifically on QF measures of alcohol use although these findings will generalize to any situation in which this measurement strategy is employed. We showed that QF measures can overestimate actual alcohol consumption, fail to capture individuals’ relative ranks, and produce non-monotonic QF estimates that are not invariant across covariates. Taken together, our results provide clear evidence that QF measures are subject to significant threats to validity that directly impact the ability to accurately measure alcohol consumption. This, in turn, limits our ability to accurately test theoretically-derived research hypotheses.

Valid and reliable measurement is essential in any scientific discipline, and this is particularly salient in studies of alcohol use and abuse. We highlighted basic illustrations of how threats to validity arise, but these threats extend to a variety of more complicated research settings. For example, in a longitudinal design, the shifts in relative ranks of alcohol consumption will not only occur between individuals (as we described earlier) but also within individuals over time. For example, using standard QF measures, the time 1 estimate of consumption for a given individual can be greater than the time 2 estimate even though the person truly consumed more drinks at time 2 relative to time 1. Further, threats to construct validity will impact the ability to appropriately test theory, regardless of the statistical modeling technique employed (e.g., generalized linear models, random effects models, latent variable models, mixture models, etc.). There is simply no statistical model that can “fix” these fundamental issues in flawed measurement.

A natural question arising from our findings relates to the impact that this scoring practice exerts on core psychometric properties such as reliability, dimensionality, and differential item functioning (DIF). Our study was not designed to assess these components of measurement so we are not able to provide definitive insights on these topics. For many instruments, especially those used in substance use research, information about psychometric properties is available (e.g., for alcohol use see Allen & Wilson, 2003). We know that in our empirical example, given specific levels of quantity and frequency, QF estimates will always be the same because there are computed by means of a deterministic multiplicative process. Moving beyond this initial work to a broader latent variable framework, our findings suggest that both Type 1 and Type 2 errors involving DIF testing may arise because QF estimates are not always equivalent as a function of covariates. Most important, regardless of these psychometric characteristics, we demonstrated that the measurement strategy depicted in this paper lacks validity. Without validity, other psychometric properties have little practical utility.

In this paper, we have focused on concerns with the multiplication of ordinal items defined by collapsed counts. These results do not apply more generally to combining other scale types such as nominal, interval, and ratio that do not collapse across ranges of values. In fact, from a quantitative standpoint, we do not expect the issues outlined to arise when multiplying interval variables or ratio variables because the crux of the problem with multiplying the ordinal QF data is that there are ranges of underlying counts. These underlying distributions do not exist for interval or ratio variables, thus multiplying these scale types does not induce problems such as switches in relative rank.

A limitation of our study is that we only used data from the NSDUH on past 30 day alcohol use. In practice, alcohol use is measured in numerous ways with different time frames and ordinal response categories. The extent to which these validity concerns do or do not arise in practice depends on the properties of ordinal measures (e.g., how the counts are collapsed) and the distribution of the counts underlying the ordinal items, which may vary substantially across studies. We did not report supporting results from the simulation study noted in Footnote 3 because of space constraints and, more importantly, it was not central to the core aims of our study. However, a summary of these simulation results is available in the supplemental appendix. Further, we are not promoting this measurement strategy for use in practice, regardless of the formulation of the ordinal items, because of the serious validity risks.

Our study examined a single QF measure that is consistent with those used in applied research. Future research should consider other substances and consumption measures. It would also be beneficial to examine experimental factors such as varying chronological reference periods, alternative response options and mid-value selections, unreliability, and reporting bias (Dawson, 2003; Dawson & Room, 2000; Del Boca & Darkes, 2003; Ivis, Bondy, & Adlaf, 1997). Methodologists should identify similar measurement issues in other research areas and investigate how these fundamental issues impact inferences drawn from statistical models. Applied researchers and quantitative methodologists alike need to make continuing investments in the ongoing evaluation and improvement of psychometric measures. Measurement serves as the foundation for testing substantive theory and making significant advances in the social and behavioral sciences.