Abstract
Aims
Left-ventricular (LV) conduction disturbances are common in heart-failure patients and a left bundle-branch block (LBBB) electrocardiogram (ECG) type is often seen. The precise cause of this pattern is uncertain and is probably variable between patients, ranging from proximal interruption of the left bundle branch to diffuse distal conduction disease in the working myocardium. Using realistic numerical simulation methods and patient-tailored model anatomies, we investigated different hypotheses to explain the observed activation order on the LV endocardium, electrogram morphologies, and ECG features in two patients with heart failure and LBBB ECG.
Methods and results
Ventricular electrical activity was simulated using reaction–diffusion models with patient-specific anatomies. From the simulated action potentials, ECGs and cardiac electrograms were computed by solving the bidomain equation. Model parameters such as earliest activation sites, tissue conductivity, and densities of ionic currents were tuned to reproduce the measured signals. Electrocardiogram morphology and activation order could be matched simultaneously. Local electrograms matched well at some sites, but overall the measured waveforms had deeper S-waves than the simulated waveforms.
Conclusion
Tuning a reaction–diffusion model of the human heart to reproduce measured ECGs and electrograms is feasible and may provide insights in individual disease characteristics that cannot be obtained by other means.
Keywords: Heart failure, Left bundle-branch block, Conduction disorders, Computer models
What's new?
Anatomically and physiologically detailed computational models were fitted to two heart-failure patients with ventricular conduction disturbances.
The models were tuned to reproduce the measured electrocardiogram and activation order on the left-ventricular (LV) endocardium.
Tuning results suggest the absence of antegrade or reentrant LV Purkinje activity, myocardial hypertrophy, reduced myocardial conductivity, and a partially preserved ventricular gradient.
To match the T-waves, we had to assume a much lower density of the delayed rectifier current than has been measured in isolated-cell experiments.
Introduction
Ventricular conduction disturbances are frequently seen in heart-failure (HF) patients. About one-third of the patients with HF have a left bundle-branch block (LBBB) morphology of the QRS complex. Clinical trials have demonstrated that cardiac resynchronization therapy (CRT) reduces mortality and hospitalization for HF in patients with complete LBBB, while results in patients with right bundle-branch block or non-specific left-ventricular (LV) conduction delay are poor.1,2 Endocardial mapping and simulation studies have suggested that many patients diagnosed with LBBB by conventional electrocardiogram (ECG) criteria are misdiagnosed, and that these patients may have a combination of ventricular hypertrophy, LV chamber dilation, scar, delayed LV activation, or other forms of electrical uncoupling in the working myocardium.3–5 The ability to distinguish between these possible factors may be important to predict the success of CRT.3,6 The purpose of this study was to improve our understanding of the activation pattern in individual HF patients, the pathological mechanisms underlying this pattern, and their relation to ECG characteristics such as the notching in lead V6 which is typical for LBBB.
Using a computational model, the relation between hypothesized disease factors and the ECG can be investigated in a perfectly controlled environment. Modelling studies have already shown important insights in HF,7 effects of CRT,8 LV hypertrophy,5 and in the problem of LBBB diagnosis. For example, it has recently been hypothesized that in complete LBBB, activation starts in the right ventricle (RV) and must proceed through the septum for 40–50 ms before it reaches the LV endocardium.3 It then takes another 50 ms to propagate to the endocardium of the posterolateral wall, and a further 50 ms to cross it. This results in a total QRS duration of 140–150 ms,9 far longer than the current criterion for LBBB.
The present state of computational modelling of the heart allows for highly realistic representation of the cardiac activation process, action potential waveforms, local electrograms, and the ECG.10 However, such purely theoretical investigations still do not allow for insight in individual cases in all their complexity. Therefore, we set out to construct computational models that mimic individual patients as well as possible, so that the predicted signals could be directly compared with their measured equivalents. By repeated model tuning, the mechanisms that best explain the observed signals can then be identified, and to some extent such findings can be validated by other diagnostic methods and by predicting follow-up data.
Methods
Patient characteristics
Two patients with moderate-to-severe HF who were eligible for CRT implantation according to the criteria from the 2011 ESC clinical practice guidelines were included in the study. Both patients were on stable drug therapy (>3 months) with maximally tolerated doses of angiotensin-converting enzyme inhibitors or angiotensin-1 receptor blockers, diuretics, aldosterone antagonists, and beta-blockers. Antiarrhythmic drugs, if any, were stopped before the procedure for at least five half-lives. The patients underwent a standard 12-lead ECG, a clinically indicated cardiac magnetic resonance (CMR) procedure, an electrophysiological study, and a coronary angiography procedure. The patients provided oral and written consent to each procedure, and the studies were performed according to institutional ethics guidelines.
Data collection
Standard 12-lead ECGs were recorded using a novel ECG machine (CS200 excellence, Schiller AG) with a sampling rate of 1000/s and an amplitude resolution of 1.0 µV.
In addition to standard electrophysiological catheters deployed in the right atrium and ventricle, a reference catheter (REF-STAR, Biosense Webster, a Johnson & Johnson company) was placed on the back of the patient. The electromechanical mapping system (NOGA XP, Biosense Webster) and the navigation and mapping method were described previously.11 In brief, a conventional 7F deflectable-tip mapping catheter (NAVI-STAR, Biosense Webster) was deployed in the LV via a retrograde aortic approach from the femoral artery. Intracardiac unipolar and bipolar electrograms and spatial position of the catheter tip were recorded at ∼200 equally distributed LV endocardial locations. The sequentially recorded intracardiac electrogram and position data were temporally aligned using the simultaneously recorded 12-lead body surface ECG. For the three-dimensional (3D) LV reconstruction during the acquisition process, the geometric filling threshold was set at 10 mm to reduce artificial interpolation.
Cardiac magnetic resonance data were acquired with a 3T Siemens Magnetom Skyra scanner with 36 channel coils. Following localizer acquisitions, cine ECG-triggered segmented steady-state free precession images were acquired in the two-, three-, and four-chamber orientations, as well as in a stack of contiguous short-axis slices covering the ventricles (slice thickness 8 mm, 20% inter-slice gap, 25 phases). After intravenous bolus injection of gadolinium (Gadobutrol, 0.2 mmol/kg body weight) ultra-fast gradient-echo ‘VIBE’ images were obtained to describe thoracic anatomy and to detect the location of the precordial ECG electrodes on the chest. Axial, coronal, and sagittal images (slice thickness 2.5 mm, slice oversampling 15%) were used. Finally, a navigator-gated, ECG-triggered whole-heart ‘FLASH’ angiography was acquired with a T1-weighted inversion-recovery echo-gradient sequence with a slice thickness of 0.9 mm, with inversion time (TI) adjusted using TI-scout images.
Construction of anatomical models
Patient-specific anatomical models were reconstructed using CMR data. The outline of the ventricular musculature was traced semi-automatically in the end-diastolic frame of the short-axis cine dataset. The base of the ventricles, outflow tracts, outline of the atrial cavities, aortic arch, and caval veins were traced manually in the FLASH dataset. The lungs and the torso surface were traced from the VIBE data. From the contours thus obtained surfaces were created using Blender (The Blender Foundation) as 3D editing software. A computational mesh was constructed and mesh nodes were labelled as myocardium, blood, connective tissue, lung, or skeletal muscle, depending on the surfaces in which they were enclosed. Fibre orientations were assigned to the ventricular nodes using a rule-based method.12
Cardiac magnetic resonance images of the ventricles typically have a ‘grey zone’ consisting of trabeculated myocardium between the wall and the intracavitary blood. We segmented this zone separately, and will refer to it as the ‘non-compact myocardium’.
A thin, rapidly conducting subendocardial layer was created in both ventricles to mimic the function of the Purkinje network,13,14 since the Purkinje system cannot be imaged in vivo. Early activation sites similar to those published by Durrer et al.15 mimicked the action of the upstream Purkinje fibres.
To allow comparison between measured and simulated activation times, the set of catheter locations from the electroanatomical mapping system was aligned to the LV endocardial surface obtained from CMR imaging. The data could be inspected in 3D as well as in a polar diagram of the LV.
Computer simulations
Simulations were performed using a ventricular model at 0.2 mm resolution and an inhomogeneous torso model at 1 mm resolution as in previous studies.5,10,16,17 The heart model had anisotropic tissue with transmurally rotating fibre orientation. All individual heart anatomies included the roof of the RV. The torso model included intracavitary blood, lungs, and an anisotropic skeletal muscle layer. A list of conductivity values in the heart and torso was published previously.18 Propagating electrical activity was simulated based on ionic transmembrane currents by a monodomain reaction–diffusion equation.12 Membrane ionic currents at each of the ∼25 million points that represented the ventricular myocardium were computed with the Ten Tusscher-Noble-Noble-Panfilov (TNNP) membrane model for human ventricular myocytes.19 This model distinguishes subendocardial, mid-myocardial, and subepicardial cell types. We added differences between LV and RV cells as published previously.20
At 1 ms intervals, computed transmembrane currents were injected in the torso model and the bidomain equation was solved for the electric potential throughout the torso, from which the 12-lead ECG and local electrograms were extracted.18 Wilson's central terminal was used as reference for electrograms and precordial ECG leads.
All simulations were performed using propag-5, a cardiac simulation package suitable for large-scale parallel computers.12,21 The computations were performed on 2048 cores of a Cray XE 6 supercomputer and took about 20 min for a single heartbeat.
Tuning procedure
The initial model parameters were those that we previously used to reproduce a normal QRS complex.5 In each subject, the first step of model tuning was the choice of an initial activation site in the RV free wall, near the observed LV breakthrough. This location was fine-tuned to optimize the match between the observed and the simulated LV endocardial activation order. If necessary, more sites were added towards the inferior side of the RV.
Next, tissue conductivities and cell surface-to-volume ratio were considered. Reduced myocardial coupling was simulated by reducing the ‘intracellular’ component of the bidomain conductivities.22 This is equivalent to the compound electrical conductivity of the cytoplasm and the gap junctions.23 Longitudinal and transverse conductivity, i.e. the conductivity along and across the dominant myocyte orientation, were tuned individually, both for the bulk myocardium and for the rapid endocardial layer. The aim of this tuning process was to optimize the match for both the activation order and the ECG. Local electrogram morphology was not taken into account.
When tuning of the QRS complex was completed, repolarization parameters were adjusted to match the T-wave. Heterogeneity in the maximum conductivity of the slow delayed rectifier current (IKs) was introduced using a linear relation with the activation time in a previous simulation. The slope of this relation was used to tune the T-wave amplitude. The maximum conductivity of the inward rectifier current (IK1) was reduced to make the peaks of the T-waves less sharp.
Results
Pathogenesis was assessed in both patients by coronary artery angiography, confirming the absence of significant coronary artery disease in Patient 1 and a two-vessel disease in Patient 2. During the mapping procedure, 181 contact points were acquired in the LV of Patient 1 and 97 in Patient 2. Left-ventricular ejection fraction, end-diastolic volume, and end-systolic volume were 39%, 138 mL, 84 mL in Patient 1 and 35%, 248 mL, 160 mL in Patient 2.
The final model parameters that were common in both patients were the following: (i) the fast endocardial layer in the LV was given the same conductivity as the bulk myocardium, to approximate the observed conduction velocity along the endocardium; (ii) the surface-to-volume ratio for the cell membrane was reduced to 60% of its original value to increase transmural conduction velocity; (iii) the non-compact myocardium was omitted to reduce R-wave amplitude in left precordial leads; (iv) the maximum conductivity of IK1 was reduced to 20% of its original value to flatten the T-waves; and (v) the conductivity of IKs was configured as a linear function of activation time to match T-wave amplitude.
Patient 1
Patient 1 was a 72-year-old woman with an idiopathic dilated cardiomyopathy diagnosed by CMR and coronary angiography. Her ECGs fulfilled conventional criteria for LBBB, which include a QRS duration >120 ms, QS or rS morphology in lead V1, and a monophasic R-wave with no Q-waves in leads V6 and I. Moreover, a broad notched or slurred R-wave in leads I, aVL, V5, and V6 was noted, which is consistent with the ECG criteria of the American Heart Association, American College of Cardiology Foundation, and the Heart Rhythm Society.
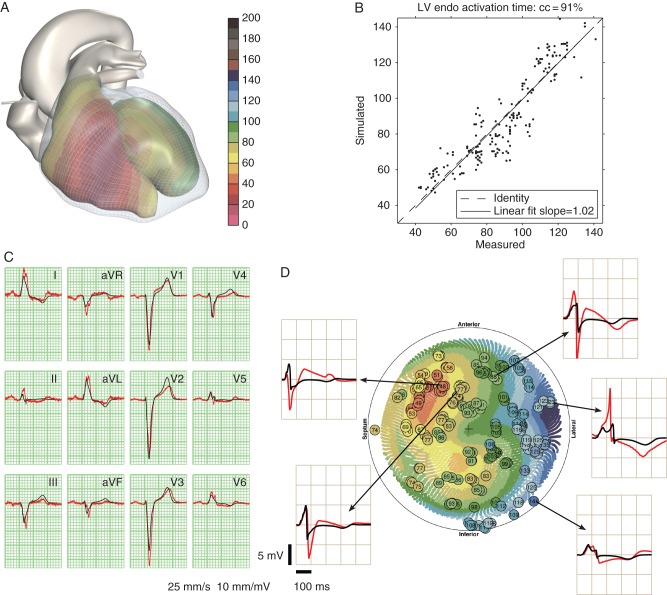
The comparison between the measured and simulated data for this patient is shown in Figure 1. The correlation coefficient between measured and simulated activation times was r = 0.91. Measured surface QRS duration (130 ms) was very close to the simulated QRS duration. Slurring in lead V4 was well reproduced. Notching was present in both the measured and simulated leads V5, but with different timing. Notching in V6 was not reproduced. Unipolar electrogram morphologies matched qualitatively at some sites, but large differences were also observed. Especially, the measured electrograms had deeper S-waves and sometimes much higher R-waves than the corresponding simulated electrograms (e.g. the lateral site in Figure 1D). Some measured electrograms had ST elevations suggestive of (catheter-induced) injury currents (all anterior sites in Figure 1D), which we did not attempt to reproduce with the model.
Figure 1.
Comparison of measured and simulated data in Patient 1. (A) Simulated activation times on the endocardia of both ventricles; the colour scale is in millisecond. (B) Simulated against measured activation times on the LV endocardium; scales in millisecond. (C) Measured ECG (red) and simulated ECG (black). (D) Polar diagram of the LV endocardium showing measured activation times (circles with time in millisecond) and simulated activation times (coloured dots). Same colour scale as panel A. Measured (red) and simulated electrograms (black) from five indicated locations are shown.
The following model parameters were specific to this patient: (i) three early activation sites on the lateral RV free wall were used, together with a fast endocardial layer in the RV; (ii) the LV myocardium was made less anisotropic than normal; (iii) the depth of RV early activation sites was fine-tuned to obtain the right amplitude of the small R-waves in leads V2 and V3; and (iv) the skeletal muscle layer, which is normally strongly anisotropic in our models, was made isotropic, consistent with the observation that the patient was a non-athletic female. This intervention increased the amplitude of the precordial leads relative to the limb leads.
Patient 2
Patient 2 was a 69-year-old man with a QRS duration of 190 ms with previous anterior myocardial infarction diagnosed by cardiac CMR and coronary angiography. With a QS complex in lead V1 and broad, notched, monophasic R-waves in leads I and V6, his ECG fulfilled conventional criteria for LBBB.
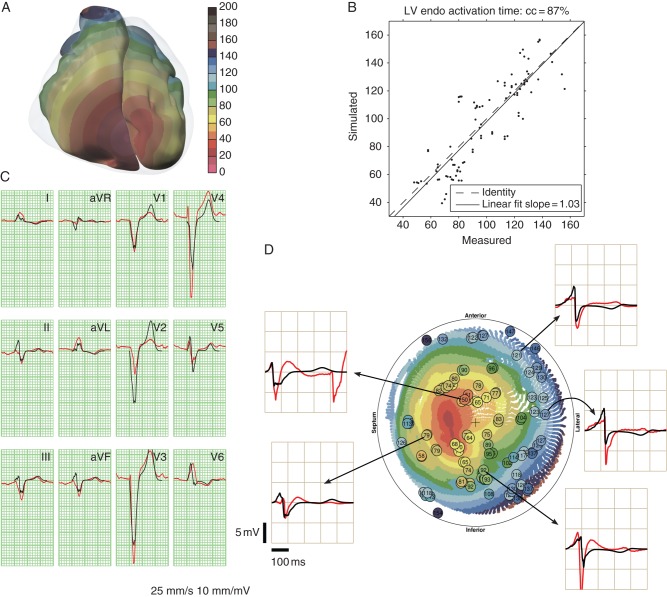
The comparison between the measured and simulated data for this patient is shown in Figure 2. The correlation between measured and simulated activation times was r = 0.87. The measured LV breakthrough was in the anterior wall, far from the septum. Attempts were made to reproduce this in the model by increasing the tissue anisotropy ratio, but the simulated breakthrough was still closer to the septum. The simulated leads I and V6 were more notched than the measured signals, while in lead V5 the opposite was true. The large J-point elevations in V3 and V4 were only partially reproduced. The following model parameters were specific to this patient: (i) five early activation sites on the anterior and inferior RV free wall; and (ii) the transverse conductivity of the myocardium was reduced.
Figure 2.
Comparison of measured and simulated data in Patient 2. See caption of Figure 1 for explanation.
Discussion
To increase the reliability of patient-specific predictions with electrophysiological and electromechanical models of the heart, several groups have worked on patient-tailored models.24–29 To the best of our knowledge though, the present study reports the first two HF cases in which a model was accurately tuned to the measured surface and intracardiac ECG. In both patients, the LV activation pattern could be reproduced by assuming a small number of early activation sites in the free wall of the RV in combination with a thin, rapidly conducting layer on the RV endocardium, and tuning of the surface-to-volume ratio of the cell membrane and the anisotropic bidomain conductivities of the tissue. We reduced the surface-to-volume ratio in both patients to represent a state of hypertrophy. This increases conduction velocity in the model without increasing the ECG amplitude.
In simulations of normal hearts (unpublished results), we use a rapidly conducting layer in both ventricles in combination with a small number of early activation sites. However, in both patients the fit was clearly improved by assuming that there was no rapidly conducting layer (Purkinje network) on the LV endocardium. This appears to contradict the assumption of Strauss et al.3 that activation from the RV enters the LV Purkinje network in LBBB patients and the observation, by Strik et al.14, of entry in some form of rapidly conducting subendocardial layer in canine LV.
The original TNNP model, of which the parameters are tuned to reproduce the result of patch-clamp experiments, produces sharp T-wave peaks.17 To produce realistic T-waves, we had to reduce the conductivity of IK1 to 20% of its original value.19 There is experimental support for reduced IK1 in HF,30–32 but not of this magnitude. The magnitude of IK1 in the TNNP model corresponds with canine and human data.32 It is, however, five times larger than in the (human atrial) Courtemanche model,33 near the 5.6-fold difference reported by Koumi et al.34 in human cells.
A positive correlation between activation time and IKs density, which results in a negative correlation between activation time and action potential duration, was found to be crucial to reproduce the T-waves in both patients. This suggests that a certain amount of ventricular gradient35,36 is still present in these patients, although it does not suffice to produce T-waves with a sign that is concordant with the QRS complex as observed in normal subjects.
We have not yet been able to reproduce the deep S-waves seen in many measured endocardial electrograms. Such S-waves are caused by activation propagating away from the measurement electrode after local depolarization. Such propagation, both in endocardial-to-epicardial and circumferential direction, was certainly present in our simulations. A possible explanation for the discrepancy is the underestimation of wall thickness in our models, which results from the omission of the non-compact myocardium. A thicker wall, with faster propagation to arrive at the same QRS duration, would produce stronger S-waves on the endocardium. Including the non-compact myocardium with improved conductivity values may solve the problem.
Limitations
Although matching both ECG and endocardial electrograms restricts the solution much more than matching the ECG alone, an optimal match with our models is not guaranteed to be unique. In principle, it can never be excluded that a completely different set of parameters may lead to an equally close fit. In addition, shortcomings in the model may influence the solution. Our conclusions should therefore be seen in the first place as research hypotheses, which are to be investigated by targeted clinical or experimental research.
Conclusion
Our model-fitting results in two HF patients with LBBB ECG morphology suggest the absence of antegrade or reentrant LV Purkinje activity, hypertrophied myocytes, reduced myocardial conductivity, and a partially preserved ventricular gradient. In addition, these and previous results suggest that the density of IK1 in the in situ human heart is smaller than in isolated-cell experiments.
The method presented here may in the future become a new diagnostic method to determine the origin of ventricular conduction abnormalities that lead to LBBB patterns in the ECG and to improve patient selection for CRT.
Conflict of interest: none declared.
Funding
This work was supported by a grant from the Swiss National Supercomputing Centre (CSCS) under project ID 397. The authors gratefully acknowledge financial support by the Theo Rossi di Montelera Foundation, the Mantegazza Foundation, and FIDINAM. This work was previously supported by the ‘Iniziativa Ticino in Rete’ and the ‘Swiss High Performance and Productivity Computing’ (HP2C) Initiative. Funding to pay the Open Access publication charges for this article was provided by …
References
- 1.Rossi A, Rossi G, Piacenti M, Startari U, Panchetti L, Morales MA. The current role of cardiac resynchronization therapy in reducing mortality and hospitalization in heart failure patients: a meta-analysis from clinical trials. Heart Vessels. 2008;23:217–23. doi: 10.1007/s00380-008-1039-8. [DOI] [PubMed] [Google Scholar]
- 2.Kutyifa V, Solomon SD, Bourgoun M, Shah AM, Pouleur AC, Knappe D, et al. Effects of cardiac resynchronization therapy on left ventricular mass and wall thickness in mild heart failure patients in MADIT-CRT. Heart Rhythm. 2013;10:354–60. doi: 10.1016/j.hrthm.2012.11.007. [DOI] [PubMed] [Google Scholar]
- 3.Strauss DG, Selvester RH, Wagner GS. Defining left bundle branch block in the era of cardiac resynchronization therapy. Am J Cardiol. 2011;107:927–34. doi: 10.1016/j.amjcard.2010.11.010. [DOI] [PubMed] [Google Scholar]
- 4.Auricchio A, Fantoni C, Regoli F, Carbucicchio C, Goette A, Geller C, et al. Characterization of left ventricular activation in patients with heart failure and left bundle-branch block. Circulation. 2004;109:1133–9. doi: 10.1161/01.CIR.0000118502.91105.F6. [DOI] [PubMed] [Google Scholar]
- 5.Bacharova L, Mateasik A, Krause R, Prinzen FW, Auricchio A, Potse M. The effect of reduced intercellular coupling on electrocardiographic signs of left ventricular hypertrophy. J Electrocardiol. 2011;44:571–6. doi: 10.1016/j.jelectrocard.2011.06.004. [DOI] [PubMed] [Google Scholar]
- 6.Zareba W, Klein H, Cygankiewicz I, Hall WJ, McNitt S, Brown M, et al. Effectiveness of cardiac resynchronization therapy by QRS morphology in the multicenter automatic defibrillator implantation trial-cardiac resynchronization therapy (MADIT-CRT) Circulation. 2011;123:1061–72. doi: 10.1161/CIRCULATIONAHA.110.960898. [DOI] [PubMed] [Google Scholar]
- 7.Constantino J, Hu Y, Trayanova NA. A computational approach to understanding the cardiac electromechanical activation sequence in the normal and failing heart, with translation to the clinical practice of CRT. Prog Biophys Mol Biol. 2012;110:372–9. doi: 10.1016/j.pbiomolbio.2012.07.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Hu Y, Gurev V, Constantino J, Trayanova N. Efficient preloading of the ventricles by a properly timed atrial contraction underlies stroke work improvement in the acute response to cardiac resynchronization therapy. Heart Rhythm. 2013;10:1800–6. doi: 10.1016/j.hrthm.2013.08.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Grant RP, Dodge HT. Mechanisms of QRS complex prolongation in man: left ventricular conduction disturbances. Am J Med. 1956;20:834–52. doi: 10.1016/0002-9343(56)90204-2. [DOI] [PubMed] [Google Scholar]
- 10.Potse M. Mathematical modeling and simulation of ventricular activation sequences: implications for cardiac resynchronization therapy. J Cardiovasc Transl Res. 2012;5:146–58. doi: 10.1007/s12265-011-9343-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Perin EC, Silva GV, Sarmento-Leite R, Sousa ALS, Howell M, Muthupillai R, et al. Assessing myocardial viability and infarct transmurality with left ventricular electromechanical mapping in patients with stable coronary artery disease: validation by delayed-enhancement magnetic resonance imaging. Circulation. 2002;106:957–61. doi: 10.1161/01.cir.0000026394.01888.18. [DOI] [PubMed] [Google Scholar]
- 12.Potse M, Dubé B, Richer J, Vinet A, Gulrajani RM. A comparison of monodomain and bidomain reaction-diffusion models for action potential propagation in the human heart. IEEE Trans Biomed Eng. 2006;53:2425–35. doi: 10.1109/TBME.2006.880875. [DOI] [PubMed] [Google Scholar]
- 13.Myerburg RJ, Gelband H, Nilsson K, Castellanos A, Morales AR, Bassett AL. The role of canine superficial ventricular muscle fibers in endocardial impulse distribution. Circ Res. 1978;42:27–35. doi: 10.1161/01.res.42.1.27. [DOI] [PubMed] [Google Scholar]
- 14.Strik M, Rademakers LM, van Deursen CJM, van Hunnik A, Kuiper M, Klersy C, et al. Endocardial left ventricular pacing improves cardiac resynchronization therapy in chronic asynchronous infarction and heart failure models. Circ Arrhythm Electrophysiol. 2012;5:191–200. doi: 10.1161/CIRCEP.111.965814. [DOI] [PubMed] [Google Scholar]
- 15.Durrer D, van Dam RT, Freud GE, Janse MJ, Meijler FL, Arzbaecher RC. Total excitation of the isolated human heart. Circulation. 1970;41:899–912. doi: 10.1161/01.cir.41.6.899. [DOI] [PubMed] [Google Scholar]
- 16.Hoogendijk MG, Potse M, Vinet A, de Bakker JMT, Coronel R. ST-segment elevation by current-to-load mismatch: an experimental and computational study. Heart Rhythm. 2011;8:111–8. doi: 10.1016/j.hrthm.2010.09.066. [DOI] [PubMed] [Google Scholar]
- 17.Potse M, Krause D, Bacharova L, Krause R, Prinzen FW, Auricchio A. Similarities and differences between ECG signs of left bundle branch block and left-ventricular uncoupling. Europace. 2012;14(Suppl. 5):v33–9. doi: 10.1093/europace/eus272. [DOI] [PubMed] [Google Scholar]
- 18.Potse M, Dubé B, Vinet A. Cardiac anisotropy in boundary-element models for the electrocardiogram. Med Biol Eng Comput. 2009;47:719–29. doi: 10.1007/s11517-009-0472-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.ten Tusscher KHWJ, Noble D, Noble PJ, Panfilov AV. A model for human ventricular tissue. Am J Physiol Heart Circ Physiol. 2004;286:H1573–89. doi: 10.1152/ajpheart.00794.2003. [DOI] [PubMed] [Google Scholar]
- 20.Potse M, Vinet A, Opthof T, Coronel R. Validation of a simple model for the morphology of the T wave in unipolar electrograms. Am J Physiol Heart Circ Physiol. 2009;297:H792–801. doi: 10.1152/ajpheart.00064.2009. [DOI] [PubMed] [Google Scholar]
- 21.Krause D, Potse M, Dickopf T, Krause R, Auricchio A, Prinzen FW. Hybrid parallelization of a large-scale heart model; In Keller R, Kramer D, Weiss JP (eds) Facing the Multicore-Challenge II, volume 7174 of Lecture Notes in Computer Science. Berlin: Springer, 2012. [Google Scholar]
- 22.Henriquez CS. Simulating the electrical behavior of cardiac tissue using the bidomain model. CRC Crit Rev Biomed Eng. 1993;21:1–77. [PubMed] [Google Scholar]
- 23.Jongsma HJ, Wilders R. Gap junctions in cardiovascular disease. Circ Res. 2000;86:1193–7. doi: 10.1161/01.res.86.12.1193. [DOI] [PubMed] [Google Scholar]
- 24.Gurev V, Lee T, Constantino J, Arevalo H, Trayanova NA. Models of cardiac electromechanics based on individual hearts imaging data; image-based electromechanical models of the heart. Biomech Model Mechanobiol. 2011;10:295–306. doi: 10.1007/s10237-010-0235-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Ashikaga H, Arevalo H, Vadakkumpadan F, Blake RC, III, Bayer JD, Nazarian S, et al. Feasibility of image-based simulation to estimate ablation target in human ventricular arrhythmia. Heart Rhythm. 2013;10:1109–16. doi: 10.1016/j.hrthm.2013.04.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Geerts L, Kerckhoffs R, Bovendeerd P, Arts T. Towards patient specific models of cardiac mechanics: a sensitivity study. In: Goos G, Hartmanis J, van Leeuwen J, editors. FIMH 2003 Conference Proceedings, Berlin: Springer-Verlag; 2003. volume 2674 of Lecture Notes in Computer Science. [Google Scholar]
- 27.Aguado-Sierra J, Krishnamurthy A, Villongco C, Chuang J, Howard E, Gonzales MJ, et al. Patient-specific modeling of dyssynchronous heart failure: a case study. Prog Biophys Mol Biol. 2011;107:147–55. doi: 10.1016/j.pbiomolbio.2011.06.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.MacLeod RS, Stinstra JG, Lew S, Whitaker RT, Swenson DJ, Cole MJ, et al. Subject-specific, multiscale simulation of electrophysiology: a software pipeline for image-based models and application examples. Phil Trans R Soc A. 2009;367:2293–310. doi: 10.1098/rsta.2008.0314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Krueger MW, Rhode K, Weber FM, Keller DUJ, Caulfield D, Seemann G, et al. Patient-specific volumetric atrial models with electrophysiological components: a comparison of simulations and measurements. Biomed Tech. 2010;55(Suppl 1):54–7. [Google Scholar]
- 30.Priebe L, Beuckelmann DJ. Simulation study of cellular electric properties in heart failure. Circ Res. 1998;82:1206–23. doi: 10.1161/01.res.82.11.1206. [DOI] [PubMed] [Google Scholar]
- 31.Kääb S, Nuss HB, Chiamvimonvat N, O'Rourke B, Pak PH, Kass DA, et al. Ionic mechanism of action potential prolongation in ventricular myocytes from dogs with pacing-induced heart failure. Circ Res. 1996;78:262–73. doi: 10.1161/01.res.78.2.262. [DOI] [PubMed] [Google Scholar]
- 32.Aiba T, Hesketh GG, Barth AS, Liu T, Daya S, Chakir K, et al. Electrophysiological consequences of dyssynchronous heart failure and its restoration by resynchronization therapy. Circulation. 2009;119:1220–30. doi: 10.1161/CIRCULATIONAHA.108.794834. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Courtemanche M, Ramirez R, Nattel S. Ionic mechanisms underlying human atrial action potential properties: insights from a mathematical model. Am J Physiol Heart Circ Physiol. 1998;275:H301–21. doi: 10.1152/ajpheart.1998.275.1.H301. [DOI] [PubMed] [Google Scholar]
- 34.Koumi S, Backer KL, Arentzen CE. Characterization of inwardly rectifying K channel in human cardiac myocytes. Circulation. 1995;92:164–74. doi: 10.1161/01.cir.92.2.164. [DOI] [PubMed] [Google Scholar]
- 35.Plonsey R. A contemporary view of the ventricular gradient of Wilson. J Electrocardiol. 1979;12:337–41. doi: 10.1016/s0022-0736(79)80001-1. [DOI] [PubMed] [Google Scholar]
- 36.Conrath CE, Opthof T. Ventricular repolarization: an overview of (patho)physiology, sympathetic effects and genetic aspects. Prog Biophys Mol Biol. 2006;92:269–307. doi: 10.1016/j.pbiomolbio.2005.05.009. [DOI] [PubMed] [Google Scholar]