Impact of Sequence on the Molecular Assembly of Short Amyloid Peptides

Abstract

The goal of this work is to understand how the sequence of a protein affects the likelihood that it will form an amyloid fibril and the kinetics along the fibrillization pathway. The focus is on very short fragments of amyloid proteins since these play a role in the fibrillization of the parent protein and can form fibrils themselves. Discontinuous molecular dynamics simulations using the PRIME20 force field were performed of the aggregation of 48-peptide systems containing SNQNNF (PrP (170–175), SSTSAA (RNaseA(15–20), MVGGVV (Aβ(35–40)), GGVVIA (Aβ(37–42) and MVGGVVIA (Aβ(35–42)). In our simulations SNQQNF, SSTTSAA and MVGGVV form large numbers of fibrillar structures spontaneously (as in experiment). GGVVIA forms β-sheets that do not stack into fibrils (unlike experiment). The combination sequence MVGGVVIA forms less fibrils than MVGGVV, hindered by the presence of the hydrophobic residues at the C-terminal. Analysis of the simulation kinetics and energetics reveals why MVGGVV forms fibrils and GGVVIA does not, and why adding I and A to MVGGVVIA reduces fibrillization and enhances amorphous aggregation into oligomeric structures. The latter helps explain why Aβ(1–42) assembles into more complex oligomers than Aβ(1–40), a consequence of which is that it is more strongly associated with Alzheimer’s disease.

INTRODUCTION

There are currently forty known protein deposition diseases or “amyloidoses.”¹ These diseases affect multiple organs and are characterized by the abnormal deposition of ordered aggregates of proteins, called fibrils. Notable amyloidoses are Alzheimer’s disease, which is linked to the abnormal deposition of the β-amyloid protein in the brain, Mad Cow disease, which is related to the aggregation of prion proteins in the central nervous system, and chronic inflammatory diseases, which are caused by an immune response triggered by the deposition of precursor Protein A in the liver. Although a different protein and a different organ system are involved in each of these diseases, the fibrils associated with all of them share a common basic structural feature, the so called “cross-β structure,” which consists of layers of β-sheets running parallel to the fibril axis containing strands that run perpendicular to the fibril axis. This paper focuses on understanding how variations in the sequence affect the likelihood that a particular sequence will form a fibril and the kinetic events that occur along the fibrillization pathway.

The cross-β structure was first identified by Sunde et al. based on high-resolution x-ray diffraction studies on a range of synthetic and natural amyloid fibrils.² In this structure, β strands are connected by backbone hydrogen bonds to form β-sheets which are parallel to the fibril axis and have a 15° axial twist; the hydrogen bonding distance is 4.7–4.8 Å intra-sheet and the inter-sheet spacing is approximately 10 Å.² Amyloid fibrils are ordered, insoluble structures 70–120 Å in diameter and of any length.^2–5 These observations, along with work in Dobson’s laboratory showing that non-disease-related proteins could also form fibrils,⁶ prompted the suggestion that fibril or protofibril⁷ formation was an inherent property of proteins, regardless of the sequence.^8–11 The idea here was that all protein backbones can form hydrogen bonds and that backbone-backbone hydrogen bonds are the glue that holds proteins together in a fibril. More recent evidence suggests however that the primary sequence of a protein also plays a role in determining its ability to adopt the cross-β structure necessary for fibril formation^12–15 and that the side chains influence the unique molecular arrangement of amyloid peptides in a fibril.

Proteins do not need to be sizeable in order to form fibrils; in fact selected fragments of amyloidogenic peptides form fibrils themselves.^16,17 For example, Aβ, the peptide associated with Alzheimer’s Disease, has several fragments that can independently aggregate into β-sheets.^18–20 These short peptide sequences, or “core sequences” as they are called, are believed to play a role in determining whether or not the parent peptide will form fibrils²¹; in fact, the identity and position of specific side chains in these short peptides dictates whether or not the peptide can adopt the cross-β structure and the type of aggregation pathway and kinetics that are followed.

The factors described above lead to the hypothesis that short core sequences from fibril forming peptides are central to amyloid formation, acting as the “Velcro” that holds these structures together. It follows then that understanding the fibrillization of core sequences should help us to better understand the fibrillization of the parent protein. Accordingly, the long term goal of this work has been to learn: which sequences will form fibrils, what types of side chains disrupt assembly, and how sequence affects molecular arrangement. Knowing the answers to these questions should help us to improve our understanding of amyloid fibril structure and the events leading to its formation.

Eisenberg and coworkers have identified several fibril-forming segments from disease-linked proteins and characterized their structure using x-ray diffraction on microcrystals formed by each short peptide.¹⁴ They grouped the types of cross-β spines into eight classes. The classes are defined according to whether: 1) the β-strands within each sheet are parallel or antiparallel, 2) the sheets pack face-to-face or face-to-back, and 3) the sheets are stacked parallel (up-up) or antiparallel (up-down). They found six different sequences, including SSTSSA, which have parallel β-strands, sheets packed face-to-face and stacked in an antiparallel conformation (Class 1). They also determined the molecular arrangement of short sequences related to the human prion protein (SNQNNF) and amyloid-β (GGVVIA).

Since the Sawaya et al.¹⁴ publication of the measured atomic structures of the fibrils formed by the thirteen amyloid-related peptides, many researchers have used atomistic molecular dynamics simulations to answer questions about assembly kinetics, details of fibril structure, preference for a particular arrangement for these peptides.^13,22–27 Atomistic molecular dynamics is used to perform stability calculations to determine if the predicted crystal structure is the free energy minimum (thermodynamically most stable) and how peptide sequence contributes to its stability. Park et al.²³ simulated five different peptide sequences containing : GNNQQNY, NNQQ, VEALYL, KLVFFAE, and STVIIE. These peptides were placed in all possible arrangements of β-sheet bilayers and the free energy of binding for each arrangement was calculated using the generalized Born solvation model. Interestingly, the greatest energetic contribution to the binding energies seemed to come from the free energies of the non-bonded interactions, i.e. side chains. Based upon this work, Park and coworkers concluded that the steric zipper forms most easily when the β-sheets are parallel because this allows similar or identical side chains to interact at the interface. In addition, since the backbone hydrogen bonds accounted for almost one-quarter of the total non-bonded interaction energy in their simulations, they concluded that the long-held idea that hydrogen bonding plays a significant role in the formation of the universal fibril structure is correct.²³

Several other groups have used molecular dynamics simulations to study the short, truncated amyloid-forming sequences identified by Sawaya et al.¹⁴ De Simone et al. performed GROMACS-based all-atom, explicit-solvent, 20 ns molecular dynamics on a pair of β-sheets composed of either two, three, four, ten or fifty SNQNNF peptides²⁴ associated together into the measured crystal structures. (Twenty nanoseconds was not enough time for the fifty SNQNNF peptides system to equilibrate.) The smallest system that remained stable over the time course of the simulation was the tetramer bilayer structure. Interestingly, they observed β-sheet twisting with a face-to-back orientation of the side chains between the two sheets and F6 packed tightly into the core. Vitagliano et al.²⁵ performed 60 ns all-atom molecular dynamics on a bilayer of β-sheets composed of ten strands of SSTSAA and of VQIVYK using the GROMACS package with explicit solvent. Over the time course of the simulation the inter-sheet interactions taken from the measured crystal structure of SSTSAA (face-to-face) completely deteriorated although the β-structure remained, suggesting that SSTSAA cross-β spines are unstable. The VQIVYK bilayer with face-to-face cross-β spine composed of V1, I3 and V4, was more stable than the SSTSAA bilayer and retained much of its β-structure, although it did not preserve the cross-β spine motif. Ho and coworkers have also used all-atom molecular dynamics simulations with DISCOVER 2.9.8 to study β-sheets of GGVVIA²⁶ and VEALYL.²⁷ For GGVVIA their starting configurations were single-layered parallel β-sheets with two, three, four, or five strands and bilayers of two, three, four or five parallel β-strands arranged in antiparallel β-sheets face-to-back as predicted by the crystal structure of Sawaya et al. Over the 10 ns simulation, the oligomers of GGVVIA remained relatively stable, indicating that the hydrophobic contacts I5, V4 and V3 play a significant role in holding the cross-β spine together. Lin et al. performed 10 ns stability simulations using DISCOVER 3 on the crystal structure of VEALYL, with the β-strands anti-parallel within a sheet and sheets stacked in parallel, face-to-back.²⁷ Over the course of the simulation, the β-sheet bilayer remained relatively stable, again suggesting the importance of the hydrophobic residues at the interface.

Although the atomistic-resolution simulations described above provide insights into the stability of particular fibrillar structures, they do not provide information about the pathway to fibril formation. An increasingly-popular way to elicit this information computationally is coarse-grained simulations where the combination of a simplified protein representation and an alternative simulation technique such as Monte Carlo or discontinuous (also called discrete) molecular dynamics (DMD) simulation allows access to much longer time scales. For example, the Irbäck group has used Monte Carlo simulations in conjunction with a simplified force field, PROFASI, to investigate the fibrillization of Aβ16–22 peptides²⁸ and of amyloid tau fragment²⁹. Urbanc et al. applied DMD to a coarse-grained model, similar to the one used in this paper to study Aβ oligomerization mechanisms.³⁰ Ding et al. have used DMD to study the prion-like conformational conversion of a model peptide from an α-helix to a β-strand when in proximity to other β-sheets.³¹ Auer et al. examined the nucleation and structural changes associated with fibrillar assembly using a flexible tube model.^32,33 The dependence of fibril formation pathways on the energy difference between two possible peptide conformers was examined by Pellarin et al. using a simple model peptide with four backbone and six side-chain spheres.³⁴ The Shea group introduced a peptide model with single-sphere side-chains of four types (hydrophobic, polar, positive charge, negative charge) to examine how side chain characteristics influence the fibrillization pathway.^35,36 Lattice models have been employed by Li et al. to study fibril growth mechanisms.^37,38 A review of the application of coarse-grained models to protein aggregation simulations can be found in reference.³⁶ Our strategy has been to use coarse-grained models of intermediate resolution that incorporate just enough detail to account for amino acid specificity and yet allow for simulations that are fast enough to look at kinetics along the whole fibril formation pathway.

In this paper we simulate the spontaneous assembly of large systems containing four of the peptides whose fibril crystal structures were measured by Sawaya et al.: SNQNNF (PrP(170–175)), SSTSAA (RNaseA(15–20)), MVGGVV(Aβ(35–40)), and GGVVIA(Aβ(37–42)).¹⁴ We also simulate the sequence MVGGVVIA (Aβ(35–42)) an overlapping combination of the last two sequences in the previous list. This is accomplished by combining PRIME20, an intermediate–resolution description of the protein geometry for all twenty amino acids³⁹ that we have developed.^40–45 It was designed to be used with discontinuous molecular dynamics (DMD), a fast alternative to traditional molecular dynamics applicable to systems interacting via discontinuous potentials, such as the square-well potential.^30,46–51 The motions of 48 peptides are monitored. An initial configuration of random coils at high temperatures is slowly cooled to the temperature of interest and then simulated until an equilibrium structure is reached. Our goals are to test the ability of PRIME20 to distinguish the role played by each of the twenty different amino acids in fibril formation, to validate PRIME20’s ability to predict each sequence’s propensity to form fibrils, and to contribute to the fundamental understanding of the fibril formation pathway. An additional goal is to learn how combining different fragments from the same protein (herein Aβ (35–40, 37–42, and 35–42)) impacts their ability to form fibrillar structures. We explore how changing sequence and temperature affect the aggregation pathway by monitoring the formation of different structures such as β-sheets (dimers, trimers, tetramers, pentamers, hexamers and other large oligomers), amorphous aggregates and fibrils as a function of time.

Highlights of our results are the following. Depending upon the sequence and the temperature, we are able to observe the spontaneous formation of fibrillar structures in 48-peptide systems starting from a random configuration of random coil conformations. The fragments SNQNNF, SSTSAA and MVGGVV form large numbers of fibrils at low to moderate reduced temperatures and cease to form fibrils above the so-called fibrillization temperature, T_fibril, in agreement with our previous results on KLVFFAE⁵² and STVIIE⁵³. However, in contrast to KLVFFAE and STVIIE, which exist primarily as monomers at T > T_fibril, the more hydrophobic sequences SSTSAA and MVGGVV continue to aggregate into large numbers of amorphous aggregates above the fibrillization temperature. MVGGVVIA forms moderate numbers of fibrils at low to moderate reduced temperatures and has disordered aggregates over the entire temperature range. GGVVIA forms β-sheets but does not stack into fibrils over the whole range of temperatures at least for the simulation times we have studied even though its crystal structures has been observed experimentally. It may be that our simulations are not long enough or that this is a relatively slow process compared to the spontaneous fibrillization of other sequences. In an effort to understand why β-sheets of MVGGVV stack to form fibrils while β-sheets of GGVVIA do not, even though they have four residues in common, we examined their aggregation pathways and the different possibilities for strand- and side-chain arrangements within and between sheets. We find that the glycines at the end of GGVVIA make it easier for out-of-register strand arrangements to occur and that these in turn reduce the energy available for stacking. We also find that the addition of IA to MVGGVV to form MVGGVVIA hinders the process of sheet stacking in favor of more disordered aggregates, likely due to the formation of trapped asymmetric configurations. The two C-terminal residues I and A on Aβ42 make the system more likely to form long-lasting oligomers on the path towards creation of protofilaments This yields insights into the differences between Aβ40 and Aβ42 fibrillation kinetics.

This paper is organized as follows. In the next section, we describe the peptide model and simulation method. In the following section, we present the results obtained from simulations of multi-peptide systems at various conditions. The last section is a discussion of our results.

Materials and Methods

Model Peptide and Forces

In this work we use our implicit solvent force field, PRIME20, to describe the geometry and energetics of the short segments of heteropeptides sequences considered here. PRIME20 was introduced by Cheon et al.³⁹ as an extension of PRIME, an implicit solvent intermediate-resolution protein model previously used in simulations of the aggregation of polyalanine and polyglutamine. PRIME was originally developed by Smith and Hall^41,54 and later improved by Nguyen et al.⁴³ More recently the PRIME model was extended to the study of polyglutamine peptides.⁴⁴ In PRIME, the protein backbone is represented by three united atom spheres, one for the amide group (NH), one for the carbonyl group (CO), and one for the alpha-carbon and its hydrogen (C_αH). In the original version of PRIME, each side chain was represented by a single sphere for polyalanine and by a chain of four spheres for polyglutamine. In PRIME 20, the twenty possible side chains are modeled as single spheres of unique size, atomic mass and C_α—R bond length. All backbone bond lengths and angles are set to their ideal values. In order to maintain the trans-configuration we fix the consecutive C_α—C_α distance. The side chains are positioned relative to the protein backbone so that all residues are L-isomers. The solvent molecules in our system are modeled implicitly.

All forces between the united atom spheres are modeled with discontinuous potentials, e.g. hard-sphere and square-well interactions. The excluded volume of each of the peptide’s four united atoms is modeled using a hard sphere interaction. The covalent bond lengths are maintained using a hard sphere interaction that prevents them from moving outside of the range (1+δ)l to (1-δ)l, where l is the ideal bond length and δ is the tolerance, which is set at 2.375% (41). Ideal backbone bond angles, C_α—C_α distance, and the residue L-isomerization are maintained by imposing a series of pseudobonds whose lengths are also allowed to fluctuate by 2.375%.

Hydrogen bonding is represented in PRIME 20 as a square well attraction of depth ε_HB and width 4.5Å between the backbone amide and carbonyl groups. Hydrogen bonds are anisotropic in nature so we must constrain their formation to occur only when the NH united atom vector and the CO united atom vector point towards each other and the angle between those vectors is restricted between 120° and 180°. In order to accomplish this, a set of conditions must be met which is described in detail in our earlier work.^42,43,45

The non-hydrogen-bonding interactions in PRIME20 are all modeled as square well interactions between the spherical units on each amino acid with strength (well depth) and range determined individually for each pair. Since solvent is modeled implicitly these are all effective interactions or potentials of mean force. In PRIME20, the energy parameters that describe the side chain / side chain interactions and the hydrogen bonding interactions between backbone NH and CO, and between side chain and side chain are derived in the following way. Briefly, the twenty possible amino acids are classified into 14 groups: [LVI] [F] [Y] [W] [M] [A] [C] [ED] [KR] [P] [ST] [NQ] [H] [G], according to their side chain size, hydrophobicity, and possibility of hydrogen bonding. The aforementioned energy parameters were determined by Cheon et al.³⁹ who applied a perceptron-learning algorithm and a modified stochastic learning algorithm to optimize the energy gap between 711 known native states from the PDB and decoy structures generated by gapless threading. The number of independent pair-interaction parameters was chosen to be small enough to be physically meaningful yet large enough to give reasonably accurate results in discriminating decoys from native structures. A total of nineteen interaction parameters with a 5.75Å heavy atom criteria were used to describe the side chain energetics.

The system temperature is scaled by the hydrogen bonding energy between the backbone NH and CO, ε_HB, so that the reduced temperature is T* = k_BT/ε_HB.

Discontinuous Molecular Dynamics

Discontinuous molecular dynamics (DMD) is a variant on standard molecular dynamics that is applicable to systems of molecules interacting via discontinuous potentials (e.g., hard sphere and square-well potentials). Unlike soft potentials such as the Lennard-Jones potential, discontinuous potentials exert forces only when particles collide, enabling the exact (as opposed to numerical) solution of the collision dynamics. This imparts great speed to the algorithm, allowing sampling of longer time scales and larger systems than traditional molecular dynamics. The particle trajectories are followed by locating the time between collisions and then advancing the simulation to the next collision (event).^55,56 DMD on chain-like molecules is generally implemented using the "bead string" algorithm introduced by Rapaport^57,58 and later modified by Bellemans et al.⁵⁹ Chains of square-well spheres can be accommodated in this algorithm by introducing well-capture, well-bounce, and well-dissociation "collisions" when a sphere enters, attempts to leave, or leaves the square well of the adjacent sphere. DMD simulations are performed in the canonical ensemble (NVT) with the initial velocities chosen randomly from a Maxwell-Boltzmann distribution about the desired system temperature.

Details of the simulation are as follows. The initial positions of the particles or spheres are chosen randomly while still ensuring that no geometrical constraints are violated. The number of particles in the system is determined by specifying the concentration, c = N/L³, where N is the number of molecules in the box and L is the simulation box length. Periodic boundary conditions are imposed. Since we are simulating large systems at high concentrations starting from random initial configurations we must ensure that the box length is large enough to prevent the molecules from interacting with themselves but still allow them to interact with their periodic image. We set L = 200Å in this study. The simulation proceeds according to the following schedule: identify the first event (e.g., a collision), move forward in time until that event occurs, calculate new velocities for the pair of spheres involved in the event and calculate any changes in system energy resulting from hydrogen bond events or side chain interactions, find the second event, and so on. Types of events include excluded volume events, bond events, and square-well hydrogen bond and side chain interaction events. For more details on DMD simulations with square-well potentials, see articles by Alder and Wainwright⁵⁵ and Smith et al.⁵⁶

A total of five model systems are studied in this work; all contain 48 peptides at concentrations c = 10mM. The peptides considered are SNQNNF, SSTSAA, MVGGVV, GGVVIA and MVGGVVIA. Each simulation is started at high temperature to ensure a random initial configuration and then slow-cooled to the temperature of interest to minimize kinetic trapping. Slow-cooling is achieved by decreasing the temperature in discrete steps starting from a high temperature until we reach the desired simulation temperature. The simulation temperature is maintained using the Andersen thermostat.⁶⁰ Five simulations are run for each sequence at the given temperature and concentration (state). Error bars are taken to be the standard deviation at each state. All simulations are run for an average of 100–200 billion collisions depending on simulation conditions, sequence, temperature and concentration.

The formation of β-strands, β-sheets, amorphous aggregates and fibrils are monitored and analyzed. We check to see if the β-strands in a β-sheet are arranged in a parallel or anti-parallel configuration. The criteria for assigning the types of structures formed are the following. If each peptide in a group of peptides has at least two inter-peptide hydrogen bonds or side chain interactions with a neighboring peptide in the same group, then that group is classified as an aggregate. Aggregates can be either ordered or amorphous. If an aggregate contains β-sheets or fibrils, we classify it as an ordered aggregate. If each peptide in a group of peptides has at least n/2, where n = chain length, inter-peptide β-hydrogen bonds to a particular neighboring peptide in the group, we classify this group as a β-sheet. (A β-hydrogen bond is a hydrogen bond between two residues whose backbone angles are in the β-region of the Ramachandran plot.) If at least two β-sheet structures form inter-sheet side chain interactions (at least four side chain interactions per peptide per β-sheet), we classify this as a fibril; otherwise, we classify this and isolated β-sheets as non-fibrillar β-sheet structures. If an aggregate does not contain β-sheets but the peptides in the aggregate have any side chain contacts, then the aggregate is considered amorphous. If an aggregate contains peptides with less than n/2 inter-peptide β-hydrogen bonds between neighboring chains then this is also considered to be an amorphous aggregate.

Results

Table I summarizes our simulation results on SNQNNF, SSTSAA, MVGGVV, MVGGVVIA, and GGVVIA and includes a comparison to STVIIE from our earlier work.⁵³ The table is organized into four sections, each containing the results of multiple runs at temperatures that span the range over which each sequence is most likely to form a fibrillar structure. Table I lists the percentage of peptides at the end of the simulation runs that are monomers, in non-fibrillar β-sheets, in amorphous aggregates or in fibrils. The final structures formed are categorized as “ordered” (greater than 40% fibril and β-sheet), “slightly ordered” (low or no observed fibrils and high β-sheet), “slightly disordered” (high amorphous content but still containing fibrils or β-sheets), and “disordered” (high amount of monomers or amorphous aggregates).

Table I.

Percentage of peptides in each sequence that are in monomer, non-fibrillar β-sheet, disordered aggregates and fibril conformations at the end of low, intermediate, and high reduced temperature simulations at 10mM concentration.

Sequence	T*	% of monomers	% of non-fibril β-sheets	% of amorphous aggregates	% of fibrils	Structure
STVIIE	0.13	0.0(0.0)	8.5(8.4)	1.0(0.8)	90.5(7.8)	Ordered
SNQNNF	0.13	0.0(0.0)	10.2(16.9)	0.1(0.1)	89.8(16.8)	Ordered
SSTSAA	0.13	0.0(0.0)	52.1(36.2)	2.3(0.6)	47.6(36.1)	Ordered
MVGGVV	0.13	0.0(0.0)	25.0(5.7)	4.8(2.7)	70.2(6.8)	Ordered
MVGGVVIA	0.13	0.0(0.0)	51.9(14.0)	7.8(2.7)	40.3(14.1)	Ordered
GGVVIA	0.10	1.1(0.9)	94.9(3.6)	1.1(0.6)	2.9(3.3)	Slightly Ordered
STVIIE	0.15	0.0(0.0)	24.8(14.0)	0.0(0.0)	75.2(14.0)	Ordered
SNQNNF	0.15	0.6(0.8)	1.4(2.4)	0.1(0.1)	97.9(3.0)	Ordered
SSTSAA	0.15	0.4(0.4)	10.5(7.2)	0.2(0.2)	88.9(7.2)	Ordered
MVGGVV	0.15	0.1(0.1)	36.1(13.5)	4.1(2.0)	59.7(14.4)	Ordered
MVGGVVIA	0.15	0.0(0.0)	57.2(11.4)	8.7(2.9)	34.1(12.7)	Slightly Ordered
GGVVIA	0.12	5.2(1.4)	93.9(1.8)	0.7(0.3)	0.2(0.2)	Slightly Ordered
STVIIE	0.16	0.2(0.3)	24.4(14.3)	0.1(0.1)	75.3(14.0)	Ordered
SNQNNF	0.16	4.6(2.1)	3.6(3.3)	0.4(0.2)	91.4(4.3)	Ordered
SSTSAA	0.16	5.4(1.3)	11.2(5.9)	1.3(0.3)	82.1(6.4)	Ordered
MVGGVV	0.16	0.2(0.2)	40.9(21.1)	9.0(5.8)	49.9(26.5)	Ordered
MVGGVVIA	0.16	0.0(0.0)	66.1(7.7)	8.4(3.2)	25.5(8.4)	Slightly Ordered
GGVVIA	0.13	15.6(2.4)	80.2(3.0)	3.9(0.7)	0.3(0.1)	Slightly Ordered
STVIIE	0.17	2.2(1.4)	11.3(0.6)	0.5(0.3)	86.0(7.4)	Ordered
SNQNNF	0.17	33.2(4.0)	50.8(11.6)	9.3(2.5)	6.8(14.7)	Slightly Ordered
SSTSAA	0.17	33.1(1.1)	47.8(1.8)	18.0(0.8)	1.2(0.5)	Slightly Ordered
MVGGVV	0.17	2.2(0.6)	52.6(15.3)	30.1(8.2)	15.4(23.3)	Slightly Disordered
MVGGVVIA	0.17	0.1(0.1)	68.1(5.2)	13.7(3.4)	18.1(7.2)	Slightly Ordered
GGVVIA	0.15	55.7(0.5)	21.0(0.5)	23.2(0.2)	0.1(0.0)	Disordered

Values in parenthesis indicate error bars.

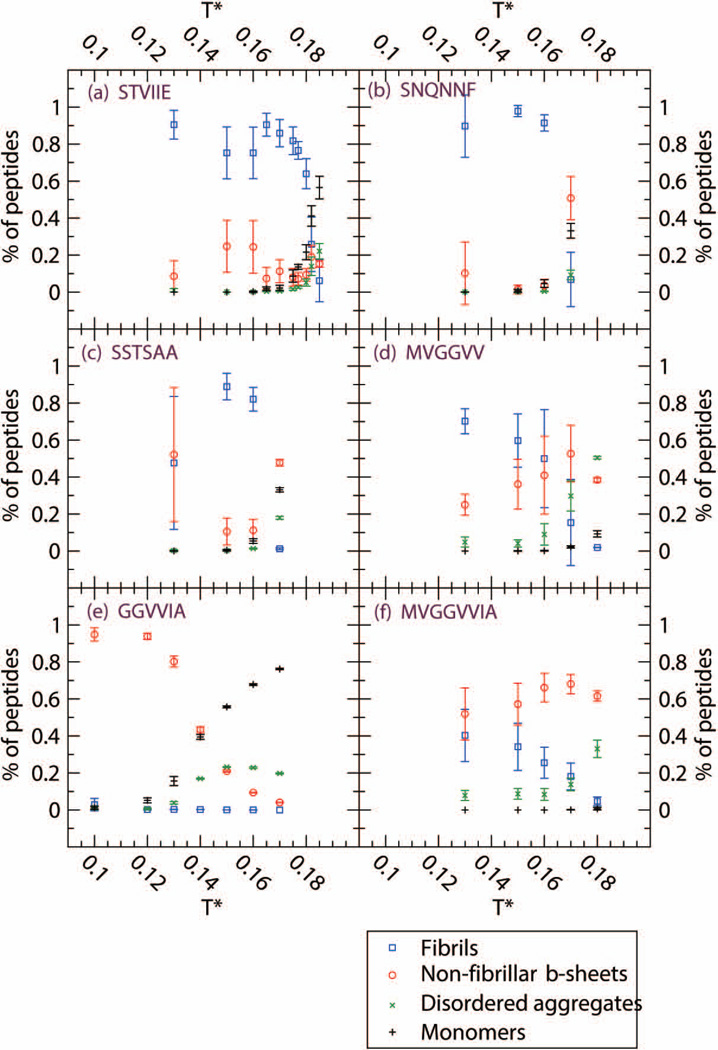
From the upper panel of Table I, we can see that at low temperature T* = 0.13, STVIIE, SNQNNF and MVGGVV readily form fibrils and that SSTSAA and MVGGVVIA form fibrils to a lesser extent but have high non-fibrillar β-sheet content. MVGGVVIA also has some amorphous aggregate content. At the lowest temperature T*=0.10 that we ran for GGVVIA, almost all of the GGVVIA peptides assemble into β-sheets but no fibrils are observed. As we increase to intermediate temperatures in the middle panels of Table I, we see that STVIIE, SNQNNF, SSTSAA, and MVGGVV continue to form fibrils, with SNQNNF and SSTSAA forming considerably more fibrils and MVGGVV forming less. As expected, to compensate for this change in fibrillar content, MVGGVV forms more non-fibrillar β-sheets while SNQNNF and SSTSAA form less. MVGGVVIA forms less fibrils, moving to the “slightly ordered” category and more non-fibrillar β-sheets and amorphous aggregates. As we increase to the highest temperature (T*=0.15 for GGVVIA and 0.17 for other sequences) in the bottom panel of Table I only STVIIE continues to form fibrils. SSTSAA, MVGGVV and GGVVIA form a considerable number of amorphous aggregates; SNQNNF, SSTSAA, MVGGVV and MVGGVVIA form large numbers of non-fibrillar β-sheets which do not stack into fibrils. The robust β-sheet former, GGVVIA, however has begun to lose β-sheet content. GGVVIA did not form fibrils in our simulations at any temperature even though its crystal structure has been observed¹⁴ and a two–layer structure remained stable during simulations by Chang et al.²⁶ Figure 1 displays the temperature dependence of the four observables described in table I for the six sequences. Error bars are taken to be the standard deviation at each temperature. (The data on STVIIE is taken from our previous paper.⁵³

Figure 1.

Four observables at c=10mM for six sequences (a) STVIIE (b) SNQNNF (c) SSTSAA (d) MVGGVV (e) GGVVIA and (f) MVGGVVIA. Percentage of peptides in fibrils (blue circle), non-fibrillar β-sheets (red circle), amorphous aggregates (green X) and monomers (black cross). Non-fibrillar β-sheets refer to β-sheets in disordered aggregates or single β-sheets without cross-β spine structure.

The fact that STVIIE, SNQNNF, SSTSAA and MVGGVV form fibrils over a wide range of temperatures, including low temperatures (where it is usually more challenging to form fibrils in a simulation) indicates that these are very strong fibril formers, especially compared to the other sequences studied. We have found in previous work on STVIIE and KLVFFAE (Aβ(16–22)) that the fraction of peptides that form fibrils increases with temperature up until the so-called fibrillization temperature, T_fibril, beyond which fibrils do not form.^52,53 The higher the value of T_fibril, the more stable the fibril is. The relatively high values of T_fibril for STVIIE (T*_fibril =0.18), SNQNNF (T*_fibril =0.165), SSTSAA (T*_fibril =0.165) and MVGGVV ( T*_fibril =0.16) suggests that their fibrils are more stable than fibrils formed by the other sequences that we have considered. This has yet to be confirmed experimentally however since fibrillization is generally measured only at a single temperature. The ease with which STVIIE, SNQNNF, SSTSAA and MVGGVV form fibrils may be due to the fact that these fragments are composed of bulky side chains which have a combination of hydrophobic residues and polar residues like S, N and Q in SSTSAA and SNQNNF.

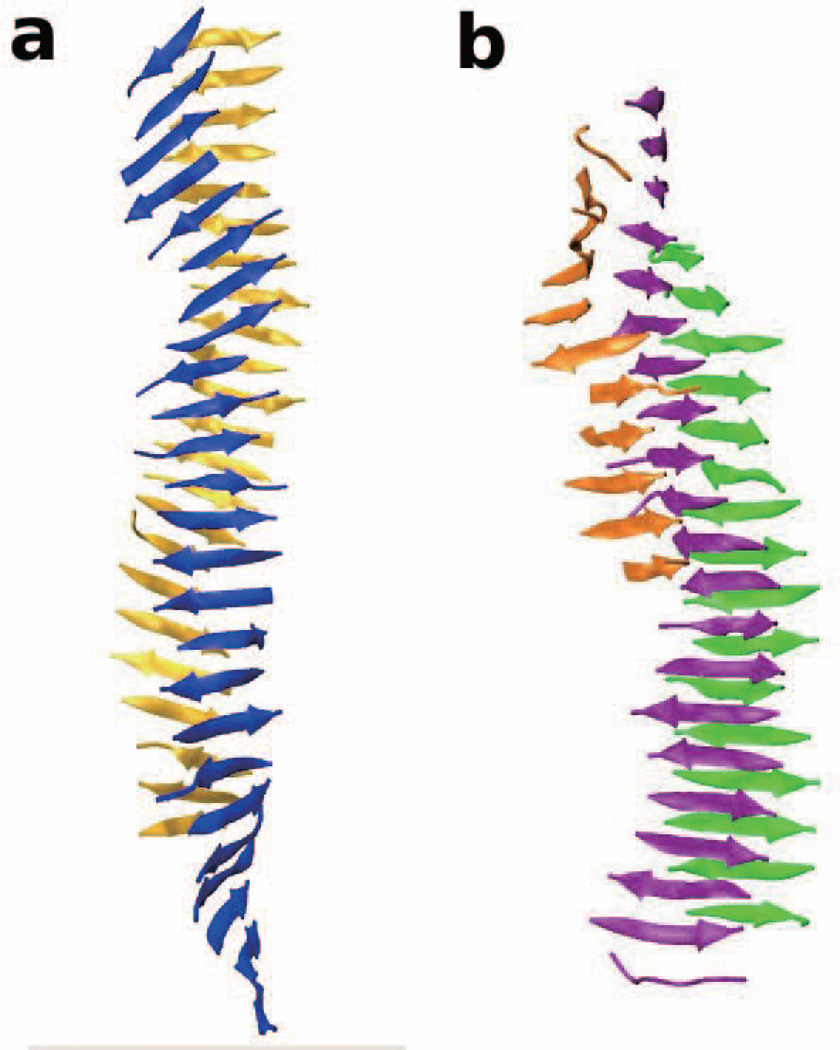
Figure 2 shows a snapshot of the best fibrils formed by SNQNNF (Fig. 2a) and SSTSAA (Fig. 2b) at T*=0.15. The fibril for SNQNNF is a bilayer (with one β-sheet colored blue and one β-sheet colored yellow) with a moderate twist. The fibril for SSTSAA is a tri-layer (with two large β-sheets colored purple and green, and a smaller β-sheet colored orange). The SSTSAA structure is less twisted than the SNQNNF structure. This may be because the single-sphere side-chains on SSTSAA based on the PRIME20 geometry are smaller than those on SNQNNF, allowing the two β-sheets to lay flat without tilting. The amount of twist in the SNQNNF fibril is similar to those for the STVIIE, STVIFE, STVIVE fibrils whereas the amount of twist for SSTSAA is similar to those for STAIIE and STVIAE, as can be seen by reference to Fig. 4 of our previous simulations-based work.⁵³ Since the structures formed by MVGGVV resemble cylinders rather than two-layer β-sheets (as we will see later), it is hard to comment about their twist.

Figure 2.

The fibril structures formed by (a) SNQNNF and (b) SSTSAA at T*=0.15.

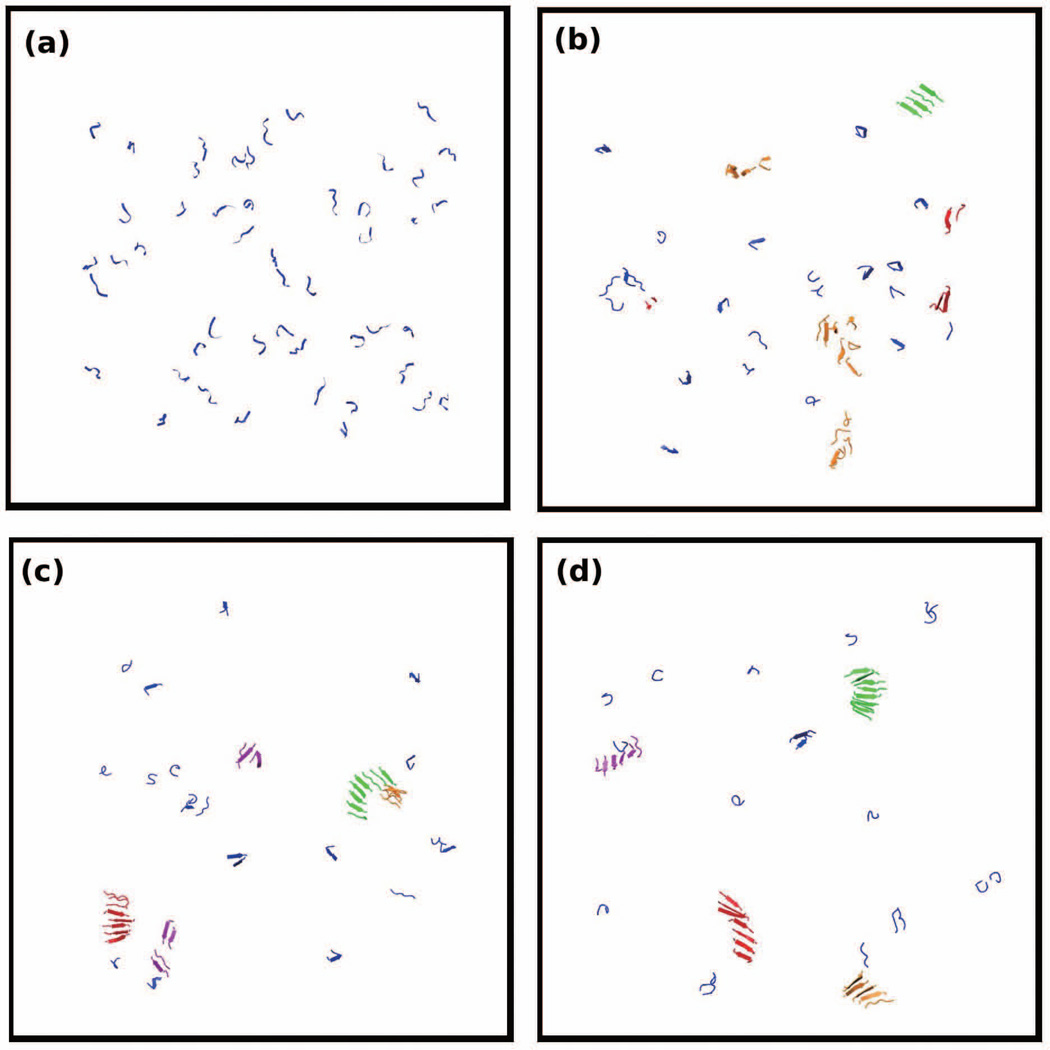
Figure 4.

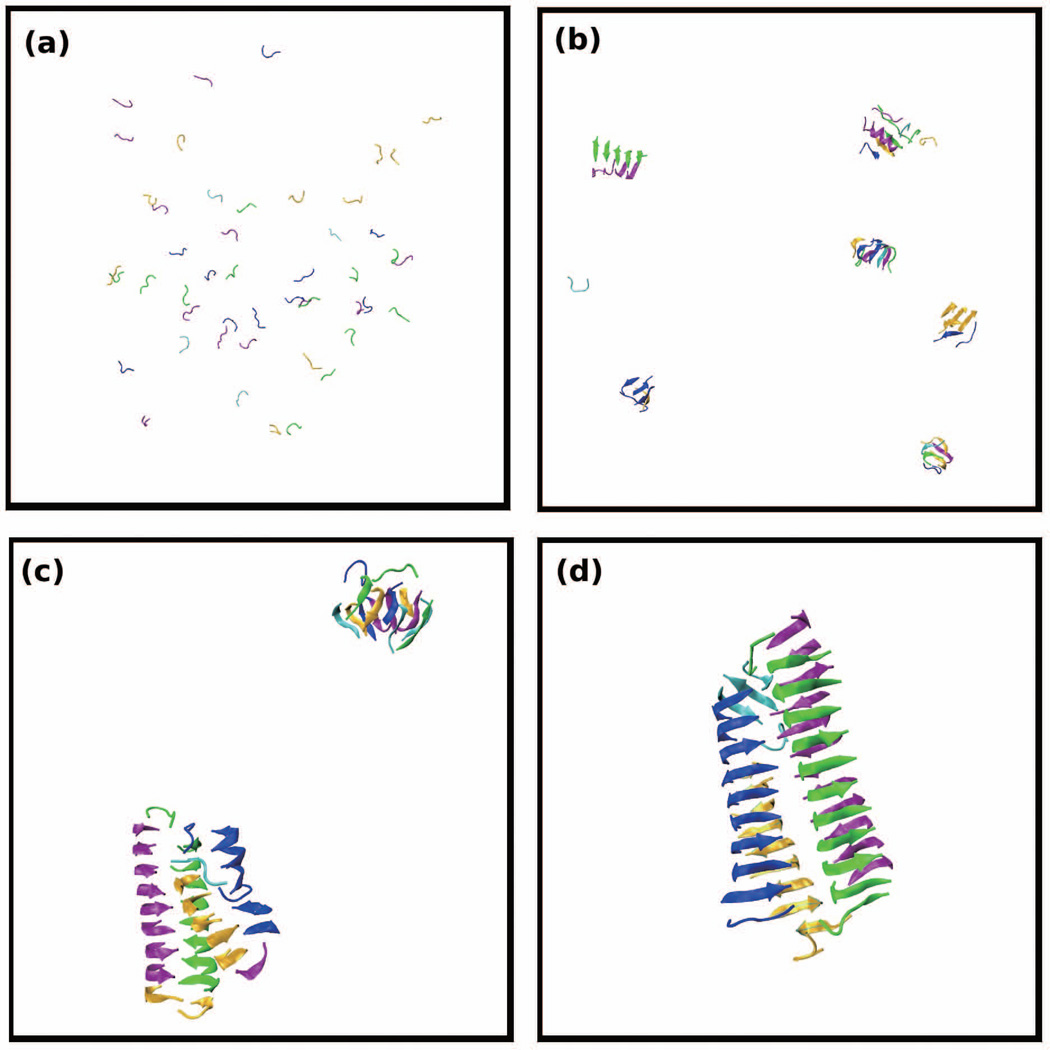
Simulation snapshots of 48 peptides of GGVVIA at T*=0.13 and c=10mM. Snapshots are selected at reduced times (a) t*=20 (b) t*=1163 (c) t*=2568 and (d) t*=17529.

We examined the assembly of MVGGVV, GGVVIA and MVGGVVIA at low, intermediate, and high temperatures. These sequences are of particular interest because the first two sequences overlap (have four residues in common) and together form the third sequence, Aβ35–42. Fibrils for three sequences have been isolated experimentally.^14,61 Fibrils were observed for MVGGVV in our simulations at low-to-intermediate temperatures, but at higher temperatures it forms less fibrils and instead forms an equal percentage of β-sheets and amorphous aggregates. In fact, MVGGVV is not the best fibril former considered in our simulations, as mentioned earlier its T*_fibril is lower than those for STVIIE, SNQNNF and SSTSAA. The fragment GGVVIA did not form fibrils over the entire range of temperatures selected. Instead it formed a high percentage of β-sheets and almost no amorphous aggregates. It is unclear why our simulations of GGVVIA do not result in fibrils as is found experimentally. GGVVIA certainly likes to form β-sheets, forming them at temperatures as low as T*=0.10, but the sheets do not stack. It may be that our simulation times are too short or our temperatures are too high to allow the GGVVIA β-sheets to find each other and structurally reorganize into fibrils. The combination of MVGGVV and GGVVIA, MVGGVVIA formed relatively few fibrils (≤40%) over the range of temperatures considered, including the low-to-moderate temperatures where MVGGVV formed fibrils. MVGGVVIA also forms a sizeable number of β-sheets (≥50%) at all temperatures and more amorphous aggregates (≥7%) than any other sequence at low-to-moderate temperatures. Again, much longer simulations and/or more detailed force fields may be necessary in order to observe the structural reorganization necessary for obtain a fibrillar structure for MVGGVVIA. In the next few paragraphs we present analyses aimed at learning why MVGGVV forms fibrils while GGVVIA does not in our simulations. After that we discuss the behavior of the combination sequence MVGGVVIA.

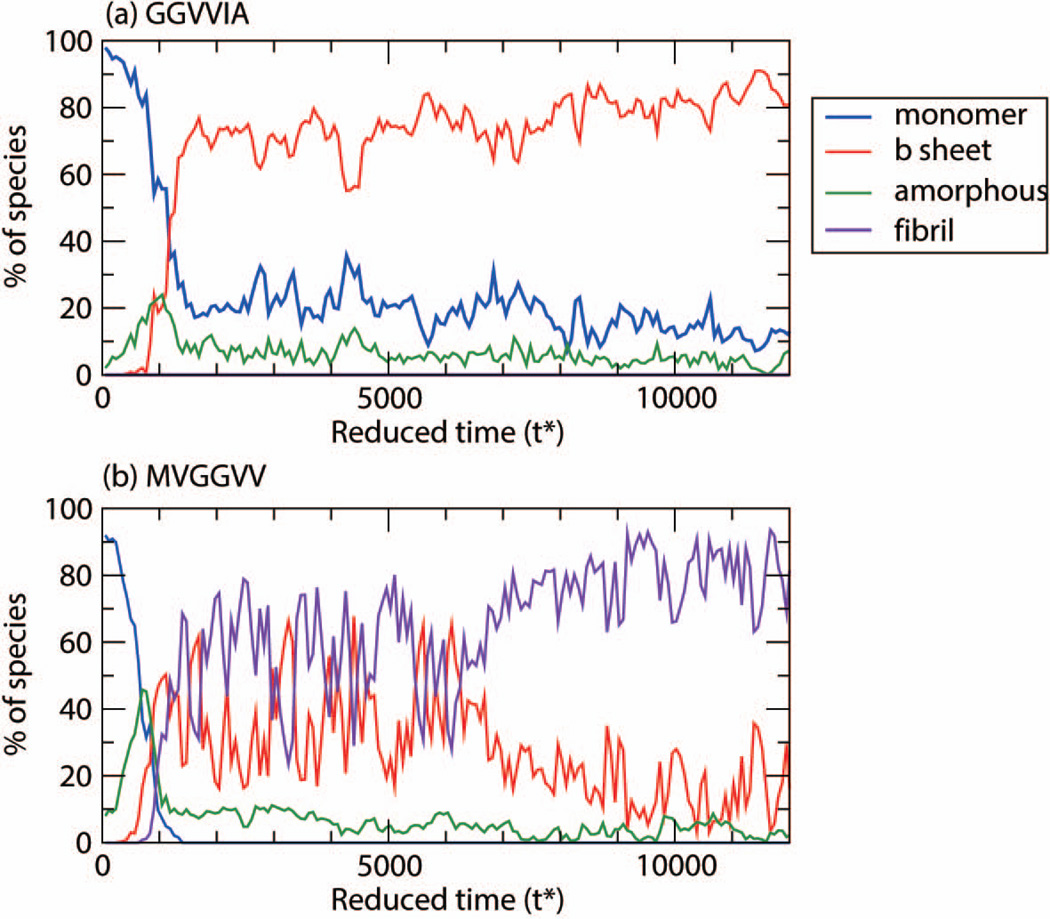
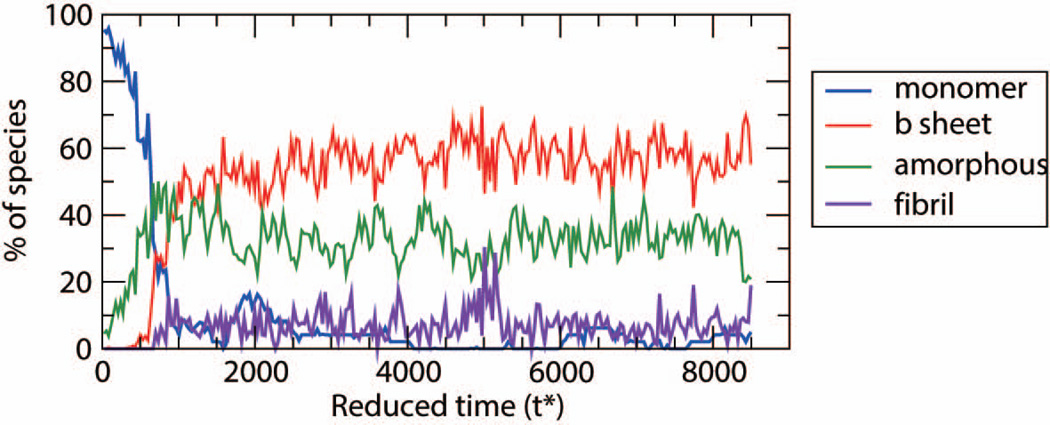
In an attempt to learn why MVGGVV formed fibrils in our simulations and GGVVIA did not, we examine their aggregation pathways. Figures 3(a) and (b) show the percentage of GGVVIA peptides and MVGGVV peptides at low temperature, T*=0.13, respectively, in each species (monomer, β-sheet, amorphous aggregate, fibril) as a function of simulation time. Both sequences start out at time t*=0 as monomers (blue curve) but quickly begin to form amorphous aggregates (green curve) at very early times. For GGVVIA (Fig. 3(a)) the competition between β-sheet and amorphous aggregate formation begins at time t*=700 and ends at t*=900, when amorphous aggregates disappear and β-sheet growth takes off; no fibrils appear after that. For MVGGVV (Fig. 3(b) there is a competition between β-sheet and amorphous aggregate formation starting at t* = 400 and ending at t* = 900 during which amorphous aggregates begin to disappear and both β-sheets (red curve) and fibrils (purple curve) begin to grow. Thus it is apparent that the early steps in the aggregation assembly pathways for MVVGGV and GGVVIA are similar except that the β-sheets for MVGGVV have the ability to associate together into fibrillar structures and the β-sheets for GGVVIA do not. Figure 3(b) for MVGGVV sequence shows a relatively long time period of coexistence, t*=1000 to t*= 6000, between fibril and non-fibrillar β-sheet structures followed by a long slow rearrangement or settling into a fibrillar structure after t*=7000. Evidently the enthalpic contribution to the energy of the system for MVGGVV is great enough to overcome the entropic loss associated with fibril formation, but that of GGVVIA is not.

Figure 3.

Population of each species: monomer, β-sheets, amorphous, and fibril for (a) GGVVIA at T*=0.13 and (b) MVGGVV at T*=0.13

Figures 4 and 5 show simulation snapshots that illustrate the kinetic pathways at T*=0.13 for GGVVIA and MVGGVV, respectively. Figure 4 shows a series of configurations for GGVVIA at: (a) t = 20, (b) t=1163 where disordered oligomers (orange) and β-sheets (green) have begun to form, and (c) t=2568 where the blue and red β-sheets have grown to form larger oligomers but have not associated to form a fibril. Even though we have run extremely long simulations (to t*=17529) we see only β-sheets (red, green, orange, purple) but no fibrils. Figure 5 shows a series of configurations for MVGGVV at T* = 0.15 at: (a) t=25 (b) t=1324 where there are a few β-sheets and amorphous aggregates, (c) t=4356 where most of the small oligomers have disappeared and a fibril-like structure has begun to form, and (d) t=17433 which shows a close up of the fibril-like structure that has formed. Figure 5(e) also shows a view of the structure in Fig. 5(d) down the fibril axis. This structure contains two cross β-spines that are attached; each cross β-spine looks like a half-cylinder with two curved β-sheets. The curving is likely due to the two glycine residues at the center of each peptide.

Figure 5.

Simulation snapshots of 48 peptides of MVGGVV at T*=0.15 and c=10mM. Snapshots are selected at reduced times (a) t*=25 (b) t*=1324 (c) t*=4356 and (d) t*=17433. (e) Fibril axis view of (d). Figures (c) and (d) are close-ups of the structures that form.

Figure 6 shows the population curves (monomers, β-sheets, amorphous aggregates and fibrils) as a function of time for MVGGVV at high temperature, T*=0.17. From the very beginning of the simulation at time, t=0 until t* = 700, the monomers (blue curve) are rapidly depleted in favor of amorphous aggregates (green curve) whose population is fairly stable. From t* = 700 to 1000, the remaining monomers come together to form β-sheets (red curve) whose population increases slowly thereafter but whose number never exceeds the number of amorphous aggregates. Since the population of β-sheets remains small there are not enough β-sheets to encourage fibril growth (purple curve) and the system remains in the amorphous state. In contrast, at lower temperatures, T* = 0.13, as shown in Figure 3(a), the MVGGVV peptides first associate to form amorphous aggregates which, along with the remaining monomers, rearrange into more ordered β-sheets that can then associate into a fibrils. Comparison of the population vs. time data in Figures 3(a) and 6 underscores the importance of temperature in fibril formation.

Figure 6.

Population of each species: monomer, β-sheets, amorphous, and fibril for MVGGVV at T*=0.17

It is of interest to ask why MVGGVV, which prefers ordered conformations at lower temperatures such as T* = 0.15 undergoes a shift towards considerable amorphous aggregate formation as temperature increases (See Table I). This large increase in the number of amorphous aggregates as temperature increases above the fibrillization temperature is also seen here for SSTSAA, and for STVIVE and VAGAAAGAV in our previous simulations. It is not seen here for SNQNNF, and for STVIIE and AGAAAAGA in our previous simulations.^53,62 The difference can be traced to the differences in the types of amino acids in the various sequences. For example although the amino acids in SNQNNF are of similar size to those in MVGGVV (with the exception of F and G) the biophysical characteristics of their side chains are vastly different. Methionine and valine are mainly hydrophobic whereas asparagine (N) and glutamine (Q) are polar and capable of side-chain hydrogen bonding. Similarly VAGAAAGAV has more hydrophobic side chains than AGAAAAGA. We conclude that it is the side chain functionality, particularly the hydrophobicity, which is most likely contributing to the presence of amorphous aggregates at temperatures above the fibrillization temperature.

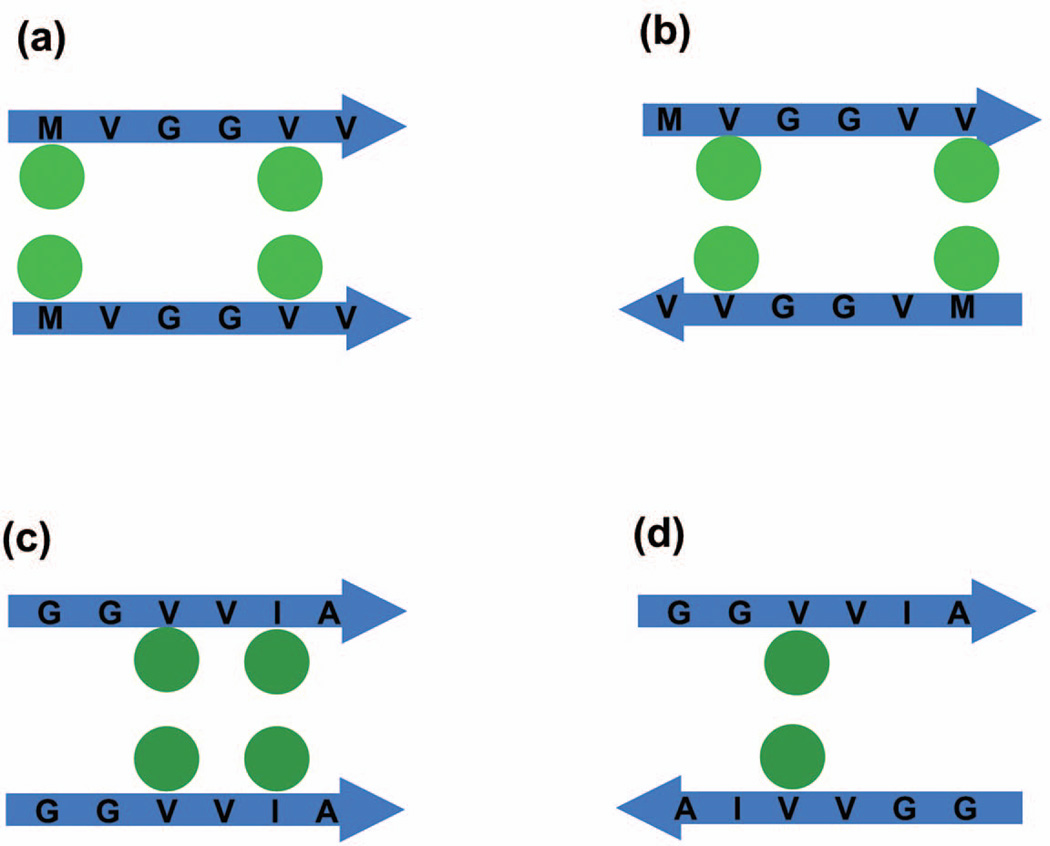
To understand why the β-sheets for MVGGVV stack into fibrillar structures and the β-sheets for GGVVIA do not, we examine the types of β-sheet and stacked structures that each could form, and relate this to the energies associated with these conformations and their alignment (parallel vs. antiparallel) within sheets and between sheets. Figure 7 shows schematics of the interactions between side chains on two adjacent sheets in a stack for (a) parallel MGVVVV β-sheets, (b) antiparallel MVGGVV β-sheets, (c) parallel GGVVIA β-sheets, and (d) antiparallel GGVVIA sheets. Since ε_MM = ε_{VV =} ε_VM = ε_II = 0.198 ε_HB, and ε_{AA =} 0.086 ε_HB the side chain interactions energies for these four cases, respectively are (a) ε_MM+ε_VV = 0.396ε_HB for the configuration shown or alternatively ε_VV+ε_VV = 0.396ε_HB (b) ε_VV+ε_VM = 0.396ε_HB for the configuration shown or alternatively ε_MV+ε_VM=0.396ε_HB (c) ε_VV+ε_II=0.396ε_HB for the configuration shown or alternatively ε_VV+ε_AA=0.284ε_HB, (d) ε_VV=0.198ε_HB for the configuration shown. Thus, assuming that the strands within the individual sheets are in register (as in this schematic) and that parallel and antiparallel configurations are equally likely, the average energy of a stacked MVGGVV conformation is considerably greater in magnitude than the average energy of a stacked GGVVIA conformation. (By average here we mean the average over all possible equally-weighted configurations.) The assumption that the MVGGVV strands within the β-sheets and between the sheets tend to be in register regardless of whether they are parallel or antiparallel is a good one as can be seen in Fig. 5(d). This is because within the context of PRIME20 the sidechain–sidechain V-V, M-M and M-V interactions are all the same, making the sequence relatively symmetric. In contrast, we have found in our simulations that when GGVVIA forms β–sheets, the strands within the sheet tend to be mostly out of register. As an example, the green β-sheet in Fig. 4(d) is presented in Fig. S1. The lack of registry between strands on the same sheet makes it more likely that the β-sheets will stack in an out-of registry fashion, reducing the stacking energy further. This is because the Gs do not have side chains that contribute to a stacking energy and thus the sequence is very unsymmetrical. This relative absence of registry for GGVVIA compared to MVGGVV makes the energy of a stacked GGVVIA configuration even lower than the value one would get if the average was taken over the energies for the configurations in Fig 7 (c) and (d) mentioned above. The energy differences discussed here explain in part why MVGGVV forms fibrils and GGVVIA does not in our simulations.

Figure 7.

Schematic side-chain pair interactions between two stacked β-strands. (a) Parallel stack of MVGGVV peptides with pair interactions ε_MM+ε_VV =0.396ε_HB shown in figure or alternatively ε_VV+ε_VV=0.396ε_HB (b) Antiparallel stack of MVGGVV peptides with two pair interactions ε_VV+ε_VM=0.396ε_HB shown in figure alternatively ε_MV+ε_VM=0.396ε_HB (c) Parallel stack of GGVVIA peptides with two pair interactions ε_VV+ε_II=0.396ε_HB shown in figure or alternatively ε_VV+ε_AA=0.284ε_HB (d) Antiparallel stack of GGVVIA peptides with one pair interactions ε_VV=0.198ε_HB.

It is of interest to ask why the addition of isoleucine and alanine to MVGGVV makes fibril formation less likely to occur and amorphous aggregation more likely to occur. Recall that 70% of the MVGGVV peptides form fibrils whereas only 40% of the MVGGVVIA peptides form fibrils at low-to-moderate T*. Although the presence of hydrophobic residues usually seems to promote the stacking of β-sheets, in these simulations it seems to be hindering stacking. We speculate that this happens to these particular sequences because the additional hydrophobic residues are located at one peptide end rather than in the middle. These residues stick out and promote the initial association of peptides into non-aligned configurations (micelle-like), allowing them to get stuck in kinetic traps. (Note that this argument only applies to sequences where there are intervening non-hydrophobic resides close to the affected end such as happens in MVGGVVIA.) Here the addition of the I and A makes the strength of the hydrophobic pull lopsided (4 hydrophobic residues on one side of the glycines and two on the other) in comparison to MVGGVV which is more balanced ( 2 hydrophobic residues on each end.) The idea that the addition of hydrophobic residues to the end of the chain is less effective in promoting stacking than the addition of hydrophobic residues to the middle is consistent with our earlier simulation work on prion-like peptides which showed that the percent of peptides that form fibrils for VAGAAAAGAV and GAVAAAAVAG are 46% and 74.5%, respectively whereas the percent of peptides that form amorphous aggregates are 18% and 4.1%& respectively.⁶²

Generalization of the ideas presented here about the connection between the stacking tendencies of MVGGVV and MVGGVVIA and asymmetric placement of hydrophobic residues along the chain to other C-terminal fragments of Aβ is not warranted. The reason is that the argument depends critically on the fact that the fragment starts at Aβ35 (M). As has been shown by Li et al,⁶³ the impact of the addition of I and A to the C terminal fragments of Aβ appears to be context specific. For example, in examining the solubility and fibrillization tendencies of short C-terminal fragments (CTFs), they found that that CTFs like Aβ(29–42) and Aβ(30–42), which adopt a β-hairpin turn, rapidly form short fibrils whereas those that don’t, such as Aβ(31–42) and Aβ(30–40) aggregate more slowly into longer fibrils. They also point out that Aβ (30–40) assembled into β-rich fibrils while Aβ(32–42) did not. Finally we should note that they found that MVGGVV did not form fibrils at concentrations < 200µM. Our concentration is much higher, however.

Although our observations on MVGGVV and MVGGVVIA suggest that the two C-terminal residues on Aβ(1–42) peptides might drive it to make fibril formation more difficult than Aβ(1–40), this is not necessarily the case. In fact many papers in the literature find the opposite --that Aβ(1–42) fibril nucleation and growth rates are faster than those for Aβ(1–40).^64–68 The ease with which fibrils form might depend, however, on the method of preparation, e.g. concentration, temperature, pH, buffer, agitation, etc., as do many other aspects of fibril formation. For example in private communication, R Tycko states that under certain conditions, Aβ(1–42) seems to form "oligomer" blobs (probably containing >20 molecules) that persist for a long time (weeks) before eventually converting to fibrils but Aβ(1–40) doesn't do this.”⁶⁹ It is well known that different preparation conditions, particularly quiescent vs agitated conditions can lead to diverse polymorphic fibril structures.^70,71 We expect that those conditions also play an important role in fibrillation rate, including the differences between the fibrillization rates for Aβ(1–40) and Aβ(1–42).

Our observations that the addition of I and A to MVGGVV make amorphous aggregation more likely are consistent with experimental observations that oligomers of Aβ(1–42) are more numerous, complex and longer lived than those for Aβ(1–40).^72–77

Conclusions

Recent improvements in our intermediate-resolution protein model, PRIME20, have enabled us to observe the spontaneous formation of amyloid fibrils starting from an initial configuration of random coils. Using the PRIME20 force field, we performed discontinuous molecular dynamics simulations of the aggregation of 48-peptide systems containing the following fragments of amyloidogenic peptides: SNQNNF (PrP(170–175)), SSTSAA (RNase A(15–20)), MVGGVV(Aβ(35–40)), MVGGVVIA (Aβ(35–42)) and GGVVIA (Aβ(37–42)). The short amyloid peptide fragments MVGGVV, SNQNNF, and SSTSAA all formed fibrils as is observed experimentally. For GGVVIA we observed β-sheet formation and an assembly pathway very similar to that of MVGGVV, but no fibril formation. The strength of the sidechain-sidechain interactions in GGVVIA is apparently insufficient to overcome the energetic barrier to β-sheet stacking. This is due mainly to the positioning of the glycines along the chain and not to the amino acid content, since the amino acids in MVGGVV and GGVVIA have similar levels of hydrophobicity. Although MVGGVVIA forms fibrils it forms less fibrils and more non-fibrillar β-sheets and amorphous aggregates than MVGGVV.

Our studies of three different peptide fragments (MVGGVV, GGVVIA and MVGGVVIA) from the C-terminal of Aβ42 show clear differences in their ability to form fibrils. Although all three peptides have been crystallized experimentally by the Eisenberg group and have been found to have steric-zipper interfaces, our simulations suggest that the driver sequence for fibrillization here is MVGGVV. Adding two more residues I and A to MVGGVV induces the system to form more disordered aggregates, consistent with the observation that Aβ(1–42) oligomers form more rapidly and are more stable than Aβ(1–40) oligomers. There are two reasons why I and A at the C terminal enhance oligomerization: (1) the strong hydrophobic interactions at the C-terminal promote aggregation in general, and (2) they hinder β-sheet stacking. The former explanation is likely applicable to full length Aβ while the latter is not. In fact many papers in the literature suggest that Aβ(1–42) form fibrillar structures more easily that Aβ(1–40) although this is a matter of debate.

Our simulations show that the fibril structure of SNQNNF is more twisted that of SSTSAA. This is due to the difference in the sizes of the side-chain centroids. Having larger side-chain centroids usually makes the β-sheets twist more. This effect is even more pronounced in our PRIME20 model because it uses a single-sphere representation for each side-chain. The fibril structures for STVIIE and SNQNNF sequences in experiment or in all-atom situations might be less twisted than in our simulations because the shape complementarity associated with the steric zipper interface, especially in the dry phase is more faithfully represented.

We observed amorphous aggregates for MVGGVV at temperatures greater than the fibrillization temperature, the temperature above which no fibrils are observed. Amorphous aggregates are found at high temperatures in our simulations only for sequences having strong hydrophobic residues such as MVGGVV, MVGGVVIA and VAGAAAAGAV. This means that the thermal energy can destroy the formation of fibrils but not the formation of oligomers. In other words, the strong hydrophobic interactions can still be effective at high temperature even though the hydrogen bonding is destroyed by thermal fluctuations. This conclusion should be tempered, however, by the fact that the PRIME20 energy parameters are temperature-independent and hence do not accurately account for the temperature dependence of hydrogen bonding and the hydrophobic effect. We expect that the trend is qualitatively correct, as the ratio of the strengths of the hydrophobic and hydrogen bonding interactions are likely less temperature-dependent than the values of the individual interactions.

Since the range of relative temperatures in this study is large, it is of interest to ask how experimental studies of temperature dependence for fibril formation and stability support the trends observed computationally. Unfortunately there are few experimental studies for temperature dependence of fibril structures corresponding to conformational conversion of high concentration condition. Experiments studying temperature dependence of fibrillization rate have been performed at low concentration where monomer addition is a key role in fibrillization.⁷⁸ Morphological studies in which temperature was varied did not show any systematic temperature dependence, as other conditions such as agitation and buffer were controlled simultaneously.^71,79 An additional question that arises is how to relate the reduced temperatures studied here to real temperature. The relative temperature T* depends on the strength of the backbone-backbone hydrogen bond interaction. If we were to calculate the real temperature directly based on a hydrogen bond energy ranging from 1.9 to 2.5×10⁻²⁰ J given in ref (33), T*=0.17 would correspond to 234 to 308 K and T*=0.12 would correspond to 166 to 218 K. Thus the estimated temperature ranges obtained in this manner are much lower than the physiological temperature range and includes temperatures in which water freezes. Clearly this is incorrect; the problem lies with the neglect of the kinetic energy of water (water is only accounted for implicitly in this model) and the fact that the hydrogen bond energy in our model is a potential of mean force due to surrounding water as opposed to a direct interaction We are currently working on a more meaningful way to relate reduced temperature to real temperature. The best way to scale the reduced temperature in PRIME 20 to real temperature is to compare the fibrillization temperatures determined in our model with those determined experimentally for a variety of sequences. We are in discussion with potential collaborators about the possibility of performing these experiments.

While the PRIME20/DMD approach has many advantages for simulating fibril and oligomer self-assembly, it does have limitations. We have already discussed the difficulty of relating the reduced temperature scale to a real temperature. Another limitation is the inability to relate reduced time to real time. Again this springs from our use of an implicit solvent model which means that the peptides are traveling in straight lines in a vacuum rather than in a solvent that hinders peptide diffusion. Hence we cannot at the present time directly relate the time scales for fibril formation to those in the laboratory in more than a qualitative fashion. Use of implicit solvent also prevents us from directly measuring the effects associated with internal waters captured or lost when a steric zipper interface forms. This can affect both the aggregation kinetics as well as the fibrillar structure that is ultimately formed.

It would be of interest to use the DMD/ PRIME20 approach to study the "dock and lock" mechanism that has been proposed for fibril elongation. To do this we would need to choose our simulation temperature and concentration such that there are sufficient monomers around to have good statistics on monomer addition and relatively few oligomers lest the fibrils form mostly by oligomer aggregation. This work is performed at high concentrations (c=10mM) so that oligomerization is prevalent at most low temperatures. There the mechanism of fibril formation is most similar to nucleated conformational conversion. However at higher temperatures like T*=0.18 for STVIIE, the fibril growth mechanism switches to template assembly by monomer addition, which is similar to the dock-and-lock mechanism.⁸⁰ A potential problem at this near fibrillation temperature is that there are as many monomer dissociation as association events at the fibrillar template, making it difficult to focus on monomer addition. To observe the dock and lock mechanism we would need to reduce the temperature and concentration to the point where we would see more monomer addition and less dissociation, In that case we could systematically study the dock and lock phase during monomer addition. It would be interesting to investigate the sequence dependence of dock-and-lock to see if and how the mechanism depends on the balance of hydrophobic and polar residues.⁸¹