Using Data Augmentation to Facilitate Conduct of Phase I–II Clinical Trials with Delayed Outcomes

Abstract

A practical impediment in adaptive clinical trials is that outcomes must be observed soon enough to apply decision rules to choose treatments for new patients. For example, if outcomes take up to six weeks to evaluate and the accrual rate is one patient per week, on average three new patients will be accrued while waiting to evaluate the outcomes of the previous three patients. The question is how to treat the new patients. This logistical problem persists throughout the trial. Various ad hoc practical solutions are used, none entirely satisfactory. We focus on this problem in phase I–II clinical trials that use binary toxicity and efficacy, defined in terms of event times, to choose doses adaptively for successive cohorts. We propose a general approach to this problem that treats late-onset outcomes as missing data, uses data augmentation to impute missing outcomes from posterior predictive distributions computed from partial follow-up times and complete outcome data, and applies the design’s decision rules using the completed data. We illustrate the method with two cancer trials conducted using a phase I–II design based on efficacy-toxicity trade-offs, including a computer stimulation study.

1 Introduction

Phase I–II clinical trial designs combine conventional phase I and phase II trials by determining a dose of a new agent based on both toxicity and efficacy (Gooley et al., 1994; Thall and Russell, 1998; O’Quigley et al., 2001; Braun, 2002; Thall and Cook, 2004; Bekele and Shen, 2005; Zhang et al., 2006; Yin et al., 2006; Yuan and Yin, 2011a). Most commonly, a small phase I trial based on toxicity (Storer, 1989; O’Quigley et al., 1990; Babb et al., 1998; Conaway et al., 2004) first is conducted to choose a putatively safe dose, the “maximum tolerated dose” (MTD), and a phase II trial then is conducted (Gehan, 1969; Fleming, 1982; Simon, 1989; Thall and Simon, 1994; Thall et al., 1995; Bryant and Day, 1995), using the MTD, with efficacy the primary outcome. This conventional approach may lead to several problems. (1) Informal dose adjustments often are made in phase II if excessive toxicity is observed, which invalidates assumed properties of any efficacy-based design. (2) Operating characteristics of the entire phase I – phase II process are seldom computed. (3) Separate designs ignore the trade-off between efficacy and toxicity that often underlies therapeutic decision making. Since phase I–II designs address these problems explicitly, a natural question is why such designs are used infrequently for actual trials. While these are complex issues, the following logistical problem may play a prominent role.

In outcome-adaptive clinical trials, a major practical impediment arises if patient outcomes are not observed quickly enough to apply decision rules that choose treatments or doses for newly accrued patients. Because it is undesirable, and often impossible, to delay a new patient’s treatment while waiting for previous patients’ outcomes to be scored so that an adaptive statistical rule can be applied, outcome-adaptive rules may be at odds with clinical practice. In phase I–II, this problem arises if either toxicity or efficacy is not scored quickly, relative to the accrual rate. One solution is to turn away new patients and treat them off protocol. This may be less desirable than giving the experimental regimen, or impossible if no alternative treatment exists. Another solution is to give all new patients the dose or treatment that is optimal based on the most recent data. This may have very undesirable consequences if the most recent optimal dose later turns out to be overly toxic, and it is the main reason that dose-finding usually is done sequentially with small cohorts of 1, 2, or 3 patients. In Phase I–II, the opposite effect can occur if the most recent optimal dose is safe but inefficacious. A third solution when some patients’ outcomes have not yet been evaluated fully is to treat all new patients immediately, but use a dose one level below the design’s current optimal dose. In Phase I, the problem of dealing with delayed (“late onset”) toxicity was first addressed by Cheung and Chappell (2000), who introduced the time-to-event continual reassessment method (TiTE-CRM), and later by Braun (2006), Bekele et al. (2008), and Yuan and Yin (2011b).

As an illustration, consider a phase I–II clinical trial of chemotherapy for acute leukemia, both toxicity and efficacy events may occur at any time during a common 6-week evaluation period, doses chosen adaptively for cohorts of size 3, and accrual rate 1 patient per week. On average, the first cohort will be accrued in 3 weeks with all of their outcomes scored by week 9, when adaptive rules are applied using their data to choose the second cohort’s dose. Since one also can expect to accrue 6 new patients between weeks 3 and 9, the question is how to deal therapeutically with these new patients. A second example is an autologous stem cell transplantation trial for multiple myeloma (MM) where toxicity may occur at any time during the first 30 days, but efficacy is evaluated only at 90 days post-transplant, and is defined as no detectable MM protein in the urine or blood serum and < 5% plasma cells in the bone marrow. If the accrual rate is 3 patients per month, one may expect to accrue 9 patients before efficacy is scored for any patients, so applying an adaptive rule to choose a dose for patients 4, 5, and 6, (cohort 2), using the data from patients 1, 2, and 3, (cohort 1), is not possible without delaying the second cohort’s therapy. The severity of this problem increases with accrual rate and persists throughout the trial.

In this paper, we consider phase I–II designs where both efficacy (E) and toxicity (T) are characterized as binary variables, Y_E and Y_T, evaluated either during or at the end of specified time intervals, [0, U_E] for Y_E and [0, U_T] for Y_T. We refer to Y_E and Y_T as “delayed outcomes” because they are not observed immediately. Denote accrual rate by α. We quantify the severity of the problem using the logistical difficulty indexes ζ_j = U_jα for each outcome j = E, T, and overall index ζ = max{ζ_E, ζ_T}. For example, if α = 1 patient/month and U_E = U_T = 3 months, then ζ = 3. Doubling the accrual rate to α = 2 gives the problematic value ζ = 6.

We propose a methodology that handles the problem of delayed outcomes in phase I–II by accounting for each patient’s follow up time prior to evaluation of Y_E and Y_T, and treating all Y_j’s that have not yet been observed as missing values. We use data augmentation (Tanner and Wong, 1987) to impute each missing Y_j using partial follow-up times and complete outcome data. Combining observed and imputed (Y_E, Y_T) data for all patients who have been treated, we then apply the phase I–II design’s decision rules. Our approach of treating delayed outcomes as missing data is similar to that of Yuan and Yin (2011b), who deal with the phase I setting with Y_T but not Y_E. Key differences are that the bivariate distribution and missingship patterns of (Y_E, Y_T) are much more complicated than those of Y_T alone. In addition, Yuan and Yin (2011b) use the EM algorithm under a frequentist framework to estimate toxicity probabilities, whereas we rely on predictive probabilities and imputatation to obtain a completed data set under a Bayesian formulation.

In Section 2, we propose a general approach to delayed outcomes in phase I–II trials. In Section 3, we present imputation and Bayesian data augmentation methods. Section 4 illustrates the method with two trials designed using an extended version of the efficacy-toxicity (Eff-Tox) trade-off based design of Thall and Cook (2004). In Section 5, we present simulations of the proposed method and comparison with alternative methods. We conclude with a discussion in Section 6.

2 Observed Outcomes and Missing Values

2.1 Data Structures

The data structure assumed by most phase I–II dose-finding method consists of assigned doses and two binary outcomes. We denote this by 𝒟(Y) = {(d_[1], Y_1,E, Y_1,T), …, (d_[n], Y_n,E, Y_n,T)}, where d_[i] is the dose given to the ith patient and interim sample size n = 1, ⋯, N_max. To account for the fact that, at any interim decision, one or both of Y_E and Y_T may not yet be observed for a given patient, we denote the data including only the observed Y_j’s by 𝒟_obs(Y) and the unobserved (“missing”) Y_j’s by 𝒟_mis(Y). Our strategy will be to use 𝒟_obs(Y) and partial follow up time data to impute any missing Y_j’s in 𝒟_mis(Y) and thus construct a completed version of 𝒟_obs(Y) that has the form of 𝒟(Y), and then apply the phase I–II method.

Let X_j denote time to outcome j = E, T. Corresponding to the acute leukemia trial and the stem cell transplantation trial described previously, we distinguish between two data structures, depending on how Y_E is observed. In Case 1, Y_E is observed in real time, and Y_E = I(X_E ≤ U_E). In Case 2, Y_E is evaluated only at U_E, and there is no X_E. In both cases, Y_T = I(X_T ≤ U_T). To simplify exposition, we focus primarily on Case 1 since it is more complex, and later explain how to deal with Case 2. For trials where efficacy is evaluated periodically X_E is interval censored. We include this by smoothing the interval censored data, placing X_E at the midpoint or a randomly chosen value of the interval where efficacy was known to occur. We accommodate patient death during therapy by defining X_T as the time to either non-fatal toxicity or death. For efficacy, if the patient dies prior to U_E we define Y_E = 0, which is implied by defining X_E = ∞. Denote U = max {U_T, U_E} and V = follow up time, where by design V ≤ U.

2.2 Missingship Mechanism

Denote π_j(d, θ) = Pr(Y_j = 1 | d, θ) for j = E, T, where θ is the model parameter vector. In the sequel, we often will suppress d and θ for brevity. The observed follow up time of X_j during the evaluation interval [0, U_j] is $X_j^o=V\wedge X_j$. We assume that V is independent of X_j. The key to our method is that $X_j^o$ provides useful information about Y_j, because

$$\text{Pr}(Y_j=1|X_j^o=V<X_j)=1-\frac{\text{Pr}(U_j<X_j)}{\text{Pr}(X_j^o=V<X_j)}$$

must decrease as $X_j^o$ increases from 0 to U_j. This fact also underlies the TiTE-CRM (Cheung and Chappell, 2000). To account for missing values, we use V to extend the previous definitions of Y_E and Y_T, as follows. We define

$$Y_j=\{\begin{array}{ccc}\hfill \mathit{\text{missing}}\hfill & \text{if}{X}_j>V\text{and}V<U_j\hfill & (X_j^o=V),\hfill \\ \hfill 1\hfill & \text{if}{X}_j\le V\le U_j\hfill & (X_j^o=X_j),\hfill \\ \hfill 0\hfill & \text{if}{X}_j>V=U_j\hfill & (X_j^o=U_j).\hfill \end{array}$$

That is, Y_j = missing if the patient has not yet experienced the event and has not been fully followed to U_j, while Y_j is observed if the patient either has experienced the event (Y_j = 1) or has completed the defined follow-up time without the event (V = U_j and Y_j = 0). Denote the missingship indicators M_j = I(Y_j = missing) for j = E, T, and M = (M_E, M_T). The ith patient’s data are ${\mathbf{𝒟}}_i=(d_{[i]},Y_{i,E},Y_{i,T},X_{i,E}^o,X_{i,T}^o)$, and 𝒟_i determines M_i. Our methodology uses the actual interim data from n patients, by 𝒟= (𝒟₁, ⋯, 𝒟_n), to impute missing Y_j’s and construct a completed binary data set 𝒟(Y) for implementing the phase I–II method.

2.3 Event Time Distributions

To construct flexible survival functions, we assume piecewise exponential marginals for [X_j|d, Y_j = 1], j = E, T, by partitioning [0, U_j] into K_j intervals, [0, h_j,1), [h_j,1, h_j,2), ⋯, [h_j,Kj−1, h_j,Kj], and assuming hazard λ_j,k on [h_j,k−1, h_j,k). The marginal survival function for X_j is

$$S_j(x|Y_j=1,{\lambda }_j)=\text{exp}\{-\sum _{k=1}^{K_j}{w}_{j,k}(x){\lambda }_{j,k}\},x>0,$$

denoting λ_j = (λ_j,1, ⋯, λ_j,Kj), and weights w_j,k(x) = h_j,k − h_j,k−1 if x > h_j,k, w_j,k(x) = x − h_j,k−1 if x ∈ [h_j,k−1, h_j,k), and w_j,k(x) = 0 otherwise. Initially, we considered a more elaborate form of S_j, in which each λ_j,k was replaced by ${\lambda }_{j,k}{\gamma }_j^d$ where γ_j > 1, so that the event time distributions varied with dose in a proportional hazard model with piecewise exponential baseline hazard. However, we found that fixing γ_E = γ_T = 1 did not change the method’s operating characteristics, due to the fact that there is little or no information to estimate the γ_j’s. To determine whether a more parsimonious survival model might give a design with similar performance, we replaced the piecewise exponential with a Weibull. However, simulations across eight dose-outcome scenarios (Supplementary Table S9) showed that the Weibull gave larger probabilities of incorrectly stopping early, and either similar or lower probabilities of selecting desirable doses.

Our imputation method requires the joint conditional survival probabilities S(x_E, x_T |a, b) = Pr(X_E > x_E, X_T > x_T |Y_E = a, Y_T = b) for (a, b) = (0,1), (1,0), (1,1). Assuming conditional independence, S_j(x_j |Y_E, Y_T) = S_j(x_j |Y_j) for j = E, T, implies that S(x_E, x_T |1, 0) is determined by the marginal of X_E and S(x_E, x_T |0, 1) is determined by the marginal of X_T. Determining S(x_E, x_T |1, 1) requires accounting for association between X_E and X_T. We do this by defining a joint distribution using the Clayton copula (Clayton, 1978), given for ϕ ≥ 0 by

$$S(x_E,x_T|1,1)={\{S_E{(x_E|Y_E=1)}^{-1/\varphi }+S_T{(x_T|Y_T=1)}^{-1/\varphi }-1\}}^{-\varphi }={\left\{\text{exp}\right\{\sum _{k=1}^{K_E}{\lambda }_{E,k}{w}_{E,k}/\varphi \}+\text{exp}\{\sum _{k=1}^{K_T}{\lambda }_{T,k}{w}_{T,k}/\varphi \}-1\}}^{-\varphi }.$$

The likelihood of 𝒟 depends on Y_E, Y_T, and the censoring patterns of X_E and X_T. Denote $\lambda =({\lambda }_E,{\lambda }_T),\xi =(\varphi +1)/\varphi ,{\epsilon }_j=I(X_j^o=X_j)$, the pdf of X_j by f_j(·), and

$$W(X_E^o,X_E^o)=S_E{(X_E^o|Y_E=1)}^{-1/\varphi }+S_T{(X_T^o|Y_T=1)}^{-1/\varphi }-1.$$

When Y_E = Y_T = 1, there are four possible likelihoods,

$$L(𝒟|\lambda ,\varphi )=\{\begin{array}{cc}\xi W{(X_E^o,X_E^o)}^{-\varphi -2}{\prod }_{j=E}^T{f}_j(X_j^o|Y_j=1){\{{\prod }_{j=E}^T{S}_j(X_j^o|Y_j=1)\}}^{\xi }\hfill & \text{if}({\epsilon }_E,{\epsilon }_T)=(1,1)\hfill \\ W{(X_E^o,X_E^o)}^{-\varphi -1}{f}_E(X_E^o|Y_E=1)S_E{(X_E^o|Y_E=1)}^{\xi }\hfill & \text{if}({\epsilon }_E,{\epsilon }_T)=(1,0)\hfill \\ W{(X_E^o,X_E^o)}^{-\varphi -1}{f}_T(X_T^o|Y_T=1)S_T{(X_T^o|Y_T=1)}^{\xi }\hfill & \text{if}({\epsilon }_E,{\epsilon }_T)=(0,1)\hfill \\ W{(X_E^o,X_E^o)}^{-\varphi }\hfill & \text{if}({\epsilon }_E,{\epsilon }_T)=(0,0)\hfill \end{array}$$

For the cases (Y_E, Y_T) = (1,0) or (0,1), the likelihoods are given by

$$L(𝒟|\lambda ,\varphi )={[{\{f_E(X_E^o|Y_E=1)\}}^{{\epsilon }_E}{\{S_E(X_E^o|Y_E=1)\}}^{1-{\epsilon }_E}]}^{Y_E(1-Y_T)}\times {[{\{f_T(X_T^o|Y_T=1)\}}^{{\epsilon }_T}{\{S_T(X_T^o|Y_T=1)\}}^{1-{\epsilon }_T}]}^{Y_T(1-Y_E)}.$$

Denoting the likelihood for n patients by $L(\mathbf{𝒟}|\lambda ,\varphi )={\prod }_{i=1}^{n}L({𝒟}_i|\lambda ,\varphi )$, the posterior is f(λ, ϕ|𝒟) ∝ f(λ)f(ϕ)L(𝒟|λ, ϕ), for priors f(λ) and f(ϕ) of λ and ϕ.

3 Imputation Method

Let π_a,b(d, θ) = Pr(Y_E = a, Y_T = b|d, θ) for a, b ∈ {0, 1} denote the joint distribution of [Y_E, Y_T | d], so π_E(d, θ) = π_1,1(d, θ) + π_1,0(d, θ) and π_T(d, θ) = π_1,1(d, θ) + π_0,1(d, θ). If no outcomes are missing the likelihood is the usual product

$$L(\mathbf{𝒟}(Y)|\theta )=\prod _{i=1}^n\prod _{a=0}^1\prod _{b=0}^1{\{{\pi }_{a,b}(d_{[i]},\theta )\}}^{I\{(Y_{i,E},Y_{i,T})=(a,b)\}},$$ (1)

with posterior f(θ|𝒟(Y)) ∝ L(𝒟(Y)|θ)f(θ); for prior f(θ). Since L(𝒟(Y)|θ) cannot be computed if some Y_i,j’s are missing, we obtain a completed version of the likelihood, of the form (1), by using Bayesian data augmentation (Tanner and Wong, 1987). We iterate between an imputation step sampling missing Y_j’s from their full conditionals, and a step computing the posterior using the completed data. Importantly, the imputation depends on the dose-outcome model.

Missing Y_j’s are nonignorable because, at follow up time V, a patient who will not experience outcome j by U_j is more likely to have Y_j = missing (M_j=1) than a patient for whom outcome j will occur (Yuan and Yin, 2011b). By Bayes’ Law, Pr(M_j = 1|Y_j = 0) > Pr(M_j = 1|Y_j = 1) implies that

$$\frac{{\pi }_j}{1-{\pi }_j}>\frac{\text{Pr}(Y_j=1|M_j=1)}{\text{Pr}(Y_j=0|M_j=1)}.$$

This says that the odds that Y_j = 1 decreases if Y_j is missing, so the missingship indicator M_j contains information about the future value of Y_j.

A complication in carrying out the imputation is that there are three possible missingship patterns: (1) Y_E = missing and Y_T is observed, (2) Y_T = missing and Y_E is observed, and (3) both Y_E = missing and Y_T = missing. Since we impute missing values by sampling from their full conditional posteriors, these distributions must be specified for each missingship pattern. These posteriors are defined in terms of the following conditionals for X_E and X_T, given each of the four possible future outcome pairs, which for brevity we denote by

$$S_{ab}=\text{Pr}(X_E>V,X_T>V|Y_E=a,Y_T=b),a,b\in \{0,1\}.$$ (2)

In any case, S₀₀ = 1 due to the fact that Pr(X_j > V |Y_j = 0) = 1 for 0 ≤ V ≤ U_j, which also implies that S₁₀ = Pr(X_E > V |Y_E = 1, Y_T = 0) and S₀₁ = Pr(X_T > V |Y_E = 0, Y_T = 1). Thus, only S₁₁ involves a joint distribution for (X_E, X_T) given Y_E = Y_T = 1.

To obtain consistent estimates when imputing the missing Y_j’s, we condition on the actual data 𝒟. The following posterior conditional distributions are derived in the Appendix. When Y_E = missing and Y_T is observed, we impute Y_E from its conditional posterior

$$\mathrm{p}\mathrm{r}(Y_E=1|𝒟)={\left\{\frac{{\pi }_{1,1}{S}_{10}}{{\pi }_{1,1}{S}_{10}+{\pi }_{0,1}}\right\}}^{Y_T}{\left\{\frac{{\pi }_{1,0}{S}_{10}}{{\pi }_{1,0}{S}_{10}+{\pi }_{0,0}}\right\}}^{1-Y_T}.$$

When Y_T = missing and Y_E is observed, we impute Y_T from its conditional posterior

$$\mathrm{p}\mathrm{r}(Y_T=1|𝒟)={\left\{\frac{{\pi }_{1,1}{S}_{01}}{{\pi }_{1,1}{S}_{01}+{\pi }_{1,0}}\right\}}^{Y_E}{\left\{\frac{{\pi }_{0,1}{S}_{01}}{{\pi }_{0,1}{S}_{01}+{\pi }_{0,0}}\right\}}^{1-Y_E}.$$

When both Y_E and Y_T are missing, we impute (Y_E, Y_T) from the joint conditional posterior

$$\mathrm{p}\mathrm{r}(Y_E=y,Y_T=z|𝒟)=\frac{{\pi }_{y,z}{S}_{yz}}{{\sum }_{a=0}^1{\sum }_{b=0}^1{\pi }_{a,b}{S}_{ab}},\text{for}y,z=0,1$$

At the posterior step using the completed data, we sample parameters from their full conditional posteriors in two steps: (1) Sample θ from f(θ|𝒟(Y)) and (2) sample ϕ and λ_j,k for each k = 1, ⋯, K_j and j = (E, T) from f(λ, θ|𝒟). This is iterated until the Markov chain converges, with posteriors computed using adaptive rejection Metropolis sampling (Gilks et al., 1995).

We now turn to Case 2, in which Y_E is evaluated only at U_E. Analytically, Case 2 is much simpler than Case 1 because in Case 2 efficacy is Y_E with no random event time involved, and Y_E is missing completely at random (MCAR) at all V < U_E. For the same reason, trial conduct in Case 2 is much harder logistically than in Case 1. This is because there is no X_E in Case 2 and hence no partial information about Y_E when V < U_E. Inference for π_E relies entirely on observed Y_E values from previously treated patients, while Y_T may be imputed by exploiting the event time data $(X_T^o,{\delta }_T)$ using the marginal of X_T.

Our proposed method can be applied to any phase I–II combination of probability model and decision rules based on [Y_E, Y_T | d] with delayed outcomes. To make things concrete, we apply the method to the Efficacy-Toxicity (EffTox) trade-off method of Thall and Cook (2004). Case 1 is illustrated by the trial of chemotherapy for acute leukemia where U_T = U_E = 42 days, and Case 2 by the stem cell transplantation trial with U_T = 30 days and U_E = 90 days.

4 EffTox Designs

4.1 The Design Assuming Complete Data

We first briefly review the EffTox phase I–II design (Thall and Cook, 2004) assuming complete data 𝒟(Y). The model for [Y_E, Y_T | d] assumes marginal probabilities π_E = logit⁻¹{μ_E + β_E,1d + β_E,2d²} and π_T = logit⁻¹{μ_T + β_T,1d + β_T,2d²} and uses a Gumbel copula (Murtaugh and Fisher, 1990) to obtain a joint distribution,

$${\pi }_{a,b}={({\pi }_E)}^a{(1-{\pi }_E)}^{1-a}{({\pi }_T)}^b{(1-{\pi }_T)}^{1-b}+{(-1)}^{a+b}{\pi }_E(1-{\pi }_E){\pi }_T(1-{\pi }_T)\left(\frac{e^{\psi }-1}{e^{\psi }+1}\right),$$ (3)

where ψ parameterizes association between Y_E and Y_T. To prevent mis-estimation with small sample sizes, we require that β_E,1 + 2β_E,2d > 0 and β_T,1 + 2β_T,2d > 0, corresponding to agents where both π_T and π_E increase with dose.

The desirability of a dose is defined by first defining the desirability δ(π_E, π_T) of each probability pair π = (π_E, π_T) in [0, 1]²; with δ(π_E, π_T) increasing in π_E and decreasing in π_T. Denoting the posterior means ${\pi }_{j,d}^{*}=\mathrm{E}\{{\pi }_j(d,\theta )|𝒟(Y)\}$ for j = E, T, the desirability of d is $\delta ({\pi }_{E,d}^{*},{\pi }_{T,d}^{*})$, for use as a decision criterion. The function δ may be obtained from a target efficacy-toxicity tradeoff contour, 𝒞, in [0, 1]² in several ways (cf. Thall, Cook and Estey, 2006). To avoid doses that are too toxic or inefficacious, two admissibility criteria are imposed. Given elicited fixed lower limit π̲_E on π_E and upper limit π̄_T on π_T, a dose d is acceptable if

$$\text{Pr}\{{\pi }_E(d,\theta )>{\mathrm{\pi ̲}}_E|𝒟(Y)\}>p_E\text{and}\text{Pr}\{{\pi }_T(d,\theta )<{\mathrm{\pi ̄}}_T|𝒟(Y)\}>p_T$$ (4)

for prespecified cutoffs p_E and p_T. The trial starts at a dose chosen by the physician and each new cohort is treated with the acceptable dose having largest δ(d). An untried dose may not be skipped when escalating, and when escalating to an untried dose only the toxicity admissibility rule is imposed. If no dose is acceptable the trial is stopped with no dose selected.

We refer to the new version of the EffTox design that incorporates our proposed imputation methodology as the late onset (LO)-EffTox design. It differs from the EffTox design in one fundamental way, namely that event time data are exploited to compute posterior decision criteria using the Bayesian data augmentation methodology described in Section 3.

4.2 Prior Specification

In any model-based Bayesian adaptive clinical trial design, the prior must be sufficiently vague that the accumulating data dominates the posterior distribution, and thus the adaptive decisions. Thall and Cook (2004) provided a framework for establishing priors from elicited mean values of π_E(d, θ) and π_T (d, θ) that solves for prior hyperparameters using nonlinear least squares. We derive a prior based on the weakly informative prior for logistic regression proposed by Gelman et al. (2008). Following Gelman et al. (2008), for priors we assume μ_T, μ_E, β_T,1, β_E,1, β_T,2, β_E,2 ~ iid Cauchy(0, 2.5), and then shift the six Cauchy prior location parameters from 0 to μ̃ = (μ̃_μT, μ̃_βT,1, μ̃_βT,2, μ̃_μE, μ̃_βE,1, μ̃_βE,2), to reflect prior opinion. To obtain μ̃, similarly to Thall and Cook (2004), we first elicit the means m̃_E,dr and m̃_T,dr of π_E(d_r, θ) and π_T(d_r, θ) from the physician for each dose d_r, r = 1, …, R. For each j = E, T, we use least squares to solve for (μ̃_μj, μ̃_βj,1, μ̃_βj,2) by assuming $\mathrm{E}\{\text{logit}({\mathrm{m̃}}_{j,d_r})\}={\mathrm{\mu ̃}}_{{\mu }_j}+{\mu }_{{\beta }_{j,1}}{d}_r+{\mathrm{\mu ̃}}_{{\beta }_{j,2}}{d}_r^2$.

To obtain a vague prior on λ, we assume [X_j |Y_j = 1] ~ Unif(0, U_j), which implies that the hazard at the midpoint of the subinterval [h_j,k−1, h_j,k) of the partition is λ̃_j,k = K_j/{U_j(K_j − k+0.5)}. We assume that λ_j,k ~ Gam(λ̃_j,k/C, 1/C), where Gam(a, b) denotes the gamma distribution with mean a/b and variance a/b². Thus, λ_j,k has prior mean λ̃_j,k and variance Cλ̃_j,k, so C is a tuning parameter that determines var(λ_j,k) and that can be calibrated by simulation. In preliminary simulations, we found that C = 2 yields a reasonably vague prior and a design with good operating characteristics. Finally, we assume ψ ~ Normal(0, 1) and ϕ ~ Gam(0.2, 0.2).

5 Computer Simulations

5.1 Clinical Trial Designs

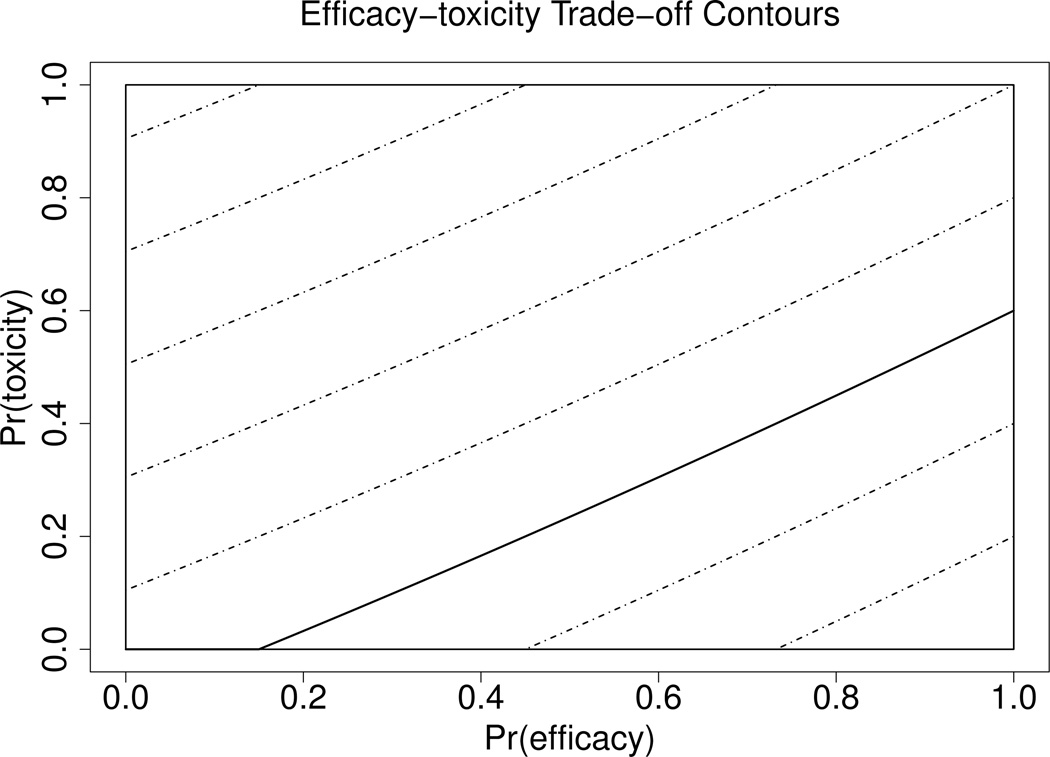
We simulated our proposed methodology to study its behavior when applied to the EffTox design for phase I–II trials in each of Cases 1 and 2. To assess robustness, we conducted a second set of simulations in which we varied several model, design, and simulation scenario parameters. In all simulations, we considered hypothetical phase I–II trials with five raw doses (2.5, 5.0, 7.5, 10.0, 12.5). In the model, we replaced each raw dose $d_r^o$ by the standardized dose $d_r=(.5/s)\{\text{log}(d_r^o)-\overline{\text{log}(d^o)}\}$, where s is the standard deviation of the centered log doses, so d₁, ⋯, d₅ are centered around 0 and have standard deviation .5. The trade-off contour, 𝒞, was determined by fitting a quadratic curve to the trade-off target probability pairs (π_E, π_T) = (0.15, 0), (0.45, 0.20), (1, 0.60), which gives target contour function ${\pi }_T=-0.0952+0.6239{\pi }_E+0.0713{\pi }_E^2$. Figure 1 illustrates the target contour by a solid line, with contours on which all (π_E, π_T) have the same desirability θ(π_E, π_T) shown as dashed lines. Dose acceptability was determined by π̲_E = 0.25 for efficacy and π̄_T = 0.35 for toxicity, with decision cutoffs p_E = p_T = 0.10. In Case 2, a dose could be declared inefficacious due to the first inequality in (4) being violated only after at least one cohort was fully evaluated at that dose. In the first set of simulations, we considered trials with 16 cohorts of size three, so N_max = 48. In practice, N_max should be chosen via simulation by doing a sensitivity analysis that evaluates a design’s properties over a range of practically feasible N_max values.

Figure 1.

Desirability Contours: The target contour is represented by a solid line. Other contours on which all (π_E, π_T) have the same desirability are shown as dashed lines.

The following designs are constructed to mimic dose-finding trials of either chemotherapy for acute leukemia in Case 1, or an agent that is part of a preparative regimen in the stem cell transplantation trial for multiple myeloma in Case 2. Recall that, in Case 1, X_E may occur at any time during [0, U_E], and, in Case 2, Y_E is observed at U_E. For Case 1, we assumed that U_E = U_T = 6 weeks with accrual rate α = 1.5 patients per week. For Case 2, we assumed U_E = 90 days, (12.85 weeks), toxicity evaluation interval U_T = 30 days (4.3 weeks), and accrual rate α = 2.1 patients per week. The logistical difficulty indices are ζ = 1.5 × 6 = 9 for Case 1 and ζ = 2.1 × 12.85 = 27 for Case 2. We kept all other parameters for Case 2 the same as those in Case 1.

We assumed prior means 0.15, 0.20, 0.25, 0.30, 0.35 for π_E(d₁, θ), …, π_E(d₅, θ) and 0.15, 0.20, 0.27, 0.35, 0.45 for π_T (d₁, θ), …, π_T(d₅, θ). Applying the method described in Section 4.2, this gave location parameters (μ̃_μE, μ̃_βE,1, μ̃_βE,2) = (−1.21, 0.96, 0.35) and (μ̃_μT, μ̃_βT,1, μ̃_βT,2) = (−1.16, 1.39, 0.85) for the shifted Cauchy priors. For the Gamma piecewise exponential event rate priors, we assumed K = 6. The formula in Section 4.2 gives (λ̃_E,1, ⋯, λ̃_E,6) = (λ̃_T,1, ⋯, λ̃_T,6) = (0.182, 0.222, 0.286, 0.400, 0.667, 2.000) in Case 1, and (λ̃_T,1, ⋯, λ̃_T,6) = (0.364, 0.444, 0.571, 0.800, 1.333, 4.000) in Case 2. We used tuning parameter C = 2. Thus, for example, λ_E,1 ~ Gam(0.093, 0.5) in Case 1.

5.2 Simulation Study Design

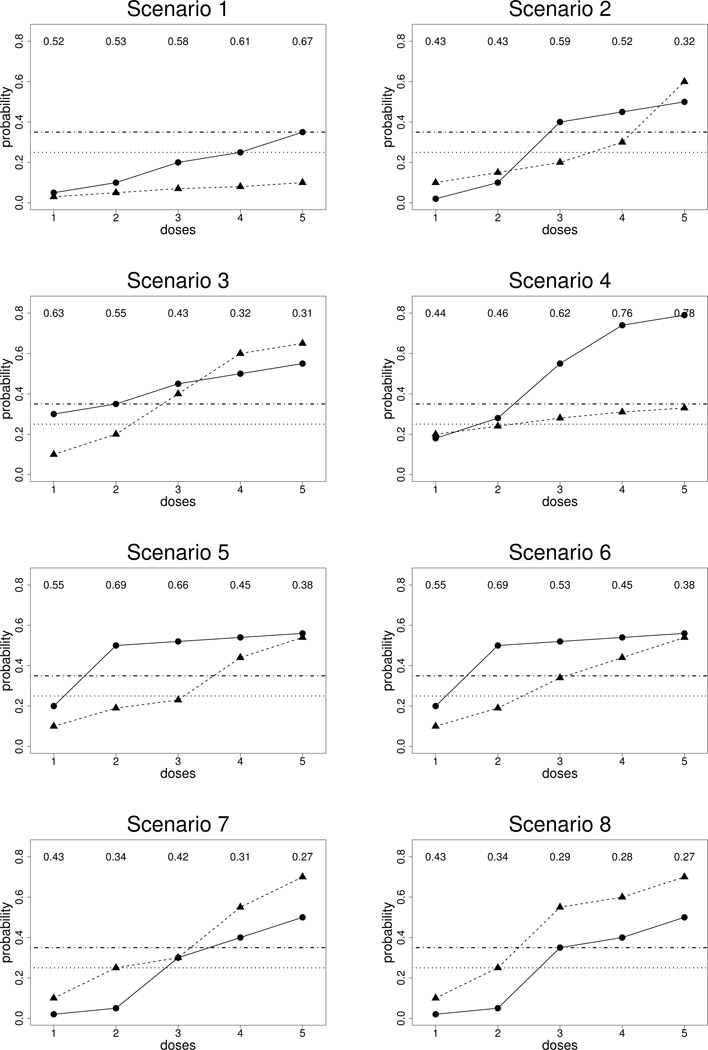
Each simulation scenario was specified in terms of assumed true efficacy and toxicity probabilities at each dose, π_j(d_r)^true, for j = E, T and r = 1, …, 5. We modeled association between X_E and X_T by assuming a Clayton copula (Clayton, 1978) with ϕ = 1.0. We considered eight scenarios, illustrated in Figure 2. In Scenario 8, no dose is admissible, since d = 1,2 are inefficacious and d = 3,4,5 are too toxic. For the first simulation study, we generated X_E, X_T from Weibull distributions. For each j and d_r, the Weibull scale and shape parameters were chosen so that (1) Pr(X_j ≤ U_j |d_r)^true = π_j(d_r)^true and (2) π_j,late(d_r)^true = Pr(U_j/2 ≤ X_j ≤ U_j |d_r)^true = 0.50, that is, 50% of the events occurred in the second half of the evaluation interval. Because π_E(d_r)^true and π_T (d_r)^true vary with d_r in each scenario, the scale and shape parameters of the corresponding true Weibull distributions both vary with d_r. Each scenario was simulated 1000 times.

Figure 2.

Illustration of scenarios: The solid lines with circles represent true probabilities of efficacy and the dashed lines with triangles represent true probabilities of toxicity. The horizontal lines represent π̄_T and π̲_E.

5.3 Simulation Results for Case 1

For Case 1, we compared the LO-EffTox design to three methods that are used in practice to deal with the late onset problem. The first method is the “One Level Down” rule. With this method, if some of the patients treated at the current optimal dose, d^opt = d_r have not yet been evaluated fully, i.e. Y_i,E,dr = missing or Y_i,T,dr = missing, then any new patient is treated at d_r−1. The second method is the “Look Ahead” rule (Thall et al., 1999) which says that, for each possible value 𝒟̃_mis(Y) that 𝒟_mis(Y) may take on, use the completed data 𝒟_obs(Y) ∪ 𝒟̃_mis(Y) to compute d^opt. If this dose is the same for all possible 𝒟̃_mis(Y), then use that dose to treat the next patient immediately. Otherwise, the only two options for new patients are to make them wait to be treated, which usually is impossible in practice, or to turn them away and treat them off protocol. The third method uses all complete cases, where both Y_E and Y_T are observed, to compute d^opt and treat the next patient immediately.

We will use two summary criteria to evaluate each method’s performance and compare the three methods. Denote the true desirability of dose d_r by ${\delta }_r^{\mathit{\text{true}}}$ and the true set of acceptable doses by 𝒜^true. The first criterion is the desirability-weighted selected percentage,

$$\mathrm{\delta ̄}=\frac{{\sum }_{r=1}^5{\delta }_r^{\mathit{\text{true}}}\text{Pr}(\text{select}{d}_r)I(d_r\in {𝒜}^{\mathit{\text{true}}})}{{\sum }_{r=1}^5{\delta }_r^{\mathit{\text{true}}}I(d_r\in {𝒜}^{\mathit{\text{true}}})},$$

which quantifies dose selection reliability and thus potential benefit for future patients. The second criterion is the ratio N_E/N_T where N_E and N_T denote the number of patients who experienced efficacy and toxicity, respectively. This criterion quantifies benefit to the patients in the trial, hence may be considered an index of ethical desirability.

Table 1 gives the operating characteristics of the LO-EffTox design and three competing methods. The percentage of trials with no dose selected is denoted by “None,” with the numbers of patients turned away from the trial by the Look Ahead method given in parentheses. In general, LO-EffTox outperforms the One Level Down, Look Ahead rule, and Complete Case method. The One Level Down rule has much smaller correct selection rate and mean N_E. The Look Ahead rule design performs roughly equivalently to LO-EffTox in terms of dose selection percentages and N_E/N_T, but the trial durations under the Look Ahead rule are dramatically larger compared to LO-EffTox. This is because the Look Ahead rule turns many patients away, while LO-EffTox treats all patients. Compared to the Complete Case method, LO-EffTox has either similar or higher correct selection percentages and more patients treated at doses with higher desirability. In Scenario 8, where all doses are inefficacious or too toxic, LO-EffTox has by far the largest probability of correctly stopping early and selecting no dose.

Table 1.

Simulation study comparing the four phase I–II designs in Case 1. The probability pairs given in parentheses for each dose level are (π_E(d_r)^true, π_T(d_r)^true).

Method		Dose Level						NE/NT	Duration (Weeks)
		1	2	3	4	5	None
	Scenario 1	(0.05, 0.03)	(0.10, 0.05)	(0.20, 0.07)	(0.25, 0.08)	(0.35, 0.10)
	δtrue	0.52	0.53	0.58	0.61	0.67
LO-EffTox	% selected	0.0	0.1	2.6	2.5	91.7	3.1	11.8/3.8	36.9
	# patients	6.15	6.80	6.94	4.96	22.80
One Down	% selected	0.0	0.7	6.0	16.1	76.6	0.6	5.7/2.4	37.0
	# patients	18.89	13.69	10.42	4.46	0.50
Look Ahead	% selected	0.0	0.2	2.4	2.5	88.7	6.2	13.1/4.0	69.7
	# patients	3.40	3.84	4.30	3.97	30.90	(52.07)
Complete Case	% selected	0.0	0.2	2.4	3.4	91.8	2.2	9.8/3.3	37.6
	# patients	11.18	8.11	6.76	5.43	16.40
	Scenario 2	(0.02, 0.10)	(0.10, 0.15)	(0.40, 0.20)	(0.45, 0.30)	(0.50, 0.60)
	δtrue	0.43	0.43	0.59	0.52	0.32
LO-EffTox	% selected	0.0	11.9	61.6	20.5	5.0	1.0	15.5/13.1	36.9
	# patients	5.90	9.31	13.79	9.60	9.14
One Down	% selected	0.0	1.0	5.1	24.3	69.1	0.5	8.3/7.6	37.2
	# patients	18.73	13.51	10.49	4.67	0.51
Look Ahead	% selected	0.0	8.0	67.5	19.0	4.6	0.9	16.7/12.5	74.2
	# patients	3.39	7.14	20.58	9.95	6.67	(57.54)
Complete Case	% selected	0.0	8.9	44.3	27.4	18.5	0.9	13.1/11.9	37.0
	# patients	11.27	10.19	9.86	8.56	7.95
	Scenario 3	(0.30, 0.10)	(0.35, 0.20)	(0.45, 0.40)	(0.50, 0.60)	(0.55, 0.65)
	δtrue	0.63	0.55	0.43	0.32	0.31
LO-EffTox	% selected	75.0	22.5	2.3	0.2	0.0	0.0	16.2/8.9	37.4
	# patients	26.21	14.21	5.11	1.88	0.59
One Down	% selected	77.6	14.4	4.7	2.6	0.0	0.7	15.5/7.3	37.1
	# patients	31.30	12.79	3.34	0.33	0.00
Look Ahead	% selected	63.8	32.6	3.3	0.1	0.0	0.2	16.4/8.9	62.4
	# patients	24.79	16.39	5.32	1.23	0.23	(39.65)
Complete Case	% selected	78.5	17.2	2.0	1.2	0.0	1.1	15.7/8.1	37.0
	# patients	28.99	12.44	4.61	1.27	0.30
	Scenario 4	(0.18, 0.20)	(0.28, 0.24)	(0.55, 0.28)	(0.74, 0.31)	(0.79, 0.33)
	δtrue	0.44	0.46	0.62	0.76	0.78
LO-EffTox	% selected	3.4	3.0	7.1	19.5	65.2	1.8	25.5/13.1	36.8
	# patients	9.63	6.87	7.77	9.98	13.08
One Down	% selected	9.1	5.8	9.2	29.3	40.4	6.2	13.9/10.6	35.7
	# patients	23.22	12.06	7.57	2.76	0.23
Look Ahead	% selected	8.5	6.1	11.1	21.0	51.8	1.5	26.5/13.2	70.8
	# patients	9.45	5.48	6.77	9.85	15.83	(52.81)
Complete Case	% selected	6.9	2.8	8.2	18.5	57.6	6.0	20.3/11.8	35.7
	# patients	15.70	7.79	8.02	7.67	6.73
	Scenario 5	(0.20, 0.10)	(0.50, 0.19)	(0.52, 0.23)	(0.54, 0.44)	(0.56, 0.54)
	δtrue	0.55	0.69	0.66	0.45	0.38
LO-EffTox	% selected	13.9	46.8	31.4	6.8	0.6	0.5	21.1/10.2	37.3
	# patients	11.35	16.31	14.22	4.63	1.33
One Down	% selected	10.8	22.6	39.3	22.1	4.0	1.2	17.5/7.7	37.2
	# patients	21.61	16.20	8.29	1.42	0.03
Look Ahead	% selected	10.7	48.3	37.7	3.1	0.1	0.1	21.9/10.4	76.1
	# patients	8.23	18.61	15.77	4.36	0.98	(60.26)
Complete Case	% selected	13.2	40.7	34.4	9.7	1.1	0.9	19.6/9.4	37.2
	# patients	15.67	15.23	11.96	3.97	0.85
	Scenario 6	(0.20, 0.10)	(0.50, 0.19)	(0.52, 0.34)	(0.54, 0.44)	(0.56, 0.54)
	δtrue	0.55	0.69	0.53	0.45	0.38
LO-EffTox	% selected	20.0	60.6	17.5	1.6	0.2	0.1	20.4/10.8	37.5
	# patients	13.32	19.09	11.05	3.38	1.13
One Down	% selected	14.9	37.5	35.1	9.7	1.6	1.2	17.3/8.4	36.9
	# patients	21.78	17.25	7.68	0.83	0.01
Look Ahead	% selected	16.1	65.4	17.1	1.2	0.1	0.1	21.2/10.8	73.8
	# patients	10.18	23.41	10.76	2.87	0.74	(56.73)
Complete Case	% selected	21.7	50.3	21.5	5.3	0.4	0.8	18.9/9.7	37.3
	# patients	17.69	17.31	9.65	2.50	0.56
	Scenario 7	(0.02, 0.10)	(0.05, 0.25)	(0.30, 0.30)	(0.40, 0.55)	(0.50, 0.70)
	δtrue	0.43	0.34	0.42	0.31	0.27
LO-EffTox	% selected	0.0	3.5	60.4	8.3	1.7	26.1	11.0/15.5	33.4
	# patients	6.27	9.08	16.71	6.28	5.91
One Down	% selected	10.9	4.3	10.9	29.7	37.4	6.8	13.9/10.7	35.5
	# patients	23.48	11.90	7.48	2.62	0.19
Look Ahead	% selected	9.6	8.3	22.1	47.2	11.8	1.0	25.4/14.9	74.3
	# patients	10.00	6.26	9.31	15.72	6.38	(57.84)
Complete Case	% selected	0.0	3.0	49.3	11.4	6.6	29.7	8.8/13.8	34.1
	# patients	11.27	12.21	11.94	5.28	4.44
	Scenario 8	(0.02, 0.10)	(0.05, 0.25)	(0.35, 0.55)	(0.40, 0.60)	(0.50, 0.70)
	δtrue	0.43	0.34	0.29	0.28	0.27
LO-EffTox	% selected	0.0	1.8	17.0	0.8	0.1	80.3	8.0/14.5	25.7
	# patients	6.09	10.12	13.10	4.13	2.40
One Down	% selected	0.0	1.8	33.9	14.8	7.2	42.3	5.4/11.9	34.3
	# patients	18.71	14.62	9.86	2.28	0.07
Look Ahead	% selected	0.0	1.8	18.7	0.5	0.1	78.9	8.3/13.6	59.7
	# patients	3.33	7.93	16.40	3.73	1.26	(50.76)
Complete Case	% selected	0.0	2.3	22.1	2.9	1.2	71.5	7.3/13.9	29.6
	# patients	11.25	12.78	10.99	4.07	1.91

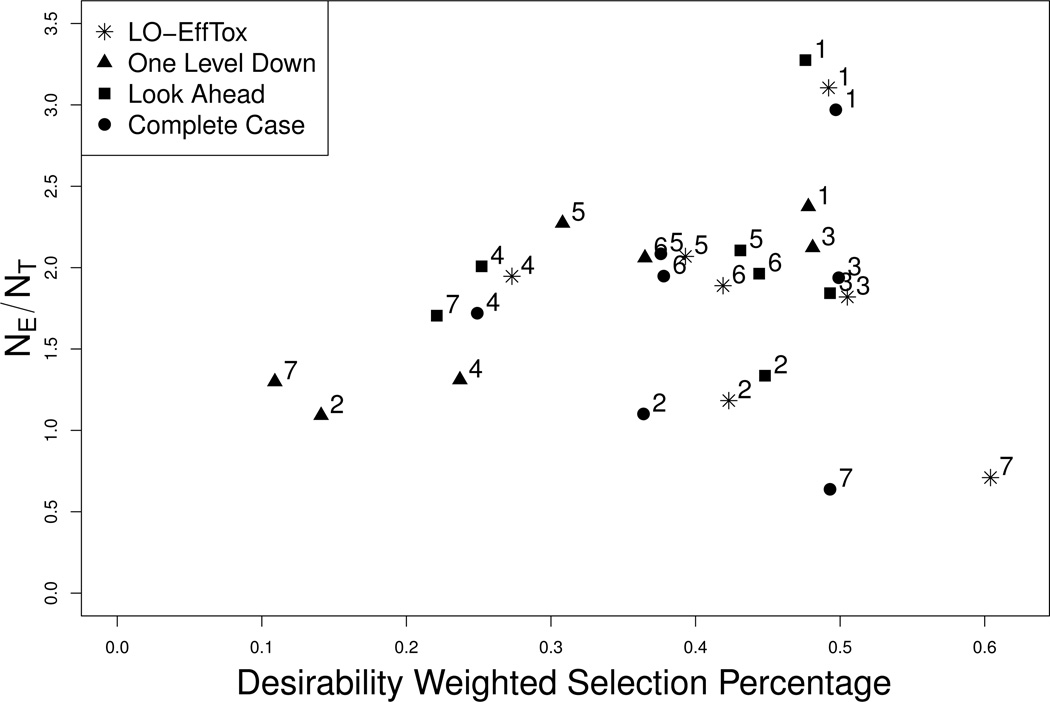
Figure 3 illustrates the results in Table 1 in terms of δ̄ plotted on the vertical axis and N_E/N_T on the horizontal axis, under each of Scenarios 1 – 7. Scenario 8 is not included in Figure 3 since in this case no dose is acceptable, so δ̄ is not relevant. Values in the upper right portion of the figure are more desirable, while values in the lower left are less desirable. Figure 3 shows that the One Level Down rule produces designs with very poor properties, in terms of both δ̄ and N_E/N_T. These two criteria are roughly equivalent for LO-EffTox and the Look Ahead version of EffTox for each of Scenarios 1 – 6, In Scenario 7, which has true desirability not monotone in dose, LO-EffTox has much greater δ̄ and much smaller N_E/N_T compared to the “Look Ahead” version of EffTox, so in this case there is no clear winner. However, since the Look Ahead rule turns away many patients and produces a very long trial, the apparent equivalence in terms of the two criteria in Figure 3 only tells part of the story. Compared to the Complete Case method, LO-EffTox has either similar or much larger δ̄ values and similar N_E/N_T.

Figure 3.

Comparison of the Late Onset Eff-Tox, One Level Down, Look Ahead, and Complete Case methods. The X-axis is δ̄, the desirability weighted selection percentage, and the Y-axis is N_E/N_T. Simulation scenarios are identified by integers.

5.4 Simulation Results for Case 2

For Case 2, we compared the LO-EffTox design to the One Level Down, Look Ahead, and Complete Case rules, and also the TiTE-CRM (Cheung and Chappell, 2000). We included the TiTE-CRM because, when the efficacy indicator Y_E is observed at U_E, the only time-to-event variables are X_T and V, which are the basis for the TiTE-CRM, so the TiTE-CRM is a reasonable alternative in Case 2. To implement the TiTE-CRM, we assumed the dose-toxicity model ${\pi }_T(d_r)=p_r^{\text{exp}(\alpha )}$ with fixed skeleton (p₁, ⋯, p₅) = (0.15, 0.20, 0.27, 0.35, 0.45), parameter α having N(0, σ² = 2) prior, and target toxicity probability 0.35.

The simulation results for the Case 2 under six of the eight scenarios are summarized in Table 2. Results for the other two scenarios are summarized in Table S1. Table 2 shows that, across all scenarios, LO-EffTox greatly outperforms the One Level Down, Look Ahead, and Complete Case methods, in terms of both selection percentages and N_E/N_T. The “One Level Down” rule is most likely to select d₃ or lower doses, and almost never selects d₄ or d₅, regardless of their δ values. It thus greatly sacrifices efficacy in many cases, as shown by the extremely small N_E values. As in Case 1, the “Look Ahead” rule has selection percentages similar to those of the LO-EffTox design, but the price is a much longer trial with many patients turned away. Because the TiTE-CRM design completely ignores efficacy, it is unlikely to select doses having acceptable toxicity and high efficacy, which is the case in nearly all scenarios. As in Case 1, for Scenario 8 LO-EffTox has by far the largest probability of correctly stopping early and selecting no dose.

Table 2.

Simulation study comparing the five phase I–II designs in Case 2. The probability pairs given in parentheses for each dose level are (π_E(d_r)^true, π_T(d_r)^true).

Method		Dose Level						NE/NT	Duration (Days)
		1	2	3	4	5	None
	Scenario 1	(0.05, 0.03)	(0.10, 0.05)	(0.20, 0.07)	(0.25, 0.08)	(0.35, 0.10)
	δtrue	0.52	0.53	0.58	0.61	0.67
LO-EffTox	% selected	0.0	0.4	1.1	2.2	90.9	5.4	12.7/3.9	237
	# patients	3.58	4.25	5.99	4.91	27.75
One Down	% selected	0.0	4.8	94.2	1.0	0.0	0.0	2.9/1.6	246
	# patients	38.74	9.23	0.03	0.00	0.00
Look Ahead	% selected	0.0	0.0	1.6	1.9	91.0	5.5	13.3/4.0	399
	# patients	3.25	3.49	4.54	6.11	29.26	(49.2)
Complete Case	% selected	0.0	2.7	7.3	6.3	80.7	3.0	6.2/2.4	244
	# patients	28.96	3.64	3.91	3.35	7.97
TiTE-CRM	% selected	0.0	0.0	0.0	0.0	99.9	0.1	14.2/4.3	240
	# patients	3.22	3.23	3.18	3.40	34.92
	Scenario 2	(0.02, 0.10)	(0.10, 0.15)	(0.40, 0.20)	(0.45, 0.30)	(0.50, 0.60)
	δtrue	0.43	0.43	0.59	0.52	0.32
LO-EffTox	% selected	0.0	9.4	62.5	21.4	5.4	1.3	16.4/12.6	244
	# patients	3.35	8.30	18.77	10.09	7.03
One Down	% selected	0.0	1.8	96.3	1.4	0.0	0.5	1.6/5.2	246
	# patients	38.72	9.17	0.04	0.00	0.00
Look Ahead	% selected	0.1	8.9	56.9	27.9	5.7	0.5	17.3/13.2	436
	# patients	3.27	6.46	17.54	13.38	7.24	(58.8)
Complete Case	% selected	0.0	5.3	29.2	32.0	33.2	0.3	7.9/9.1	246
	# patients	29.11	3.65	5.10	5.09	5.04
TiTE-CRM	% selected	0.0	0.7	14.0	70.8	13.3	1.2	18.3/15.7	238
	# patients	3.99	4.39	8.27	18.97	11.89
	Scenario 3	(0.30, 0.10)	(0.35, 0.20)	(0.45, 0.40)	(0.50, 0.60)	(0.55, 0.65)
	δtrue	0.63	0.55	0.43	0.32	0.31
LO-EffTox	% selected	68.1	27.9	3.4	0.4	0.0	0.2	16.4/9.2	247
	# patients	26.19	13.53	5.82	1.99	0.46
One Down	% selected	44.9	8.0	47.0	0.1	0.0	0.0	14.8/5.6	246
	# patients	38.98	8.99	0.02	0.00	0.00
Look Ahead	% selected	58.3	32.2	8.7	0.7	0.0	0.1	16.7/9.7	420
	# patients	22.21	16.28	7.54	1.69	0.23	(54.0)
Complete Case	% selected	85.1	11.3	2.0	1.5	0.1	0.0	14.9/6.2	247
	# patients	39.77	5.24	2.39	0.57	0.03
TiTE-CRM	% selected	1.1	30.1	62.3	5.1	0.0	1.4	20.1/17.4	238
	# patients	5.32	12.13	18.08	8.98	2.90
	Scenario 4	(0.18, 0.20)	(0.28, 0.24)	(0.55, 0.28)	(0.74, 0.31)	(0.79, 0.33)
	δtrue	0.44	0.46	0.62	0.76	0.78
LO-EffTox	% selected	3.5	3.8	10.4	20.9	61.0	0.4	27.0/13.5	246
	# patients	9.02	5.84	7.97	11.51	13.52
One Down	% selected	17.0	7.5	73.1	1.2	0.0	1.2	9.6/9.9	245
	# patients	38.64	9.09	0.05	0.00	0.00
Look Ahead	% selected	6.4	6.1	14.8	23.1	48.5	1.1	27.1/13.4	445
	# patients	7.58	6.17	9.38	10.55	13.93	(62.0)
Complete Case	% selected	11.4	6.1	7.8	20.1	54.4	0.2	15.3/11.0	246
	# patients	31.64	4.12	3.79	3.82	4.60
TiTE-CRM	% selected	1.1	5.6	19.1	28.0	40.2	6.0	25.9/12.8	231
	# patients	6.37	6.89	9.16	10.50	12.62
	Scenario 6	(0.20, 0.10)	(0.50, 0.19)	(0.52, 0.34)	(0.54, 0.44)	(0.56, 0.54)
	δtrue	0.55	0.69	0.53	0.45	0.38
LO-EffTox	% selected	20.3	63.4	13.9	1.8	0.4	0.2	20.8/10.9	246
	# patients	11.86	20.78	10.87	3.45	0.96
One Down	% selected	8.0	12.4	79.2	0.4	0.0	0.0	12.4/5.6	247
	# patients	38.73	9.24	0.03	0.00	0.00
Look Ahead	% selected	16.7	52.2	26.3	3.8	0.9	0.1	21.6/11.5	402
	# patients	9.10	20.03	13.71	4.26	0.86	(48.6)
Complete Case	% selected	27.8	40.2	22.8	7.1	2.0	0.1	14.4/7.6	246
	# patients	32.84	7.63	5.38	1.82	0.33
TiTE-CRM	% selected	0.0	11.8	51.6	30.2	4.6	1.8	23.5/16.7	237
	# patients	4.47	7.42	14.68	13.57	7.10
	Scenario 8	(0.02, 0.10)	(0.05, 0.25)	(0.35, 0.55)	(0.40, 0.60)	(0.50, 0.70)
	δtrue	0.43	0.34	0.29	0.28	0.27
LO-EffTox	% selected	0.0	1.9	8.1	0.4	0.1	89.5	7.9/13.6	117
	# patients	3.36	7.21	13.99	4.18	1.79
One Down	% selected	0.0	4.2	90.1	1.4	0.0	4.3	1.3/6.1	247
	# patients	38.62	9.31	0.05	0.00	0.00
Look Ahead	% selected	0.0	1.6	18.8	1.1	0.1	78.4	8.2/13.4	367
	# patients	3.22	8.10	16.11	3.79	1.17	(53.5)
Complete Case	% selected	0.0	8.2	33.5	8.7	3.9	45.7	5.0/10.6	204
	# patients	28.81	4.85	7.18	2.84	1.15
TiTE-CRM	% selected	5.8	58.7	31.7	0.9	0.0	2.9	9.1/17.5	236
	# patients	8.00	17.23	14.29	5.65	1.69

5.5 Sensitivity Analyses

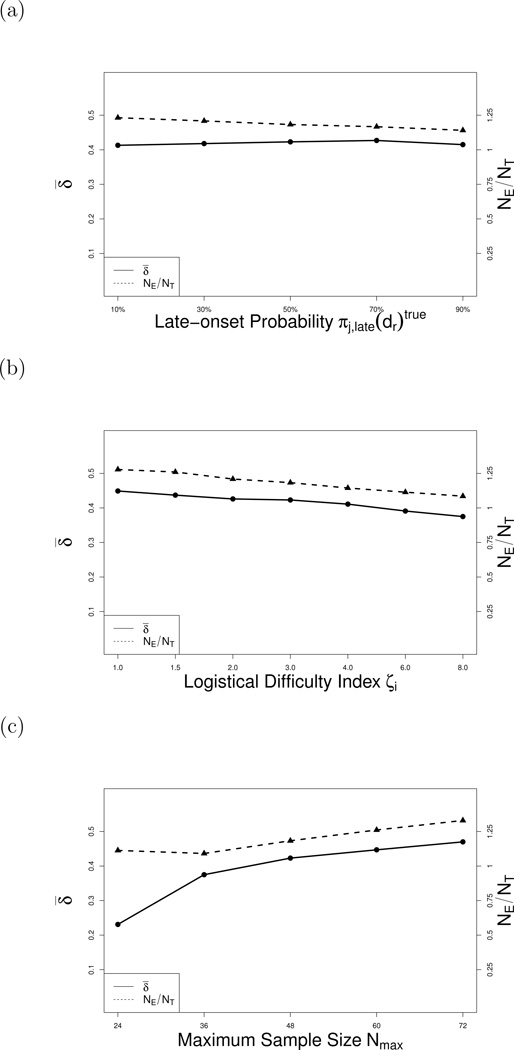
To investigate robustness, we conducted additional simulations in which we varied each of π_j,late(d)^true, logistical difficulty index ζ, N_max, the event time distributions, K = number of sets in the piecewise exponential event time distribution partition, and the association parameter, ϕ. Each sensitivity analysis was conducted for all scenarios, and the results are summarized in Supplementary Tables S2 – S8. Table S2 shows that the design is not sensitive to changes in values of π_j,late(d)^true over the range 0.10 to 0.90, illustrated in Figure 4a. Tables S3 and S4 summarize sensitivity to the logistical difficulty index for the values ζ = 3.0 to 24.0 in Case 1 and ζ = 9.0 to 54.0 in Case 2. As ζ increases, the ratio N_E/N_T and δ̄ both decrease, illustrated in Figure 4b. Table S5 shows, as expected, that the design’s performance improves with larger N_max, illustrated in Figure 4c. Simulations with X_E and X_T generated from several combinations of the Weibull and Log-logistic(Table S6) showed that LO-EffTox is robust to the true event time distributions. Table S7 shows that the number of sets in the partition of the piecewise exponential has little effect on the method’s performance for K = 6 to 12. Varying the association parameter from ϕ = 0.1 to 2.5 had almost no effect on performance (see Table S8).

Figure 4.

Sensitivity analyses under Scenario 2. Solid lines represent the desirability weighted selection percentages δ̄. Dashed lines represent the means of N_E/N_T.

6 Discussion

We have proposed a general methodology to address the problem of late-onset outcomes in phase I–II clinical trials. The method treats unobserved binary outcomes are as nonignorable missing data, uses data augmentation to impute the missing outcomes, and applies the design’s decision rules using the completed data. Simulations show that, in most cases, the proposed design performs better than alternative approaches to the late onset problem in phase I–II trials. Our results suggest that the general approach of imputing binary vectors Y by utilizing time-to-event variables used to define Y may improve the logistics of any outcome-adaptive procedure based on the distribution of Y.

Appendix

The probability of Y_E = 1 with the known Y_T value is

$$\mathrm{p}\mathrm{r}(Y_E=1|X_E>V,Y_T)=\frac{\mathrm{p}\mathrm{r}(Y_E=1)\mathrm{p}\mathrm{r}(Y_T,X_E>V|Y_E=1)}{{\sum }_{a=0}^1\mathrm{p}\mathrm{r}(Y_E=a)\mathrm{p}\mathrm{r}(Y_T,X_E>V|Y_E=a)}=\frac{\mathrm{p}\mathrm{r}(Y_E=1)\mathrm{p}\mathrm{r}(Y_T|Y_E=1)\mathrm{p}\mathrm{r}(X_E>V|Y_T,Y_E=1)}{{\sum }_{a=0}^1\mathrm{p}\mathrm{r}(Y_E=a)\mathrm{p}\mathrm{r}(Y_T|Y_E=a)\mathrm{p}\mathrm{r}(X_E>V|Y_T,Y_E=a)}=\frac{\mathrm{p}\mathrm{r}(Y_T,Y_E=1)\mathrm{p}\mathrm{r}(X_E>V|Y_E=1)}{{\sum }_{a=0}^1\mathrm{p}\mathrm{r}(Y_T,Y_E=a)\mathrm{p}\mathrm{r}(X_E>V|Y_E=a)}=\{\begin{array}{cc}\hfill \frac{{\pi }_{1,1}\mathrm{p}\mathrm{r}(X_E>V|Y_E=1)}{{\pi }_{1,1}\mathrm{p}\mathrm{r}(X_E>V|Y_E=1)+{\pi }_{01}}=\frac{{\pi }_{1,1}{S}_{10}}{{\pi }_{1,1}{S}_{10}+{\pi }_{0,1}}\hfill & \text{if}{Y}_T=1,\hfill \\ \hfill \frac{{\pi }_{1,0}\mathrm{p}\mathrm{r}(X_E>V|Y_E=1)}{{\pi }_{1,0}\mathrm{p}\mathrm{r}(X_E>V|Y_E=1)+{\pi }_{0,0}}=\frac{{\pi }_{1,0}{S}_{10}}{{\pi }_{1,0}{S}_{10}+{\pi }_{0,0}}\hfill & \text{if}{Y}_T=0.\hfill \end{array}$$

where S_ab and π_a,b are defined by equation (2) and (3), respectively.

The probability of Y_T = 1 with the known Y_E value is

$$\mathrm{p}\mathrm{r}(Y_T=1|X_T>V,Y_E)=\frac{\mathrm{p}\mathrm{r}(Y_T=1)\mathrm{p}\mathrm{r}(Y_E,X_T>V|Y_T=1)}{{\sum }_{b=0}^1\mathrm{p}\mathrm{r}(Y_T=b)\mathrm{p}\mathrm{r}(Y_E,X_T>V|Y_T=b)}=\frac{\mathrm{p}\mathrm{r}(Y_T=1)\mathrm{p}\mathrm{r}(Y_E|Y_T=1)\mathrm{p}\mathrm{r}(X_T>V|Y_E,Y_T=1)}{{\sum }_{b=0}^1\mathrm{p}\mathrm{r}(Y_T=b)\mathrm{p}\mathrm{r}(Y_E|Y_T=b)\mathrm{p}\mathrm{r}(X_T>V|Y_E,Y_T=b)}=\frac{\mathrm{p}\mathrm{r}(Y_E,Y_T=1)\mathrm{p}\mathrm{r}(X_T>V|Y_T=1)}{{\sum }_{b=0}^1\mathrm{p}\mathrm{r}(Y_E,Y_T=b)\mathrm{p}\mathrm{r}(X_T>V|Y_T=b)}=\{\begin{array}{cc}\hfill \frac{{\pi }_{1,1}\mathrm{p}\mathrm{r}(X_T>V|Y_T=1)}{{\pi }_{1,1}\mathrm{p}\mathrm{r}(X_T>V|Y_T=1)+{\pi }_{1,0}}=\frac{{\pi }_{1,1}{S}_{01}}{{\pi }_{1,1}{S}_{01}+{\pi }_{1,0}}\hfill & \text{if}{Y}_E=1,\hfill \\ \hfill \frac{{\pi }_{0,1}\mathrm{p}\mathrm{r}(X_T>V|Y_T=1)}{{\pi }_{0,1}\mathrm{p}\mathrm{r}(X_T>V|Y_T=1)+{\pi }_{0,0}}=\frac{{\pi }_{0,1}{S}_{01}}{{\pi }_{0,1}{S}_{01}+{\pi }_{0,0}}\hfill & \text{if}{Y}_E=0.\hfill \end{array}$$

where S_ab and π_a,b are defined by equation (2) and (3), respectively.

When Y_T and Y_E are unknown, the probability of (Y_E, Y_T) is

$$\mathrm{p}\mathrm{r}(Y_E=1,Y_T=1|X_E>V,X_T>V)=\frac{\mathrm{p}\mathrm{r}(X_E>V,X_T>V|Y_E=1,Y_T=1)\mathrm{p}\mathrm{r}(Y_E=1,Y_T=1)}{{\sum }_{a=0}^1{\sum }_{b=0}^1\mathrm{p}\mathrm{r}(X_E>V,X_T>V|Y_E=a,Y_T=b)\mathrm{p}\mathrm{r}(Y_E=a,Y_T=b)}=\frac{{\pi }_{1,1}{S}_{11}}{{\sum }_{a=0}^1{\sum }_{b=0}^1{\pi }_{a,b}{S}_{ab}},\mathrm{p}\mathrm{r}(Y_E=1,Y_T=0|X_E>V,X_T>V)=\frac{\mathrm{p}\mathrm{r}(X_E>V,X_T>V|Y_E=1,Y_T=0)\mathrm{p}\mathrm{r}(Y_E=1,Y_T=0)}{{\sum }_{a=0}^1{\sum }_{b=0}^1\mathrm{p}\mathrm{r}(X_E>V,X_T>V|Y_E=a,Y_T=b)\mathrm{p}\mathrm{r}(Y_E=a,Y_T=b)}=\frac{{\pi }_{1,0}{S}_{10}}{{\sum }_{a=0}^1{\sum }_{b=0}^1{\pi }_{a,b}{S}_{ab}},\mathrm{p}\mathrm{r}(Y_E=0,Y_T=1|X_E>V,X_T>V)=\frac{\mathrm{p}\mathrm{r}(X_E>V,X_T>V|Y_E=0,Y_T=1)\mathrm{p}\mathrm{r}(Y_E=0,Y_T=1)}{{\sum }_{a=0}^1{\sum }_{b=0}^1\mathrm{p}\mathrm{r}(X_E>V,X_T>V|Y_E=a,Y_T=b)\mathrm{p}\mathrm{r}(Y_E=a,Y_T=b)}=\frac{{\pi }_{0,1}{S}_{01}}{{\sum }_{a=0}^1{\sum }_{b=0}^1{\pi }_{a,b}{S}_{ab}}.$$

where where S_ab and π_a,b are defined by equation (2) and (3), respectively, and S₀₀ = 1.