Towards modelling the flexible timing of shoot development: simulation of maize organogenesis based on coordination within and between phytomers

Abstract

Background and Aims

Experimental evidence challenges the approximation, central in crop models, that developmental events follow a fixed thermal time schedule, and indicates that leaf emergence events play a role in the timing of development. The objective of this study was to build a structural development model of maize (Zea mays) based on a set of coordination rules at organ level that regulate duration of elongation, and to show how the distribution of leaf sizes emerges from this.

Methods

A model of maize development was constructed based on three coordination rules between leaf emergence events and the dynamics of organ extension. The model was parameterized with data from maize grown at a low plant population density and tested using data from maize grown at high population density.

Key Results

The model gave a good account of the timing and duration of organ extension. By using initial conditions associated with high population density, the model reproduced well the increase in blade elongation duration and the delay in sheath extension in high-density populations compared with low-density populations. Predictions of the sizes of sheaths at high density were accurate, whereas predictions of the dynamics of blade length were accurate up to rank 9; moderate overestimation of blade length occurred at higher ranks.

Conclusions

A set of simple rules for coordinated growth of organs is sufficient to simulate the development of maize plant structure without taking into account any regulation by assimilates. In this model, whole-plant architecture is shaped through initial conditions that feed a cascade of coordination events.

INTRODUCTION

Plant development responds strongly to the environment by changing individual organ size. The relative contributions of rate and duration of elongation to changes in organ sizes are not known. Therefore, in many plant models the elongation duration of each organ is fixed while only elongation rate can be modulated by environmental factors (Fournier and Andrieu, 1998; Evers et al., 2005; Guo et al., 2006; Vos et al., 2010). However, this fixed duration is challenged by experimental evidence that duration does vary in different environments (Sugiyama and Gotoh, 2010), and this is relevant both for understanding the distribution of organ size along a shoot (Andrieu et al., 2006) and plant responses in organ size to environmental factors such as temperature stress (Louarn et al., 2010) and shading by neighbouring plants (Zhu et al., 2014).

Andrieu et al. (2006) showed that the onset of sheath extension and duration of blade extension are major determinants of the response of blade length of maize (Zea mays) to plant density. Louarn et al. (2010) showed that, under chilling conditions, maize leaves (blade + sheath) have a longer duration of elongation that compensates for the slower rate of growth. All these authors confirmed the positive effects of the length of the sheath tube (Fig. 1) on the elongation rates and durations of the blades and sheaths that grow within it (Davies et al., 1983; Wilson and Laidlaw, 1985; Casey et al., 1999). Thus, early growth processes appear to affect later growth processes by affecting the length of the sheath tube. Because of the positive effect of the length of a sheath n on the length of the next sheath, n + 1 (Andrieu et al., 2006), changes in the length of lower sheaths would continue to propagate to upper sheaths and thus also to blades. The positive effect of the length of sheath n on the length of sheath n + 1 likely acts through a coordination mechanism in which a decline in the elongation rate of a given sheath n, leading to cessation of sheath growth, is coordinated with the emergence of its collar (Fournier and Andrieu, 2000a, b). Such coordination rules can result in flexible timing of organ development because the time of events is partly controlled by the architecture itself (Verdenal et al., 2008). However, no structural model has been set up based mainly on coordination rules, e.g. synchrony between emergence events and the dynamics of organ extension. Hence, there are no tools for explaining the change in leaf elongation duration under various growth conditions. The aims of this study were to (1) set up a structural development model of maize based on a set of coordination rules at the organ level that regulate elongation duration and (2) show how the timing of organ development can be influenced by initial conditions through coordination rules.

Fig. 1.

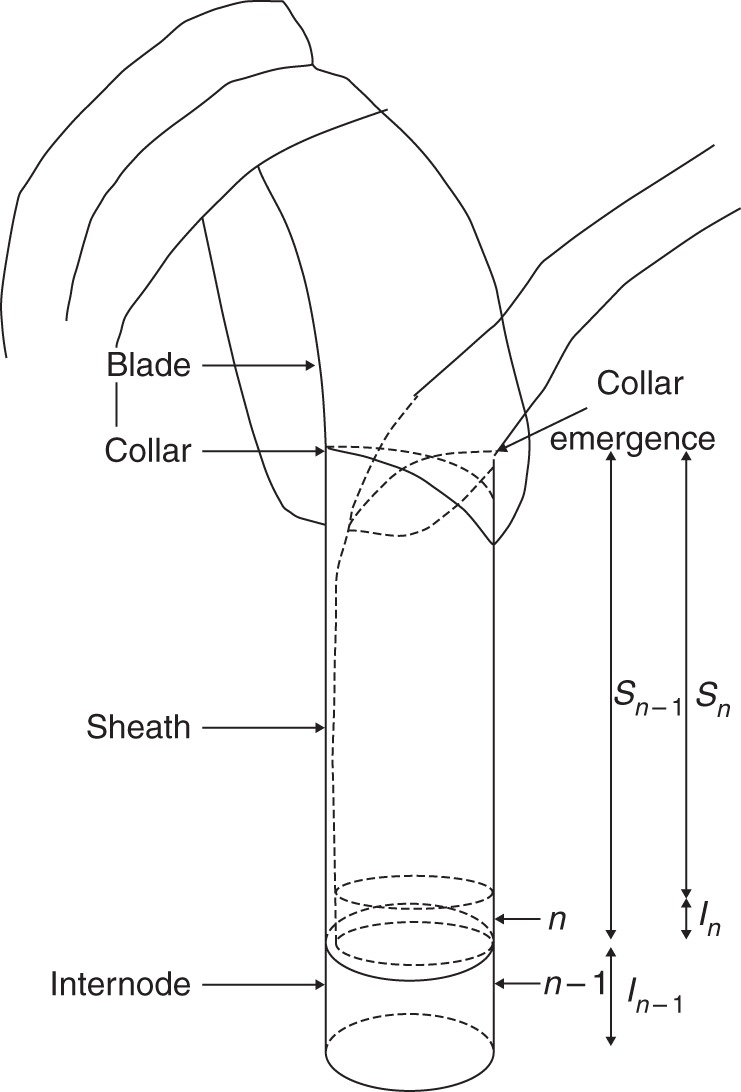
Schematic diagram of two successive phytomers, showing the relationships among the time of collar emergence, the lengths of the sheaths (S_n and S_n–1) and the length (I_n) of internode n. Adapted from Fournier and Andrieu (2000a).

In this study we integrated three coordination rules, in sequence of succession of leaf emergence events: (I) tip emergence of leaf n is coordinated with initiation of sheath n and stabilization of the elongation zone length of blade n (Andrieu et al., 2006); (II) collar emergence of leaf n – 1 is coordinated with the start of linear elongation of sheath n (newly postulated rule); and (III) collar emergence of leaf n is coordinated with the decline in elongation rate of sheath n and the rapid increase in the elongation rate of internode n (Fournier and Andrieu, 2000a). These three coordination rules were implemented in a model of maize shoot development, using the principles of functional–structural plant modelling (Vos et al., 2010). Modelling of this type is suited to simulate morphogenesis as a coordinated growth process, and allows the generation and study of hypotheses drawn from experimental data. The model was parameterized using parameters derived from the growth of maize plants at low density (Andrieu et al., 2006) and was tested by simulating the growth of maize plants at high density by adapting only the initial conditions, but keeping model parameters the same. Thus, testing of the model allows evaluation of the effect of coordination on the emergence of a modified structure of the whole plant over time, based on a change in the initial conditions only. These initial conditions were the dynamics of the length of the first three sheaths, which could therefore be used to reflect the environmental influence on the early growth of the plant. The sensitivity of time of leaf tip emergence to changes in the relative rate of blade elongation was analysed. A scenario study was carried out to assess the effects of early competition by varying the initial conditions of the model. The model is described according to the protocol of Grimm et al. (2006).

MATERIALS AND METHODS

Model concepts

The novel model concept developed in this study represents a holistic system view of plant development and contains coordination rules governing whole-plant development during both the vegetative and reproductive phases (Fig. 2). Concepts taken from earlier work are (1) the synchrony between collar emergence of a leaf and the rapid increase in the elongation rate of the associated internode (Fournier and Andrieu, 2000a); (2) a model for elongation of individual grass leaves in the vegetative phase (Fournier et al., 2005); and (3) the synchrony between sheath initiation and leaf tip appearance before tassel initiation, and sheath initiation at a constant time interval after tassel initiation (Andrieu et al., 2006). A novel element of our current model is the new coordination rule II, which was derived from experimental observations and allows simulation for all phytomers instead of individual phytomers. Also, our model takes into account the reproductive phase in which rules for sheath initiation and start of linear elongation are different from those for the vegetative phase, and in which internode elongation plays an important role in the timing of events.

Fig. 2.

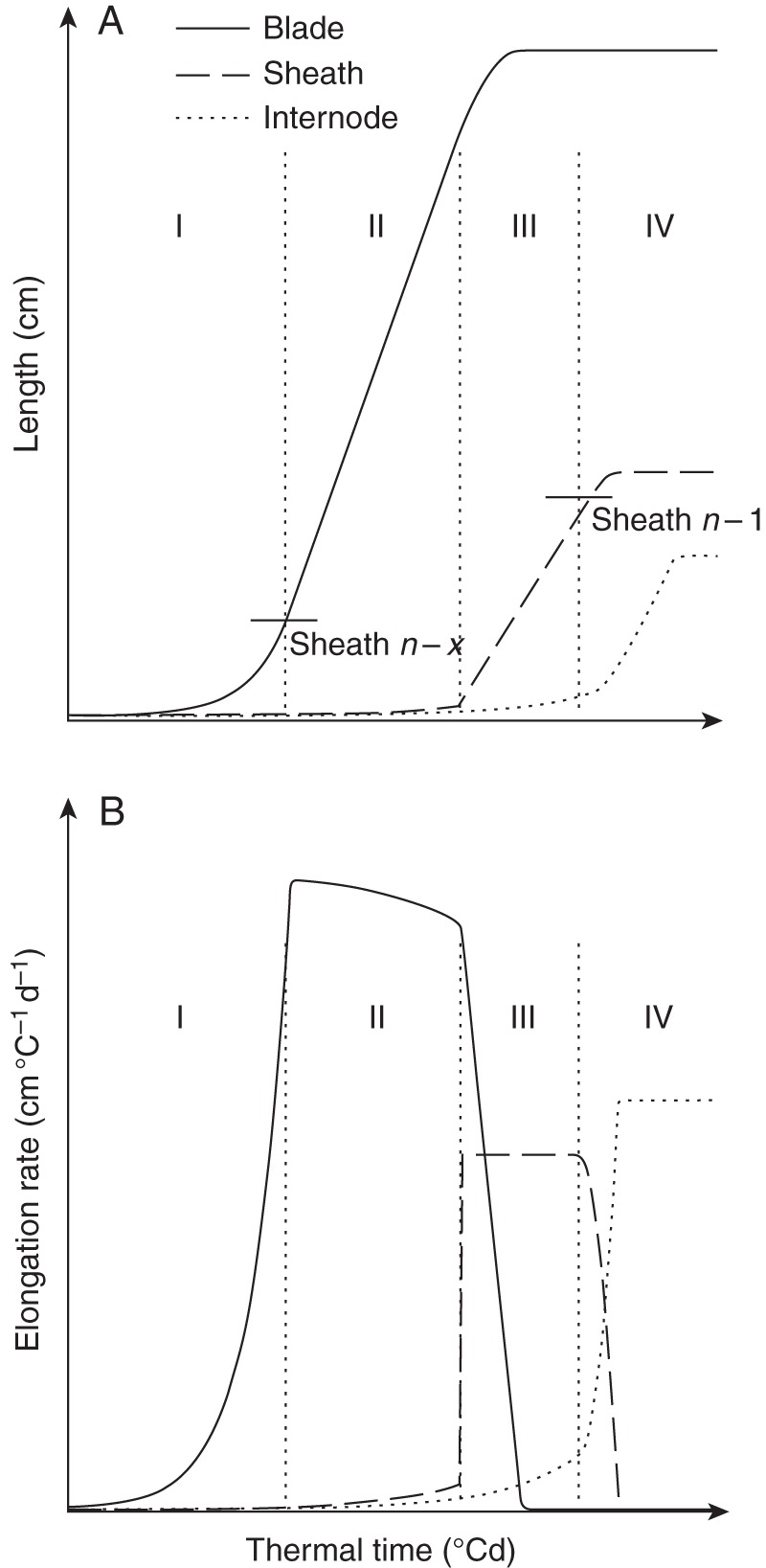
Conceptual model of lengths (A) and elongation rates (B) of blade, sheath and internode (see key) of a phytomer n with leaf tip emergence before tassel initiation, plotted against thermal time. Vertical dotted lines separate four phases of growth of the phytomer. Phase I: from blade initiation until tip emergence. Phase II: from tip emergence until collar emergence of the preceding leaf. Phase III: from collar emergence of the preceding leaf until collar emergence of the leaf itself. Phase IV: from collar emergence until completion of growth. The short horizontal line segments in (A) represent the length of the sheath that has the highest ligule on the plant at tip emergence (left line) and collar emergence (right line). The succession of leaf emergence events that linked with coordination rules comprised tip emergence, collar emergence of the preceding leaf and collar emergence of the leaf itself. Further explanation is given in the text. Adapted from Zhu et al. (2014).

The model is implemented in the interactive modelling platform GroIMP (Buck-Sorlin et al., 2005; Kniemeyer, 2008) and simulates growth of individual blades, sheaths and internodes (Supplementary Data Fig. S1). The state of each of these organs is characterized by their attributes (Table 1). Whole plant growth emerges as a result of three coordination rules. In the current paper, following Andrieu et al. (2006), we define emergence as the event in which a leaf tip or collar grows past the highest collar of the preceding sheaths (Fig. 1), while appearance is the event in which the blade tip appears visibly out of the whorl formed by preceding growing blades. Phyllochron here was defined as the thermal time interval between emergences of successive leaf blades.

Table 1.

List of model attributes and parameters, their definitions, units and values

Attributes	Definition	Value/unit
Phytomer rank	Phytomer number counting from bottom to top
Bn, Sn, In	Length of blade, sheath and internode of phytomer n	cm
En	Length of the blade elongation zone of phytomer n	cm
En,max	Maximum length of the elongation zone that was reached by blade n	cm
$I_n^{\ast }$	Length of internode n at collar emergence	cm
hasInitiated	True when organ is initiated	True/false
hasTipEmerged	True when the sum of the length of blade, sheath and internode of rank n is larger than the length of the sheath with its ligule at the highest position of the plant at that time	True/false
hasReachedEn,max	True when En,max has been reached for blade n	True/false
hasCollarEmerged	True when the sum of the length of sheath and internode of rank n is larger than the length of the sheath with its ligule at the highest position of the plant at that time	True/false
hasMatured	True when elongation rate of an organ is smaller than 1 × 10–3 cm °Cd	True/false

The general concepts of how the growth of blades, sheaths and internodes is coordinated are as follows (Fig. 2). The extension of one phytomer can be seen as four phases delineated by emergence events on the phytomer itself or on the preceding phytomer (phases I–IV in Fig. 2). During phase I (from blade initiation until tip emergence), blade and internode are present and grow exponentially. The internode is initiated at half a plastochron after initiation of the blade at the lower half of the disc of leaf insertion (Sharman, 1942). During phase II (from tip emergence until collar emergence of the preceding leaf), blade, sheath and internode are present. The blade grows approximately linearly. The sheath and internode both grow exponentially. Tip emergence limits further increase in the length of blade elongation zone, which has been attributed to a direct effect of light absorbed by the emerged leaf tip (Casey et al., 1999). Tip emergence also triggers the initiation of the associated sheath at the base of the blade. Since blade and sheath evolve from the same elongation zone (Schnyder et al., 1990), the extended length of the sheath is subtracted from the length of the blade elongation zone, which results in a gradual decrease in blade elongation rate. In phase III (from collar emergence of the preceding leaf until collar emergence of the leaf itself), collar emergence of the preceding leaf triggers the linear phase of sheath growth, which causes a rapid decrease in the length of blade elongation zone, and thus the rate of blade elongation declines rapidly to zero. During this phase, the internode still grows exponentially. In phase IV (from collar emergence until completion of growth), the blade is completely out of the sheath tube and has stopped growing. Collar emergence triggers the fading of the elongation rate of the sheath while the elongation rate of the internode increases rapidly, and their sum remains more or less constant. During this phase, in which the sheath is protruding from the sheath tube, the elongation rate of the internode reaches a constant rate within a short time. Subsequently, the internode grows linearly until it reaches its final length. The final length of internode n is obtained from the final length of the encapsulating sheath (rank n – 1) according to an empirical relationship (Supplementary Data Methods S1 and Fig. S2). Thus, the final internode length is not directly obtained from coordination rules.

The time of tip emergence is defined as the thermal time when the total length of blade plus sheath plus internode of rank n exceeds the length of encapsulating sheath within that time step. Collar emergence occurs when the total length of the sheath plus internode of rank n exceeds the length of encapsulating sheath that has the highest collar on the plant. Detailed justifications for the methods used for organ extension are provided in Supplementary Data Methods S2 . The dynamics of blade, sheath and internode extension in our model are described below.

Blade extension was calculated according to eqn 1 and eqn 2:

$$\frac{\text{d}{B}_n}{\text{d}t}=r_{\mathrm{B},n}{E}_n$$ (1)

$$E_n^{}=\{\begin{array}{cc}{B}_n& B_n<E_{n,\max }^{}\\ E_{n,\max }^{}-S_n& B_n\ge E_{n,\max }^{}\end{array}$$ (2)

where B_n is the length of blade n (cm), r_B,n is the relative elongation rate of the elongation zone of blade n (°Cd^–1), E_n is the length of the elongation zone of blade n and S_n is the length of sheath n, E_n,max is the maximum length of the elongation zone that is reached by blade n. After tip emergence of blade n, E_n,max is set by taking the minimum value of the length of the elongation zone at tip emergence plus 2 cm (p, Table 2) and the ratio between maximum elongation rate (e) and relative elongation rate of blade n (r_B,n). The maximum elongation rate e is a parameter that is identical for all leaves. The length of the elongation zone was set back to E_n,max when the length of blade n exceeded E_n,max within one time step. A blade or sheath was mature when its elongation rate was less than 1 × 10^–3 cm °Cd^–1.

Table 2.

List of model parameters, their definitions, values and units

Attributes	Definition	Value	Unit
Plastochron	Thermal time interval between the initiations of successive blades	19·2	°Cd
Tassel initiation	The moment when the length of the apex meristem of main shoot reaches 0·5 mm	237	°Cd
Ear initiation	The moment when the length of the axillary meristem of the top ear reaches 0·5 mm.	350	°Cd
Initial blade length	Length of a blade at initiation	2·5 × 10–2	cm
Initial sheath length	Length of a sheath at initiation	0·1	cm
Initial internode length	Length of an internode at initiation	2·5 × 10–3	cm
rB,n	Relative elongation rate of blade n	3 × 10–2 –6 × 10–2	°Cd–1
rS	Constant relative elongation rate of sheath	2 × 10–2	°Cd–1
rI	Constant relative elongation rate of internode	2·3 × 10–2	°Cd–1
p	Maximum length by which the elongation zone of the blade can increase after tip emergence	2	cm
e	Maximum elongation rate that can be reached by each individual blade	0·5	cm °Cd–1
kS	Constant linear elongation rate of sheath	0·25	cm °Cd–1
d	Decline coefficient of the elongation rate of sheath, per unit of exposed sheath lengtha	3·0 × 10–3	°Cd–1
a1	Average blade age when the associated sheath is initiated for those blades that emerged after tassel initiation	150	°Cd
a2	Average blade age when the associated sheath starts the linear phase of extension for those blades that emerged after tassel initiation	300	°Cd

^aThe value obtained directly from the ‘optim’ function was 7·5 × 10^–3. It was fine-tuned to 3·0 × 10^–3 such that final sheath length was close to the observed values at normal density.

Sheath extension was calculated according to eqn 3:

$$\frac{\mathrm{d}{S}_n}{\mathrm{d}t}=\{\begin{array}{cc}{r}_{\mathrm{S}}{S}_n& t<c_{n-1}\\ k_{\mathrm{S}}& c_{n-1}\le t<c_n\\ k_{\mathrm{S}}-d\ast (I_n+S_n-S_{n-1})& t\ge c_n\end{array}$$ (3)

where S_n is the length of sheath n (cm), t is thermal time (°Cd), c_n–1 and c_n are the thermal times of the collar emergence on ranks n–1 and n, respectively, r_S is the relative elongation rate of the sheath (°C d^–1) and k_S is the linear elongation rate of the sheath (cm °Cd^–1). Since there was little variation in r_S and k_S among ranks, average values over ranks were used. d (°Cd^–1) is the decline coefficient of the elongation rate after collar emergence. The decline in the growth rate of sheath n equals the decline coefficient (d) times the exposed length of sheath n (I_n + S_n – S_n−1), which is calculated as the length of the internode n (I_n) plus the length of sheath n (S_n) minus the length of encapsulating sheath (S_n–1) (adapted from Fournier and Andrieu, 2000a). d was estimated by minimizing the sum of squared residuals comparing observed and estimated exposed sheath length at normal density (eqn S2, Supplementary Data Methods S3) using the ‘optim’ function in the ‘stas’ package of the R programming language (R Development Core Team, 2012).

Equation 3 applies to sheaths that initiated after tassel initiation, but with one difference: the start of the linear phase of growth is controlled by parameter a₂ instead of c_n–1. a₂ is defined as the average blade age when the associated sheath starts the linear phase of extension for those blades that emerged after tassel initiation.

Internode extension was calculated according to eqn 4:

$$\frac{\mathrm{d}{I}_n}{\mathrm{d}t}=\{\begin{array}{cc}{r}_{\mathrm{I}}{I}_n& t<c_n\\ k_{\mathrm{S}}+r_{\mathrm{I}}{I}_n^{\ast }-\frac{\mathrm{d}{S}_n}{\mathrm{d}t}& t\ge c_n\end{array}$$ (4)

where I_n is the length of internode n (cm), r_I is the relative elongation rate of internodes and $I_n^{\ast }$ is the length of internode n at collar emergence. The equation applies from ear initiation onwards. The extension of internode n stops when it reaches the final length. The length of internodes 1–4 was set to zero.

Data set

The model was parameterized using complete records of the dynamics of blade, sheath and internode length (typically from 1–3 mm to maturity) of all the phytomers of maize. The experiment was conducted outdoors at the INRA campus of Thiverval-Grignon, France (48°51′N, 1°58′E) on a silty loam soil. Hybrid maize Zea mays ‘Déa’ was sown on 15 May 2000 at two population densities: 9·5 and 30·5 plants m^–2, referred to as normal density and high density. Fifteen plants in each treatment were tagged at the time at which leaf 3 was exposed. Two or three times a week, the number of visible and collared leaves, the exposed lengths of the two youngest visible leaves and the length of the youngest mature blades were measured for each of the tagged plants. The median values for these lengths served as references to select between two and four (usually three) plants, which were dissected to enable measurement of the length of all blades, sheaths and internodes. Destructive measurements were performed under a binocular microscope for the early stages of development, and with a ruler once the dimension of the organ exceeded 1 cm. In both treatments, the temperature of the elongation zone was represented by soil temperature before stem extension and by the temperature behind a sheath at the height of the shoot apex, which were both measured by thermocouples. Details of experimental procedures and measurements are described by Andrieu et al. (2006).

The data were fitted using multi-phase regression models to derive the relative elongation rates and linear elongation rates of the extension of blades, sheaths and internodes. An exponential linear plateau model was used for the extension of blades and sheaths, and an exponential exponential linear plateau model was used for the extension of internodes (Andrieu et al., 2006). Details of the fitting procedures and choice of models are described by Hillier et al. (2005). Here we calculated the time of leaf tip or collar emergence by determining when the height of a leaf tip or collar equalled the height of the highest collar on the plant, based on multi-phase models for the growth of each organ, as parameterized by Andrieu et al. (2006).

Model verification and model validation

The normal-density data set was used for model parameterization and verification, and the high-density data set was used for model validation. The dynamics of the lengths of the first three sheaths at normal density and high density were input as the initial condition of the model (Supplementary Data Fig. S3). The start of model simulation was set at the time of initiation of blade 4, which was 23 °Cd after sowing. The output of the model comprised the moments of leaf tip and collar emergence and dynamics of organ extension and the final lengths of blades, sheaths and internode of ranks 4 and higher. The operation of the model and the correct estimation of its parameters were verified by comparing simulated and observed thermal times of leaf tip and collar emergence, which was done by plotting simulated and observed final lengths of blade, sheath and internode versus rank and by comparing simulated and observed dynamics of extension.

Model validation was done using data on maize at high density by adapting the initial conditions of the model to represent high density (Supplementary Data Fig. S3B) while all parameters were kept at their values estimated from maize growth at normal density.

Goodness of fit between observed values and model output was expressed as the root mean square error (RMSE):

$$\text{RMSE=}\sqrt{\frac{1}{n}{\displaystyle \sum _{i=1}^n{\left(X_{\text{sim,}i}-X_{\text{obs,}i}\right)}^{\text{2}}}}$$ (5)

where i is the sample number, n is the total number of measurements, X_sim,i is the simulated value and X_obs,i is the observed value. The units of RMSE are the same as those of the data.

Sensitivity analysis

To assess the sensitivity of model output to changes in relative elongation rate of the blade (r_B,n) at normal density, a sensitivity analysis was performed using the time of tip emergence versus phytomer rank as the test output variable. Initial conditions representing normal-density maize were used. The standard values of r_B,n were changed at 10 % intervals from –30 % to + 30 %.

Effects of initial sheath length

To assess the power of the model in predicting plant development as influenced by the effects of early competition, a scenario analysis was carried out. Typically, plants in general respond to early competition by producing longer sheaths in response to a drop in the red:far red ratio, aiming to maximize light interception (Franklin and Whitelam, 2007). Therefore, in our model the effects of early competition were represented by variations in the final lengths of the first three sheaths, mimicking the effects of early competition on sheath length. The final sheath lengths of the first three ranks at normal density were changed jointly in 10 % increments from –30 % to +30 %. The scenario in which initial final sheath length was increased by 30 % corresponded to the condition of maize plants at high density. The dynamics of blade and sheath extension on phytomers 5 and 7 were used as test output. Note that, due to the rules used for the sheaths that initiated after tassel initiation, blade development was not influenced by initial sheath length from rank 9 onwards.

Extra scenarios were simulated to explore the causes of reduction in final blade length at high ranks. The results are presented in Supplementary Data Table S1 and Fig. S5. Explorations were done by replacing r_B,n at normal density with values of r_B,n derived from the measurements at high density for ranks beyond 8 for simulations under the high-density condition, and by replacing the single value of e by the linear elongation rate estimated for each rank for ranks beyond 8.

RESULTS

Experimental support for model design choices

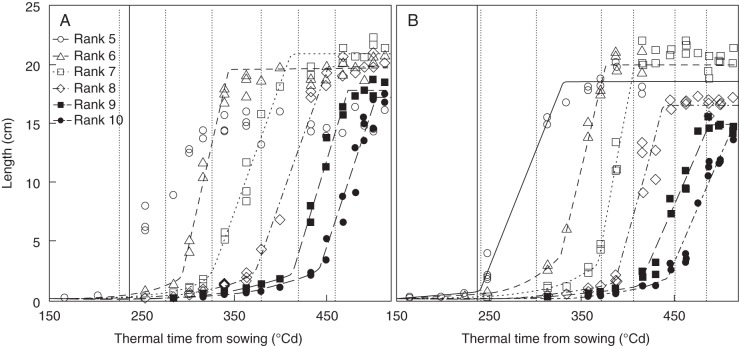
The time of sheath initiation was estimated separately for each rank by extrapolating the exponential growth of the sheath back to the time at which sheath length was 1 mm. The moment of sheath initiation was synchronized with the moment of tip emergence of the same phytomer for phytomers that emerged before tassel initiation (Supplementary Data Fig. S4). For phytomers that emerged after tassel initiation (ranks 9–15 at normal density and ranks 8–15 at high density), initiation of the sheath happened before tip emergence and around a constant blade age (a₁) of 150 °Cd of the same phytomer. The difference at the initiation of the sheath before and after tassel initiation has been reported by Andrieu et al. (2006), and is supported by an earlier finding that sheath initiation is controlled by different genes before and after tassel initiation (Harper and Freeling, 1996). The start of linear sheath growth was close to the moment of collar emergence of the preceding phytomer for ranks below 9 at normal density (Fig. 3A) and below 8 at high density (Fig. 3B), the phytomers whose tip emergence occurred before tassel initiation. For upper ranks, the start of the linear phase was earlier than the moment of collar emergence of the previous phytomer. An average blade age, a₂, was used to control the start of the linear phase of the sheaths that initiated after tassel imitation.

Fig. 3.

Dynamics of sheath length of ranks 5–10, as indicated in the key, at (A) normal density and (B) high density. The vertical solid line indicates the time of tassel initiation. Vertical dotted lines indicate collar emergence times of ranks 4–9. Symbols are measurements on maize ‘Déa’ in 2000 and lines are fitted curves. Filled symbols and rank 8 in panel B represent the sheaths that initiated after tassel initiation. No line is shown for rank 5 at normal density since fitting was not successful due to lack of data points between 200 and 250 °Cd.

Model verification and validation

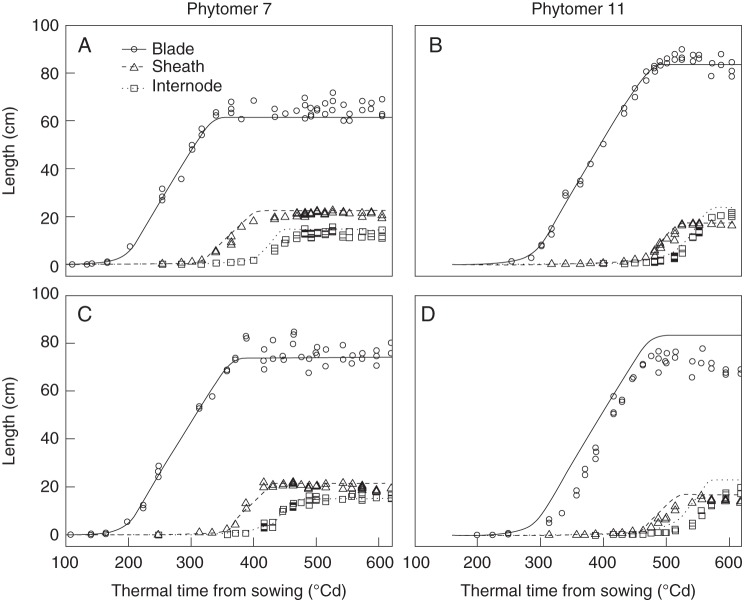
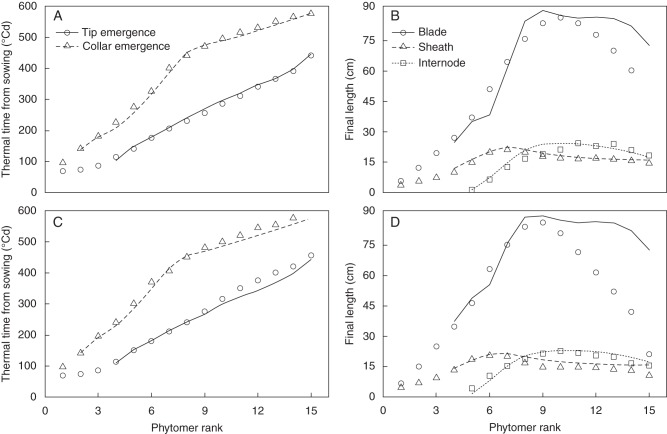
The model satisfactorily reproduced the changes in blade, sheath and internode lengths over time for maize at normal density (Fig. 4A, B), when using the parameter values listed in Table 2. The predicted major phase changes in the extension of blade, sheath and internode were all well consistent with the data, i.e. the decline in blade elongation rate, the start of the linear phase of sheath extension, and the transition from the exponential phase to the linear phase of the internode extension. The simulated moments of tip and collar emergence were close to the observed values (Fig. 5A). The model well reproduced the acceleration of collar emergence beyond rank 8 (Fig. 5A). This is due to the change in the way the start of linear sheath extension was coordinated: synchronization with collar emergence of the preceding leaf before tassel initiation, and based on leaf age after tassel initiation. The coordination rule used before tassel initiation predicted a linear relationship between time of collar emergence and phytomer rank, which resulted in a delay in the time of collar emergence of ranks 9–15. Furthermore, the model produced final blade lengths close to experimentally observed values for phytomers 4–11 (Fig. 5B). Only final blade length of ranks 12 and above was overestimated.

Fig. 4.

Model verification (A, B) and model validation (C, D) of the dynamics of blade length, sheath length and internode length (see key) of phytomers 7 and 11. Symbols are measurements on maize ‘Déa’ in 2000 and lines are simulations. RMSE values for blade, sheath and internode of phytomer 7 in (A) were 3·7, 1·8 and 2·5 cm respectively, and those for phytomer 11 in (B) were 2·8, 1·5 and 2·4 cm, respectively. RMSE values for blade, sheath and internode of phytomer 7 in (C) were 3·8, 1·8 and 1·3 cm, respectively, and those for phytomer 11 in (D) were 11·2, 2·5 and 4·8 cm, respectively.

Fig. 5.

Model verification (A, B) and model validation (C, D) of tip emergence and collar emergence (see key in A), and final lengths of blade, sheath and internode (see key in B) versus phytomer rank. Symbols are measurements from maize ‘Déa’ in 2000 and lines are simulations. RMSE values of model verification were 8·6 °Cd for tip emergence, 12·4 °Cd for collar emergence, 12·3 cm for final blade length, 1·2 cm for sheath length and 2·4 cm for internode length. RMSE values of model validation were 17·9 °Cd for tip emergence, 16·7 °Cd for collar emergence, 21·8 cm for final blade length, 2·6 cm for sheath length and 1·7 cm for internode length.

By using initial conditions associated with high population density and parameter values listed in Table 2, the model well reproduced the sigmoid extension patterns of the blade, sheath and internode (Fig. 4C, D). The increase in blade elongation duration and the delay in sheath linear extension compared with normal density for rank 7 were well captured by the model (Fig. 4C). Also, predicted tip and collar emergence of high-density maize up to rank 9 were consistent with the data (Fig. 5C). Beyond rank 9, the model estimated sheath extension correctly but overestimated the elongation rate and final length of the blades, and slightly underestimated tip and collar emergence (Fig. 5C, D). All blade lengths were predicted with high accuracy when the model was run with close to real relative elongation rate and linear elongation rate fitted for each individual blade, while elongation duration was controlled by the coordination model (Supplementary Data Table S1 and Fig. S5).

Model sensitivity

Tip emergence was delayed when r_B,n was decreased and vice versa (Fig. 6) for ranks beyond 4. The responses of tip emergence to changes in r_B,n differed between ranks 4–6 and ranks beyond 6. For leaf ranks above 6 a linear relationship between tip emergence and phytomer rank, with an unchanged phyllochron, was preserved at different values of r_B,n. Timing of tip emergence was more sensitive to a decrease in r_B,n than to an increase (Fig. 6).

Fig. 6.

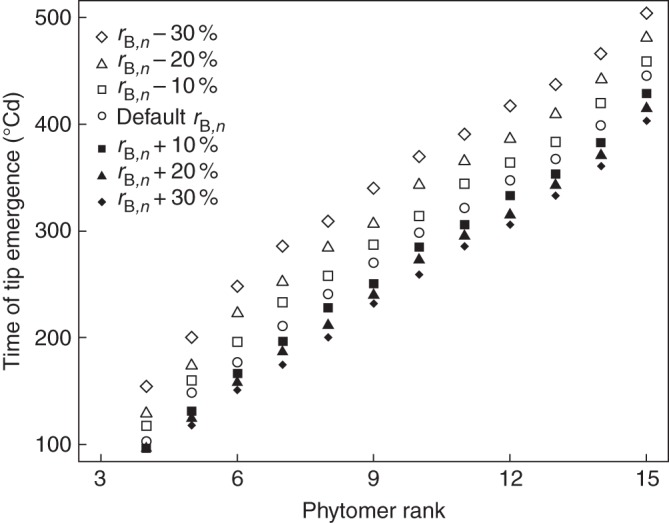
Analysis of the sensitivity of the time of leaf tip emergence to changes in r_B,n at normal density.

Effects of initial sheath length

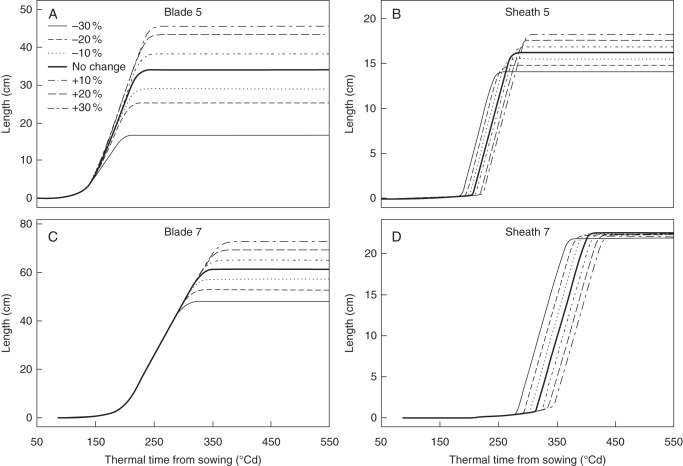
Final lengths of blades 5 and 7 were positively related to the change in final sheath lengths of the first three ranks, as reduction in the value of the initial sheath length by 30 % resulted in the shortest final blade lengths while setting the value 30 % higher resulted in the longest lengths (Fig. 7A, C). Blade elongation rates and durations at rank 5 were positively affected by changes in sheath length at ranks 1–3, while for rank 7 elongation durations were positively affected but elongation rates were not. The start of the phase of linear sheath extension was delayed with increasing initial sheath length (Fig. 7B, D). The final length of sheath 5 was increased considerably whereas final length of sheath 7 was only slightly increased.

Fig. 7.

Simulated effects of changes in final sheath length of ranks 1–3 on the dynamics of blade and sheath extension of phytomers 5 and 7. The final sheath lengths of ranks 1–3 were changed jointly by –30 % (solid lines), –20 % (dashed lines), –10 % (dotted lines), no change (bold solid lines), +10 % (dot-dashed lines), +20 % (long-dashed lines) and +30 % (two dashed lines).

DISCUSSION

The purpose of this study was to show that: (1) key aspects of whole plant development, such as rate of leaf emergence, dynamics of organ extension and distribution of organ size along the stem, can all emerge from a set of simple coordination rules without the need to include effects of carbon assimilation and biomass allocation; and (2) a flexible time of organ development can emerge from a model based on coordination rules. The model gave a good account of the timing and duration of blade and sheath extension at both plant population densities, which were different in both aspects. This supports the plausibility of phase transitions in organ extension being coordinated with leaf emergence events (Fig. 4). Using the coordination model, we showed that events early in the life of the plant, such as increase in sheath length as a result of interplant competition at high density (Fig. 7), may set in motion a cascade of linked developmental events at the organ level that shape the development of the structure of the whole plant over its entire growth duration.

A novel coordination rule implemented in our model is that the start of the linear phase of sheath extension is related to collar emergence of the preceding leaf in those sheaths that were initiated before tassel initiation. This rule was derived from the observation that the linear phase of sheath growth took place later at high density than at normal density for low ranks (Fig. 3), and was supported by the accurate prediction of the dynamics of blade and sheath extension and the final blade length of the considered phytomers in both the normal- and the high-density treatment. Another novel element in this model was to take into account the reproductive phase which results in changes in the profile of blade length along the stem without considering the competition for assimilates among leaves, stem and ears.

Early competition shapes structural plasticity at high density

In another study, we found that the initial modification of the light environment experienced by maize seedlings in a wheat–maize intercrop in which maize was sown after wheat caused longer sheath lengths at ranks below 6 (Zhu et al., 2014). Consistent with Andrieu et al. (2006), these longer sheaths resulted in a longer blade length for phytomers below 10 by increasing leaf elongation duration. The scenario simulation of changes in final sheath length of ranks 1–3 and model validation for high density confirms the role of the sheath length of low phytomers in determining the dynamics of organ extensions and final organ sizes of subsequent ranks through the three coordination rules. The rule that defines the start of the decrease in sheath elongation rate and the rapid increase in internode elongation rate is most responsible for propagating differences created on low phytomers from leaf to leaf. This rule results in a monotonous increase in final sheath length at low ranks and a decrease at high ranks. The increase in sheath length over ranks can be seen as the length increase after collar emergence. The decrease occurs because (1) the slow extension of the internode before collar emergence pushes up the leaf and consequently reduces the length of the sheath of the same phytomer at collar emergence (Figs 1 and 2A), and (2) the rapid extension of the internode after collar emergence accelerates the decline in the elongation rate of the sheath and shortens the increase in sheath length after collar emergence (Fig. 2B). This supports the idea that early competition and differences created on low ranks influence whole plant structure, which would highlight the importance of early growth conditions and the crucial role of the sheath in whole-plant development.

A constant leaf emergence rate emerges from the interplay between leaf initiation, leaf elongation and sheath tube construction

The timing of leaf emergence depends on the processes of leaf initiation and leaf elongation, and on the depth of the sheath tube (Skinner and Nelson, 1995). Despite the complexity of these dynamic processes, field experiments have often shown a linear relationship between leaf appearance and thermal time (McMaster, 2005). Consistent with this, the current modelling exercise showed that, for a large range of relative blade elongation rates, the time interval between emergence of successive leaves remains stable (Fig. 6). The value of the phyllochron would be equal to that of the plastochron if all blades emerged from a sheath tube of constant length. However, the depth of the sheath tube is not constant, but increases during plant development until maturity of sheath 7, when most leaves have emerged (Supplementary Data Fig. S6). This explains why a phyllochron that is both constant and larger than the plastochron is generally observed in experiments, and also why we see it in our modelling exercise. Nevertheless, the plastochron value may vary under different light conditions because of the influence of assimilates (Sugiyama and Gotoh, 2010) or signals from leaf to the apex (Chuck and Hake, 2005; Pautler et al., 2013). Our current model provides the foundation necessary to simulate the feedback of leaf emergence on leaf initiation based on ecophysiological mechanisms in the future.

Strengths and weaknesses of the model

Our model was able to satisfactorily capture the close coordination between the dynamics of blade, sheath and internode extension and leaf emergence events within the structural development of the maize plant. The model successfully predicted the rank numbers for the peak in sheath length distribution, and in blade length distribution, which is usually around two-thirds of the final leaf number in field conditions (Dwyer and Stewart, 1986; Birch et al., 1998). The exercise of optimizing prediction of final blade length of high ranks indicates that assimilates are probably a limiting factor for blade size at high ranks. However, the model was not designed to consider the influence of environmental conditions and the availability of assimilates on organ extension. The aim of the modelling exercise was to provide a conceptual framework of how whole-plant structural development emerges from the coordinated growth of organs.

By using coordination rules, we reduced the number of parameters needed for the timing of phase transitions in organ extension. Nevertheless, the model still needs a considerable number of parameters to specify the relative blade elongation rate for each organ. The necessity for these parameters could be eliminated by adding the effect of assimilates on organ growth: organ extension would then become dependent on assimilate supply.

The model requires the input of the dynamics of first three sheaths as initial conditions. When this was reduced to only the first sheath, the model overestimated the final sheath length of the subsequent ranks and thus ran with less accuracy (Supplementary Data Fig. S7). This was because the linear elongation rate of the first three sheaths is lower than that of the subsequent ranks due to a short elongation zone of the leaf in question.

Conclusions

The current model presents a framework for the structural development of a maize plant and shows the plausibility of coordination rules underlying the structural development. Based on three coordinating rules, whole-plant structural development in terms of leaf tip and collar emergence, dynamics of organ extension and the distribution of organ size along the stem emerged as model output, without considering any process related to biomass formation. The model gave a good account of the timing and duration of the extension of blade and sheath, but not the changes in elongation rate at high ranks. To further improve model predictions, a next step could be to include the effect of assimilates on organ and whole-plant growth, and to take into account the possible effects of resource capture and assimilate supply on relative growth rates of the leaves. Nevertheless, we show that many aspects of maize plant development can be captured using relatively simple rules, which illustrates the relative resource independency of several developmental events. In addition, models based on such rules can be used to study plant plasticity, such as shade avoidance, as responses of this kind are typically triggered by cues that precede any drop in light capture (Pierik and de Wit, 2013) and therefore do not depend on changes in carbon assimilation.

SUPPLEMENTARY DATA

Supplementary data are available online at www.aob.oxfordjournals.org and consist of the following. Methods S1: estimation of the ratio between the final length of internode n and sheath n – 1. Methods S2: justification of coordination rules used in the model. Methods S3: calculation of the decline coefficient (d) of the elongation rate of sheath. Table S1: simulation scenarios for exploring the cause of reduction in final length of the blade at high ranks. Fig. S1: model visualization of the blade, sheath and internode on separated phytomers 1–15. Fig. S2: ratio between the final length of internode n and sheath n – 1 versus phytomer rank. Fig. S3: dynamics of length growth of sheaths 1–3 at normal and high density. Fig. S4: relationship between blade age at sheath initiation and blade age at tip emergence. Fig. S5: final blade lengths of ranks 4–15 under different simulation scenarios. Fig. S6: dynamics of the depth of the sheath tube over time. Fig. S7 : simulation results of the time of tip and collar emergence and organ sizes when only input the length dynamics of the first sheath.