Abstract
Background and Aims
Predicting light partitioning in crop mixtures is a critical step in improving the productivity of such complex systems, and light interception has been shown to be closely linked to plant architecture. The aim of the present work was to analyse the relationships between plant architecture and light partitioning within wheat–pea (Triticum aestivum–Pisum sativum) mixtures. An existing model for wheat was utilized and a new model for pea morphogenesis was developed. Both models were then used to assess the effects of architectural variations in light partitioning.
Methods
First, a deterministic model (L-Pea) was developed in order to obtain dynamic reconstructions of pea architecture. The L-Pea model is based on L-systems formalism and consists of modules for ‘vegetative development’ and ‘organ extension’. A tripartite simulator was then built up from pea and wheat models interfaced with a radiative transfer model. Architectural parameters from both plant models, selected on the basis of their contribution to leaf area index (LAI), height and leaf geometry, were then modified in order to generate contrasting architectures of wheat and pea.
Key results
By scaling down the analysis to the organ level, it could be shown that the number of branches/tillers and length of internodes significantly determined the partitioning of light within mixtures. Temporal relationships between light partitioning and the LAI and height of the different species showed that light capture was mainly related to the architectural traits involved in plant LAI during the early stages of development, and in plant height during the onset of interspecific competition.
Conclusions
In silico experiments enabled the study of the intrinsic effects of architectural parameters on the partitioning of light in crop mixtures of wheat and pea. The findings show that plant architecture is an important criterion for the identification/breeding of plant ideotypes, particularly with respect to light partitioning.
Keywords: Architectural parameters, functional–structural plant model, intercropping, LAI, light interception, L-systems, Pisum sativum, pea, plant architecture, plant height, Triticum aestivum, wheat
INTRODUCTION
In the current context of improving the sustainability of agriculture, there is renewed interest in the growing of crop mixtures, referred to as intercropping (Willey, 1979; Anil et al., 1998). Crop mixtures can indeed produce high and stabilized yields; they can also enable a reduction in the use of fertilizers and pesticides and enhance biodiversity conservation (Ofori and Stern, 1987; Jensen, 1996; Corre-Hellou et al., 2006; Malézieux et al., 2009). These benefits result from the trade-off between the complementarity and competition between mixed species with respect to resource capture and use. In particular, the ability of component species in the canopy to capture light strongly determines both their potential productivity and their proportion in the mixture at harvest. Understanding the modalities of light partitioning is therefore a crucial area of study.
The partitioning of light among mixed species is closely linked to their temporal and spatial development. On the one hand, the period of time during which one of the crops has not yet developed has important effects on the partitioning of light and hence on the growth of the mixture. These situations are notably encountered in relay cropping (Malézieux et al., 2009), in which mixed crops do not grow simultaneously but tend to exhibit a partial overlap (e.g. maize–bean, groundnut–cotton). On the other hand, the interception of light by plant stands is also closely related to the physical structure of the canopy (Ross, 1981a; Sinoquet and Caldwell, 1995), which itself is determined by the architecture (Godin, 2000) of the individuals growing within the stand (Moulia et al., 1998). Such a multi-scale description of canopy structure highlights the fact that architectural parameters defined at the organ scale can significantly affect light partitioning. Unlike homogeneous monospecific stands, where plants have roughly the same architecture, intercropping systems involve at least two species which may display differing architectural patterns (e.g. agroforestry systems, cereal–legume mixtures). Characterizing the architecture of intercropped plants and its variability (genotypic and environmental) is therefore a critical issue that could guide the choice of species/cultivars to be mixed in intercropping systems and hence their degree of complementarity (Sinoquet and Caldwell, 1995; Sonohat et al., 2002).
Exploiting the variability of plant architecture is of great interest in the context of intercropping systems; however, few methods are available to assess and quantify the impact of different architectural patterns on the partitioning of light between mixed species. To the best of our knowledge, and because of experimental and cost constraints, light partitioning within interspecific mixtures cannot be assessed directly by radiation sensors (Sonohat et al., 2002). The only feasible alternative at present is a modelling approach that involves various concepts and formalisms for representation of the canopy and the calculation of light interception. Most studies are based on the turbid medium approach, in which the canopy is represented using a statistical model and light interception is given by the Beer–Lambert law (Sinoquet et al., 1990; Monsi and Saeki, 2005). The turbid medium paradigm has thus been applied to several intercropping systems, such as pea–barley (Corre-Hellou et al., 2009), maize–bean (Tsubo and Walker, 2002; Tsubo et al., 2005), perennial mixtures (Faurie et al., 1996; Lantinga et al., 1999) and agroforestry systems (Noordwijk and Lusiana, 1999). These approaches were based on a simplified description of the canopy given by integrative parameters such as leaf area index (LAI), plant height and mean leaf inclination. However, due to their underlying hypotheses, crop models coupled to the turbid medium approach cannot explicitly account for plant architecture sensu stricto. Therefore, such models are not suitable for the assessment of relationships between light partitioning and architectural parameters (organ scale) of the component species. Moreover, the turbid medium analogy applied to intercropping systems has also been shown to produce inaccurate estimates of light partitioning in some complex canopy structures (Sonohat et al., 2002; Combes et al., 2008; Barillot et al., 2011). Furthermore, alternative modelling concepts, such as functional–structural plant models (FSPMs), are able to take account of interactions between plant architecture, their physiological functioning and environmental conditions (for reviews see Fourcaud et al., 2008; Vos et al., 2010; DeJong et al., 2011). FSPMs therefore represent a suitable framework for understanding the modalities of light partitioning within intercropping systems. Such approaches have been used to quantify light partitioning within contrasting canopies: agroforestry (Lamanda et al., 2008), a legume-weed system (Cici et al., 2008) and grass–legume mixtures involving perennial and annual species (Sonohat et al., 2002; Barillot et al., 2011).
The aim of the present study was therefore to investigate the influence of architectural variations on the partitioning of light among mixed species using an FSPM approach. To achieve this, we decided to use grass–legume mixtures, a commonly used intercropping system in temperate regions (e.g. wheat–pea, triticale–broad bean, tall fescue–alfalfa) and tropical zones (e.g. maize–bean). Our approach consisted in using a wholly in silico framework based on dynamic architectural models of both species in a grass–legume mixture. For the grass species, we used an existing wheat model (ADEL-wheat; Fournier et al., 2003), while for the legume species we chose pea, for which we developed a new model. The two models were combined to analyse the effects of architectural changes on the level of light partitioning in virtual wheat–pea mixtures. These architectural models do not account for any plastic responses of plants to their environment. This approach thus enabled us to assess the intrinsic effect of specific architectural traits on the partitioning of light.
MATERIALS AND METHODS
Description and parameterization of the L-Pea model
The virtual plant model for pea (Pisum sativum; L-Pea) was developed using the L-Py platform (Boudon et al., 2012), which combines the formalism of L-systems (Lindenmayer, 1968; Prusinkiewicz and Lindenmayer, 1990) with Python, an open source, dynamic programming language. The structural organization of stems was described as a modular system (Godin et al., 1999), i.e. as a collection of repeated basic units called ‘phytomers’ (Gray, 1849; White, 1979). Using this formalism, the main vegetative organs of pea were represented by a bracketed string made up of the following modules: apex (apical meristem), A; internodes, I; stipules, S; and axillary buds, B. Thus, the apex production rule used in the L-Pea model is:
meaning that the initiation of a phytomer by the apex (A) is associated with the production (→) of an internode (I), two stipules (S), n axillary buds (B) and an ongoing apex. Square brackets are topological rules that indicate branches. Each module (virtual organ) bears its own state, i.e. identification (cultivar, plant, stem and phytomer to which they belong), age, length and amount of intercepted light.
In the model proposed here, the morphogenesis of pea is dependent on the number of growing degree-days (GDD) cumulated since sowing (base temperature = 0 °C). Thermal time drives the two main modules represented in the L-Pea model: (1) vegetative development and (2) the extension of vegetative organs. Parameterization of the vegetative development module (Table 1) was derived from an experiment conducted under field conditions on pea (‘Lucy’) intercropped with wheat. Details of growing conditions and measurements were as described by Barillot et al. (2014). Moreover, these data were completed by a supplementary experiment designed to characterize the extension kinetics of stipules and internodes. Measurements were performed on isolated pea plants grown in growth cabinets (for details see Supplementary Data).
Table 1.
Parameters of the L-Pea model. Main stems are denoted as Axis 0 and branches are distinguished according to their nodal position on the main stem. Axis 1, branches developing at the first node; Axis 2, second node
| Module | Function | Parameter | Unit | Value | Source |
|---|---|---|---|---|---|
| Vegetative development | Phytomer appearance rate | RL | Phytomer °C d–1 | Axis 0: 0·0165 | Barillot et al. (2014) |
| Axis 1: 0·0183 | |||||
| Axis 2: 0·0171 | |||||
| phyto_ final | Phytomer | Axis 0: 11 | Barillot et al. (2014) | ||
| Axis 1: 25 | |||||
| Axis 2: 20 | |||||
| Branching | nbbranch | Branch | Axis 1: 1·7 | Barillot et al. (2014) | |
| Axis 2: 1·6 | |||||
| bud_break | C °d | Axis 1: 335 | Barillot et al. (2014) | ||
| Axis 2: 289 | |||||
| Organ extension | Organ length | Lfinal | mm | - | Fitted to dataa |
| tbase | °C d | Internode: 34·88 | Fitted to dataa | ||
| Stipule: 0 | |||||
| tmax | °C d | Internode: 87·71 | Fitted to dataa | ||
| Stipule: 71·28 | |||||
| tend | °C d | Internode: 171·51 | Fitted to dataa | ||
| Stipule: 197·66 | |||||
| Allometric coefficient | k | Dimensionless | 0·57 | Fitted to dataa | |
| Senescence | lifespan | °C d | 480 | Adapted from Lecoeur (2005) |
aSee experiment described in Supplementary Information.
Vegetative development module
Rate of phytomer appearance
The L-Pea model does not account sensu stricto for the initiation of vegetative primordia by the apical meristem (plastochron). In fact, the leaf appearance rate (RL) as measured by Barillot et al (2014) was used directly in the model to initiate the production of a new phytomer which immediately starts its visible growth, i.e. no hidden growth period was considered. Therefore, the production and appearance of phytomers (concomitant events in the model) were implemented as a linear function of the leaf appearance rate:
| (1) |
where Nphyto(p,s) (t) is the number of visible phytomers at a given thermal time t (GDD since sowing) for plant p and stem s; parameter RL(p,s) is the rate of leaf appearance, used as the rate of phytomer appearance (phytomer C ° d–1); and phyto_ final(p,s) is the final number of phytomers. Parameters RL(p,s) and phyto_ final(p,s) are input parameters of the model, which can be specified for each plant (p) and stem (s), i.e. main stems and each lateral branch. Note that the phyto_ final(p,s) of main stems measured by Barillot et al.((2014) was low so that the model could account for death of the apical meristem of main stems, which frequently occurs in winter pea cultivars that experience cold temperatures (Jeudy and Munier-Jolain, 2005; Barillot et al., 2014).
Branching
Based on our previous experiment on intercropped peas (Barillot et al., 2014), we only considered first-order branches. Branching is therefore handled by the model through two main input parameters (Table 1), which are: (1) the number of axillary buds (nbbranch,n) located at each node (n) of the main stem and (2) the time of bud break (bud_breakrk). Branches were denoted according to their topological position, i.e. main stems were denoted as Axis 0, and then branches emerging from node n of the main stem were referenced as Axis n. Properly speaking, the axillary buds should rather be called ‘active buds’ as they represent those that actually lead to the development of a branch and not all buds. Based on the measurements made by Barillot et al. (2014), the L-Pea model was set as follows:
Organ extension module
Organ growth kinetics
The extension of internodes and stipules is assumed to follow a β function (Yin et al., 2003):
| (2) |
where Lfinal (mm) is the final organ length, t (°C d) is the current age of the organ, tbase is the beginning of organ extension (°C d), tmax (°C d) is the time point at which the maximum rate of organ extension is reached, and tend (°C d) is the duration of organ extension. The values for the parameters tbase, tmax and tend shown in Table 1 were normalized by the time at which the first organ started its extension in a phytomer. Our results showed that the development of phytomers was initiated by the emergence of stipules (tbase = 0 °C d), which started to grow slightly earlier than internodes (see Supplementary Data). The final length reached by organs (Lfinal) is defined as a function of the normalized phytomer rank (see Supplementary Data).
The width of stipules (Wstipule) at time t was derived from an allometric rule:
| (3) |
where k is the allometric coefficient and Lt,stipule is stipule length.
Senescence
In the L-pea model, shoot senescence only concerns stipules that are removed once their lifetime has elapsed (Table 1). The values for leaf lifespan were derived from Lecoeur (2005).
Geometric interpretation of the model
Internodes were associated with generalized cylinders. Stipules were reconstructed from a library of ∼200 geometric objects obtained from the photographs used to extract stipule shape.
ADEL-wheat model
Virtual wheat plants were obtained from a dynamic and 3-D architectural model of wheat (Triticum aestivum) development (Fournier et al., 2003). This model is available on the Openalea platform (Pradal et al., 2008). The dataset was derived from an experiment carried out by Bertheloot et al. (2009) in which wheat (‘Caphorn’) was grown under field conditions with low nitrogen fertilization at a density of 250 plants m–2. The model simulates the elongation kinetics of individual organs and their geometric shape. The development and death of tillers was also accounted for in the model and was kept constant in our simulations.
The input parameters of both the ADEL-wheat and the L-Pea model used to build up the virtual mixtures were thus based on experiments with low nitrogen levels similar to those applied by farmers in Western Europe.
Virtual wheat–pea mixtures: interfacing the L-Pea and ADEL-Wheat models
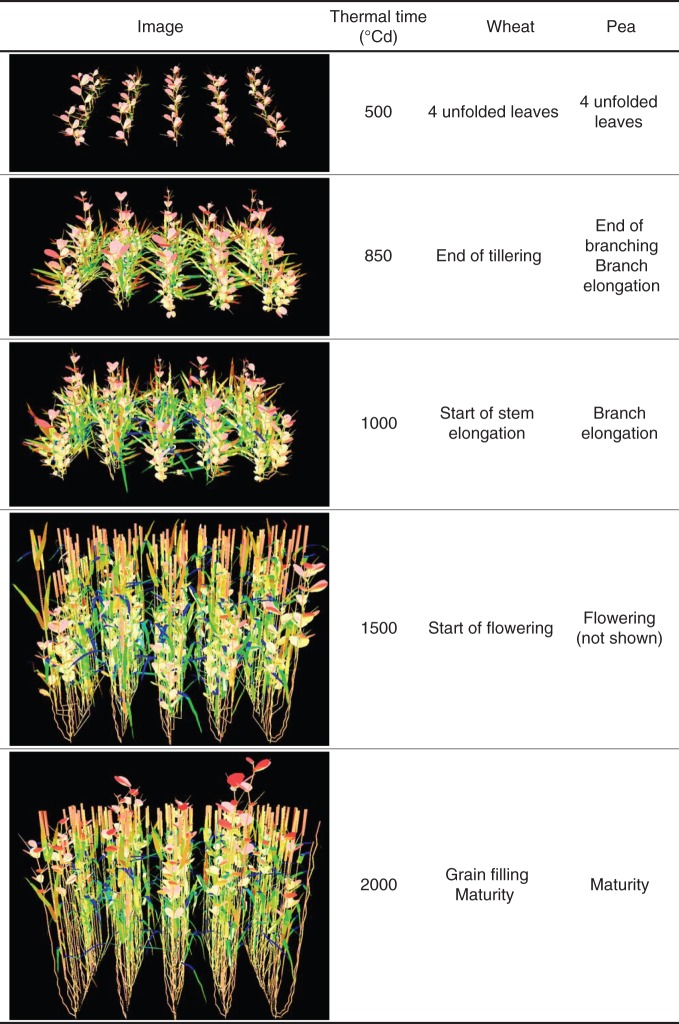
The L-Pea model was implemented on the Openalea platform so that it could be interfaced with ADEL-Wheat. Wheat and pea mock-ups were merged in scene graphs using the PlantGL graphic library (Pradal et al., 2009). Simulations were processed from 0 to 2000 GDD with a time step of 50 GDD (Fig. 1). The inter-row spacing of mixtures was 0·17 m, with a final density of 125 plants m–2 for wheat and 45 plants m–2 for pea, i.e. 50 % of the optimum density of each crop as generally encountered in Western European farming practices (Corre-Hellou et al., 2006). The component species were mixed within each row in virtual mixtures of 0·5 × 0·5 m (two rows including 18 wheat plants and 6 pea plants).
Fig. 1.
Specific stages of the development of wheat and pea illustrated by side views of the virtual mixtures. The colour gradient is a function of the light intercepted by different organs (from blue to red).
Light partitioning within virtual wheat–pea mixtures
The virtual wheat–pea mixtures were coupled with a radiative transfer model that estimates the dynamics of photosynthetically active radiation (PAR) partitioning at each step of the growing cycle. Calculations of light interception were provided by the nested radiosity model Caribu, developed by Chelle and Andrieu (1998). The computations only considered diffuse radiations according to the uniform overcast sky radiation distribution (Moon and Spencer, 1942). Diffuse radiations were approximated using a set of 20 light sources. Light interception by each organ was computed for each direction and then integrated over the sky vault by summing the weighted values obtained from all 20 directions. In order to prevent any border effects, the basic mixture plot of 0·25 m–2 was duplicated using an option of the Caribu model.
Building contrasting wheat and pea architectures
The architectural parameters of both models were set initially to ensure the smallest possible difference in LAI and height dynamics between wheat and pea. This first simulation is hereinafter called the ‘reference simulation’ (Table 2 and Fig. 2).
Table 2.
Input parameters of the ADEL-Wheat and L-Pea models as used for the reference simulation
Fig. 2.
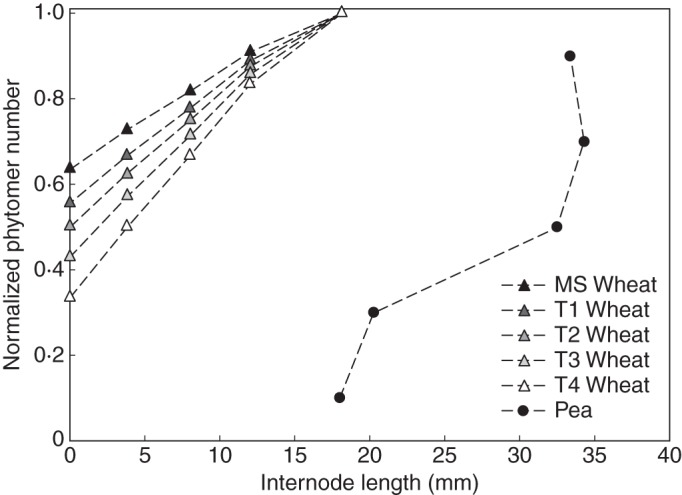
Vertical profile of the final length of the wheat and pea internodes used in the reference simulation. The internode length of wheat is specified for the main stem (MS) and four tillers (T1–T4).
Architectural alterations were then applied to both plant models in order to quantify their impact on light partitioning throughout the growing cycle of the mixture. These architectural parameters were selected as a function of their contribution to LAI, plant height and leaf geometry. (1) Variations in LAI were obtained by increasing and decreasing the number of tillers and branches produced by wheat and pea, respectively. (2) Variations in plant height were obtained by altering the final length of internodes. (3) During previous studies (Barillot et al., 2011, 2012), it was found that leaf inclination had minor effects on light partitioning within virtual wheat–pea mixtures when compared with the LAI and height of the species. In order to validate this assumption, light partitioning was also estimated within mixtures in which the leaf inclination of pea was altered. Based on the initial values set for the reference simulation, 25 and 50 % variations in both directions were applied to each architectural parameter.
All simulations were performed by modifying one parameter at a time, giving a total of 21 simulations. The effects of each architectural parameter (Simul) on plant LAI and height and on light partitioning were compared with the reference simulation (Ref) by calculating the relative variation:
| (4) |
Based on these simulations, we were able to analyse the relationships between light partitioning and variations in the species ratios of LAI and height. To this end, five particular stages during development were selected (Fig. 1). The first dates represented the vegetative stages of the two species and onset of their lateral development (branching and tillering). Vertical elongation phases were then selected, as well as the flowering periods of wheat and pea. The relationships between light partitioning and species LAI and height were finally studied during the last stages of development, nearing physiological maturity (2000 GDD).
RESULTS
Reference simulation
The dynamics of LAI, height and light interception efficiency (LIE; the fraction of incident light intercepted by a species or the whole mixture) for the reference simulation are shown in Fig. 3. Between 200 and 2000 GDD after sowing (Fig. 3A), the LAI kinetics of the whole mixture and of each component species followed kinetics typical of those observed in pea–barley mixtures (e.g. Corre-Hellou et al., 2009). The mixture reached a maximum LAI of 6·30 at the time of wheat and pea flowering (1400 GDD). After 1700 GDD, the senescence of wheat and pea leaves led to a fall in the mixture LAI to 4·45. Differences between the LAI of wheat and pea did not exceed 0·66.
Fig. 3.
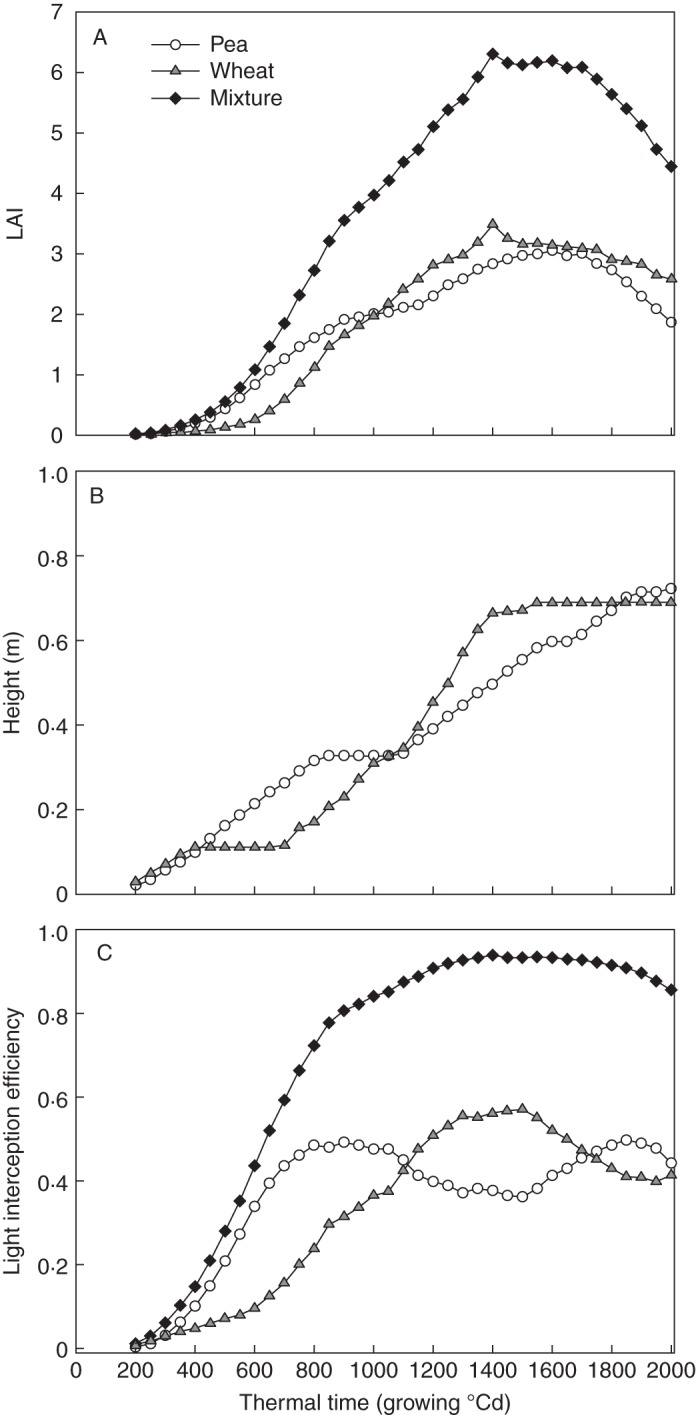
Dynamics of LAI (A), plant height (B) and light interception efficiency (C) in the reference simulation as a function of thermal time. These dynamics are shown for both the overall mixture and the component species (pea and wheat).
Pea was taller than wheat from the early stages of development to 1000 GDD, a period that corresponds to the elongation of wheat internodes (Fig. 3B). The stable height of pea observed between 800 and 1000 GDD could be explained by (1) the death of the main stem, causing a cessation of vertical growth, and (2) the delayed growth of branches, which overtopped the main stems from 1100 GDD and led to a final height of 0·70 m. The height of wheat also remained at 0·11 m between 400 and 700 GDD, i.e. before internode elongation, which resulted in a maximum height of 0·70 m.
The LIE of the mixture increased rapidly until the final height of species had nearly been reached (1500 GDD) and then stabilized at 0·9, meaning that 90 % of incident light was intercepted by the canopy (Fig. 3C). As a consequence of these greater LAI and height values, pea captured on average 62 % of the light intercepted by the overall mixture up to 1100 GDD. The contribution of wheat to light interception by the mixture subsequently averaged 57 % until 1700 GDD.
Variations in species LAI and height in response to architectural alterations
LAI variations
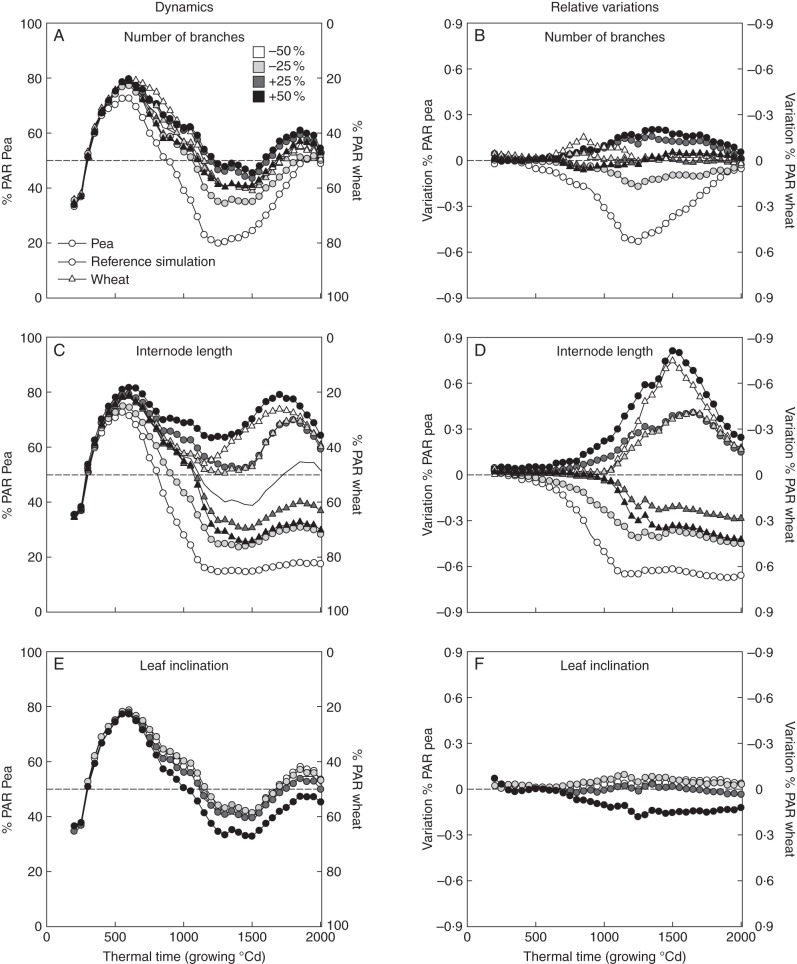
Alterations in the number of branches produced by pea dramatically affected its LAI from the early stages of development (400–500 GDD; Fig. 4). Based on the reference simulation, similar absolute variations in LAI were observed after an equivalent increase or decrease in the number of branches, thus defining symmetrical variations. As expected, the greatest differences in LAI were observed when the number of branches increased or decreased by 50 % (+0·50 and –0·52, respectively).
Fig. 4.
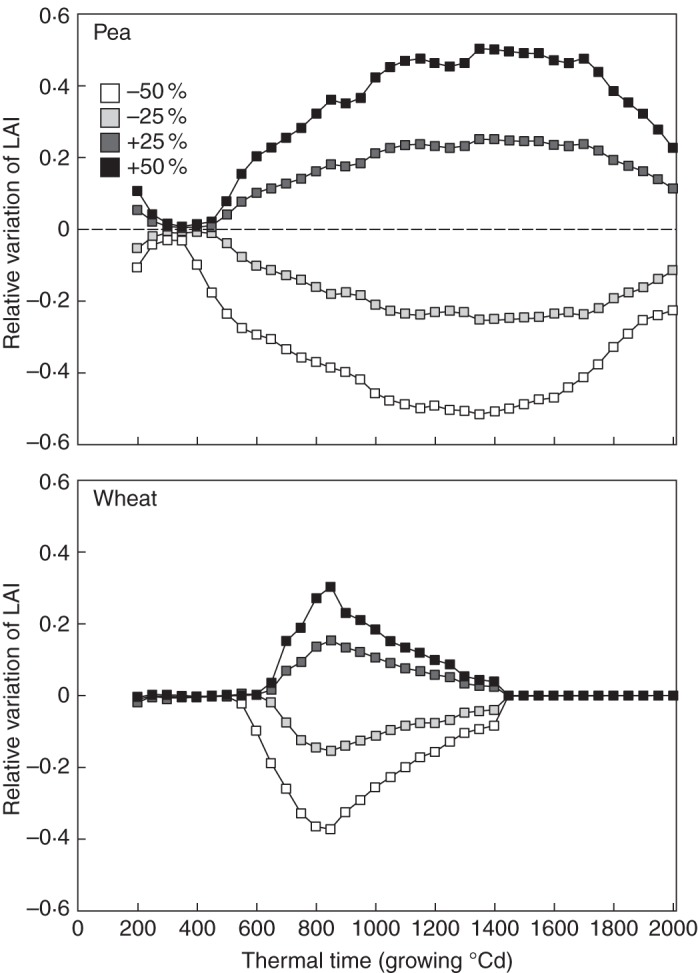
Relative variations in the LAI of pea (upper panel) and wheat (lower panel) estimated from the reference simulation. Variations were obtained by modifying the number of branches or tillers. The shading gradient indicates the amplitude of the modifications applied to the architectural parameters.
Alterations in the number of tillers produced by wheat also led to strong relative variations in LAI, although the amplitude was less marked than in pea (Fig. 4). These effects were observable from 600 to 650 GDD, i.e. during tiller production. Maximum relative variations of + 0·30 and –0·37 in wheat LAI were observed at the end of tillering (850 GDD) and resulted from a 50 % increase and decrease in the number of tillers, respectively. Relative variations in LAI then rapidly diminished from 900 GDD under each scenario. After flowering (∼1500 GDD), these plants reached the same LAI values as those of the reference simulation. This was due to a parameter relative to tiller death that led to the same final number of tillers as the reference simulation, because (1) the tillers removed under the –25 and –50 % scenarios were also intended to regress in the reference simulation, and (2) the tillers added (+25 and + 50 % scenarios) were set to regress at the same time as those in the reference simulation.
Height variations
Symmetrical absolute variations in the height of pea and wheat were observed after an equivalent increase or decrease in internode length (Fig. 5). Relative variations in pea height were constant from 800 GDD to the end of the growing cycle (maximum variations of 0·47 and –0·47 under the + 50 % and –50 % scenarios, respectively).
Fig. 5.
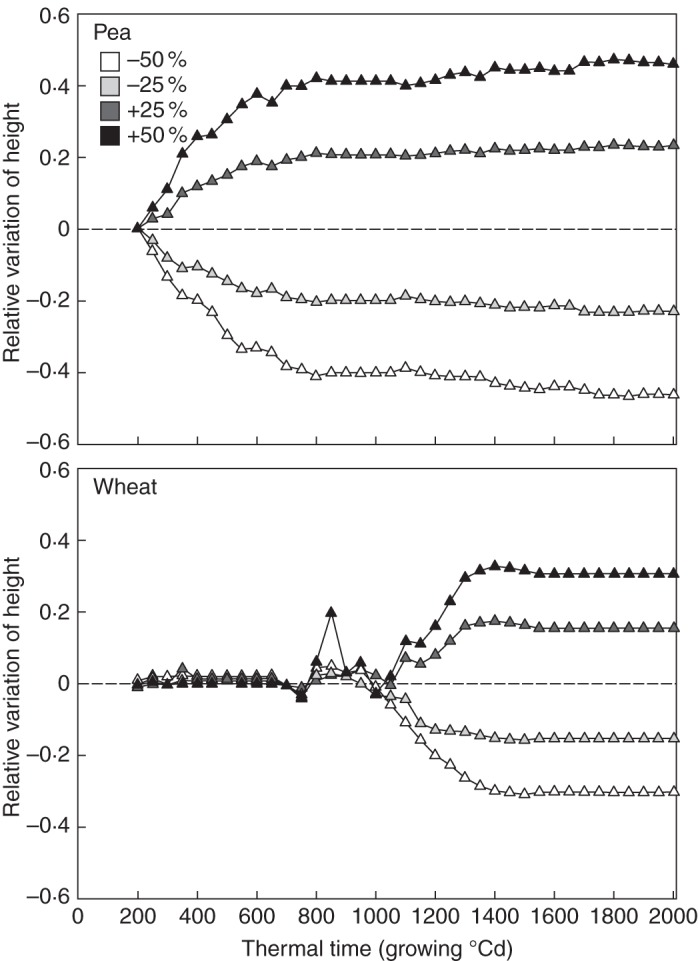
Relative variations in the height of pea (upper panel) and wheat (lower panel) estimated from the reference simulation. Variations were obtained by modifying the final length of internodes. The shading gradient indicates the amplitude of the modifications applied to the architectural parameters.
The effect of internode length on plant height was observed later in wheat than in pea, as the elongation of wheat internodes started from 1000 GDD. Maximum relative variations were observed at 1400 GDD (0·33) and 1500 GDD (–0·31) consecutive to a 50 % increase and decrease in internode length, respectively.
Effects of architectural modifications on light partitioning
Figure 6 shows (1) the effects of branching/tillering, internode length and leaf inclination (pea) on the ratio of light intercepted by a species to the interception of the whole mixture (%PAR) (values are thus complementary between pea and wheat), and (2) variations in %PAR expressed as a function of the reference simulation. Interestingly, the modifications made to architectural parameters led to asymmetrical responses of light partitioning even though they affected LAI and plant height symmetrically (same absolute variations observed after an increase or decrease in a given parameter). Indeed, increasing or reducing the value of an architectural parameter (branching, height or leaf inclination) did not result in similar absolute variations in light partitioning but rather defined asymmetrical responses.
Fig. 6.
Dynamics (left) and relative variations (right, estimated from the reference simulation, in straight lines) of light partitioning (%PAR). %PAR is the ratio of light intercepted by a species (left and right axes for pea and wheat, respectively) to the interception of the whole mixture. Therefore, %PAR values are complementary between pea and wheat and those of relative variations are the opposite. The number of branches, internode length and leaf inclination (for pea only) were altered for both pea (circles) and wheat (triangles) as indicated by the shading gradient.
Branching
Alterations in the number of branches/tillers led to greater variations in light partitioning in pea than in wheat. This was particularly the case when the number of branches was reduced, as this dramatically decreased the proportion of light intercepted by pea from the early stages of development (500 GDD). Reducing the number of pea branches by 25 or 50 % caused maximum losses of light interception, of 17 and 53 %, respectively, just before the flowering stages (1250 GDD, Fig. 6B). By contrast, increasing the number of branches resulted in smaller variations in light partitioning than those caused by their reduction (a 20 % maximum gain of light capture under both the + 25 and + 50 % scenarios). Compared with the branch modifications applied to pea, the number of wheat tillers led to slight relative variations in light partitioning (15 % at most). The variations in wheat LAI that can be seen in Fig. 4 (30–35 %) therefore had little effect on light.
Internode length
Modifications to internode length (Fig. 6C, D) appeared to have the most dramatic effects on light partitioning when compared with branching (at most 81 % gain and 65 % loss in light capture). In both pea and wheat, longer internodes resulted in a marked increase in light interception when compared with the reference simulation. For both species, strong asymmetry was found regarding variations in light partitioning between plants subjected to an increase in their internode length and in those whose internodes were reduced, especially from 1500 GDD. From this stage of development, the effects of internode length that had caused a gain in light interception by pea (i.e. longer internodes for pea and shorter for wheat) started to decline until maturity. By contrast, alterations that increased wheat height (i.e. shorter internodes for pea and longer for wheat) maintained wheat dominance in terms of light interception until maturity. Figure 6D also shows that similar variations in light partitioning could result from an increase in the internode length of pea, or an equivalent reduction in wheat internodes. By contrast, increasing the internode length of wheat did not cause a gain in light interception similar to that caused by an equivalent reduction in pea internodes. Indeed, wheat was the most dominant species in terms of light capture when the internodes of pea were shortened by 25 or 50 % (up to 76 and 85 %, respectively, of light captured by wheat). Increasing the internode length of wheat by 50 % resulted in a gain in light interception similar to that seen when the internode length of pea was reduced by 25 %.
Leaf inclination of pea
Alterations in the inclination of pea leaves clearly had minor effects on light partitioning when compared with the changes applied to branching and internode length (Fig. 6E and F). Nevertheless, increasing leaf inclination by 50 % (i.e. the leaves became more erect) reduced light capture of pea by 18 % at most.
Light partitioning as a function of the ratios of species LAI and height
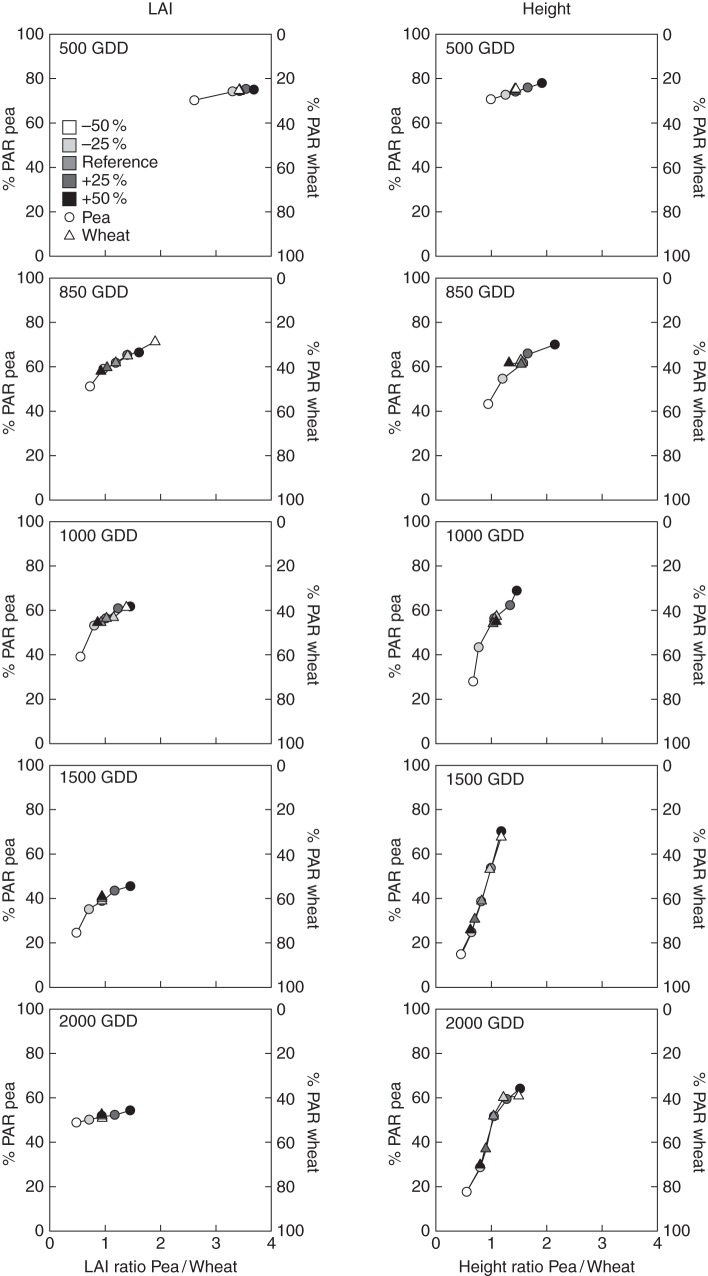
The results described above evidenced the dynamics of light partitioning in response to contrasting plant architectures. As illustrated in Figs 4 and 5, such architectural alterations induced a broad range of variations in the LAI and height of the component species. The next step was therefore to analyse the relationships between light partitioning and variations affecting both ratios of species LAI and height (Fig. 7). This analysis was performed at five stages of development (Fig. 1).
Fig. 7.
Relationship between light partitioning (%PAR is the ratio of light intercepted by a species (left and right axes for pea and wheat, respectively) to the interception of the whole mixture) and the species ratios of LAI (left) and height (right) at five particular stages of development. Variations in the ratios of LAI and height resulted from architectural alterations applied to pea (circles) and wheat (triangles) as indicated by the shading gradient.
During the early stages of development (500 GDD), the architectural modifications made mainly affected the height of pea plants (Figs 4 and 5). Therefore, the ratio of the species LAI (Fig. 7) did not display any marked variations (except when the number of pea branches was reduced by 50 %). By contrast, changes in the internode length of pea led to different height ratios, ranging from 1 to 1·92. Despite the reduction in its internode length, pea remained the dominant species in terms of light capture, mainly due to its higher LAI compared with wheat. At the end of the branching and tillering stages (850 GDD), wheat and pea developed contrasting levels of LAI in response to architectural variations (the LAI ratio ranged from 0·7 to 1·9). This resulted in marked variations in light partitioning as pea intercepted between 51 and 71 % of the light captured by the whole mixture. Whether the architectural variations were applied to pea or wheat, the LAI ratios were similar, although they were obviously affected in contrasting ways. Like the results observed at 500 GDD, light partitioning was also linked to the height ratio, which was modified by alterations made to pea internodes (wheat internodes had not started their elongation). The relationship between light partitioning and the LAI ratio no longer appeared to be linear at 1000 GDD. Indeed, increasing the number of branches/tillers still modified the LAI ratio but this only resulted in slight variations of light partitioning. However, the sharing of light among the component species was linearly related to the variations in height ratio, which originated from modifications to the internode length of pea. Under these scenarios, light intercepted by pea ranged from 28 to 69 % of the total light interception. At flowering (1500 GDD), the onset of internode elongation in wheat generated contrasting vertical dominance (the height ratio ranged from 0·63 to 1·20), which markedly affected light partitioning (between 15 and 70 % of light captured by pea). Figure 7 also shows that alterations in internode length at 1500 and 2000 GDD led to similar absolute variations in height ratio and light partitioning, whether they were made to pea or wheat. The effect of the LAI ratio on light partitioning continued to decline at maturity (2000 GDD). The LAI ratio ranged from 0·48 to 1·45 but only increased the light interception of pea by 10 %. Variations in the height ratio at this stage of development were similar to those observed at 1500 GDD. However, the link with light partitioning appeared to become non-linear, particularly with the most marked alterations to internode length (±50 %).
DISCUSSION
The L-Pea model: a deterministic approach to modelling the aerial morphogenesis of pea
For the purposes of our study, we developed a deterministic model that generated a simplified and dynamic representation of pea architecture. Pea morphogenesis was modelled as a function of thermal time, in line with the work of Turc and Lecoeur (1997), who found stable linear relationships between thermal time and the number of expanded leaves in pea whatever the plant growth rate, cultivar and period of the cycle. As mentioned by Prusinkiewicz (1998), the design of developmental models necessitates the definition of rules to describe the emergence of new modules during development as well as the growth kinetics of modules produced previously. During the present study, these rules were considered in the light of the results of two separate experiments, one conducted under field conditions (Barillot et al., 2014) and the other in a growth cabinet. The latter measurements, dedicated to characterizing stipules and internode elongation, were obtained on pea plants that had not been grown in a mixture with wheat. These kinetics were not therefore intended to accurately quantify the extension of pea internodes and stipules in an intercropping system, but rather to capture the main characteristics of their extension and coordination. Furthermore, the kinetics of organ extension were likely to have a limited influence on our results as we performed an analysis of the sensitivity of light partitioning to alterations in the number of branches/tillers and internode length.
Moreover, the L-Pea model was used to represent realistic/measured architectures of pea plants (resulting from the integration of environmental effects) but was not designed to reproduce the responses of plants to the environment. Indeed, the current version of the L-Pea model does not account for environmental influences on pea morphogenesis (e.g. intra-/interspecific competition, abiotic and biotic factors). Although this goes beyond the scope of this paper, future studies on the L-Pea model could be performed in order to develop a more mechanistic approach to pea development that might include feedback between the resource status of plants and their morphogenesis.
An in silico experiment to assess the effects of contrasting architectures on light partitioning within mixtures
The ability to manipulate light partitioning in multi-specific stands is crucial to managing the balance between component species and also determining the final yield of the mixture (Ofori and Stern, 1987; Keating and Carberry, 1993; Sinoquet and Caldwell, 1995; Malézieux et al., 2009; Louarn et al., 2010). The present work therefore focused on the architectural determinants (i.e. physical modalities) of light partitioning in intercropping systems, but did not aim to study competition for this resource. As a first step towards understanding competition for light within intercropping systems, in silico experiments were performed using two deterministic FSPMs of wheat and pea morphogenesis, without taking account of the plastic responses of plants to their environment. The tripartite simulator (wheat–pea–light) built up for this study therefore represented a heuristic tool to assess the intrinsic effects of individual architectural parameters. More generally, this simulator could be used to test hypotheses that are inaccessible to ‘conventional’ experiments because of technical or time constraints. Although the environmental responses of plants were not taken into account, the contrasting architectures of plants that were generated during this work could mimic the situations encountered in different intercropping systems subject to particular environmental conditions (e.g. agroforestry systems in which one species largely overtops another).
By scaling down our analysis to the organ level, this study provided novel information on the temporal sensitivity of light partitioning to the architecture of component species. Some previous studies had also aimed to analyse the relationships between light partitioning and the simplified or explicit architecture of component species (Sinoquet and Caldwell, 1995; Louarn et al., 2012). However, these studies focused on integrative parameters (height, LAI) which could not discriminate the effects of explicit architectural parameters defined at the organ scale. As reported by several studies (Sinoquet and Caldwell, 1995; Barillot et al., 2011, 2012; Louarn et al., 2012), the present results further confirmed that light partitioning is strongly related to the ratio of the component species LAI and height. However, this relationship appeared to be dependent on the species considered and was not constant throughout the growing cycle. Light partitioning during the early stages of development was closely linked to the contribution of each component species to the LAI of the mixture. Species with high capacity for branching therefore displayed marked competitiveness for light capture. As the mixture grew, the interception of each plant started to be altered by its neighbours (e.g. foliage clumping, mutual shading) and interspecific competition (for light) thus started to modify the relative importance of architectural parameters. When species started their vertical growth (internode elongation), the relationship between light partitioning and the ratio of the component species LAI was no longer linear. During later stages of the growing cycle, light partitioning tended to be related to height ratio. These results were consistent with a previous study carried out on virtual wheat–pea mixtures derived from the digitization of several pea cultivars grown under greenhouse conditions (Barillot et al., 2012). The present work, based on dynamic models of both wheat and pea, has therefore provided new information on the temporal variations of light partitioning throughout the growing cycle of the two species. Furthermore, the use of architectural models enabled us to assess the effects of specific parameters with respect to both wheat and pea architectures.
Leaf inclination also affected light partitioning but to a lesser extent than alterations in branching or internode length. This architectural trait does not appear to be a factor that should be targeted as a priority when manipulating the partitioning of light within mixtures. Nevertheless, Sarlikioti et al. (2011) reported that the leaf inclination of tomato impacted the distribution of light interception rather than total light interception. Further, the effect of leaf inclination should probably be related to plant height, i.e. planophile leaves would significantly improve the light interception of plants that are already the tallest in the mixture (e.g. the alfalfa–tall fescue mixtures described by Barillot et al., 2011). In our simulations based on wheat–pea mixtures, light partitioning was found to be highly sensitive to the number of tillers/branches and to internode length. Although they were significant, the effects of wheat internode length on light capture were less marked than in pea. Cici et al. (2008) also reported that, in chickpea, changes in internode length did not lead to the strongest competition with sow-thistle when compared with phyllochron variations, for example. By contrast, Lemerle et al. (2001) suggested that wheat plants with longer internodes had enhanced competitive ability for light capture versus weeds. It therefore appears that an assessment of the effects of a given architectural parameter (e.g. branching, internode length and leaf inclination) on light partitioning should be carried out with respect to both the whole plant structure (i.e. other architectural parameters) and the morphogenesis of the neighbouring plant/species. Indeed, the determinant parameters that are known to affect light interception in pure stands (e.g. number of tillers and internode length) do not necessarily have the same quantitative effects in multispecific stands, depending on the behaviour of the component species. Moreover, modifications made to branching and internode length triggered asymmetrical variations in light partitioning, which means that (1) other ranges of variation in architectural parameters should be tested in order to better explore the responses of light partitioning, and (2) interactions with other parameters need to be taken into account, e.g. leaf area distribution and clumping (Ross, 1981b; Lantinga et al., 1999).
Conclusions
The questions addressed in this paper necessitated the development of a 3-D dynamic architectural model of pea (L-Pea) which, to our knowledge, is the first pea model to have become available in the literature. The L-Pea model is based on a deterministic approach that enables the generation of simplified representations of pea architecture. Although they may go beyond the scope of the present paper, further studies should be performed in order to obtain a more mechanistic approach to the modelling of pea morphogenesis. For instance, mechanistic rules could be implemented for branching, a process that is known to be closely dependent on genotype (Arumingtyas et al., 1992; Barillot et al., 2012) and environmental factors such as low temperatures (Jeudy and Munier-Jolain, 2005) and plant density (Spies et al., 2010) which affects light quality within the canopy (Casal et al., 1986; Ballaré and Casal, 2000). Integrating such responses in a model would nevertheless require further studies in order to enhance our understanding of the regulation of branching and in particular how internal factors (e.g. hormone balance) respond to environmental signals (Evers et al., 2011).
During the present study, the L-Pea model was used within a complex modelling framework that integrated an architectural model of wheat as well as a light model. Such virtual environments can facilitate approaches designed to define plant ideotypes adapted to intercropping by targeting morphological traits that need to be integrated in breeding programmes. Indeed, scaling the analysis at the organ level can facilitate links with geneticists and breeders. Taking the example of wheat–pea mixtures, several genes that govern pea architecture (branching, height, leaf type) have already been identified (e.g. for pea, Arumingtyas et al., 1992; Kusnadi et al., 1992; Huyghe, 1998). For wheat (and other cereals), the studies performed during the Green Revolution also enabled the control of plant height (Evenson, 2003), notably by introducing dwarf genes (Hedden, 2003). Our study also highlights the importance of considering plant architecture in the choice of the species/genotypes used for intercropping systems. Thus, alongside standard criteria, such as crop earliness, disease sensitivity and yield, attention should also be paid to the architectural traits involved in LAI and plant height. In particular, we showed that both branches and internode length are crucial architectural parameters that determine the ability of component species to compete for light. Integration of these architectural traits should also take account of the fact that their impact on light partitioning will vary during the growing cycle, thus requiring greater knowledge of the dynamic aspects of plant morphogenesis.
SUPPLEMENTARY DATA
ACKNOWLEDGEMENTS
This research is supported by ‘La Région Pays de la Loire’, France through a PhD fellowship to R.B. The research of D.C. and A.J.E-G. is partially funded by ‘La Région Poitou-Charentes’, France.
LITERATURE CITED
- Anil L, Park J, Phipps RH, Miller FA. Temperate intercropping of cereals for forage: a review of the potential for growth and utilization with particular reference to the UK. Grass and Forage Science. 1998;53:301–317. [Google Scholar]
- Arumingtyas EL, Floyd RS, Gregory MJ, Murfet IC. Branching in Pisum: inheritance and allelism tests with 17 ramosus mutants. Pisum Genetics. 1992;24:17–31. [Google Scholar]
- Ballaré CL, Casal JJ. Light signals perceived by crop and weed plants. Field Crops Research. 2000;67:149–160. [Google Scholar]
- Barillot R, Louarn G, Escobar-Gutiérrez AJ, Huynh P, Combes D. How good is the turbid medium-based approach for accounting for light partitioning in contrasted grass-legume intercropping systems? Annals of Botany. 2011;108:1013–1024. doi: 10.1093/aob/mcr199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barillot R, Combes D, Chevalier V, Fournier C, Escobar-Gutiérrez AJ. How does pea architecture influence light sharing in virtual wheat-pea mixtures? A simulation study based on pea genotypes with contrasting architectures. 2012. AoB PLANTS2012: pls038; doi:10.1093/aobpla/pls038. [DOI] [PMC free article] [PubMed]
- Barillot R, Combes D, Pineau S, Huynh P, Escobar-Gutiérrez AJ. Comparison of the morphogenesis of three genotypes of pea (Pisum sativum) grown in pure stands and wheat-based intercrops. 2014. AoB PLANTS6: plu010; doi:10.1093/aobpla/plu010. [DOI] [PMC free article] [PubMed]
- Bertheloot J, Andrieu B, Fournier C, Martre P. Modelling nitrogen distribution in virtual plants, as exemplified by wheat culm during grain filling. In: Li B, Jaeger M, Guo Y, editors. Third International Symposium on Plant Growth Modeling, Simulation, Visualization and Applications (PMA) 2009. pp. 126–133. [Google Scholar]
- Boudoon F, Pradal C, Cokelaer T, Prusinkiewicz P, Godin C. L-Py: an L-system simulation framework for modeling plant development based on a dynamic language. Frontiers in Plant Science. 2012;3:76. doi: 10.3389/fpls.2012.00076. doi:10.3389/fpls.2012.00076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Casal JJ, Sanchez RA, Deregibus VA. The effect of plant density on tillering: the involvement of R/FR ratio and the proportion of radiation intercepted per plant. Environmental and Experimental Botany. 1986;26:365–371. [Google Scholar]
- Chelle M, Andrieu B. The nested radiosity model for the distribution of light within plant canopies. Ecological Modelling. 1998;111:75–91. [Google Scholar]
- Cici SZ-H, Adkins S, Hanan J. A canopy architectural model to study the competitive ability of chickpea with sowthistle. Annals of Botany. 2008;101:1311–1318. doi: 10.1093/aob/mcn040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Combes D, Chelle M, Sinoquet H, Varlet-Grancher C. Evaluation of a turbid medium model to simulate light interception by walnut trees (hybrid NG38 × RA and Juglans regia) and sorghum canopies (Sorghum bicolor) at three spatial scales. Functional Plant Biology. 2008;35:823–836. doi: 10.1071/FP08059. [DOI] [PubMed] [Google Scholar]
- Corre-Hellou G, Fustec J, Crozat Y. Interspecific competition for soil N and its interaction with N2 fixation, leaf expansion and crop growth in pea–barley intercrops. Plant and Soil. 2006;282:195–208. [Google Scholar]
- Corre-Hellou G, Faure M, Launay M, Brisson N, Crozat Y. Adaptation of the STICS intercrop model to simulate crop growth and N accumulation in pea–barley intercrops. Field Crops Research. 2009;113:72–81. [Google Scholar]
- DeJong TM, Da Silva D, Vos J, Escobar-Gutiérrez AJ. Using functional–structural plant models to study, understand and integrate plant development and ecophysiology. Annals of Botany. 2011;108:987–989. doi: 10.1093/aob/mcr257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Evenson RE. Assessing the impact of the Green Revolution, 1960 to 2000. Science. 2003;300:758–762. doi: 10.1126/science.1078710. [DOI] [PubMed] [Google Scholar]
- Evers JB, van der Krol AR, Vos J, Struik PC. Understanding shoot branching by modelling form and function. Trends in Plant Science. 2011;16:464–467. doi: 10.1016/j.tplants.2011.05.004. [DOI] [PubMed] [Google Scholar]
- Faurie O, Soussana JF, Sinoquet H. Radiation interception, partitioning and use in grass–clover mixtures. Annals of Botany. 1996;77:35–46. [Google Scholar]
- Fourcaud T, Zhang X, Stokes A, Lambers H, Körner C. Plant growth modelling and applications: the increasing importance of plant architecture in growth models. Annals of Botany. 2008;101:1053–1063. doi: 10.1093/aob/mcn050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fournier C, Andrieu B, Ljutovac S, Saint-Jean S. ADEL-wheat: a 3D architectural model of wheat development. In: Hu B-G, Jaeger M, editors. Proceedings PMA03: 2003 International Symposium on Plant Growth Modeling, Simulation, Visualization and their Applications; 2003. pp. 54–63. Beijing, China: IEEE Computer Society. [Google Scholar]
- Godin C. Representing and encoding plant architecture: a review. Annals of Forest Science. 2000;57:413–438. [Google Scholar]
- Godin C, Costes E, Sinoquet H. A method for describing plant architecture which integrates topology and geometry. Annals of Botany. 1999;84:343–357. [Google Scholar]
- Gray A. On the composition of the plant by phytons, and some applications of phyllotaxis. Proceedings of the American Association for the Advancement of Science. 1849. pp. 438–444.
- Hedden P. The genes of the Green Revolution. Trends in Genetics. 2003;19:5–9. doi: 10.1016/s0168-9525(02)00009-4. [DOI] [PubMed] [Google Scholar]
- Huyghe C. Genetics and genetic modifications of plant architecture in grain legumes: a review. Agronomie. 1998;18:383–411. [Google Scholar]
- Jensen ES. Grain yield, symbiotic N2 fixation and interspecific competition for inorganic N in pea-barley intercrops. Plant and Soil. 1996;182:25–38. [Google Scholar]
- Jeudy C, Munier-Jolain N. Developpement des ramifications. In: Munier-Jolain N, Biarnes V, Chaillet I, Lecoeur J, Jeuffroy M-H, editors. Agrophysiologie du pois protéagineux. Paris: INRA-Quae; 2005. pp. 51–58. [Google Scholar]
- Keating BA, Carberry PS. Resource capture and use in intercropping: solar radiation. Field Crops Research. 1993;34:273–301. [Google Scholar]
- Kusnadi J, Gregory M, Murfet IC, Ross JJ, Bourne F. Internode length in Pisum: phenotypic characterisation and genetic identity of the short internode mutant Wt11242. Pisum Genetics. 1992;24:64–74. [Google Scholar]
- Lamanda N, Dauzat J, Jourdan C, Martin P, Malézieux E. Using 3D architectural models to assess light availability and root bulkiness in coconut agroforestry systems. Agroforestry Systems. 2008;72:63–74. [Google Scholar]
- Lantinga EA, Nassiri M, Kropff MJ. Modelling and measuring vertical light absorption within grass-clover mixtures. Agricultural and Forest Meteorology. 1999;96:71–83. [Google Scholar]
- Lecoeur J. Developpement vegetatif. In: Munier-Jolain N, Biarnes V, Chaillet I, Lecoeur J, Jeuffroy M-H, editors. Agrophysiologie du pois protéagineux. Paris: INRA-Quae; 2005. pp. 27–45. [Google Scholar]
- Lemerle D, Gill GS, Murphy CE, et al. Genetic improvement and agronomy for enhanced wheat competitiveness with weeds. Australian Journal of Agricultural Research. 2001;52:527–548. [Google Scholar]
- Lindenmayer A. Mathematical models for cellular interactions in development I. Filaments with one-sided inputs. Journal of Theoretical Biology. 1968;18:280–299. doi: 10.1016/0022-5193(68)90079-9. [DOI] [PubMed] [Google Scholar]
- Louarn G, Corre-Hellou G, Fustec J, et al. Déterminants écologiques et physiologiques de la productivité et de la stabilité des associations graminées-légumineuses. Innovations Agronomiques. 2010;11:79–99. [Google Scholar]
- Louarn G, Da Silva D, Godin C, Combes D. Simple envelope-based reconstruction methods can infer light partitioning among individual plants in sparse and dense herbaceous canopies. Agricultural and Forest Meteorology. 2012;166–167:98–112. [Google Scholar]
- Malézieux E, Crozat Y, Dupraz C, et al. Mixing plant species in cropping systems: concepts, tools and models. A review. Agronomy for Sustainable Development. 2009;29:43–62. [Google Scholar]
- Monsi M, Saeki T. On the factor light in plant communities and its importance for matter production. Annals of Botany. 2005;95:549–567. doi: 10.1093/aob/mci052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moon P, Spencer DE. Illumination from a non-uniform sky. Illuminating Engineering. 1942;37:707–726. [Google Scholar]
- Moulia B, Edelin C, Jeuffroy MH, Allirand JM, Loup C, Chartier M. Premiers éléments d'analyse du développement architectural des herbacées cultivées. In: Maillard P, Bonhomme R, editors. Fonctionnement des peuplements végétaux sous contraintes environnementales. Paris: INRA; 1998. pp. 149–184. [Google Scholar]
- Noordwijk M, Lusiana B. WaNuLCAS, a model of water, nutrient and light capture in agroforestry systems. In: Auclair D, Dupraz C, editors. Agroforestry for Sustainable Land-Use Fundamental Research and Modelling with Emphasis on Temperate and Mediterranean Applications. Netherlands: Springer; 1999. pp. 217–242. [Google Scholar]
- Ofori F, Stern WR. Cereal-legume intercropping systems. Advances in Agronomy. 1987;41:41–90. [Google Scholar]
- Pradal C, Dufour-Kowalski S, Boudon F, Fournier C, Godin C. OpenAlea: a visual programming and component-based software platform for plant modelling. Functional Plant Biology. 2008;35:751–760. doi: 10.1071/FP08084. [DOI] [PubMed] [Google Scholar]
- Pradal C, Boudon F, Nouguier C, Chopard J, Godin C. PlantGL: a Python-based geometric library for 3D plant modelling at different scales. Graphical Models. 2009;71:1–21. [Google Scholar]
- Prusinkiewicz P. Modeling of spatial structure and development of plants: a review. Scientia Horticulturae. 1998;74:113–149. [Google Scholar]
- Prusinkiewicz P, Lindenmayer A. The algorithmic beauty of plants. New-York: Springer; 1990. [Google Scholar]
- Ross J. Role of phytometric investigations in the studies of plant stand architecture and radiation regime. In: Ross J, editor. The radiation regime and architecture of plant stands. The Hague: Dr W Junk; 1981a. pp. 9–11. [Google Scholar]
- Ross J. Spatial distribution of phytoelements in stands. In: Ross J, editor. The radiation regime and architecture of plant stands. The Hague: Dr W Junk; 1981b. pp. 66–89. [Google Scholar]
- Sarlikioti V, de Visser PHB, Marcelis LFM. Exploring the spatial distribution of light interception and photosynthesis of canopies by means of a functional-structural plant model. Annals of Botany. 2011;107:875–883. doi: 10.1093/aob/mcr006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sinoquet H, Caldwell MM. Estimation of light capture and partitioning in intercropping systems. In: Sinoquet H, Cruz P, editors. Ecophysiology of tropical intercropping. Paris: INRA; 1995. pp. 79–97. [Google Scholar]
- Sinoquet H, Moulia B, Gastal F, Bonhomme R, Varlet-Grancher C. Modeling the radiative balance of the components of a well-mixed canopy: application to a white clover-tall fescue mixture. Acta Oecologica. 1990;11:469–486. [Google Scholar]
- Sonohat G, Sinoquet H, Varlet-Grancher C, et al. Leaf dispersion and light partitioning in three-dimensionally digitized tall fescue-white clover mixtures. Plant, Cell and Environment. 2002;25:529–538. [Google Scholar]
- Spies JM, Warkentin T, Shirtliffe S. Basal branching in field pea cultivars and yield-density relationships. Canadian Journal of Plant Science. 2010;90:679–690. [Google Scholar]
- Tsubo M, Walker S. A model of radiation interception and use by a maize-bean intercrop canopy. Agricultural and Forest Meteorology. 2002;110:203–215. [Google Scholar]
- Tsubo M, Walker S, Ogindo HO. A simulation model of cereal-legume intercropping systems for semi-arid regions: I. Model development. Field Crops Research. 2005;93:10–22. [Google Scholar]
- Turc O, Lecoeur J. Leaf primordium initiation and expanded leaf production are co-ordinated through similar response to air temperature in pea (Pisum sativum L.) Annals of Botany. 1997;80:265–273. [Google Scholar]
- Vos J, Evers JB, Buck-Sorlin GH, Andrieu B, Chelle M, de Visser PHB. Functional-structural plant modelling: a new versatile tool in crop science. Journal of Experimental Botany. 2010;61:2101–2115. doi: 10.1093/jxb/erp345. [DOI] [PubMed] [Google Scholar]
- White J. The plant as a metapopulation. Annual Review of Ecology and Systematics. 1979;10:109–145. [Google Scholar]
- Willey RW. Intercropping—its importance and research needs. Part 1. Competition and yield advantages. Field Crop Abstracts. 1979;32:1–10. [Google Scholar]
- Yin X, Goudriaan J, Lantinga EA, Vos J, Spiertz HJ. A flexible sigmoid function of determinate growth. Annals of Botany. 2003;91:361–371. doi: 10.1093/aob/mcg029. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.